0 引言
陆空两栖平台是指以陆地行驶功能为主、兼备应急作战飞行的陆空两用平台[1]。在当前战场环境中,传统的无人机、无人车受限明显[2]。无人机无法完成室内区域等环境的侦察任务,无人车则无法通过坑洼、废墟等具有障碍限制的地面。为了避免陆空单一作战模式的短板,迫切需要研究设计一种具有变结构功能、通过性强、具备较强抵抗外界干扰能力的陆空两栖平台。
目前,许多高校从结构设计、控制方法等多个角度针对陆空两栖平台展开了研究。马建等[3]采用旋翼与车轮交叉排布的设计方案,通过PID和反步法对位置、姿态回路进行控制律设计,实现了平台小范围下的姿态稳定。朱航等[4]将PID与模糊控制方法相结合完成了对陆空两栖机器人的姿态、位置控制。钟地长[5]、陶彦隐[6]等将旋翼与轮式相结合,分别采用串级PID和模糊控制实现了两栖平台的姿态稳定。吴冲[7]、韩晓男等[8]采用旋翼与履带相结合的设计思路,针对陆空两栖平台模型非线性的特点,通过反步法设计控制律完成了姿态、位置控制。黄楠[9]、黄彬等[10]将螺旋桨与轮式相结合,通过优化算法完成了对陆空两栖平台模型的配平计算。文献[3-10]虽然实现了陆地行驶与空中飞行的功能,但其结构为简单的旋翼、螺旋桨与轮式或者履带的叠加,缺乏变结构设计,灵活性与通过性不足。在飞行控制方面,以上方法虽然考虑到两栖平台模型非线性、强耦合性等特点,但未考虑系统在具体场景下如外界扰动下的飞行情况。
综上,在前人的研究基础上,本文进一步设计了一种变结构的陆空两栖平台。首先,通过流体力学仿真和气动力学分析对两栖平台进行变结构设计;其次,对平台模型参数优化、选型和模型校核;然后,设计自抗扰控制方法实现平台在扰动下的稳定飞行;最后,通过原理样机实际测试了陆空两栖平台性能,为后续两栖平台的长航时、大载重和强稳定性等功能的实现提供了技术参考。
1 陆空两栖平台构型设计及分析
1.1 陆空两栖平台变结构设计
通常情况下,陆空两栖平台处于陆地行驶状态。在该状态下,旋翼置于车轮中心并且与地面保持垂直状态。当收到切换指令后,平台将进入空中飞行模态。在该状态下,舵机带动与之相连的旋翼和多旋翼电机向车轮内侧旋转90°,使旋翼与地面保持平行,从而具备越障等功能以适应复杂地面环境。因此,陆空2种模式的切换有效提高了平台在复杂环境下的通过性,并且最大程度保证了平台的隐蔽性。平台在2种工作模态下的示意如图1所示。
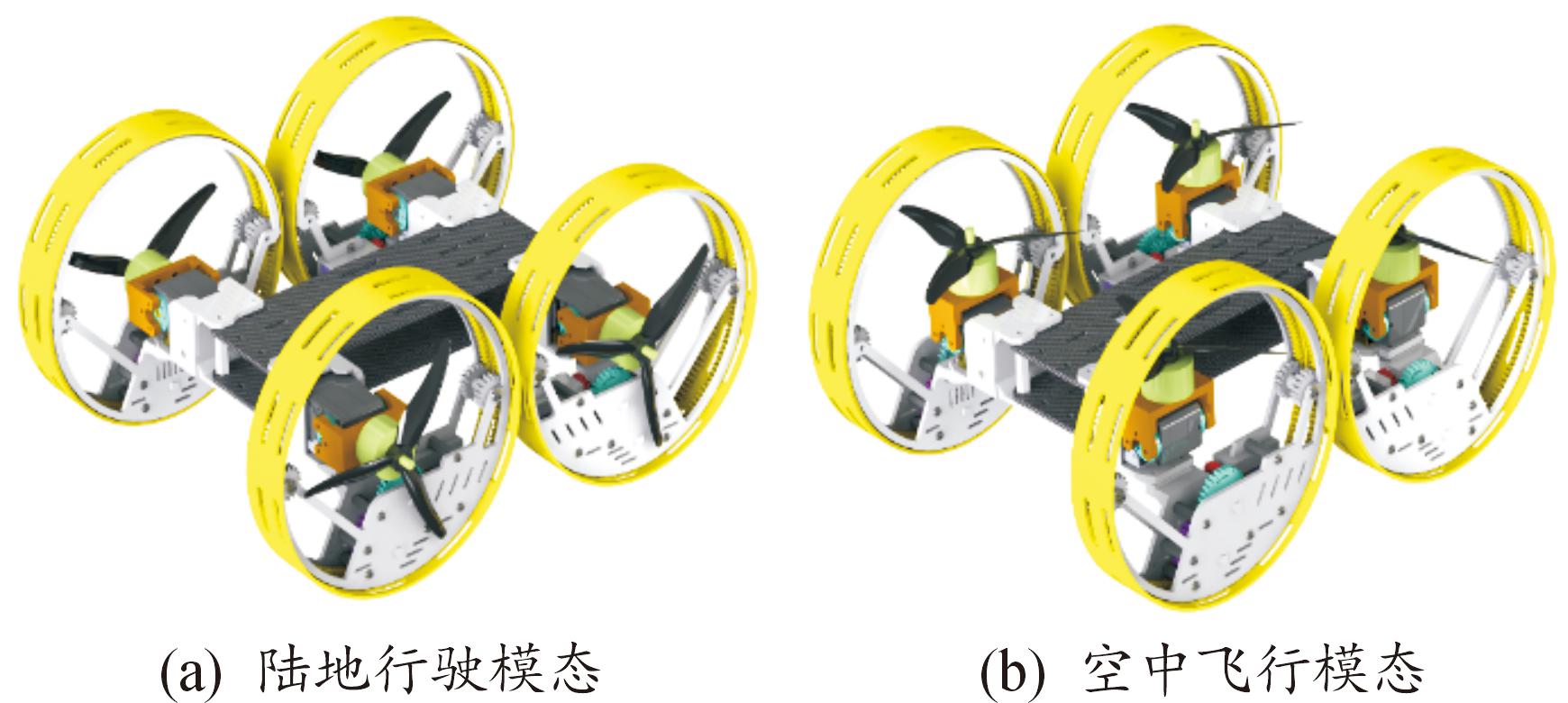
图1 平台2种工作模态下的示意图
Fig.2 Diagram of two working modes of the platform
在陆地行驶模式下,为了使旋翼不干扰平台的正常行进,采取隐藏式设计方法,将旋翼藏于车轮中并与地面保持平行。因此,采用行星齿轮传动方法进行设计,如图2所示。
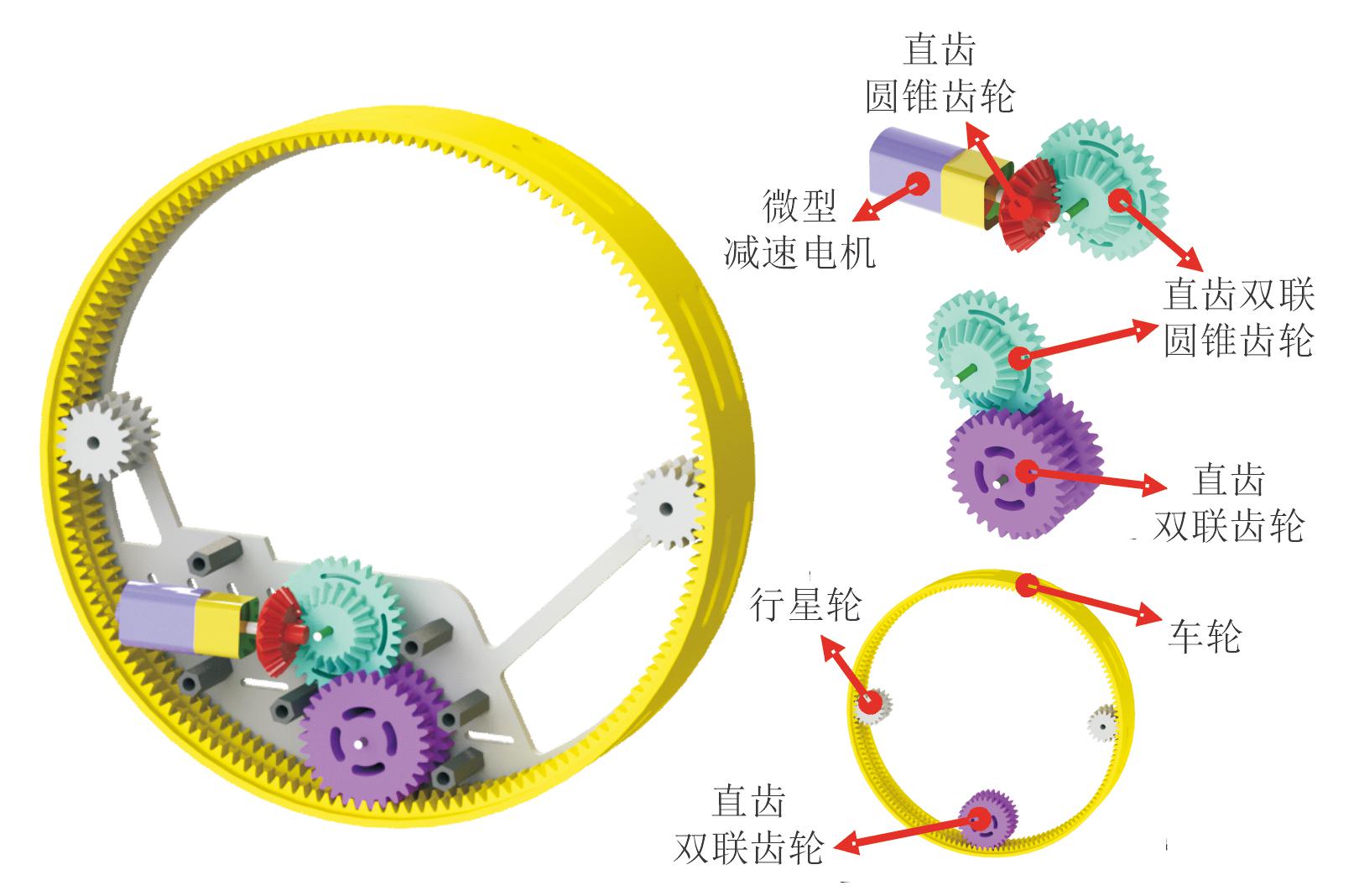
图2 陆地模式齿轮系设计
Fig.2 Ground mode gear train design
第1级齿轮传动方式为1对直齿圆锥齿轮啮合,2个锥齿轮之间的交角等于90°,改变了电机输出轴的旋转方向。第2级齿轮传动采用直齿圆柱齿轮啮合,参与该级传动的齿轮均为双联齿轮。第3级齿轮传动为内齿轮啮合,能够为平台的模式切换提供充足的空间。各级齿轮的主要传动参数如表1所示。
表1 各级齿轮传动的主要参数
Table 1 Main parameters of gear transmission at all levels

参数第1级ⅠⅡ第2级ⅠⅡ第3级ⅠⅡ分锥角/(°)45°45°齿数1717302330155分度圆直径/mm1717302330155齿宽/mm4.684.68494.55各级传动比10.775.17总传动比3.96
1.2 气动力学仿真分析
基于Adams/View动力学仿真平台,建立齿轮系的动力学仿真模型。假设电机输出转速为300 r/min,并且车轮无打滑,此时车轮会受到支持力和静摩擦力的作用。由于车轮与地面接触为面接触,还会受到滚动摩擦力矩的作用。采用Abaqus对车轮与地面的接触进行有限元仿真分析,得到当车质量为1.8 kg时,滚动摩擦力矩为0.001 95 N·m,此值较小可以忽略。在地面行驶过程中,静摩擦力会对车轮产生1个阻力矩,其大小为0.092 N·m。设定转速为300 r/min过Adams仿真得到所需平均力矩约为0.022 N·m,小于电机堵转力矩。因此,陆地行驶模态设计可行,相关计算结果如图3所示。
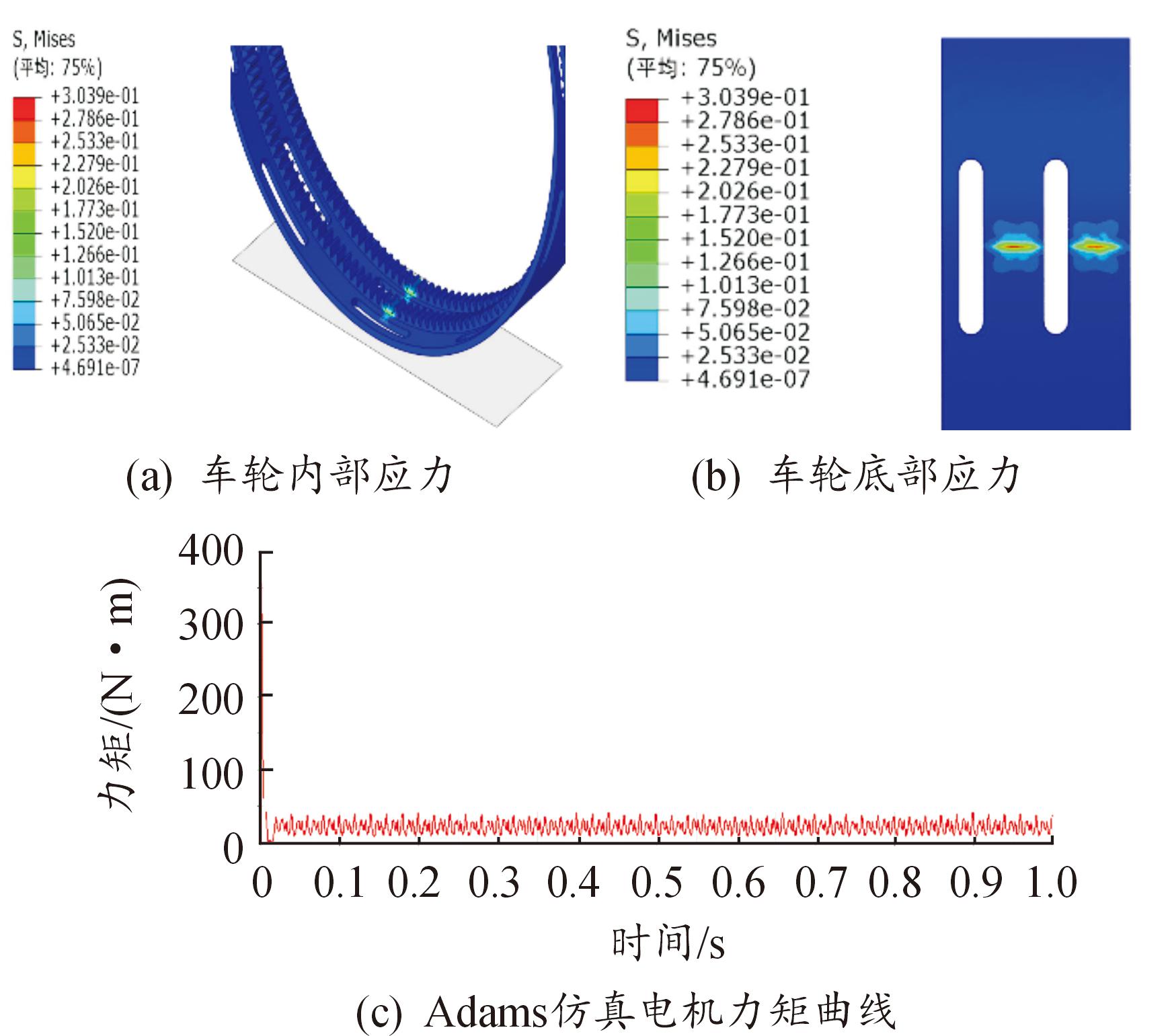
图3 陆地行驶模态气动力学分析
Fig.3 Aerodynamic analysis of ground driving mode
由于在变结构设计时旋翼会处于车轮中心的位置,所以在旋翼上下方会有障碍物对气流形成阻挡,从而对旋翼升力产生影响。为了评估空中飞行模态下的旋翼升力,基于ICEM和Fluent进行流体仿真,分别对静域、动域划分非结构化网格,划分结果如图4(a)所示。采用雅可比行列式评估网格质量,网格质量的范围为0至1,数字越大越好,通常雅可比行列式的值在0.3以上可以为大多数求解器接受。在动域中,质量在0.3以下的网格占动域网格的9.76%;在静域中,质量小于0.3的网格占静域总网格数量的0.42%,因此网格质量均可以接受。
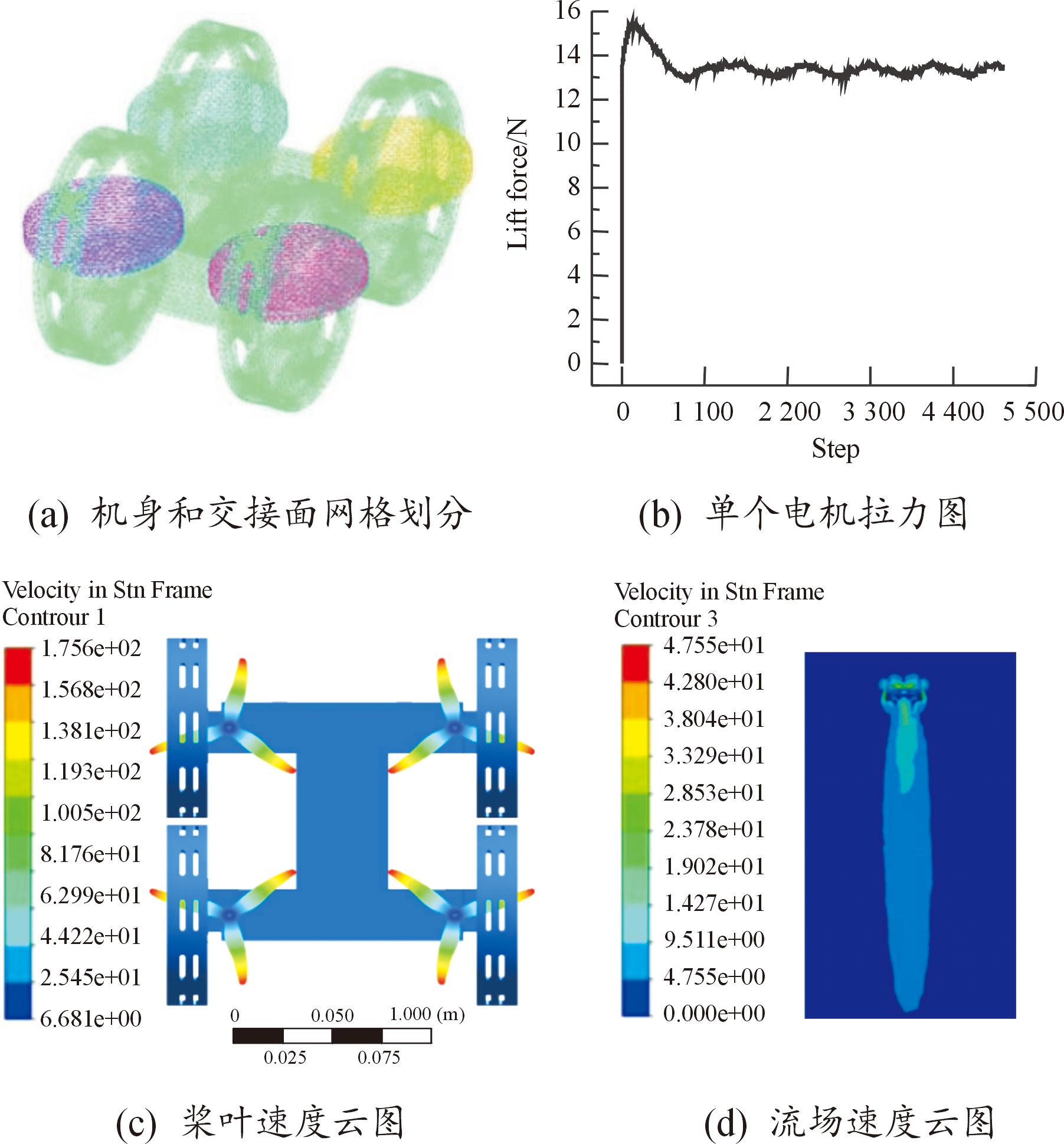
图4 陆地行驶模态气动力学分析
Fig.4 Aerodynamic analysis of flying mode
基于SST k-ω模型进行分析。图4(c)展示的是速度云图,该图可以反映出仿真中的转速设置是否合理,旋翼翼尖最大转速与理论转速相符,证明了仿真结果具有一定的可信度。图4(d)展示的是流场的速度云图,从图中可以看出,车轮确实对下洗气流产生了一定的阻挡作用,但是结合图4(c)的拉力图和厂家的电机旋翼力效数据可知,在26 420 r/min的转速条件下,仿真拉力约为13.36 N,与力效表中的12.82 N较为接近,再一次证明了仿真结果具有较高的可信度,同时也说明了在悬停状态下,车轮对旋翼气流的遮挡作用较小,电机性能满足起飞条件。
2 两栖平台参数优化及选型分析
当陆空两栖平台处于飞行模态时,平台运动模型可以等效为四旋翼飞行器。陆空两栖平台模型优化的主要目的有2点:一是确定准确的模型参数,为仿真验证奠定基础;二是进行合理选型,获得实现预期指标的最优搭配。陆空两栖平台主要参数如表2所示。
表2 陆空两栖平台模型主要参数
Table 2 Main parameters of air-ground platform model

模型主要参数表示含义Tmax/N全油门状态下拉力Thover/N悬停时拉力np电机数量thover/min悬停时间UmMax/S电机额定最大电压ImMax/A电机额定最大电流KV/(r·min-1·V-1)电压每升高1V,转速增加数值Im0/A电机空载电流Rm/Ω电机电阻Dp/inch旋翼直径φp/(°)桨距角Bp桨叶数Uemax/S电调额定最大电压Iemax/A电调额定最大电流Re/Ω电调电阻σ占空比/油门信号Ub/V电池额定电压Kb/C最大放电率Cb/mAh电池容量Rb/Ω电池电阻
假设mp、mm、me、mb分别为旋翼、电机、电调、电池质量,ηp、ηm、ηe、ηb分别为旋翼效率、电机效率、电调效率、电池效率,得到如下优化目标
minmpg,minmmg,minmeg,minmbg
(1)
minmbg⟹maxηp,maxηm,maxηe,maxηb
(2)
2.1 旋翼模型参数优化及选型分析
由叶素理论、动量定理得到旋翼气动升力(N)和气动阻力矩(N·m)为

(3)
式(3)中: CT、CM分别为旋翼升力系数和阻力系数,n为旋翼转速(r/min),ρ为空气密度(kg/m3)。考虑到模型的普适性和未确定最终的旋翼型号,由文献[11],得到悬停状态下旋翼升阻系数数学表达式为
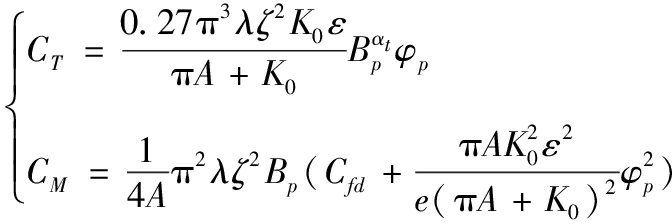
(4)
式(4)中,A、ε、ζ、λ、Cfd、e与旋翼外形相关,分别为展弦比、下洗校正系数、位置系数、叶片翼型面积修正系数、零升阻力系数、奥斯瓦尔德效率因子。由于相同系列翼型变化不大,相应系数按照常数取值,比如e取值范围在[0.6,0.8],参数含义和取值范围可参见文献[12]。其他系数如叶片间干扰系数αt由文献[13]中试验获得,取值满足αt≤0.5,K0取值为6.1[14]。
以下分析论证主要基于悬停状态。悬停状态下拉力和最大拉力为
![]()
(5)
![]()
(6)
式(5)、式(6)中:mall为陆空两栖平台总质量(kg);ax为陆空两栖平台最大加速度(m/s2)。
旋翼拉力效率ηp(N/W)表示为
![]()
(7)
将T=Thover、M=MH、n=nH代入式(3)得到
![]()
(8)
仅考虑桨叶参数Bp,将(3)式代入(8)式中化简得到
![]()
(9)
将电机与旋翼看作整体,定义整体的旋翼拉力效率为ηpm,类似式(7),得到
![]()
(10)
由无刷直流电机等效电路及欧姆定律,得到电机电压Um和电机电流Im的化简表达式为

(11)
式(11)中,Um0、Im0分别为电机空载电压和电流,为已知常量。
结合式(3)、式(11)进一步得到
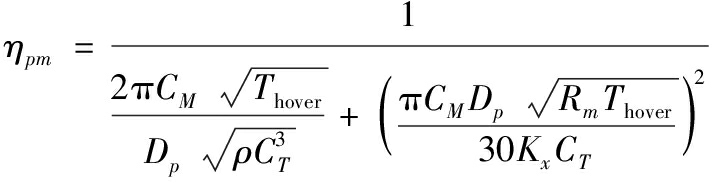
(12)
式(12)中,参数Kx定义为
![]()
(13)
结合式(4),最终化简得到ηpm与φp表达式为
![]()
(14)
通过求导可知,式(14)存在使ηpm最大化的极值。a0~a4是与电机参数相关的常值。由陆空两栖平台设计需求,仿真数据选择Thover=4.5 N,Dp=5 inch,GR2 306电机(Kv=2 750),Hp取值范围为3~8 inch。通过仿真分析,得到旋翼桨叶角与拉力效率关系,如图5所示。
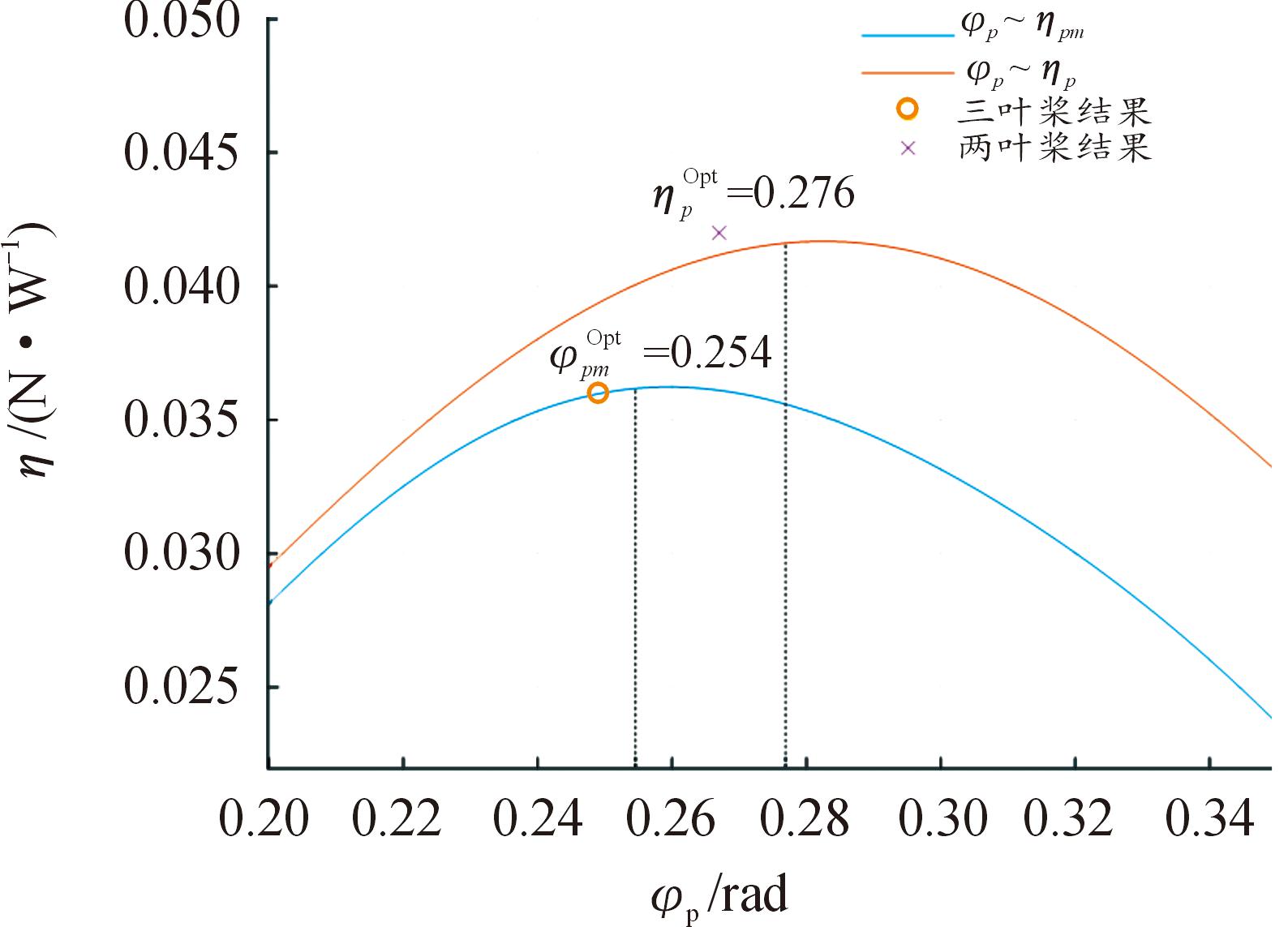
图5 旋翼拉力效率与桨叶角关系曲线
Fig.5 Curve of the relationship between rotor thrust efficiency and blade angle
考虑实际选型,桨叶角的选择应在最优桨叶角附近。图中2叶桨和3叶桨选型分别为5 043和5 045,对应拉力效率计算结果分别为0.042 N/W和0.036 N/W。通过计算比较,尽管2叶桨的理论计算拉力效率会高于3叶桨,但在考虑电机负载情况下(σ=0.5),此时负载电流为28.40 A,超过了15 s内最大电流26 A,动力系统会有损坏风险,若进一步加大油门(σ>0.5),则负载电流继续增加,反而会导致拉力效率下降。因此,在Dp=5 inch下得到
![]()
(15)
2.2 电机电调模型参数优化及选型分析
由初步的电机参数和优化后的旋翼参数进一步优化电机、电调参数。
电调模型的数学表达为
![]()
(16)
式(16)中,Ueq、σ分别为等效直流电压和电调占空比,表达式为
Ueq=Um+ImRe
(17)
![]()
(18)
电机负载电压Um和负载电流Im应满足约束条件为
Um≤UmMax, Im≤ImMax
(19)
电调模型约束条件应满足
Iemax≤30 A
(20)
令Um=UmMax、Im=ImMax、M=Mmax、n=nmax,将其代入式(3)和式(11),得到理论上旋翼最大拉力为
![]()
根据陆空两栖平台设计参数mall=1.8 kg,np=4,ax=9.8 m/s2,结合式(5)、式(6),得到Tmax=8.82 N。
由式(11)进一步化简得到电机效率ηm为
![]()
(22)
可以得到:若maxηm,则minRm。
结合式(19)—式(21),选择同系列电机符合的产品,列出接近最优解的可能结果,如表3所示。
表3 电机—电调模型参数优化结果
Table 3 Optimization results of motor and electronic speed controller parameters
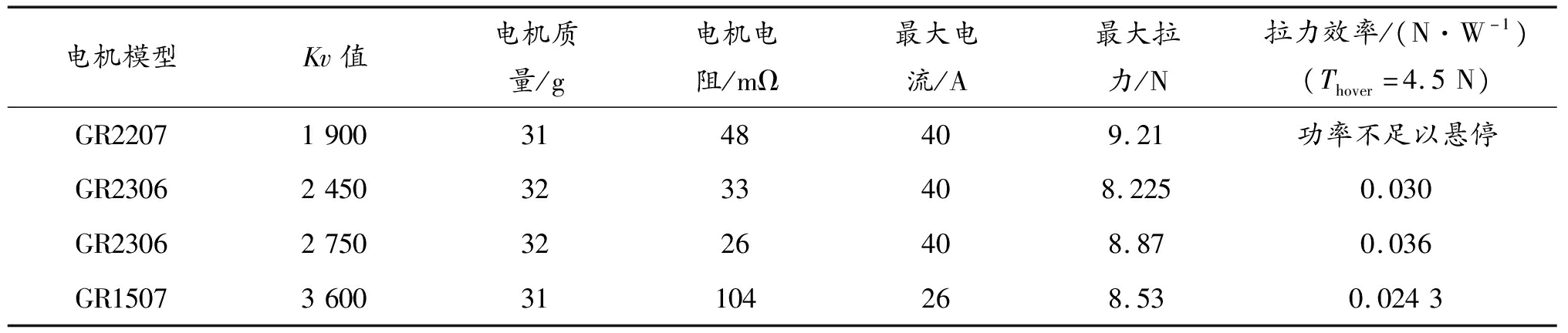
电机模型Kv值电机质量/g电机电阻/mΩ最大电流/A最大拉力/N拉力效率/(N·W-1)(Thover=4.5N)GR220719003148409.21功率不足以悬停GR230624503233408.2250.030GR230627503226408.870.036GR1507360031104268.530.0243
由表3结果可以得到,实际最大拉力8.78 N最接近Tmax=8.82 N,并且此时在悬停状态下拉力效率最高为 0.036 N/W。因此,电机—电调优化结果为
ImMax=40 A,KV=2 750,Rm=0.026 Ω,Iemax=60 A
(23)
2.3 电源电调模型参数优化及选型分析
在确定旋翼和电机后,通过研究电源质量、悬停时间关系与预期控制性能进一步优化电源和电调模型参数。
电源模型的数学表达为
Ub=Ue+IbRb
(24)
式(24)中,电源输出电流Ib为
Ib=npIe+Icontrol
(25)
式(25)中,Icontrol为飞控中电流,可假设为1 A[14]。
考虑到为避免过度放电,预留约15%余量,得到放电时间tb(min)为
![]()
(26)
电源输出功率表达式为
![]()
(27)
式(27)中,电调效率ηe计算为
![]()
(28)
由式(16)进一步化简得到
![]()
(29)
可以得到:若maxηe,则minRe。
由式(24)、式(25)化简得到电源效率表达式ηb为
![]()
(30)
可以得到,若maxηb,则minRb。
由电源密度ρb定义式可以得到悬停时间与电源质量关系,结合式(12)、式(27)化简得到
![]()
(31)
可以得到:若maxthover,则maxηe、maxηb、maxηpm、maxρb。
设m*为除电源质量外其他质量总和,则m*=mall-mb。式(5)中Thover含m*表达式,固定其他参数,得到
![]()
(32)
悬停时间thover需要满足
thover<tb
(33)
考虑到陆空两栖平台可控性,悬停拉力应满足
(mb+m*)g≤0.85Tmax
(34)
在确定电机和旋翼的情况下,悬停时间与电池质量关系曲线如图6所示。其中,实际电源质量与悬停时间数据参见表4。
表4 电源模型参数优化结果
Table 4 Optimization results of battery parameters
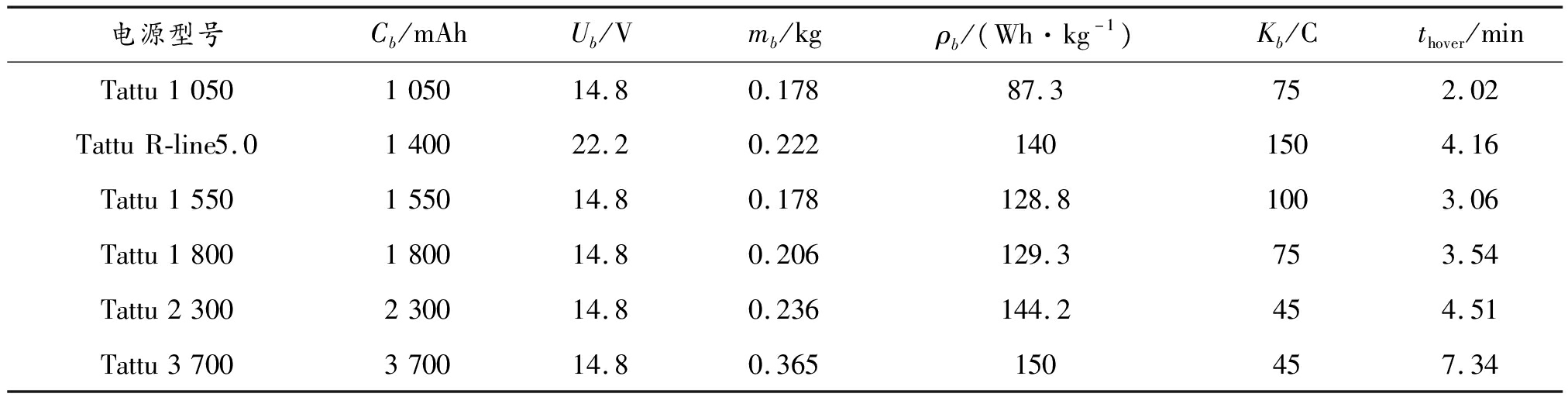
电源型号Cb/mAhUb/Vmb/kgρb/(Wh·kg-1)Kb/Cthover/minTattu1050105014.80.17887.3752.02TattuR-line5.0140022.20.2221401504.16Tattu1550155014.80.178128.81003.06Tattu1800180014.80.206129.3753.54Tattu2300230014.80.236144.2454.51Tattu3700370014.80.365150457.34
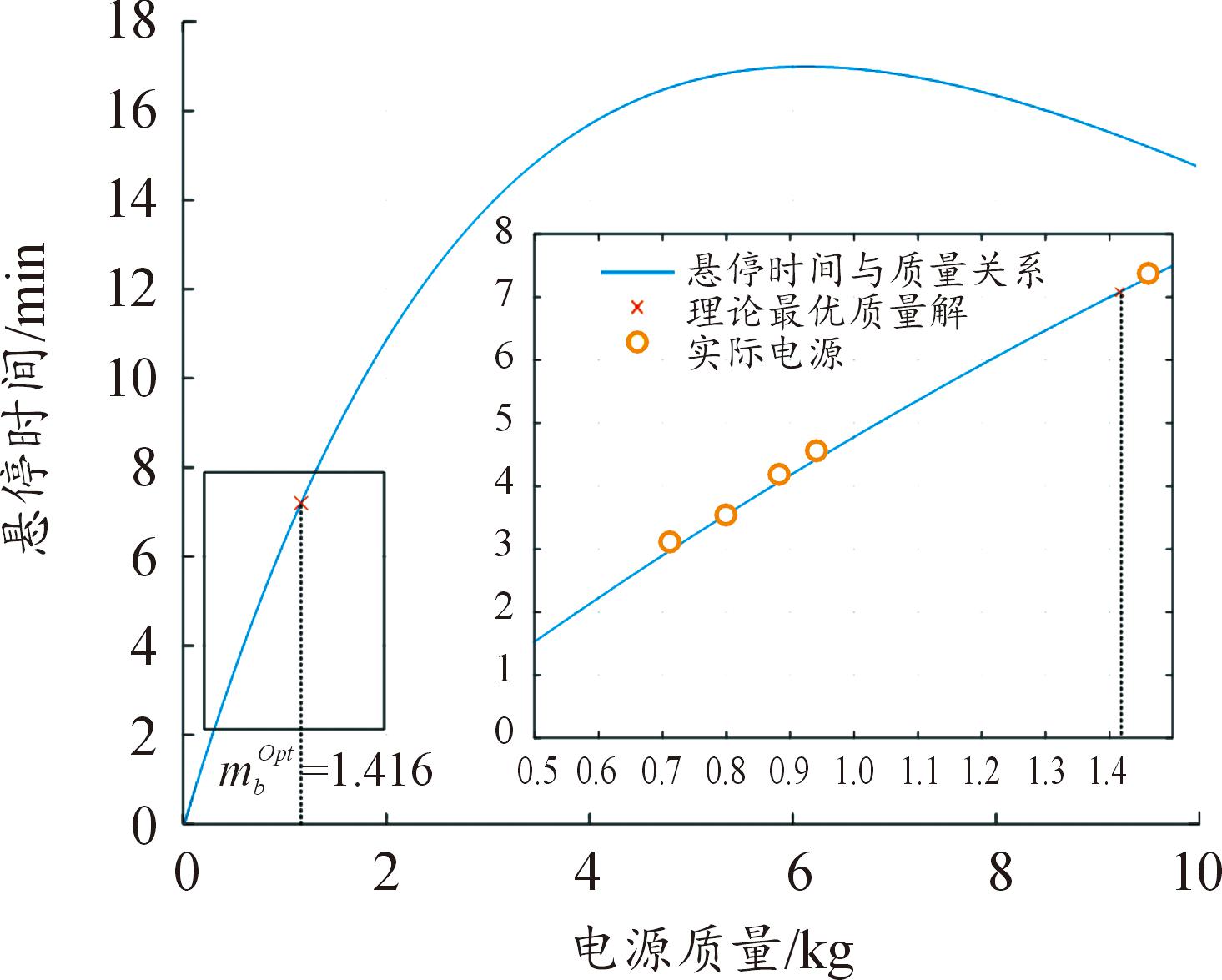
图6 悬停时间与电池质量关系曲线
Fig.6 Curve of the relationship between hover time and battery quality
从图6中看到,悬停时间并不完全随电源质量的增加而增加,随着旋翼拉力的增加,拉力效率降低,悬停时间缩短。由式(33)、式(34)的约束条件,可进一步得到在当前陆空两栖平台下电源最优质量的理论计算值。以下选择一组适合电机—旋翼的电源,列出接近最优解的可能结果,如表4所示。
电源效率的增加有助于悬停时间的延长。在其他参数一定时,电池质量、容量的增加会在一定程度上提高悬停时间,但实际也不一定完全可行。比如,尽管在Tattu3 700下理论悬停时间为7.34 min,远高于在Tattu2 300下的4.51 min,但由于电池质量的增加会导致实际悬停拉力接近旋翼最大拉力,一方面会降低旋翼拉力效率,另一方面会导致控制难度增加。
Tattu1 400参数接近最优值,但由于电机旋翼已经确定,计算得到悬停时电机电流和电调电流不满足式(23)的约束。因此,最终选择Tattu2 300电池。
在电调优化上,主要考虑电调持续电流与10 s内瞬时电流,在满足式(23)的约束下,优化结果如表5所示。
表5 电调模型参数优化结果
Table 5 Optimization results of electronic speed controller parameters
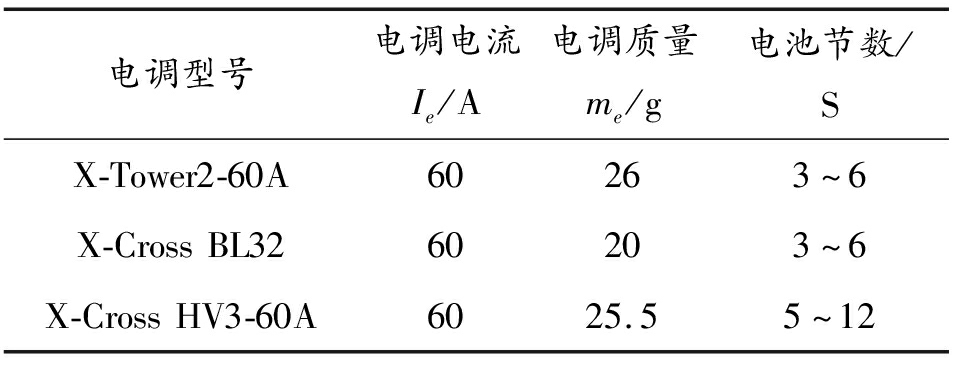
电调型号电调电流Ie/A电调质量me/g电池节数/SX-Tower2-60A60263~6X-CrossBL3260203~6X-CrossHV3-60A6025.55~12
由于电源节数为4 S,最小化me,得到X-Cross BL32结果。
综上,可得到电源—电调优化结果为
Cb=2 300 mAh, Ub=14.8 V
Kb=45 C, mb=0.236 kg, me=0.02 kg
(35)
3 陆空两栖平台模型校核
飞行控制的算法设计与验证依赖于准确的仿真平台与合理的仿真方法。因此,陆空两栖平台模型的准确度是一切仿真实验的基础。基于此,对平台模型进行校核,通过评估模型的准确程度,为后续的控制算法设计与验证创建基础。
3.1 仿真环境搭建
本文使用的陆空两栖平台仿真环境借助了由北京航空航天大学可靠飞行控制组研发的Rflysim平台[15]。该平台能够基于PX4飞控实现快速开发。软硬件连接关系如图7所示。
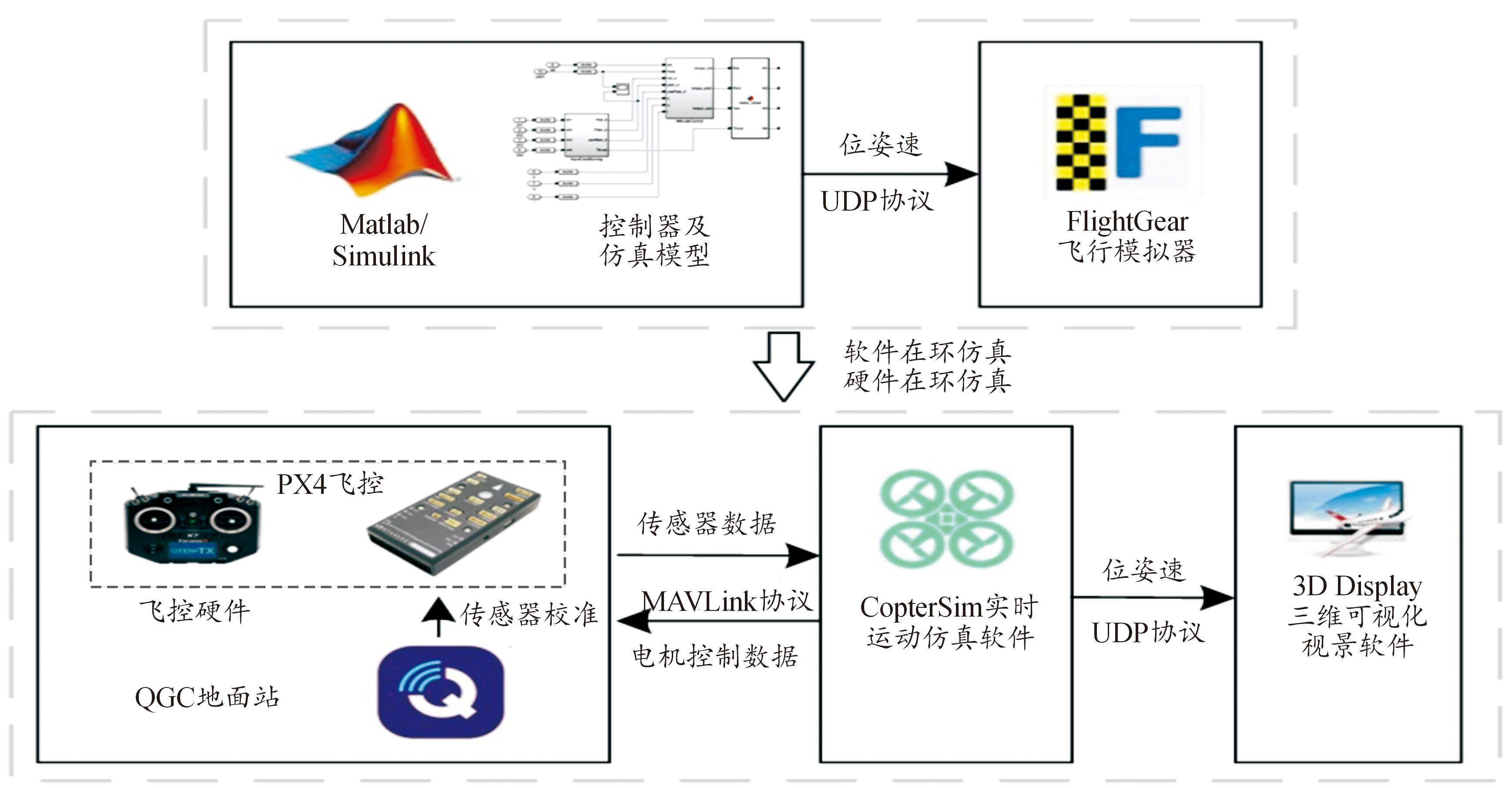
图7 Rflysim平台软硬件连接关系
Fig.7 Software and hardware connection relationship of Rflysim platform
3.2 模型校核方法
模型校核方法为首先使用相同的控制系统向真实系统和仿真系统分别输入相同信号,比较其输出误差,如图8所示。其次,由输出误差、设计经验和从相关标准中获得的误差阈值ζ,通过归一化函数将误差指数e(指标范围为e∈[0,∞])映射为统一的评估标准χ(评估标准范围为χ∈[0,1])。最后,将评估标准χ与期望的标准χration比较得出最终结论。
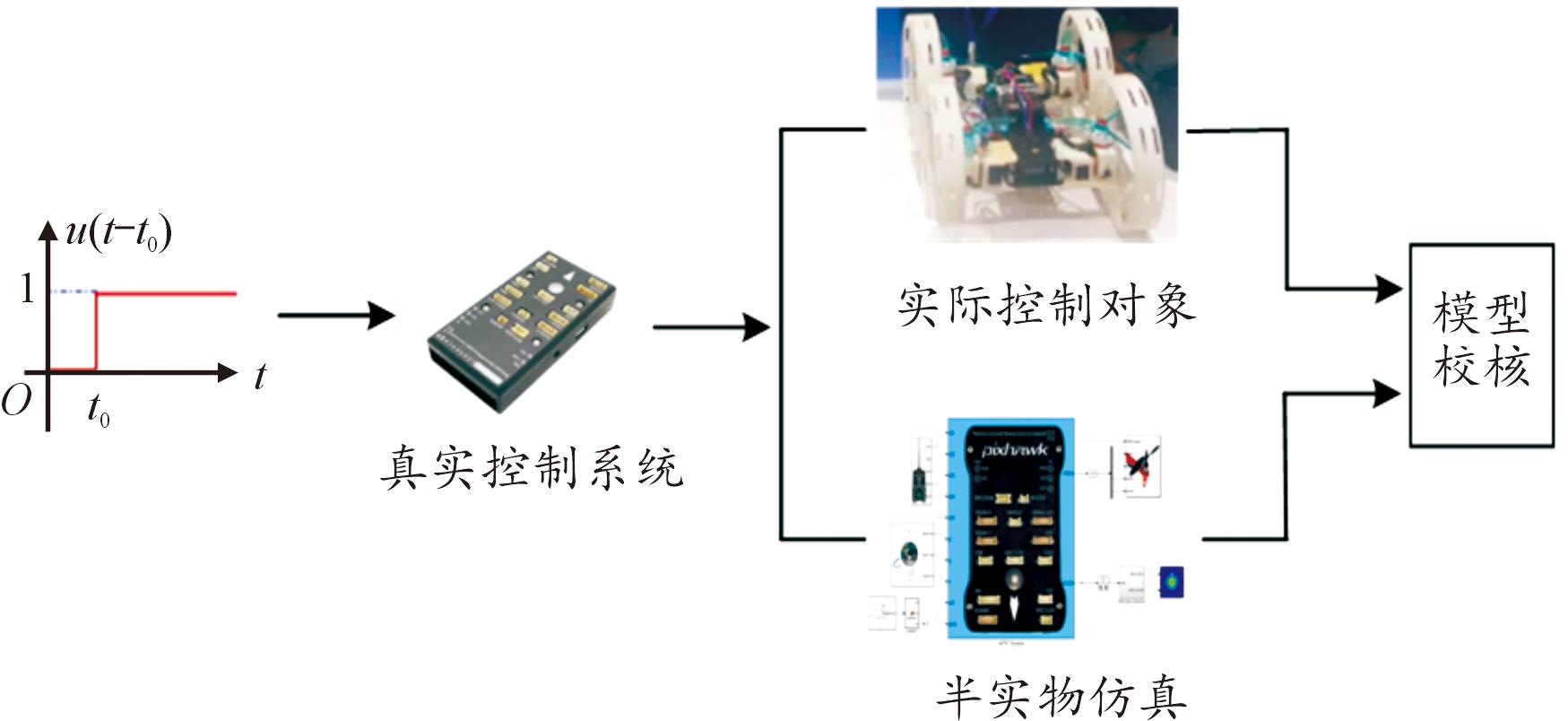
图8 模型校核验证的示意图
Fig.8 Schematic diagram for model verification
其中,评估标准χ表达式为
![]()
(36)
为保证验证精度的可信性、普适性,引入置信区间系数κ0,其取值为5%~10%,参见文献[16]。可以得到
ζ=κ0·xexp
(37)
式(37)中,xexp为实验差值。
当误差阈值ζ满足ζ=e时,比例因子κ为
![]()
(38)
从式(36)、式(38)可以看到当误差指数e→∞时,χ→0,反映出评估标准极差;反之,则可通过测试。
进行多组实验,将系统性能、时域响应取平均值,分别记为![]() 得到最终评估结果χall为
得到最终评估结果χall为
![]()
(39)
式(39)中,k1、k2为权重因子,取值侧重于某项评估指标的重要程度。参数选择为{k1,k2}={0.5,0.5}。
3.3 测试验证结果
分别从系统性能、时域响应、综合评估等方面,充分验证仿真模拟和实际试验间的可靠程度。
在平台性能表现方面,传感器数据的准确程度会直接影响后续的控制精度。因此,对传感器模型与实际样机中传感器进行比较。测试如下:在如图9(a)所示的试验平台,逐步增加电机转速,最终增加到电机最大转速的70%,得到加表噪声测试结果,如图9(b)所示。以陀螺x轴输出角速度为例,进行分析,测试结果如图9(c)所示。可以看到,仿真结果与实际测试一致程度很高。
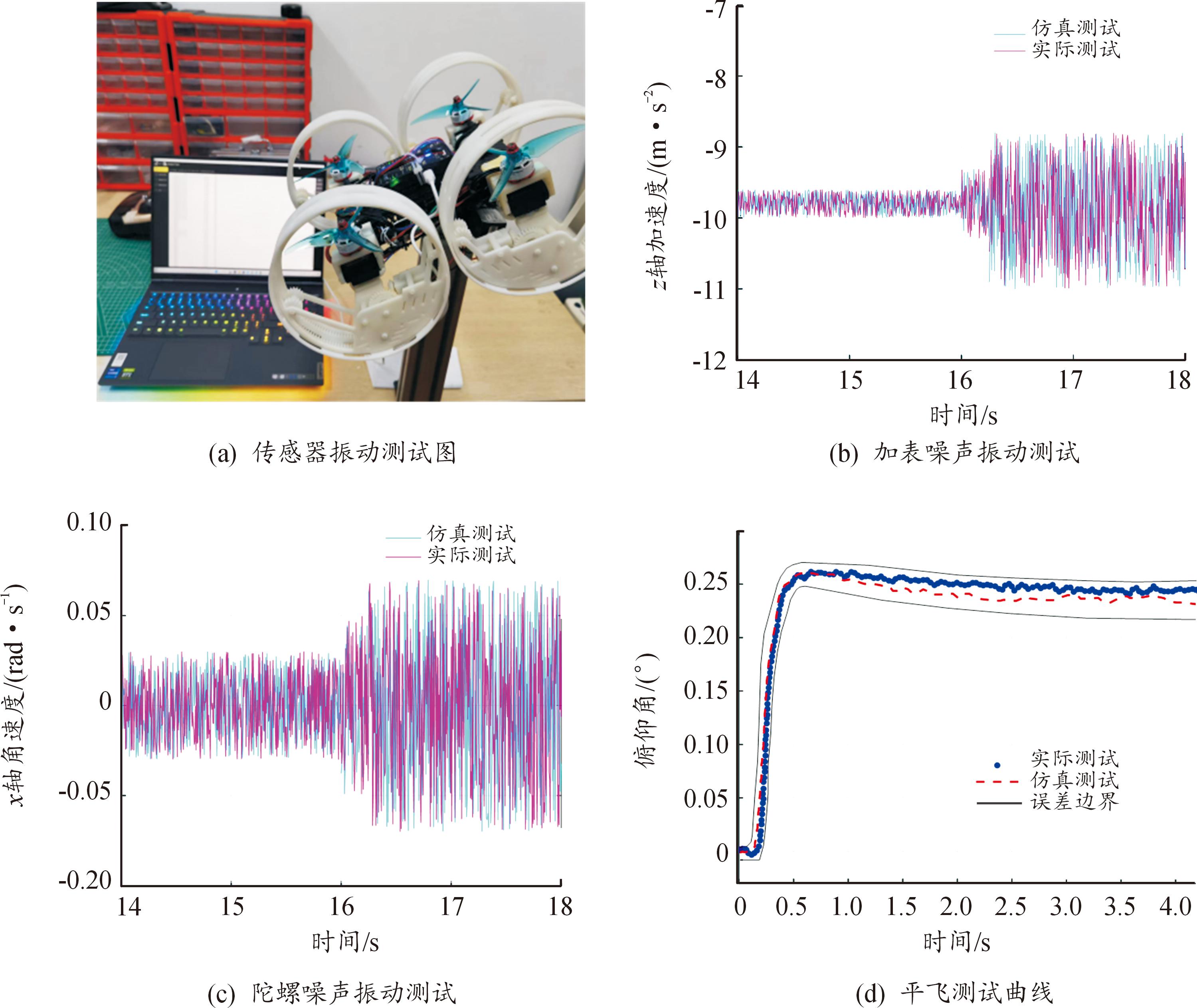
图9 基于系统性能和时域分析的测试验证
Fig.9 Testing and verification of system performance and time domain analysis
为了进一步定量说明,将加表和陀螺噪声振动数据分为14~16 s和16~18 s两组,选择方差作为性能参数指标,计算结果如表6所示。
表6 陀螺和加表噪声振动测试方差计算结果
Table 6 Calculation results of variance in Gyro and Acc noise vibration testing
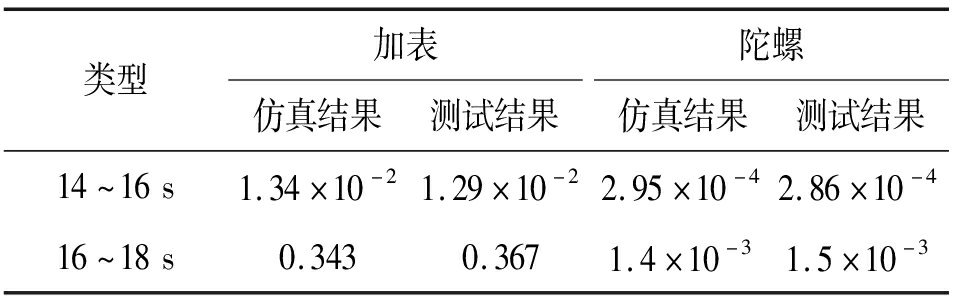
类型加表仿真结果测试结果陀螺仿真结果测试结果14~16s1.34×10-21.29×10-22.95×10-42.86×10-416~18s0.3430.3671.4×10-31.5×10-3
结合式(36)—式(38),计算误差指数e1、误差阈值ζ1及可信度标准![]() 其中,置信区间系数κ0取值为10%。期望标准χration由许多因素决定,在多数系统中取值为0.6[16-17],最终,计算结果见表7。
其中,置信区间系数κ0取值为10%。期望标准χration由许多因素决定,在多数系统中取值为0.6[16-17],最终,计算结果见表7。
表7 模型性能参数评估指标结果
Table 7 Performance evaluation index results of the model
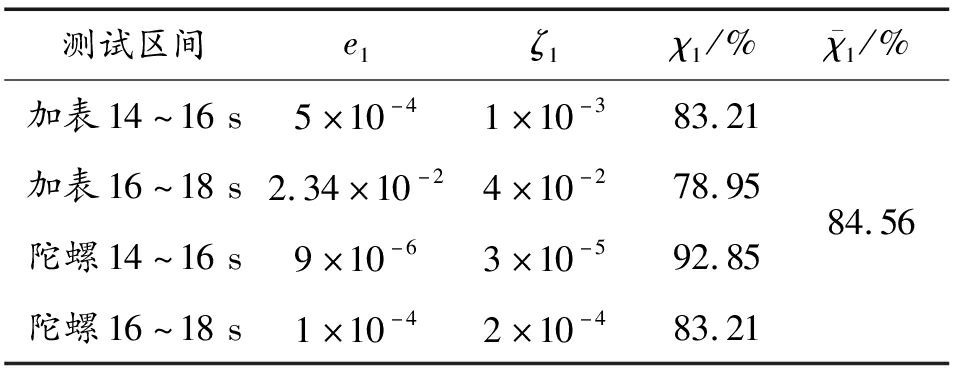
测试区间e1ζ1χ1/%χ1/%加表14~16s5×10-41×10-383.21加表16~18s2.34×10-24×10-278.95陀螺14~16s9×10-63×10-592.85陀螺16~18s1×10-42×10-483.2184.56
由表7定量结果得到,![]() 故仿真结果与实际性能较为接近。
故仿真结果与实际性能较为接近。
操作陆空两栖平台从悬停模式进入平飞状态,采集更多飞行数据进行时域评估。以俯仰通道数据为例进行分析,测试结果如图10(d)所示。其中,误差边界由实飞曲线误差阈值ζ及可信度标准χ2=0.6绘制得到。
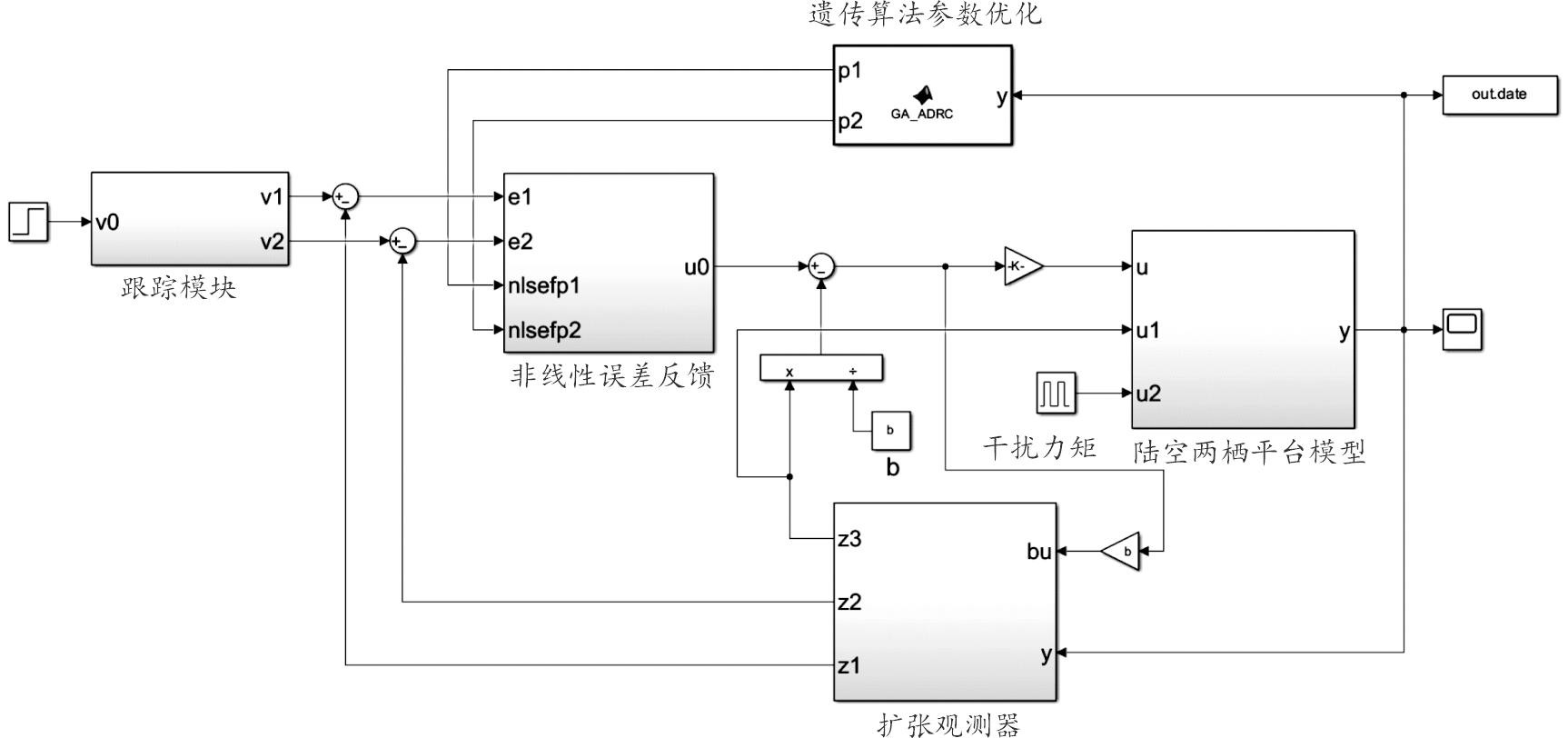
图10 基于遗传算法的ADRC仿真
Fig.10 ADRC simulation diagram based on genetic algorithm
从图10(d)中可以看到,仿真测试结果与实际测试较为接近,并且在误差边界以内,从而证明了结果的有效性。通过定量分析,结合式(36)—式(38),计算仿真结果误差e2、误差阈值ζ2及可信度标准χ2,计算结果见表8。
表8 模型时域评估指标结果
Table 8 Time domain evaluation index results of the model
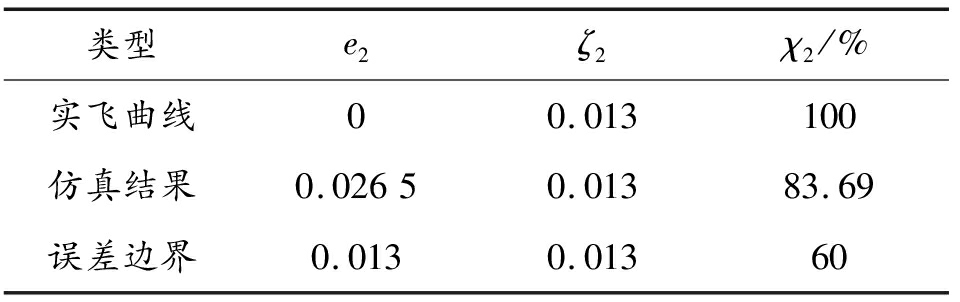
类型e2ζ2χ2/%实飞曲线00.013100仿真结果0.02650.01383.69误差边界0.0130.01360
计算得到评估结果为83.69%,远高于期望标准χration=0.6,与真实试验结果一致度高。
为了全面反映陆空两栖平台仿真模拟的可信度,结合式(39)定量计算平台综合可信度为84.12%。因此,陆空两栖模型可以较为真实地反映原理样机的实际情况。
4 自抗扰控制方案设计
从飞控方面考虑,陆空两栖平台应具有抵抗干扰,增强飞行系统稳定性和精确性的能力。经分析,采用ADRC方法对平台进行姿态控制。
4.1 自抗扰飞行控制仿真
利用陆空两栖平台仿真环境,设计基于ADRC的姿态控制器。具体由非线性自抗扰控制和参数优化2部分组成。其中,自抗扰控制用于观测系统内外总扰动,并进行反馈和补偿;参数优化部分采用遗传算法调节优化自抗扰控制中关键参数,从而使系统达到自适应调节的功能。借助Rflysim平台,采用Matlab验证自抗扰算法有效性及抗干扰能力。系统仿真如图10所示。滚动通道为例,设计姿态跟随曲线。由于系统在阶跃输入下工作条件较为严苛,具有代表性,故选择理想跟踪信号为阶跃信号。在任意时刻(实验中选择在30 s时)加入幅值为3的周期干扰力矩(单位N·cm),仿真总时间为70 s,仿真结果如图11所示。
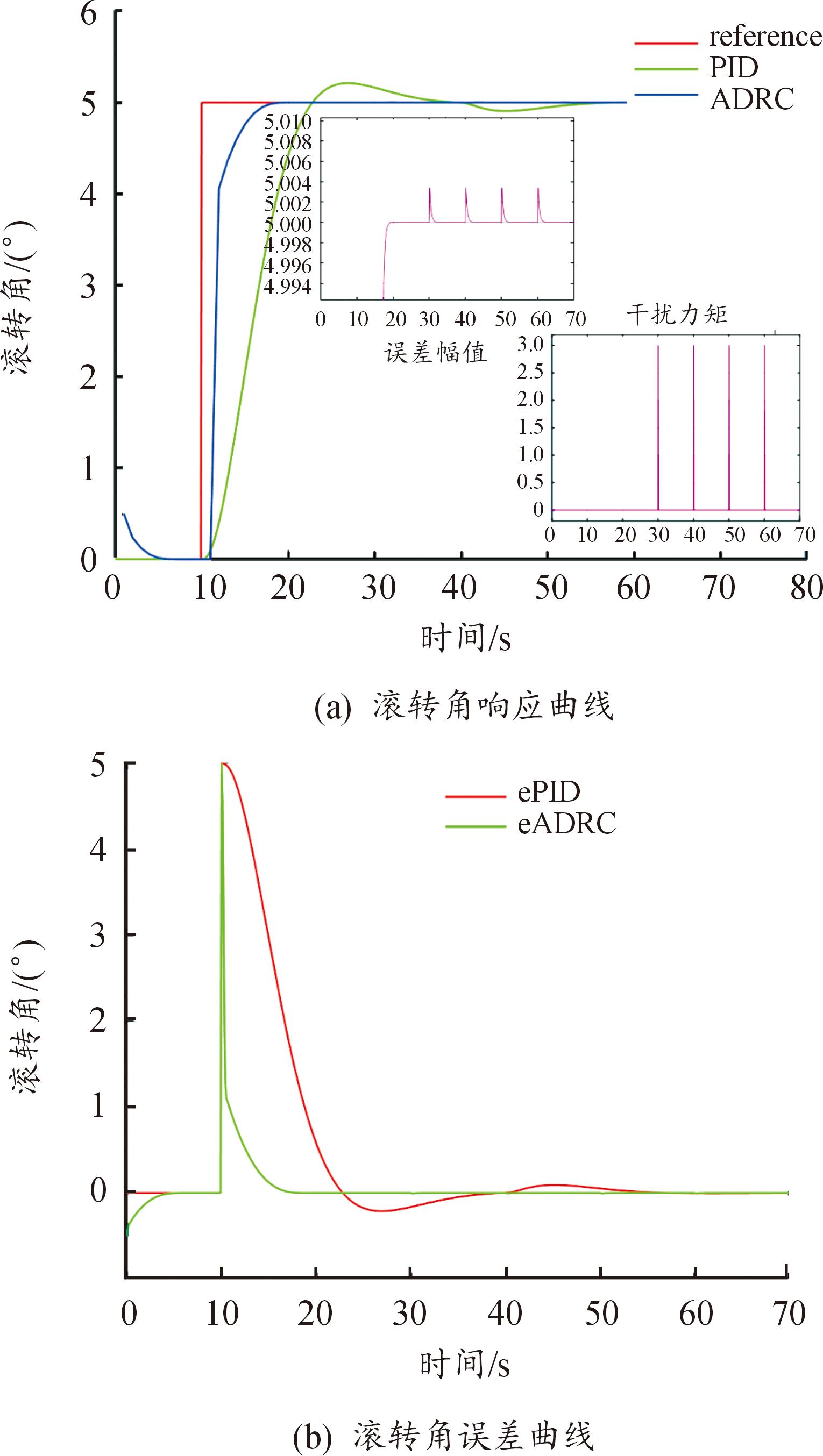
图11 姿态仿真结果
Fig.11 Attitude simulation results
从图11(a)中看到,采用PID控制时输出会有较大畸变,其抗扰动能力明显弱于ADRC控制。当在30 s时加入幅值为3的扰动信号,ADRC算法能平滑跟踪期望信号,超调仅为0.2%,显示出其强大的自抗扰能力。同时,实验结果也表明ADRC算法较好地协调了系统快速性与超调量之间的矛盾。从图11(b)中看到,改进的ADRC方法使得姿态跟踪误差最小,并且在30 s处几乎无跳变。图12表示采用遗传算法自适应优化参数时并未陷入局部最优值。自适应优化参数避免了通过经验摸索\试凑法调试参数的复杂性,提高了参数调优的可解释性与可靠性。
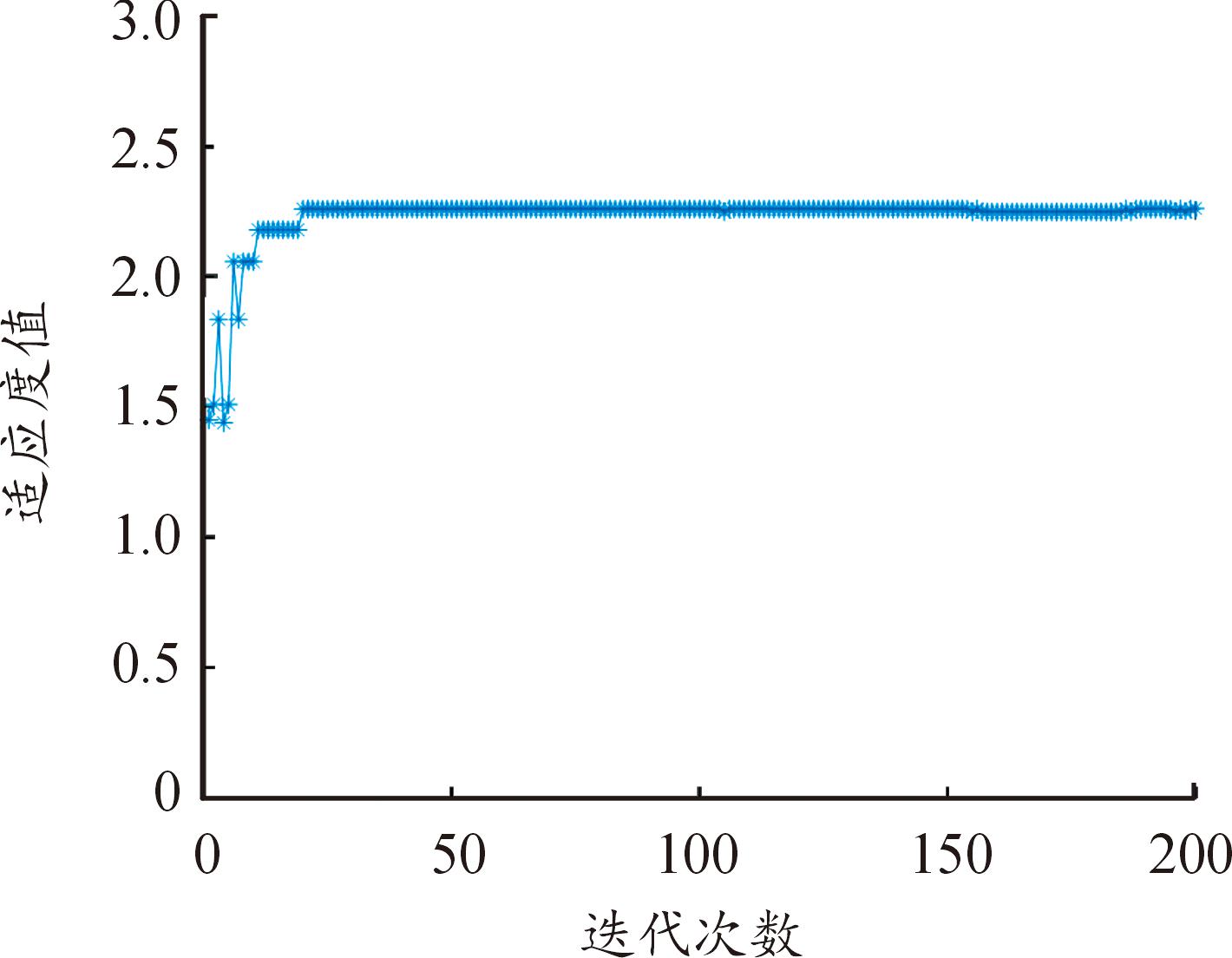
图12 自适应寻优曲线
Fig.12 Adaptive optimization curve
4.2 样机试验
陆空两栖平台总质量约1.8 kg(含电池),长334 mm,宽250 mm(空中飞行模式下287 mm),高164 mm。将样机置于地面,通过遥控进行陆地与空中模式的切换,所设计的陆空两栖平台样机兼具良好的路面行驶能力与空中飞行能力,具备一定的越障功能,试验现场如图13所示。

图13 陆空两栖平台原理样机试验
Fig.13 Principle prototype test of air-ground platform
5 结论
设计和试制了一种具有变结构功能的陆空两栖平台。通过隐藏式旋翼设计,提高了地面行驶模态下的通过性。对陆空两栖平台模型参数进行优化和选型并定量分析得到平台模型的可信度为84.12%,验证了平台模型的有效性和可信度。设计了自抗扰控制方案并验证了原理样机的性能。试验表明,所设计的陆空两栖平台兼具良好的路面行驶能力与稳定的空中飞行能力,为后续长航时、大载重和强稳定性等功能的实现提供了技术参考。
[1] 张佳林,熊大顺,毛子夏,等.新型陆空两栖平台技术发展与趋势[J].汽车工程学报,2019,9(5):332-341.ZHANG Jialin,XIONG Dashun,MAO Zixia,et al.Technology development and trends of state-of-the-art air-ground amphibious platforms[J].Chinese Journal of Automotive Engineering,2019,9(5):332-341.
[2] 樊延平,宋畅,薛中兴.陆军城市巷战作战运用构想创新研究[J].国防科技,2019,40(5):122-126.FAN Yanping,SONG Chang,XUE Zhongxing.Research on the operation conception innovation for army urban street combat[J].National Defense Science and Technology,2019,40(5):122-126.
[3] 马建.陆空两栖机器人飞行系统设计[D].北京:北京理工大学,2015.MA Jian.Flight system design of an air-ground vehicle[D].Beijing:Beijing Institute of Technology,2015.
[4] 朱航.微小型陆空两栖机器人地面移动及控制技术[D].北京:北京理工大学,2015.ZHU Hang.Terrestrial locomotion and control technique of miniature land-air hybrid robot[D].Beijing:Beijing Institute of Technology,2015.
[5] 钟地长.陆空两栖无人机控制系统设计与实现[D].南昌:南昌大学,2020.ZHONG Dichang.UAV control system design and implementation for air-ground amphibious[D].Nanchang:Nanchang University,2020.
[6] 陶彦隐.陆空两栖旋翼式无人机结构设计与控制算法研究[D].南京:南京理工大学,2018.TAO Yanyin.Research on structural design and control algorithms of air-ground rotorcraft UAV[D].Nanjing:Nanjing University of Science and Technology,2018.
[7] 吴冲.陆空两栖载物平台设计及控制算法研究[D].长春:吉林大学,2019.WU Chong.Modeling and control algorithm design of multi-rotor air-ground load platform[D].Changchun:Jilin University,2019.
[8] 韩晓男.陆空两栖载物平台模式切换与判决研究[D].长春:吉林大学,2019.HAN Xiaonan.Research on mode switching and judgment of land and air amphibious load platform[D].Changchun:Jilin University,2019.
[9] 黄彬.陆空车辆跳飞过渡控制技术研究[D].北京:北京理工大学,2016.HUANG Bing.Research on flight control of ground and air vehicles[D].Beijing:Beijing Institute of Technology,2016.
[10] 黄楠.陆空车辆飞行包线研究[D].北京:北京理工大学,2016.HUANG Nan.Research on flight envelope of ground and air vehicles[D].Beijing:Beijing Institute of Technology,2016.
[11] MERRILL R S.Nonlinear aerodynamic corrections to blade element momentum model with validation experiments[D].Utah State University,2011.
[12] DAI X,QUAN Q,REN J,et al.Efficiency optimization and component selection for propulsion systems of electric multicopters[J].IEEE Transactions on Industrial Electronics,2018,66(10):7800-7809.
[13] DAI X,QUAN Q,REN J,et al.An analytical design-optimization method for electric propulsion systems of multicopter UAVs with desired hovering endurance[J].IEEE/ASME Transactions on Mechatronics,2019,24(1):228-239.
[14] SHI D,DAI X,ZHANG X,et al.A practical performance evaluation method for electric multicopters[J].IEEE/ASME Transactions on Mechatronics,2017,22(3):1337-1348.
[15] DAI X,KE C,QUAN Q,et al.RFlySim:automatic test platform for UAV autopilot systems with FPGA-based hardware-in-the-loop simulations[J].Aerospace Science and Technology,2021,114:106727.
[16] DAI X,KE C,QUAN Q,et al.Simulation credibility assessment methodology with FP-GA-based hardware-in-the-loop platform[J].IEEE Transactions on Industrial Electronics,2020,68(4):3282-3291.
[17] TISCHLER M B,REMPLE R K.Aircraft and rotorcraft system identification[M].Reston,VA:American Institute of Aeronautics and Astronautics,2012.