0 引言
火控系统是坦克装备的核心,具有充分发挥坦克火力和提高坦克装备在战场上生存能力的重要作用。在武器系统中,火控系统的计算机和传感器子系统是其关键组成部分,负责协调瞄准子系统、炮控子系统等多个其他子系统之间的复杂信号交互。这一子系统的信号处理架构既复杂又庞大[1-2]。因此,对坦克火控系统进行故障诊断在装甲装备故障预测与健康管理(prognostics and health management,PHM)中就显得尤为重要。
随着人工智能技术快速发展,装甲装备故障诊断技术发展到现在主要分为定量和定性两大类。定性分析主要借助专家经验或者其他分析工具,分析具体装备部件或节点间的逻辑关系,难度较大。目前,大多数学者主要把研究方向放到定量分析,如粗糙集、信息融合和机器学习等一系列基于数据驱动的故障诊断方法[3-4]。在小样本数据分类方面,通过优化算法优化支持向量机建立故障诊断模型已经应用甚广[5-7]。文献[8]提出了一种基于改进灰狼算法的故障预测模型,在时间序列数据上表现良好。文献[9]和文献[10]分别提出了一种粒子群优化支持向量机和鲸鱼优化支持向量机的故障诊断模型,且取得效果良好,但高维度、复杂特征下,灰狼优化算法、粒子群优化算法、鲸鱼优化算法等协调元启发式算法均易陷入局部最优。文献[11-12]应用混沌Logistic和Tent映射于GWO算法的种群初始过程中,减少了采用随机种群初始化的不足,增强了算法的收敛能力。2020年,薛建凯等[13-14]开发了一种麻雀搜索算法,该算法与前述方法相比,显示出更高的搜索精度和更强的鲁棒性。吕鑫等[15]也通过加入混沌映射和引入高斯编译的方法,对麻雀搜索算法性能提升做进一步研究。高维度、小样本数据处理方面,Chen等[16]利用核主成分分析(kernel principal component analysis,KPCA)从信号中提取非线性特征后处理,Wang等[17]在Chen等关于KPCA融合研究的基础上,提出一种基于Pearson相关系数和KPCA融合的方法处理数据。
针对火控系统数据量少、数据维度高的特点,在扩展已有研究工作的基础上,本研究介绍了一种新的故障检测方法,即结合KPCA-ISSA-SVM技术对火控系统进行准确的故障诊断。通过KPCA对原始数据进行数据降维,处理后的数据作为诊断模型的输入。在此基础上,引入混沌Tent映射和非线性自适应权重对SSA进行改进,再通过ISSA算法对SVM核心参数进行寻优,构建火控系统故障诊断模型,相比较其他传统分类模型,提升了火控系统故障诊断的准确率和效率。
1 算法原理
1.1 核主成分分析
核心主要成分分析(kernel principal component analysis,KPCA)提供了一种扩展传统主成分分析(principal component analysis,PCA)的方式,以处理非线性数据模式。通过运用核技巧,KPCA 能够把原始数据投影到一个新的高维度空间中,该空间能够更好地揭示数据的复杂结构。在这个空间里,可以使用线性算法来解决原始空间中的非线性问题。传统的PCA是一种线性降维技术,用于在保持数据集的大部分信息的同时减少数据的维数。然而,当数据结构具有非线性特性时,传统的PCA可能就不再适用。这时,KPCA就可以发挥作用。
1) KPCA 最初将初故障样本数据投射至一个高维特征空间,形成新的数据φ(ei)={φ(e1),φ(e2),…,φ(en)}, i=1,2,…,n。
假定样本在高维特征空间已被归一化至中心,则协方差矩阵为
![]()
(1)
2) 引入核函数为K*=φφT,对S中数据进行主成分分析求解:
K*η=λη
(2)
式(2)中: λ为特征值; η为特征向量。
3) 设置累计贡献率阈值,一般设置为80%~95%之间。设置完后,降序排列选取前t个特征值λi(j=1,2,…,s)和其对应的特征向量ηj(j=1,2,…,s):
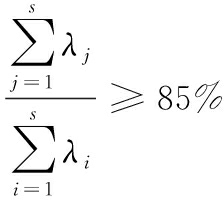
(3)
4) 当累计的贡献率达到设定要求时,计算降维映射后的非线性样本G:
![]()
(4)
1.2 支持向量机
支持向量机(support vector machine,SVM)是一个高效的监督式学习模型,常被用来处理分类与回归任务。它由Vladimir Vapnik和他的同事在1995年提出。SVM在处理线性可分以及非线性问题方面都非常有效,并且在小至中等规模的数据集上表现良好。SVM通过核函数映射,将初始数据转化到更高维度空间。核函数表达式为
![]()
(5)
当引入核函数之后,支持向量机(SVM)用于分类的决策规则变为
![]()
(6)
针对在映射到高维特征空间后若干数据点仍难以区分的情形,分类算法模型通过加入松弛变量ξi以实现更好的适应性,并通过施加惩罚项C对误分类的情况进行约束,从而优化模型的泛化能力。引入这些调整后得到的改进后模型可以表示为
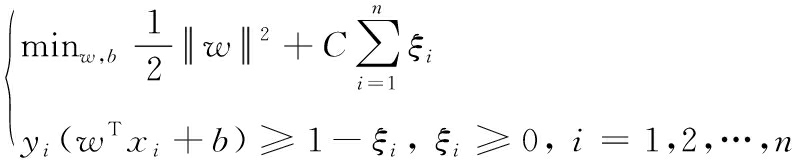
(7)
将其转换为对偶问题
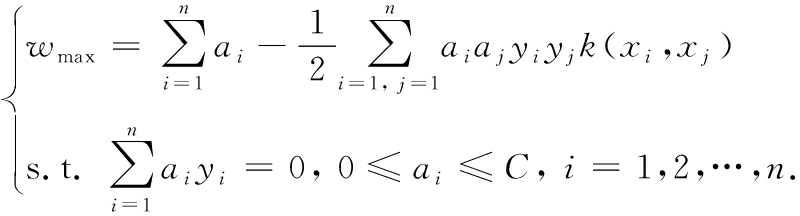
(8)
式(8)中:ai和aj表示拉格朗日乘子;yi和yj表示训练样本类别,yi和yj∈(0,1);惩罚因子C来量化机器学习模型的复杂度[19]。如果该参数设定过高,模型容易产生过度适应训练数据的情况,使得SVM的结构变得繁复,导致计算时间增加,效率降低;相反,若该参数设定过低,会减少数据样本的拟合能力,使得SVM模型可能不足以捕捉数据的特征,进而导致欠拟合。
1.3 麻雀搜索算法
麻雀搜索算法(sparrow search algorithm,SSA)是一种基于麻雀群体觅食和防御策略的集体智能优化方法,首次提出于2020年。这种算法模拟麻雀群体中发现者与追随者的角色动态,以及警戒机制的整合。在模型中,发现者角色负责探索食源并指引群体方向,追随者则依赖发现者获取食物。麻雀在求食时会根据环境切换成发现者或追随者的策略。此外,部分麻雀执行侦查预警,以便在存在威胁时放弃食源以确保生存。算法中,每只麻雀个体都由其位置属性表示,暗喻其找到食物的潜在能力。每个个体能够呈现3种行为模式:作为领航的发现者、跟随的追随者,或在预警系统作用下放弃食源以避免危险。对于麻雀种群:
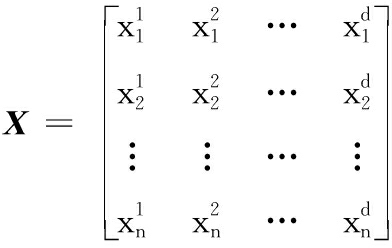
(9)
在算法实现中,拥有较优适应度且搜索能力较强的麻雀,即发现者,通常会在寻找食物时享有优先权。这些发现者不仅提供了指引全局寻食能力,还为新加入的麻雀成员指明了觅食方向。这意味着发现者需要有能力探索更广阔的搜寻区域来满足种群的需求。由此发现者其位置更新表述为
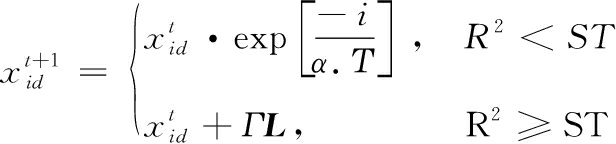
(10)
式(10)中: 在迭代过程的第t次,群体中编号为i的麻雀在空间的第d维的具体位置被确定为![]() 其中,t代表进行到的迭代轮数,α是一个落在(0,1]区间内的随机系数。Γ代表一个服从标准正态分布的随机变量。L表示由1组成的尺寸为1×d的矩阵。R2∈[0,1]和ST∈[0.5,1],分别表示预警阈值和安全阈值。当R2的值超过ST,意味着有些麻雀觉察到了威胁,探索者应在这种情况下朝着安全区域汇集,具体表现为发现者根据正态分布原则随机向其当前位置附近区域转移。而当R2小于ST时,表明当前环境不存在危险,发现者可以进行大范围的搜索操作。随着种群迭代次数的参加,
其中,t代表进行到的迭代轮数,α是一个落在(0,1]区间内的随机系数。Γ代表一个服从标准正态分布的随机变量。L表示由1组成的尺寸为1×d的矩阵。R2∈[0,1]和ST∈[0.5,1],分别表示预警阈值和安全阈值。当R2的值超过ST,意味着有些麻雀觉察到了威胁,探索者应在这种情况下朝着安全区域汇集,具体表现为发现者根据正态分布原则随机向其当前位置附近区域转移。而当R2小于ST时,表明当前环境不存在危险,发现者可以进行大范围的搜索操作。随着种群迭代次数的参加,![]() 项的取值将随之减少,种群中除去发现者,剩余麻雀均为追随者。追随者的位置更新描述如下:
项的取值将随之减少,种群中除去发现者,剩余麻雀均为追随者。追随者的位置更新描述如下:
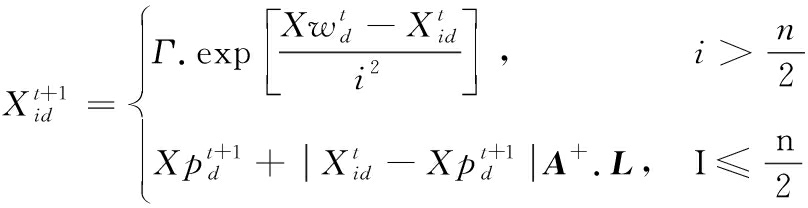
(11)
式(11)中,![]() 表示麻雀种群进行第t次迭代时,麻雀在d维的最劣位置。
表示麻雀种群进行第t次迭代时,麻雀在d维的最劣位置。![]() 表示麻雀种群进行第t+1次迭代时麻雀在第d维的最优位置。A表示一个各元素为1或-1的一行多维矩阵,且A+=AT(AAT)-1。当大于n/2的时候,表明该追求者处于十分饥饿的状态,利用一个标准正态分布随机数与以自然对数为底指数函数的积,控制其取值符合正态分布,即获取更多的能量。当i≤n/2时,其过程可解释为在当前最优位置附近随机找到一处位置,且每一维距最优适应度值位置较小,值较为稳定。
表示麻雀种群进行第t+1次迭代时麻雀在第d维的最优位置。A表示一个各元素为1或-1的一行多维矩阵,且A+=AT(AAT)-1。当大于n/2的时候,表明该追求者处于十分饥饿的状态,利用一个标准正态分布随机数与以自然对数为底指数函数的积,控制其取值符合正态分布,即获取更多的能量。当i≤n/2时,其过程可解释为在当前最优位置附近随机找到一处位置,且每一维距最优适应度值位置较小,值较为稳定。
在麻雀种群中,作为警戒麻雀的麻雀数量占麻雀种群数量的10%~20%,初始麻雀位置是随机产生的,位置更新公式如下:
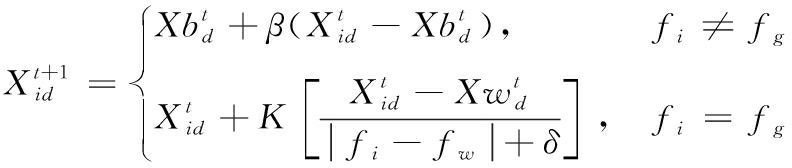
(12)
式(12)中:![]() 代表了当前全局最佳位置。β符号用于步长参数调节。其中,K表示介于[-1,1]区间内的随机数值。fi用以表示第i个麻雀的适应度值, fg以及代fw表了麻雀种群中目前的最高和最低适应度值。因此,如果警戒麻雀位于全局最优点,它将逃向其周围的位置。若不是最优位置,则逃离到当前最优位置附近。
代表了当前全局最佳位置。β符号用于步长参数调节。其中,K表示介于[-1,1]区间内的随机数值。fi用以表示第i个麻雀的适应度值, fg以及代fw表了麻雀种群中目前的最高和最低适应度值。因此,如果警戒麻雀位于全局最优点,它将逃向其周围的位置。若不是最优位置,则逃离到当前最优位置附近。
2 改进麻雀优化算法
2.1 Tent混沌算法
Tent混沌算法常用于构建优化算法的起始群体。这种方法不仅有助于维持种群的多样性,还可以增加算法探索最优解的区域,从而减少算法陷入局部最优解的风险,具有较高的适用性。Tent混沌的表达式如下:
![]()
(13)
经过贝尔努利位移转换,Tent 映射被重新表述为xi+1=(2xi)model,研究表明在可行域中生成的 Tent 映射序列可能会出现较短的周期性;并且可能会遇到不稳定的周期性点。为规避在迭代过程中遭遇短周期或不稳定周期点的情况,张娜[18]及团队在原 Tent 映射公式的基础上添加了随机变量以对混沌序列进行调整。这样在一个可控的随机界限内,同时确保了 Tent 映射序列保持随机性、穷尽性和有序性。
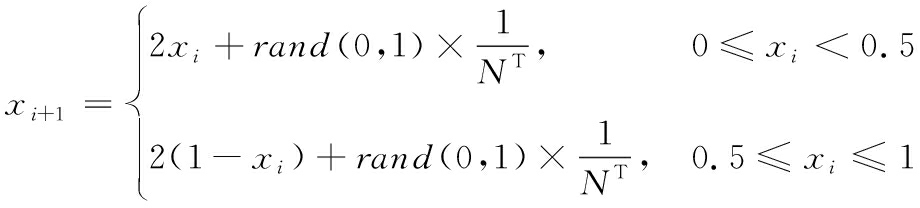
(14)
贝努利变换后的表达式为
![]()
(15)
式(15)中:NT为混沌序列内的粒子数量;rand(0,1)为[0,1]之间的随机数。
2.2 Tent混沌扰动
为保证麻雀种群的丰富性,本文提出加入Tent混沌扰动使得麻雀个体尽可能均匀的分布在寻优范围内,尽可能地增加算法的全局搜索性,降低算法陷入局部最优的概率。混沌干扰的步骤可以概述为:起初生成混沌量Zd,依照公式进行应用,然后利用相关方程将其映射到目标问题的解决方案空间,正如公式展示的那样。
![]()
(16)
式(16)中:dmax和dmin分别为第d维变量![]() 的最小和最大值。
的最小和最大值。
![]()
(17)
式(17)中:X′表示需要进行混沌扰动的个体。Xnew表示产生的混沌扰动变量,![]() 表示进行混沌扰动后产生的新个体。
表示进行混沌扰动后产生的新个体。
2.3 引入非线性惯性权重因子
协调元启发式算法的局部寻优能力和全局寻优能力是影响算法寻优性能的关键因素,由于麻雀个体位置的更新迭代与其当前所处位置息息相关,为此,引入一种非线性惯性权重因子w用于调整麻雀个体位置更新与其所处位置的关联度。迭代开始,w值较小,寻优个体受当前麻雀个体位置影响能力相对较小,全局探索能力较强,有助于防止仅限于局部最佳解的情况。随着迭代的进行,w的值逐渐增大,寻优个体受当前麻雀个体位置影响能力相对较大,局部搜索能力变强,有助于算法搜索最优解,大大提升了算法的收敛速度。更新后的追随者公式为
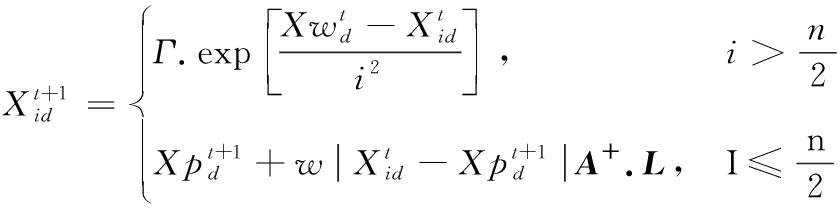
(18)
其中,非线性惯性权重因子计算公式如下:
![]()
(19)
2.4 改进麻雀搜索算法流程
步骤1 参数初始化,包括种群数N,最大迭代次数T,发现麻雀个数pn,侦察麻雀个数sn等。
步骤2 应用Tent混沌映射序列丰富初始化种群,将模型中的权值和阈值表示为ISSA算法中的d维向量,并根据式(16)载波映射到目标函数空间取值范围内。
步骤3 计算每一只麻雀的适应度值fi,并进行排名以识别最佳和最差的适应度值及其相应的位置。
步骤4 挑选排名靠前的pn只麻雀作为发现者,在此情况下,其他麻雀扮演跟随者的角色,并按照式(10)和式(18)更新它们的位置。
步骤5 随机选取只sn麻雀进行勘探,并依据公式(12)对其位置进行更新。
步骤6 根据当前麻雀种群状态更新个体最优和最差适应度对应位置。
步骤7 判断算法当前迭代次数是否达到设置阈值。如果是,则结束寻优,输出结果。否则返回步骤4继续循环。
具体过程如图1所示。
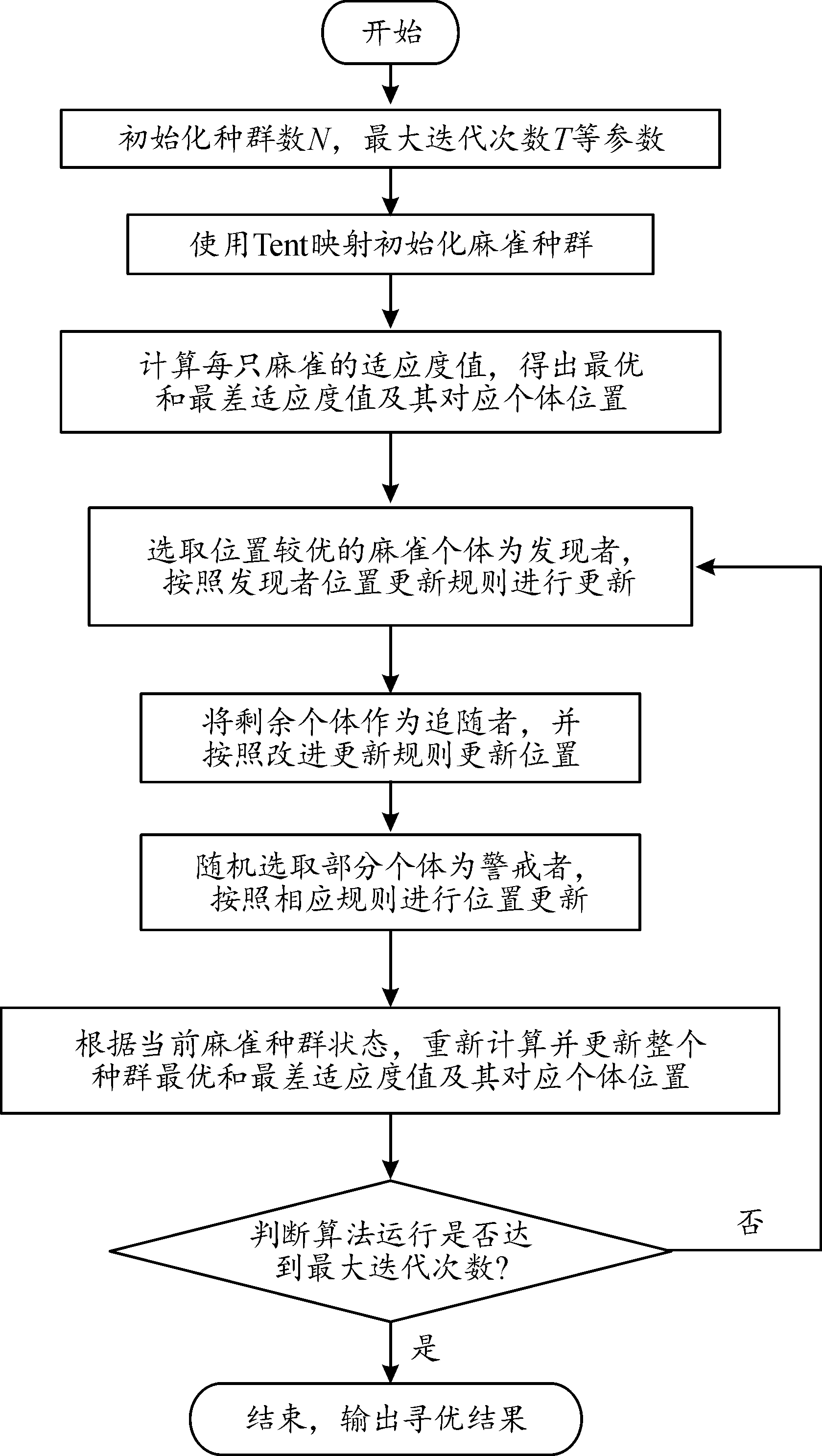
图1 改进麻雀算法搜索过程
Fig.1 Improved sparrow algorithm search process
3 火控系统故障诊断模型构建
3.1 模型输入量
坦克内部部件繁多,相互间关系错综复杂。坦克火控系统是坦克的核心部位,而火控系统当中火控计算机的电压信号更是重中之重,更能反映武器装备的退化特征和武器状态。因此,对初始测量数据进行特征抽取和数据优化是必要的。初始步骤是使用不同条件下测试元件的各个引脚信号作为评价指标,应用核主成分分析法来计算主成分,并根据累积贡献率的预设标准来选择主成分以简化数据。接下来,利用简化后的数据作为输入,对支持向量机进行模型的训练。通过加入混沌映射和非线性惯性权重来改进麻雀搜索算法,提升搜索效率和性能。使用改进后的麻雀搜索算法寻找支持向量机的最优参数,输入到算法进行故障诊断。
3.2 数据处理
由于装甲装备结构复杂,涉及参数较多,而KPCA能有效处理非线性可分的数据集,实现了将原本在原始空间无法通过线性方式区分的数据在特征空间中变得能够被线性划分。通过非线性映射发现数据的内在结构,能够将数据从一个高维空间映射到一个低维的子空间,而这个子空间能更好地表示数据的主要成分。算法流程如图2所示。
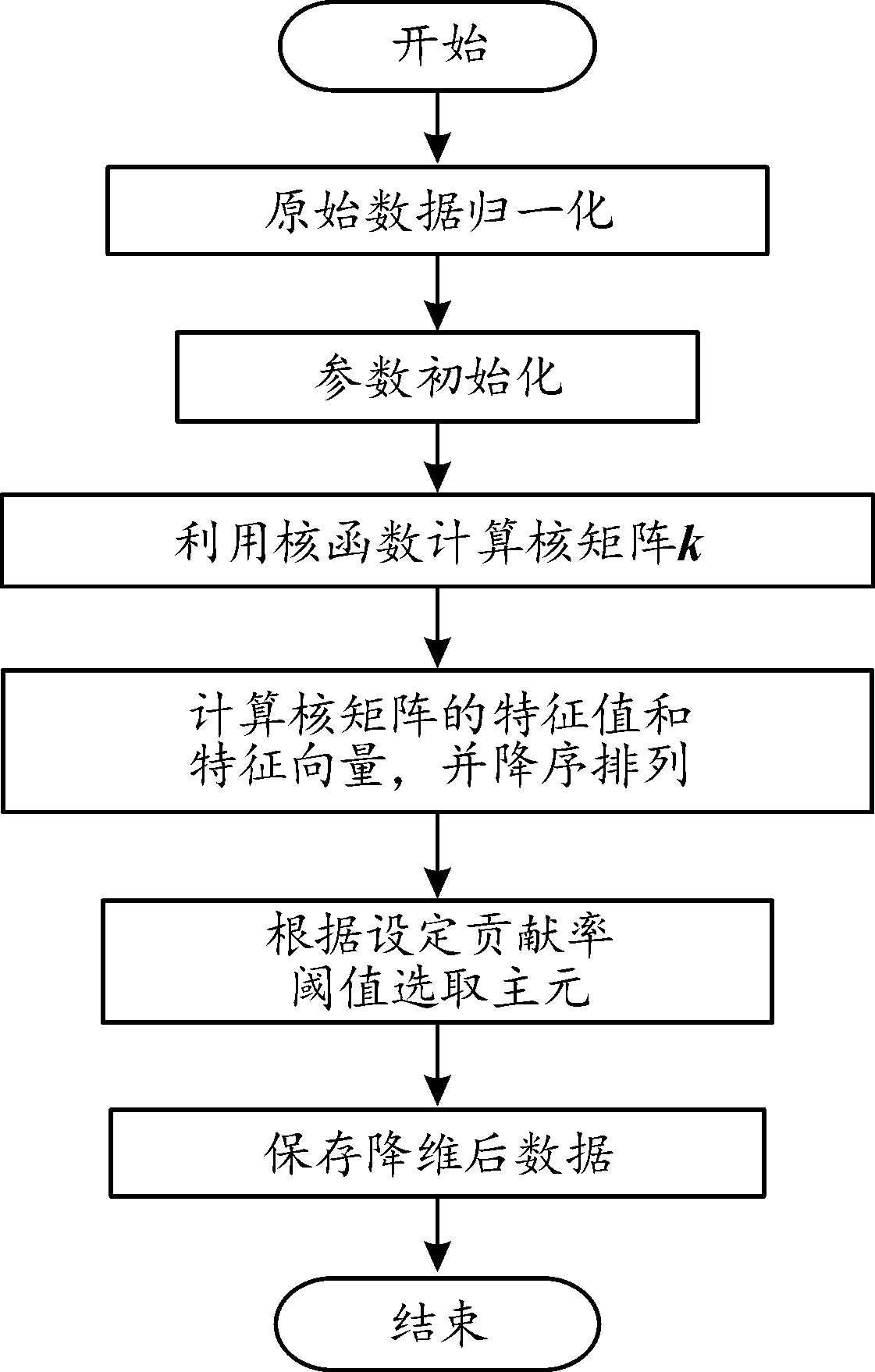
图2 KPCA算法流程图
Fig.2 KPCA algorithm flowchart
步骤1 将原始数据归一化,使所有值都落在区间[0,1]内。
步骤2 参数初始化,设定核函数参数,数据输入维度,贡献率阈值p。
步骤3 根据核函数计算输入数据对应的核矩阵K。
步骤4 确定核矩阵的特征值与对应的特征向量,并按照降序排列这些特征值及其特征向量。
步骤5 计算各特征值的累计贡献率r,若r>p,则选取前t个特征作为降维后的数据。
3.3 ISSA-SVM故障诊断方法
SVM在处理高维数据方面表现出色,因为它的工作原理并不直接依赖于数据的维度,而是通过所选的内核函数定义数据点之间的关系。即使在有限样本的情况下,SVM也能通过构造最优化的决策边界来实现良好的泛化。针对坦克火控系统数据量少、维度高的特点,采用支持向量机算法。对于SVM的2个关键参数核参数g和惩罚因子C,笔者考虑采用麻雀搜索算法进行寻优,算法初始阶段引入Tent混沌扰动,丰富初始化种群,增强全局搜索能力。随后,在算法寻优过程中,引入非线性惯性权重因子调整麻雀个体位置更新与其所处位置的关联度,协调麻雀搜索算法的搜索全局能力和局部搜索能力,提升了算法的收敛效率,诊断流程如图3所示。
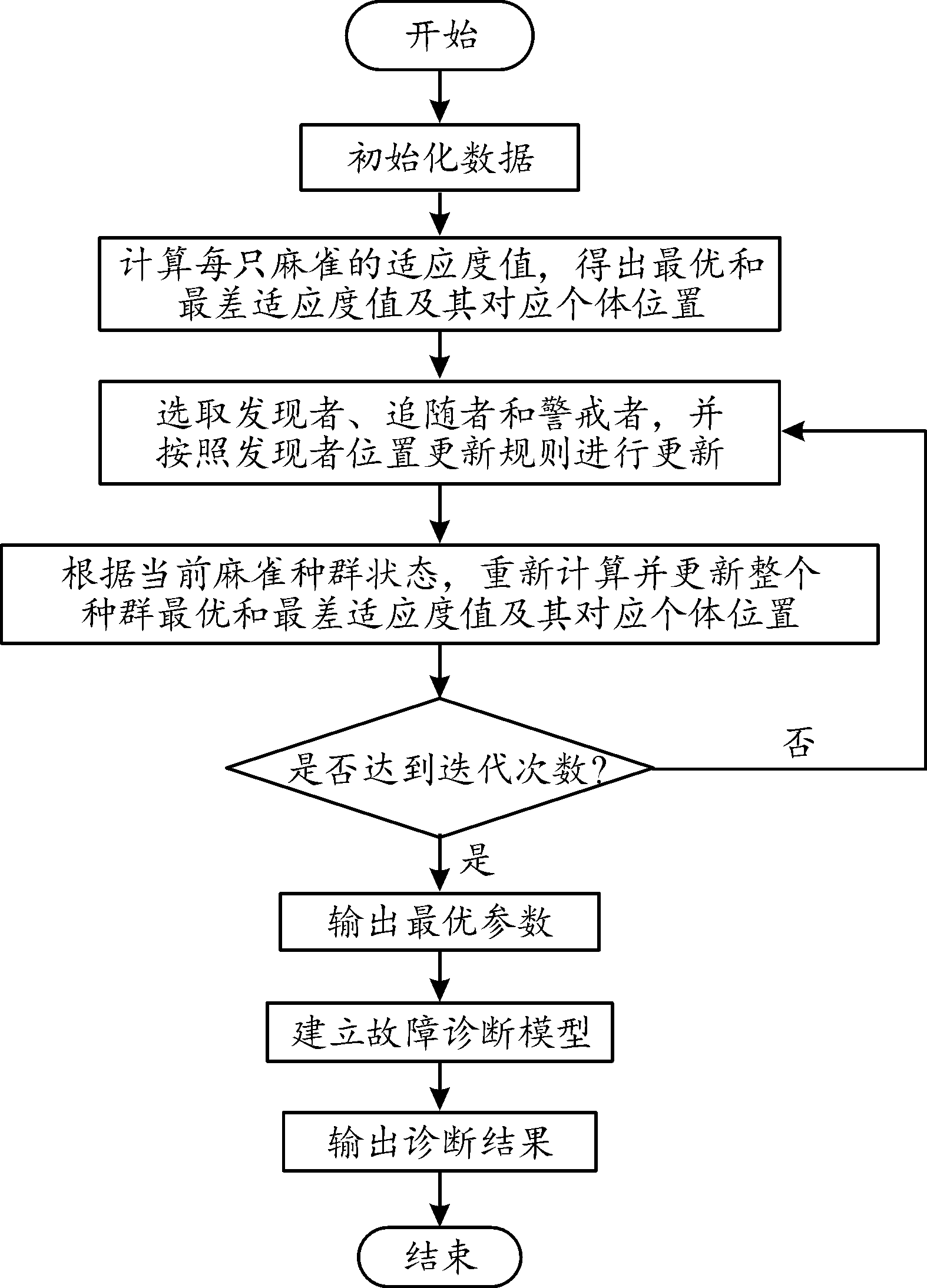
图3 ISSA-SVM故障诊断流程
Fig.3 ISSA-SVM fault diagnosis flowchart
步骤1 设定初始参数,包括种群数N,最大迭代次数T,发现麻雀个数pn,侦察麻雀个数sn等。
步骤2 取诊断准确率为适应度函数,评估每只麻雀个体的适应度,并按照此值进行排名,以识别出目前表现最好和最差的适应度值及它们各自的位置。
步骤3 根据设定参数选取发现麻雀,侦察麻雀和追随者麻雀,根据对应规则进行位置更新。
步骤4 计算位置更新后麻雀种群所有个体对应适应度值,并再次记录排序得出当前最优和最差适应度值以及其对应位置。
步骤5 判断已完成的迭代次数是否满足预定的迭代上限T,若满足条件,则停止循环并提供最终结果。否则,则返回步骤3继续循环。
步骤6 将寻优结束得到的参数输入到支持向量机模型建立故障诊断模型。
4 实例验证
火控系统结构复杂,部件繁多,但又极其重要,是坦克装备正常工作的保证,也是其战场强大战力的前提。笔者以火控系统中火控计算机及传感器子系统的控制盒输出电压信号为实验对象,其精度直接影响火控计算机的正常工作。采集信号包括火控计算机产生的+5 V、+12 V、-12 V、+26 V,其中输出的+5 V、+12 V、-12 V电压是火控计算机产生的工作电压,它们由电源的+26 V电压经火控计算机内部的DC-DC变换得到,引脚信号如表1所示。
表1 数据源引脚信号
Table 1 Data source pin signal

序号参数名称对应引脚C1U12aXS2-17C2U12bXS2-22C3U-12aXS2-19C4U-12bXS2-23C5分电源U5aXS2-25C6分电源U5bXS3-3C7分电源U5cXS3-8C8分电源U5dXS4-9C9分电源U26eXS4-38C10主电源U26aXS2-35C11主电源U26bXS2-36C12主电源U26cXS2-37C13主电源U26dXS2-38
共收集上述电压信号450组,包含故障和非故障数据,共分为5种,训练数据和测试数据的分配比例为70%和30%。,具体如表2所示。本数据集包括几种不同的数据组,正常运行数据共有90组,其标签被标为1;另外,+12 V电源出现问题的数据也有90组,相应的标签为2;-12 V电源存在故障的数据组同样为90组,对应的标签定为3;+5 V电源发生故障的数据组为90组,其标签指定为4;而+26 V电源出现故障的数据也是90组,这一类的标签被识别为5。
表2 采集数据分类
Table 2 Data collection classification
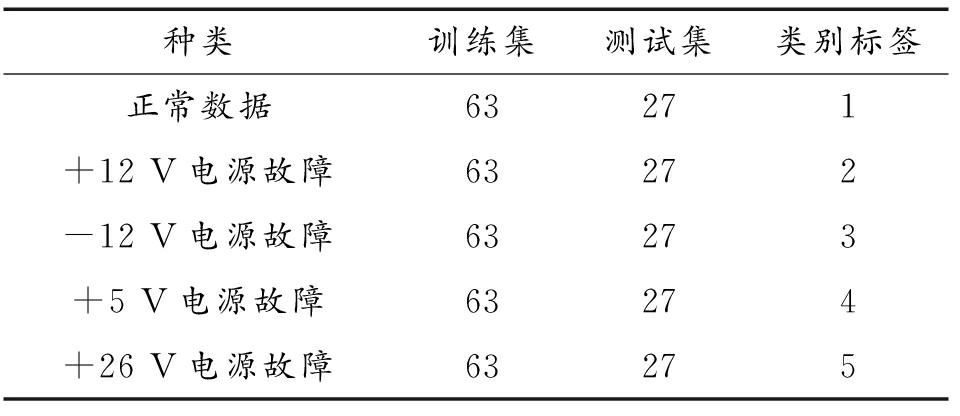
种类训练集测试集类别标签正常数据63271+12 V电源故障63272-12 V电源故障63273+5 V电源故障63274+26 V电源故障63275
4.1 基于KPCA对数据进行降维
首先对原始数据进行核主成分降维处理,在尽量保留数据信息的情况下降低数据维度,在保存加快迭代速度并降低训练时间从而提升模型性能。随后,设立不同的累计贡献率阈值,包括50%、60%、70%、80%、85%、90%和95%。在确定这些阈值之后,将筛选后的数据送入支持向量机进行处理。具体的实际累积贡献率、测试集的样本精度和主成分选择的顺序在表3中有所展示。举例来说,1-2代表选取了前2个主成分,以此类推。
表3 累计贡献率对比
Table 3 Comparison of cumulative contribution rates
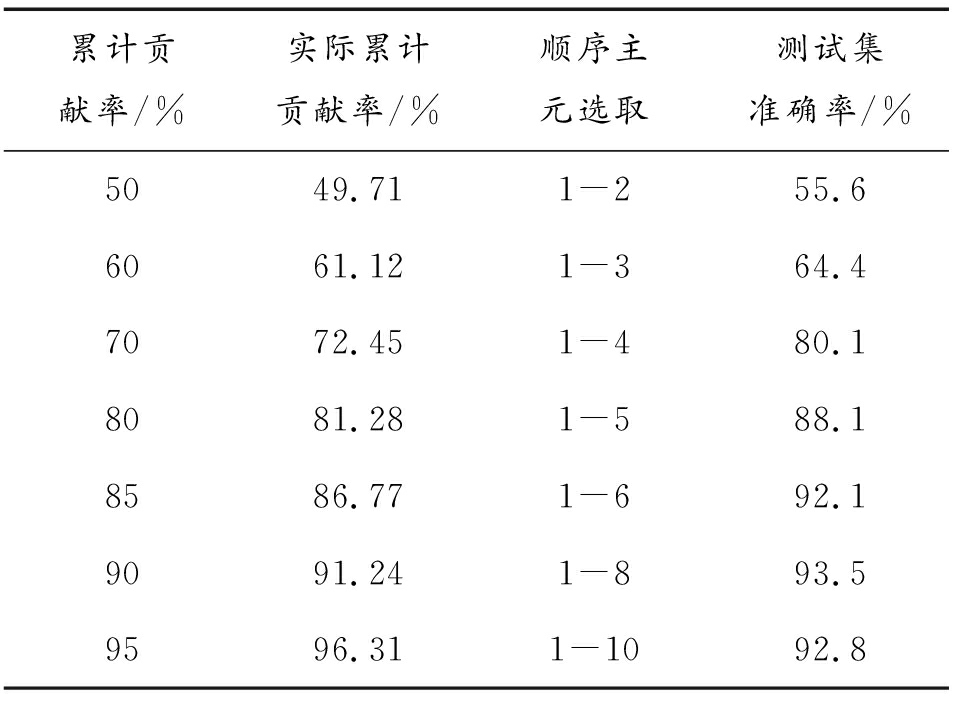
累计贡献率/%实际累计贡献率/%顺序主元选取测试集准确率/%5049.711-255.66061.121-364.47072.451-480.18081.281-588.18586.771-692.19091.241-893.59596.311-1092.8
根据表3可以看出:不同维度数据对实验结果影响较大。在一定范围内当设定累计贡献率值增加,原始数据选取主元数增加,降维数减少,实际累计贡献率增加,相应的测试集验证的准确率也增加。
但并不是实际贡献率值越多越好,当设定贡献率值达到90%时,对应测试集准确率最高,当设定贡献率值为95%时,提取数据维度较高,相应的准确率却降低。因此,设定贡献率为90%,原始数据经由KPCA处理后由13维度降为8维,降低了后续故障诊断模型训练时间,提升模型性能。
4.2 改进麻雀算法
对于SVM模型的寻优,相关学者提出了各种各样的方式。由于传统麻雀搜索算法易陷入局部最优并且初始化种群随机性较强,在此引入混沌Tent映射和非线性惯性权重因子对麻雀搜索算法进行改进,并与常规麻雀搜索算法进行对比。在Intel(R) Core(TM) i7-8750H CPU@2.20 GHz 2.20 GHz,内存16 GB,Windows10系统和Matlab 2017b下对本文算法进行仿真实验,设定最大迭代次数为50次,初始化种群数为20,发现麻雀个数pn和侦察麻雀个数sn取4,取交叉验证的准确率为适应度值,改进前后寻优曲线如图4所示。
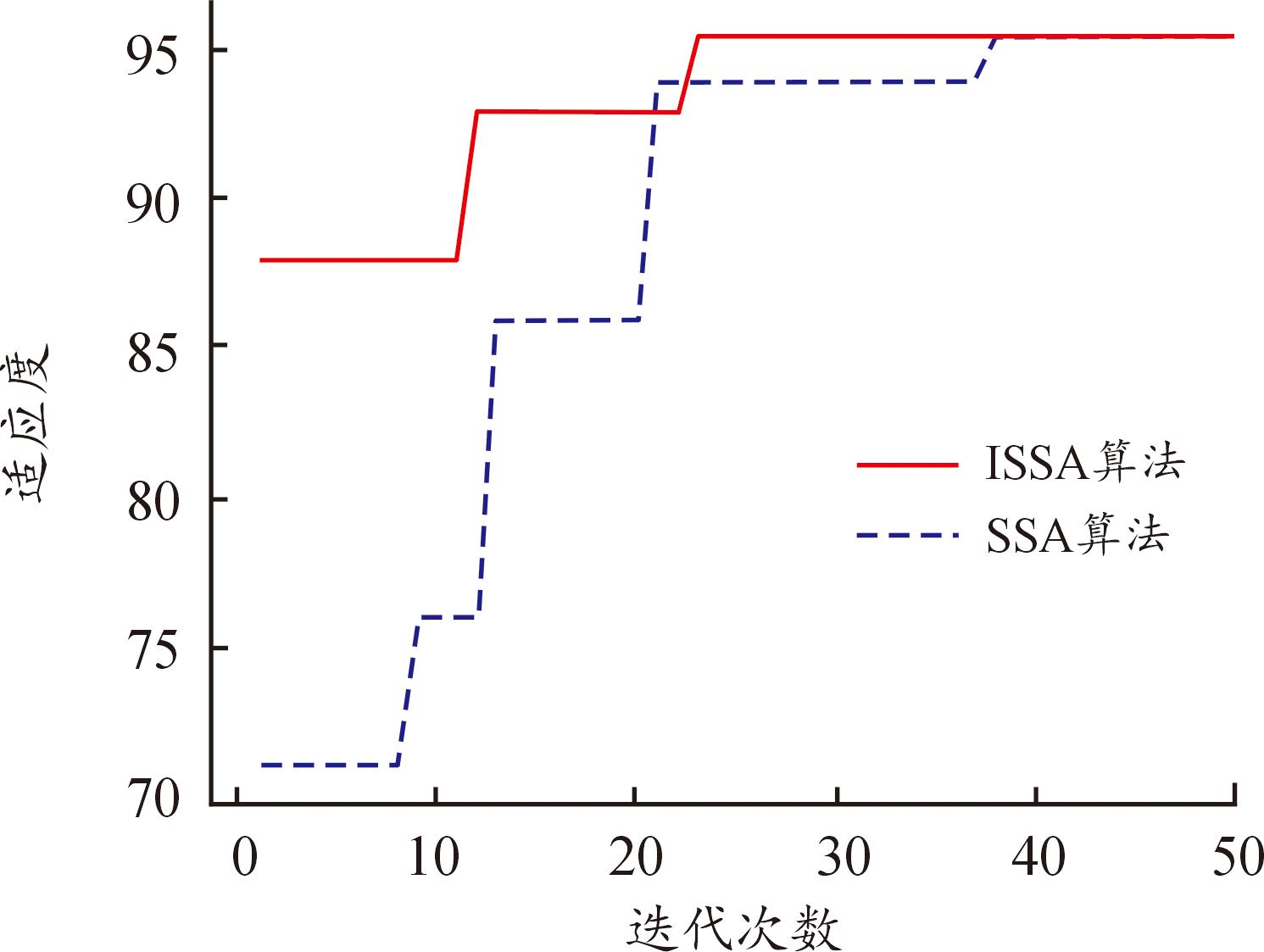
图4 分类准确率寻优曲线
Fig.4 Classification accuracy optimization curve
由图4中可以看出,引入混沌Tent映射后,丰富初始化种群。一开始ISSA算法效果就优于SSA。尽管二者最终搜索适应度值相同,但ISSA算法在第23次迭代就已经收敛到最优值,SSA算法在迭代后期陷入局部极值,直到第39次才收敛到最优值。对比改进前后SSA算法,ISSA收敛效率显著提升,验证了引入非线性惯性因子的有效性。
4.3 基于KPCA-ISSA-SVM的故障诊断
选取上述KPCA方法降维后的315组训练数据输入到建立的KPCA-ISSA-SVM故障诊断模型中,并与WOA-SVM、PSO-SVM模型进行对比,故障诊断结果如图5所示。
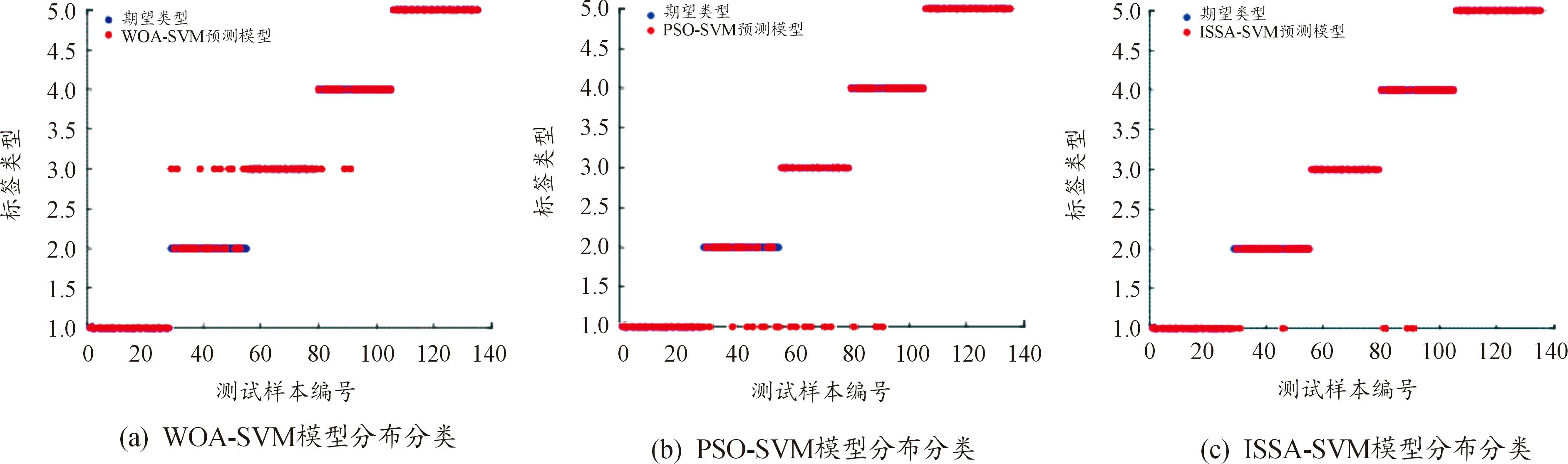
图5 SVM模型故障诊断结果对比
Fig.5 Comparison of SVM model fault diagnosis results
由图5可知,WOA-SVM的故障诊断准确率为86.7%,PSO-SVM模型的故障诊断正确率91.1%,而ISSA-SVM的故障诊断正确率达到了95.6%,相比较PSO-SVM和WOA-SVM模型的准确率分别提高了4.5%和8.9%,分类性能高于其他常规模型。在时间上,ISSA-SVM算法运行时间为5.62 s,而WOA-SVM和PSO-SVM则分别需要6.35 s和9.52 s。PSO-SVM尽管在准确率上面优于WOA-SVM,但在时间上却较为缓慢。
为了避免实验的偶然性,分别对每种算法进行了10次实验,记录实验结果并取10次实验结果的平均值作为模型最终评估依据,综合分析得出无论是故障给诊断的准确率还是模型运行时间指标,ISSA-SVM故障诊断模型都优于其他2种模型,验证了提出模型的性能较好,具体结果如表4所示。
表4 3种模型诊断结果
Table 4 Diagnosis results of three models
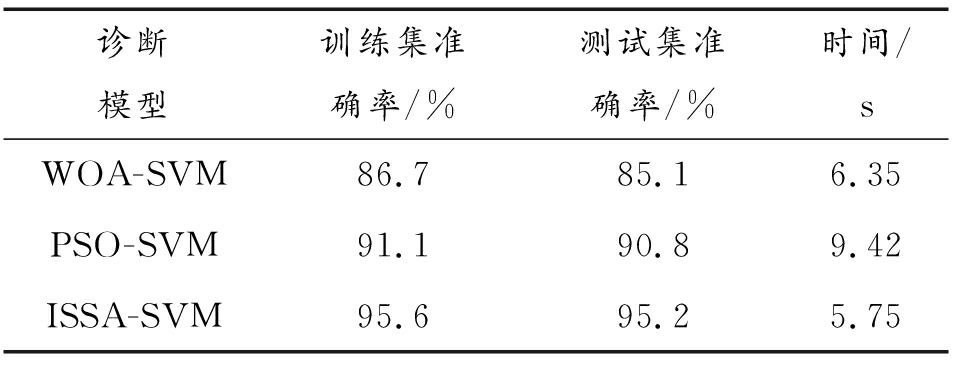
诊断模型训练集准确率/%测试集准确率/%时间/sWOA-SVM86.785.16.35PSO-SVM91.190.89.42ISSA-SVM95.695.25.75
5 结论
针对火控系统数据纬度高、参数复杂的特点,使用KPCA进行数据降维,最大限度提取原始数据有效信息,并通过实验进一步验证选取信息的科学性。针对麻雀搜索算法初始化种群随机性强,且后期收敛性差的特点,引入混沌Tent映射和非线性惯性因子加以改进,并通过实验验证。针对当前坦克装备火控系统维修现状,提出了一种KPCA-ISSA-SVM的火控系统故障诊断模型,用KPCA进行数据降维,并采用ISSA对SVM核心参数c和g进行寻优,同时与WOA-SVM和PSO-SVM模型进行多次对比试验,验证提出模型有效性,为火控系统其他部件的故障诊断提供参考。
[1]王嫒娜,李英顺,贺喆.D-S证据理论融合粗糙集的火控系统状态评估[J].控制工程,2020,27(12):2176-2184.WANG Aina,LI Yingshun,HE Zhe.D-S Evidence theory fusion rough set for fire control system state evaluation[J].Control Engineering,2020,27 (12):2176-2184.
[2]李英顺,贾薇,周建军.一种坦克火控系统健康状态评估与剩余寿命预测方法[J].火炮发射与控制学报,2020,41(4):93-97,102.LI Yingshun,JIA Wei.ZHOU Jianjun,A method for evaluating the health status and predicting the remaining life of tank fire control systems[J].Journal of Artillery Launch and Control,2020,41(4):93-97,102.
[3]赵丽琴,刘昶,曹明生,等.复杂装备健康度评估方法研究综述[J].计算机测量与控制,2021,29(11):1-7,17.ZHAO Liqin,LIU Chang,CAO Mingsheng,et al.A review of research on health assessment methods for complex equipment[J].Computer Measurement and Control,2021,29(11):1-7,17.
[4]刘奥林,古平,赵张鹏.基于深度学习的数字化装备故障诊断研究综述[J].计算机测量与控制,2024(1):1-15.LIU Aolin,GU Ping,ZHAO Zhangpeng.Review of research on digital equipment fault diagnosis based on deep learning[J].Computer Measurement and Control,2024(1):1-15.
[5]陈元峰,马溪原,程凯,等.基于气象特征量选取与SVM模型参数优化的新能源超短期功率预测[J].太阳能学报,2023,44(12):568-576.CHEN Yuanfeng,MA Xiyuan,CHENG Kai,et al.New energy ultra short term power prediction based on meteorological feature selection and SVM model parameter optimization[J].Journal of Solar Energy,2023,44(12):568-576.
[6]刘运航,宋宇博,朱大鹏.中心修正投影结合IGWO-SVM的滚动轴承故障分类方法[J].振动与冲击,2023,42(24):267-275.LIU Yunhang,SONG Yubo,ZHU Dapeng.Fault classification method for rolling bearings using center corrected projection combined with IGWO-SVM[J].Vibration and Impact,2023,42(24):267-275.
[7]张叶凯,胡亮,丰亚辉,等.基于TSO优化SVM的滚动轴承故障诊断[J].煤矿机械,2023,44(12):168-172.ZHANG Yekai,HU Liang,FENG Yahui,et al.Fault diagnosis of rolling bearings based on TSO optimized SVM[J].Coal Mining Machinery,2023,44 (12):168-172.
[8]李英顺,周通,刘海洋,等.IGWO-SVM在火控系统故障预测中的应用[J].火炮发射与控制学报,2022,43(6):57-63.LI Yingshun,ZHOU Tong,LIU Haiyang,et al.Application of IGWO-SVM in fault prediction of fire control systems[J].Journal of Artillery Launch and Control,2022,43(6):57-63.
[9]李莉云,伍忠东,芦德钊.基于PSO-SVM的硬件木马检测[J].计算机应用与软件,2023,40(6):310-314,336.LI Liyun,WU Zhongdong,LU Dezhao.Hardware trojan detection based on PSO-SVM[J].Computer Applications and Software,2023,40(6):310-314,336.
[10]梁柱,宋小春.WOA-SVM算法在钛合金端铣刀具磨损预测的研究[J].机床与液压,2022,50(15):166-174.LIANG Zhu,SONG Xiaochun.Research on WOA-SVM algorithm for predicting wear of titanium alloy end milling tools[J].Machine Tool and Hydraulic,2022,50(15):166-174.
[11]WU R,HUANG H S,WEI J N,et al.An improved sparrow search algorithm based on quantum computations and multi-strategy enhancement[J].Expert Systems with Applications,2023,215(2):408-421.
[12]TENG Z J,LV J L,GUO L W.An improved hybrid grey wolf optimization algorithm[J].Soft Computing,2019,23(15):6617-6631.
[13]薛建凯.一种新型的群智能优化技术的研究与应用[D].上海:东华大学,2020.XUE Jiankai.Research and application of a new type of swarm intelligence optimization technology[D].Shanghai:Donghua University,2020.
[14]XUE J K,SHEN B.A novel swarm intelligence optimization approach:sparrow search algorithm[J].Systems Science & Control Engineering,2020,8(1):22-34.
[15]吕鑫,慕晓冬,张钧,等.混沌麻雀搜索优化算法[J].北京航空航天大学学报,2021,47(8):1712-1720.LV Xin,MU Xiaodong,ZHANG Jun,et al.Chaotic sparrow search optimization algorithm[J].Journal of Beijing University of Aeronautics and Astronautics,2021,47(8):1712-1720.
[16]CHEN J,SG H,CHANG Y,et al.Gated recurrent unit based recurrent neural network for remaining useful life prediction of nonlinear deterioration process[J].Reliability Engineering &System Safety,2019,185(7):372-382.
[17]张娜,赵泽丹,包晓安,等.基于改进的Tent混沌万有引力搜索算法[J].控制与决策,2020,35(4):893-900.ZHANG Na,ZHAO Zedan,BAO Xiaoan,et al.Improved tent chaotic universal gravitational search algorithm[J].Control and Decision,2020,35(4):893-900.
[18]李英顺,阚宏达,王德彪,等.一种基于KPCA-WOA-SVM火控系统故障诊断方法[J].火炮发射与控制学报,2023,44(4):14-19.LI Yingshun,KAN Hongda,WANG Debiao,et al.A fault diagnosis method for fire control systems based on KPCA-WOA-SVM[J].Journal of Artillery Launch and Control,2023,44(4):14-19.