0 引言
传统RTK(real-time kinematic,RTK)定位方式为了满足定位精度,其基线长度往往不超过20 km[7]。这种约束极大限制了差分定位技术在大区域、高动态目标上面的应用。因此,Wanninger在1995年提出了使用连续运行参考站网(continuously operating reference stations,CORS)的概念,利用多个CORS站观测值,在区域中内插出以电离层延迟为主的误差模型。随后在1997年,Wanninger又提出了虚拟参考站(virtual reference station,VRS)技术,并因其在稳定性、精度与适用范围方面的优势而被广泛使用,现已成为网络RTK/RTD(real-time difference,RTD)的主要技术[2]。在定位目标运动速度较快时,其与卫星的相对运动在径向上的投影会引起载波多普勒频移发生剧烈变化,受GNSS接收机频率跟踪环路限制,容易出现载波跟踪失锁或不满足实时性要求[1]。虽然伪距差分的定位精度相对于RTK较差,但是其具有定位时间短、无需解算模糊度效率高等优势。因此导弹这类高动态目标的实时定位解算并不适合采用相位差分的定位模式,而更宜采用伪距差分的定位模式。
本研究结合网络差分定位的优点和高动态目标的定位需要,使用网络伪距差分的方法,即通过多基准站生成VRS观测值与目标进行伪距差分进而得到定位结果。基于 C++ 设计实现虚拟参考站的融合生成与差分定位算法,结合实测静态数据和弹载GNSS数据验证自研软件融合差分算法的可行性和正确性。
1 虚拟参考站技术
虚拟参考站技术是网络RTK/RTD的一种实现方法。网络RTK/RTD通常由参考站网、数据处理与控制中心、数据通信链路和用户目标等部分组成[7]。如图1所示,参考站网通常至少需要有3个基准站,数据处理与控制中心的主要任务是对各参考站的观测数据进行预处理和质量分析,并对基线进行解算,实时估计参考站网内各种系统误差并建立相应的误差模型,再由数据通信链路传递给用户。数据通信链路可根据实际情况进行设计,通常由两部分构成,一是参考站网与数据处理中心的通信,这一部分属于固定台站之间的通信,为保证通信质量常常采用有线通信;另一部分是数据中心与用户目标之间的通信,这一部分可根据用户所在位置灵活选择。通常基准站会将观测数据以PDXP(packet data exchange protocol,PDXP)协议打包为RTCM(radio technology committee of marine,RTCM)格式发送给数据处理中心,目标也可以通过这种方式将数据发送给处理中心,并进行单点定位获取概略坐标,以NMEA(national marine electronics association,NMEA)格式发送给数据处理中心进而生成虚拟观测值。
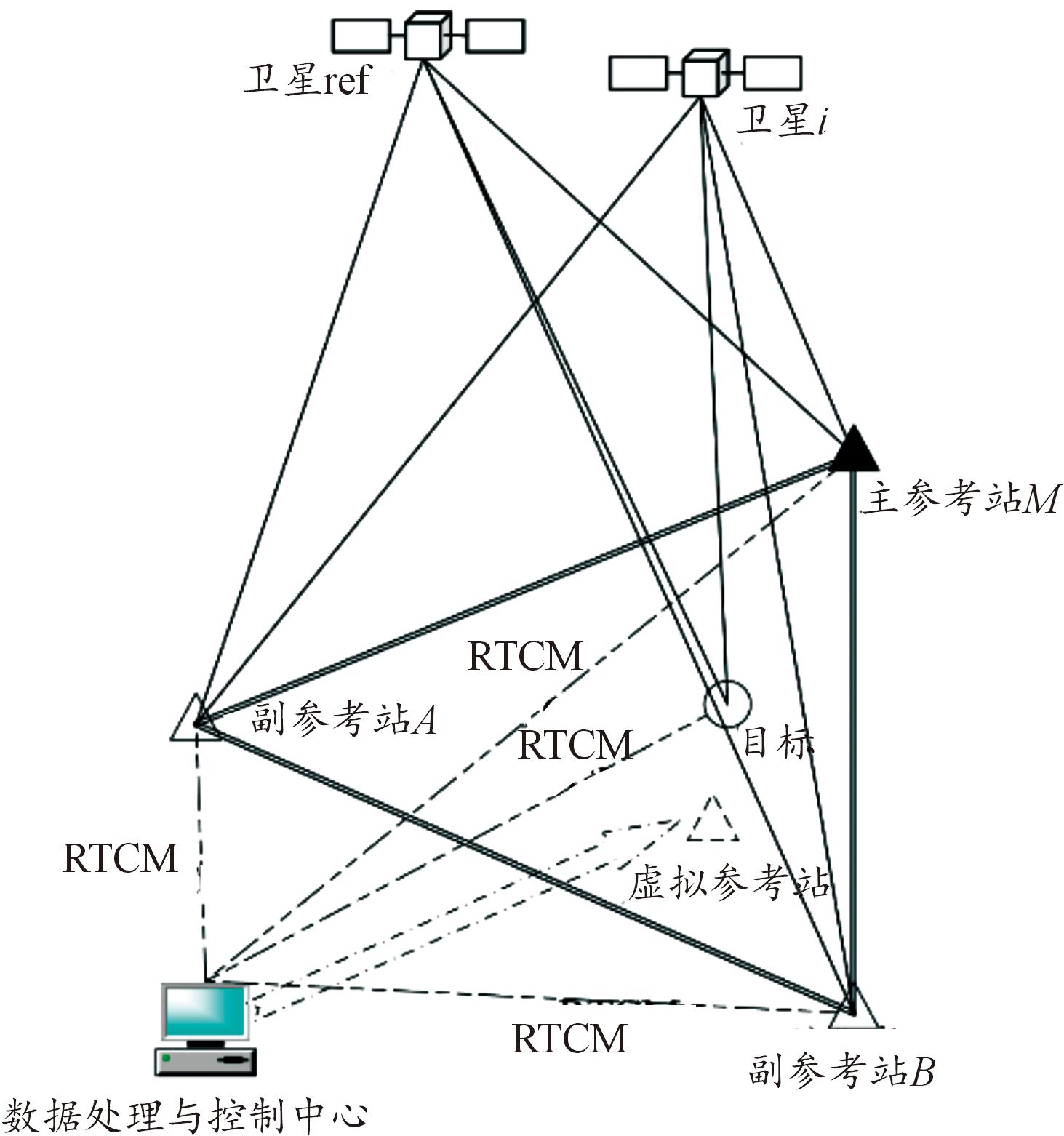
图1 VRS网络结构
Fig.1 The structure of VRS network
1.1 虚拟观测值模型
虚拟参考站技术的大体流程是处理中心实时接收至少3个参考站的观测数据与流动站的概略坐标,并建立区域内空间相关误差模型,包括电离层延迟、对流层延迟以及多路径效应等,结合参考站观测数据、流动站概略坐标与误差模型,生成虚拟参考站观测数据,最后将虚拟参考站观测数据发送给用户进行短基线差分处理[2]。
当只有一个主参考站M与2个副参考站A和B时,基线AM与BM的距离相关误差为
(1)
(2)
虚拟参考站与主参考站的关系与之类似:
(3)
其中: P为伪距观测量,ρ为测站与卫星之间的几何距离,U为参考站间基线的距离相关误差,Δ为站间单差标识,▽Δ为站星双差标识,下标中V为虚拟参考站标识,M为主参考站标识,上标i为卫星号标识,ref表示参考卫星。主参考站原则上选定为各参考站中定位精度较高的参考站,通常使用距离流动站较近的参考站。对流层和电离层的单差改正项通常使用主参考站与副参考站的双差观测值内插展开而得到[7]。
将式展开可以得到
(4)
由公式对应关系,可以得到非差伪距观测模型:
(5)
(6)
即虚拟参考站的生成需要一个主参考站的观测值,并在主参考站观测值的基础上加入站间单差改正。
1.2 几何相关改正
因为接收机t时刻接收到的信号是t-τ时刻从卫星中发出来的,所以由于虚拟参考站与主参考站所对应的空间位置不同,卫星信号传播到两参考站的时刻也不同,相应时刻的卫星位置也会有所差异。对于长基线双差几何项,这种影响会产生分米级的误差。
另外,由于卫星运动和地球自转的差异性,在信号传递过程中,地球因旋转一定角度而导致卫星发出信号时的地心地固坐标发生变化,并对主参考站和虚拟参考站的观测产生影响,需要在计算Δ ρ项时考虑地球自转影响[2]:
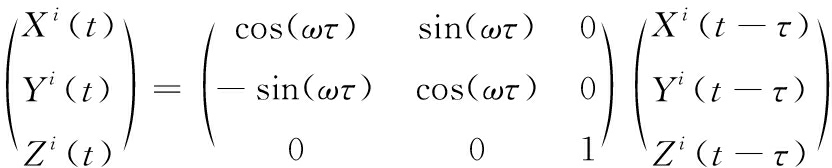
(7)
其中: ω为地球自转角速度。Xi、Yi和Zi表示卫星i在地心地固系下的坐标。
1.3 线性内插模型
线性内插模型(linear interpolation model,LIM)是Wanninger于1995年提出的用于生成内插改正数的模型方法。在目前常用的几种内插算法中,该算法精度较高,尤其是对电离层的改正建模效果明显[11]。其线性模型如下所示:
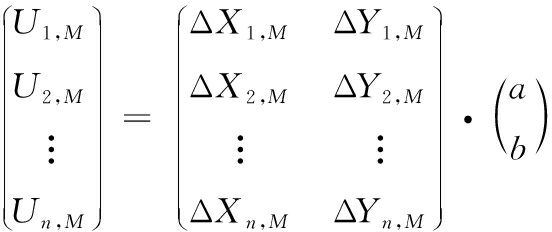
(8)
其中:下标1,2,…,n表示n个副参考站,ΔXi,M和ΔYi,M分别表示第i个副参考站于主参考站M的平面坐标之差,a和b分别为相应的内插系数。当副参考站数量不少于2个时,可以使用最小二乘法平差计算求得内插系数a和b的值:
p=(ATA)-1ATU
(9)
其中:
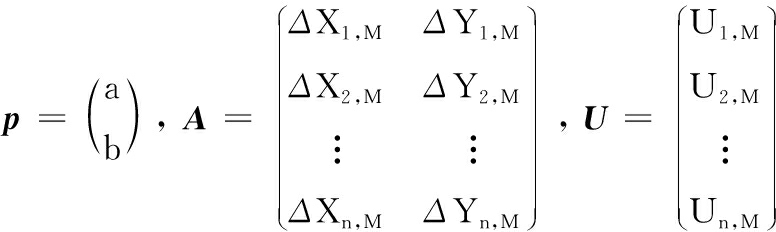
(10)
2 流动站差分定位
2.1 短基线双差观测模型
在生成虚拟参考站之后,目标与虚拟参考站之间构成短基线可进行单站双差定位。同样有双差观测方程:
(11)
其中:下标R为流动站标识。对于短基线,双差改正项
通常可以忽略[2],虚拟参考站与卫星之间的几何距离可通过目标在该时刻给出的单点定位结果求得,进而求得流动站的改正数。
而在具体实现中,需要考虑流动站的采样率与系统的差异。对于站间差分,虚拟观测站的采样率若与流动站不同,为保证解算精度,需要使用最小的差分龄期,并对差分龄期设定阈值。而不同导航系统之间的接收机信号群延迟不同,所以即便来自不同系统的信号频率相同,也不可进行星间差分。
2.2 扩展卡尔曼滤波
对于处于非线性系统的动态目标,适合使用扩展卡尔曼滤波(extended kalman filter,EKF)进行位置解算。
设在历元时刻tk的观测向量为yk,满足:
(12)
(13)
(14)
其中:
和Pk分别为历元时刻tk的状态向量估值及其协方差矩阵,上标-和+分别为EKF观测更新前和更新后的标识。h(x)、H(x)和Rk分别表示观测模型向量、偏导数矩阵和测量误差的协方差阵,Kk为卡尔曼增益矩阵。
状态向量与其协方差阵的EKF预测表达式为:
(15)
(16)
其中:
和
分别为从历元tk到历元tk+1的状态转移矩阵和系统过程噪声协方差矩阵[11]。
2.3 短基线的EKF更新与预测
现有共视卫星数目n+1,对于卫星某一频率信号f有:
(17)
H(x)=-DE
(18)
R=DRfDT
(19)
其中: D为星间单差矩阵,E为包含接收机指向卫星在地心地固系下方向向量的矩阵,Rf为对于频率f的测量误差协方差阵:
(20)
(21)
(22)
其中:
为卫星i的f信号伪距测量标准差,e表示地心地固系下接收机至单星的方向向量。
对于EKF预测表达式,设接收机为m频观测,状态转移矩阵和过程噪声协方差阵设置如下:
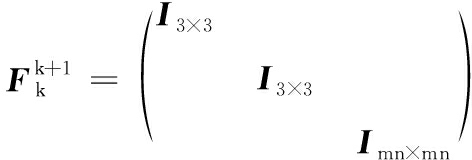
(23)
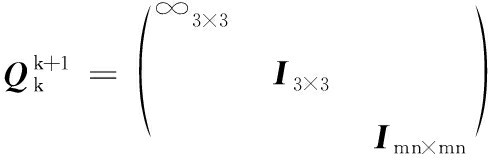
(24)
为了避免无穷大的过程噪声造成的数值不稳定性,接收机位置状态通常会在每个历元设置为一个先验值,并将相应的过程噪声设置为一个较大的值。这个先验值通常可以使用单点定位的处理结果。
3 实测数据分析
结合上述原理和方法,本研究使用 C++程序开发和实现一套具备网络RTD处理功能的软件,并基于实测数据对自研软件处理性能进行系统验证。首先,为验证软件模型算法的正确性,使用已知坐标的CORS站静态数据进行解算,将RTD差分定位结果和其高精度坐标进行比对进行对比。考虑到高动态目标位置难以精确测定,且尚无目标高速运动的真实坐标,其他测量手段的测量精度相比于GNSS定位并无显著优势。因此,对于高动态目标的精度评价以内符合精度为主,其他设备解算得到的综合轨迹作为外符合参考值。
3.1 静态数据验证
静态数据采用香港卫星定位参考站网的RTCM格式实时数据流。自2010年起,香港卫星定位参考站不间断全天候提供高精度定位数据。目前为止,已有18个CORS站投入使用,支持GPS、GLONASS、GALILEO及北斗等全球卫星导航系统的信号。这些实时原始数据流为公开信息,用户可以通过NTRIP配以适当端口设定便可获取。
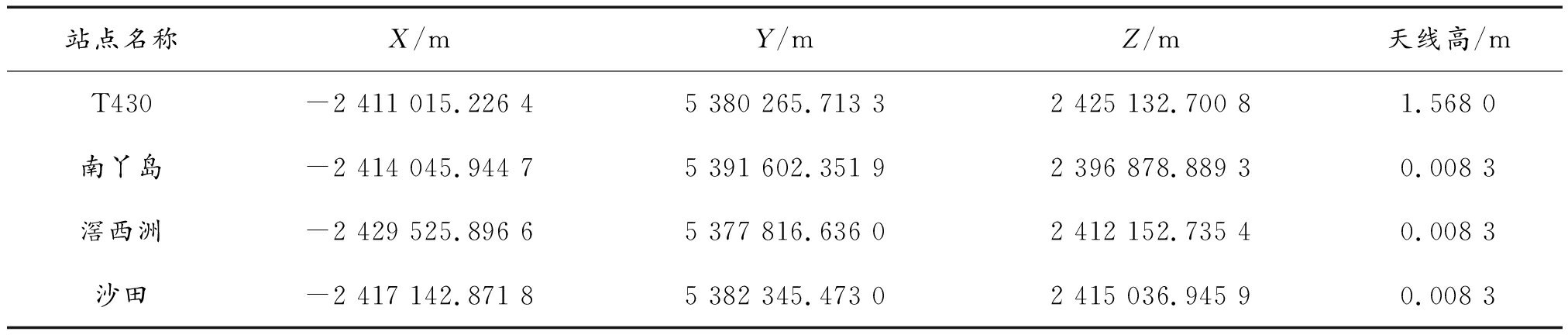
本次定位算法验证所选择的参考站为T430、南丫岛和滘西洲,流动站选用沙田,其分布在图2所示的香港地图中标出,参考站之间的基线长度也在图中标出。各站点信息见表1。定位使用各接收机收到的广播星历,卫星截止高度角取15°,各系统采用高度角定权方法,取GPS系统和北斗系统的误差因子为1.0,GLONASS系统的误差因子为1.5。根据接收机各个系统使用双频模式,GPS使用L1、L2信号,GLONASS使用G1、G2信号,北斗系统使用B1、B2信号。
表1 测站位置信息
Table 1 The information of the stations
站点名称X/mY/mZ/m天线高/mT430-2 411 015.226 45 380 265.713 32 425 132.700 81.568 0南丫岛-2 414 045.944 75 391 602.351 92 396 878.889 30.008 3滘西洲-2 429 525.896 65 377 816.636 02 412 152.735 40.008 3沙田-2 417 142.871 85 382 345.473 02 415 036.945 90.008 3
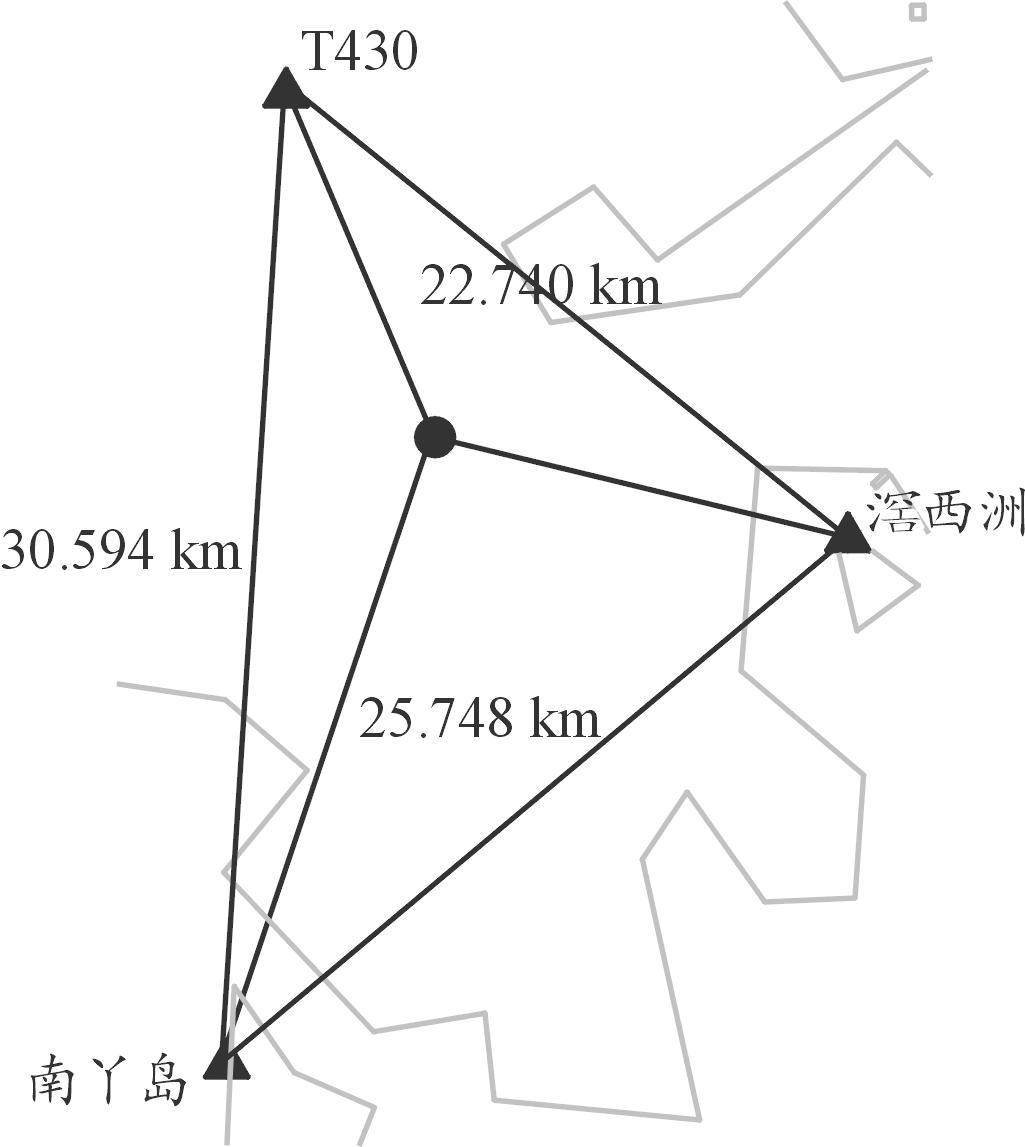
图2 静态定位基线示意图
Fig.2 The baselines in static mode
对于使用的数据,4个站点的采样率为1 Hz,观测时间选择UTC 2022年11月6日00∶00∶00—06∶00∶00的时间段,使用GPS、GLONASS和北斗三系统。解算过程中,共视卫星数不少于20,PDOP值不超过1.5,数据完整率良好,未出现丢包的情况。解算结果的伪距残差如图3所示,坐标误差如图4所示,可以看到,以沙田的真坐标为原点建立的站心坐标系中,E、N和U方向定位结果分别可达0.257、0.146、0.267 m,三维均方根误差为0.398 m。这个结果符合伪距差分定位的分米级定位精度。
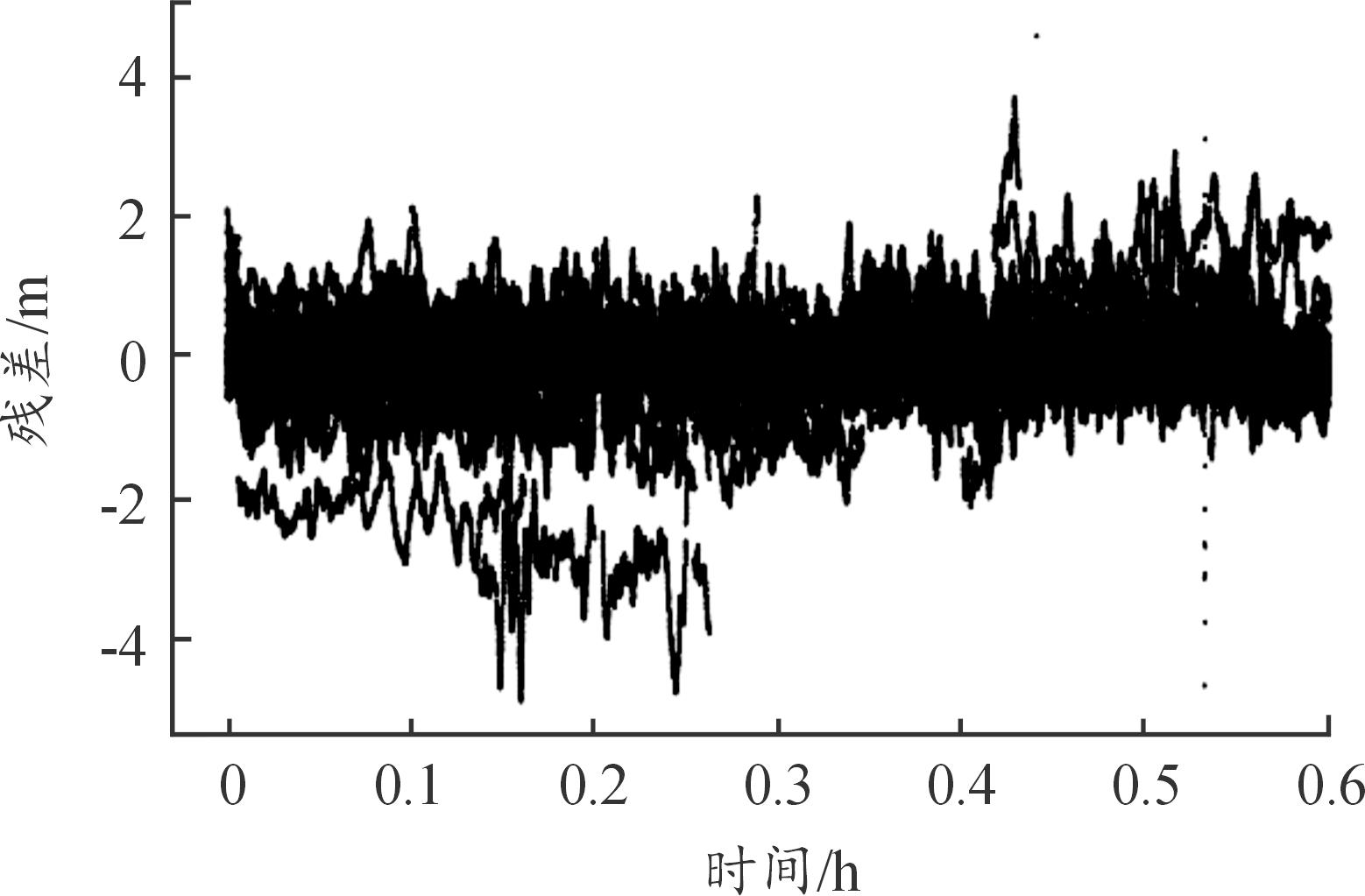
图3 静态站的伪距残差
Fig.3 The pseudorange residual of the static station
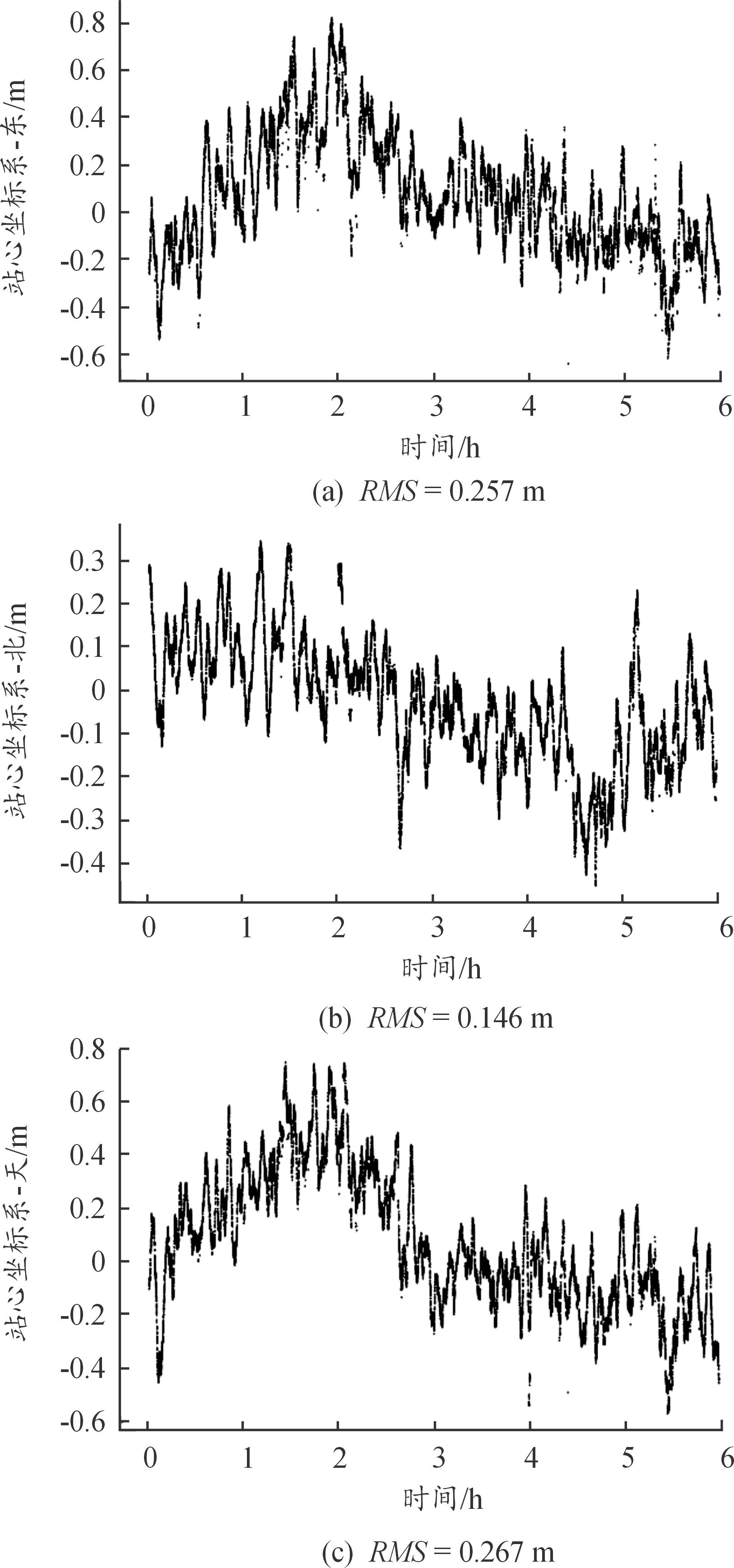
图4 静态站坐标误差
Fig.4 The error of the static position
3.2 动态数据测试
对于高动态目标,其所在环境与自身特性导致相应数据质量的大幅度降低。高动态目标运动速度大,且当飞行高度距离地面站较高时,大气环境随高程的变化幅度远大于水平距离的变化,目标所在位置的大气状况与地面参考站已有明显不同,参考站间基线的空间误差相关模型很难真实反映目标的改正信息。且在实测数据中,实时数据流存在丢包的现象,地面参考站的数据采样率与目标的采样率也不相同。
地面参考站相对位置关系如图5所示。参考站间基线长度不超过150 km,2条基线夹角不超过165°。地面参考站采样间隔为30 s,目标采样间隔为0.2 s。目标运动时间总长度约7分16.2秒。考虑数据完好性,选择其开始运动后7 s至结束前30 s数据。蓝色实线为目标投影在平面上的运动轨迹,其在水平方向的投影向南移出图示范围。目标接收机支持GPS和北斗二代系统信号。伪距残差如图6所示,每一历元的中误差如图7所示,取发射点为站心坐标系原点,目标在站心坐标系下E、N、U方向的分量分别用红色、绿色和蓝色表示。从图8可以看出,位置中误差与卫星数量联系紧密,左侧纵轴为可用共视卫星数量,在图中用黑色图线表示,当卫星数不少于6颗时,三维空间的定位中误差不超过2.75 m;右侧纵轴为三维空间中的中误差,在图中用红色图线表示。对应的PDOP随时间分布如图9所示,可以看到,随着动态目标远离地面参考站后,共视卫星的PDOP呈现增加的趋势。
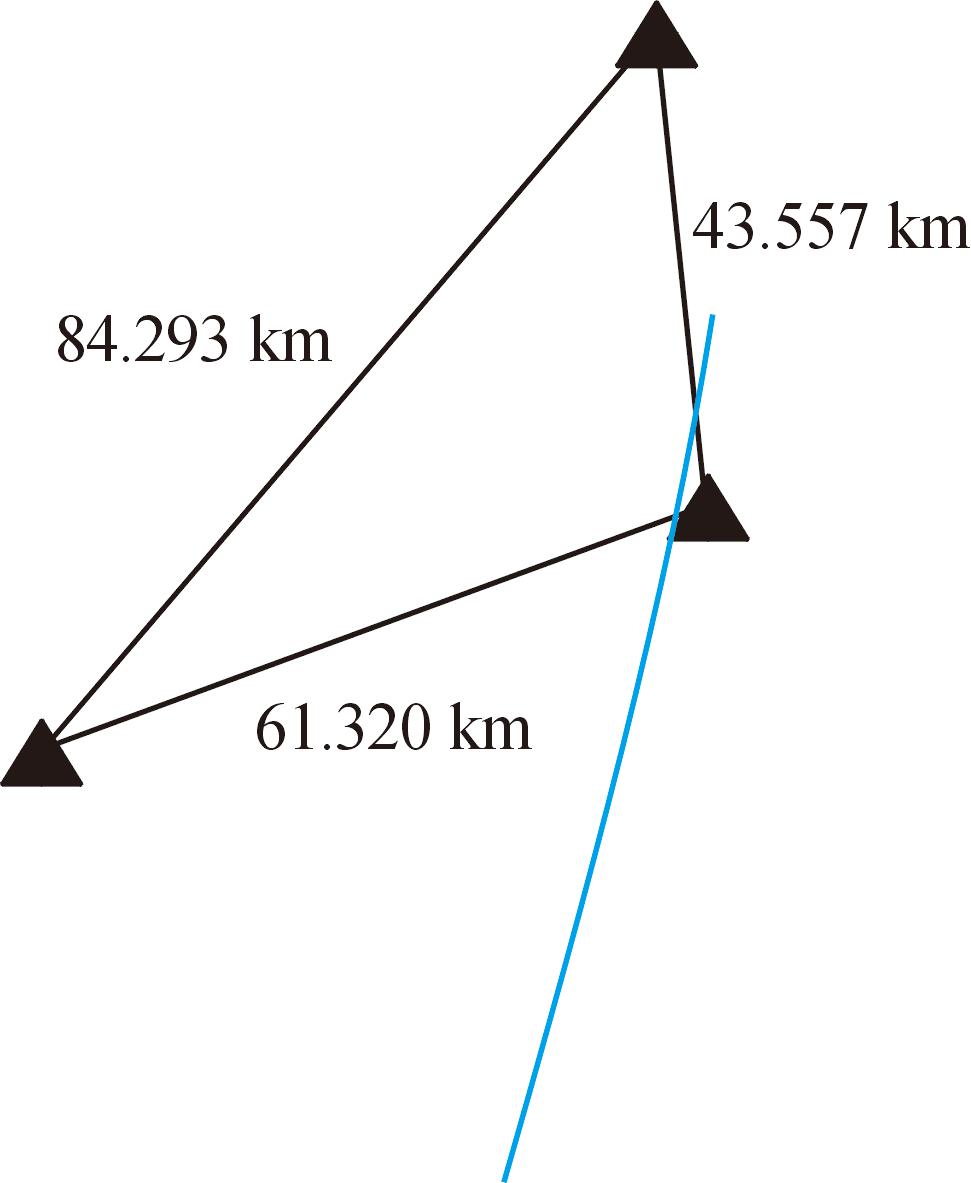
图5 动态目标所用基线
Fig.5 The baselines of the kinematic target
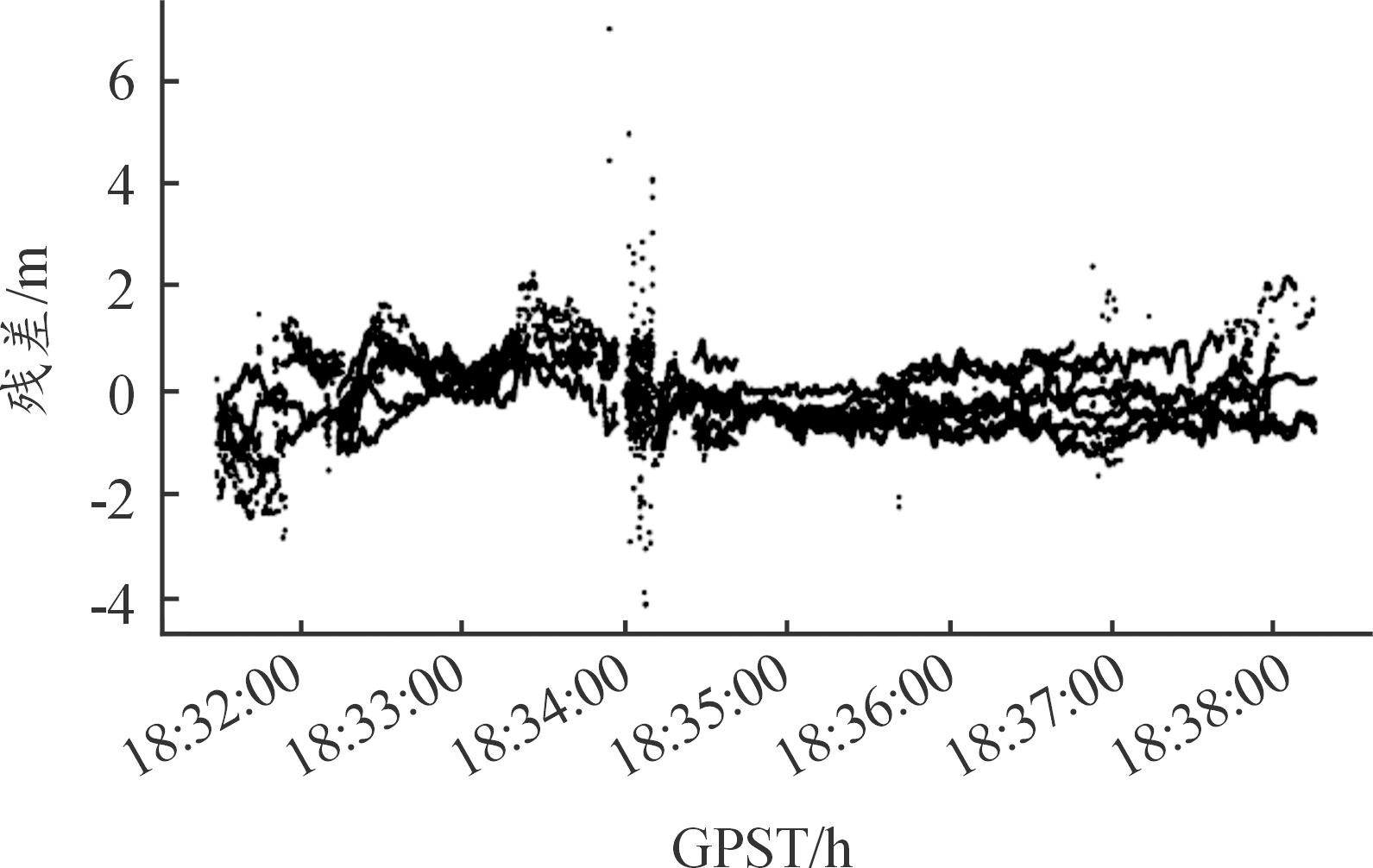
图6 动态目标的伪距残差
Fig.6 The pseudorange residual of the kinematic target
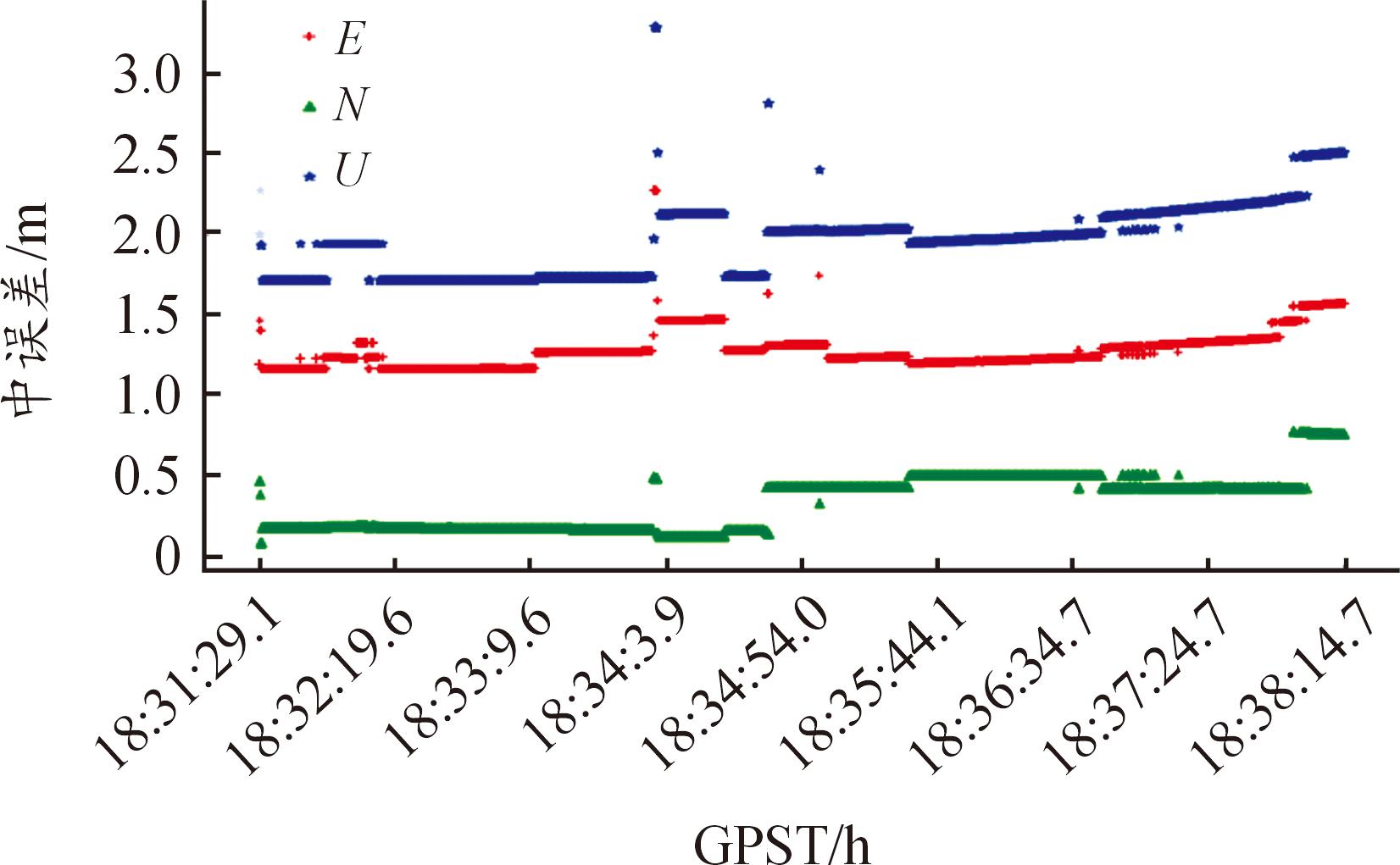
图7 动态目标的位置中误差
Fig.7 The standard deviation of the kinematic target
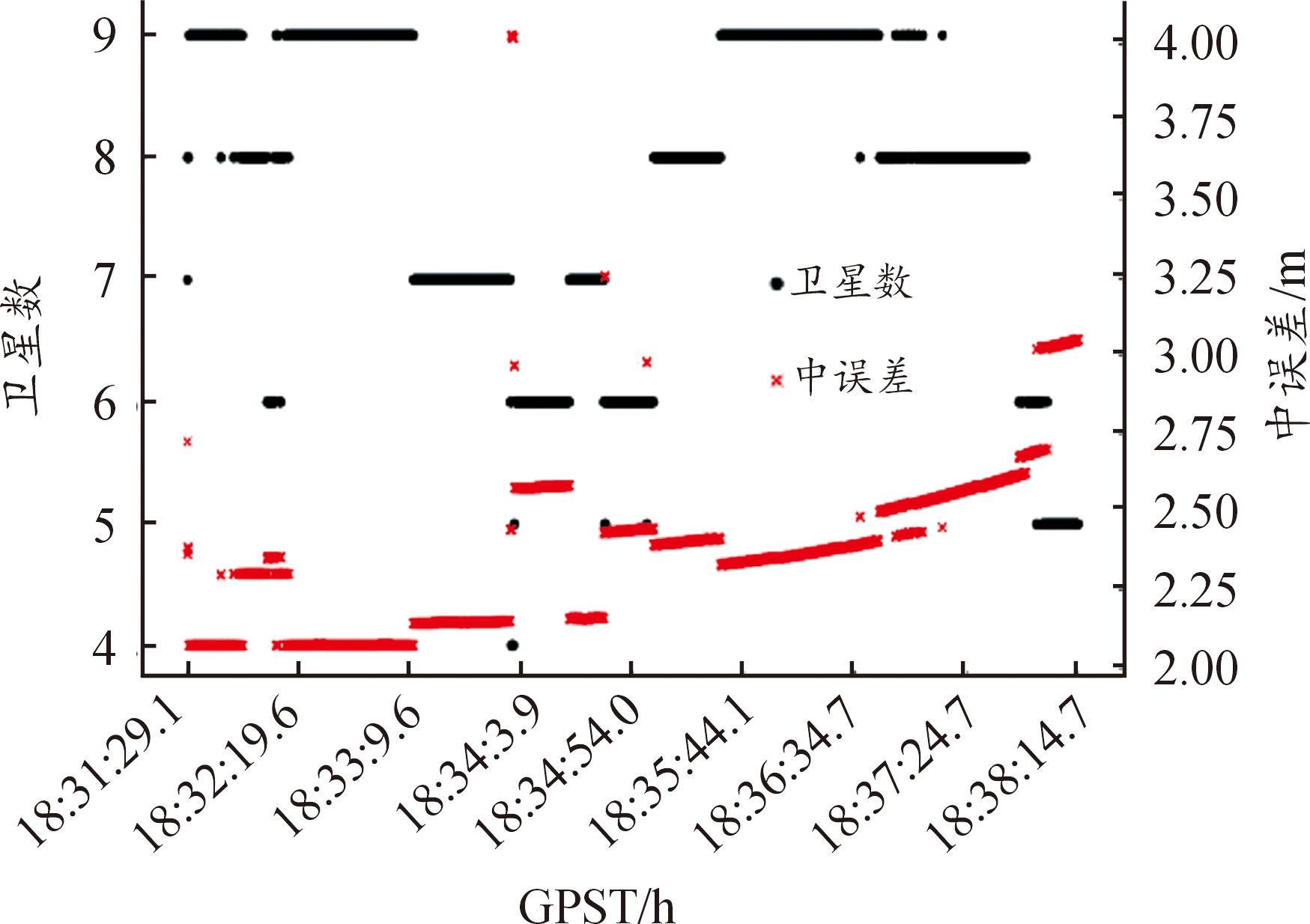
图8 共视卫星数与中误差时间分布
Fig.8 Common visible satellite number and standard deviation distribution in time field
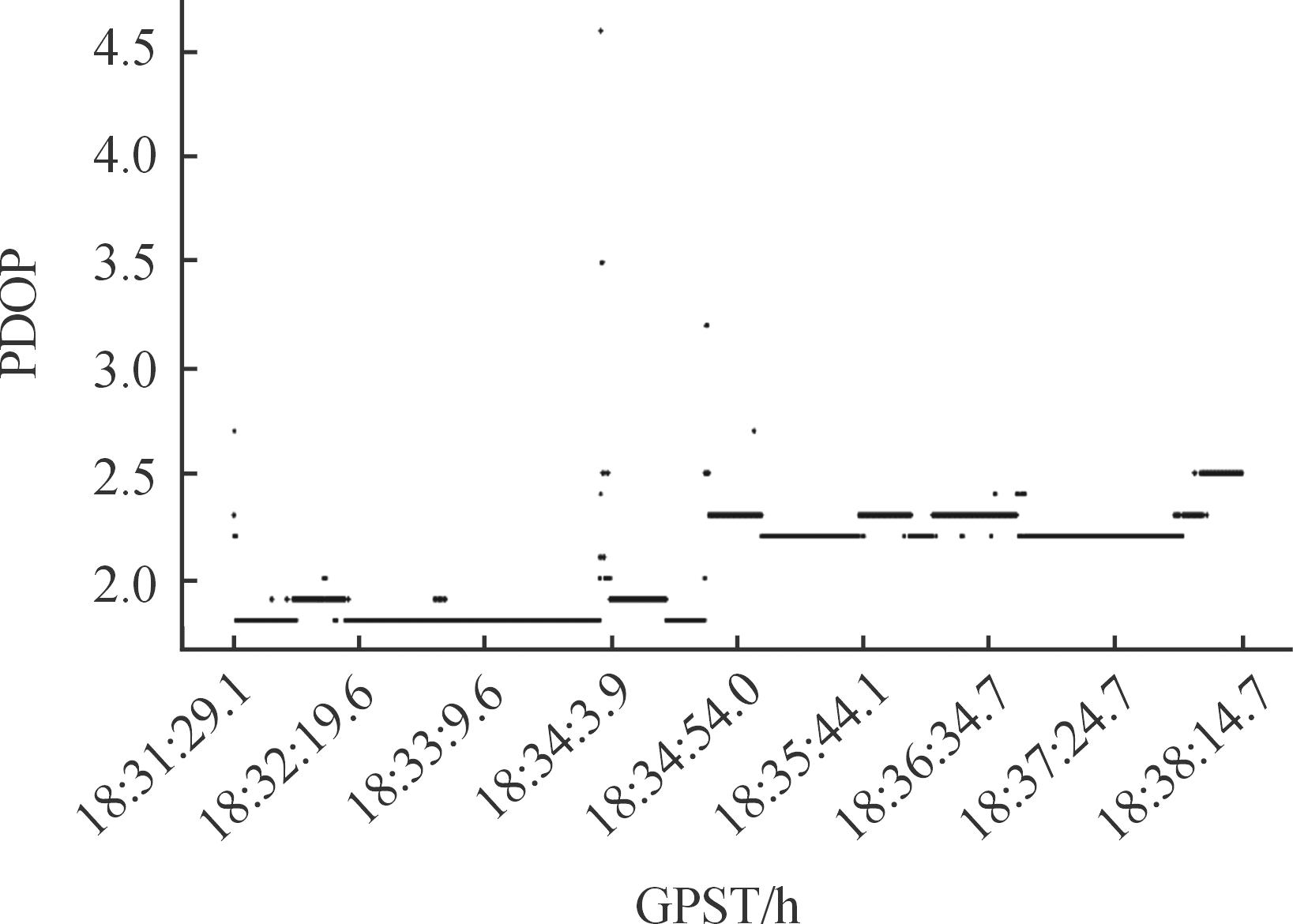
图9 PDOP分布图
Fig.9 The distribution of PDOP in time field
在目标的实际运动过程中,现场尚有光学雷达、测速雷达等其他外测手段对目标进行跟踪,通过选取不同阶段所适用的外测数据,可以拼接生成综合轨迹,综合轨迹的精度在2～10 m范围内。通过与融合差分解算轨迹进行对比,可以得到对比结果如图10所示。
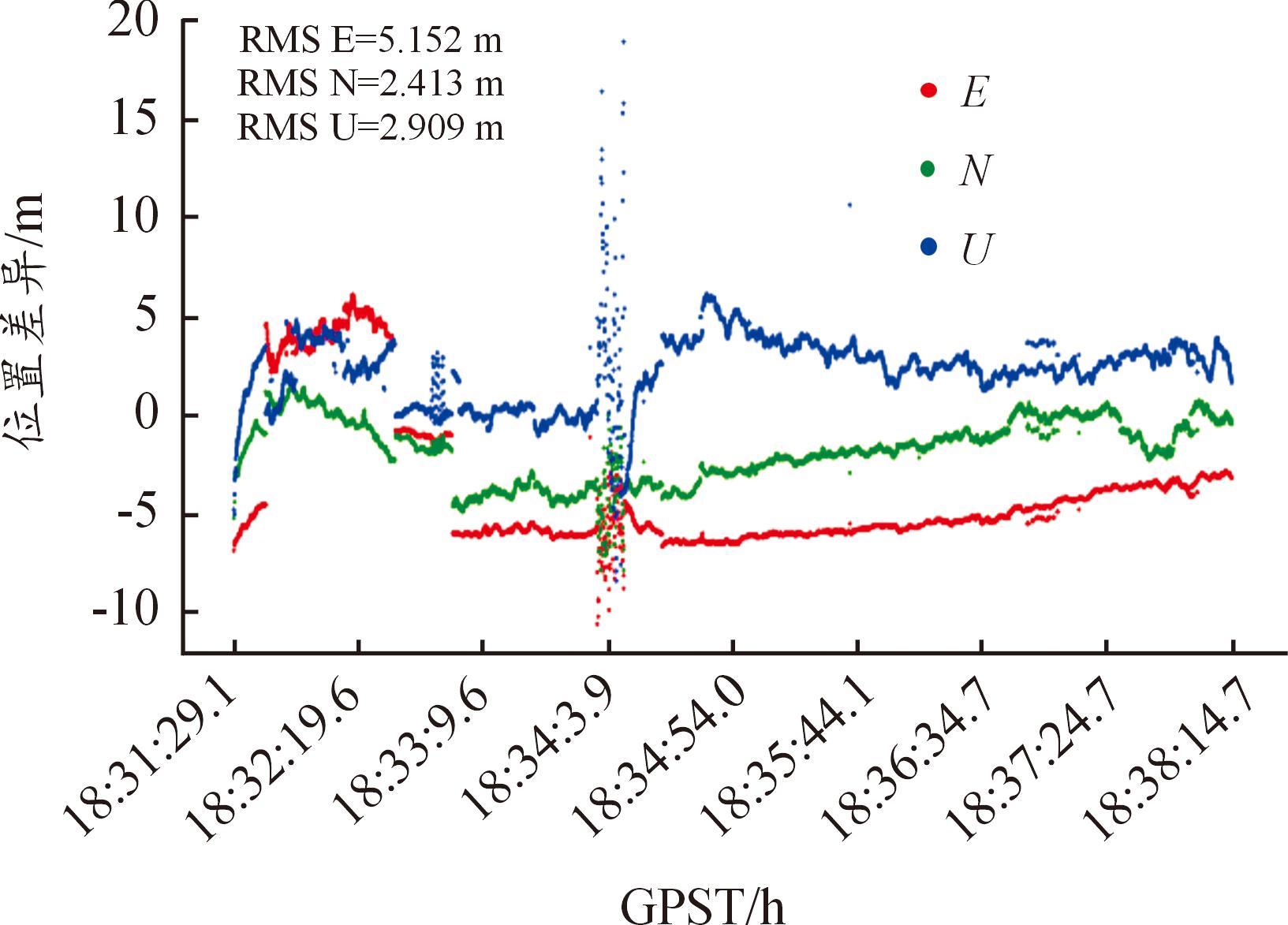
图10 其他设备数据对比
Fig.10 Comparing with the data from other equipments
从图10中可以看到,融合差分与综合轨迹数据在3个方向上对比,得到的均方根值均为米级,三维空间位置互差均方根值为6.390 m。考虑到综合轨迹的测量误差为米级,相较于GNSS并无绝对优势,该结果主要用于参考。另可注意到在大约18:34:3.90时刻左右,互差位置存在突变。结合图7和图8可以看出,该处剧烈变化源于共视卫星数量骤减至4,即刚好满足定位解算需要。而该时刻之所以观测卫星数减少,是因为目标在该时刻存在机动行为。此外,在目标运动后期,卫星数量存在下降的趋势,PDOP也有上升的趋势,这与目标的运动路线和路线上测站分布较少存在一定关系。这些因素体现了GNSS这种定位方式对共视卫星数量的依赖,是GNSS定位的局限性。随着弹载接收机的更新换代,以及各基地的军用地面参考站建设的完善,网络RTK/RTD的相关局限性也将得到一定程度的完善。
4 结论
1) 通过静态数据定位验证,说明了虚拟参考站生成与网络伪距差分算法的正确性与可行性。同时也证实了网络伪距差分具有分米级的定位精度。
2) 结合实测高动态数据的解算结果,定位精度与目标及参考站的共视卫星数高度相关。当共视卫星个数不少于6颗时,其定位中误差不超过2.75 m,高动态目标受共视卫星数目影响相比静态目标在网络伪距差分的定位模式中存在巨大的精度衰退。
3) GNSS定位模式相较于其他外测手段具有一定的局限性,通过对算法的完善、接收机的迭代和地面参考站的建设,网络伪距差分方法在高动态目标实时解算仍具有很高的提升空间。
[1]汪文韬,申宇瑶,王永庆,等.高动态场景下GNSS信号自适应载波跟踪算法[J].中国科学:物理学 力学 天文学,2021,51(1):179-186.WANG Wentao,SHEN Yuyao,WANG Yongqing,et al.Adaptive carrier-tracking algorithm for global navigation satellite system signals in high dynamic scenarios[J].Science China Physics,Mechanics &Astronomy,2021,51(1):179-186.
[2]张绍成.基于GPS/GLONASS集成的CORS网络大气建模与RTK算法实现[D]. 武汉:武汉大学,2010.ZHANG Shaocheng.The GPS/GLONASS integrated CO-RS network atmosphere modeling and RTK algorithm implementation[D].Wuhan:Wuhan University,2010.
[3]张晶晶,陈现春,秘金钟,等．BDS /GPS 格网虚拟化伪距差分和伪距改正数差分的差异化实现[J].测绘通报,2018(12):83-86．ZHANG Jingjing,CHEN Xianchun,MI Jinzhong,et al.Realization of BDS/GPS grid virtual pseudorange differential positioning and pseudorange correction differential positioning[J].Bulletin of Surveying and Mapping,2018(12):83-86.
[4]余梦洋.BDS/GPS网格伪距差分服务及移动终端实时定位算法研究与实现[D].青岛:山东科技大学,2018.YU Mengyang.Research and implementation of BDS/GPS mesh pseudorange difference service and mobile terminal real-time location algrithm[D].Qingdao:Shandong University of Science and Technology,2018.
[5]陈振.BDS/GPS网络伪距差分定位方法研究[D].北京:中国测绘科学研究院,2016.CHEN Zhen.Research on BDS/GPS network pseudo-range differential global navigation satellite system[D].Beijing:Chinese Academy of Surveying and Mapping,2016.
[6]周万振,秘金钟,李得海,等.BDS/GPS伪距差分改正数3种内插方法的比较[J].导航定位学报,2017,5(2):79-85.ZHOU Wanzhen,MI Jinzhong,LI Dehai,et al.Comparison between three interpolation methods of BDS/GPS pseudo-range differential correction[J].Journal of Navigation and Positioning,2017,5(2):79-85.
[7]张晶晶.BDS网络RTK虚拟参考站数据生成的算法研究[D].北京:中国测绘科学研究院,2014.ZHANG Jingjing.Algorithm of Generating VRS data for compass navigation system[D].Beijing:Chinese Academy of Surveying and Mapping,2014.
[8]曹宇剑.基于CORS的移动RTD及其精度评测方法[D].西安:西安科技大学,2020.CAO Yujian.Research on accuracy evaluation method of mobile RTD based on CORS[D].Xi’an:Xi’an University of Science and Technology,2020.
[9]杜文选.基于GNSS的VRS技术算法研究[D].淮南:安徽理工大学,2018.DU Wenxuan.The VRS technology algorithm research based on GNSS[D].Huainan:Anhui University of Science and Technology,2018.
[10]冷宏宇.基于GNSS基准站网的格网化动态定位算法及软件实现[D].阜新:辽宁工程技术大学,2021.LENG Hongyu.Grid-based dynamic positioning algorithm based on GNSS reference station network and its software implementation[D].Fuxin:Liaoning Technical University,2021.
[11]徐宏宇,王浩,王尔申.基于扩展卡尔曼滤波的GPS定位数据处理方法研究[J].科学技术与工程,2012,12(31):8137-8142.XU Hongyu,WANG Hao,WANG Ershen.Research of GPS positioning data processing based on extended Kalman filtering[J].Science Technology and Engineering,2012,12(31):8137-8142.
[12]邢旺.网络RTK虚拟参考站的数学模型研究[J].舰船电子工程,2018,38(8):42-45.XING Wang.Research of mathematical model based on virtual reference station in Network RTK[J].Ship Electronic Engineering,2018,38(8):42-45.
[13]CHEN X.A study of GPS/GLONASS multiple reference station technique for precise real-time carrie phase-based positioning[C]//Proc.of ION GPS-2001 Meeting.2001.
[14]WANNINGER L.Virtual reference stations for centimeter-level kinematic positioning[C]//Proceedings of the 15th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GPS 2002).2002:1400-1407.
[15]JONGRUJINAN T,SATIRAPOD C.Stochastic modeling for VRS network-based GNSS RTK with residual interpolation uncertainty[J].Journal of Applied Geodesy,2020,14(3):317-325.
[16]VOLLATH U,LANDAU H,CHEN X.Network RTK-concept and performance[C]//Proceedings of the GNSS Symposium,Wuhan,China.2002:27-30.
[17]WANNINGER L.Real-time differential GPS error modelling in regional reference station networks[M]//Advances in Positioning and Reference Frames:IAG Scientific Assembly Rio de Janeiro,Brazil,September 3-9,1997.Berlin,Heidelberg:Springer Berlin Heidelberg,1998:86-92.
[18]INAL C,BULBUL S,BILGEN B.Statistical analysis of accuracy and precision of GNSS receivers used in network RTK[J].Arabian Journal of Geosciences,2018,11:1-8.
[19]WANNINGER L.Virtual reference stations (VRS)[J].Gps Solutions,2003,7(2):143-144.
[20]ZHANG Z,GENG C,CHEN D.Research on virtual reference station (VRS) technology and differential correction information[C]//Journal of Physics:Conference Series.IOP Publishing,2021,1915(4):042068.