0 引言
航天运载器是进入太空空间的重要工具,也是开发空间资源的基础。目前航天运载器存在运输成本高、可靠性差等问题,难以满足大规模空间开发的需求[1]。因此,发展成本低、可靠性高的单级入轨技术成为改进空间交通运输能力的首选方向[2]。
单级入轨可通过预冷混合动力发动机(SABRE)[3]、火箭基组合循环推进系统(RBCC)[4]、混合推进(MAV)[5]、高度补偿喷管[6]等途径实现。其中,高度补偿喷管技术较之其他技术对航天器的适应性好、经济高效、对系统的影响较小、风险可控性强。高度补偿喷管能够比传统喷管适应更加宽泛的工作高度范围。传统喷管在工作中产生的非适应性损失较为严重可达15%[7],高度补偿喷管能有效减少传统喷管的该部分损失,提高大扩张比喷管的低空推力性能,从而拓宽喷管的最佳工作高度范围。
典型的具有高度补偿效果的先进喷管有双钟型喷管、延伸喷管、双模态喷管、塞式喷管、膨胀偏流喷管、通风喷管和缝隙喷管[8]。各种喷管的高度补偿机制有所不同,双钟型喷管[9]的特殊型面为喷管工作过程提供了两个膨胀比,可以使其在两个不同的工作高度达到最佳推力性能。延伸喷管[10]和双模态喷管[7]利用外部伺服机构或利用特定燃烧室的启/停对喷管膨胀比进行主动控制。塞式喷管[11]和膨胀偏流喷管[12]在工作高度上升过程中存在开放与闭合2种工作模态,靠喷管流动特性的变化来进行高度补偿。与前述喷管的设计概念不同,通风喷管[13]和缝隙喷管[14]关注的重点在于解决过膨胀状态下的壁面处回流和流动分离问题。这2种喷管强迫流动分离在通风孔或狭缝处发生,以减小原有喷管内部回流造成的阻力以及流动分离带来的不稳定侧向载荷。然而,各种高度补偿喷管也存在各自明显的缺点,如延伸喷管额外的作动机构可能会带来额外重量,双钟型喷管侧向载荷较大且在工作模态转化时会使得喷管推力骤降。因此,发展新型的高度补偿喷管变得尤为重要。
可渗透壁自适应高度补偿喷管(可渗透喷管)是一种新型先进喷管,这种喷管外形与传统喷管一致,但扩张段部分区域采用多孔介质材料,从而使得喷管部分壁面具有渗透性。与其他高度补偿喷管相比,可渗透喷管不改变型面、结构简单且轻便,同时保证良好的高空性能,灵巧地避免了其他现有高度补偿喷管的缺点。当飞行高度较低时,喷管壁面内外的压差较大,外界高压大气通过可渗透段进入喷管内部,提高喷管内壁面压强,减缓或改善大扩张比喷管内部过膨胀现象,从而提高发动机推力。喷管内外气体压差随着飞行高度变化而变化,但可渗透喷管始终通过压差调节喷管内壁面压强,从而改变喷管内部流场结构,实现喷管内流动状态与飞行高度的匹配。可渗透喷管利用这种自适应调节机理获得连续的高度补偿能力。当飞行高度超过一定高度时,外界大气压强小于可渗透喷管内燃气压强,但二者压差较小,喷管内会有燃气的微量泄出,从而对喷管的高空推力造成负面影响。
可渗透喷管从低海拔向高海拔飞行的过程中,其内部流场结构与推力性能表现将随飞行高度发生变化。为充分揭示可渗透喷管的动态工作特性,本文选取一定落压比范围,建立可渗透喷管瞬态数值模拟模型,对可渗透喷管的波系结构演化与推力性能进行分析,定量反映出可渗透喷管内流场与推力性能的变化规律。
1 物理模型及数值方法
1.1 物理模型
为提高计算的效率,本文使用轴对称模型如图1所示,喷管型面参数如表1所示。
表1 可渗透喷管几何参数
Table 1 Permeable nozzle geometric parameters
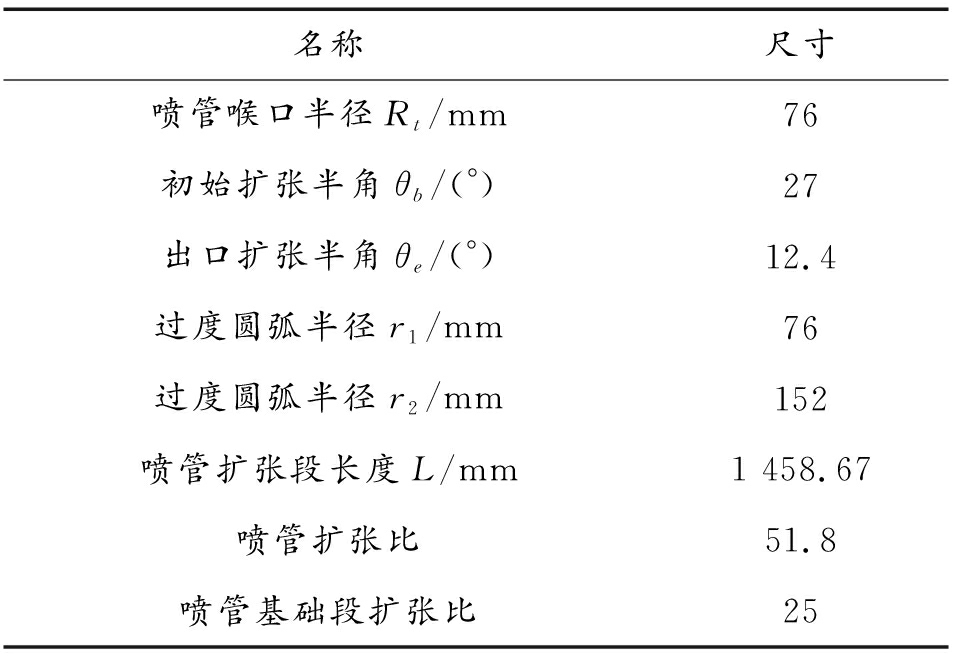
名称尺寸喷管喉口半径Rt/mm76初始扩张半角θb/(°)27出口扩张半角θe/(°)12.4过度圆弧半径r1/mm76过度圆弧半径r2/mm152喷管扩张段长度L/mm1 458.67喷管扩张比51.8喷管基础段扩张比25
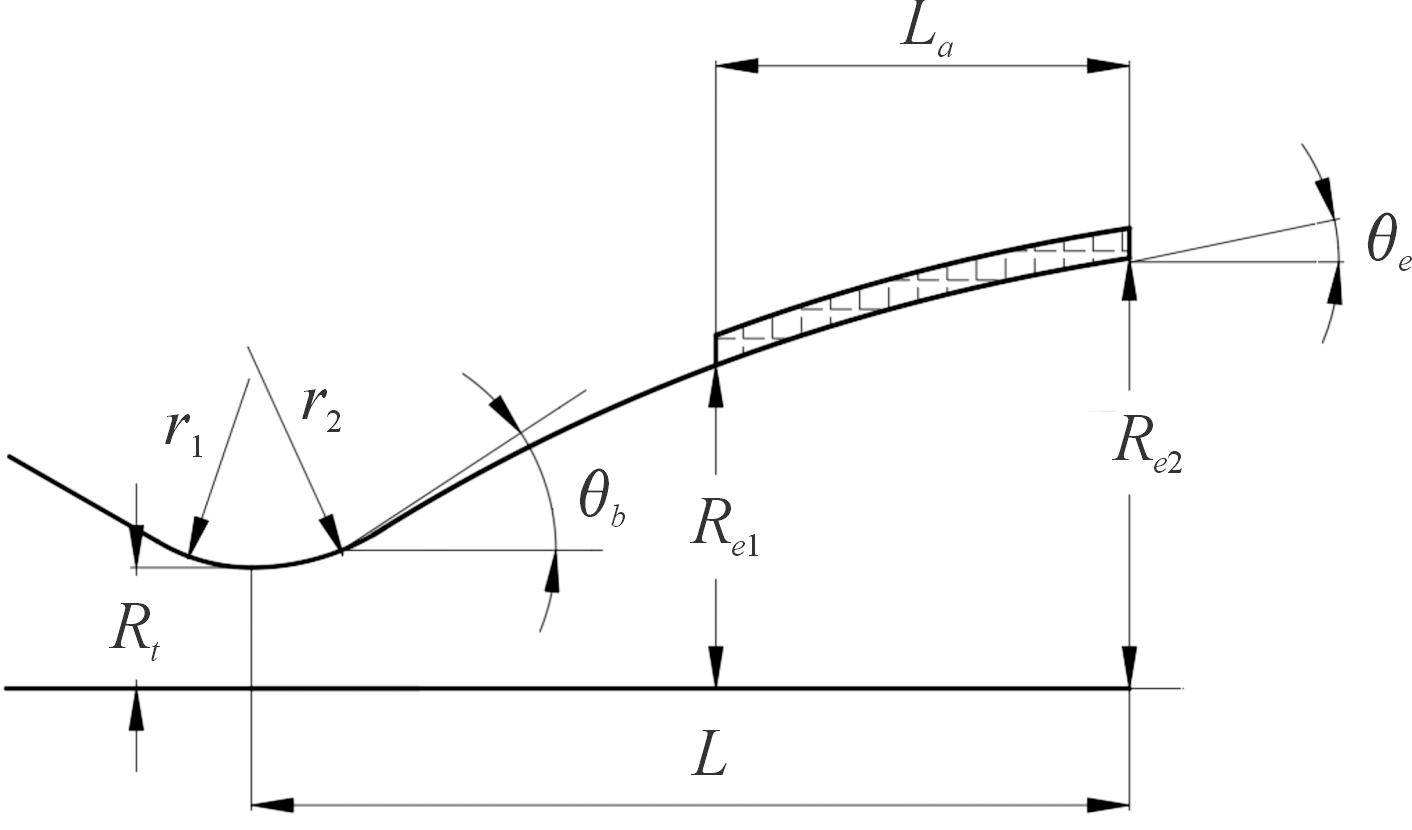
图1 喷管模型示意图
Fig.1 Schematic diagram of the nozzle model
1.2 数值方法
基于FLUENT平台进行,利用雷诺平均纳维-斯托克斯方程组对喷管流场进行求解从而捕捉喷管的流场信息,仿真过程采用SST k-ω湍流模型[15]和AUSM空间离散格式[16]。SST k-ω湍流模型在定义湍流粘度时考虑了湍流剪切应力,模型精度高,能够准确捕获喷管内可能出现的激波间断导致流动严重分离的情况。
本文模拟火箭发动机从地面上升的工作状态,工况选择NPR范围为38.49~670,其中,NPR表示燃烧室压强Pc与环境压强Pa之比,计算公式为![]()
令工作时间为0.4 s,选取5个典型工况,各相邻典型工况间工作时间为0.1 s,NPR具体变化规律为
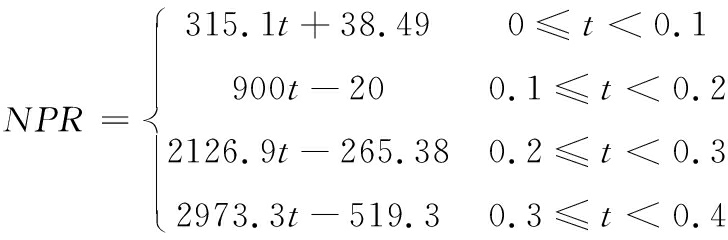
(1)
本文考虑喷管飞行速度及外流场温度,二者在动态工作过程中呈现变化的状态,其变化规律分别为

(2)
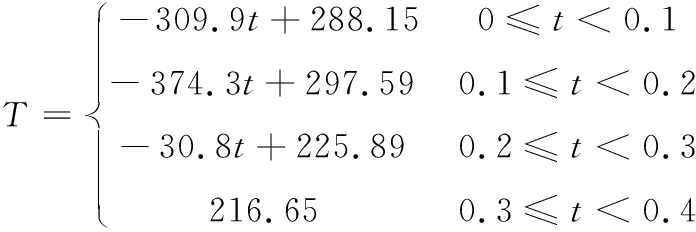
(3)
在给定的NPR、飞行速度和外流场温度条件下,存在一个与之对应的飞行高度。与上述条件所对应的飞行高度变化规律为

(4)
由于信息传递需要时间,导致边界条件变化与喷管实际工作状态之间存在微小差异,为方便对可渗透喷管工作状态进行分析,下文中所提到的喷管工作状态均为边界条件的参数值,并非喷管的实时工作状态。
1.3 网格无关性验证
由于喷管内存在复杂的激波分离现象,喷管区域需要进行局部加密,而为了满足湍流模型的要求,可渗透段部分也需要进行局部加密。为了选取合适网格数量,文中对4种不同网格数量的模型进行了网格无关性验证,网格数量范围从12万~24万。
网格数量对喷管内壁的压力分布影响较小,不同网格数量下压力分布仅在流动分离点处略有差异。随着网格数量的增加,流动分离点处壁面压力震荡幅度逐渐减小。当网格数量达到20万时,壁面压强分布不再随着网格数量的增加而产生明显变化,如图2所示。为在保证计算精度的前提下节约计算资源,本文选择采用包含20万数量的网格进行仿真计算。
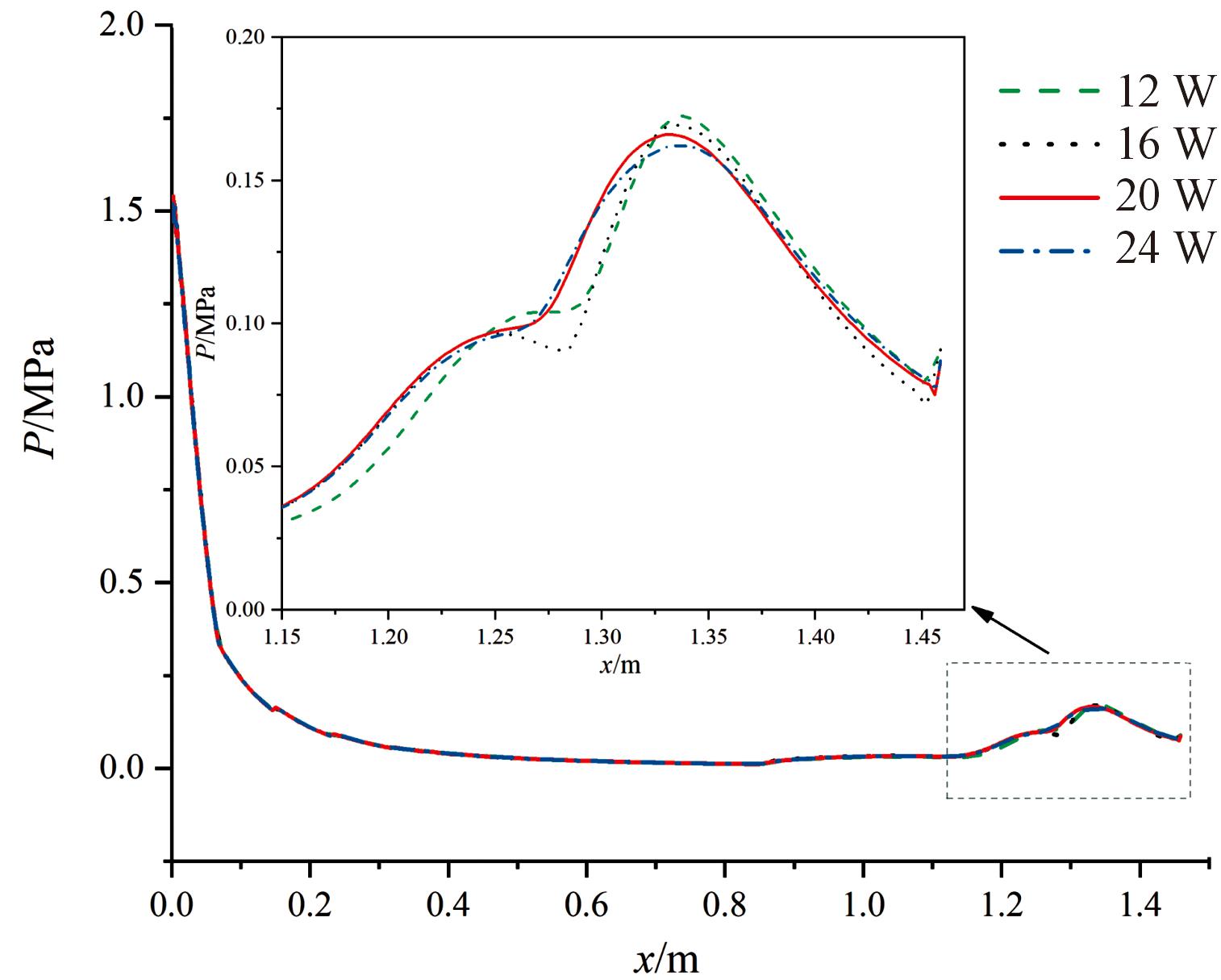
图2 不同网格数量下喷管内壁面压力分布
Fig.2 Comparison of the inner wall pressure of the nozzle with different grid quantities
2 喷管内流场结构演变
随着落压比的增大,喷管从过膨胀状态逐渐发展到欠膨胀状态[17],可渗透喷管的波系结构也随之不断变化,如图3所示,其中,喷管壁面的红色区域为可渗透段;SS为分离激波;NS为正激波;PS为可渗透段起始点激波;US为无附着激波。可渗透喷管的工作机理是改善传统喷管内部流动特征,因此本文重点讨论可渗透喷管(如不特殊说明,本节所提的喷管均默认为可渗透喷管)内部由于流动所诱导的激波演化规律。
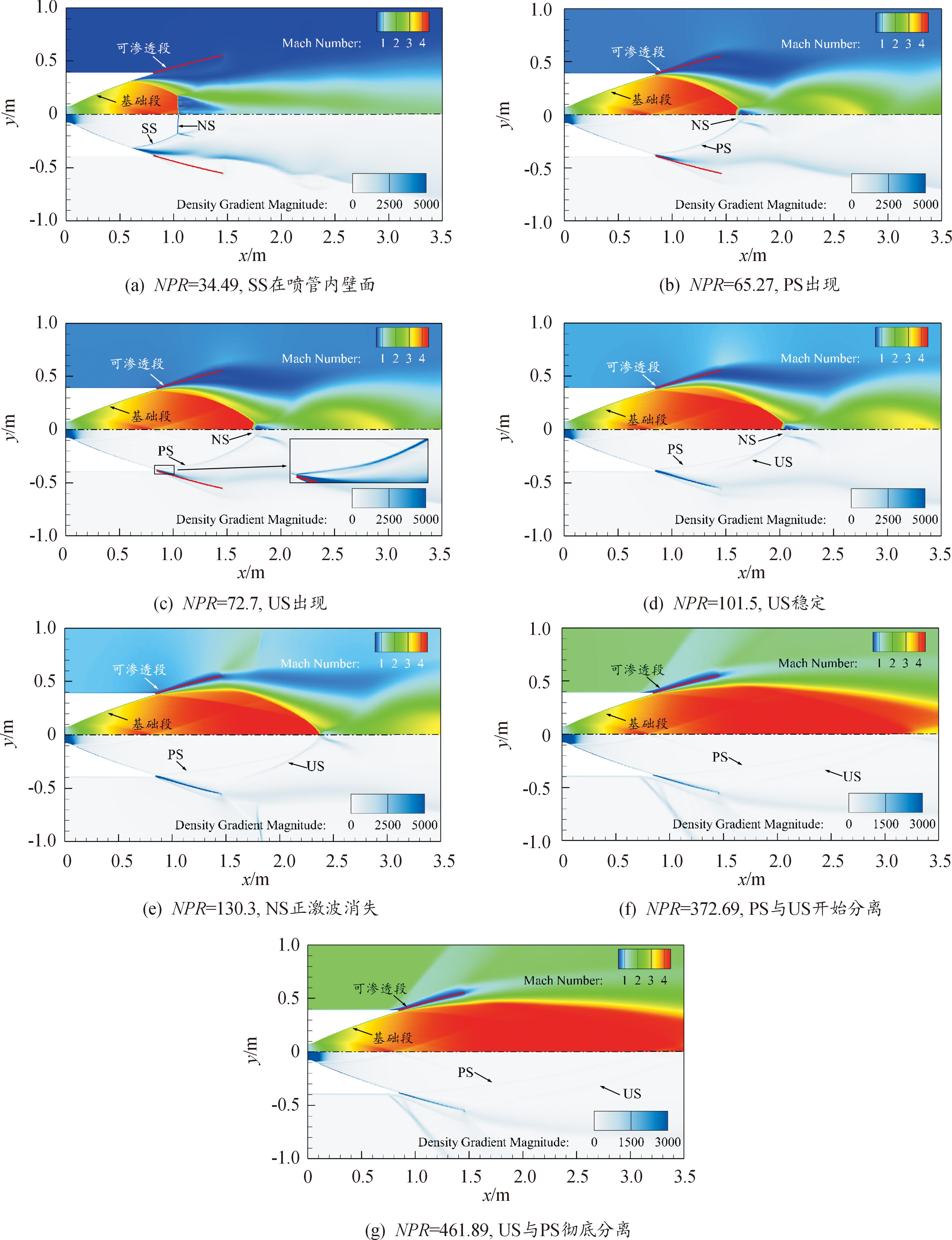
图3 动态工作过程中的典型流场
Fig.3 Typical flow field during dynamic operating conditions
在初始工况时,即在NPR=38.49时,喷管处于过膨胀状态,可渗透喷管内出现自由激波分离现象,导致喷管内出现一道分离激波SS与一道正激波NS,且SS位于可渗透喷管的基础段,如图3(a)所示。
随着NPR的增加,分离激波逐渐向下游移动,直至可渗透段起始点处(NPR=65.27),如图3(b)所示。将处于该位置的分离激波称为可渗透段起始点激波PS。燃气在经过基础段与可渗透段时,存在压力和速度的不连续变化,从宏观角度出发,即2种不同壁面对气流的阻力特性不同,因此基础段与可渗透段的连接处可近似视为一个固定的“阻力跃升”。“阻力跃升”的存在会导致喷管内超音速燃气在到达可渗透段壁面时产生PS,且PS的起点不会随着NPR的增加(喷管内燃气膨胀程度增加)而变化。
当NPR增加到72.7时,喷管内出现一道新的斜激波,这道斜激波处于PS上方,但起始点不在喷管内壁面,如图3(c)所示。将这道新的斜激波称为无附着激波US。随着NPR继续增大,US逐渐向下游推移、结构也逐渐清晰。图3(d)展现出US的典型特征,即激波上游不与任意实体壁面接触、激波下游与PS相连。
NPR在38.49~130.3范围内增长时,无论喷管内波系如何变化,始终存在一道正激波,当NPR=130.3时,正激波结构消失。此后,随着NPR的增大,US逐渐向下游移动,当NPR=372.69时,US与PS开始分离,此后,PS维持稳定状态,随着NPR的变化,仅有US不断向下游移动。
NPR从38.49到670上升的过程中可渗透喷管内流场不断演变,喷管内斜激波从分离激波SS发展为可渗透段起始点激波PS。受到“阻力跃升”的影响,PS在NPR大于65.27的工况下始终存在。为更好匹配喷管内外流场压强,当NPR等于72.7时,喷管内出现无附着激波US。随着NPR的增大,燃气膨胀程度增大,压强降低,因此PS与US强度逐渐减小。
3 US激波产生机理
US这种形式的斜激波没有在前文所述的典型高度补偿喷管内出现过,图4和图5分别为缝隙喷管和双钟型喷管的气流纹影照片[18-19]。缝隙喷管通过在传统喷管扩张段的中下游区域开一圈或多圈缝,使喷管内流场与外界大气相通。在海平面条件下,缝隙喷管内外压差驱动大气通过缝隙形成二次射流,减小实际膨胀面积比,抑制了管内气流的过膨胀现象,但激波类型依然为与壁面相接触的分离激波以及马赫盘结构。双钟型喷管由基础段和延伸段构成,在海平面条件下,随着NPR值的改变,分离激波的角度会发生改变,但都为与壁面相接触的激波,不会产生其他类型的激波。
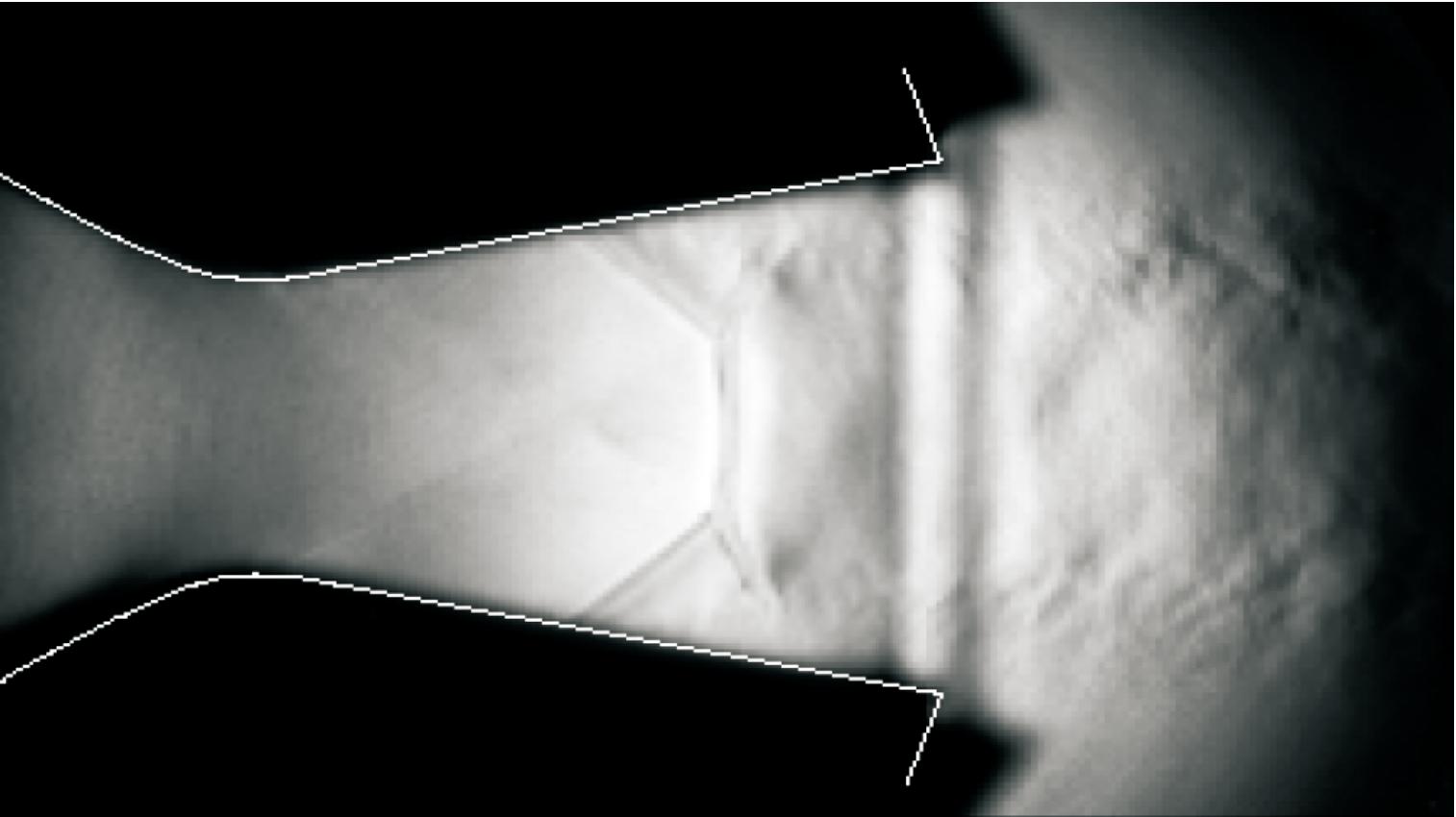
图4 缝隙喷管气体流动纹影照片
Fig.4 Schlieren picture of the slot nozzle

图5 双钟型喷管转折点处气体流动纹影照片
Fig.5 Schlieren picture of the flow in the inflection region of the dual bell nozzle
因此,可视US激波为可渗透喷管的典型特征之一。在NPR>72.7的工况下,可渗透喷管内始终存在US,但其产生机理并不一致。
3.1 机理一
当NPR较小时,US起点在可渗透喷管内部,典型结构如图3(d)(NPR=101.5)所示。这种情况下US的产生机理为气动机理,主要目的为匹配喷管周围不同区域的气动性能参数。如图6所示,区域1内为发动机燃气,区域4内为外界大气。
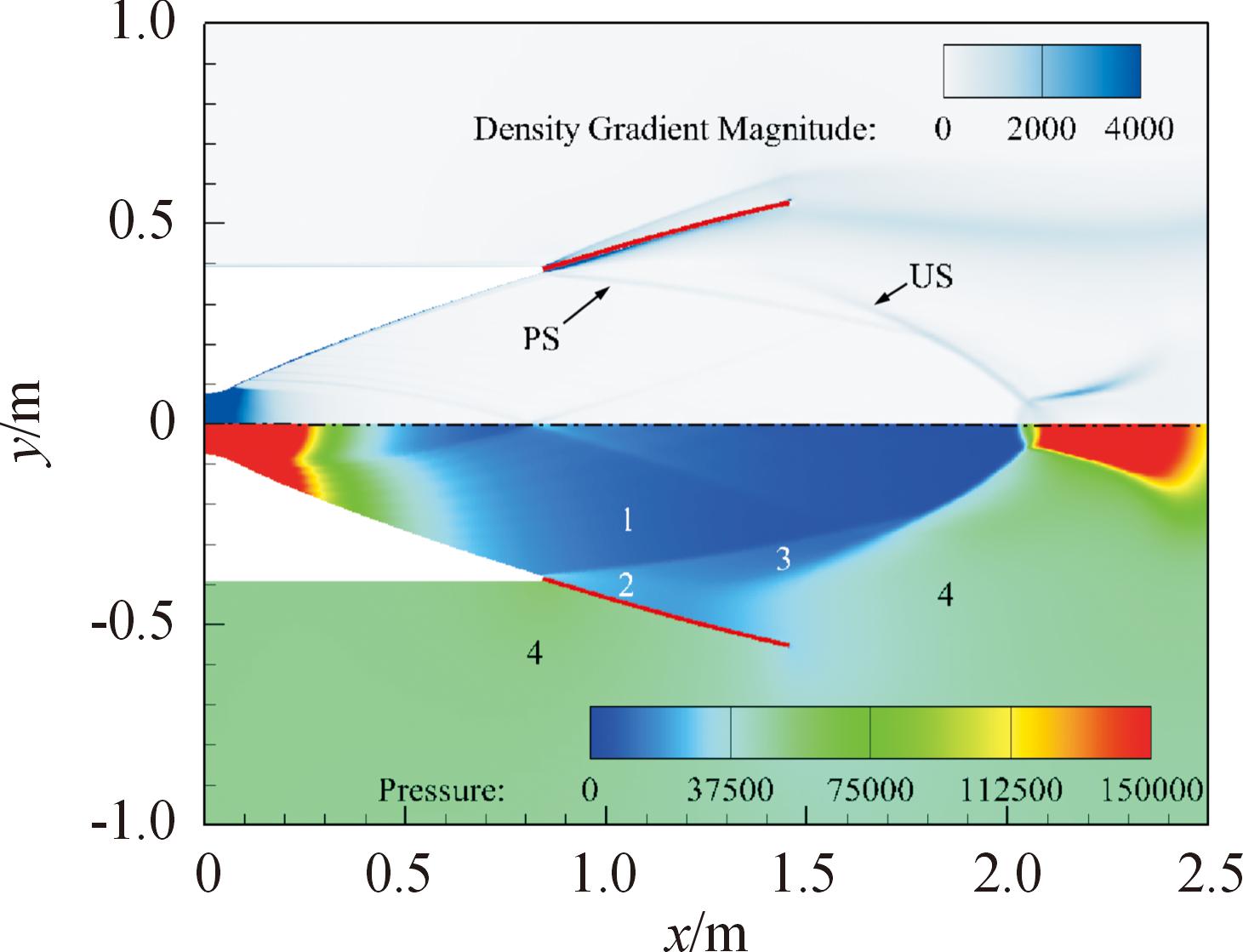
图6 US波系结构(机理一)
Fig.6 Structure of the US (The first mechanism)
喷管内燃气经过PS后进入区域2,压力上升,外界大气经过可渗透段进入区域3,压力降低,区域2与区域3压力基本一致。外界气流速度较慢,经过可渗透段时,会因为阻力产生动能耗散,当到达喷管内部时动能大大减小,难以补偿到远离喷管壁面的位置,即喷管的核心流动区,因此区域3的面积较小。在喷管内流场的核心区,燃气经过PS后虽有压力跃升,但区域2的压强与区域4压强差别较大。为匹配区域2与区域4压强,需要激波US的出现,由于区域3与区域2的压强基本一致,因此US的起点不在喷管的壁面上,表现出“无附着”的特点。
3.2 机理二
当NPR较大时,US起点在可渗透喷管外部,典型结构如图3(f)与图3(g)所示。这种情况下US的产生机理除了气动机理外,还受到喷管壁面形状的影响。如图7所示,当喷管膨胀达到一定程度时,超音速燃气抵达喷管出口壁面,在喷管出口处形成一道斜激波,随着膨胀程度的增大,斜激波逐渐向下游移动。该机理下US的结构与机理一下US的结构并无差别,但由于燃气膨胀程度较大,因此机理二下的US强度较小。
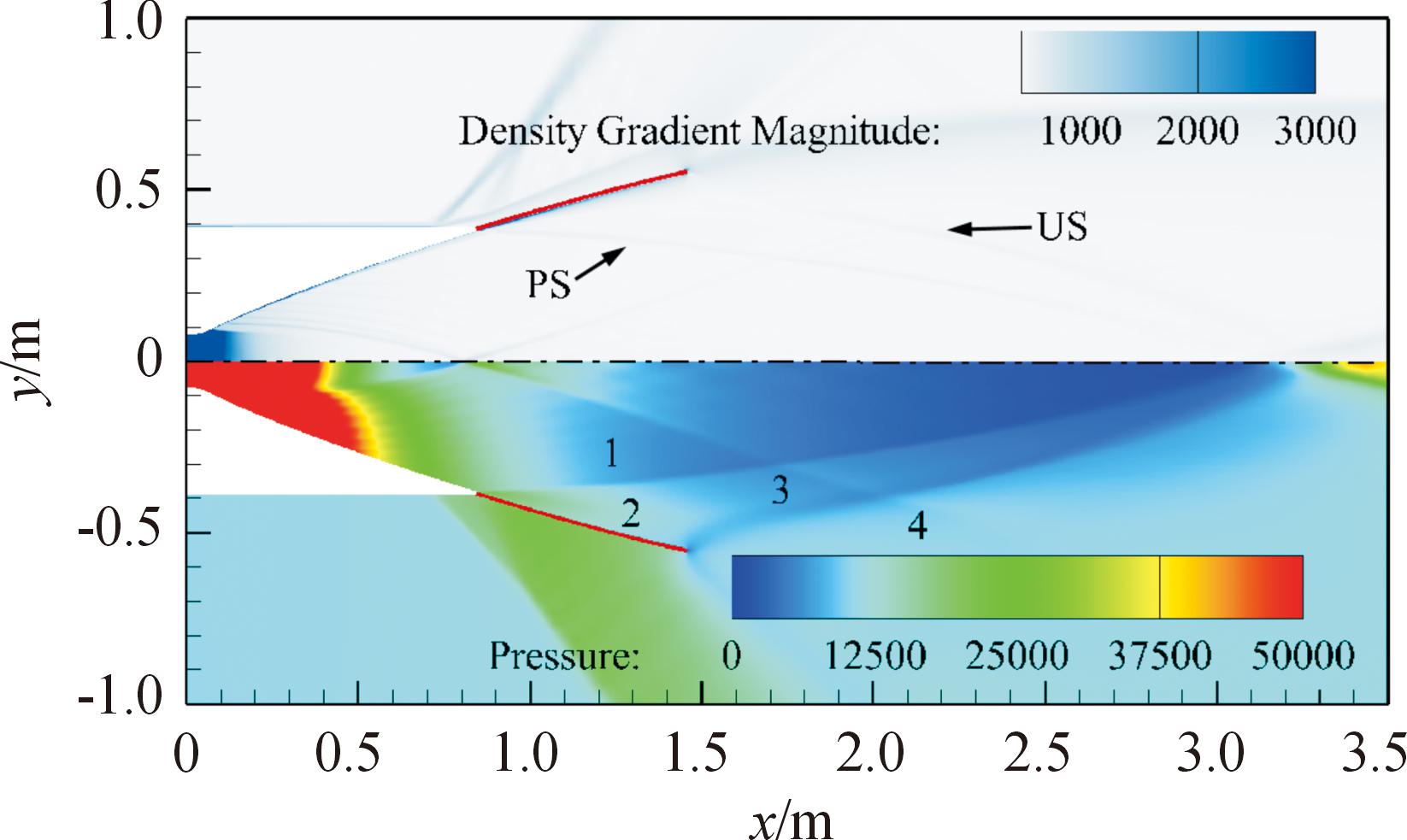
图7 US波系结构(机理二)
Fig.7 Structure of the US (The second mechanism)
4 工作特性分析
为明确可渗透喷管动态工作的特点,现选取5个典型工况,将可渗透喷管与相同工况、相同扩张比、相同型面的传统喷管进行对比,就推力性能对其进行分析。
当NPR<372.69时,可渗透喷管的推力系数始终大于钟型喷管,即在对应飞行高度之下,可渗透喷管始终具备推力补偿能力,所对应的可渗透喷管流场结构为图3(a)—图3(e)。该NPR范围内,可渗透喷管与传统喷管均处于过膨胀状态,但可渗透段的存在使得可渗透喷管的过膨胀程度轻于传统喷管,因此推力系数较高。可渗透喷管推力补偿最佳的工况是NPR=70.00,结合马赫数与飞行高度随着NPR的变化规律,得出该NPR下的飞行高度为4.77 km,马赫数为0.58,该工况下推力系数可提升24%以上。当NPR>372.69时,可渗透喷管的推力系数小于传统喷管,所对应的可渗透喷管流场结构为图3(f)与图3(g)。该工作范围内喷管膨胀程度较大,可渗透段起始点激波PS的存在使得喷管出口处的超音速气流在靠近喷管处速度降低,因此可渗透喷管推力小于传统喷管推力。推力补偿与推力损失状态下可渗透喷管流场结构的最大区别为斜激波在喷管内还是喷管外。
低NPR下,传统喷管产生流动分离现象,随着NPR的增大,传统喷管内斜激波会逐渐向喷管下游推移直至到达喷管出口。由于斜激波上游的燃气不断膨胀且压强不断降低,随着斜激波的移动,传统喷管内壁面的低压区逐渐增大。因此,在NPR=70时,传统喷管的推力系数比NPR=38.49时的推力系数小。当NPR到70后,传统喷管的推力系数随着NPR的增大而增大,如图8所示。
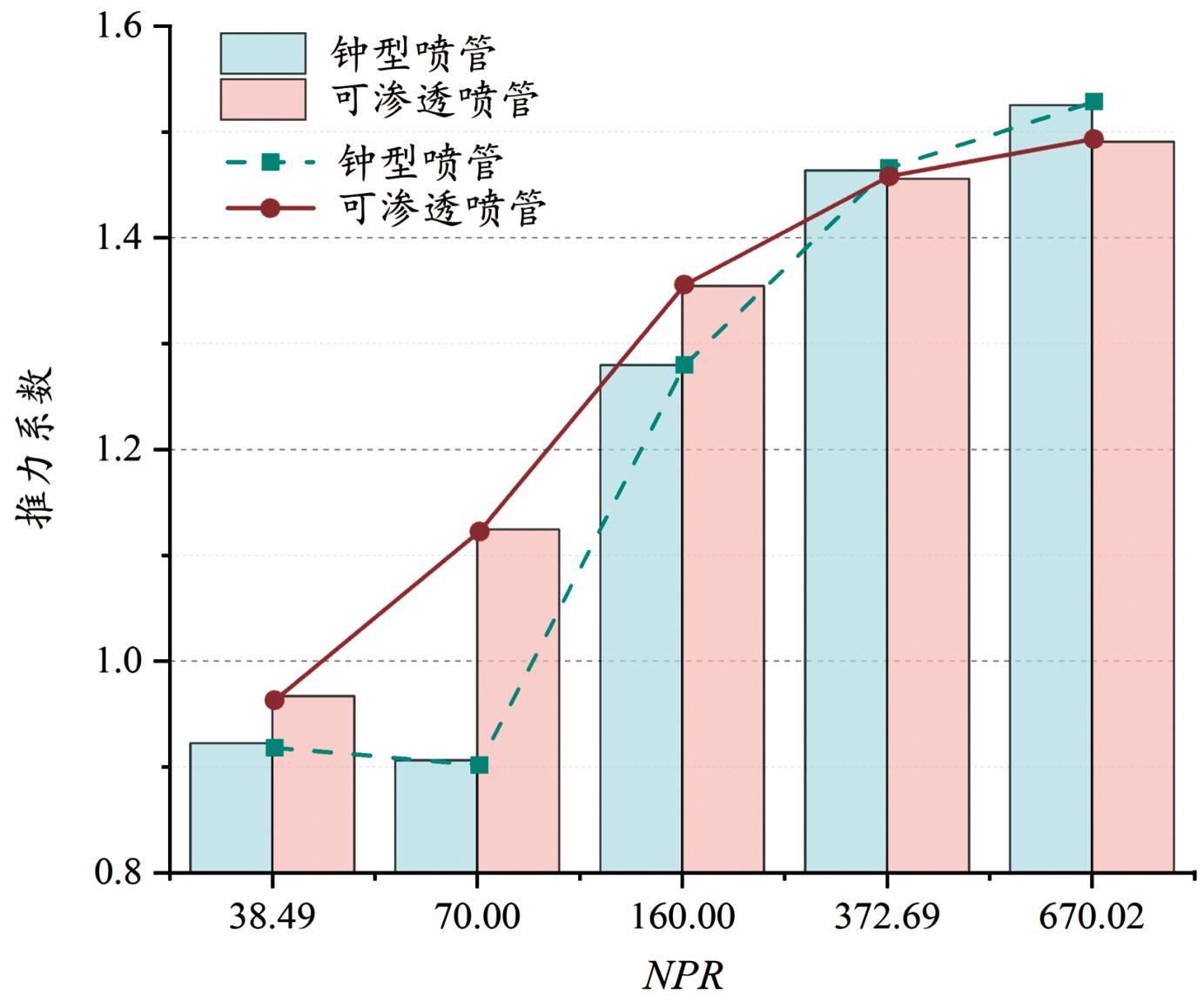
图8 推力系数
Fig.8 Thrust coefficient
结合图3(a)可得,当喷管的NPR过小(38.49)时,可渗透喷管内分离激波位于基础段壁面,即可渗透喷管也处于过膨胀状态,但可渗透段处补偿气流的存在使得可渗透喷管过膨胀程度小于传统喷管过膨胀程度,因此该工况下可渗透喷管推力系数大于传统喷管推力系数。由图3(b)至图3(e)可得,在NPR>65.27时,可渗透喷管内会将斜激波强制限制在可渗透段起点处,即PS起点位置不变,缩小了斜激波上游的低压区范围。当NPR>372.69后,喷管的膨胀程度增大,可渗透喷管PS的存在不再成为推力增益的诱因,反而会影响燃气的膨胀加速。
在喷管上升工作过程中,传统喷管推力系数呈现先减小后增大的特性,而可渗透喷管的推力单调增长,很好地提高了传统喷管的低空推力性能。可渗透喷管缓解了喷管在低空工况下与设计高度不匹配而产生的问题,改善了过膨胀效果,增强了火箭发动机的宽空域飞行性能,但在高空下会有较小的推力损失。
5 结论
本文对动态工作状态下可渗透喷管内流场进行了研究,得到如下结论:
1) 随着NPR的增大,可渗透喷管内的激波有一定的演化规律。当NPR达到65.27时,由于“阻力跃升”,喷管内斜激波从分离激波SS发展为可渗透段起始点激波PS,当NPR达到72.7时,为更好匹配喷管内外流场压强,喷管内出现无附着激波US。
2) NPR较低时,US的产生机理为气动机理;NPR较高时,US的产生机理除气动机理外,还受到喷管壁面形状的影响。
3) 当NPR<372.69时,可渗透喷管由于可渗透段的存在,推力性能优于传统喷管。
4) 可渗透喷管推力补偿最佳的工况是NPR=70.00,该工况下推力系数可提升24%以上。
5) US激波起点在可渗透喷管内部时,喷管呈现推力补偿状态,反之则呈现推力损失状态。
[1]马帅,郭健鑫,周磊,等.固体火箭发动机技术发展综述[J].火箭推进,2023,49(2):1-14.MA Shuai,GUO Jianxin,ZHOU Lei,et al.Review on the development of solid rocket motor technology[J].Rocket Propulsion,2023,49(2):1-14.
[2]SOMAN S,NAIR P P,SURYAN A.A study on the flow physics of altitude adaptive nozzle[J].Topical Problems of Fluid Mechanics,2021(16X):116-123.
[3]VARVILL R,BOND A.A comparison of propulsion concepts for SSTO reusable launchers[J].Journal-British Interplanetary Society,2003,56(3/4):108-117.
[4]ZHANG T,WANG Z,HUANG W,et al.The overall layout of rocket-based combined-cycle engines:a review[J].Journal of Zhejiang University-Science A,2019,20(3):163-183.
[5]SHOTWELL R,BENITO J,KARP A,et al.A Mars ascent vehicle for potential mars sample return[C]//2017 IEEE Aerospace Conference.IEEE,2017:1-12.
[6]KHARE S,SAHA U K.Rocket nozzles:75 years of research and development[J].Journal of Propulsion and Power,2021,46(2):1-22.
[7]HAGEMANN G,IMMICH H,VAN N T,et al.Advanced rocket nozzles[J].Journal of Propulsion and Power,1998,14(5):620-634.
[8]刘亚洲,李平,杨建文.液体火箭发动机喷管流动特性及高度补偿研究进展[J].推进技术,2022,43(1):20-39.LIU Yazhou,LI Ping,YANG Jianwen.Progress of flow characteristics and altitude compensation in liquid rocket engine nozzle[J].Journal of Propulsion Technology,2022,43(1):20-39.
[9]HORN M,FISHER S.Dual-bell altitude compensating nozzles[J].Pennsylvania State Univ,NASA Propulsion Engineering Research Center,1993(2):140-147.
[10]IINMAN F S.Extendible nozzle exit cone[P].U.S.Patent:US4489889A,1984-12-25.
[11]ANGELINO G.Approximate method for plug nozzle design[J].AIAA Journal,1964,2(10):1834-1835.
[12]RAO G V R.Analysis of a new concept rocket nozzle[J].Journal of Liquid Rockets and Propellants,1960(2):669-682.
[13]PARSLEY R,VAN S K.Altitude compensating nozzle evaluation[C]//28th Joint Propulsion Conference and Exhibit.1992:3456.
[14]FINOGENOV S,SEMENOV V,IVANOV I,et al.Advanced earth-to-orbit concept trade study[C]//42nd AIAA/ASME/SAE/ASEE Joint Propulsion Conference &Exhibit.2006:4965.
[15]MENTER F R.Two-equation eddy-viscosity turbulence models for engineering applications[J].AIAA Journal,1994,32(8):1598-1605.
[16]LIOU M S,STEFFEN J C J.A new flux splitting scheme[J].Journal of Computational Physics,1993,107(1):23-39.
[17]王宝国,刘淑艳,黄伟光.气体动力学[M].北京:北京理工大学出版社,2005.WANG Baoguo,LIU Shuyan,HUANG Weiguang.Gas dynamics[M].Beijing:Beijing Institute of Technology Press,2005.
[18]SERGEY L F,SEMENOV V V,IVANOV I E,et al.Advanced earth-to-orbit concept trade study[R].AIAA,2006:49-65.
[19]GENIN C,GERNOTH A,STARK R.Experimental and numerical study of heat flux in dual bell nozzles[J].Journal of Propulsion and Power,2013,29(1):21-26.