0 引言
高原环境下爆炸冲击波的传播规律是威力评估及研究其毁伤效果的基础。隧道工程作为交通运输的重要节点,承担着极为关键的作用,目前国外在针对高原隧道等防御工事的恐怖袭击频发,如何预测高原环境下半封闭结构内爆炸冲击波传播规律,是爆炸冲击领域研究的重点。
在空气参数对冲击波的传播规律的研究方面,奥尔连科[1]通过对空气近地面爆炸冲击波的研究,给出不同海拔条件下空气介质初始参数对爆炸冲击波特征参数的理论计算方法;Sachs[2]提出了爆炸冲击波的超压峰值、比冲量、超压持时与环境压力有相关联的比例定律;Veldman[3]通过调节密闭器内的压力测量了爆炸冲击波压力与比冲量的变化,结果表明冲击波压力与比冲量随着环境压力的升高而增加。姚成宝等[4]编写了多介质流体程序,模拟了爆炸冲击波在不均匀介质的传播过程,结果表明空气的初始密度和压强越高,冲击波超压和正压冲量衰减越慢;谢雪腾等[6]利用试验与数值模拟结合对比了平原与高原自由场环境下冲击波的传播特性,结果表明相同比例距离处冲击波的超压峰值和比冲量与海拔高度呈负相关;邓国强等[7]在分析常规装药爆炸空气冲击波标准函数的基础上,结合空气冲击波波阵面参数关系式,在给定波阵面压力时计算获得不同海拔时的波阵面参数;宋水舟[8]通过实验结果与数值模拟研究了不同真空度条件下的爆炸冲击波特性,结果表明空气初始压力越小,冲击波的超压峰值越小,正压作用时间越短,冲击波达到峰值的速度越快;甘朝虹等[9]在考虑空气密度影响下提出了冲击波超压计算模型修正方法,得到空气冲击波超压计算的修正模型。
相较于自由场内冲击波的传播,冲击波在隧道内的传播过程更加复杂,在冲击波在隧道内的传播规律的研究方面,杨科之等[10]利用三维数值模拟计算程序,对长隧道中的化爆流场进行了数值计算,并且与试验结果对比研究,归纳出空气冲击波沿隧道方向的传播规律;石成英等[11]采用数值模拟方法,分析了洞窟结构内的压力云图,总结出冲击波在半封闭结构内的不规则反射、环流等传播特性;李秀地等[12]研究了常规炸药在隧道口外爆炸情况下,长隧道中冲击波峰值压力的衰减规律,为隧道对化爆冲击波的防护理论提供依据;任新见等[13]通过试验与理论相结合,建立了炸药在等截面直隧道口部爆炸后,冲击波在隧道内传播的波速的计算模型;徐利娜等[14]进行了直隧道内部不同药量的爆炸试验,拟合了冲击波超压在隧道内的衰减计算方程,可以用于隧道内部爆炸的威力预测。罗婷等[15]采用Realizable湍流模型模拟了微型粒子在半封闭结构内的传播过程,研究了结构对流作用对粒子传播形态的影响效果。曹宇航等[16]采用数值计算方法,建立了典型钢筋混凝土框架半封闭的有限元模型,基于仿真工况的计算结果,总结了结构尺寸、爆炸当量和墙体厚度等因素对冲击波传播的影响规律。
炸药爆炸后产生的膨胀产物伴随大气运动,因此大气环境影响着冲击波的传播特性。从平原地区到高原地区,空气密度、气压随着海拔的增高而发生改变,爆炸的能量输出与隧道内冲击波传播机制也会发生改变,目前高原环境引起的空气参数的变化对冲击波在隧道内的传播规律的影响机理尚不明确。本研究中利用基于高原靶场隧道外爆试验与数值模拟相结合,通过改变大气压强与空气密度等典型参数,模拟了在典型海拔条件下,炸药口外爆炸后冲击波在隧道内的传播过程,对比了冲击波超压峰值、正压冲量、正压持时的差异,分析了海拔效应对冲击波在隧道内传播规律的影响。
1 测试方案
1.1 试验方案
在青海省某靶场建设隧道,开展外爆试验,隧道尺寸与配筋设置如图1所示。为保障工装的稳定性,隧道采用钢筋混凝土结构,混凝土衬砌内置双层网式钢筋,形成钢骨架,受场地条件限制,隧道采用分段式装配,隧道每段长3 m,共5段。
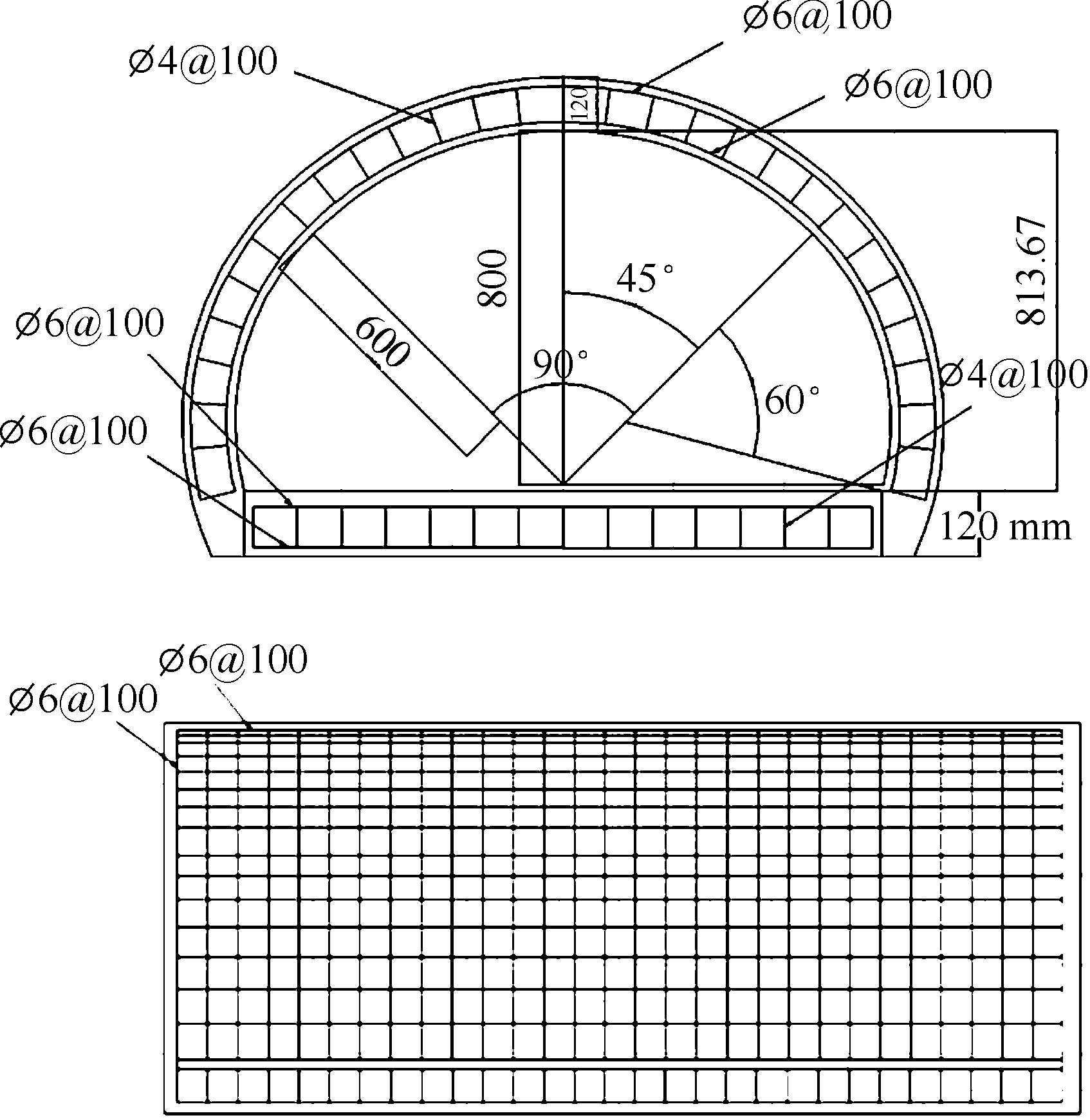
图1 隧道尺寸
Fig.1 Tunnel construction
爆炸源为定制1 kg圆柱形TNT战斗部,用电雷管进行起爆,设计专门的触发线路,爆点设在隧道口外1 m,采用空爆形式,装药位置在隧道等效截面中轴线上,装药位置如图2所示。隧道内部设置8个测试断面,每个测试断面的壁面布设PCB壁面超压传感器,壁压传感器采用的是102A压电压力传感器(美国 PCB Piezotronics 公司)。传感器型号为113B21(范围0~1.38 MPa)、113B26(范围0~3.4 MPa)和113B24(范围0~6.9 MPa)。检测面如图3所示。
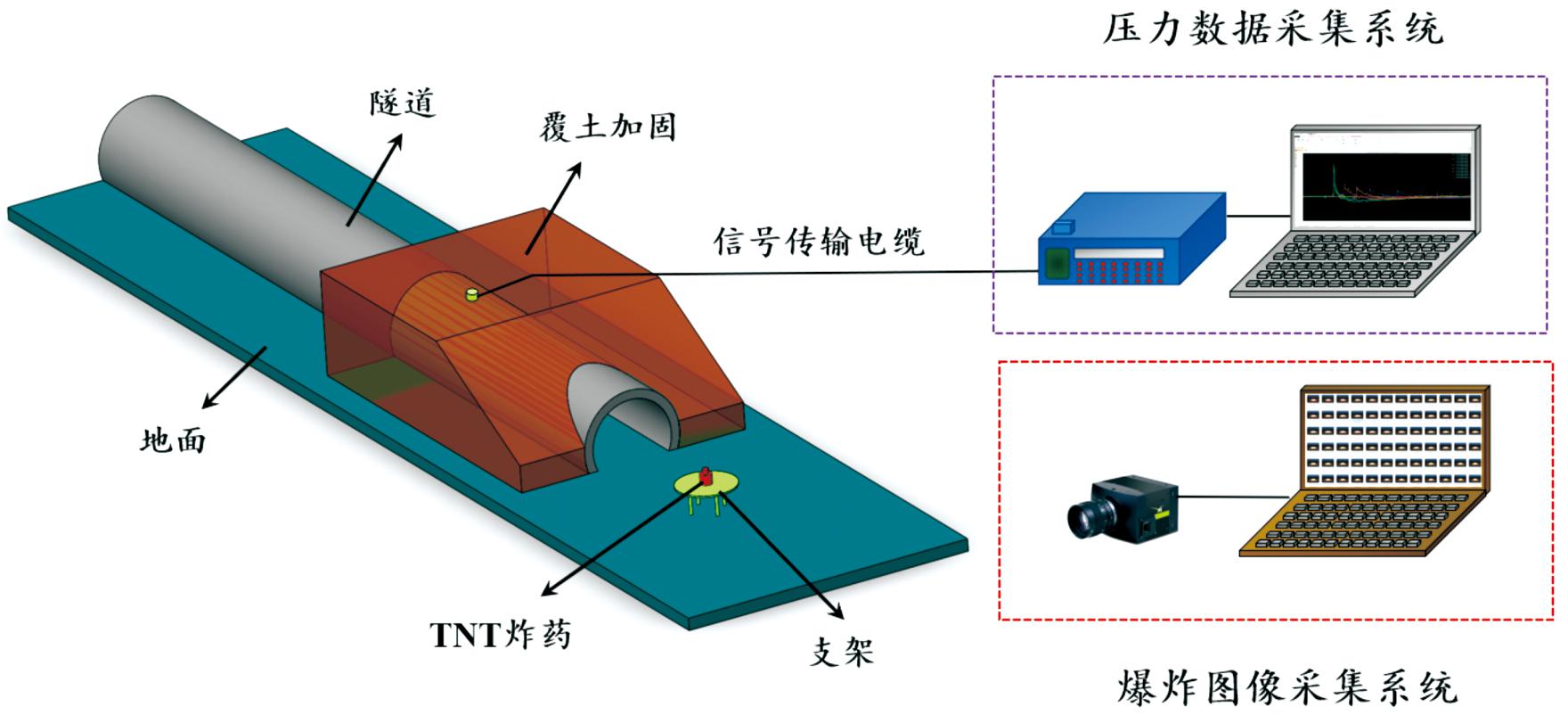
图2 隧道口外爆炸试验示意图
Fig.2 Schematic diagram of the explosion test outside the tunnel mouth
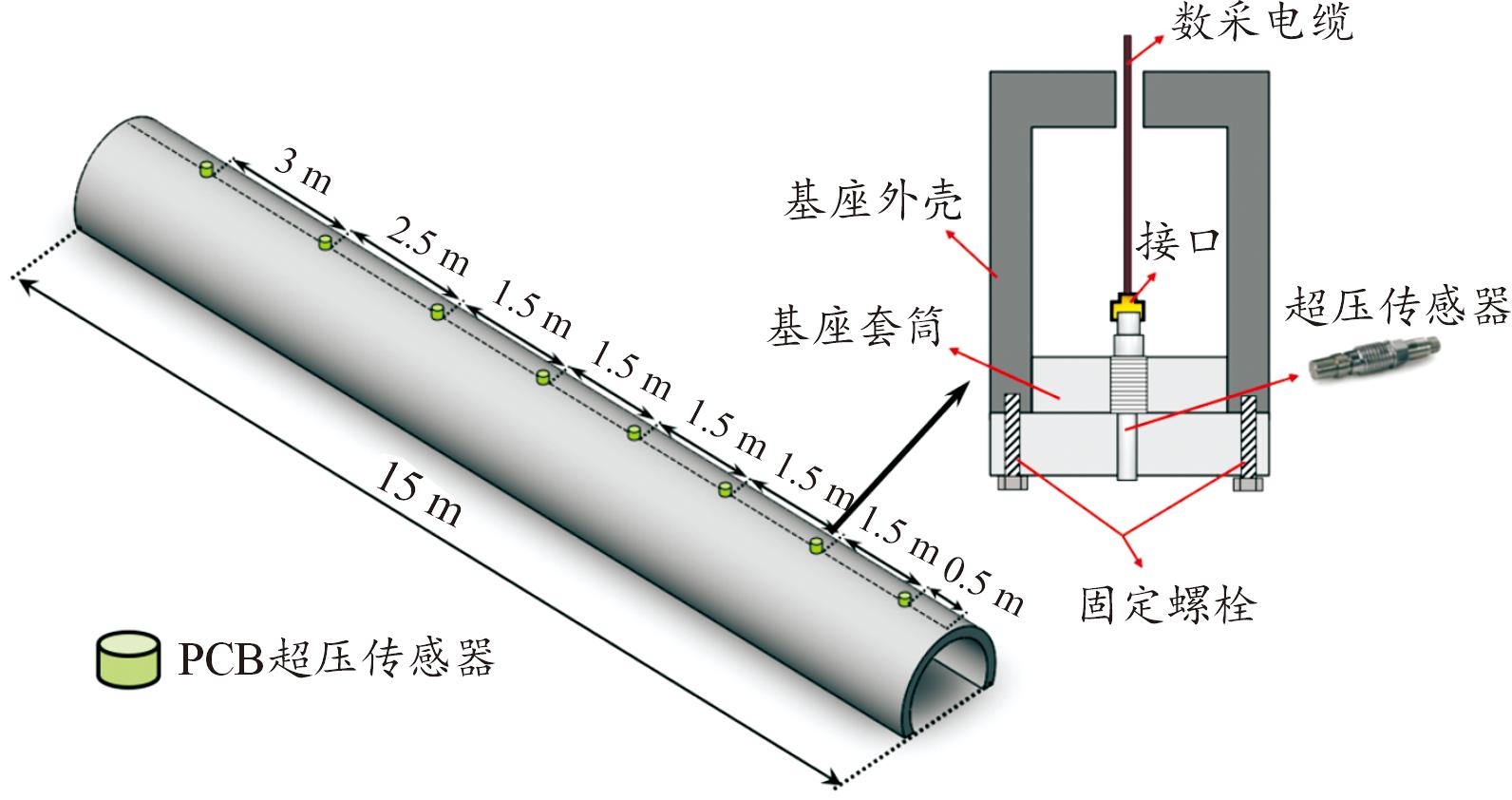
图3 检测面位置
Fig.3 Position of detection surface
1.2 数值模拟方案
1.2.1 材料参数
1) 空气材料
根据标准大气规定[18-19],对流层温度Th与环境海拔h存在线性增减关系,线性方程如式(1)所示,根据海平面气温T0与Th可以得到海拔高度h处的大气压力ph、空气密度ρh、环境声速、空气内能,按照式(2)—式(5)计算。根据标准大气规定,海平面大气温度为15 ℃(热力学温度T0=288.16 K),大气压强p0=101.35 kPa,空气密度ρ0=1.225 kg/m3。根据式(1)—式(5)计算出不同海拔下温度、大气压强与空气密度等各项参数结果如图4所示,根据图4可以看出,大气压力、密度、温度和声速都随着海拔的升高而近似线性降低。
Th=288.15-0.006 5h
(1)
Ph=P0(Th/T0)5.255 88
(2)
ρh=ρ0(Th/T0)4.255 88
(3)
![]()
(4)
E=Ph/(γ-1)
(5)
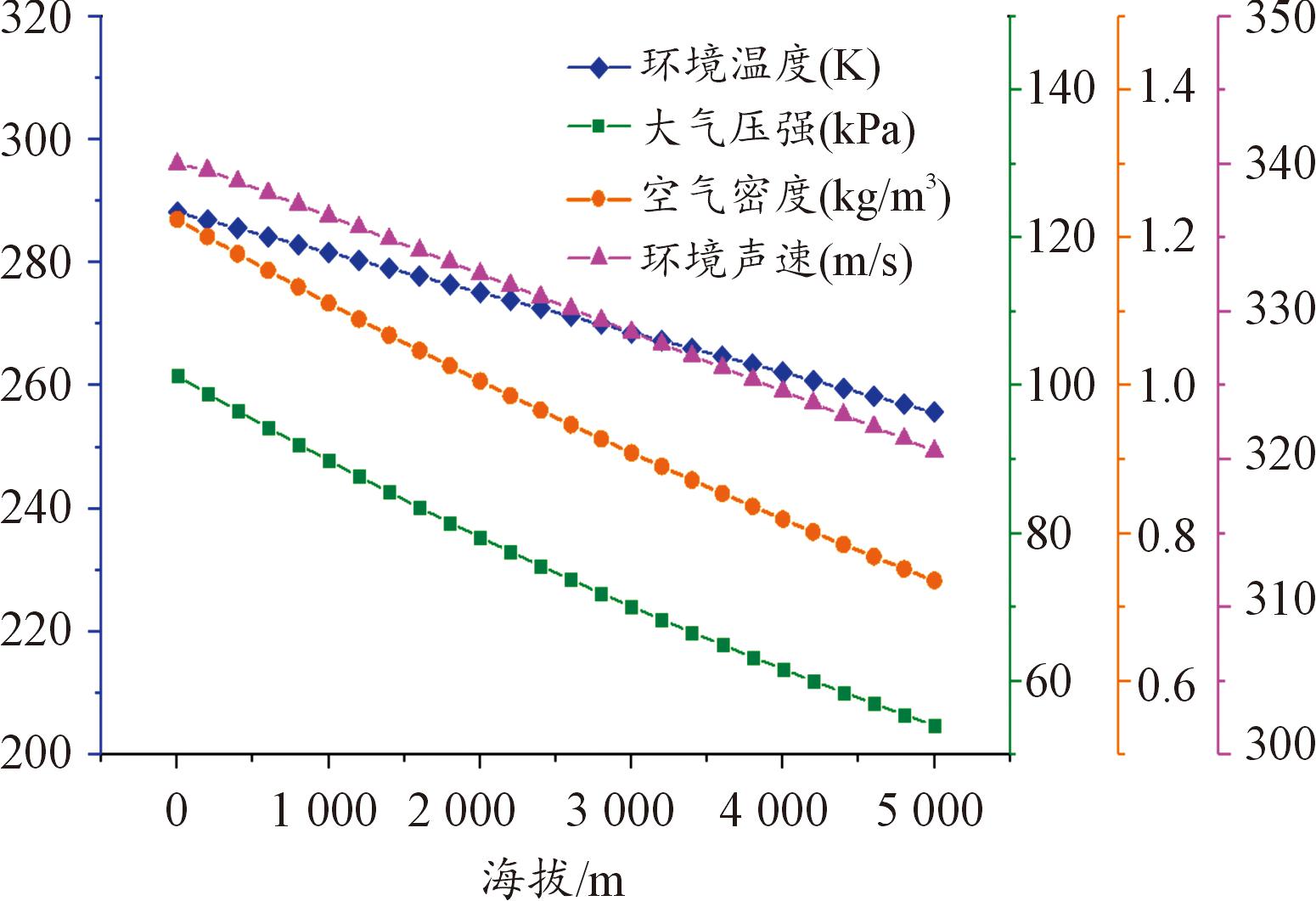
图4 大气参数比例
Fig 4 Scale of atmospheric
空气绝热指数γ=1.4,根据上述关系可以计算相应海拔下的大气参数,空气模型使用如式(6)所示多线性状态方程*EOS_LINEAR_POLYNOMIAL来描述,空气参数按照表1设定,C0~C6、μ等方程系数见表2所示。
P=[C0+C1μ+C2μ2+C3μ3]+
[C4+C5μ+C6μ2]e
(6)
表1 大气参数
Table 1 Atmospheric parameters
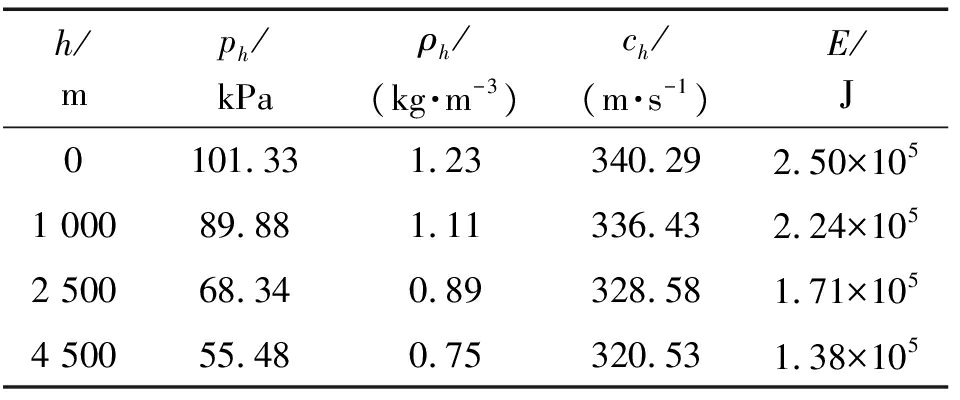
h/mph/kPaρh/(kg·m-3)ch/(m·s-1)E/J0101.331.23340.292.50×1051 00089.881.11336.432.24×1052 50068.340.89328.581.71×1054 50055.480.75320.531.38×105
表2 空气方程系数
Table 2 Coefficient of air equation

C0C1C2C3C4C5C6V0MU0.00.00.00.00.40.40.01.00.001
2) 隧道和地面材料
在爆炸问题中仅研究冲击波的传播过程,因此隧道和地面采用LS-DYNA关键字*MAT_RIGID定义为刚性部件,不发生形变与位移。
3) 炸药材料
TNT爆炸过程通过JWL状态方程(7)来描述[20]:炸药参数如表3所示,模型的单位均为kg-m-s。
![]()
(7)
表3 TNT状态方程参数
Table 3 Parameters of TNT equation of state
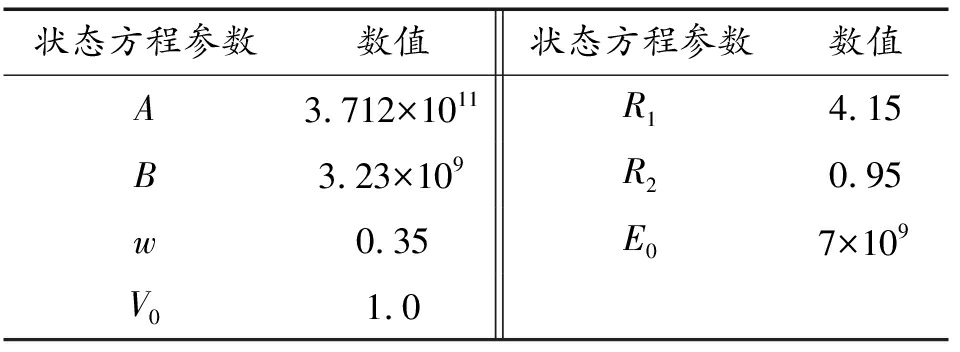
状态方程参数数值状态方程参数数值A3.712×1011R14.15B3.23×109R20.95w0.35E07×109V01.0
1.2.2 隧道外爆模型
利用有限元分析软件,建立试验隧道的三维模型进行数值模拟,模拟试验工况下各类型隧道中爆炸冲击波的传播规律,建立的试验隧道的三维有限元模型如图5所示。
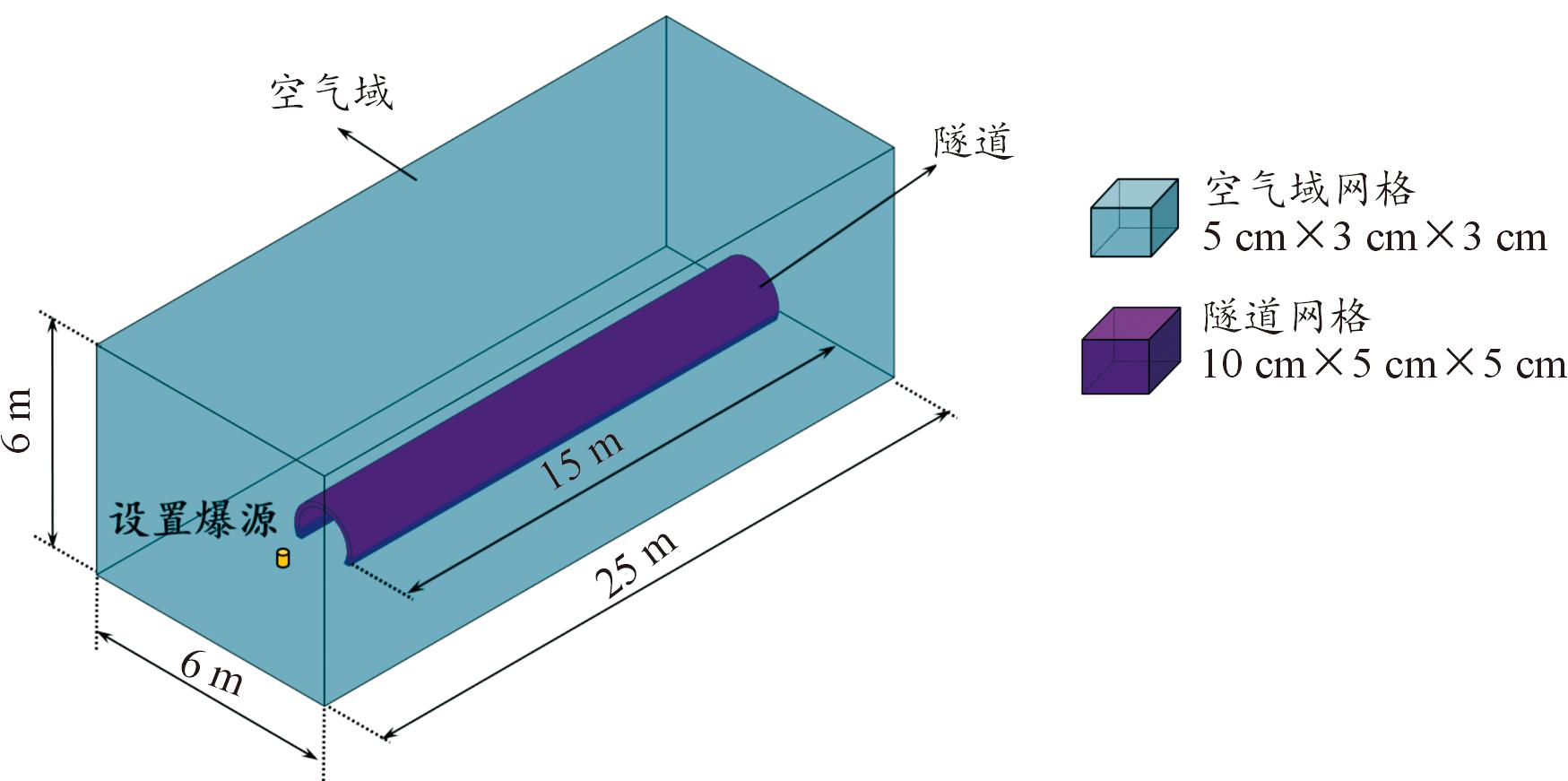
图5 隧道有限元模型示意图
Fig.5 Schematic diagram of tunnel symmetry model
数值模拟采用LS-DYNA软件模拟1 kg的TNT在隧道口外1 m位置爆炸,记录了冲击波在隧道内的传播过程。隧道内在1~14 m每隔1 m选定14个检测面用来输出冲击波的超压时程曲线。
2 结果分析
2.1 试验与数值模拟结果分析
2.1.1 爆炸火球效果
1 kg TNT炸药在隧道口外1 m爆炸后,爆炸火球效果如图6所示。TNT在隧道口外起爆后产生迅速外扩的赤橙色火球,在地面约束的作用下,向外扩张的火球发生反射后向上运动形成环状火圈,同时高温气体与火焰向上传播,火球存在分层效果,随后火焰效果逐渐减弱,自火球底部出现大量黑色烟雾跟随火球效果向四周扩散直至在火球完全消失,黑色浓烟持续向上运动直至爆轰过程完全结束。

图6 爆炸火球效果
Fig.6 Effect of explosive fireball
2.1.2 超差时程曲线分析
各个测点处采集的超压时程曲线如图7所示。根据超压时程曲线可知炸药爆炸后高速向外围扩展的冲击波到达测点后,测试断面上的超压迅速升高到达峰值,随后的超压曲线的衰减状态不同于自由场内的稳定衰减而是出现多个波峰的振荡呈锯齿状衰减,这是由于隧道的半封闭结构对入射冲击波的约束作用使冲击波不断反射叠加造成的,当波阵面压力衰减到大气压后,波形会继续衰减,压力小于大气压形成负压,负压的峰值通常小于正压的峰值。负压结束时,基本恢复为大气压力。通过超压时程曲线可以发现,在隧道前端,超压衰减迅速,正压作用时间较短,并且在负压段后会出现二次正压波段,随着冲击波在隧道内的持续传播,冲击波到达各测点的时间延长,冲击波运动速度减小,正压作用时间不断延长,波型变化轨迹逐渐平稳,超压衰减幅度减小,负压作用区后的正压波段不明显,这时已近似形成平面波。
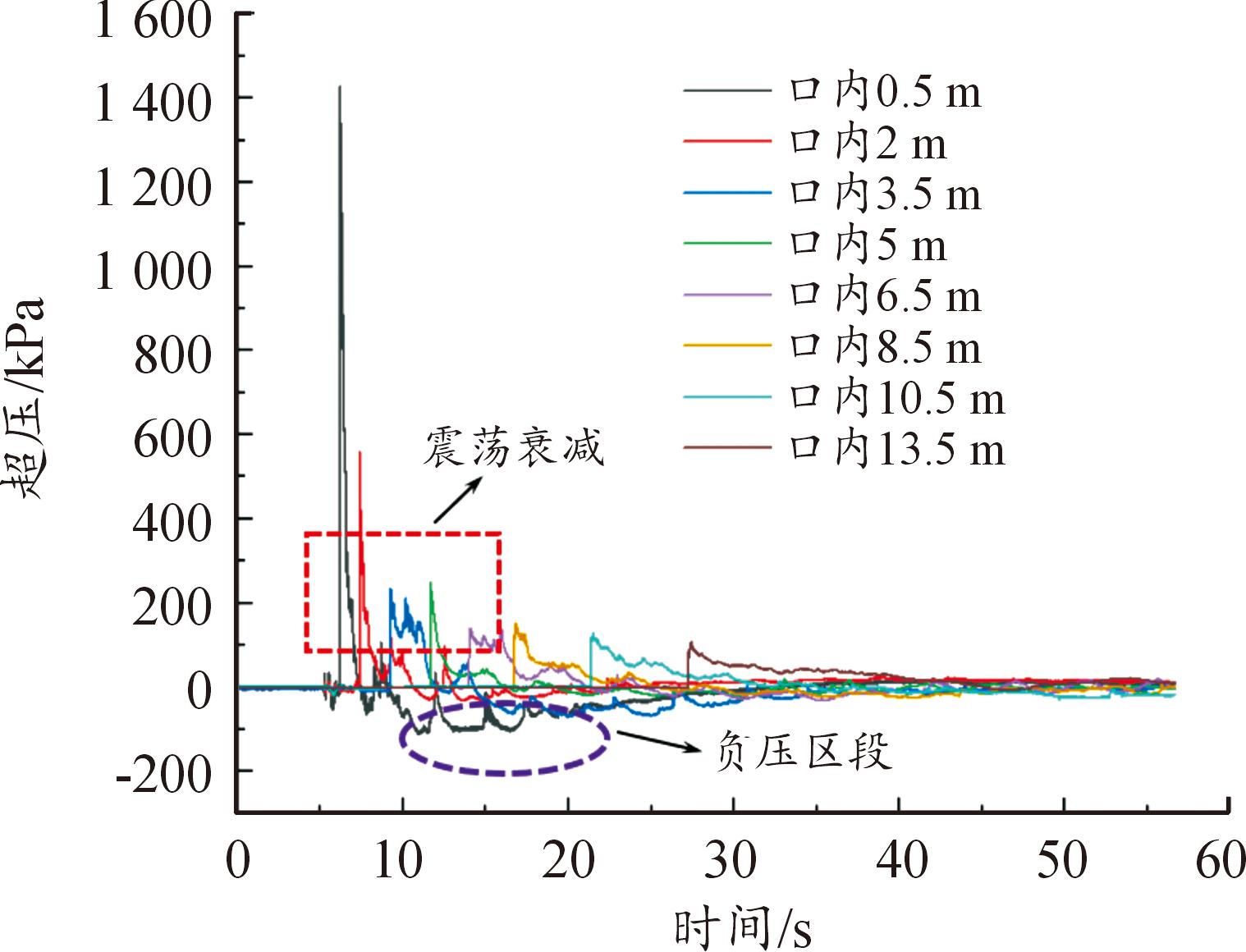
图7 1 kg TNT隧道口外1 m爆炸各测点超压
Fig.7 Overpressure of each measuring point of 1 m explosion outside the entrance of 1 kg TNT tunnel
根据数值模拟结果,不同海拔条件下冲击波在隧道内传播时,口内各检测面的超压时程输出结果如图8(a)—图8(d)所示。数值模拟结果与试验结果的超压时程曲线具有相似的变化趋势。为验证数值模拟结果的有效性,将高原靶场试验数据与4 500 m条件下数值模拟结果进行对比,对比结果如图9—图11所示,通过超压峰值、冲量与持时对比结果可知,数值模拟结果与试验数据有较好的吻合性。
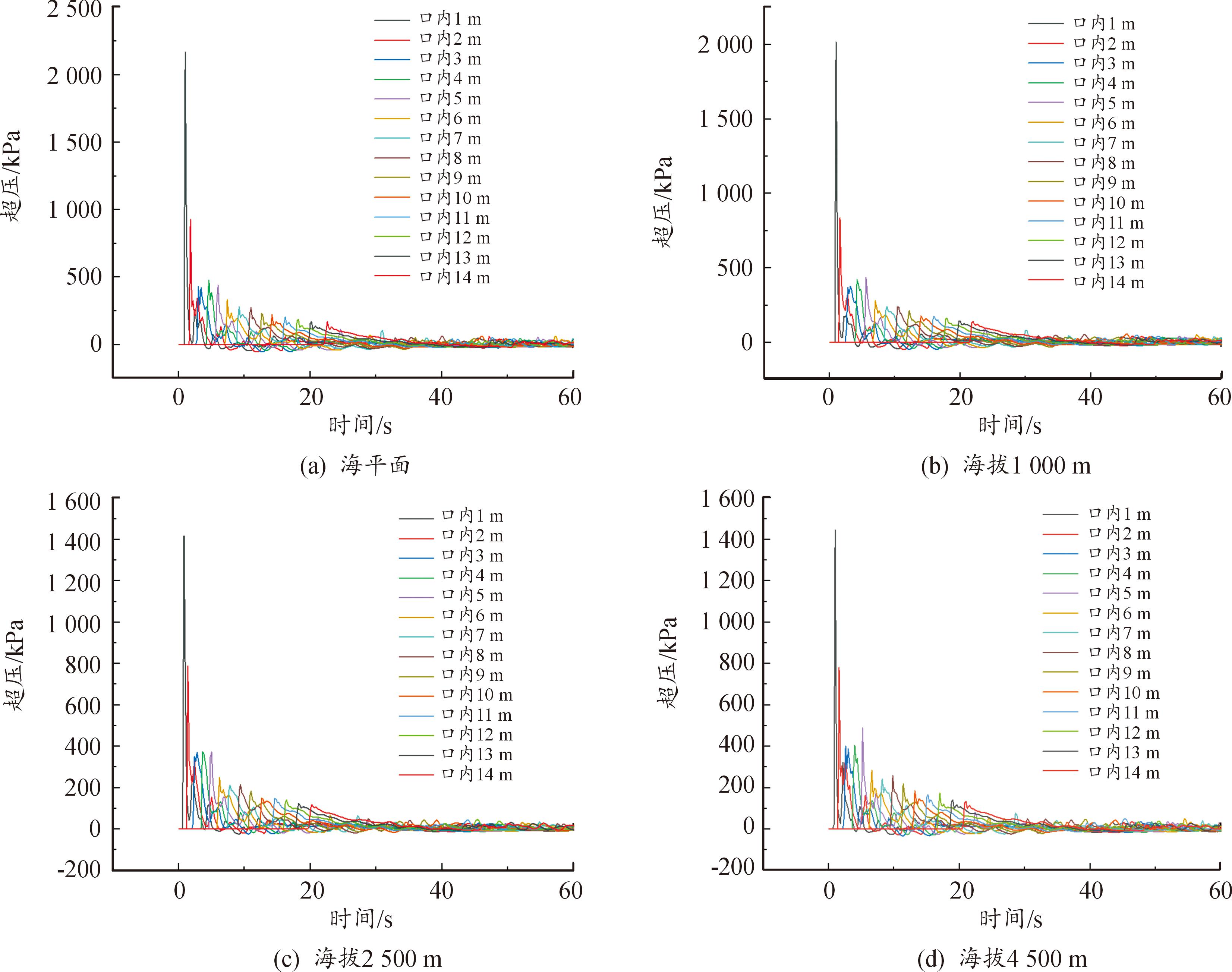
图8 数值模拟结果
Fig.8 Numerical simulation result
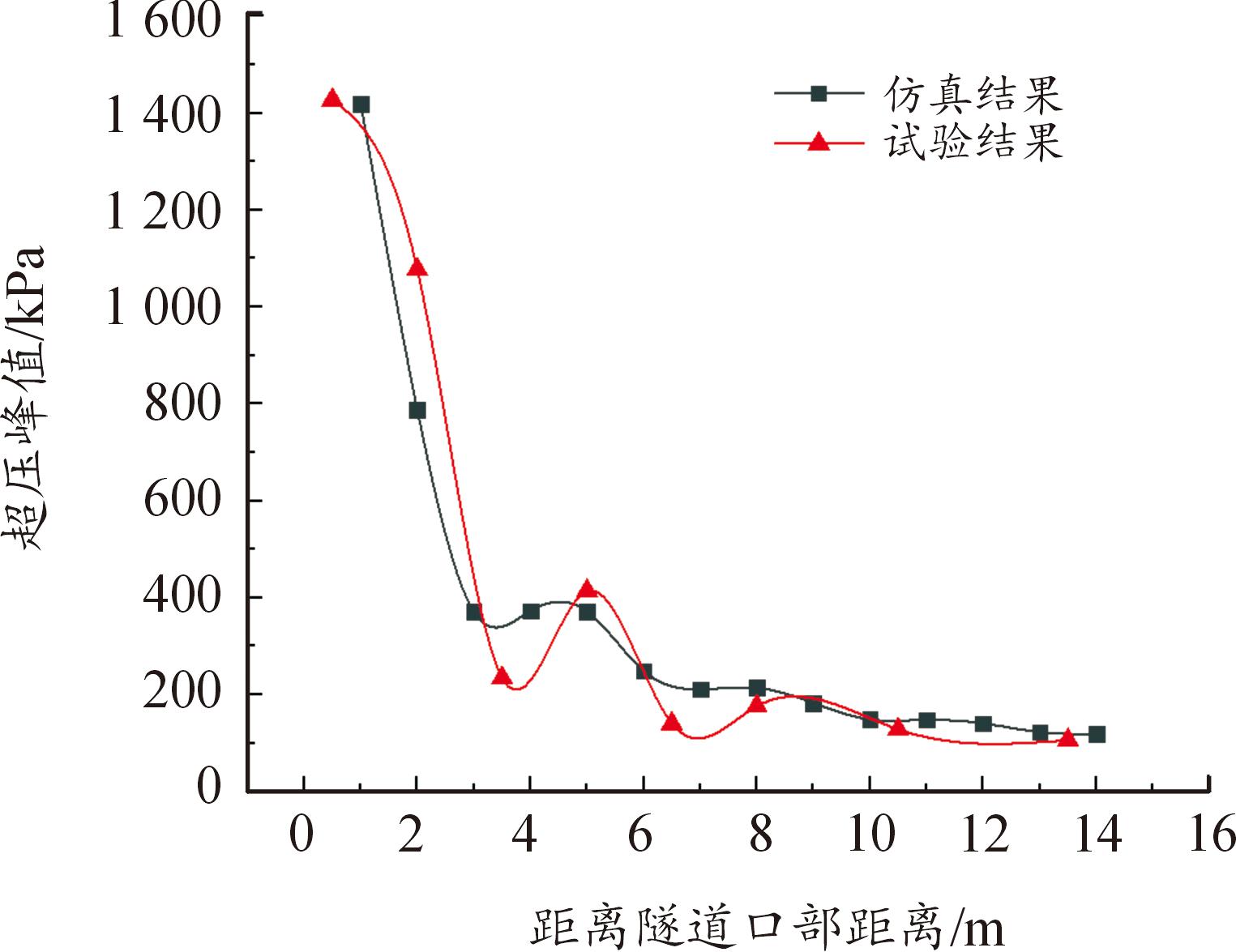
图9 超压峰值对比
Fig.9 Comparison of peak overpressure
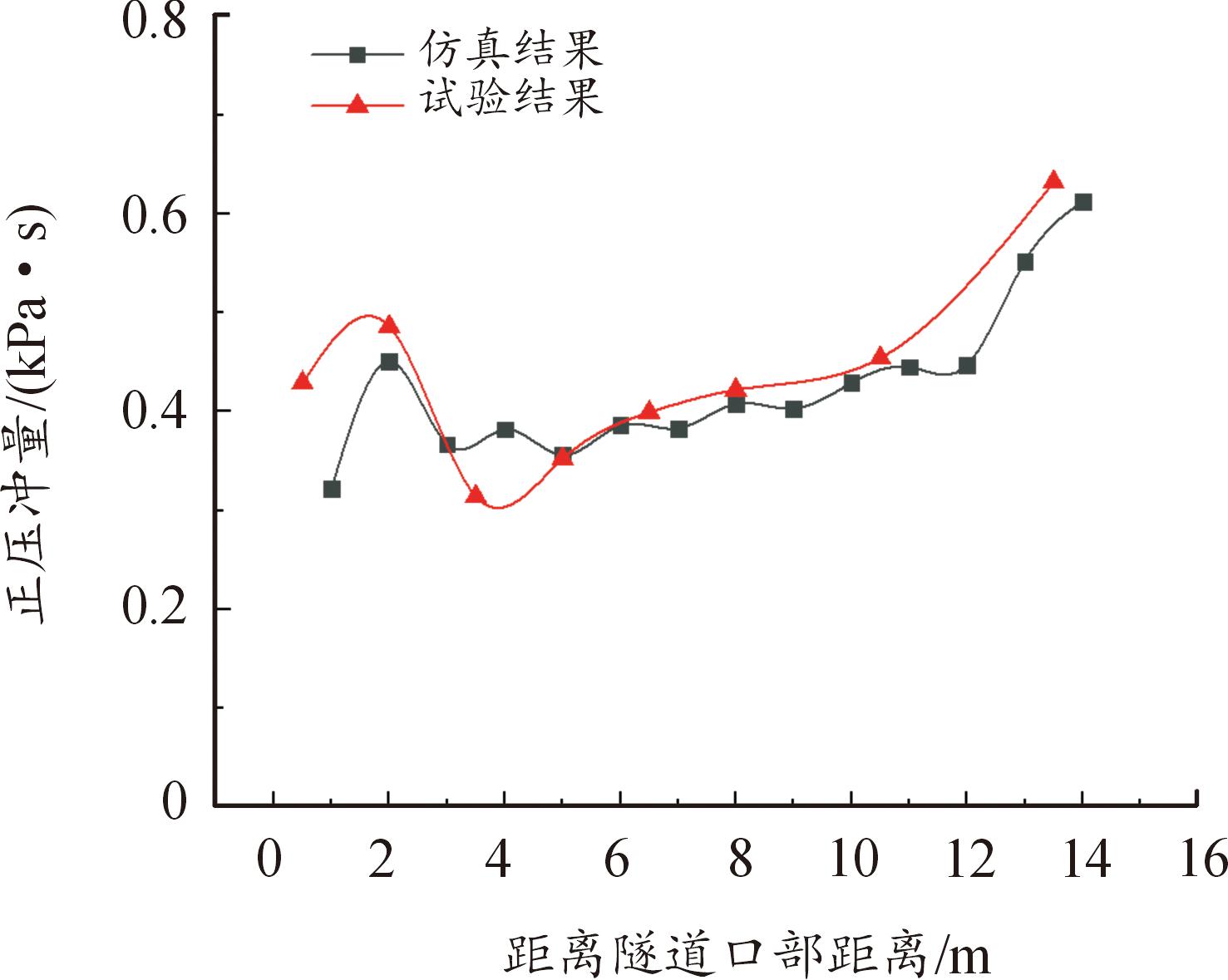
图10 正压冲量对比
Fig.10 Impulse comparison diagram
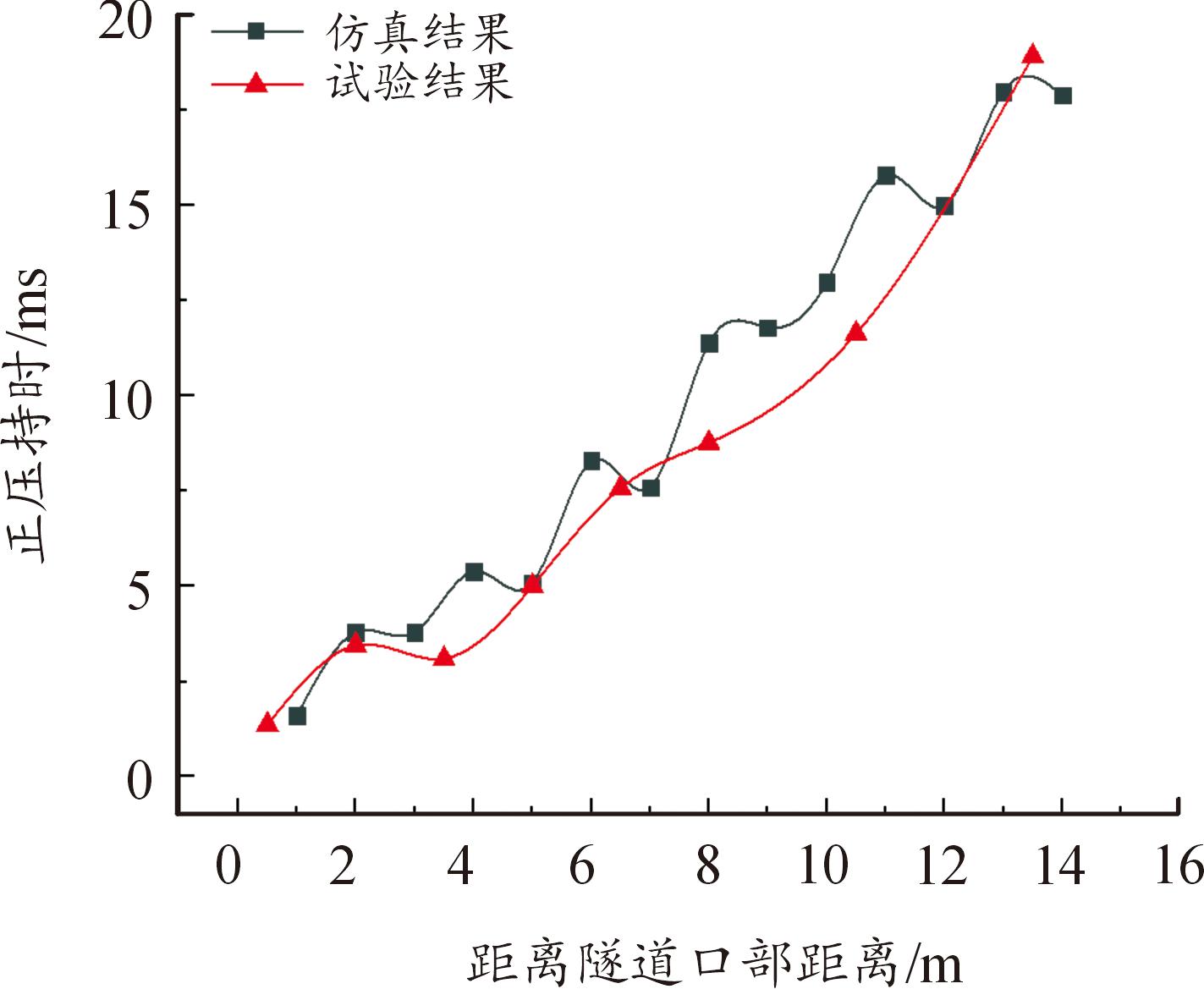
图11 正压持时对比
Fig.11 Comparison of holding time
2.2 冲击波传播参量分析
根据质量、动量与能量守恒关系结合1.2中的公式可以得出关系式(8)—式(11)[21],由理论公式可知冲击波波阵面压力与空气密度、内能以及爆轰产物的能量有关,因此不同海拔造成的大气参数的变化会影响波阵面的传播过程,根据理论公式与数值模拟结果可以验证冲击波传播过程中超压的变化情况,通常取γ绝热指数为1.4[21-22]。
Patm=(γ-1)ρatmeatm
(8)
m=ρ0(D-v0)=ρ(D-v)
(9)
ρ0(D-v0)2-ρ(D-v)2=p-p0
(10)
![]()
(11)
针对隧道口外爆炸问题,根据量纲分析确定影响冲击波超压参数(超压峰值ΔP、冲量i、持时τ+)的物理参量,主要有大气压强Ph、空气密度ρh、炸药释能E、爆源距离口部距离R、口内传播距离L、隧道截面积S(或截面积的等效直径D)等,上述物理量中有3个基本量纲,超压参数表达式可以简写为式(12),该问题中的有量纲物理量的量纲幂次指数如表4和表5所示。
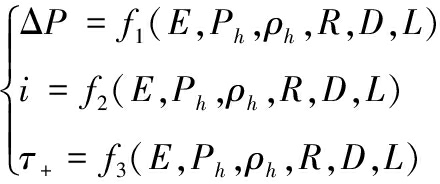
(12)
表4 隧道口外爆炸问题中变量的量纲幂次指数
Table 4 Dimensional power index of variables in the explosion problem outside the tunnel entrance
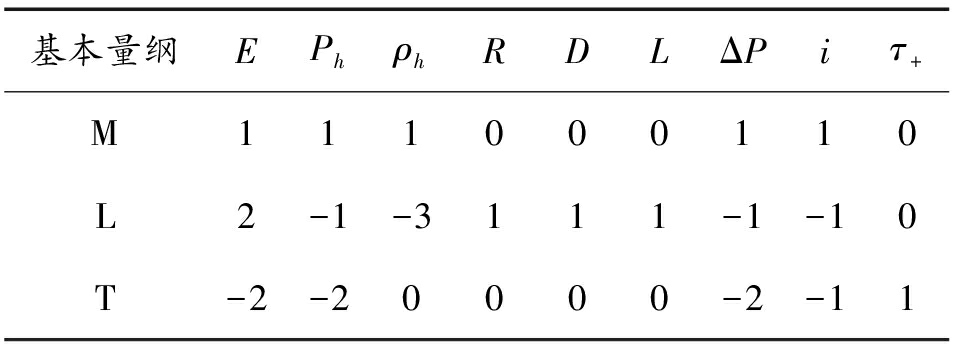
基本量纲EPhρhRDLΔPiτ+M111000110L2-1-3111-1-10T-2-20000-2-11
表5 隧道口外爆炸问题中变量的量纲幂次指数(行变换)
Table 5 Dimensional power index of variables in the explosion problem outside the tunnel entrance (after row transformation)
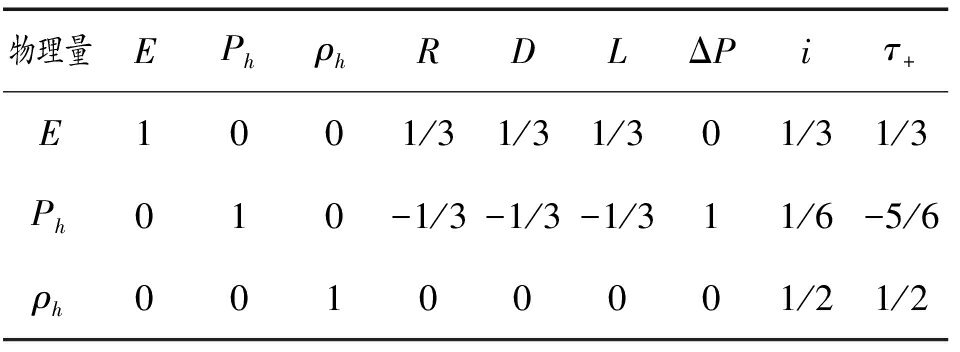
物理量EPhρhRDLΔPiτ+E1001/31/31/301/31/3Ph010-1/3-1/3-1/311/6-5/6ρh00100001/21/2
根据Π定理[23]可以得到无量纲表达式(13),基于守恒公式(8)—式(11)与无量纲表达式可知,隧道内冲击波超压峰值ΔP、冲量i、持时τ+与大气压强有关。
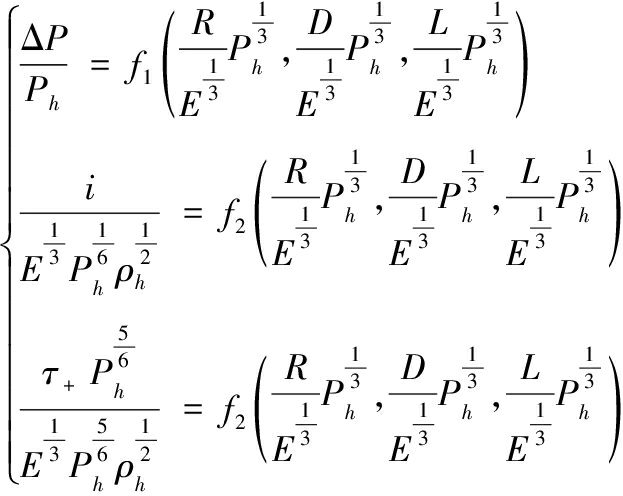
(13)
2.3 冲击波传播过程
炸药在隧道口外起爆示意图如图12所示,在半封闭空间内,由于壁面对冲击波的反射叠加作用使得冲击波的传播过程更加复杂,图13为炸药起爆后冲击波传播的几个典型时刻压力云图,根据图像可知,炸药在隧道口外爆炸后,形成高速外扩的球面波,并不断向外扩张,反射角增大,形成马赫波,在到达隧道口外和内壁壁面后发生剧烈的反射与扩散,此时冲击波的传播受到装药质量、隧道截面形状与传播距离等多个参量的影响,传播过程较为复杂,随着冲击波在隧道内持续传播,在隧道壁面的整流和定向作用下,紊乱的流场逐渐转化为近似平面的波(约5 m后)。
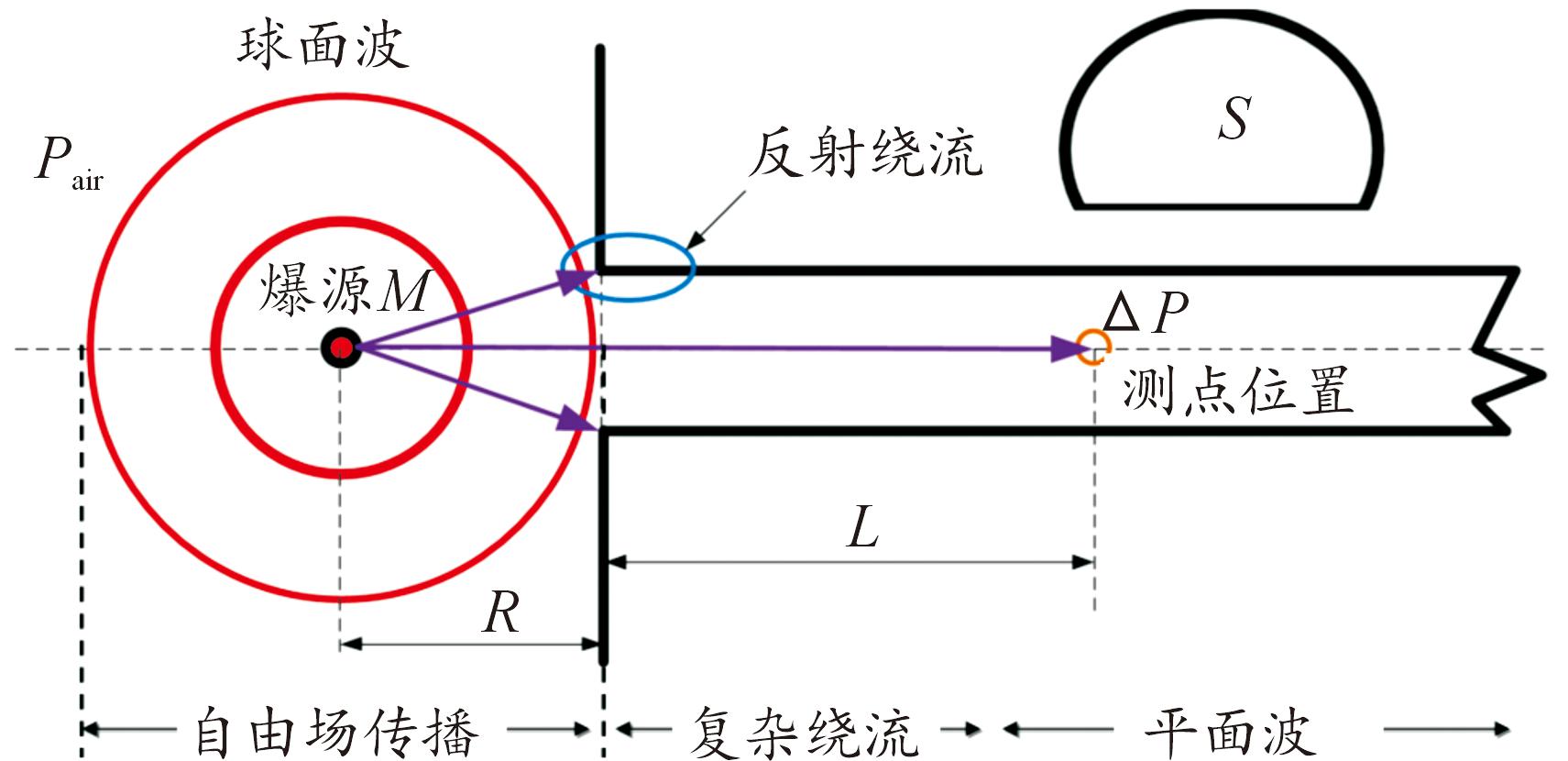
图12 隧道外爆示意图
Fig.12 Schematic diagram of tunnel explosion test
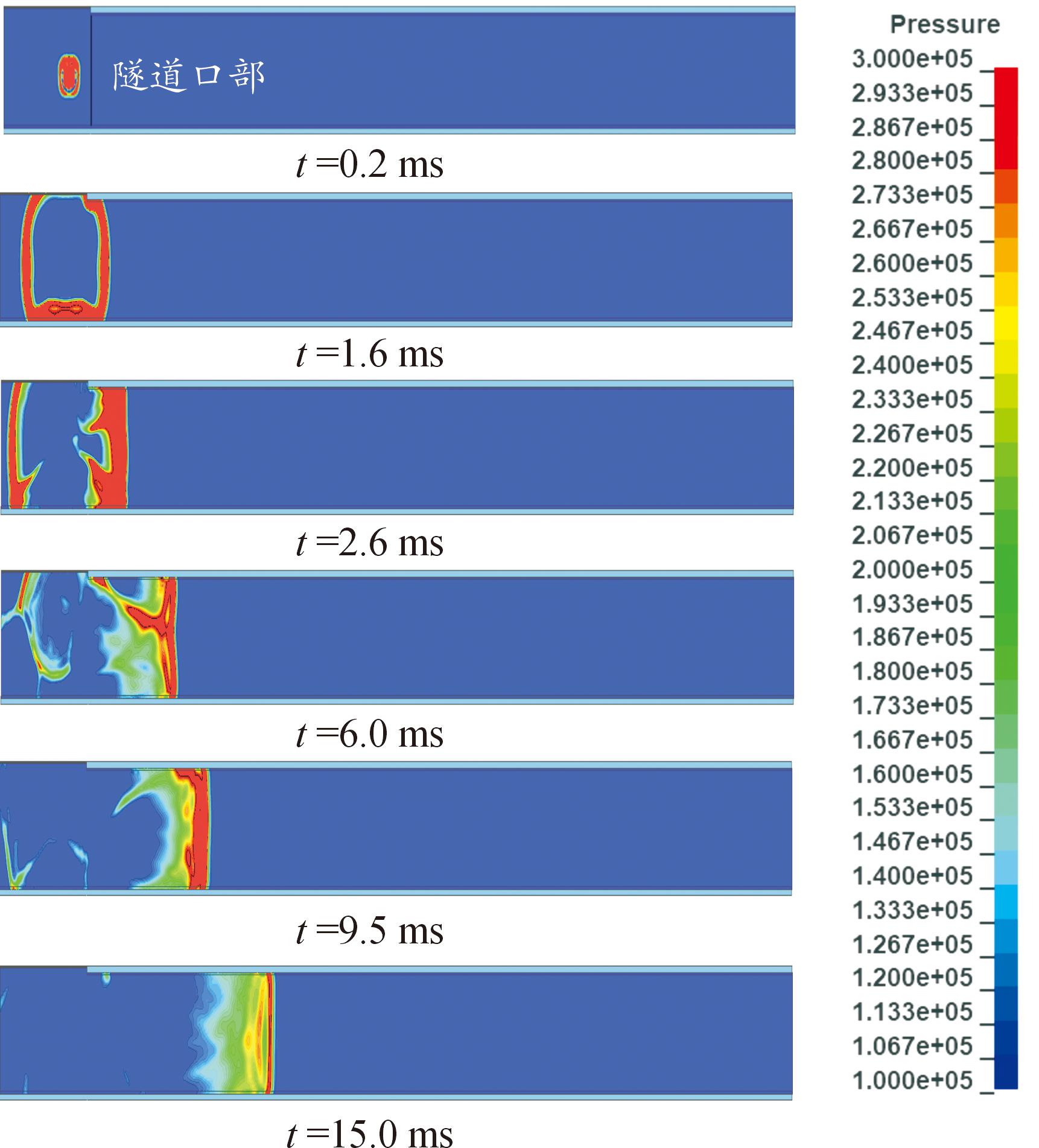
图13 几个典型时刻的压力云图
Fig.13 Pressure cloud diagrams at several typical moments
2.4 超压参数对比
2.4.1 超压峰值
不同海拔下隧道内测点处的超压峰值对比图如图14所示,数值模拟结果如表6所示,根据各个测点处超压峰值对比可以发现,海拔效应对于超压峰值具有明显的影响作用,在隧道前段,波阵面运动状态比较复杂,不同海拔下相同位置处超压峰值差距较大,随着波阵面持续运动,冲击波超压峰值随传播距离的增加而不断衰减,平面波形成后(约7 m),不同海拔下相同位置处超压峰值差值逐渐减小,相较于海平面环境,海拔1 000、2 500、4 500 m环境下,隧道内相同位置处的超压峰值平均下降10.27%、18.41%、25.45%。
表6 超压峰值对比
Table 6 Comparison of peak overpressure
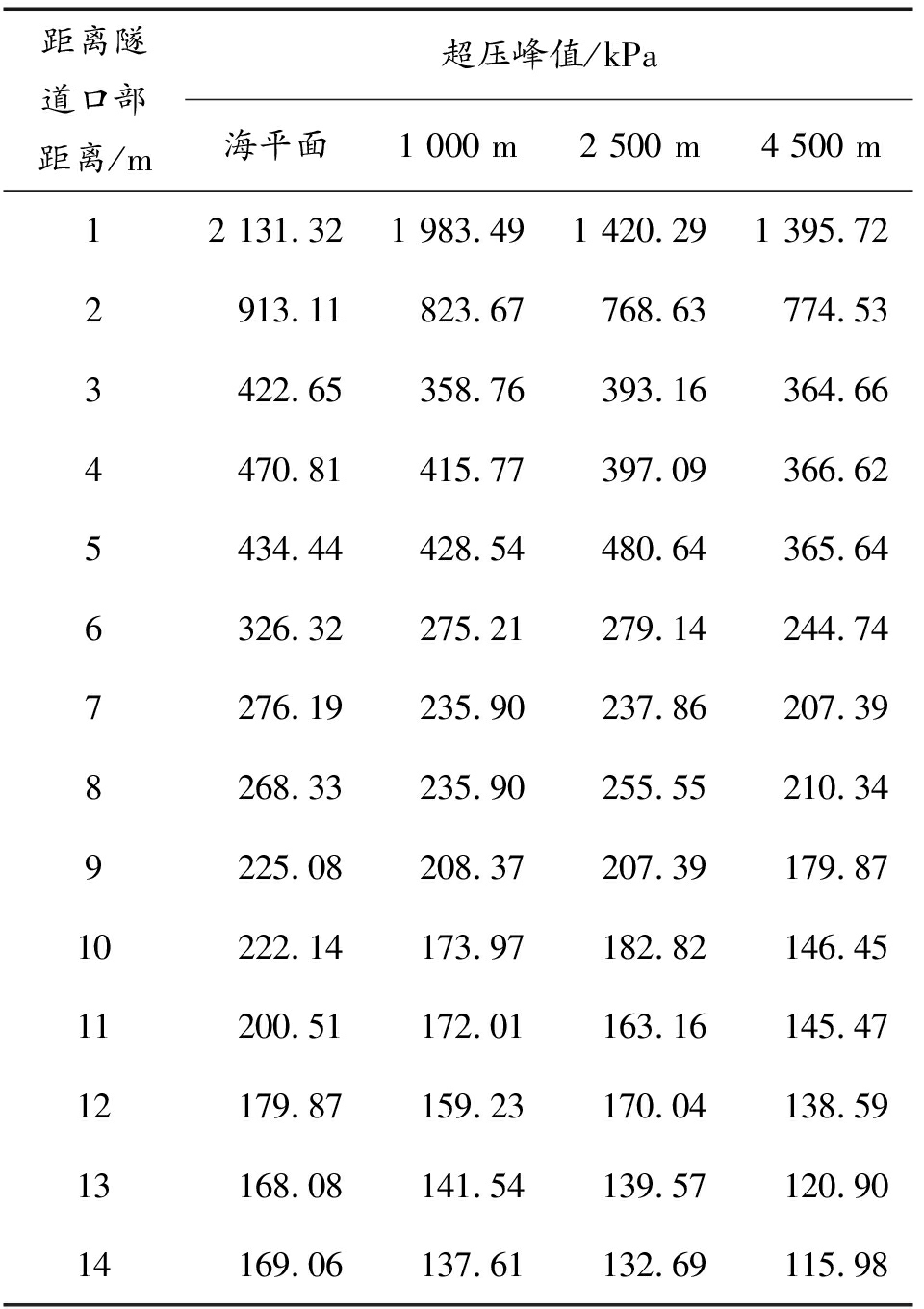
距离隧道口部距离/m超压峰值/kPa海平面1 000 m2 500 m4 500 m12 131.321 983.491 420.291 395.722913.11823.67768.63774.533422.65358.76393.16364.664470.81415.77397.09366.625434.44428.54480.64365.646326.32275.21279.14244.747276.19235.90237.86207.398268.33235.90255.55210.349225.08208.37207.39179.8710222.14173.97182.82146.4511200.51172.01163.16145.4712179.87159.23170.04138.5913168.08141.54139.57120.9014169.06137.61132.69115.98
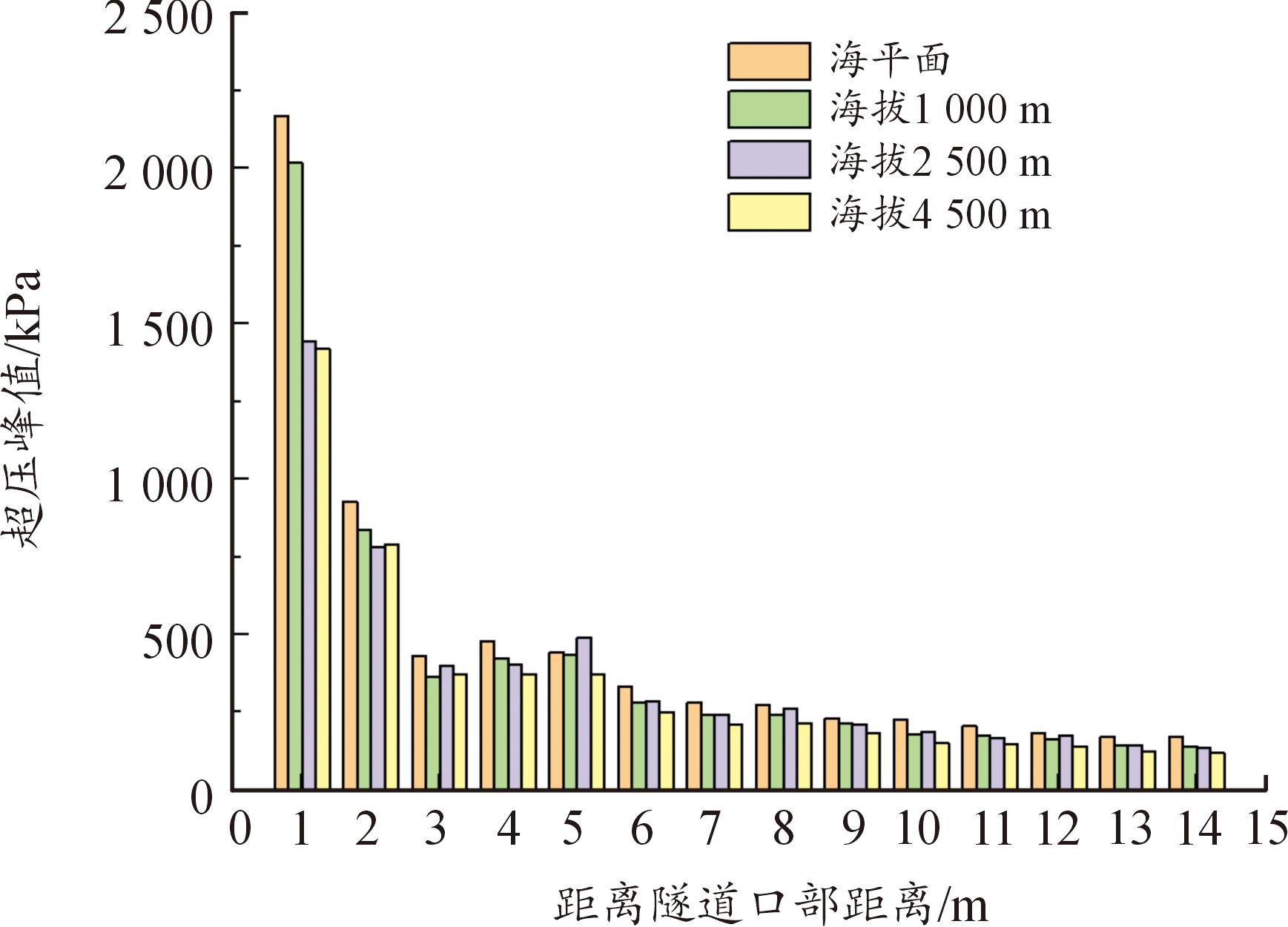
图14 超压峰值对比
Fig.14 Comparison of peak overpressure
2.4.2 正压冲量
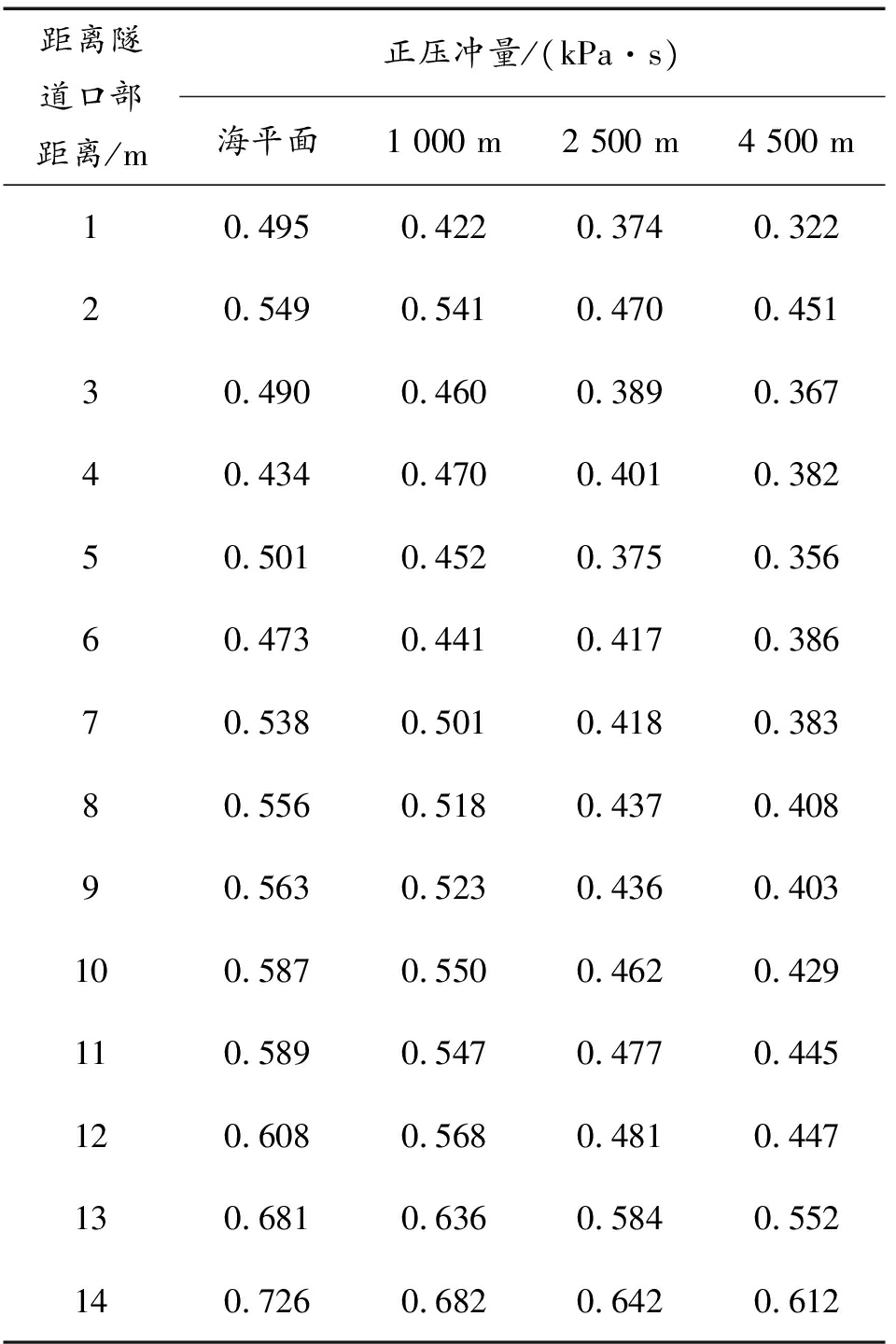
不同海拔下隧道内测点处的正压冲量对比如图15所示,数值模拟结果如表7所示,爆炸冲击波进入隧道后,近爆源区域隧道前段(0~6 m),测点处的正压冲量较小,随着冲击波在隧道内的传播,隧道壁面对冲击波的叠加反射作用,冲击波的正压冲量表现为先增加后减小;在隧道的中段(6~11 m),冲击波的正压冲量数值表现出一定的稳定性,在隧道口段(11~15 m),冲击波正压冲量上升,在此区域内靠近隧道出口,存在一定的泄压状况,对正压作用时间有一定的延长作用。根据数值对比可知海拔效应对于超压峰值具有明显的影响作用,相比较于海平面环境,海拔1 000、2 500、4 500 m环境下,隧道内相同位置处的超压冲量平均下降6.15%、18.32%、23.71%。
表7 正压冲量对比
Table 7 Comparison of positive pressure impulse
距离隧道口部距离/m正压冲量/(kPa·s)海平面1 000 m2 500 m4 500 m10.4950.4220.3740.32220.5490.5410.4700.45130.4900.4600.3890.36740.4340.4700.4010.38250.5010.4520.3750.35660.4730.4410.4170.38670.5380.5010.4180.38380.5560.5180.4370.40890.5630.5230.4360.403100.5870.5500.4620.429110.5890.5470.4770.445120.6080.5680.4810.447130.6810.6360.5840.552140.7260.6820.6420.612
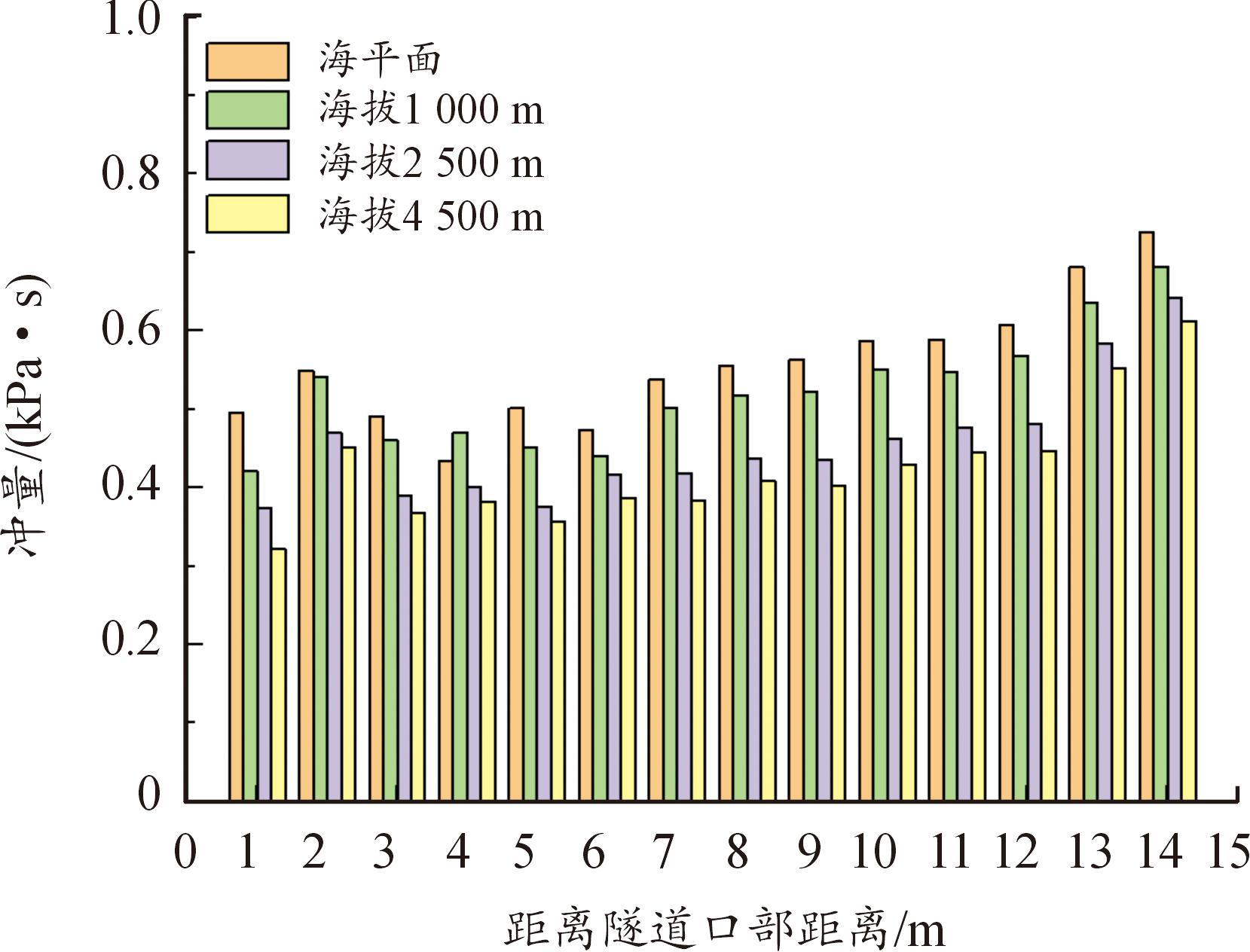
图15 正压冲量对比
Fig.15 Comparison of positive pressure impulse
2.4.3 正压持时
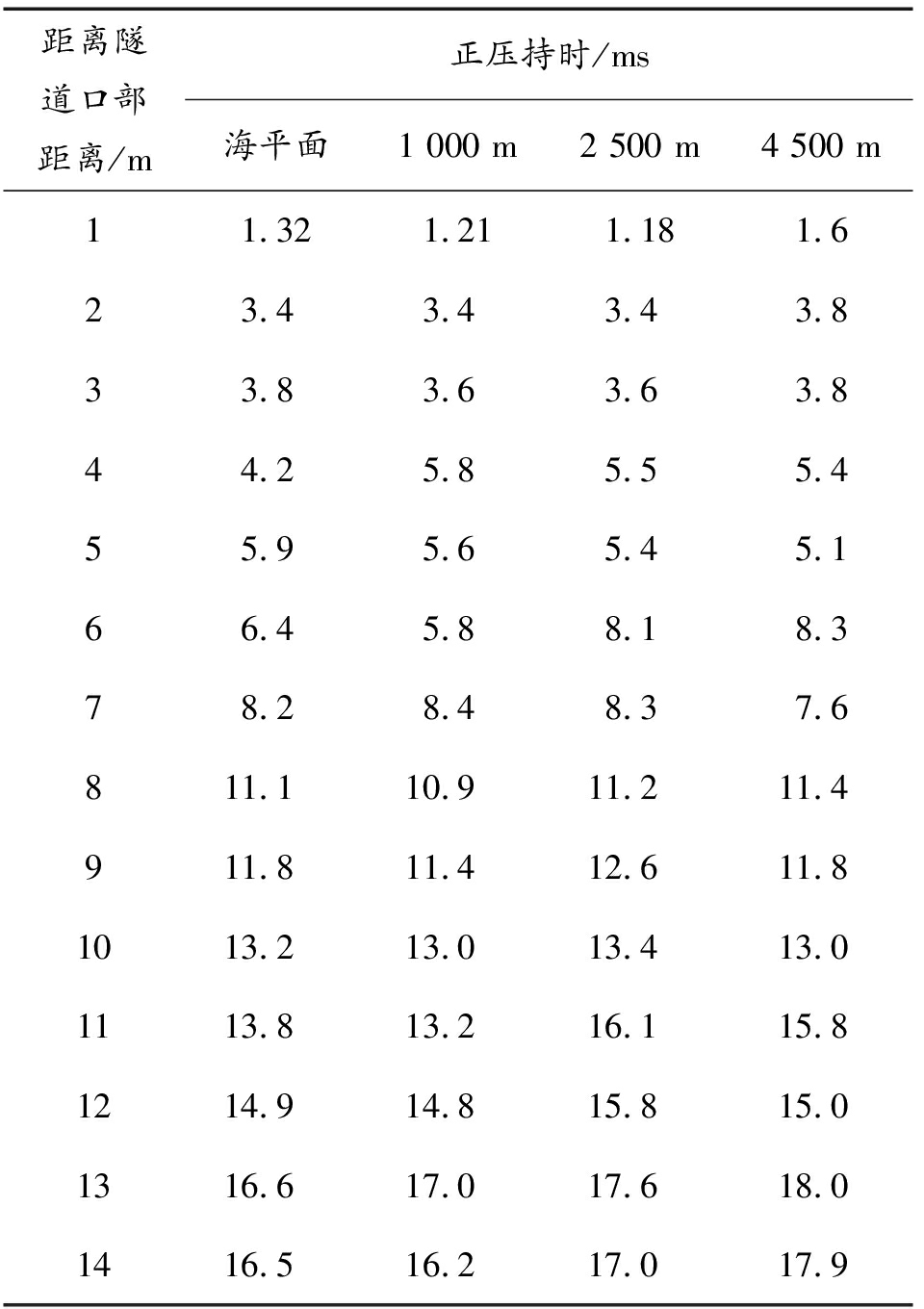
不同海拔下隧道内测点处的超压持续时间对比如图16所示,数值模拟结果如表8所示,入射冲击波正压持时沿冲击波传播方向不断增加,在隧道前段,海拔效应对于正压持时的影响不明显,随着波阵面持续传播,在形成平面波后(约7 m后),不同海拔下正压持时呈现一定差异,整体上表现为在隧道中后段,正压持时随着环境海拔的增加而增加。
表8 正压持时对比
Table 8 Comparison of overpressure holding time
距离隧道口部距离/m正压持时/ms海平面1 000 m2 500 m4 500 m11.321.211.181.623.43.43.43.833.83.63.63.844.25.85.55.455.95.65.45.166.45.88.18.378.28.48.37.6811.110.911.211.4911.811.412.611.81013.213.013.413.01113.813.216.115.81214.914.815.815.01316.617.017.618.01416.516.217.017.9
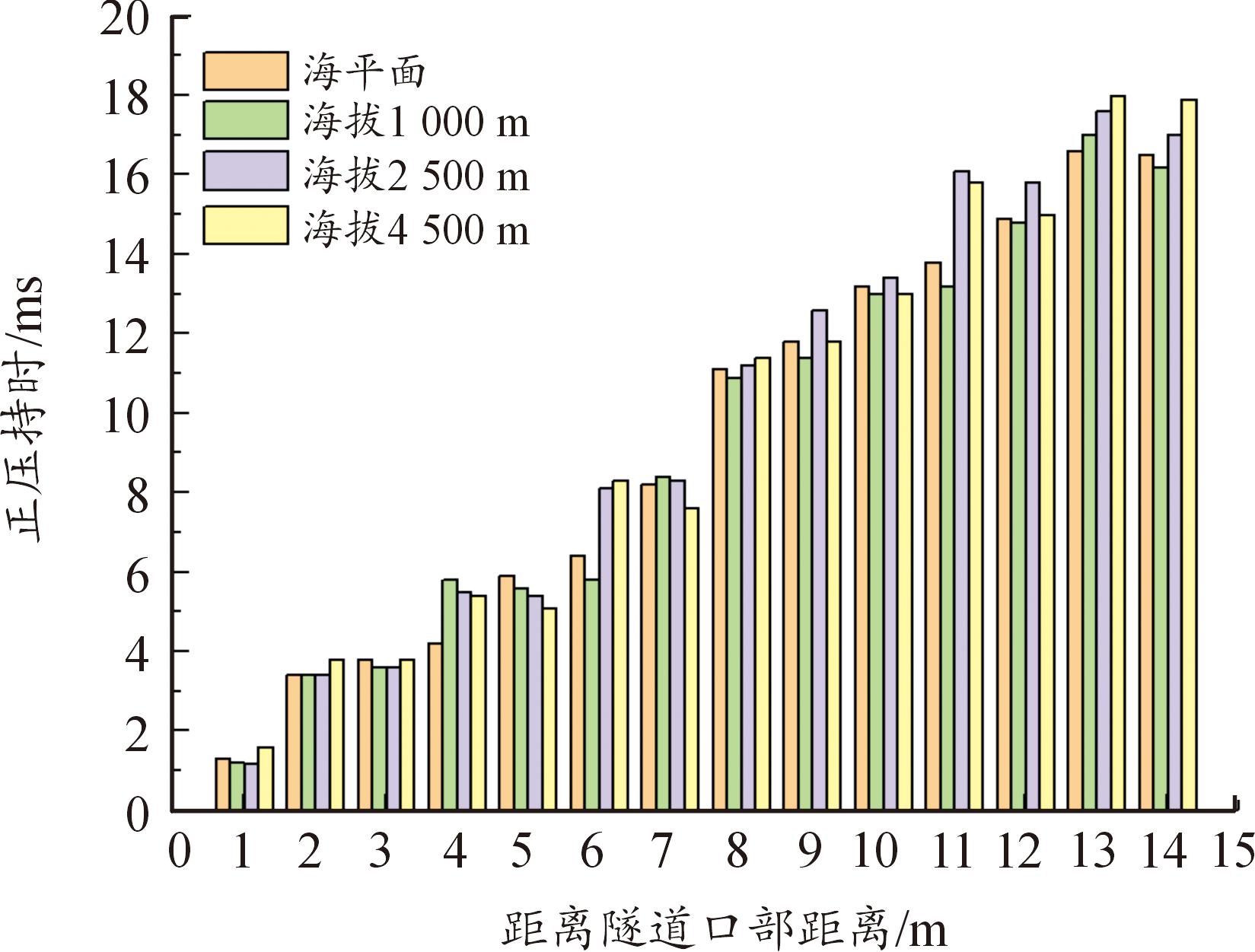
图16 正压持时对比
Fig.16 Comparison of overpressure holding time
3 结论
基于4 500 m高原靶场隧道外爆试验与LS-DYNA有限元软件分析了海拔效应对隧道内冲击波超压参数的影响效果。建立了典型海拔环境下的隧道外爆有限元模型,模拟了TNT炸药隧道口外起爆、爆炸冲击波形成与传播过程,通过试验数据与仿真结果对比验证了数值模拟的有效性,对比选定测点处的冲击波超压峰值、正压冲量、持时,得出以下结论:
1) TNT炸药在隧道口起爆后,产生向外围扩展的球状冲击波,在波阵面进入隧道后与隧道壁面发生多次反射,随着反射波不断向前叠加,反射波能量不断衰减,隧道内逐渐形成平面波;
2) 随着海拔的增高,距离隧道口部相同距离处的超压峰值降低,相比于海平面环境,海拔1 000、2 500、4 500 m条件下距离口部相同距离的测点处的冲击波的超压峰值分别降低10.27%、18.41%、25.45%;
3) 随着海拔的增高,距离隧道口部相同距离处冲击波的正压冲量降低,相比较于海平面环境,海拔1 000、2 500、4 500 m条件下距离口部相同距离的测点处的冲击波的正压冲量平均降低6.15%、18.32%、23.71%;
4) 在隧道前段不同海拔下各测点处冲击波超压持时差距不明显,在隧道中后段,超压持时随着环境海拔的增加而增加。
[1] 奧尔连科.爆炸物理学[M].孙成讳,译.3版.北京:科学出版社,2011.ERLIENKE.Explosion physics[M].Translated by Sun Chengxi.3 ed.Beijing:Science Press,2011.
[2] SACHS R G.The dependence of blast on ambient pressure and temperature:466[R].Aberdeen Proving Ground,MD,USA:Ballistic Research Laboratories,1944.
[3] VELDMAN R L,NANSTEEL M W,CHEN C C T,et al.The effect of ambient pressure on blast reflected impulse and overpressure[J].Experimental Techniques,2017,41(3):227-236.
[4] 姚成宝,浦锡锋,寿列枫.强爆炸冲击波在不均匀空气中传播数值模拟[C]//中国计算力学大会2014暨第三届钱令希计算力学奖颁奖大会论文集.中国力学学会计算力学专业委员会,2014:1-7.YAO Chengbao,PU Xifeng,SHOU Liefeng,et al.Numerical simulation of strong explosion shock wave propagation in non-uniform air[C]//Proceedings of the 2014 China Computational Mechanics Conference and the third Qian Lingxi Computational Mechanics Award presentation Conference.rofessional Committee of Computational Mechanics of Chinese Society of Mechanics,2014:1-7.
[5] 姚成宝,王宏亮,张柏华,等.TNT空中爆炸冲击波传播数值模拟及数值影响因素分析[J].现代应用物理,2014(1):39-44.YAO Chengbao,WANG Hongliang,ZHANG Baihua,et al.Numerical simulation of TNT air explosion shock wave propagation and analysis of numerical influencing factors[J].Modern Applied Physics,2014(1):39-44.
[6] 谢雪腾.高原环境爆炸冲击波传播特性的数值模拟与实验研究[D].南京:南京理工大学,2017.XIE Xueteng.Numerical simulation and experimental study on the propagation characteristics of explosion shock wave in plateau environment[D].Nanjing:Nanjing University of Science and Technology,2017.
[7] 邓国强.常规爆炸空气冲击波参数海拔高度影响分析[J].防护工程,2019,41(3):26-32.DENG Guoqiang.Analysis of the influence of altitude of conventional explosion air shock wave parameters[J].Protection Engineering,2019,41 (3):26-32.
[8] 宋水舟.不同真空度条件下结构内爆炸冲击波特性的数值模拟研究[D].太原:太原理工大学,2018.SONG Shuizhou.Numerical simulation of explosion shock wave characteristics in structures under different vacuum conditions[D].Taiyuan:Taiyuan University of Technology,2018.
[9] 甘朝虹,陈新华.一种空气冲击波超压随密度变化的计算模型[J].科技资讯,2019,17(32):57-59,62.GAN Chaohong,CHEN Xinhua.A calculation model for the variation of air shock wave overpressure with density[J].Science and Technology Information,2019,17 (32):57-59,62.
[10] 杨科之,杨秀敏.坑道内化爆冲击波的传播规律[J].爆炸与冲击,2003,23(1):37-40.YANG Kezhi,YANG Xiumin.Propagation law of chemical explosion shock wave in tunnel[J].Explosion and Shock Waves,2003,23(1):37-40.
[11] 石成英,梅宗书,王争,等.近地爆冲击波在洞库内的传播特性[J].四川兵工学报,2015(11):1-3.SHI Chengying,MEI Zongshu,WANG Zheng,et al.Propagation characteristics of near-ground burst shock wave in cave vault[J].Journal of Sichuan Ordnance,2015(11):1-3.
[12] 李秀地,郑颖人,李列胜,等.长坑道中化爆冲击波压力传播规律的数值模拟[J].爆破器材,2005,34(5):4-7.LI Xiudi,ZHENG Yingren,LI Liesheng,et al.Numerical simulation of pressure propagation of chemical explosion shock wave in long tunnel[J].Explosive Materials,2005.34 (5):4-7.
[13] 任新见,张庆明,薛一江.坑道口部B炸药爆炸冲击波传播速度模型试验研究[J].振动与冲击,2012,31(7):71-73,88.REN Xinjian,ZHANG Qingming,XUE Yijiang.Model experimental study on shock wave propagation velocity of explosive B in tunnel mouth[J].Journal of Vibration and Shock,2012,31(7):71-73,88.
[14] 徐利娜,雍顺宁,王凤丹,等.直坑道内爆炸冲击波超压传播规律研究[J].测试技术学报,2014,28(2):114-118.XU Lina,YONG Shunning,WANG Fengdan,et al.Study on overpressure propagation law of explosion shock wave in straight tunnel[J].Journal of Test and Measurement Technology,2014,28 (2):114-118.
[15] 罗婷,胡卓焕,杨茉.有限空间内飞沫颗粒传播规律的数值研究[J].流体机械,2021,49(7):83-90.LUO Ting,HU Zhuohuan,YANG Mal.Numerical study on the propagation law of droplet particles in a finite space[J].Fluid Machinery,2021,49(7):83-90.
[16] 曹宇航,张晓伟,张庆明.框架结构建筑物内爆炸冲击波传播规律研究[J].兵器装备工程学报,2022,43(3):189-195.CAO Yuhang,ZHANG Xiaowei,ZHANG Qingming.Study on the propagation law of explosion shock wave in frame structure buildings[J].Journal of Ordnance Equipment Engineering,2022,43(3):189-195.
[17] 穆朝民,任辉启,李永池,等.爆炸冲击波在复杂坑道内传播规律的数值研究[J].爆破器材,2008,37(5):1-4.MU Chaomin,REN Huiqi,LI Yongchi,et al.Numerical study on the propagation law of explosion shock wave in complex tunnel[J].Explosive Materials,2008,37(5):1-4.
[18] 钱翼稷.空气动力学[M].北京:北京航空航天大学出版社,2004.QIAN Yiji.Aerodynamics[M].Beijing:Beijing University of Aeronautics and Astronautics Press,2004.
[19] 陈龙明,李志斌,陈荣,等.高原环境爆炸冲击波传播特性的实验研究[J].爆炸与冲击,2022,42(5):51-61.CHEN Longming,LI Zhibin,CHEN Rong,et al.Experimental study on the propagation characteristics of explosion shock wave in plateau environment[J].Explosion and Shock Waves,2022,42(5):51-61.
[20] HALLQUIST J O.LS-DYNA Theoretical Manual[Z].1991.
[21] 宁建国,王成,马天宝.爆炸与冲击动力学[M].北京:国防工业出版社,2010.NING Jianguo,WANG Cheng,MA Tianbao.Explosion and impact dynamics[M].Beijing:national Defense Industry Press,2010.
[22] 李秀地,孙建虎,王起帆,等.高等防护工程[M].北京:国防工业出版社,2016.LI Xiudi,SUN Jianhu,WANG Qifan,et al.Advanced protection engineering[M].Beijing:national Defense Industry Press,2016.
[23] BRIDGMAN P W.Dimensional analysis[M].2nd ed.New Haven,USA:Yale University Press,1931:40-46.