0 引言
热防护是高空高速飞行器执行飞行任务时需要考虑的关键因素之一,在实际热防护系统的设计和数值模拟过程中,出于对问题的简化,通常认为飞行器具有连续光滑的表面,然而实际飞行过程中由于表面烧蚀等因素使得飞行器表面不可避免地出现缝隙或缺陷结构,这种结构会形成类似于空腔流动的结构。
空腔流动是由一个后台阶与一个前台阶的组合流动,当前台阶与后台阶的距离相对较远时,两个流动互不干扰,可以分解成2种流动分别进行研究;而当前后台阶的距离相对较近时,2种流动之间可能会形成相互干扰,随着距离的靠近,干扰也会变得剧烈。形成扰动的同时还会引发一些其他的流动结构,如回流旋涡、边界层与剪切层流动、声波、激波[1-6]等。在实际的应用中,往往需要在飞行器的表面增加一定的空腔结构来满足和强化具体的应用需求。例如,在高超声速飞行器钝头体前缘引入环形空腔,使飞行器头部形成“冷却环”,有效降低了局部热流[7];采用内埋式气动布局飞行器的武器舱,可以有效减小约30%的飞行阻力,然而打开武器舱门后舱内会出现空腔结构,高速气流流经此区域时会对舱内武器的安全投放产生一定影响[8];另一方面,由于制造公差、非相似材料的不均匀碰撞或者传感器的安装,也会导致飞行器的表面不可避免地出现缝隙或缺陷这种类空腔结构,使得飞行器在飞行过程中出现安全隐患[9]。因此为了更好的解决带空腔布局的高超声速飞行器几何结构的设计问题,对空腔流动特性的研究也随之而来。
Charwat等[10-11]学者较早地对空腔绕流进行研究,通过上游台阶拐角处形成的剪切层的行为来表征。根据空腔的长深比(L/D)可以分为开式空腔(1< L/D<10)、闭式空腔(L/D>14)和过渡式空腔(10< L/D<14)。开式空腔和闭式空腔内流体的流动特性并不相同。对于开式空腔,剪切层和边界层并未触及腔体底部,高速自由流对剪切层的冲击使其产生自持振荡,这使得空腔周围的气动噪声增大,给腔内的部署设施以及空腔自身结构的安全带来隐患;对于闭式空腔,边界层和剪切层逐渐触及腔体底部,空腔内回流区域一分为二,使得空腔底部的压强增大,对空腔内部组件的安全分离产生不利的影响。空腔流动分类如图1所示。Guo等[12]给出了不同长深比和改变壁面倾角对过渡流区空腔流动结构的影响,发现:当长深比L/D>7时腔内流动已变为闭式结构,改变壁面倾角可以有效减小回流区域。Palharini等[13-14]采用DSMC方法研究了80 km过渡流区几何尺寸对空腔内流动结构的影响,发现:L/D=4时空腔就已变为闭式,而连续流产生类似结果对应的L/D=14。靳旭红[15]等给出了三维效应与稀薄效应对空腔流动的影响规律,发现:飞行高度越高,三维阻塞效应约明显,表面热流与二维结果相差较大。
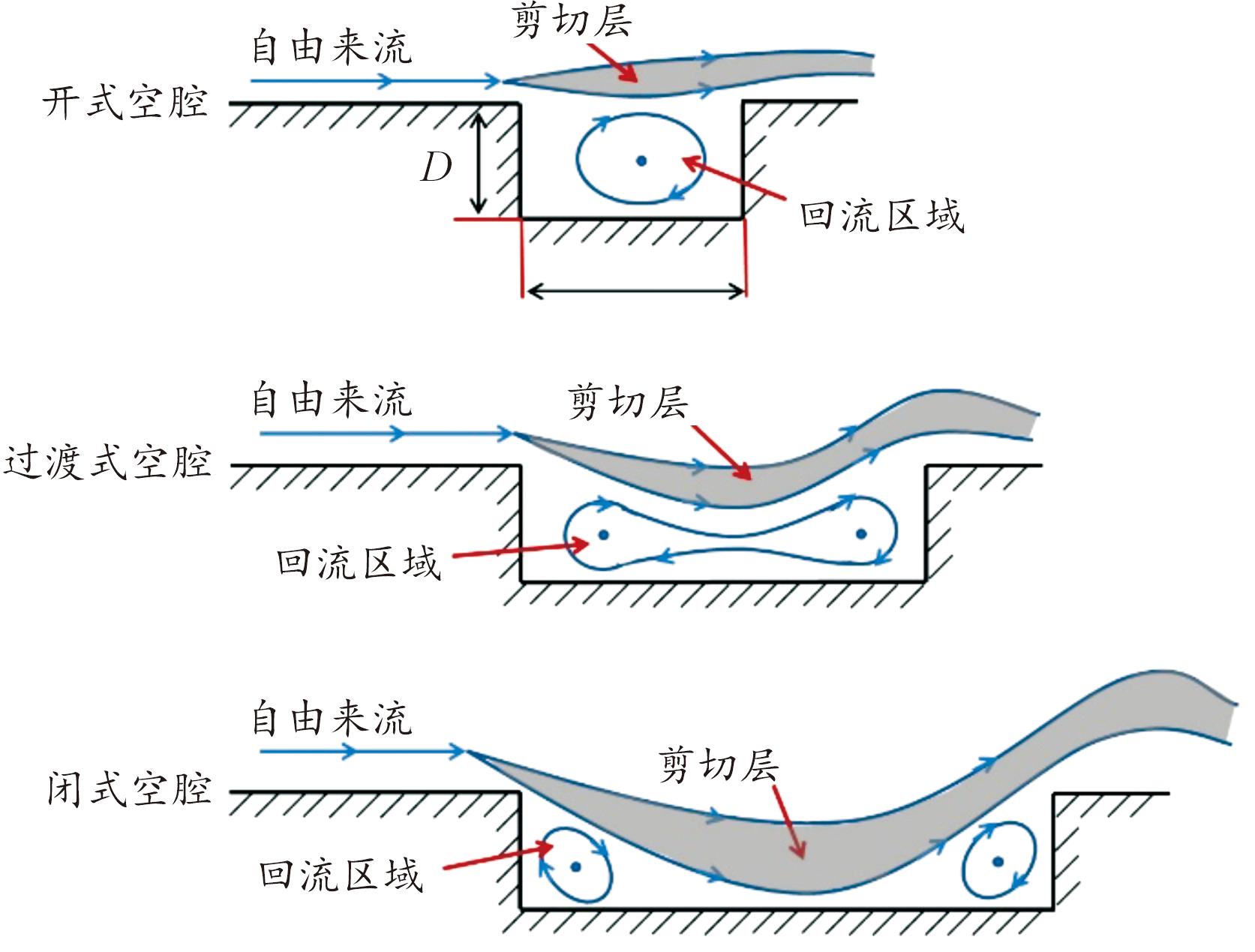
图1 不同类型空腔示意图
Fig.1 Schematic diagram of different types of cavities
目前对于高超声速空腔流动的研究主要集中在连续流区,对于过渡流区的研究相对较少,同时考虑化学反应和稀薄气体效应的研究更为匮乏。本文在Guo[12]和Palharini等[13-14]学者的工作基础上,从过渡流区高超声速空腔流动出发,对空腔内部的高热流区域进行了精确定位,定量分析了化学反应对空腔流动的影响,同时获得了发生化学反应后空腔内不同组分的粒子分布,为高空高速飞行器精细热防护设计提供参考。
1 计算方法
1.1 DSMC方法
DSMC方法是直接研究分子微观运动的统计学方法,克服了解玻尔兹曼方程的复杂性。该方法通过大量的模拟分子来仿真真实分子的微观运动情况,其本质是在Δt时间内,通过运动子程序和碰撞子程序将分子的运动和分子的碰撞这2个耦合的过程进行解耦,再通过采样子程序采集到每个流场单元的宏观流动数据,最后按单元编号将数据输出。
1.2 五组元化学反应
本文中考虑的化学反应类型有3种,分别为离解反应、单原子复合反应和交换原子反应,具体的化学反应式如下:
N2+N2→N2+N+N
(1)
N2+M→N+N+M
(2)
O2+M→O+O+M
(3)
NO+M→N+O+M
(4)
O+O→O2
(5)
N+N→N2
(6)
O+N2→NO+N
(7)
N+O2→NO+O
(8)
NO+N→O+N2
(9)
NO+O→N+O2
(10)
式(1)—式(4)为离解反应,式(5)—式(6)为复合反应,式(7)—式(10)为原子交换反应。离解反应与原子交换反应为吸热反应,复合反应为放热反应。DSMC方法中化学反应通过构造抽样概率函数,并采用取舍取样法来实现。
1.3 DSMC程序验证
本文中的DSMC程序通过与Gallis[16]的70°钝锥算例的结果进行对比验证,其具体几何参数如图2所示,其中Rb=25 mm,Rc=6.25 mm,Rn=12.5 mm。计算网格如图3所示。网格节点和网格单元数分别为46 352、95 508。下边界为对称边界条件,左边界为入口边界条件,右边界为出口边界条件,上边界为自由流动边界条件。来流气体为氮气,其分子性质见表1,来流速度为1 502 m/s,来流分子数密度为3.720 4×1020,分子平均自由程为0.003 48 m,努森数为0.032。分子与物面作用采用漫反射模型,分子碰撞模型为变径硬球模型,设置流场中模拟分子数约为2.08×106,其他详细的计算参数见表2。
表1 氮气分子性质
Table 1 Nitrogen molecular properties
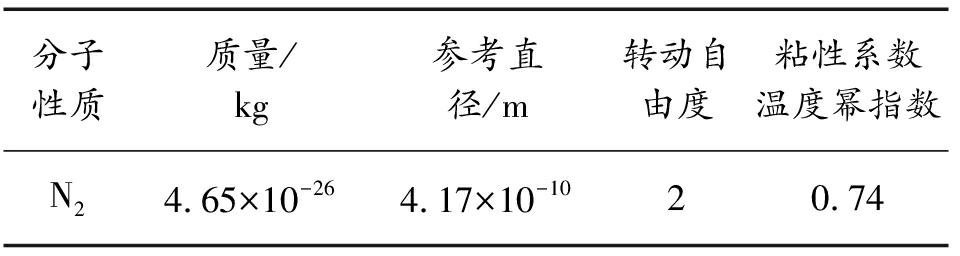
分子性质质量/kg参考直径/m转动自由度粘性系数温度幂指数N24.65×10-264.17×10-1020.74
表2 计算参数设置
Table 2 Parameter settings
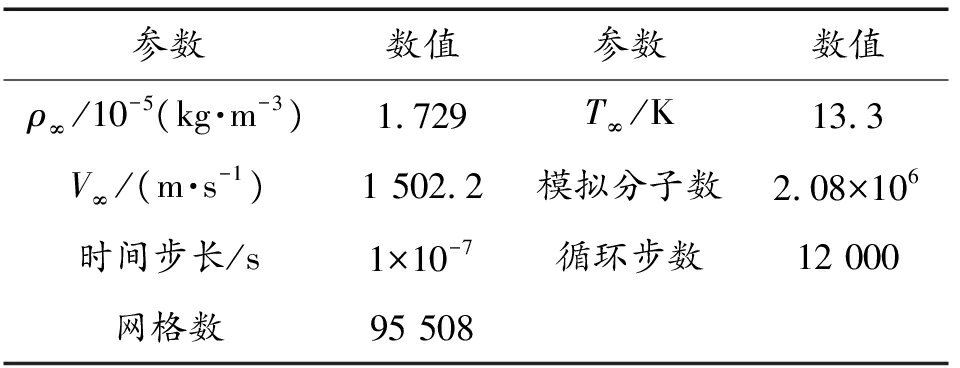
参数数值参数数值ρ∞/10-5(kg·m-3)1.729T∞/K13.3V∞/(m·s-1)1 502.2模拟分子数2.08×106时间步长/s1×10-7循环步数12 000网格数95 508
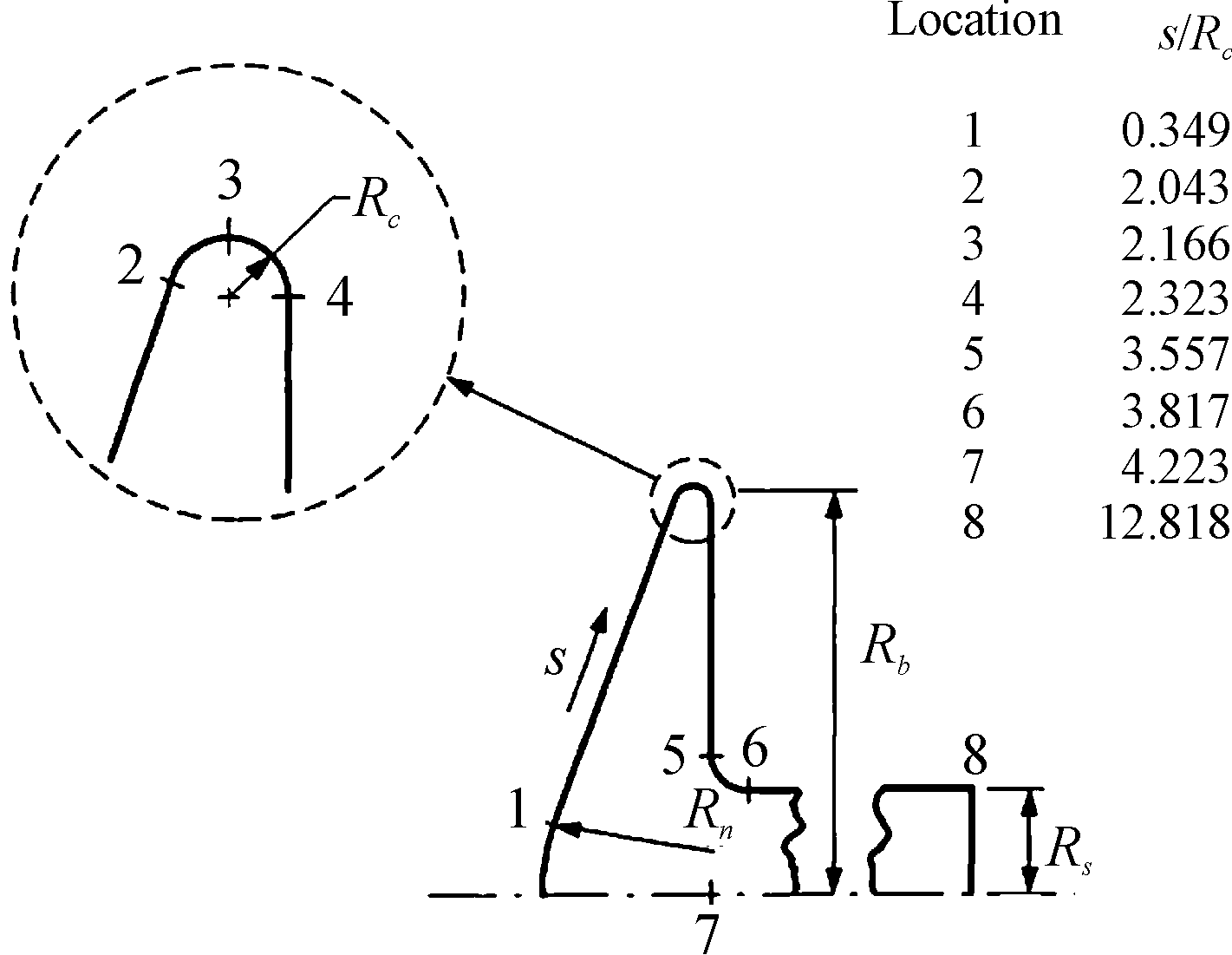
图2 70°钝锥几何参数
Fig.2 Geometric parameters for a 70 ° blunt cone
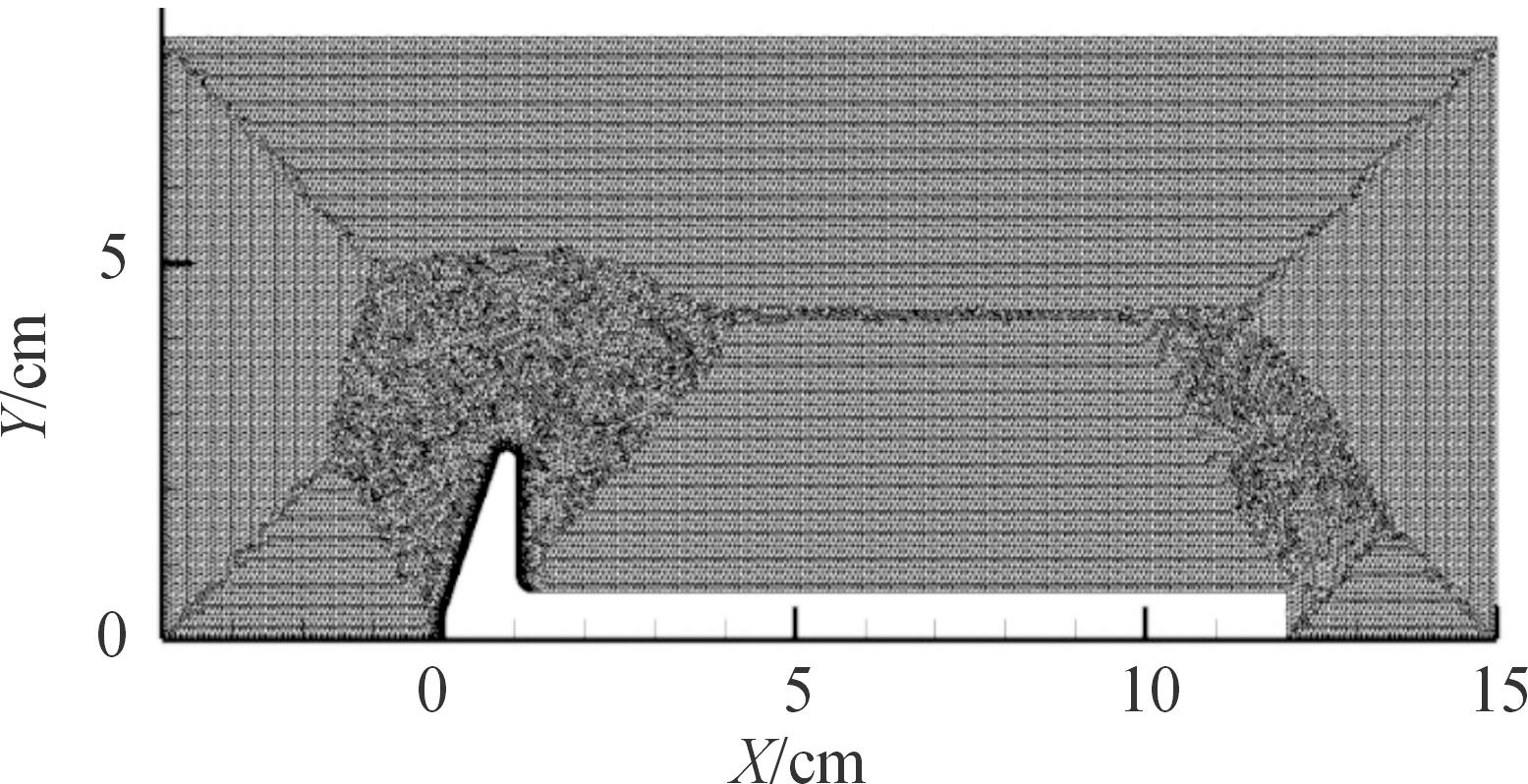
图3 70°钝锥计算网格
Fig.3 70° blunt cone computational grid
图4为70°钝锥绕流算例的密度、温度和压力云图。图5为本文中程序计算结果与文献值得对比,钝锥头部至顶端处的压力和热流与文献值稍有差异,原因在于该处的分子碰撞与化学反应较为剧烈,导致随机值的误差增大所致,尾部分子运动程度较为平缓,总体来看结果与文献值吻合较好。
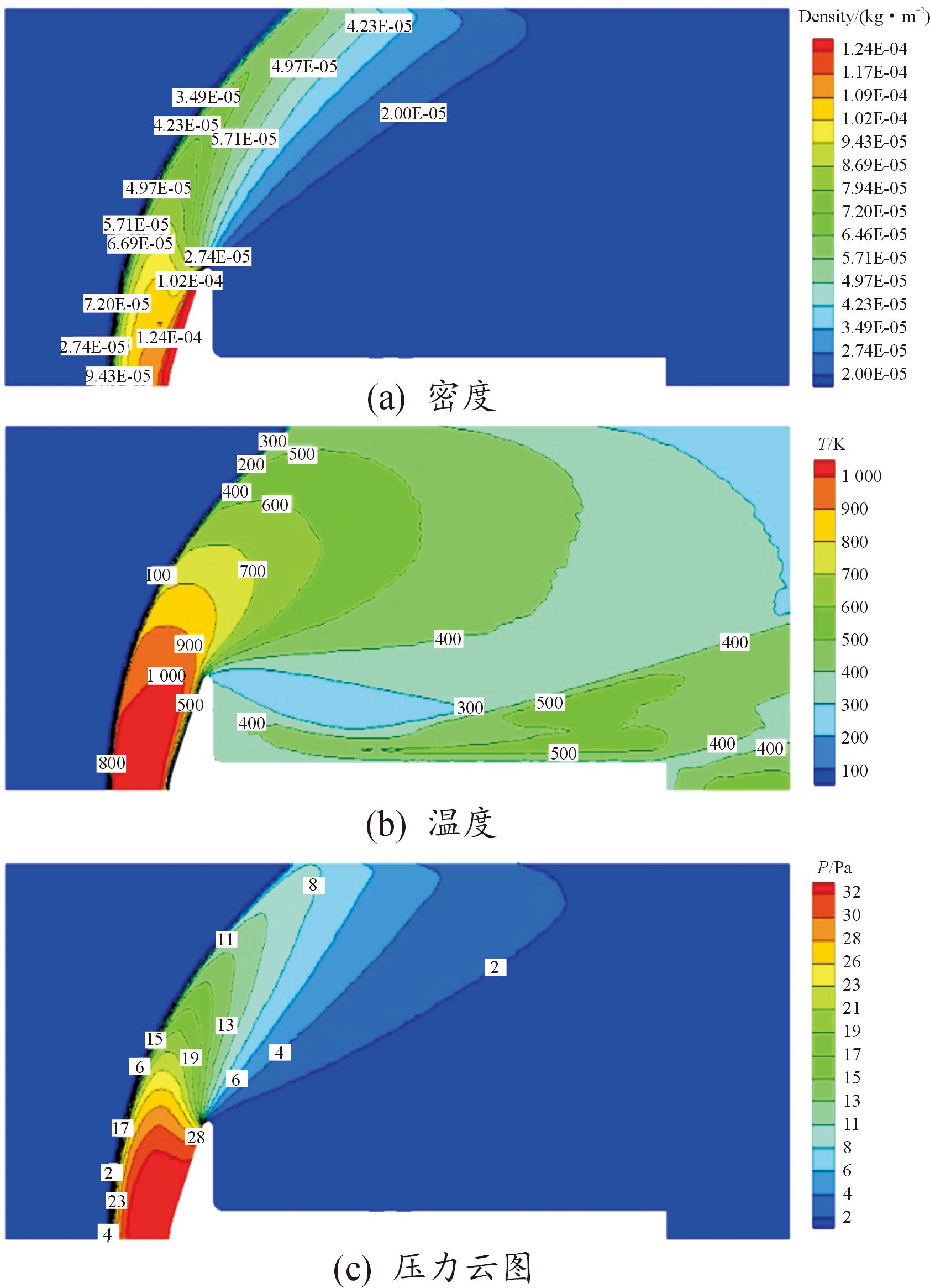
图4 70°钝锥算例(a)密度、(b)温度、(c)压力云图
Fig.4 70° blunt cone calculation example (a) density, (b) temperature,(c) pressure
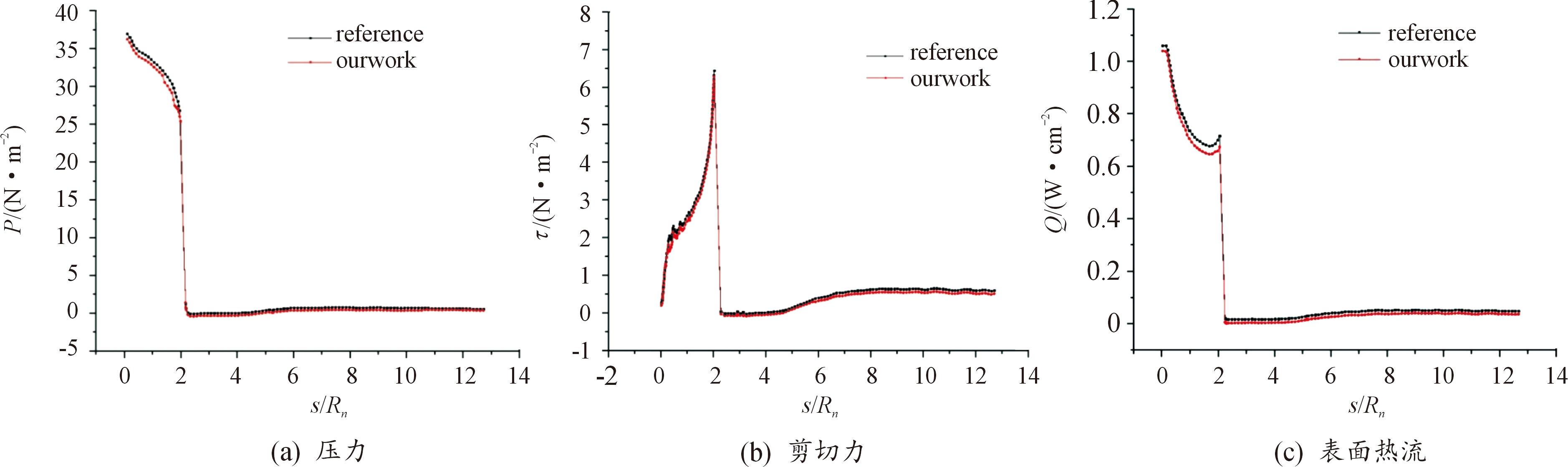
图5 70°钝锥算例算例与文献值对比结果
Fig.5 Comparison of 70° blunt cone calculation examples and literature values
2 计算结果
2.1 空腔几何特性对流动的影响
用于研究计算的空腔模型如图6所示,空腔的深度D=0.1 m,前缘壁面的长度为0.3 m,后缘壁面的长度为0.1 m。空腔的长深比L/D=1-10,间隔为1。时间步长的确定受到来流速度和网格尺度的共同影响,一般约定时间步长与来流速度的乘积要小于网格的线性尺度。模拟分子数的大小主要由计算域中的网格数决定,一般约定每个网格单元中的模拟分子数约为20~30个,这样才能确保每个网格单元中取样值的准确性。自由来流条件见表3。表4给出了长深比为6算例中网格数、分子数与时间步长等计算参数的具体设置。
表3 自由来流条件
Table 3 Free stream conditions

H/kmP∞/PaT∞/Kρ∞/(kg·m-3)n∞/m-36021.96247.03.10×10-46.54×1021
表4 L/D=6算例的计算参数
Table 4 Computational parameters for L/D=6
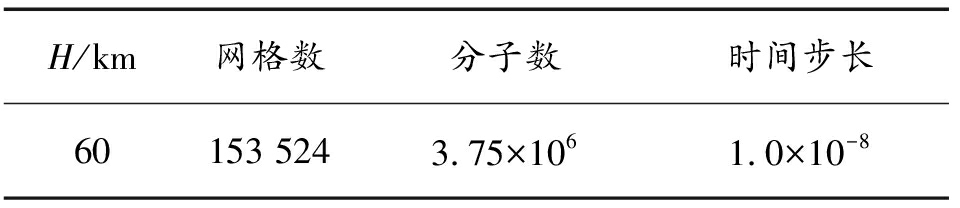
H/km网格数分子数时间步长60153 5243.75×1061.0×10-8
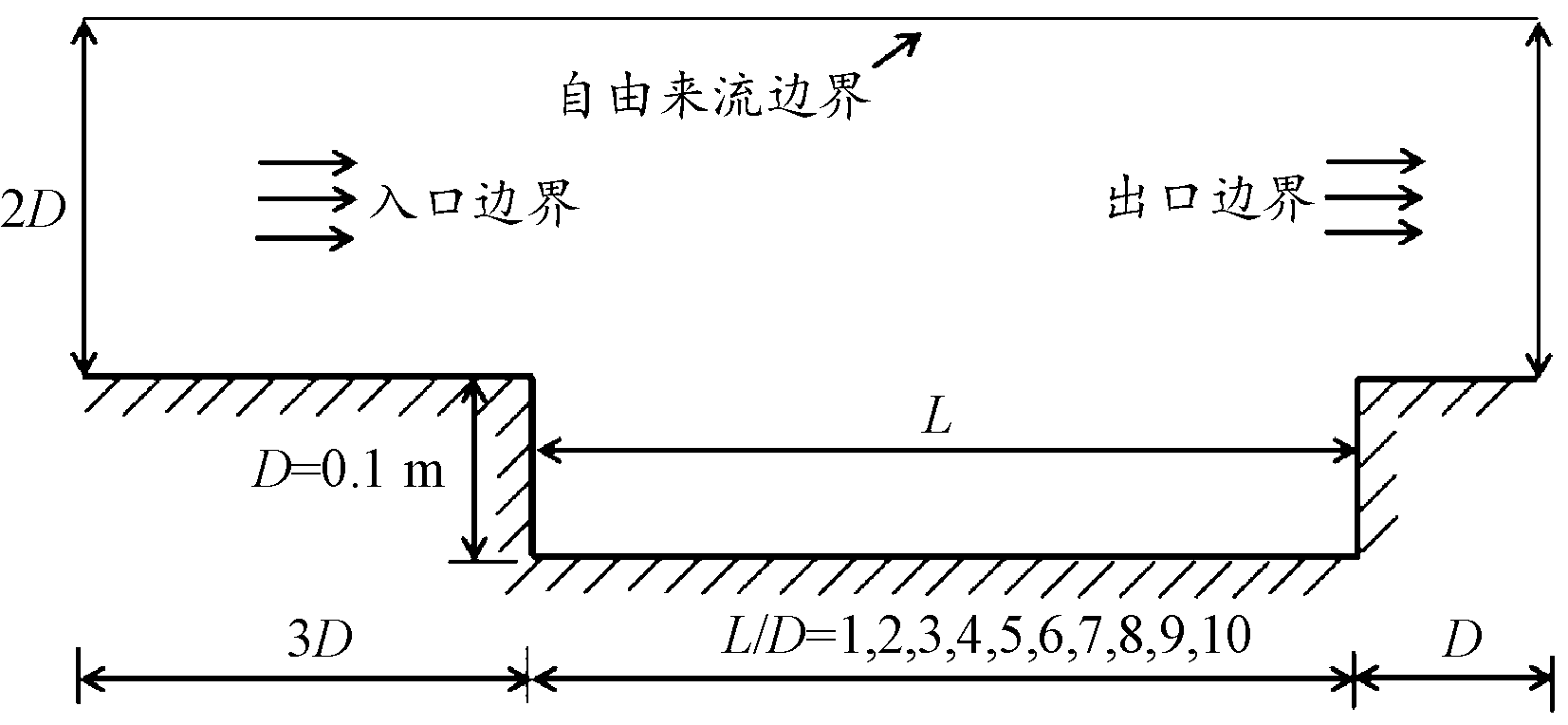
图6 空腔模型几何参数
Fig.6 Geometric parameters of cavity model
图7给出了高度为60 km时不同长深比下马赫数云图,图中以流线的形式标识了空腔中的回流区域以及剪切层内的流动。从图中可以看到,当长深比从1逐渐增加到10时,剪切层也经历着显著的变化,图中黄色绿色和浅蓝色区域为边界层及剪切层区域,该区域通过白色流线表示,如图7的图例标识所示。
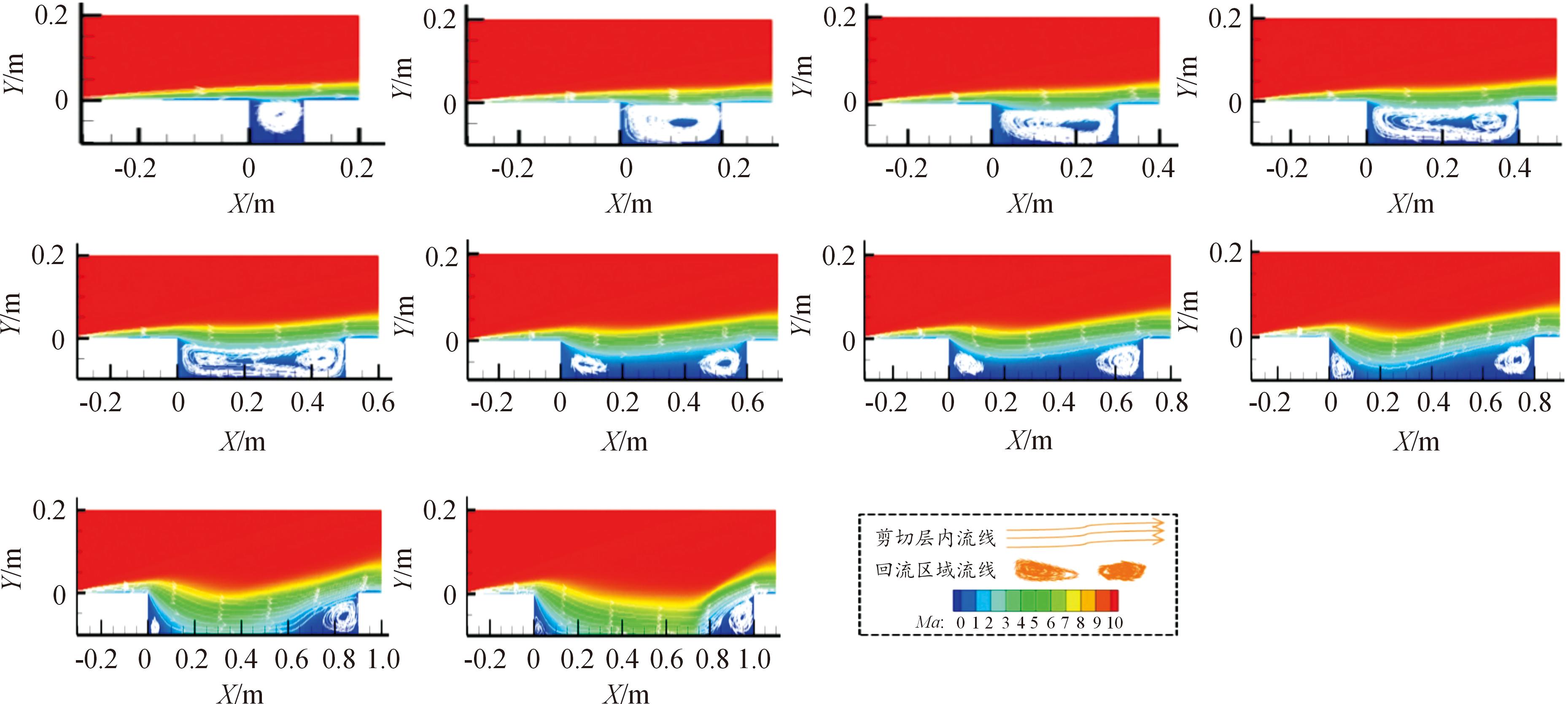
图7 60 km处不同长深比的马赫数云图
Fig.7 Mach number cloud map with different aspect ratios at 60 km
当长深比L/D=1时,空腔内部的回流区域近似为圆形,剪切层对空腔内部的流动几乎没有影响;L/D增加到2时,回流区域的中心向右发生移动,整个回流区域变为一个近椭圆形的区域,剪切层仍未进入空腔内部;L/D=3时,回流中心继续右移,此时剪切层开始对腔内流动产生挤压;当L/D增加到4时,回流区域仍布满了整个空腔,腔体左右两侧已正在形成各自的回流中心,此时腔体内部的回流区域仍为1个;当长深比L/D继续增大到5时,由于剪切层对空腔内部的流动的近一步影响,使得空腔内部形成了2个回流中心,左侧的回流中心与右侧的相比较小,并且2个回流区域之间仍有流线连接,可以相互影响;L/D=6时空腔内的流动结构发生明显改变,剪切层更进一步地进入空腔,逐渐触及到了空腔底部,使得腔内的回流区域完全一分为二,左右2个回流区域互不影响;随着长深比L/D的继续增大,剪切层越来越多的汇入空腔内,对左右两侧的回流区域都进行了不同程度的挤压,右侧的回流区域受到的影响小于左侧;L/D>9时左侧回流区域由于剪切层的挤压逐渐消失,右侧的回流区域也进一步减小。
综上所述,随着长深比L/D的增大,剪切层对空腔内部的流动逐渐挤压,回流区域的中心逐渐右移。左侧的回流区域随着L/D的增大也会逐渐形成,然后逐渐消退。可以从图7中明显看出,当长深比小于4时,空腔内的回流区域仅有一个,随着边界层的挤压效应,空腔内的回流区域逐渐地一分为二。当长深比大于等于6时,剪切层逐渐触及到空腔底板,使得回流区域分为两个独立的循环区域,此时我们称空腔由开式变为闭式。因此,我们可以对高度H=60 km,来流马赫数Ma=10的工况下的空腔流动进行分类,L/D=1~5为开式空腔,L/D=6~10为闭式空腔,L/D=6为空腔发生形变的阈值。
不同长深比空腔底部壁面的压力系数变化规律如图8(a)所示,从图中可以发现压力系数沿着流动方向逐渐增大,下面我们以L/D=1的算例来解释该趋势,由于回流区域的流动为顺时针方向,因此壁面最左侧的流动方向向上,气体分子对该位置处的法向力较小,而随着流动的发展,气体分子的流动方向逐渐向下,当到达壁面的最右侧时,分子的运动方向几乎竖直向下,所以压力系数沿流动方向逐渐增大。随着L/D的增加,壁面的压力系数也呈增大趋势,这是因为空腔的长深比增大后,剪切层会逐渐地进入腔体内部,这对空腔内部的流动造成挤压,导致该壁面压力系数的逐渐增大。
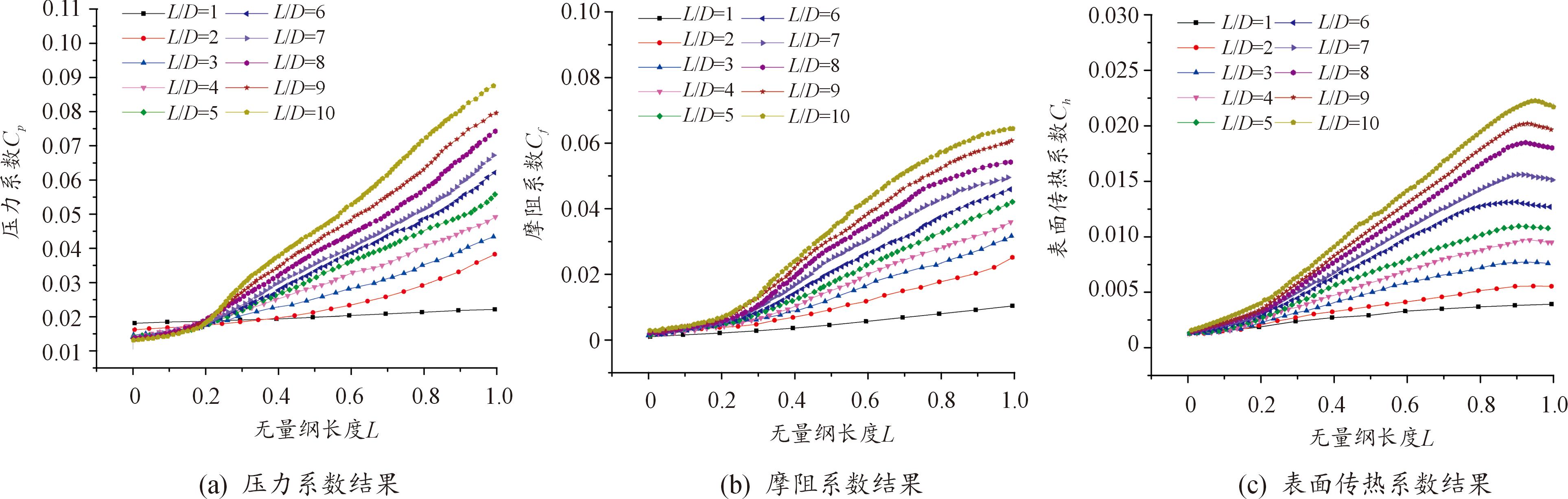
图8 空腔底部物面(a)压力系数(b)摩阻系数(c)表面传热系数计算结果
Fig.8 Computational results of the bottom surface of the cavity (a) pressure coefficient (b) friction coefficient (c) surface heat transfer coefficient
图8(b)给出了底部壁面的摩阻系数分布图,该分布趋势与该壁面处的压力系数分布趋势基本相同,因为随着流动沿着空腔底部的发展,底部壁面处分子的速度也逐渐增大,使得分子的切向力逐渐增大,壁面的摩阻系数也就随之增大。随着空腔长深比的增大,摩阻系数也呈增大趋势,原因同样在于,长深比增大后,更多的自由来流分子汇入空腔内部,使得该壁面分子的切向力增大,摩阻系数也随之增大。
图8(c)为空腔底部表面传热系数的分布趋势,图中我们发现沿着自由流动的方向,表面传热系数逐渐增大,在无量纲长度L=0.9附近处达到最大值,随后有了略微的减小,这是由空腔右侧形成的回流区域使得壁面附近的分子速度略微减小所致。随着长深比L/D的增大,传热系数也随之增大,原因在于长深比增大,更多的自由来流分子汇入空腔,使得更多的分子有机会触及空腔底部,增大了底部壁面处分子的流动速度,壁面处分子的热流密度主要由分子的动能提供,所以表面传热系数也随之增大。
2.2 化学反应空腔流场分析
60 km处气体分子的来流密度为3.1×10-4 kg/m3,氮气和氧气所占比例分别为0.78和0.22,因此可以得到氮气的来流密度为2.418×10-4 kg/m3,氧气的来流密度为6.82×10-5 kg/m3。
图9为L/D=6,Ma=10空腔算例各组分的分布云图,图9(a)—图9(d)分别为N2、O2、N、O以及 NO粒子。可以看出,N2分子与O2分子的密度云图规律一致,这2种粒子浓度的变化受化学反应发生的影响很小,我们主要研究N、O原子和NO分子的密度分布情况。从图9(c)-图9(e)不难看出,N与NO粒子的分布规律相似,主要集中在腔体内部,O原子主要分布在腔体的后半段。O原子密度的最大值约为来流O2分子1.52%,N原子密度的最大值约为来流N2分子0.66%,NO分子密度的最大值约为N原子35.24%,根据对上述粒子的浓度分析我们可以得到O2分子的离解反应,即公式(3)与公式(4),在本文中所考虑的化学反应类型中占据主导地位;N2分子与O原子以及O2分子与N原子之间的交换原子反应,即公式(7)—公式(10),占据的比例紧随其后;N2分子的离解反应,即公式(1)与公式(2)在化学反应类型中所占比例更少;N原子与O原子的复合反应,即公式(5)与公式(6),在所有化学反应中所占比例最少。
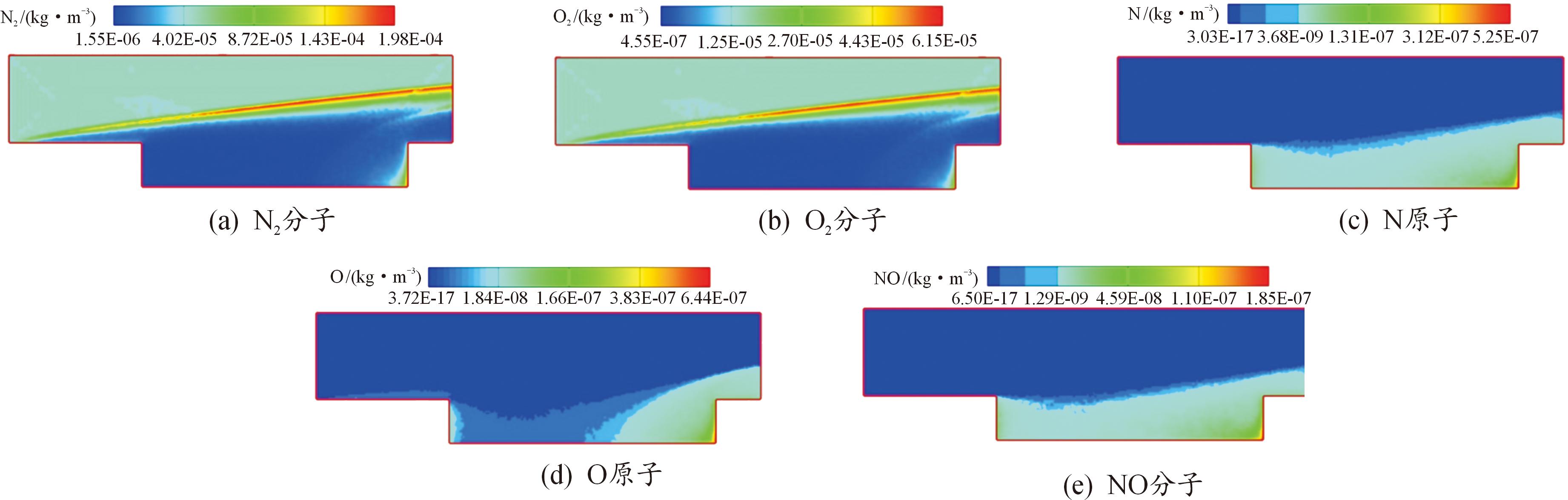
图9 空腔各组分密度分布云图
Fig.9 Density distribution of each component in the cavity
图10为空腔底部壁面有无化学反应的热流结果对比,可以看出壁面的前半段受化学反应影响较小,当无量纲长度L>0.7时,表面传热系数出现略微下降,原因在于剪切层进入空腔后,在底部壁面的后半段触及到了腔体底部,因此前半段受来流的影响较弱,分子运动较为缓慢,而后半段在剪切层的作用下分子的运动变得剧烈,化学反应碰撞的频率也同样剧烈,由于离解反应为吸热反应,因此热流会略微减小,图9(c)—图9(e)也验证了此结果。表面传热系数的最大偏差为5.50%。
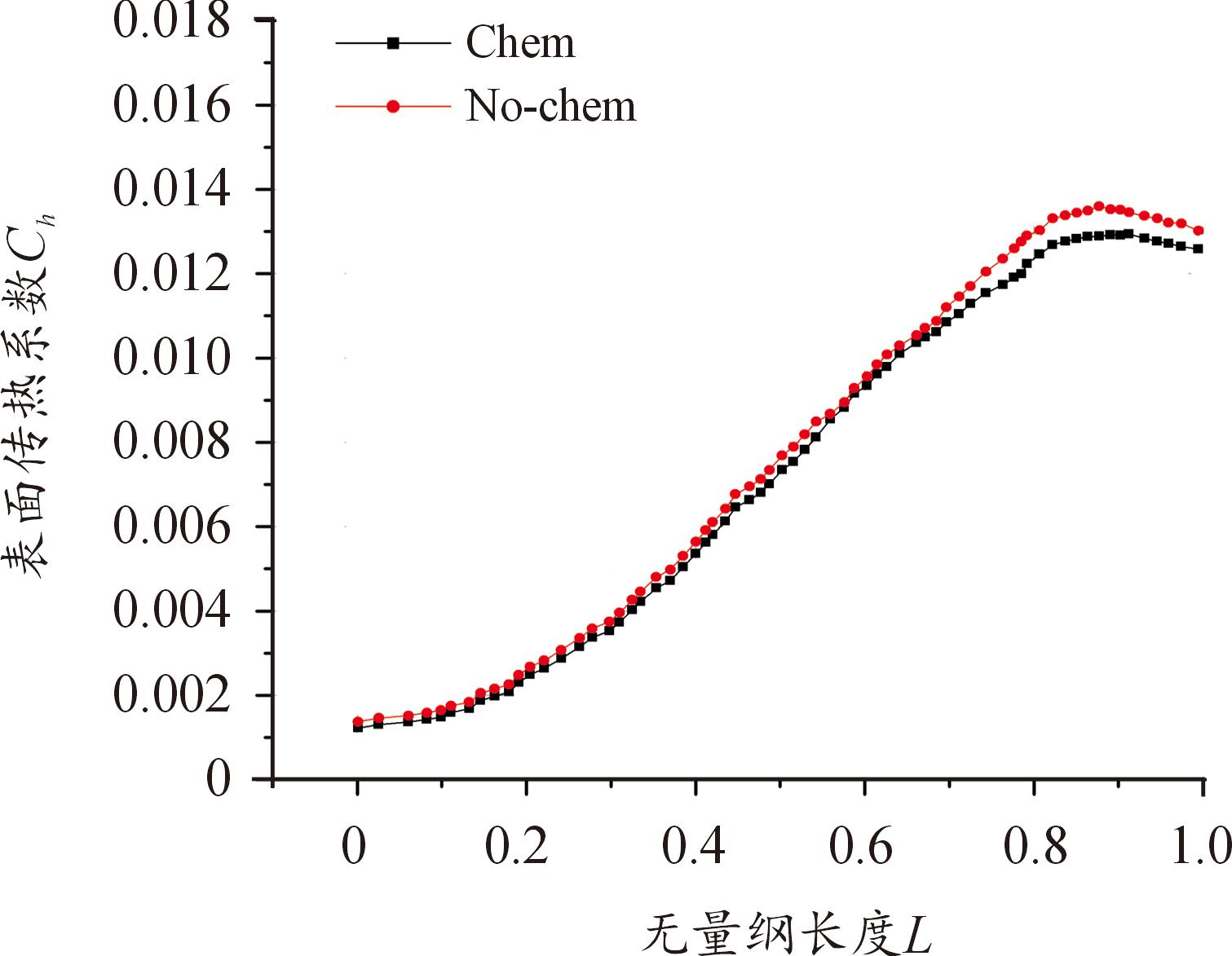
图10 空腔底部热流分布
Fig.10 Heat flux distribution atthe bottom of the cavity
3 结论
本文研究了临近空间流域高超声速空腔的流动特性和化学反应特性。得到以下结论:
1) 高度H=60 km,来流马赫数Ma=10的工况下,长深比L/D=1~5为开式空腔,L/D=6~10为闭式空腔,L/D=6为空腔发生形变的阈值。
2) H=60 km,Ma=10来流条件下发生的化学反应主要为O2和NO分子的离解反应,后壁面处和空腔底部的化学反应较为剧烈。
3) 空腔底部壁面的热流峰值出现在无量纲长度L=0.95处(底部壁面与后壁面交汇处附近),引入化学反应使得空腔底部壁面的表面传热系数最大减小为5.50%。
[1] 刘俊,蔡晋生,杨党国,等.超声速空腔流动波系演化及噪声控制研究进展[J].航空学报,2018,39(11):18-36.LIU Jun,CAI Jinsheng,YANG Dangguo,et al.Research progress in wave evolution and noise control for supersonic cavity flows[J].Acta Aeronautica et Astronatutica Sinica,2018,39(11):022366.
[2] 于靖波,向星居,黄湛,等.高超声速风洞开式空腔PSP试验研究[C]//第十一届全国流动显示学术会议.2016.YU Jingbo,XIANG Juxing,HUANG Zhan,Experimental study using PSP on open cavity in hypersonic wind tunnel[C]//The 11th Chinese Flow Visualization Conference.2016.
[3] 侯中喜,易仕和,王承尧.超声速开式空腔流动的数值模拟[J].推进技术,2001,22(5):400-403.HOU Zhongxi,YI Shihe,WANG Chengyao.Numerical analysis of supersonic open cavity[J].Journal of Propulsion Technology,2001,22(5):400-403.
[4] 陈伟芳,尹乐,吴雄,等.开式空腔流动的蒙特卡罗直接模拟[J].力学季刊,2003,24(3):341-345.CHEN Weifang,YIN Le,WU Xiong,et al.Flow simulation in open cavity by direct simulation Monte-Carlo method[J].Chinese Quarterly of Mechanics,2003,24(3):341-345.
[5] 张培红,唐银,唐静,等.基于自适应混合网格的高马赫数空腔流动模拟[J].北京航空航天大学学报,2023,49(6):1311-1318.ZHANG Peihong,TANG Yin,TANG Jing,et al.Simulation of cavity flow at high Mach number based on adaptive unstructured hybrid mesh[J].Journal of Beijing University of Aeronautics and Astronautics,2023,49(6):1311-1318.
[6] 龚淼,何安南,马存原.涡轮叶片前缘气膜冷却机理及流场分析[J].兵器装备工程学报,2022,43(9):232-239.GONG Miao,HE Annan,MA Cunyuan.Film cooling mechanism and flow field analysis of leading edge of turbine blade[J].Journal of Ordnance Equipment Engineering,2022,43(9):232-239.
[7] 耿云飞,阎超.高超声速前缘空腔数值模拟研究[J].空气动力学学报,2011,29(4):470-475.GENG Yunfei,YAN Chao.Numerical simulation on the hypersonic leading edge cavity[J].Acta Aerodynamica Sinica,2011,29(4):470-475.
[8] 宋威,鲁伟,蒋增辉,等.内埋武器高速风洞弹射投放模型试验关键技术研究[J].力学学报,2018,50(6):72-81.SONG Wei,LU Wei,JIANG Zenghui,et al.The crucial technique investigation of wind-tunnel drop-model testing for the supersonic internal weapons[J].Chinese Journal of Theoretical and Applied Mechanics,2018,50(6):72-81.
[9] PALLHARINI R C,SCANLON T J,REESE J M.Aerothermodynamic comparison of two and three-dimensional rarefied hypersonic cavity flows[J].Journal of Spacecraft &Rockets,2014,51(5):1619-1630.
[10] CHARWAT A F,ROOS J N,DEWEY C F,et al.An investigation of separated flows:Part Ⅰ the pressure field[J].Journal of Aerospace Sciences,1961,28(6):457-470.
[11] CHARWAT A F,DEWEY C F,ROOS J N,et al.An investigation of separated flows:Part Ⅱ flow in the cavity and heat transfer[J].Journal of Aerospace Sciences,1968,7(7):513-527.
[12] GUO G,LUO Q.DSMC investigation on flow characteristics of rarefied hypersonic flow over a cavity with different geometric shapes[J].International Journal of Mechanical Sciences,2018,148:496-509.
[13] PALLHARINI R C,SANTOS W F N.The impact of the length-to-depth ratio on aerodynamic surface quantities of a rarefied hypersonic cavity flow[J].Aerospace Science and Technology,2019,88:110-125.
[14] PALLHARINI R C,SCANLON T J,WHITE C.Chemically reacting hypersonic flows over 3D cavities:Flowfield structure characterisation[J].Computers &Fluids,2018,165:173-187.
[15] 靳旭红,黄飞,程晓丽,等.稀薄流区高超声速飞行器表面缝隙流动结构及气动热环境的分子模拟[J].航空动力学报,2019,34(1):201-209.JIN Xuhong,HUANG Fei,CHENG Xiaoli,et al.Monte Carlo simulation for the flow-field structure and aerodynamic heating due to cavities on hypersonic vehicle surfaces in the rarefied flow regime[J].Journal of Aerospace Power,2019,34(1):201-209.
[16] MICHAEL A,GALLIS,JOHN K,et al.Modelling of chemical reactions in hypersonic rarefied flow with the direct simulation Monte Carlo method[J].Journal of Fluid Mechanics,1996,312(1):149-172.