0 引言
航空重油活塞发动机具有功率密度高、安全性高、燃油经济性好的特点,在军、民用教练机、无人机上得到了非常广泛的应用。双质量飞轮作为航空重油活塞发动机一个重要部件,具有隔离发动机曲轴扭振和改善发动机使用性能的特点,其可靠性直接决定了航空重油活塞发动机运行安全。双质量飞轮毂盘(下文简称“毂盘”)将发动机的扭矩传递给减速器,是双质量飞轮的核心部件。在实际运行中,航空重油活塞发动机输入扭矩呈现出波动大且非线性的特点,导致毂盘有发生提前疲劳的风险[1-2]。近些年,国内发生多起由于毂盘疲劳断裂导致的航空重油活塞发动机功率无法输出的事故/事故征候。因而,毂盘结构不仅要具备基本承载功能,更要兼顾高强度、耐疲劳和运行经济性等要求。基于此,在双质量飞轮结构设计过程中,亟待创新结构优化方法,以实现毂盘的结构高性能轻量化设计。
目前双质量飞轮的研究主要是集中在双质量飞轮整体的综合设计与减振方面。张贵辉等[3]通过仿真分析的手段研究了双质量飞轮性能对发动机扭振衰减效果的影响,得出共振解决方案并进行了试验验证。郭政[4]等研究了双质量飞轮对离合器及整车动力传动系统的影响,建立以离合器滑黏比、整车冲击度为目标函数的多目标优化模型,得到双质量飞轮最优参数组合。对于双质量飞轮扭转振动问题,学者们从参数建模、改进结构等方面出发,改善了双质量飞轮扭转振动的问题[5-9]。蔡芸等[10]采用遗传算法对客车传动系扭转振动问题进行了优化,结果表明,加装双质量飞轮方案对降低扭振幅值效果更加明显。Lu等[11]研究了某型号航空重油活塞发动机双质量飞轮中的毂盘疲劳断裂机制,但是并未对毂盘结构进行优化设计。
上述优化设计研究主要是针对汽车用双质量飞轮结构,展开了相关研究,但是针对于航空重油活塞发动机毂盘优化设计研究鲜有报。针对上述实际运行问题,提出一种基于响应面模型辅助多目标优化的毂盘优化设计方法。该方法通过对比优化设计中响应面精度确定响应面模型,参与多目标优化设计,响应面法(response surface methodology,RSM)与多目标遗传算法(multi-objective genetic algorithm,MOGA)相结合,提升了优化效率,从而达到提升多目标优化效果的目的。
1 基于响应面模型的多目标联合优化
1.1 Kriging响应面模型
Kriging响应面模型是一种精确的多维插值方法[12],Kriging响应面模型假设了一个多项式模型,再加上高斯过程给定的偏差形式,则Kriging模型响应面模型可表示为
y=f(x)+Z(x)
(1)
式(1)中:y为未知函数;f(x)为关于x的多项式函数;Z(x)为正态高斯随机过程。Z(x)是均值为0,方差为σ2,协方差为
Cov[Z(xi),Z(xj)]=σ2R[r(xi,xj)]
(2)
式(2)中:R为关联矩阵,是在任意2个样本点xi和xj之间的空间相关系数,是对称正定矩阵;r(xi,xj)为高斯相关函数,r(xi,xj)具体表示为
![]()
(3)
式(3)中:θk为拟合模型的位置参数;M为设计变量的数量;![]() 为样本点i的组成部分;
为样本点i的组成部分;![]() 为样本点j的组成部分。
为样本点j的组成部分。
1.2 非参数回归响应面模型
非参数回归响应面模型是一种用于建立输入变量与输出变量之间关系的统计方法,特别适用于那些无法简单用参数化函数(如线性或多项式)来描述的复杂非线性关系[13-15]。在非参数回归中,模型不依赖于事先指定的参数化形式,而是根据数据本身的特征进行建模。非参数回归响应面模型可表示为
y=[w,x]+b
(4)
式(4)中:y为未知函数;w为加权向量;x为样本点;b为误差。在一般非参数情况下,式(4)可改写为
![]()
(5)
式(5)中:![]() 为核映射;Ai和
为核映射;Ai和![]() 为拉格朗日乘子;b为误差。
为拉格朗日乘子;b为误差。
1.3 多目标优化理论
多目标优化是指在一个优化问题中,同时考虑和优化多个(通常是2个或多个)相互竞争的目标或指标[16-20]。其目的是找到一个能够在各个目标之间实现平衡或最优的权衡方案,多目标优化模型可表示为

(6)
式(6)中:x为设计变量;D为决策空间;min f1(x), min f2(x),…,min fn(x)为优化目标,min fn(x)为第n个优化目标,可以为质量、刚度、强度、体积等相关性能参数;g1(x)和g2(x)为约束条件,gn(x)≤0是第n个约束条件。
2 多目标优化流程
为了提高优化效率、节省计算时间,采用灵敏度分析筛选出关键设计变量。利用试验设计法获得初始样本空间和构建响应面模型,使用多目标优化对毂盘结构进行优化设计,提出一种响应面法的多目标联合优化设计流程,如图1所示。
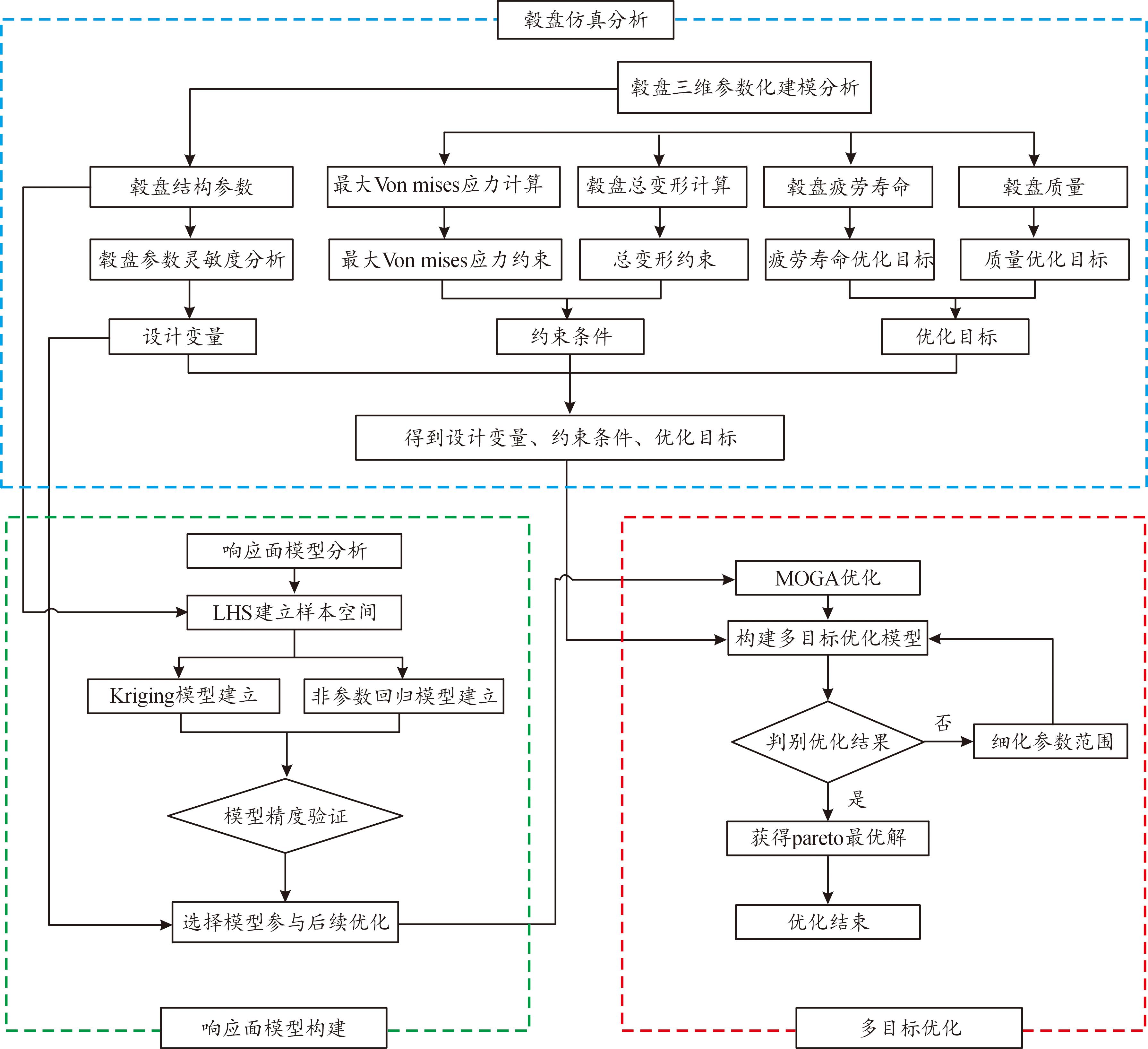
图1 毂盘多目标优化流程框图
Fig.1 Multi-objective optimization flow chart of flywheel hub
该流程包括3个部分。
第1部分:毂盘有限元仿真分析。对毂盘进行三维建模并进行仿真计算,得到毂盘最大Von mises应力、最大总变形、毂盘质量、疲劳寿命;对毂盘结构参数进行灵敏度分析,确定用于优化的结构参数。
第2部分:响应面模型构建。使用拉丁超立方法(latin hypercube sampling,LHS)进行DOE (design of experiment) 试验设计生成样本空间。使用Kriging响应面模型与非参数回归响应面模型对样本空间进行响应面拟合,对拟合出的两种响应面模型进行精度验证,确定参与后续多目标优化的响应面模型。
第3部分:多目标优化。根据第1部分有限元仿真计算结果构建多目标优化模型,对第2部分拟合出的响应模型使用MOGA进行优化迭代并判别结果是否满足要求。
3 毂盘多目标优化设计
3.1 毂盘仿真分析
毂盘起到传递发动机与减速器输出轴之间扭矩的作用,通过8个螺栓与双质量飞轮连接,其花键孔与减速器的输出轴花键相啮合(如图2所示)。在实际工作中,毂盘的花键轴孔与减速器的输入轴花键啮合,将发动机的输出功率传递给减速器。

图2 双质量飞轮示意图
Fig.2 Diagram of dual mass flywheel
文献[11]中的图6,通过分析飞机上数据采集系统记录了该型航空重油发动机的实际运行(约76 min)的转速与输出扭矩数据,得到其在实际运行中的转速和输出扭矩随时间变化的曲线(工况曲线)。该发动机最大转速为2 300 r/min;减速比为1.69;最大功率为123.5 kw[11]。实际采集到的扭矩与公式计算出的扭矩载荷一致。航空重油活塞发动机工作时,毂盘受到初级飞轮和次级飞轮共振冲击的影响,导致毂盘实际受到的扭矩是发动机最大输出扭矩的5倍[21]。根据文献[11,21]的发动机功率计算公式计算得出发动机最大输出扭矩与实际采集一致。发动机功率计算公式为
![]()
(7)
式(7)中:Tm为发动机输出扭矩,N·m;ωrpm为发动机转速, r/min;Pkw为发动机功率, kW。由式(7)可计算出发动机输出扭矩为303.39 N·m。
毂盘材质为SAE-4340合金钢,其材料性能参数如表1所示。
表1 SAE-4340合金钢性能参数
Table 1 Performance parameters of SAE-4340 alloy steel

参数数值参数数值密度/(kg·m-3)7 850泊松比0.3剪切模量/MPa1.725×105屈服极限/MPa1.371×105弹性模量/MPa2.07×105抗拉极限/MPa1.167×105
使用Ansys Workbench软件进行有限元仿真计算,选用Static Structural模块进行静力学分析。本研究中有限元仿真的输入载荷为工况曲线中的毂盘承受最大载荷实际载荷,与毂盘在实际运行中的工况一致,定义毂盘所受到的载荷与约束条件,如图3(a)所示,在图3(a)中A处(红色)施加的扭矩,其大小为1 517 N·m,B处(蓝色)为固定约束。静力学仿真计算结果如图3(b)、图3(c)所示,图3(b)为毂盘最大总变形云图,毂盘最大总变形发生在毂盘外围处,大小为 0.278 mm,图3(c)为毂盘最大Von mises应力云图,毂盘最大Von mises应力发生在辐条底部圆角半径处,大小为635.53 MPa,且在辐条底部圆角半径处发生了应力集中现象,最大Von mises应力为SAE-4340合金钢屈服极限的一半,此时毂盘仍具有较大的安全裕度。
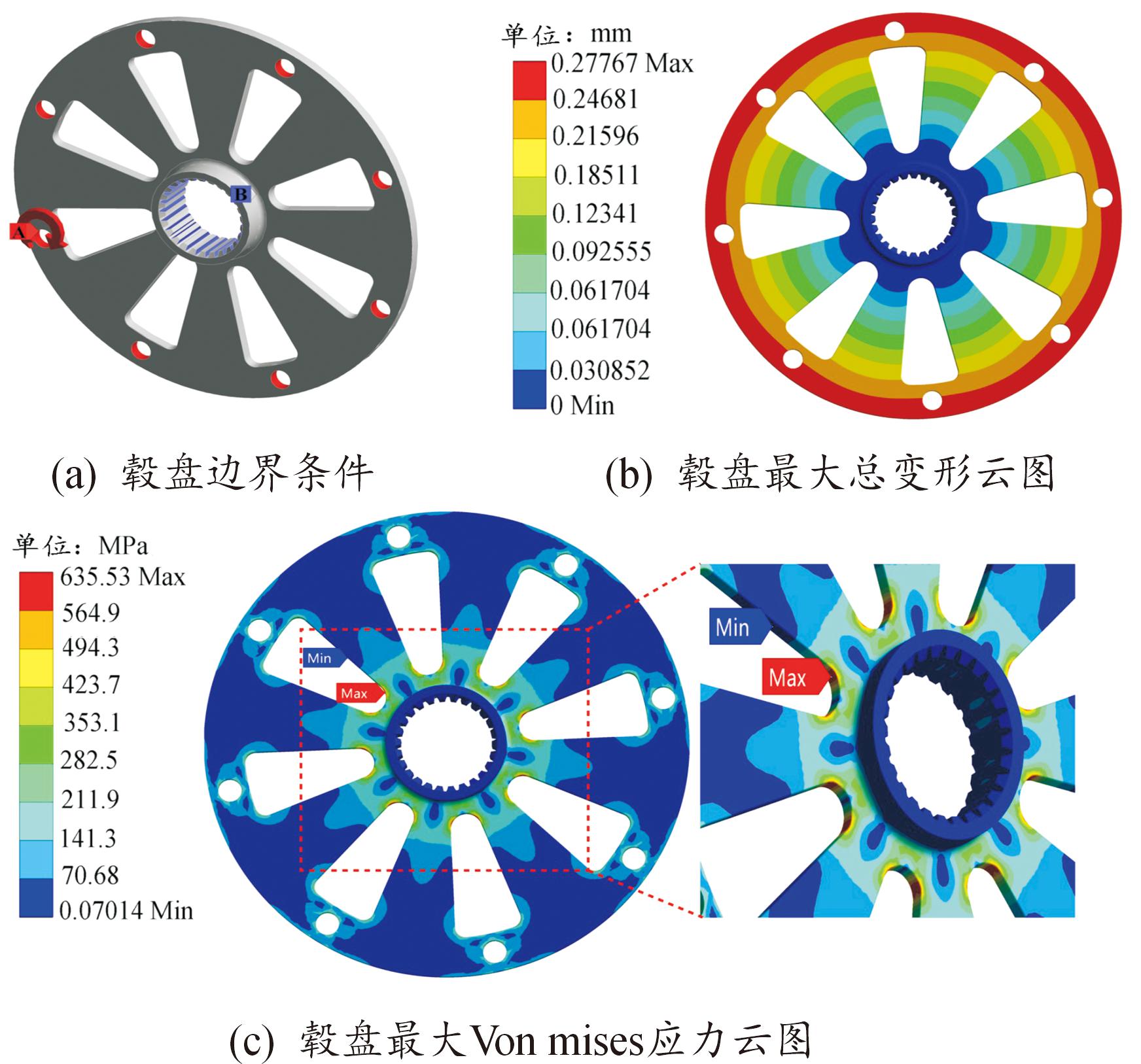
图3 毂盘边界条件及静力学计算结果
Fig.3 Boundary conditions of flywheel hub and results of statics calculation
根据静力学分析结果,将静力学分析结果导入Ansys Workbench中的nCode-Designlife模块,采用应力寿命法[22]对毂盘疲劳寿命进行分析计算,并利用SAE-4340合金钢疲劳性能曲线(S-N曲线,如图4所示)与毂盘所受的载荷谱计算出毂盘的疲劳寿命。毂盘疲劳寿命计算结果如图5所示,发现毂盘最小疲劳寿命发生在辐条底部圆角半径处,其大小为7.209×104次(折算为20 h),与图3(c)中最大Von mises应力发生区域一致,表明应力越大,疲劳寿命越小。

图4 SAE-4340合金钢材料S-N曲线
Fig.4 S-N curve of SAE-4340 alloy steel material

图5 毂盘疲劳寿命计算结果
Fig.5 Calculation result of flywheel hub fatigue life
3.2 毂盘优化参数确定
毂盘的结构参数如图6所示。在进行参数灵敏度分析前,确定毂盘结构参数取值范围。毂盘辐孔个数只能是整数,因此将辐孔个数P2设置为离散化参数,取值范围为3~9个。毂盘结构设计变量及取值范围如表2所示。
表2 毂盘设计变量及初始值范围
Table 2 Initial value and value range of flywheel hub design variables

参数名称初始值优化上限优化下限辐条长度P1/mm155157135辐条倒角P4/mm0.20.180.22辐条底部圆角半径P5/mm65.56.6辐条顶部圆角半径P6/mm43.44.4分度夹角P9/(°)107.510.5花键圆角P10/mm21.82.2
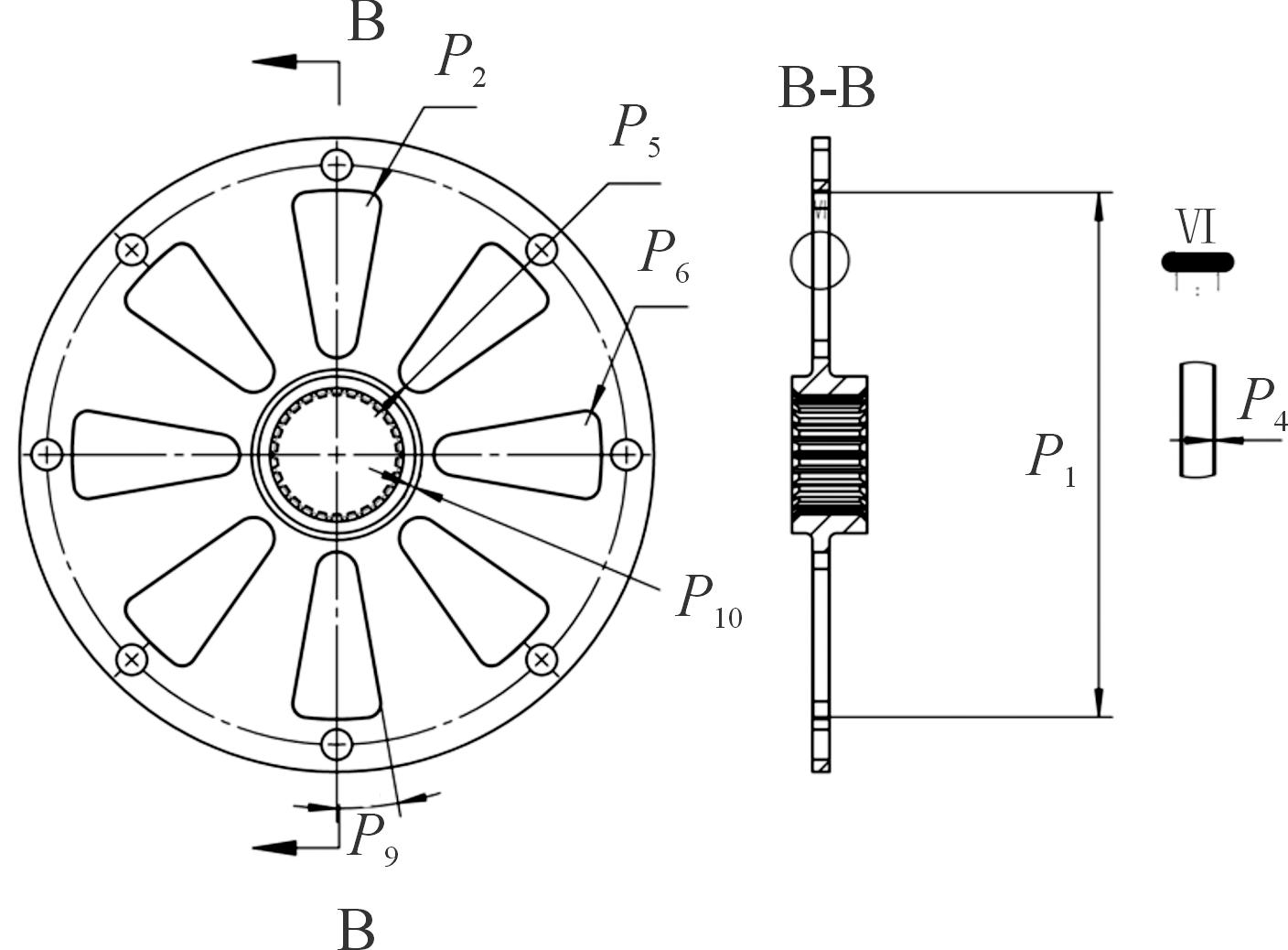
图6 毂盘结构参数
Fig.6 Flywheel hub structural parameters
为了在不影响计算精度的前提下进一步缩减设计变量、减小计算规模,通过灵敏度分析筛选出对优化目标作用效果显著的结构参数。因此,在进行优化前,需要对毂盘结构参数进行灵敏度分析[23]。灵敏度分析主要是研究设计变量对输出参数的影响,灵敏度计算表达式为
![]()
(8)
式(8)中:S为灵敏度;yi为约束条件或目标函数;xi为设计变量。
表3为毂盘结构参数与优化目标(毂盘质量、疲劳寿命)间的灵敏度分析表。由表3可知,所有的设计变量参数中,辐条长度P1和分度夹角P9对毂盘质量影响最明显,呈现负相关。通过计算可知,当辐条长度与分度夹角逐渐增大时,毂盘质量会逐渐减小;辐条底部圆角半径P5与分度夹角P9对毂盘疲劳寿命影响最明显,呈现负相关。依据灵敏度分析结果,选择辐条长度P1、辐条底部圆角半径P5和分度夹角P9作为后续优化的变量。
表3 参数灵敏度分析
Table 3 The result of parameter sensitivity analysis
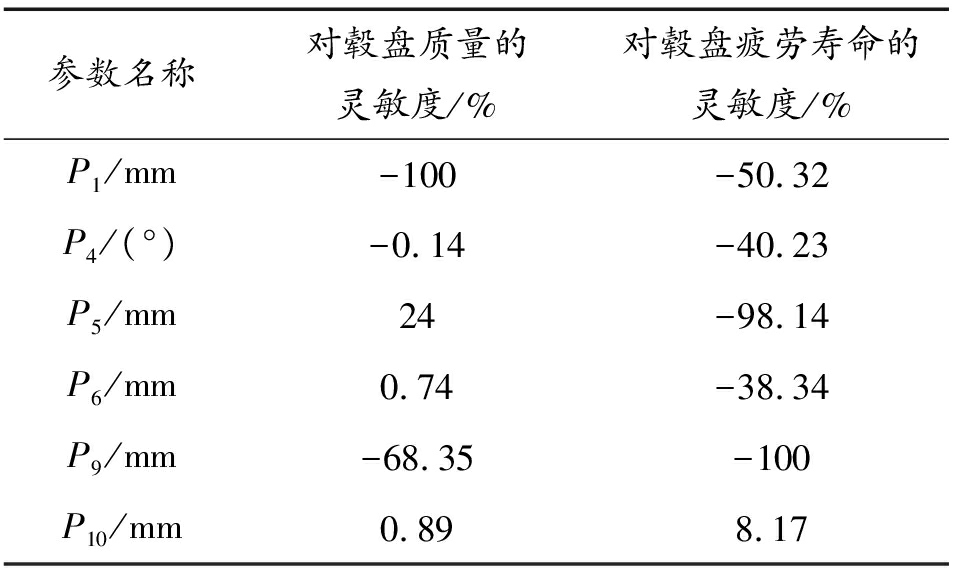
参数名称对毂盘质量的灵敏度/%对毂盘疲劳寿命的灵敏度/%P1/mm-100-50.32P4/(°)-0.14-40.23P5/mm24-98.14P6/mm0.74-38.34P9/mm-68.35-100P10/mm0.898.17
3.3 响应面模型建立
上述分析完成后,使用Ansys Workbench的Design Exploration模块进行优化设计。将毂盘结构参数设定为设计变量,以毂盘质量、毂盘最大Von mises应力、最大总变形、疲劳寿命为结构响应进行试验设计。利用拉丁超立方试验设计法(LHS)获得315个试验样本[23]。
本文采用Kriging响应面模型与非参数回归响应面模型拟合通过拉丁超立方试验设计法生成的315个试验样本点生成响应面。通过归一化拟合曲线与决定系数R2来评价拟合的Kriging响应面模型和非参数回归模型的精确度[24-26]。
3.3.1 响应面模型归一化拟合曲线分析
在归一化拟合曲线中,观察值与预测值越接近,两者越接近45°直线,表示响应面模型拟合出的响应曲面效果越准确。Kriging响应面模型与非参数回归响应面模型的归一化拟合曲线如图7所示。在图7(a)中只有较少点离散在45°直线附近,而图7(b)中,有较多点离散在45°曲线附近,表明Kriging响应面模型拟合出的响应曲面更适用于对毂盘的优化。
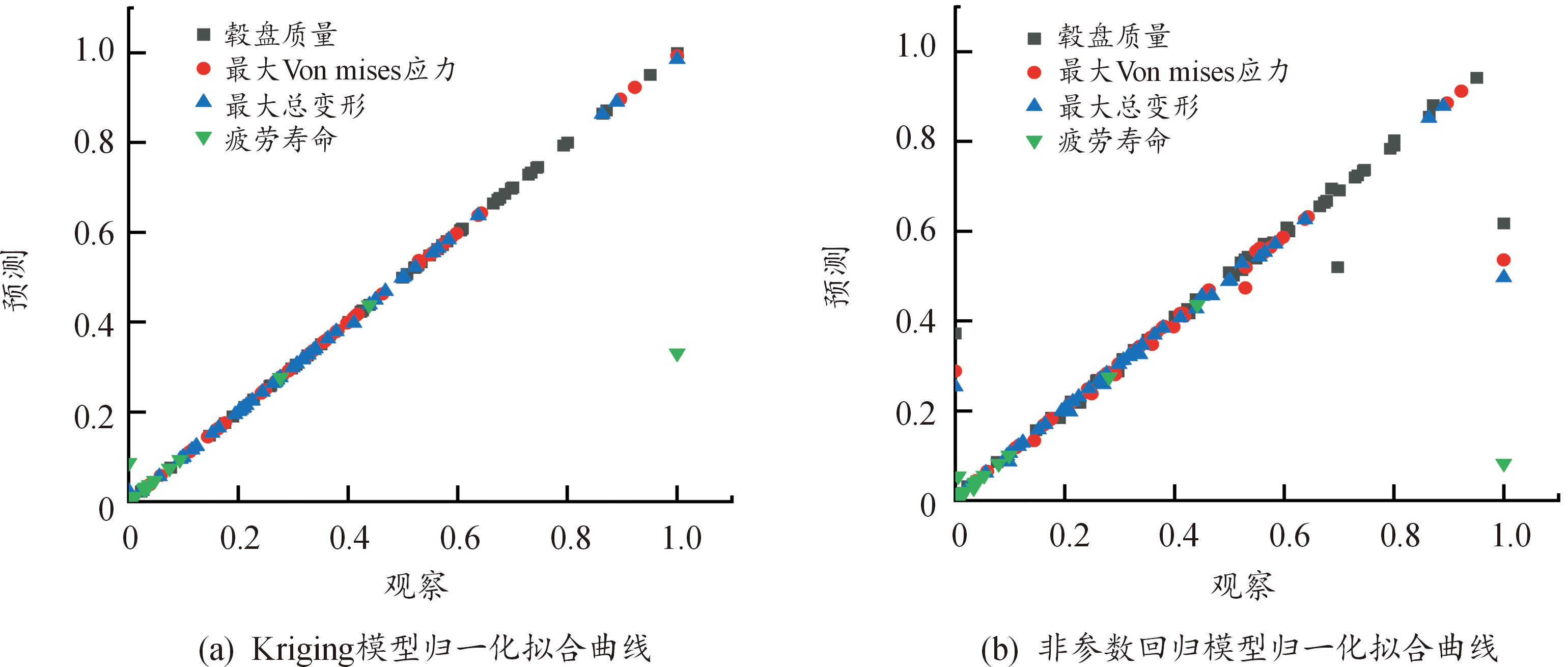
图7 2个响应面模型归一化拟合曲线
Fig.7 Fitting curve of two response surface models
3.3.2 响应面模型决定系数分析
通过决定系数R2验证生成的Kriging响应面模型与非参数回归响应面模型精度,对于第i个样本的决定系数R2为

(9)
式(9)中:R2为决定系数;yi为真实值;![]() 为近似值;
为近似值;![]() 为均值。由式(9)计算出的决定系数R2越趋近于1,表明拟合出的响应曲面精确度越高。
为均值。由式(9)计算出的决定系数R2越趋近于1,表明拟合出的响应曲面精确度越高。
2个模型决定系数R2如表4所示。Kriging响应面模型计算的毂盘质量P11、最大Von mises应力P12以及最大总变形P13的决定系数都大于0.9,毂盘质量的决定系数为1(达到最优),毂盘的疲劳寿命P14为0.7;非参数回归模型计算的毂盘质量P11决定系数为0.88,最大Von mises应力P12决定系数为0.86,最大总变形P13决定系数为0.85,疲劳寿命P14决定系数为0.29(最差)。由上述决定系数R2分析可知,拟合出的Kriging响应面模型精度高于非参数回归响应面模型。
表4 2个响应面模型精度评价
Table 4 Two response surface model accuracy evaluation
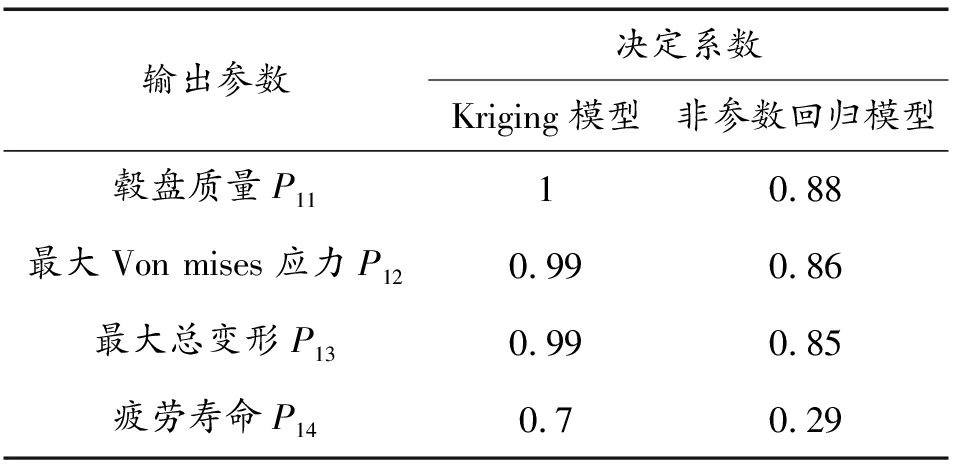
输出参数决定系数Kriging模型非参数回归模型毂盘质量P1110.88最大Von mises应力P120.990.86最大总变形P130.990.85疲劳寿命P140.70.29
3.3.3 响应面分析结果
归一化拟合曲线及决定系数分析表明:Kriging响应面模型满足毂盘的后续优化要求。对辐条长度P1、辐条底部圆角半径P5和分度夹角P9生成Kriging响应面,如图8所示。由图8(a)可知,毂盘质量P11随着辐条长度P1的增大而逐渐减小,随着辐条底部圆角半径P5逐渐减小而减小。同理,由图8(b)可知,毂盘质量P11随着辐条长度P1的增大而逐渐减小,随着分度夹角逐渐增大而减小。由图8(c)—图8(d)可知,毂盘结构参数与毂盘疲劳寿命P14呈现的是非线性关系,且在图8(c)—图8(d)中均出现了下凹面,这解释了图7(a)中毂盘疲劳寿命拟合度差的原因。

图8 P1、P5及P9拟合的毂盘质量响应面(a)—(b)和毂盘疲劳寿命响应面(c)—(d)
Fig.8 Weight response surface (a)—(b) and fatigue life response surface (c)—(d) of flywheel hub by P1,P5 and P9
3.4 毂盘多目标优化与结果验证
根据本文的优化目标,以最大Von mises应力和最大总变形为约束条件,以最小化毂盘结构质量和毂盘疲劳寿命最大化为优化目标,建立毂盘结构多目标优化模型:

(10)
式(10)中: X=[x1,x2,…,x10]T为毂盘结构设计变量P1,P2,…,P10;XL和XH分别为设计变量的下限值与上限值;P11为毂盘质量,kg;P14为毂盘疲劳寿命,次;P12为最大Von mises应力,MPa;P13为最大总变形,mm。
使用MOGA对毂盘结构多目标优化模型进行优化迭代,经过17 867次迭代后得到1 403组毂盘结构多目标优化解。兼顾轻量化与结构安全,在1 403组优化解集中选出符合毂盘结构多目标优化的3组优化解集,如图9所示。在图9中,蓝色球体为一般解集,3个立方体为符合毂盘结构多目标优化模型的3组最优解。
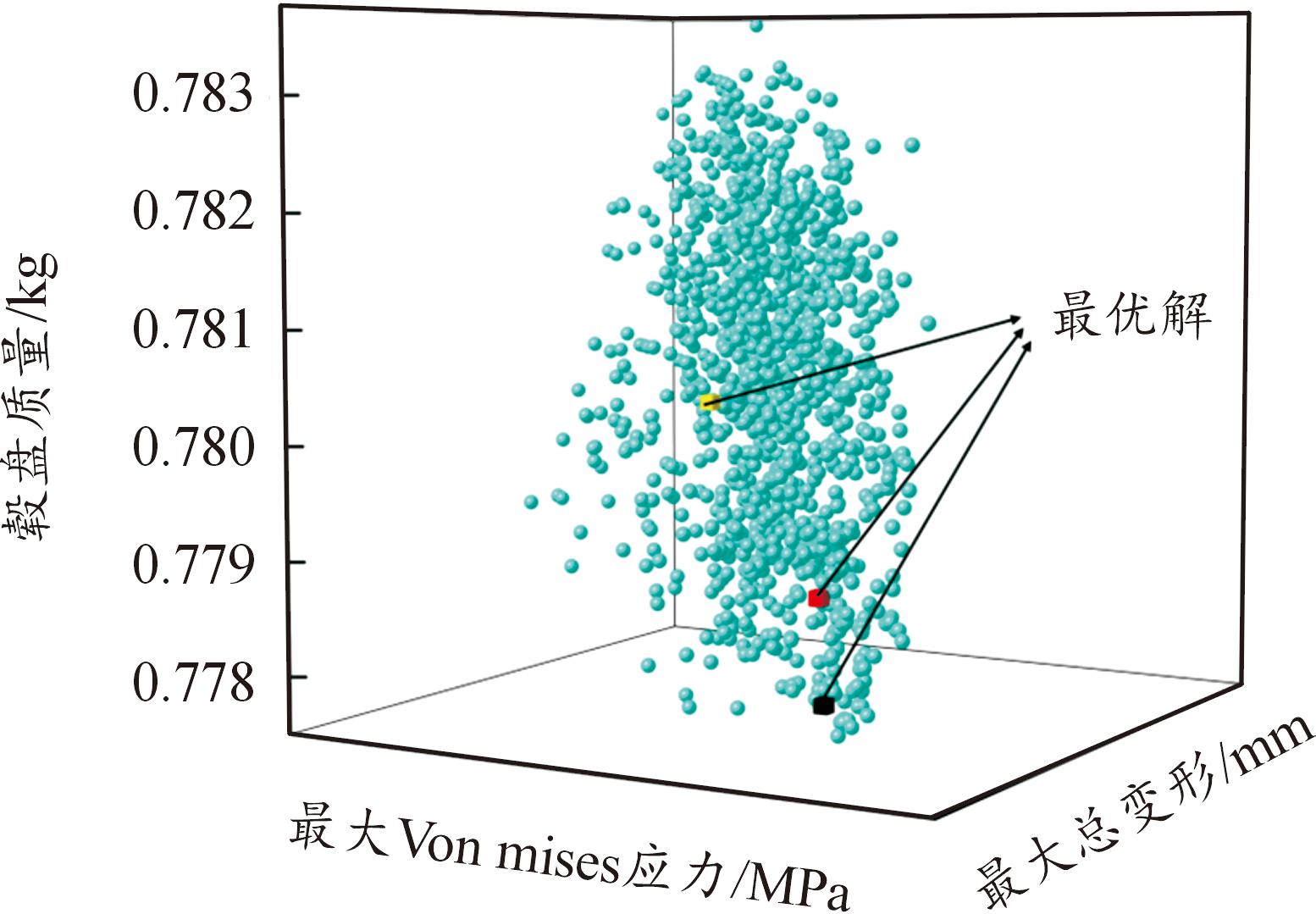
图9 MOGA最优解
Fig.9 MOGA optimal solution
为确保毂盘结构优化达到轻量化与疲劳寿命最大化的目的,对图9中的3组最优解进行计算验证,验证结果如表5所示。由表5可知,毂盘的3组优化解性能指标均有提升。毂盘优化前疲劳寿命与优化后3组最优解的疲劳寿命云图,如图10所示。由图10可知,3组最优解的疲劳寿命较优化前毂盘疲劳寿命均得到提升,其中第2组最优解疲劳寿命优化效果达最佳。结合式(10)、表5及图10,在3组最优解中选择第2组最优解作为优化结果。
表5 3组最优解
Table 5 Three optimal solutions
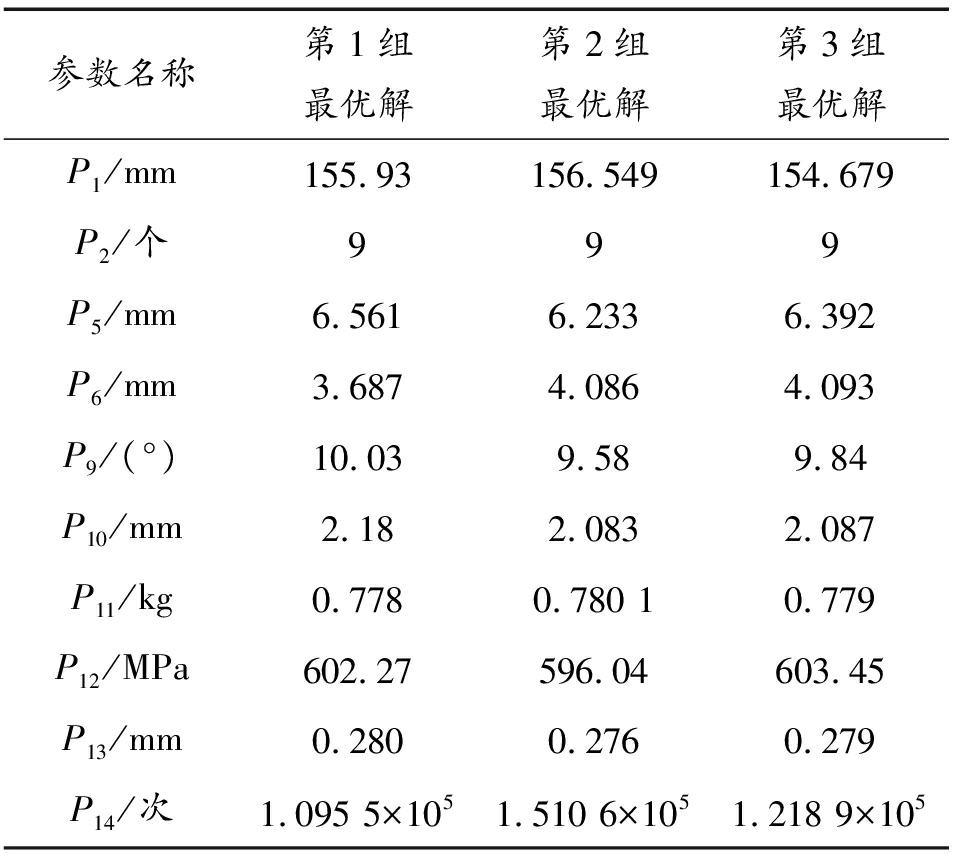
参数名称第1组最优解第2组最优解第3组最优解P1/mm155.93156.549154.679P2/个999P5/mm6.5616.2336.392P6/mm3.6874.0864.093P9/(°)10.039.589.84P10/mm2.182.0832.087P11/kg0.7780.780 10.779P12/MPa602.27596.04603.45P13/mm0.2800.2760.279P14/次1.095 5×1051.510 6×1051.218 9×105
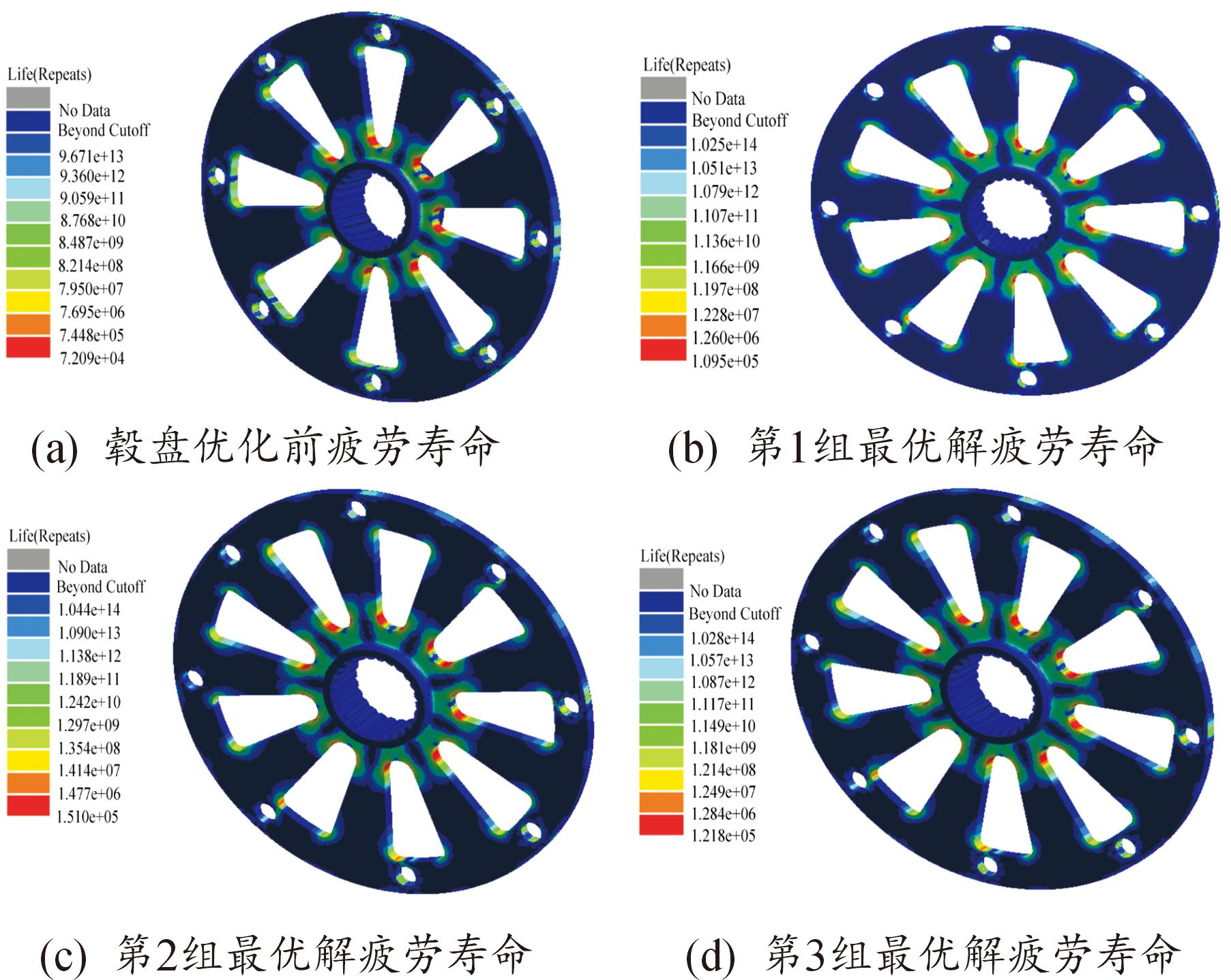
图10 优化前后毂盘疲劳寿命云图对比
Fig.10 Comparison of fatigue life of flywheel hub before and after optimization
对第2组最优解的结构参数进行圆整处理,圆整结果如表6所示。对圆整后的结构参数仿真计算,如表7所示。由表7可知优化后毂盘质量较原毂盘质量降低3.3%,优化后疲劳寿命较原毂盘提升87.5%,优化后毂盘最大Von mises应力较原毂盘降低5.4%,优化后毂盘最大总变形较原毂盘降低2.1%,优化结果达到了本文优化目的。
表6 第2组最优解设计变量圆整
Table 6 Roundness data of design variable for the second optimal solution

参数名称初始值优化结果圆整后结果指标变化P1/mm155156.549157+2P2/个899+1P5/mm66.236.2+0.2P6/mm44.0864.1+0.1P9/(°)109.589.6-0.4P10/mm22.082.1+0.1
表7 第2组最优解毂盘设计变量圆整后性能变化
Table 7 Performance changes of the second optimal solution flywheel hub design variable after roundness

目标性能初始值优化结果指标变化P11/kg0.8070.78-3.3%P12/MPa635.53601.06-5.4%P13/mm0.2780.272-2.1%P14/次7.209×1041.352×105+87.5%
4 结论
以航空重油活塞发动机双质量飞轮中的毂盘为研究对象,提出了一种响应面的多目标联合优化设计流程,并对优化结果进行了验证,得到如下结论:
1) 对原毂盘模型进行仿真计算得出:毂盘质量为0.807 kg;疲劳寿命约为20 h;最大Von mises应力发生在辐条底部圆角半径处,大小为635.53 MPa;最大总变形为0.278 mm。
2) 通过参数灵敏度分析筛选出对于优化目标作用明显的结构参数,LHS生成初始样本空间,对样本空间使用Kriging响应面模型和非参数回归响应面模型进行响应曲面拟合,并比较2个模型的拟合精度,选出Kriging响应面模型进行多目标优化。
3) 通过对毂盘进行多目标优化,获得了1 403组优化解集,并在1 403组优化解集中选取3组符合毂盘优化目标的解集,兼顾轻量化与安全,在3组最优解中选出优化目标的最优解,毂盘质量减少3.3%,疲劳寿命提升87.5%,最大Von mises应力降低5.4%,最大总变形降低2.1%。
[1] 礼平,徐宇鲲,吴浪武.双质量飞轮关键传动零件受力与疲劳寿命分析[J].机械设计与制造,2023(3):263-266. LI Ping,XU Yukun,WU Langwu.Force and fatigue life analysis of key transmission part in dual mass flywheel[J].Machinery Design and Manufacture,2023(3):263-266.
[2] 何柏林,王斌.疲劳失效预测的研究现状和发展趋势[J].机械设计与制造,2012 (4):279-281. HE Bolin,WANG Bin.Research status and development trend of fatigue failure prediction[J].Machinery Design and Manufacture,,2012(4):279-281.
[3] 张贵辉,石磊,陈闯,等.双质量飞轮共振问题的分析与改善[J].噪声与振动控制,2023,43(6):190-195. ZHANG Guihui,SHI Lei,CHEN Chuang,et al.Analysis and improvement of resonance problem of dual mass flywheels[J].Noise and Vibration Control,2023,43(6):190-195.
[4] 郭政,秦大同,李盛炜,等.考虑DCT车辆起步过程离合器接合稳定性的双质量飞轮参数优化[J].振动与冲击,2023,42(14):162-169,219. GUO Zheng,QIN Datong,LI Shengwei,et al.Parameter optimization of a dual mass flywheel considering clutch engagement stability during the starting of a DCT vehicle[J].Journal of Vibration and Shock,2023,42(14):162-169,219.
[5] 曾礼平,黄杰,宋立权,等.计及间隙和转矩滞回变化的双质量飞轮冲击特性及动态响应分析[J].振动与冲击,2022,41(23):330-338. ZENG Liping,HUANG Jie,SONG Liquan,et al.Shock characteristics and dynamic response analysis of a DMF considering clearance and hysteretic vari-ation of torque[J].Journal of Vibration and Shock,2022,41(23):330-338.
[6] WU G,ZHAO G.Parameter influence law analysis and optimal design of a dual mass flywheel[J].International Journal of Mechanical System Dynamics,2022(2),165-177.
[7] 史文库,陈龙,陈志勇,等.分段刚度双质量飞轮非线性振动特性研究[J].汽车工程,2019,41(4):417-425. SHI Wenku,CHEN Long,CHEN Zhiyong,et al.A research on nonlinear vibration characteristics of piecewise stiffness dual mass flywheel[J].Automotive Engineering,2019,41(4):417-425.
[8] 史文库,陈龙,张贵辉,等.多级刚度双质量飞轮扭转特性建模与试验验证[J].吉林大学学报(工学版),2020,50(1):44-52. SHI Wenku,CHEN Long,ZHANG Guihui,et al.Modeling and tests for torsional characteristics of multistage stiffness dual mass flywheel torsional dampers[J].Journal of Jilin University (Engineering and Technology Edition),2020,50(1):44-52.
[9] ZHOU Y,SHI X,RAO W,et al.Feasibility study of single-mass flywheels with centrifugal pendulum vibration absorbers in vehicles with dual clutch transmissions[J].Journal of Vibration and Control,2023,29:3213-3226.
[10] 蔡芸,董大伟,闫兵,等.汽车传动系统扭振问题的遗传算法优化[J].机械设计与制造,2020(3):198-202. CAI Yun,DONG Dawei,YAN Bing,et al.Optimization of driveline torsional vibration using genetic algorithm[J].Machinery Design and Manufacture,2020(3):198-202.
[11] LU J,ZHENG H,HAIDER M H,et al.Fracture failure analysis of flywheel hub served in heavy-fuel aviation piston engine[J].Engineering Failure Analysis,2023,151:107363.
[12] 韩忠华.Kriging模型及代理优化算法研究进展[J].航空学报,2016,37(11):3197-3225. HAN Zhonghua.Kriging surrogate model and it’s application to design optimization:A review of recent progress[J].Acta Aeronautica et Astronautica Sinica,2016,37(11):3197-3225.
[13] 阳吉初,屈小章,翟方志.基于非参数回归模型轨道风机叶轮的可靠性分析方法[J].机械设计与制造,2016(7):100-103. YANG Jichu,QU Xiaozhang,ZHAI Fangzhi.Reliability analysis method of fan impeller based on nonparametric regression model[J],Mechanical Design and Manufacturing,2016(7):100-103.
[14] 王少渤.基于蚁群算法与非参数回归模型的交通分析关键技术研究[D].淄博:山东理工大学,2022. WANG Shaobo.Research on key technologies of traffic analysis based on ant colony algorithm and nonparametric regression model[D].Zibo:Shandong University of Technology,2022.
[15] 杨郡守,周振伟,林晓亮,等.基于非参数回归响应面法的高精车铣复合机床床身多目标联合优化设计[J].制造技术与机床,2024,(5):128-133. YANG Junshou,ZHOU Zhenwei,LIN Xiaoliang,et al.Multi-objective joint optimization design of high-precision turn-milling compound machine tool bed based on nonparametric regression response surface method[J].Manufacturing Technology &Machine Tool,2024(5):128-133.
[16] 陈立娜,张维刚.基于Kriging模型的发动机罩多目标优化设计[J].中国机械工程,2013,24(22):3014-3018. CHEN Lina,ZHANG Weigang.Multi-objective optimization design of engine hood based on kriging model[J].China Mechanical Engineering,2013,24(22):3014-3018.
[17] 万云发,孙文磊,王宏伟,等.基于Kriging模型与MOGA算法的风力机主轴轻量化设计[J].太阳能学报,2022(3):388-395. WAN Yunfa,SUN Wenlei,WANG Hongwei,et al.Lightweight design of wind turbines main shaft based on Kriging model and moga algorithm[J].Acta Energiae Solaris Sinica,2022(3):388-395.
[18] 贾连辉,李晓科,袁文征,等.基于拓扑优化和Kriging模型的前中盾结构轻量化设计[J].中国机械工程,2022,33(23):2888-2897. JIA Lianhui,LI Xiaoke,YUAN Wenzheng,et al.Lightweight design of front and middle shield structures based on topology optimization and Kriging model[J].China Mechanical Engineering,2022,33(23):2888-2897.
[19] 朱孙科,孙永刚,董绍江,等.基于参数敏度分析的轮毂轴承寿命多目标优化[J].重庆交通大学学报:自然科学版,2023,42(8):147-154. ZHU Sunke,SUN Yonggang,DONG Shaojiang,et al.Multi-objective optimization of hub bearing life based on parameter sensitivity analysis[J].Journal of Chongqing Jiaotong University(Natural Science),2023,42(8):147-154.
[20] 王普毅,范天峰,张太平,等.武器装备轻量化结构正向设计方法及应用[J].兵器装备工程学报,2024,45(6):150-158. WANG Puyi,FAN Tianfeng,ZHANG Taiping,et al.A forward design method and application for light-weight structure of weaponry[J].Journal of Ordnance Equipment Engineering,2024,45(6):150-158.
[21] MARTYR A J,PLINT M A.Dynamometers:The measurement of torque,speed,and power,science direct[M].Fourth Edition.Engine Testing,2012:227-258.
[22] 孙艳坤,陈银,张威,等.飞机牵引滑行工况下前起落架疲劳寿命仿真分析[J].兵器装备工程学报,2024,45(6):246-252. SUN Yankun,CHEN Yin,ZHANG Wei,et al.Simulation analysis of nose landing gear fatigue life under aircraft towing taxiing condition[J].Journal of Ordnance Equipment Engineering,2024,45(6):246-252.
[23] 柴山,尚晓江,刚宪约.工程结构优化设计方法与应用[M].北京:中国铁道出版社,2015. CHAI Shan,SHANG Xiaojiang,GANG Xianyue.Optimized design methods and applications for engineering structures[M].Beijing:China Railway Publication House,2015.
[24] 李美求,赵志远,宋德双,等.超高压旋流除砂器结构响应面优化及数值模拟[J].液压与气动,2023,47(6):29-39. LI Meiqiu,ZHAO Zhiyuan,SONG Deshuang,et al.Optimization and numerical simulation of response surface of ultra-high pressure cyclone desander structure[J].Chinese Hydraulics and Pneumatics,2023,47(6):29-39.
[25] 张孟阳,陈志华,郑纯,等.基于代理模型的制导子弹气动外形优化设计[J].装备环境工程,2023,20(12):102-110. ZHANG Mengyang,CHEN Zhihua,ZHENG Chun,et al.Aerodynamic shape optimization design of guided bullet based on surrogate model[J].Equipment Environmental Engineering,2023,20(12):102-110.
[26] 吴勃夫,吴姚烨,贝璟,等.铸铝一体化车门的多目标可靠性优化设计[J].工程设计学报,2024,31(2):188-200. WU Bofu,WU Yaoye,BEI Jing,et al.Multi-objective reliability optimization design for cast aluminum integrated car door[J].Chinese Journal of Engineering Design:2024,31(2):188-200.