冲击波是弹药爆炸的重要毁伤元，弹药在实际工作过程中都是在运动状态下爆炸的，当弹药有一定运动速度时，相比静爆，冲击波的分布特征会发生变化，研究运动条件下的爆炸冲击波特性对爆炸威力评价具有着重要意义。
20世纪50年代，Ф·А鲍姆等[1]关于装药运动速度对于爆炸效应的影响进行了初步理论分析研究。桑希尔(C.K.Thornhill)和海塞林顿(R.Hetherington)从理论上分析了装药爆炸时刻的运动速度对爆炸冲击波特性的影响[2]。美国陆军弹道研究所(BRL)利用滑膛炮对B炸药和Pentolite两种球形装药进行了动态加载实验，得到了装药运动速度下的爆炸冲击波分布参数[3-4]。
国内关于动爆冲击波研究方面较少，目前的工作以计算仿真为主。张光莹等[5]提出了一种理论方法与计算机仿真实验方法相结合研究运动装药在距地面一定高度发生爆炸产生冲击波特性的方法，给出了100 kg TNT装药在速度为200 m/s时的爆炸冲击波压力-时程曲线。谢美华[6]针对不同类型的导弹实验之间存在的差异，利用回归分析方法对异类实验数据进行联合建模，给出了动爆与静爆实验数据差异分析的一种参数化方法。蒋海燕等[7]采用AUTODYN对不同速度装药的爆炸冲击波场进行数值模拟，获得动爆条件下的冲击波场演化过程及冲击波超压分布特征，建立动爆冲击波超压的工程计算模型。聂源等[8]对球形装药动态爆炸冲击波超压场计算模型，采用Baker计算公式加入修正因子进行修正。畅博等[9]利用AUTODYN研究了运动炸药近地爆炸冲击波场分布特性，认为3倍比例距离外运动速度对地面峰值超压的增益无明显差异。
由于动爆实验爆点位置难以精确控制，国内针对动爆冲击波开展实验研究较少，理论模型尚未建立，仿真数据缺乏验证，不能对动爆冲击波给予很好描述。本文通过设计动爆实验，获取了动爆冲击波初始变化图像及冲击波压力参数，为动爆冲击波场研究提供了依据。
1 实验
为研究动爆条件下的冲击波分布特征，选取某榴弹进行了静爆与动爆实验并对二者进行比较。实验样弹装药量约8.7 kg TNT当量，装药长径比为3.4。其中静爆实验炸高为2 m，采用8#电雷管起爆。动爆实验采用火炮对样弹进行水平动态加载，预设加载炮口速为680 m/s，在距炮口轴线方向设置目标靶，靶面与炮口中线垂直，中心距地高度2 m，采用短延期瞬发引信前端起爆。动态实验经过调试，样弹可在穿靶后约2 m处起爆，现场布设如图1所示。
图1 实验方法示意图
实验在距离静爆爆点及动态预设爆点位置地面投影中心2 m、3 m、4 m、6 m、8 m、10 m布设了测点。以样弹弹头方向为0°方向，沿逆时针0°、90°、180°三个方向布设地面冲击波超压传感器，采用的是美国PCB 113B系列冲击波传感器，其谐振频率≥250 kHz，单通道采样速率1 MS/s，实验前对传感器采取隔振及热防护处理。
在90°方向架设激光高速摄影系统，帧频5 000帧/s，存储长度可完整记录样弹撞击靶板、样弹起爆到爆轰产物传播到压力测点范围变化过程，如图2所示。
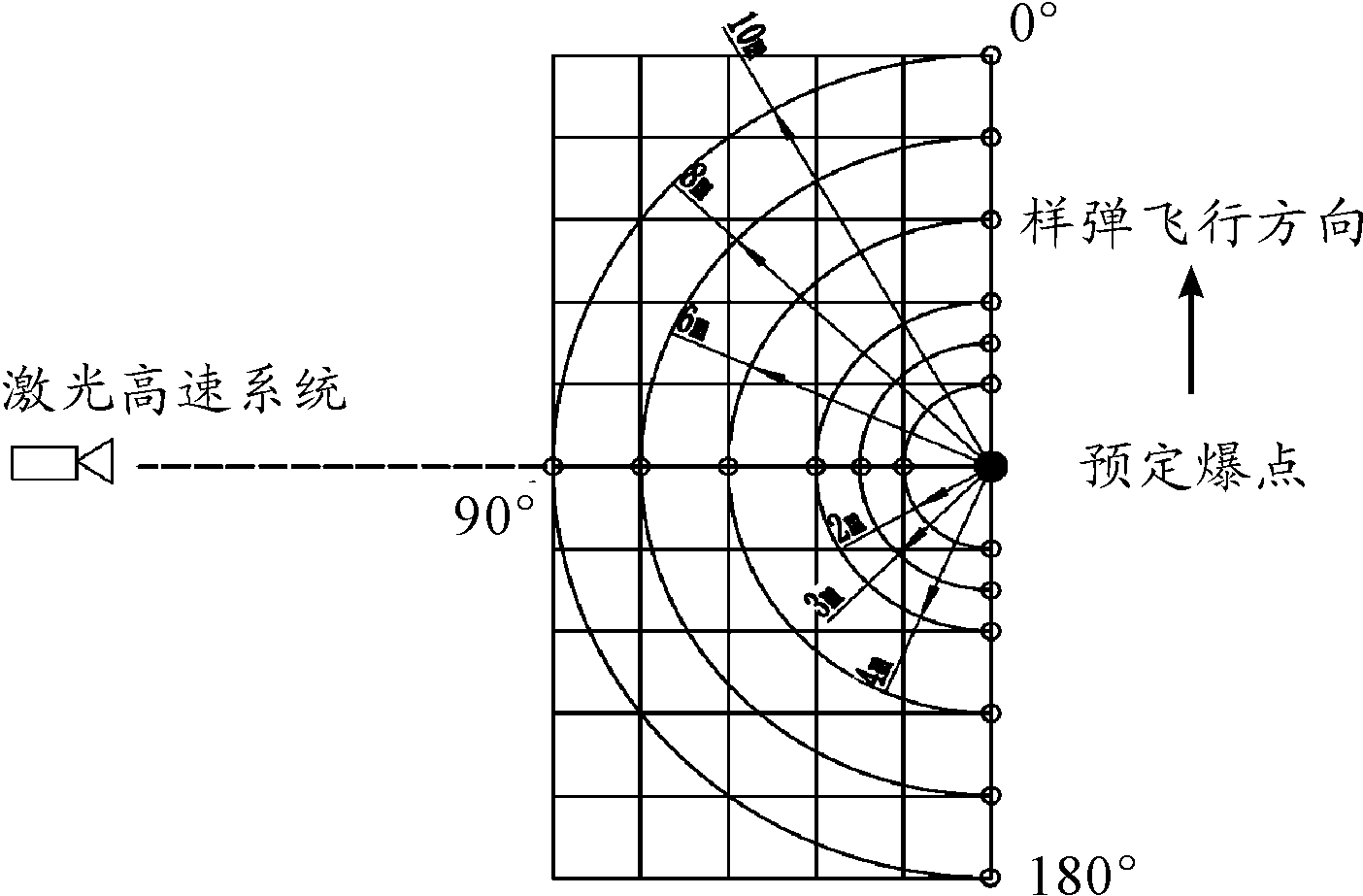
图2 测点布设示意图
2 结果与分析
2.1 静爆与动爆冲击波变化过程
利用激光高速摄影系统获取了样弹静爆及动爆后的动态影像，并对其进行了图像处理。为便于比较，取样弹瞬时爆轰时间为0时刻，其中右侧为弹头方向，定义为正向；左侧为弹底方向，定义为负向。
样弹静爆过程如图3所示，初始时爆轰产物在冲击波作用下快速膨胀，受弹体形状的影响，爆轰产物在正向与负向分布存在差异，冲击波阵面并不规则；在800 μs时冲击波与爆轰产物逐渐分离。在1 000 μs时两侧冲击波阵面基本对称分布；随着冲击波的扩展，约2 000 μs时可观察到地面反射冲击波，并在3 000 μs时可清晰观测到马赫杆。其后冲击波进一步扩展，逐步形成较为光滑的冲击波。
图3 静爆实验影像图
样弹动态起爆过程如图4所示。经专用软件判读，样弹实际起爆瞬时速度为618 m/s,弹体几何中心距预定爆心向速度方向前移0.56 m，高度方向较预设位置下偏0.4 m，横向位置沿测线方向偏移0.1 m。
通过图4可以看出：受弹药运动速度的影响，爆轰产物在起爆后仍以一定的速度向前运动，在向外膨胀过程中爆轰产物形态上较为“光滑”，受弹体形状影响较小。分析认为该过程与速度引起的阻力变化关系密切，有待进一步深入研究。约800 μs时，负向冲击波先于正向冲击波从产物中分离；而正向冲击波约1 000 μs时才开始该过程。随着冲击波的逐步扩展，与地面作用后产生反射冲击波，并对入射冲击波“追赶”，约2 000 μs时正向已出现马赫杆，而负向马赫杆出现时间则大于3 000 μs。
图4 动态实验影像图
取起爆时刻样弹几何中心为参考点，对不同时刻正向与负向冲击波阵面所在位置进行判读，得到静爆与动爆条件下冲击波阵面传播速度，如图5所示。可以看出，静爆时正向与负向冲击波速度较为接近；而在动爆条件下，正向冲击波速度明显大于静爆冲击波速度，负向冲击波速度则明显小于静爆冲击波速度。
2.2 冲击波中心位移变化
仍取起爆时刻实验样弹几何中心为参考点，根据爆炸冲击波波阵面变化图像，以沿弹轴中心线为x轴，正向及负向冲击波阵面所在位置取平均值作为“冲击波中心”，如图6所示，获得弹药在不同运动速度下的冲击波中心沿装药爆炸时刻速度方向的位移随时间的变化曲线，以及冲击波传播中心速度随时间的变化曲线。
可以看出，动爆冲击波中心位移随时间沿弹药运动正向移动，但运动速度逐渐降低，并趋于稳定值，接近300 m/s。而静爆冲击波中心在约100 mm附近波动，可能与样弹中心位置选取有关，即初始冲击波阵面中心与其几何中心并不重合，但中心速度在0 m/s附近波动，如图7所示。
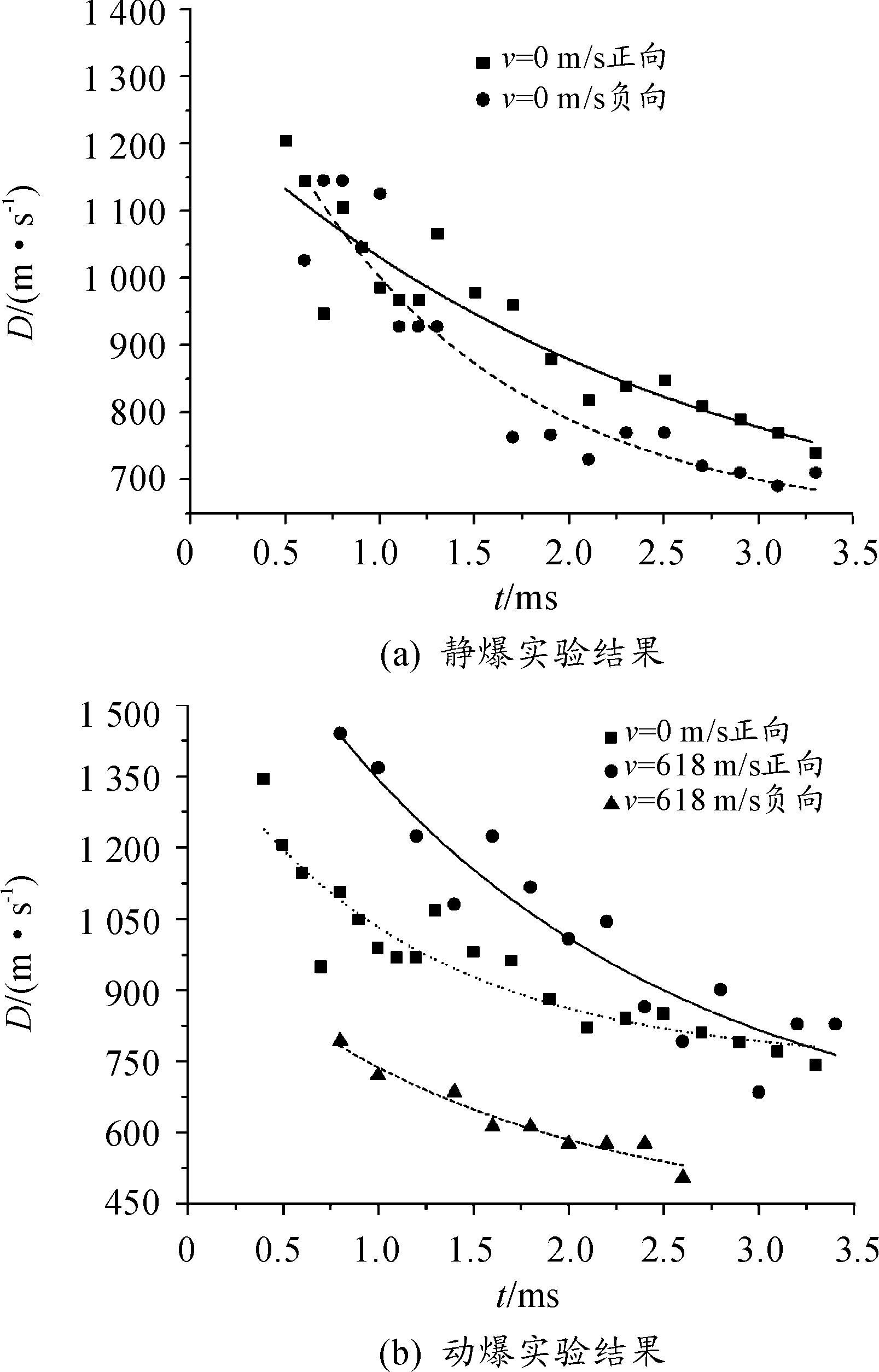
图5 静爆与动爆冲击波速度
图6 冲击波传播中心选取示意图
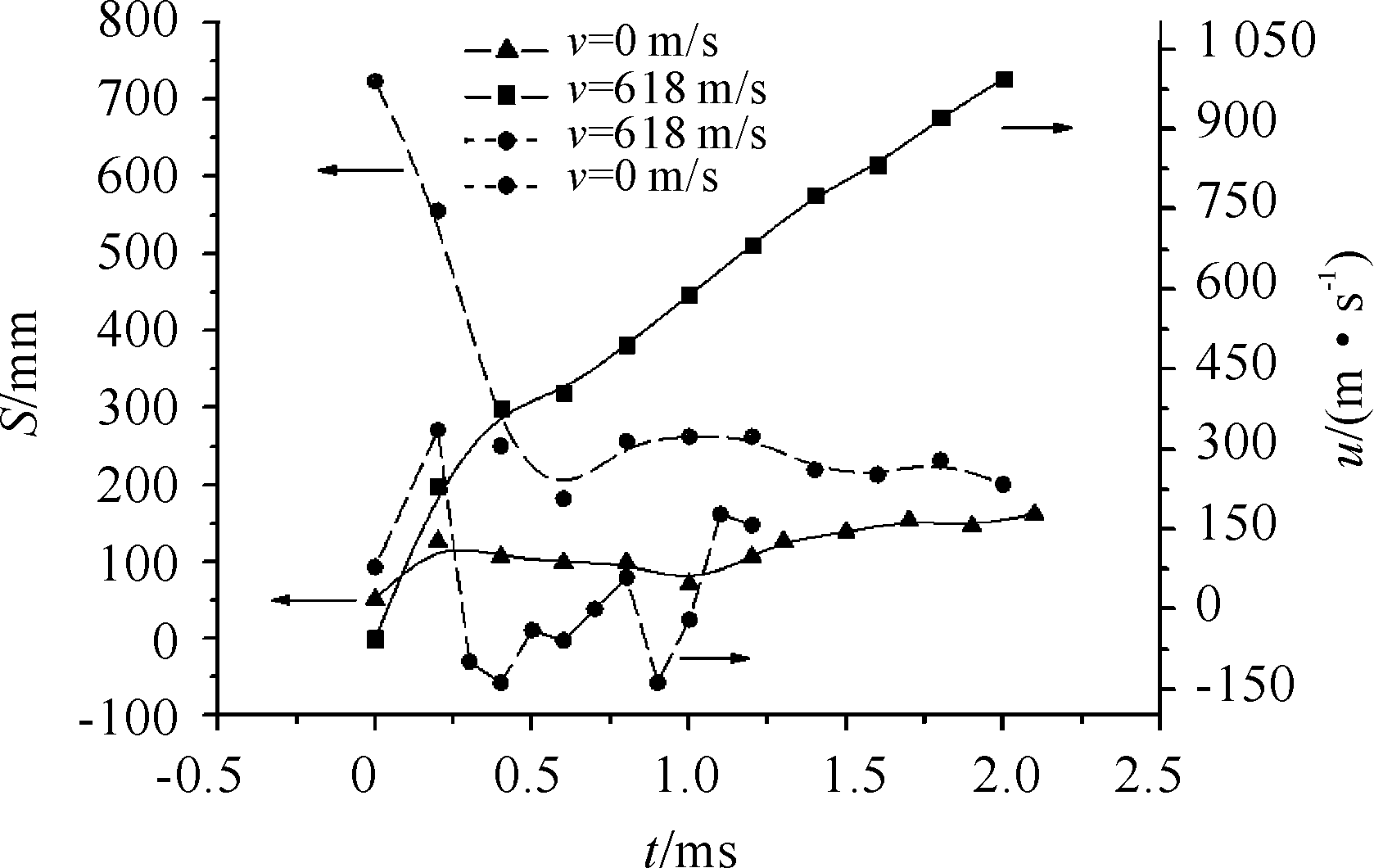
图7 冲击波中心位移/速度随时间变化曲线
2.3 冲击波超压比较
2.3.1 冲击波超压测试曲线
实验测试结果受破片影响较大，90°测线方向破片较为密集，0°(正向)测线方向与180°(负向)测线方向破片较少，对于90°测线方向数据未能全面获取，典型静爆冲击波超压曲线如图8所示。
图8 静爆0°方向冲击波超压测试曲线
动态加载情况下由于破片受弹药运动速度影响，整体向前飞散，导致冲击波超压数据获取率较低，且所获信号较差，对可信度较低的测量结果予以剔除，典型波形曲线如图9所示。
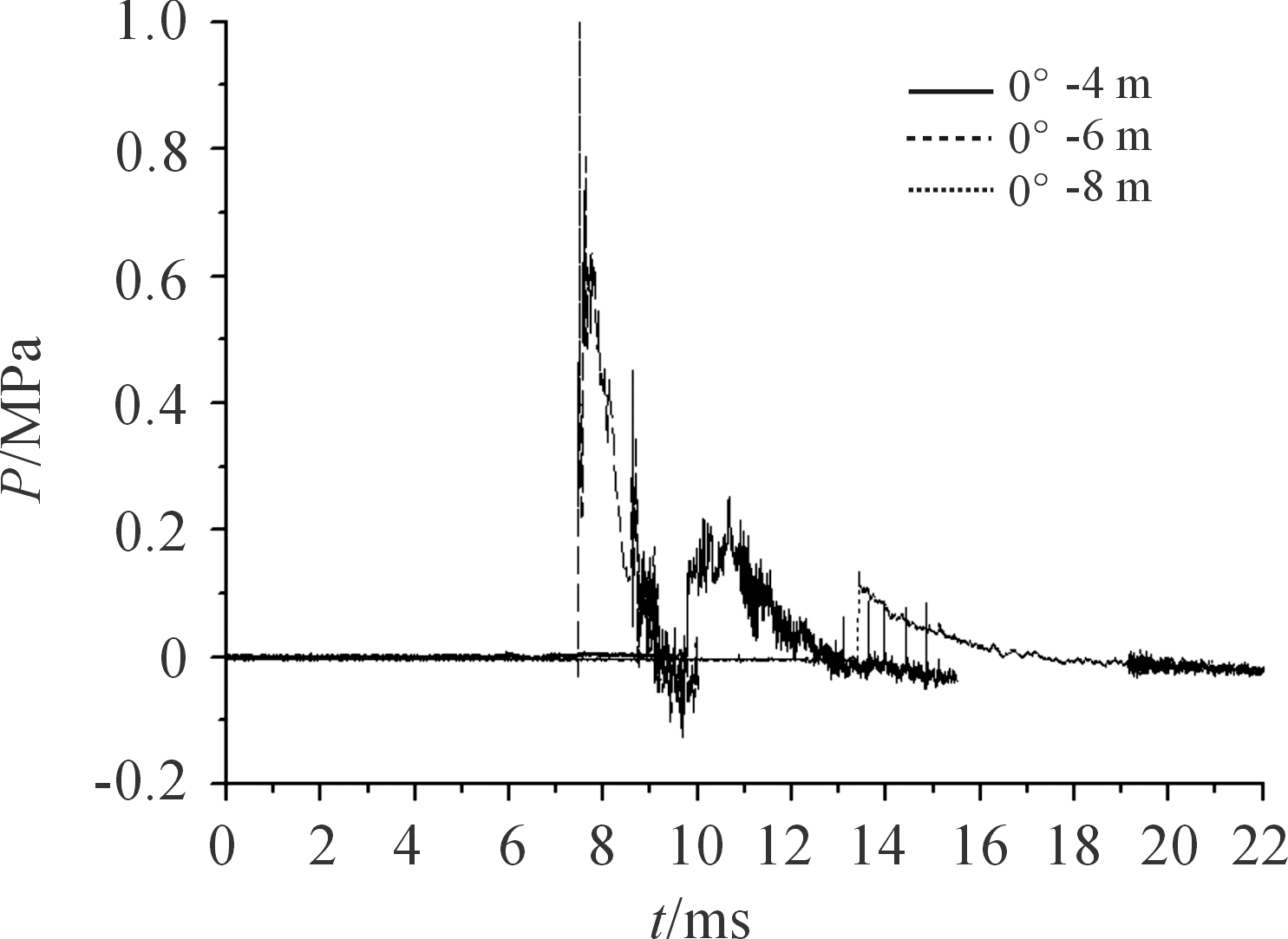
图9 动爆0°方向冲击波超压测试曲线
2.3.2 冲击波超压结果分析
实验利用冲击波压力传感器获取了静爆冲击波超压与动爆冲击波超压，静爆结果如表1所示。
表1 静爆冲击波超压
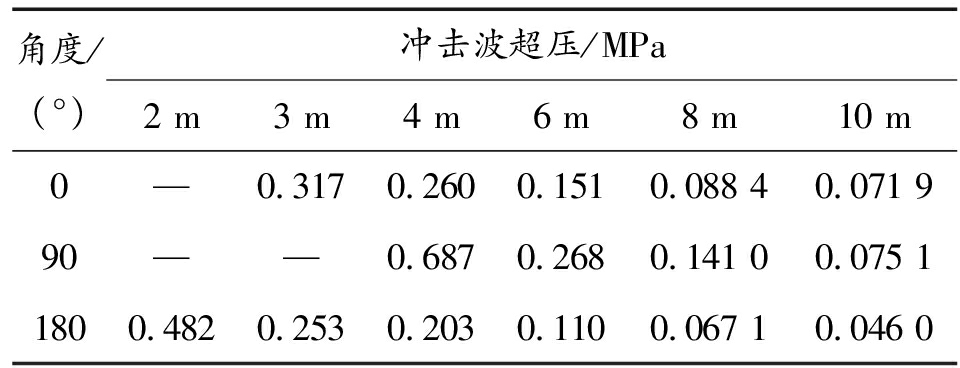
角度/(°)冲击波超压/MPa2 m3 m4 m6 m8 m10 m0—0.3170.2600.1510.088 40.071 990——0.6870.2680.141 00.075 11800.4820.2530.2030.1100.067 10.046 0
由于样弹在动爆过程中，实际位置与预定位置有偏差，为便于与静爆实验结果分析，需要对其进行修正。由于实验弹位置的偏差主要来源于高度方向(-0.4 m)和水平方向(-0.56 m)，依据实际距离对冲击波超压进行换算。
由炸药爆炸理论可知，当弹药有一定炸高时，对于非正规反射，若在地面上测量冲击波超压，则存在一临界角φ0(一般认为约为42°)。当入射角φ>φ0时，该处所测应为马赫波压力，当φ0<φ<90°时，存在式(1)～式(3)关系：
ΔPR=ΔPmg(1+cosφ)
(1)
(2)
(3)
其中，ΔPmg为装药地面爆炸时冲击波超压(MPa)；ΔPR为马赫波压力
为对比距离；φ为测点位置相对爆心连线与爆心垂直投影夹角；H为爆心高度(m)；R为测点距离(m)。
对于实验弹，对于同一处测点，设样弹预设高度为H1，实际高度H2，则测点处相对爆心角度分别为
则存在
ΔPR1/ΔPR2=(1+cosφ1)/(1+cosφ2)
(4)
利用式(4)，根据样弹沿速度方向的偏移量对实验结果进行修正，即将静爆与动爆中心点统一到同一参考坐标系下，结果见表2所示。
表2 修正后的冲击波超压
方向序号实际距离/m修正后冲击波超压/MPa0°13.4401.313 025.4400.269 037.4400.141 090°42.0760.687 054.0390.268 066.0260.141 078.0190.075 1180°84.5600.078 896.5600.059 0108.5600.038 7
从表2可以看出：对0°方向及180°方向，实际距离变化较大。90°方向实际距离与静爆预设距离最大偏差不超过4%(2 m处)，将其动爆与静爆实验结果直接进行比较。将静爆实验表1中各测线数据进行拟合，得到
关系，即
0°测线：
(5)
90°测线：
(6)
180°测线：
(7)
通过式(5)～式(7)及表2，计算得到相同
下的动爆超压值Pd及静爆超压值Ps，进一步得到Pd/Ps-r关系，如图10所示。其中0°方向在1.440 m处测点所在位置与爆心之间角度大于临界角φ0，不作比较予以舍弃。
从图10可以看出：在0°测线方向，沿运动速度方向冲击波超压具有增强作用，实验中在
处增压系数可达2.5倍，而在90°测线方向和180°测线方向冲击波则减弱，平均减压系数分别为0.70倍和0.57。
对冲击波正压时间也进行了对比分析，记静爆与动爆冲击波正压时间分别为ts和td,取(td-ts)随距离变化进行对比，如图11所示，可以看出，对于0°测线，冲击波正压时间明显减小，而对于90°与180°测线，冲击波正压时间较为接近。
图
关系曲线
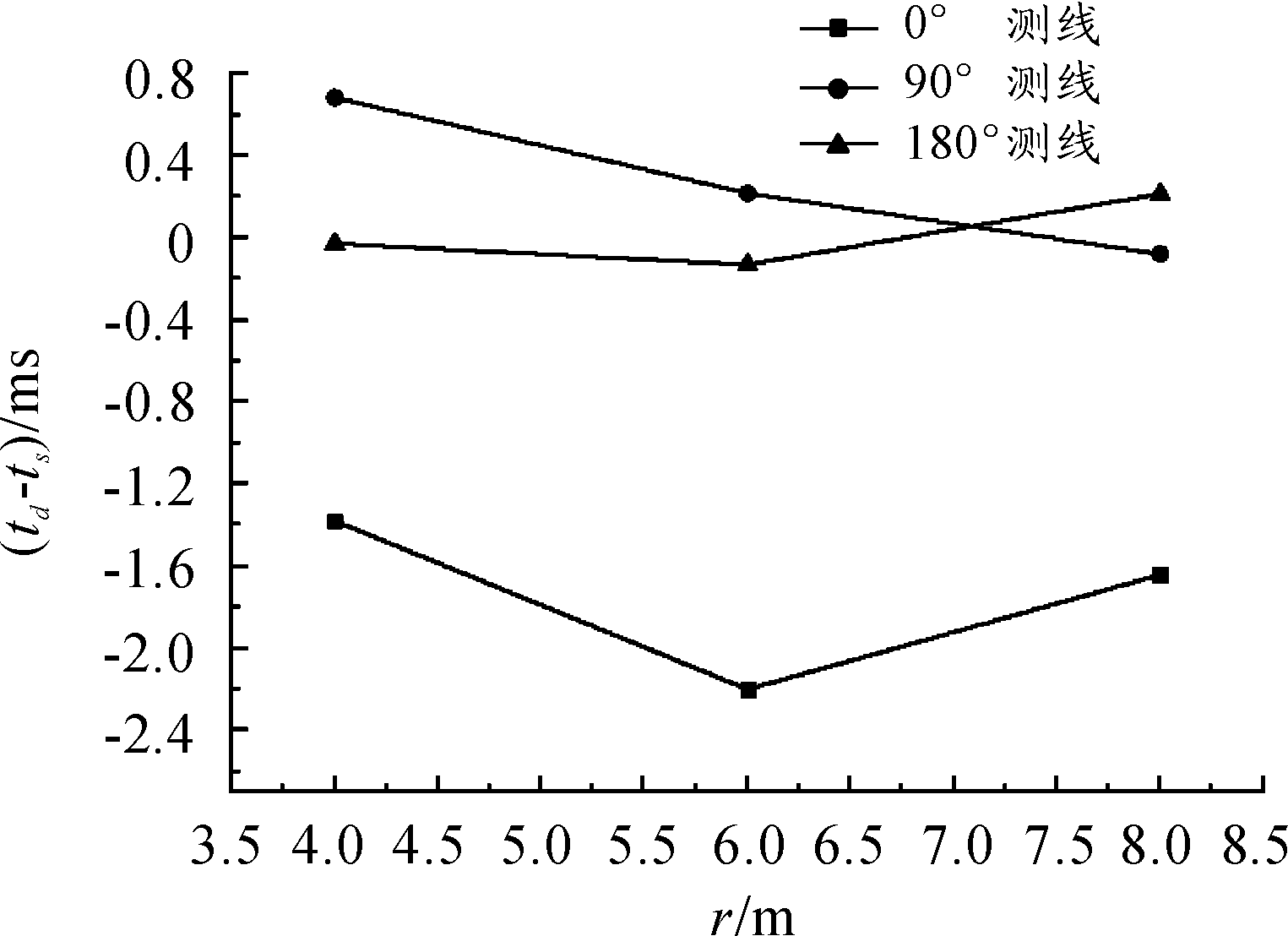
图11 (td-ts)-r关系曲线
关于不同方向的动爆冲击波特性，分析认为根据文献[3]提到的动爆冲击波模型，冲击波中心较样弹几何中心向运动速度正向移动，其中R为冲击波波阵面到爆心的距离，r为冲击波波阵面到“冲击波中心”的距离。
根据Rankine-Hugoniot方程，冲击波速度D与冲击波超压峰值P存在以下关系：
(8)
式中：P0为大气压力，γ为绝热指数，c0为当地空气声速。
由式(8)可知，动爆冲击波超压峰值Pd与静爆冲击波超压峰值Ps的关系为
(9)
式中：Dd和Ds分别为动爆冲击波速度和静爆冲击波速度。
根据图5冲击波速度对比，以及文献[3]动爆冲击波模型，结合式(9)可知，对于动爆冲击波超压，沿运动速度正向应具有增强作用，沿运动速度负向应减弱。同时注意到在90°方向，由于运动速度影响，爆轰产物仍向前移动，实际测点布设是以样弹几何中心为参照，故冲击波超压值也应减弱，这与实际冲击波超压测试是吻合的。
实验过程中由于破片的作用，未获取到全部测点有效数据，关于动爆威力场的形成机理仍有待进一步深入研究。
3 结论
1) 沿弹药运动正向冲击波速度大于静爆冲击波速度，而运动速度负向冲击波速度小于静爆冲击波速度；
2) 沿运动速度正向冲击波超压具有增强作用，本次实验中增压系数最高可达2.5倍；而在90°方向和运动速度负向冲击波则减弱，平均减压系数分别为0.70倍和0.57倍。
3) 动爆与静爆过程中形成马赫波的时间不一致，受运动速度的影响，沿动态运动速度正向三波点出现时间早于静爆，负向三波点出现的时间晚于静爆。
[1] Ф·А鲍姆,К·П斯达纽柯维奇.爆炸物理学[M].众智,译.北京:科学出版社,1963:624-627.
[2] THORNHILLl C K,HETHERINGTON R.Some notes on explosions of moving charges[M].British:Armament Research Establishment,1953.
[3] PATTERSON J D,WENIG J.Air blast measurements around moving explosive charges:AD0033173[M].Aberdeen:Army Ballistics Research Laboratory,1954.
[4] ARMENDT B F,SPERRAZZA J.Air blast measurements around moving explosive charges,Part III:AD0114950[M].Aberdeen:Army Ballistics Research Laboratory,1956.
[5] 张光莹,周旭,黄咏政,等.动爆冲击波特性分析方法研究[C]//第四届全国计算爆炸力学会议论文集.中国力学学会爆炸力学专业委员会，西安：2008:282-287.
[6] 谢美华.导弹动、静实验差异的参数化建模及补偿[J].控制理论与应用，2009,26(10):1130-1132.
[7] 蒋海燕,李芝绒,张玉磊,等.运动装药空中爆炸冲击波特性研究[J].高压物理学报，2017,31(3):286-294.
[8] 聂源,蒋建伟,李梅.球形装药动态爆炸冲击波超压场计算模型[J].爆炸与冲击，2017,37(5):951-956.
[9] 畅博,谷鸿平,牛晨伟,等.运动装药近地爆炸冲击波场特性研究[J].爆破，2018,35(3):49-54.