分离速度是衡量飞行器分离过程的重要指标之一,建立对应计算模型可快速评估不同影响因素下飞行器的分离可靠性。其中针对飞行器静态分离速度的计算模型较为常见[1],而动态分离过程由于飞行环境恶劣,气动与运动特性变化剧烈,与静态分离存在差异,静态分离速度无法准确描述动态过程[2]。因此研究飞行器的动态分离速度计算模型非常必要。
国内外学者针对飞行器级间分离速度的计算问题进行了广泛的研究[3-5],大多采用仿真与理论方法。且对于分离速度计算模型而言,目前关于静态分离速度计算模型主要以内弹道原理[6-7]及能量法[8-9]居多。而针对动态分离速度计算模型,不少学者也开展了相关研究。杨涛、王鑫[10-11]等开展了导弹级间多体分离过程理论研究,建立了导弹前级分离过程六自由度运动方程,但模型所需参数较多,直观性不强。姬龙、蔡薇[12-13]等进行了串联战斗部动态分离研究,建立了动态条件下前级战斗部内弹道模型,但仅研究了某一特定飞行速度。黄伟[14]开展了降落伞弹射分离过程理论研究,建立了不同飞行速度下降落伞最小弹射速度计算模型,但未探讨其他影响因素。综上所述,这些研究并未给出多种因素综合影响下且较为直观的动态分离速度计算模型。而在实际分离过程中,除飞行速度外,飞行攻角、平均膛压等因素均共同影响动态分离速度,同时在工程应用中直观便捷的计算公式更具有实用性。
本文基于CFD-FASTRAN软件计算两级高速飞行器动态分离过程,得到不同工况下前级动态分离速度,并在仿真数据的基础上,通过建立前级关于初始飞行速度、攻角与平均膛压的速度修正因子,得到基于静态分离速度的前级动态分离速度计算模型,并采用仿真验证该模型的正确性。该模型综合考虑了三种影响因素对动态分离的影响,适用范围更广,提高了对实际工况的预测能力,计算直观便捷,具有一定的工程意义。
1 模型建立
1.1 问题描述
图1为两级高速飞行器结构示意图,由图1可知飞行器分为前级、后级、分离套筒与分离机构。前级通过分离机构作用,经分离套筒实现分离,前级头部为球缺型,弹径30 mm,弹长100 mm,弹重0.3 kg,分离套筒有效长度与弹长相同。由于本文中分离机构作用时间短,选用平均膛压进行计算[15]。后级口径与质量均远大于前级,假定后级以恒定速度飞行,且分离过程空气阻力均匀作用于前级。定义变量:v∞为两级高速飞行器初始飞行速度,α为两级高速飞行器初始攻角,P为平均膛压。
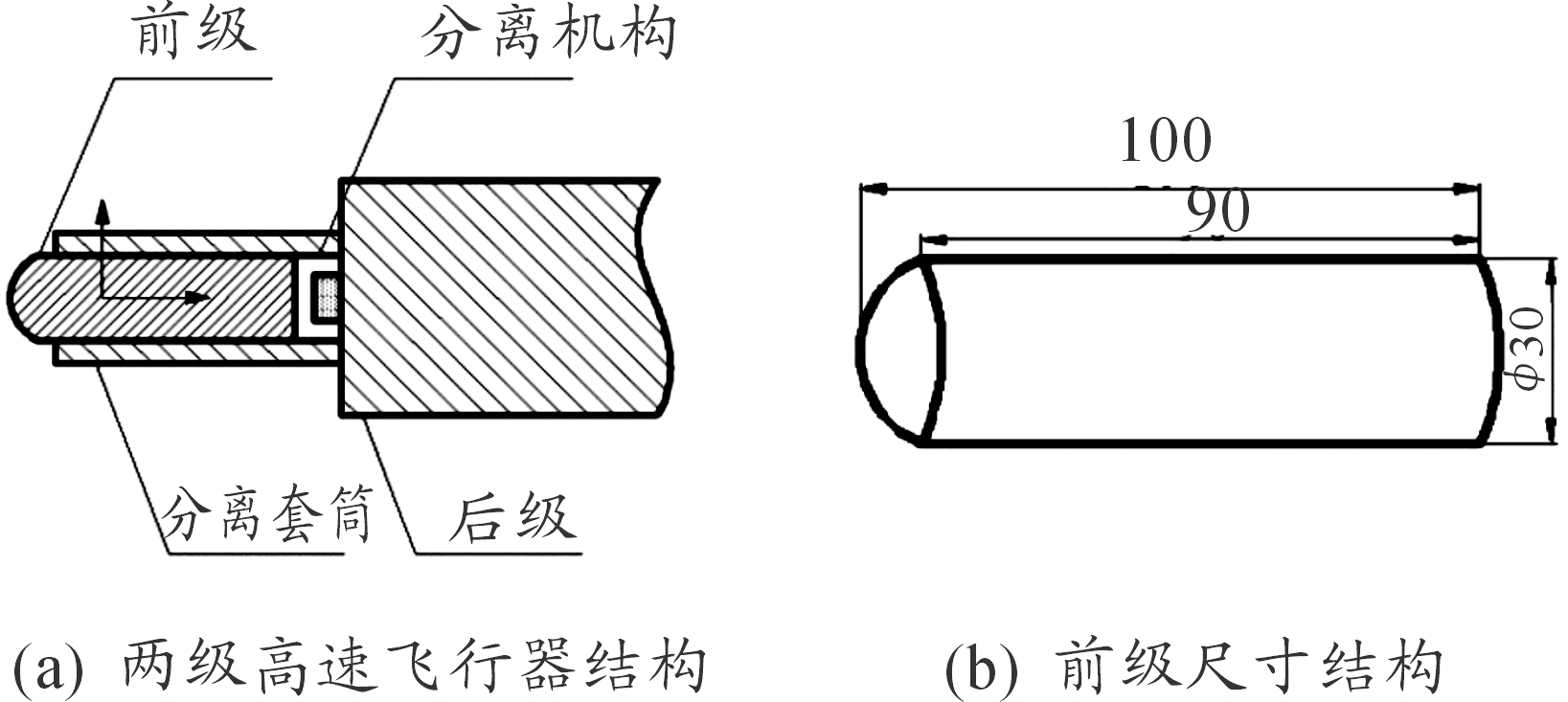
图1 两级高速飞行器结构及坐标位置示意图
1.2 动态分离速度计算模型建立
针对前级的动态分离速度进行量纲分析,得到动态分离速度是关于初始飞行速度、攻角、平均膛压与静态分离速度的函数,对不同工况下前级的动态分离速度进行数值计算,基于静态分离速度,并由仿真结果拟合得到速度修正因子,最终由速度修正因子得到动态分离速度计算模型[16]。
通过量纲分析[17]可知,决定动态分离速度的参数包括三类:
1) 气动参数:初始飞行速度v∞、攻角α、阻力系数Cx、当地声速c、前级参考长度lc、参考面积Sm、空气密度ρ∞。
2) 结构参数:前级质量m、套筒长度lt、前级长度ld、前级口径D。
3) 膛内参数:平均膛压P。
动态分离速度与上述参量存在确定的函数关系,即:
vd=F(v∞,α,Cx,c,lc,Sm,ρ∞,m,lt,ld,D,P)
(1)
本文中飞行器尺寸固定,分离过程发生于大气标准状态,阻力系数是初始飞行速度与飞行器外形特征的函数,因此结构参数、标准大气参数与阻力系数均可消去。选取vd为因变量,v∞,α,P为基本量,依据π定理可知,动态分离速度可表示为:
(2)
对基本量进行归一化处理,得到无量纲参量为:
(3)
式(3)中:Ma为初始飞行马赫数;α为攻角;Pd为无量纲平均膛压。
计算静态分离速度,采用平均膛压进行计算,忽略分离过程前级与套筒之间的摩擦力,由能量法可得理想状态下的静态分离速度为:
![]()
(4)
式(4)中:P为平均膛压;S为弹底面积;lt为套筒长度;m为前级质量。
定义速度修正因子δ,即:
![]()
(5)
式(5)中:v0为静态分离速度;vd为动态分离速度。
用速度修正因子计算动态分离速度,变换式(5)可得:
vd=(1-δ)v0
(6)
采用初始飞行马赫数Ma、攻角α和无量纲平均膛压Pd来反映不同工况条件对动态分离速度的影响,即δ= f (v∞/c,α,SltP/mc2),因三变量间相互独立,定义f(Ma)为初始飞行速度修正因子,f (α)为攻角修正因子,f (Pd)为平均膛压修正因子,则修正因子δ可表示为:
δ= f (Ma)·f (α)·f (Pd)
(7)
式(7)中, f (Ma)为特定攻角α*及平均膛压P*条件下,不同初始飞行马赫数时的δ值,即:
(8)
f (α)为特定平均膛压P*条件下,取一系列初始飞行马赫数时,不同攻角α处的δ与特定攻角α=α*时δ的比值,即:

(9)
f (Pd)为取一系列初始飞行马赫数Ma和攻角α时,不同平均膛压的δ与特定平均膛压![]() 的δ的比值,即:
的δ的比值,即:
(10)
以上为基于速度修正因子的动态分离速度计算模型建立方法。选取不同初始飞行速度v∞=[500,1 000,1 500,2 000,2 500]m/s、攻角α=[0,π/45,2π/45,3π/45,4π/45,5π/45]及平均膛压P=[50,70,90,110,130]MPa进行计算。根据式(8)-(10)可知,速度修正因子求解时需选取特定攻角及平均膛压参与速度修正因子拟合过程,为方便计算选取α*=0,P* =30 MPa(即![]()
2 修正因子的获取
2.1 仿真模型的建立与计算
为获得速度修正因子求解过程所需的动态分离速度,本节基于CFD-FASTRAN软件,对两级高速飞行器动态分离过程进行计算,该软件采用嵌套网格技术进行多体运动仿真。图2为前级嵌套网格有限元模型,由图2可知,计算区域分为前级近壁面流场和外流场模型。在前处理软件CFD-GEOM中分别划分结构化网格,并进行自动嵌套。求解过程采用三维Farve平均N-S方程与描述刚体运动的6DOF运动方程耦合求解,对于近壁面网格,采用k-ε湍流模型,计算条件为标准大气环境,其中大气密度ρ∞=1.225 kg/m3,大气温度T0=288.15 K,大气压力P0=101 325 Pa。

图2 嵌套网格有限元模型
由于动态分离过程为非定常问题,需先对前级近壁面流场进行稳态计算,当计算收敛后,以稳态流场环境为初始条件,求解动态分离过程,即可获得前级动态分离速度的精确解。图3(a)为30 MPa平均膛压、0攻角下一系列初始飞行速度的前级膛内相对运动速度随行程变化曲线,图3(b)为2 500 m/s初始飞行速度、30 MPa平均膛压下一系列攻角的前级膛内相对运动速度随行程变化曲线。
由图3可知,前级膛内相对运动速度在平均膛压与空气阻力的共同作用下近似幂函数形式增加,且随初始飞行速度增大而下降,随攻角增大而增大。选用CFD-FASTRAN计算获得的膛内相对运动速度-相对行程曲线的终点值作为动态分离速度vd,进行修正因子的计算。
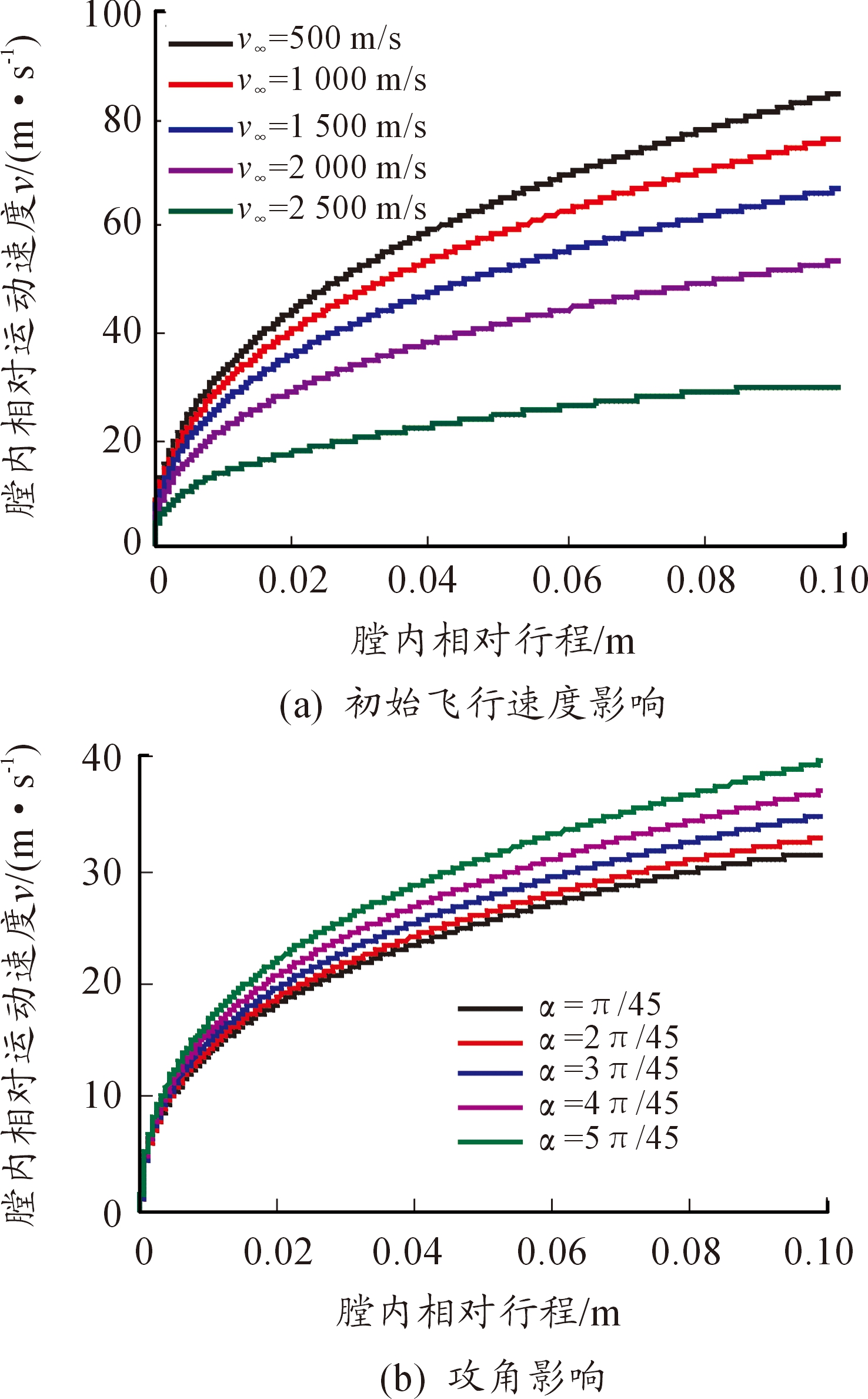
图3 典型工况下的前级膛内相对运动速度-行程曲线
2.2 初始飞行速度修正因子
为获取初始飞行速度修正因子,选取攻角为0、平均膛压为30 MPa时,一系列初始飞行速度v∞=[500,1 000,1 500,2 000,2 500]m/s(即初始飞行马赫数Ma=[1.47,2.94,4.41,5.88,7.35]),计算典型初始飞行速度下前级动态分离速度。
图4为根据式(8)计算得到的 f (Ma)及其拟合曲线。由图4可知,f (Ma)随初始飞行马赫数增大而增大,且增大趋势逐渐变陡。说明初始飞行速度修正因子随初始飞行马赫数增大而增大,这是由于初始飞行速度增大后,前级所受空气阻力增大,导致动态分离速度减小,其对应数值逐渐远离静态分离速度。对 f (Ma)函数进行拟合,得到:
f (Ma)=0.01Ma2-0.006Ma+0.28
(1.47<Ma<7.35)
(11)
2.3 攻角修正因子
为获取攻角修正因子,选取平均膛压为30 MPa时,一系列初始飞行速度下的不同攻角α=[0,π/45,2π/45,3π/45,4π/45,5π/45],计算典型攻角下前级动态分离速度。
图5为根据式(9)计算得到的 f (α)、平均值及拟合曲线。由图5可知,f (α)随攻角增大而减小,且减小趋势逐渐变陡。说明攻角修正因子随攻角增大而减小,这是由于攻角增大时,前级轴向空气阻力在攻角和特征面积的综合作用下减小,导致动态分离速度增大,其对应数值逐渐逼近静态分离速度所致,取不同初始飞行速度时f (α)的平均值,可以拟合得到:
f(α)=-0.29α2-0.04α+1
(0<α<π/9)
(12)
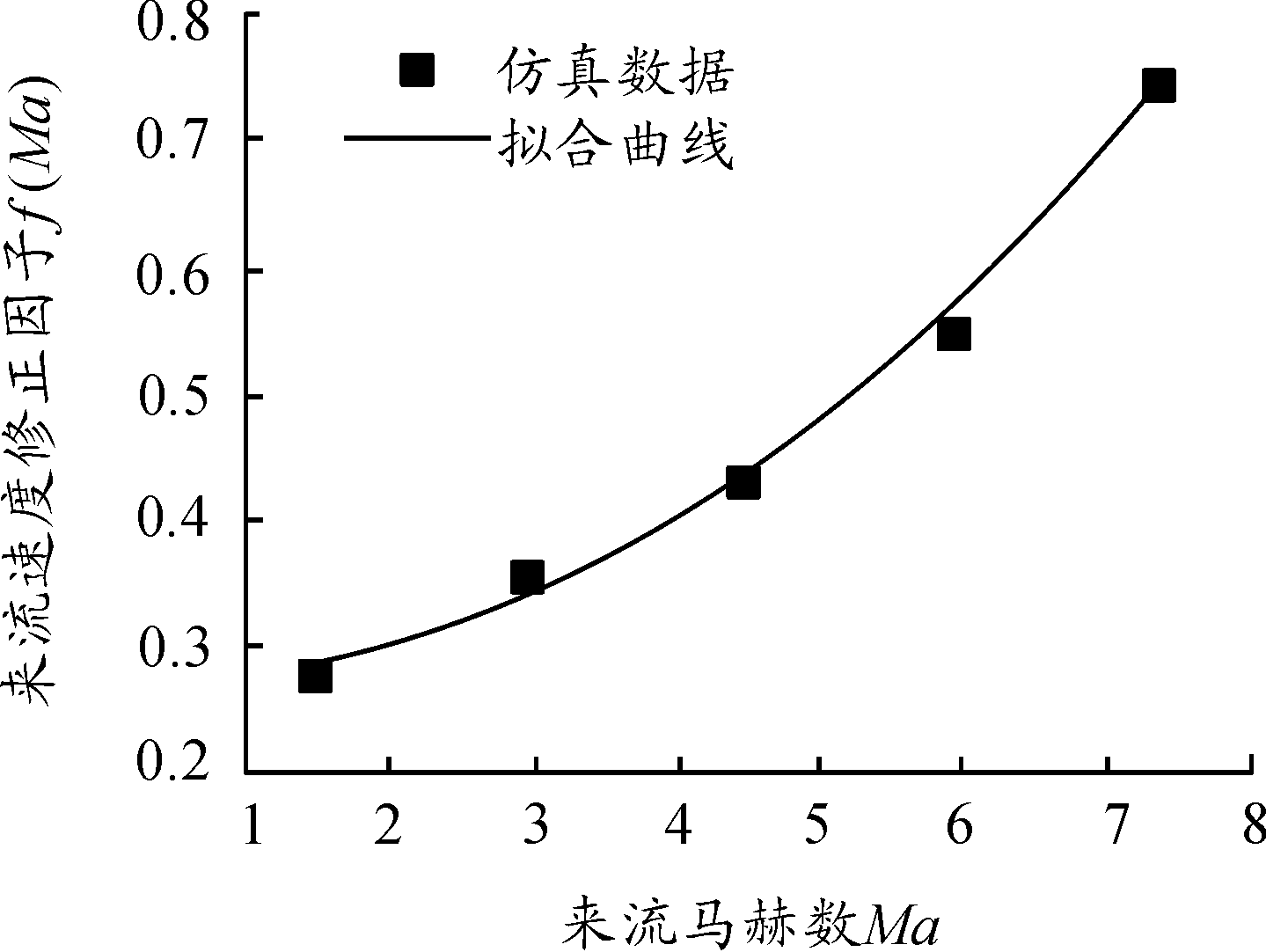
图4 f (Ma)拟合曲线
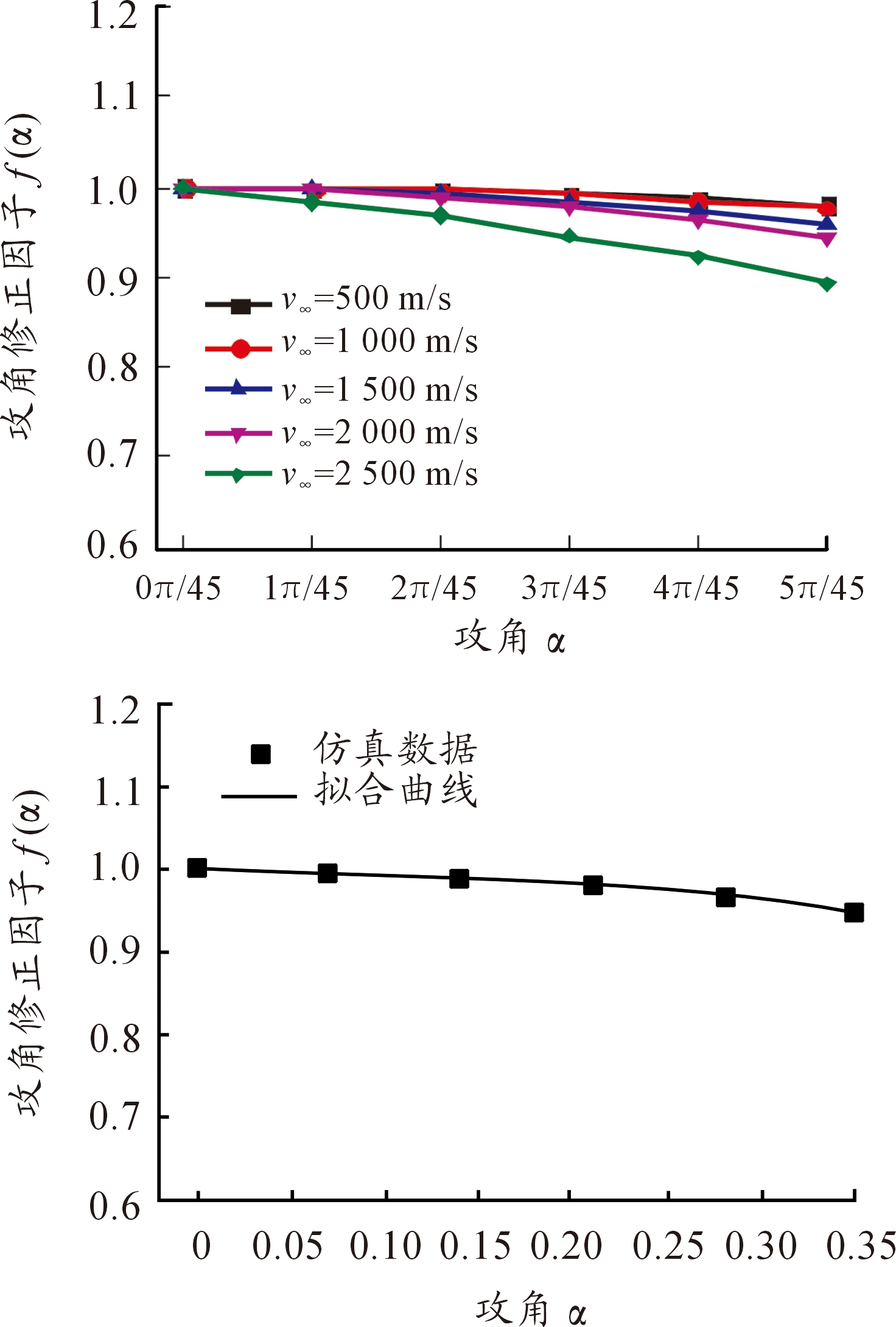
图5 不同α时f (α)的曲线、平均值及拟合曲线
2.4 平均膛压修正因子
为获取平均膛压修正因子,选取一系列初始飞行速度及攻角条件下的平均膛压P=[30,50,70,90,110,130]MPa(即无量纲平均膛压Pd=[0.06,0.1,0.14,0.18,0.22,0.26]),计算典型平均膛压下前级动态分离速度。
图6为根据式(10)计算得到的f (Pd)、平均值及拟合曲线。由图6可知, f (Pd)随无量纲平均膛压增大而减小,且减小趋势逐渐变缓。说明平均膛压修正因子随无量纲平均膛压增大而降低,这是由于平均膛压增大时,空气阻力在大平均膛压作用下对两级高速飞行器分离过程影响较小,导致动态分离速度逼近静态分离速度。取不同初始飞行速度与攻角时f (Pd)曲线平均值拟合可得:
(0.06<Pd<0.26)
(13)
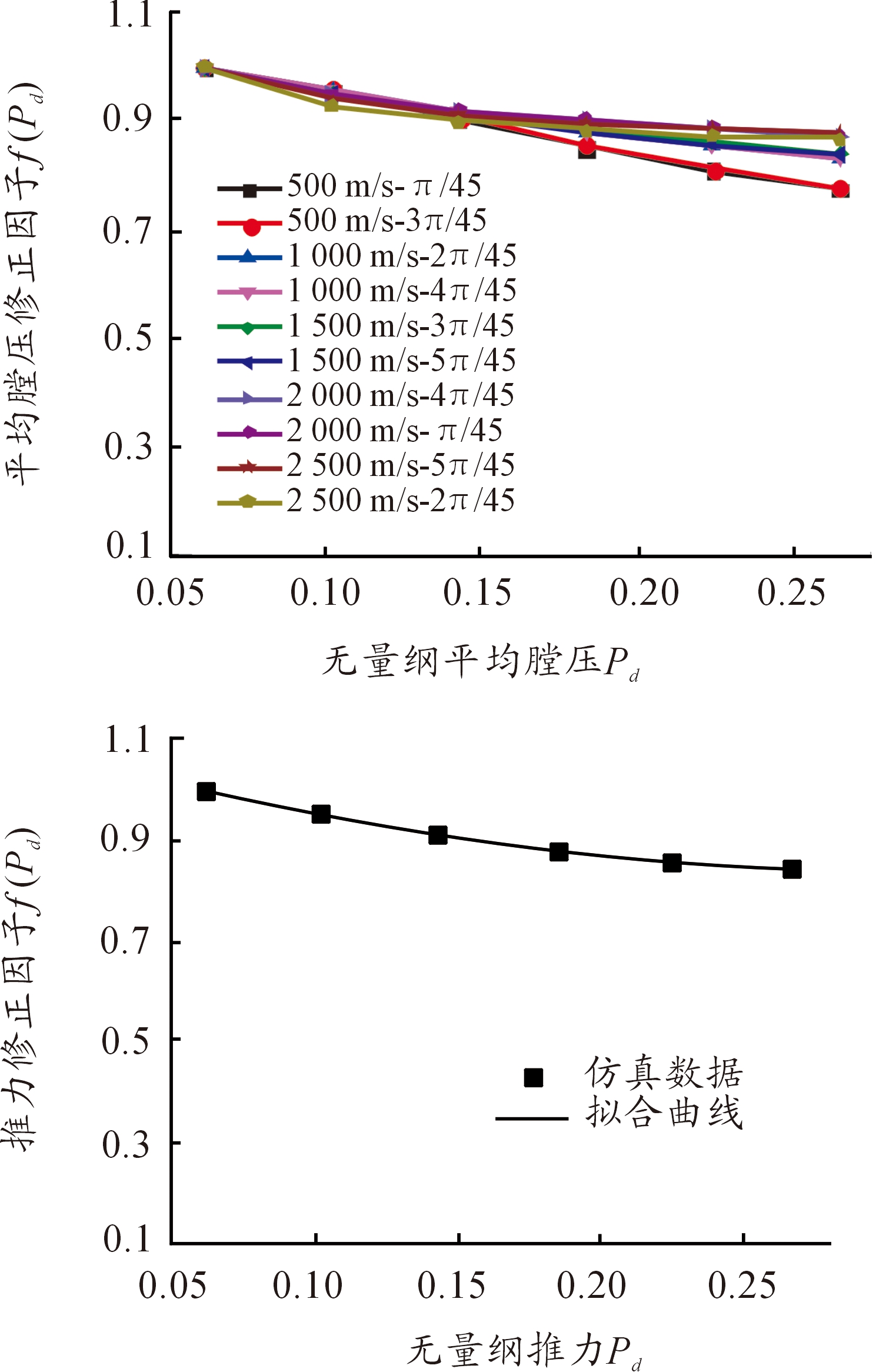
图6 不同Pd时的f (v0)曲线、平均值及拟合曲线
综上所述,得到了动态分离速度修正因子的计算公式(11)-(13),将其应用于式(6),得到标准大气条件下两级高速飞行器前级的动态分离速度计算模型表达式(14),即:
vd=[ 1-(0.01Ma2-0.006Ma+0.28)×
(-0.29α2-0.04α+1)×
(1.47<Ma<7.35, 0<α<π/9,
0.06<Pd<0.26)
(14)
3 模型验证
式(14)是在固定飞行器结构下以特定工况为参考得到的动态分离速度计算模型,为验证该模型能否计算非典型工况条件下的动态分离速度,采用CFD-FASTRAN对两组非典型工况进行计算,其中工况1,P=65 MPa,v∞=830 m/s(即Pd=0.13,Ma=2.44);工况2,P=125 MPa,v∞=2 450 m/s,(即Pd=0.25,Ma=7.21),计算非典型工况下不同攻角的前级动态分离速度。
图7为在工况1、2条件下仿真数据与速度计算模型[式(14)]结果图。由图7可见,动态分离速度计算模型与仿真结果基本吻合,变化趋势相同,该计算模型能正确表征该两级高速飞行器结构下不同初始飞行速度、攻角及平均膛压下前级的动态分离速度。

图7 非典型工况下仿真与计算模型速度
4 结论
1) 通过量纲分析研究了前级动态分离速度影响因素,引入了包含初始飞行速度、攻角与平均膛压的速度修正因子,对静态分离速度进行修正,建立了应用范围更广,计算更加便捷的两级高速飞行器前级动态分离速度计算模型式(6)、式(7)-式(9)。
2) 基于CFD-FASTRAN对两级高速飞行器动态分离过程进行了气动仿真,得到了分离结束时刻前级动态分离速度计算模型[式(14)]。对该模型的校验结果表明,计算模型具有较好的预测能力,能准确计算不同初始飞行速度、攻角与平均膛压下前级的动态分离速度,具有一定工程价值。
[1] 袁亚.带头罩折叠翼飞行器多体分离数值模拟[D].北京:中国航天科技集团公司第一研究院,2017.
[2] 程修妍,范博超,荣吉利,等.柔性整流罩地面展开试验仿真分析与飞行状态飞行预测[J].兵器装备工程学报,2018,39(3):608-616.
[3] ROCK S,HABCHI S.Validation of an automated chimera methodology for aircraft escape systems analysis[C]//Proc.of AIAA Aerospace Sciences Meeting & Exhibit.Virginia,US:AIAA,1998:209-225.
[4] PETER A.Liever and Sami D.Habchi.Stage Separation Analyesis of the X-43A Research Vehicle[C] //Proc.of Applied Aerodynamics Conference and Exhibit.Rhode Island,US:AIAA,2004:1-9.
[5] 罗宗熠,张久云,张世林.小口径高低压发射系统内弹道数值模拟及试验[J].水雷战与舰船防护,2017,25(3):48-51.
[6] 边朝阳,姚养无,刘怡.高初速度榴弹发射器内弹道特性仿真[J].兵器装备工程学报,2018,39(5):75-78.
[7] WANG J G,YU Y G,ZHOU L L,et al.Numerical simulation and optimized design of cased telescoped ammunition interior ballistic[J].Defence Technology,2018,14(2):39-45.
[8] 郭支明,王志军,吴国东.一种有效的EFP速度计算方法[J].弹箭与制导学报,2006,26(2):213-215.
[9] 王哲,蒋建伟,王树有,等.双层药型罩形成的串联爆炸成型弹丸速度计算模型[J],兵工学报,2017,38(7):1301-1306.
[10]杨涛.地空导弹级间分离过程仿真分析研究[D].长沙:国防科学技术大学,2005.
[11]王鑫,袁晓光,杨星.基于拉格朗日方法的飞行器多体分离姿态动力学分析研究[J],西北工业大学学报,2014,32(1):18-21.
[12]姬龙.反爆炸反应装甲理论与关键技术研究[D].南京:南京理工大学,2013.
[13]蔡薇.战斗部分离技术研究[D].南京:南京理工大学,2008.
[14]黄伟.降落伞最小弹射分离速度的计算方法[J].航天返回与遥感,2018,39(2):26-33.
[15]王力,谷良贤.导弹助推器分离过程数值模拟研究[J].航空动力学报,2008,23(2):342-346.
[16]聂源,蒋建伟,李梅,等.球形装药动态爆炸冲击波超压场计算模型[J]爆炸与冲击,2017,37(5):951-956.
[17]谈庆明.量纲分析[M].北京:中国科学技术大学出版社,2005.