控制力矩陀螺(Control Moment Gyro,CMG)自平衡车是一类依靠CMG进动产生的陀螺力矩效应保持姿态稳定的新型无人驾驶装置，当其处于低速或静止状态时由于自身静不稳定特性会出现倾倒现象，需要设计控制器实现其侧倾稳定控制[1-2]。同时在自平衡车稳定控制过程中需要及时调整CMG进动角回到零位，防止其超出进动幅度造成系统失稳。Lam等[3]采用双闭环PD控制实现了倾角稳定，但经典输入输出反馈无法克服模型中的耦合项影响，未能有效控制进动角回零。赵明国等[4]采用极点配置方法设计状态反馈控制器，在模型等效平台上实现了稳定及回零控制，但极点位置选择对经验依赖程度较大且无法保证良好的动态性能。Sergio等[5]基于扩张状态观测器设计了一种双回路状态反馈控制器并得到了较好的仿真控制效果，但控制器结构复杂、能量消耗大且并未在实验平台上对控制效果加以验证。
LQR控制器通过建立状态变量和控制量构成的目标函数并求取最优解实现状态反馈控制，对于耦合系统的姿态稳定控制具有较好的控制效果[6-7]。本文基于CMG自平衡车系统模型设计了一种粒子群算法优化的LQR状态反馈控制器，根据优化流程通过Simulink仿真确定满足系统性能指标的控制器参数，并在实验平台上实现了自平衡车实时侧倾稳定控制，同时能够有效抑制进动角耦合和外加干扰力矩对系统的影响。
1 CMG自平衡车动力学模型
1.1 系统组成及平衡原理
如图1所示，CMG自平衡车采用单轨式前后两轮结构布局，车身后部安装有CMG及其驱动设备作为控制执行机构，中部是以NI my RIO控制板为核心器件的控制单元，底部固定IMU姿态测量单元，车身前部为电源供电装置，最外侧安装有安全隔离架。
图1 CMG自平衡车结构
其中，CMG及其驱动设备组成如图2所示，包括飞轮转子，自转驱动电机，陀螺框架，陀螺进动电机及增量式编码器。
图2 控制力矩陀螺组成
自转电机驱动飞轮转子保持高速旋转，当自平衡车产生一定的倾斜角时，进动电机施加扭矩使飞轮转子在自转的同时相对车体进动，根据陀螺力矩效应，陀螺进动过程中受到沿进动轴方向的外力矩同时会对车体产生一个反作用力矩抵消重力矩分量以及外界干扰力矩
M=H×ω
(1)
方向与飞轮自转轴方向和进动轴方向均正交，如图3所示。
图3 陀螺力矩示意图
1.2 模型建立
将CMG自平衡车系统视为由车体、高速旋转的飞轮转子和陀螺框架3部分刚体组成的刚体系，建立正视、侧视示意模型及坐标系如图4所示。点O为平衡车后轮与地面接触点，Ob为车体的质心，考虑飞轮转子相对于陀螺框架仅有绕Ygf轴角速度为ω的自转运动，因此它们共同的质心为Ogf，自平衡车绕X轴的倾斜角定义为θ，倾角角速度为
飞轮和陀螺框架绕轴Zb的进动角定义为α，进动角速度为
车体质心与地面的垂直距离为db,飞轮和陀螺框架质心与地面的垂直距离为dgf；车体质量为mb,沿X轴方向转动惯量Ib，飞轮和陀螺框架总质量为mgf，极向转动惯量分别为Ipf、Ipg，径向转动惯量分别为Irf、Irg。
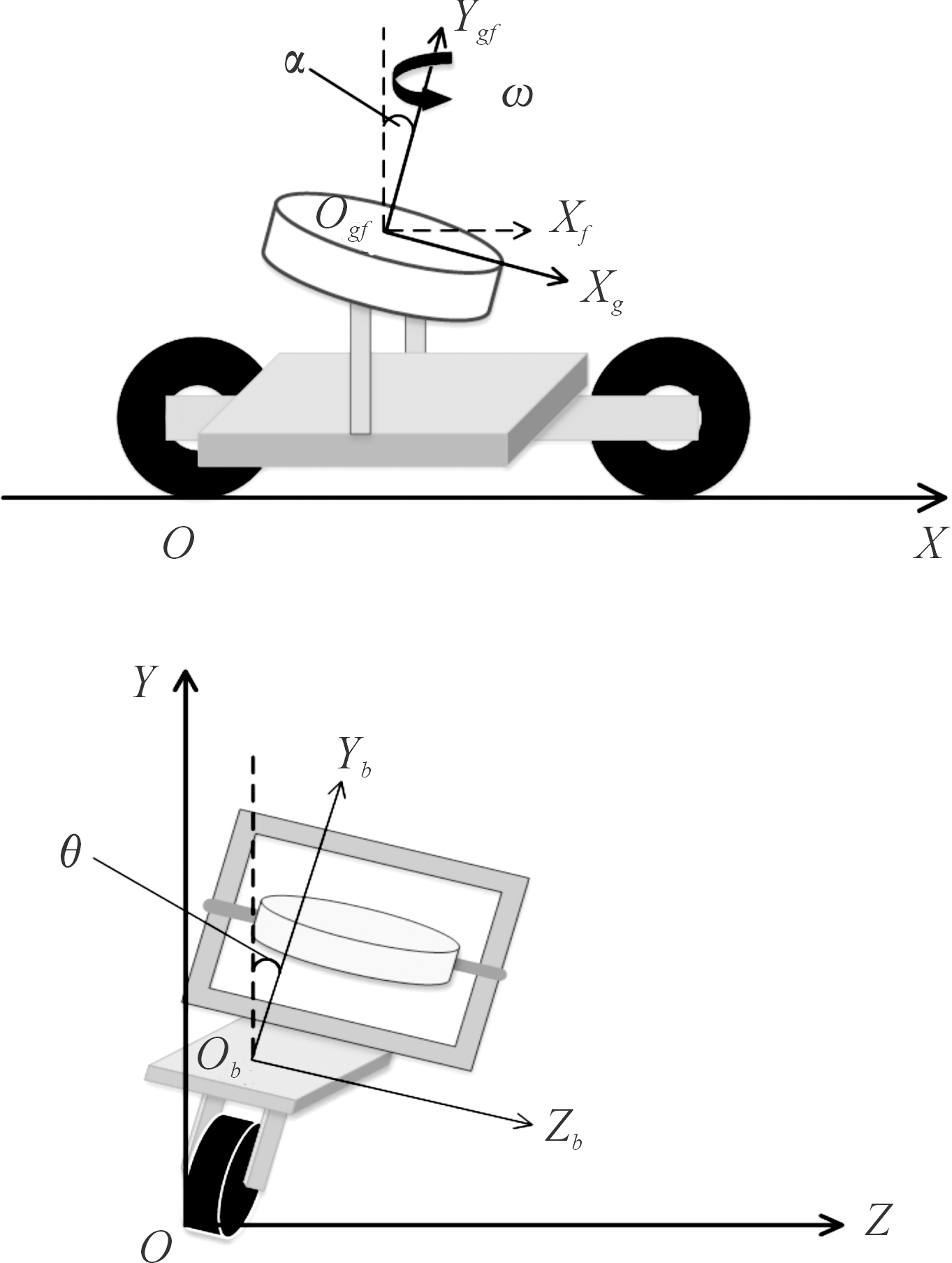
图4 自平衡车模型及坐标系
由上述假设和参数设置，可以得到自平衡车系统的动能：
(2)
忽略不确定性外力作用，系统所受广义力中重力为有势力，则系统势能为
V=mbgdbcosθ+mgfgdgfcosθ
(3)
选取车体的侧倾运动和陀螺框架的进动两个自由度为系统的广义坐标，根据包含有势力的拉格朗日方程
对于广义坐标θ，受到的非有势广义力矩为
令q1=θ可得关于侧倾角动力学方程为
(4)
对于广义坐标α，受到的非有势广义力矩为
其中Km为进动电机的力矩放大系数，令q2=α可得进动角动力学方程
(5)
2 侧倾稳定控制系统设计
2.1 系统性能分析
由方程式(4)、式(5)可知，CMG自平衡车模型中有非线性项和耦合项存在，直接基于非线性模型设计非线性控制器复杂度较高、实现困难，且实际稳定控制范围小并伴随有抖动现象[8]。考虑自平衡车在实际应用中偏离平衡位置范围一般在-20°～20°，为降低控制器设计复杂度，对非线性模型在平衡点附近进行线性化处理，可近似认为有：
(6)
选取状态量
输出量
控制量u=i，可得自平衡车动力学模型的线性状态空间表达式
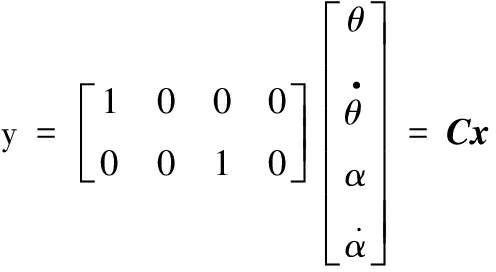
(7)
其中：
CMG自平衡车模型中涉及到的具体参数值如表1所示，将其代入状态空间表达式中可以得到系统矩阵A和控制矩阵B分别为
求得系统极点[0,0,±0.860 6i]，可以发现系统有两个零极点和两个位于虚轴上的极点，因此该自平衡车系统是不稳定的，但对系统可控性矩阵求秩得
rank(B AB A2B A3B)=4
显然可控性矩阵满秩，系统可控并可设计状态反馈控制器改变系统极点使其达到稳定状态。
表1 自平衡车参数
参数数值车体质量mb/kg26.52飞轮及框架质量mgf/kg17.96飞轮及框架质心到地面距离dgf/cm35.65车体质心到地面距离db/cm20.36车体沿X轴转动惯量Ib/(kg·cm-2)7 328.80飞轮轴向转动惯量Ipf/(kg·cm-2)860.55框架轴向转动惯量Ipg/(kg·cm-2)675.02飞轮径向转动惯量Irf/(kg·cm-2)456.10框架径向转动惯量Irg/(kg·cm-2)357.86进动电机力矩放大系数Km/(N·m/A)0.097飞轮自转角速度ω/(r·min-1)2 160
2.2 粒子群优化LQR控制器设计
对于CMG自平衡车的侧倾稳定控制，主要考虑系统是否能快速、平稳地达到平衡状态，以及解决平衡车倾角和CMG进动角控制耦合问题。同时采用CMG作为控制执行机构虽然具有力矩放大显著、响应快等优点，但其耗费能量较大，因此设计以状态变量θ、α和控制量u为性能指标的线性定常系统无限时间状态调节控制器：
其中，对于状态约束矩阵Q和控制约束矩阵R的选取并没有明确指标，较难通过解析方式得到，本文采用粒子群优化算法结合Simulink仿真迭代的方式进行求解[9]，各权重系数变换相同倍数并不影响相互之间比例关系，不妨假设Q、R矩阵具有如下形式：
粒子群优化算法采用带惯性权重的速度和位置更新式[10]：
(7)
其中，
为惯性权重；xk、Vk表示当前时刻粒子位置和速度；xk+1、Vk+1表示下一时刻粒子位置和速度；c1、c2是非负的加速度常数；r1、r2是区间[0,1]上的随机数，Pbest为当前代数最优粒子位置坐标，Gbest为全局最优粒子位置坐标。
适应度函数选择能够反映控制系统稳定性和快速性的ITAE误差指标[11]：
f =
t|e(t)|dt=t(|x1(t)|+|x3(t)|)dt
(8)
LQR控制器权重系数优化流程和Simulink仿真模型分别如图5、图6所示。
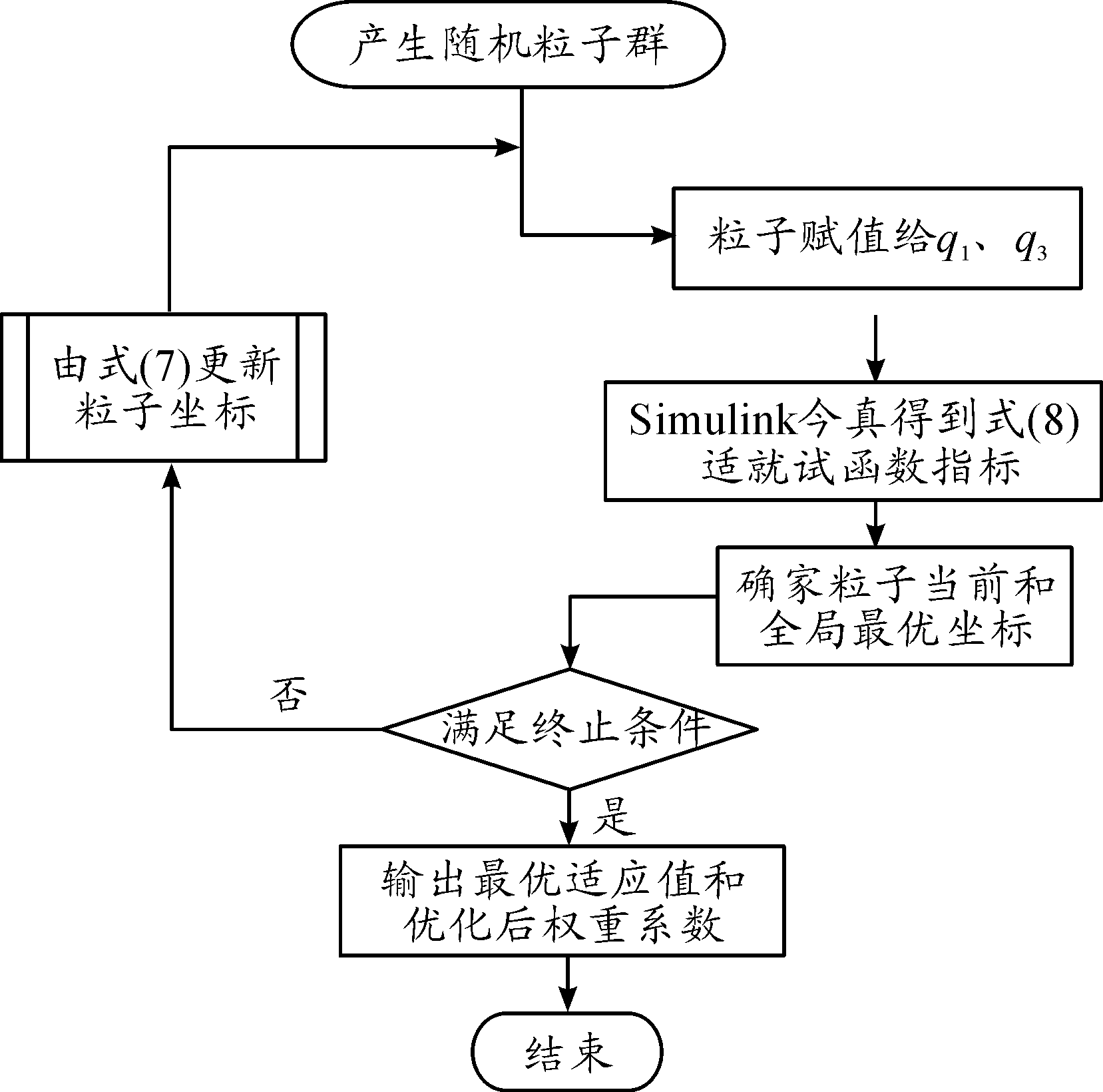
图5 LQR权重系数优化流程框图
图6 Simulink仿真模型示意图
3 实验验证
搭建自平衡车实验平台如图7，NI myRIO控制板集成了双核 ARM Cortex-A9实时处理器以及Xilinx FPGA可编程器件，基于Real-Time模块能够编译并执行LabVIEW实时控制程序，并通过Xsens三轴IMU和增量式编码器NI-CompactRio-9114实时敏感车体姿态和控制力矩陀螺进动角信息。实验中设定控制力矩陀螺进动幅度±45°，采样频率100 Hz，LQR控制器参数经粒子群算法优化后，最优适应度函数值 f=2.058，权重系数q1=150.32,q3=501.85，结合Riccati方程可以计算得到反馈控制矩阵K=[-1 328.3-223.6-15.818.8]。
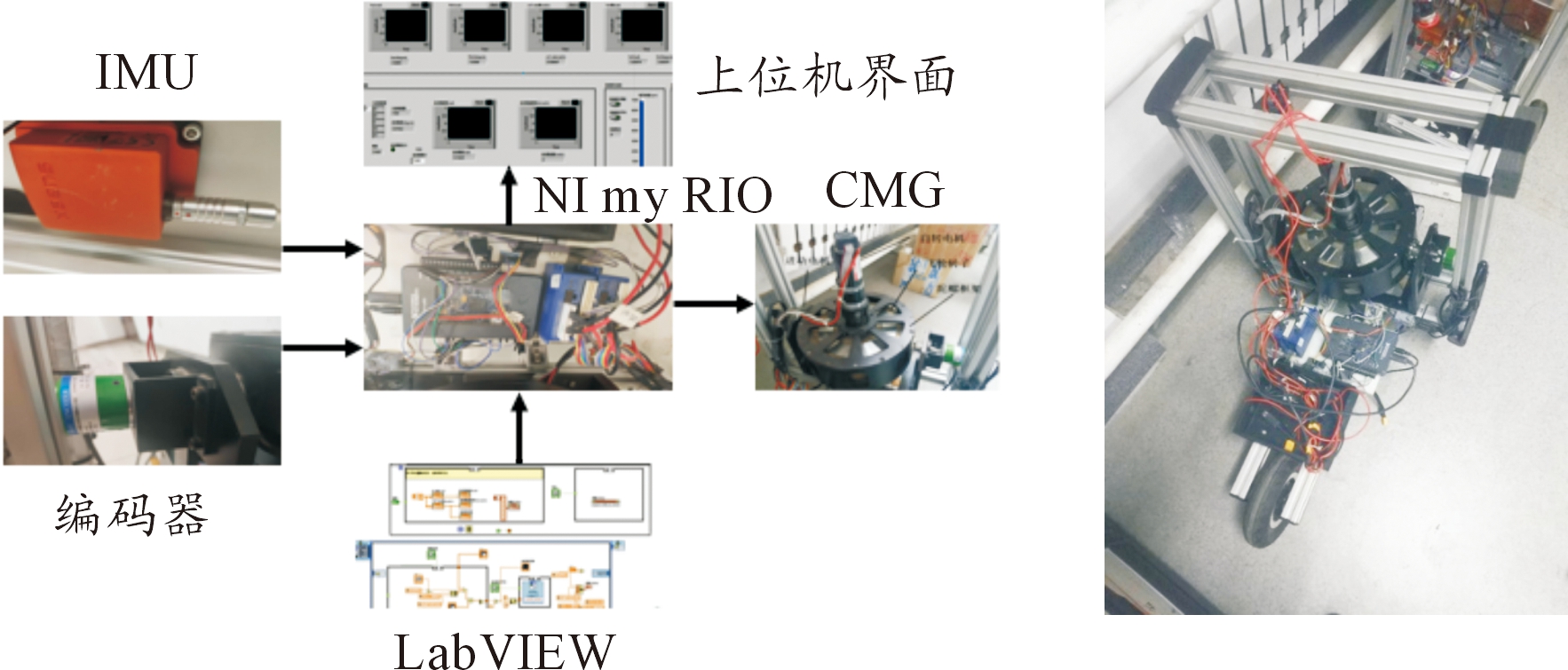
图7 实验验证平台
1) 具有初始倾角的姿态稳定控制。分别设定平衡车倾角初始值为6°、8°、10°，姿态稳定控制曲线如图8所示，可以看出在平衡范围内随着初始倾角增大，系统仍能保持较好地控制效果，在1.7 s左右回到平衡状态，超调角度均在2°左右，调节过程平稳。倾角在平衡点附近稳态误差为0.25°，证明粒子群优化LQR控制器具有较高的控制精度。
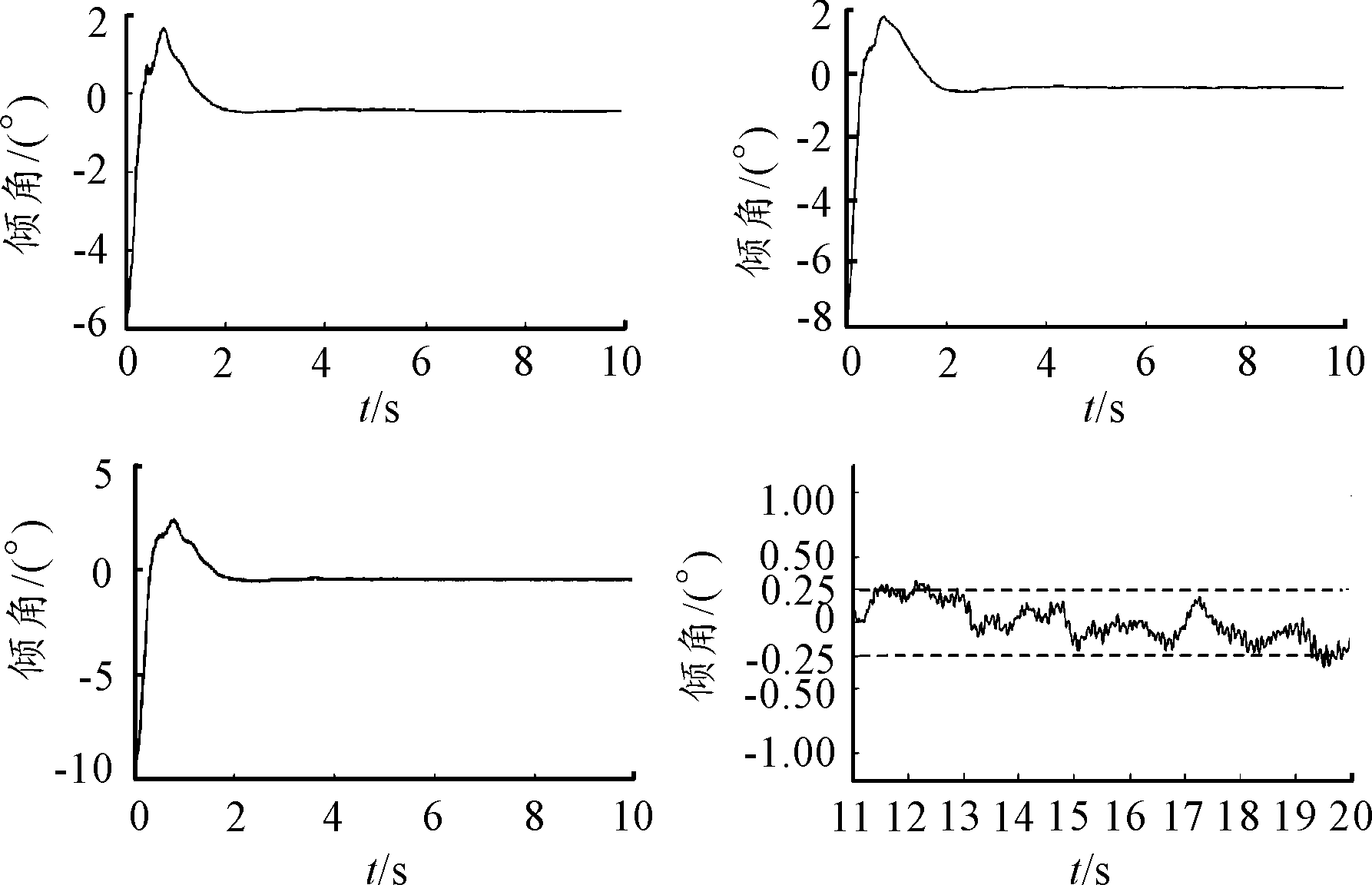
图8 具有初始倾角的姿态稳定控制曲线
2) CMG进动回零控制。自平衡车侧倾稳定控制过程中伴随有CMG进动作用产生，平衡车姿态回到平衡位置后CMG进动角仍然存在，当进动角达到限定幅度时，CMG无法由进动效应产生陀螺力矩保持系统姿态稳定，为了提升系统鲁棒性能设定进动角零位期望值，控制曲线如图9所示，可以看出所设计的控制器受耦合影响较小，能够在实现侧倾稳定控制的同时(2 s左右)快速、平稳控制进动角回到零位。
图9 CMG进动角回零控制曲线
3) 外加力矩干扰姿态稳定控制。为了进一步验证控制器对自平衡车姿态稳定控制的抗干扰能力，在t=3 s时对处于平衡状态的平衡车施加脉冲力矩干扰，实验结果如图10所示，经过2 s左右倾角恢复平衡状态，证明系统在外界环境突变情况下仍能保持姿态稳定，具有一定的抗干扰能力。
图10 外加干扰姿态稳定实验结果
4 结论
设计了一种粒子群算法优化的控制力矩陀螺自平衡车LQR控制器；将LQR控制器应用于控制力矩陀螺自平衡车侧倾稳定控制，基于粒子群算法设计控制器Q、R权重系数矩阵优化流程，结合Simulink仿真确定控制器参数值并计算得到最优状态反馈控制律，最后在搭建的实验平台上进行实时控制实验，结果表明本文所设计的控制器能够快速、平稳实现自平衡车侧倾稳定控制，稳态误差小，同时能够有效调节CMG进动角回到零位，使系统具有抗干扰能力。
[1] 梁文宇,周惠兴,曹荣敏.双轮载人自平衡控制系统研究综述[J].控制工程,2010,17(S2)：140-144.
[2] YAMAKITA M,UTANO A.Automatic control of bicycles with a balancer[C]//Proceedings of IEEE/ASME International Conference on Advanced Intelligent Mechatronics.IEEE,2005：1245-1250.
[3] POM Y L.Gyroscopic stabilization of a kid-size bicycle[C]//Proceedings of IEEE International Conference on Cybernetics & Intelligent Systems.IEEE,2011：247-252.
[4] HE J,ZHAO M.Control System Design of Self-balanced Bicycles by Control Moment Gyroscope[J].Lecture Notes in Electrical Engineering,2015,338(11)：205-214.
[5] SERGIO T L,SANTIAGOE P G,HORACIO C E.Self-Stabilization of a Riderless Bicycle With a Control Moment Gyroscope via Model-based Active Disturbance Rejection Control[C]//Proceedings of 2017 IEEE 3rd Colombian Conference on Automatic Control (CCAC).IEEE,2017：1-6.
[6] DUAN H B,SUN C H.Pendulum-like oscillation controller for micro aerial vehicle with ducted fan based on LQR and PSO[J].Science China：Technological Sciences,2013,56(2)：423-429.
[7] 夏浩军,邱荣华.倒立摆线性二次型最优控制方法研究[J].机械制造与自动化,2018,47(1)：218-221.
[8] YETKIN H,KALOUCHE S,VERNIER M,et al.Gyroscopic stabilization of an unmanned bicycle[C]//Proceedings of American Control Conference.IEEE,2014：4549-4554.
[9] GHOREISHI S A,NEKOUI M A.Optimal Weighting Matrices Design for LQR Controller Based on Genetic Algorithm and PSO[J].Advanced Materials Research,2012,433-440：7546-7553.
[10]杨维,李歧强.粒子群优化算法综述[J].中国工程科学,2004,6(5)：87-93.
[11]杜文正,谢政,童国林.基于粒子群优化算法的桥式起重机PID控制参数优化[J].计算机测量与控制,2013,21(2)：371-373.