随着导弹等飞行技术的发展,传统制导律已经不能满足现代日益复杂的反导拦截要求[1-2],新型导引律的研究和应用已成为导航领域的重点与热门方向。
变结构控制系统对外界干扰和参数摄动具有良好的鲁棒性[3],为解决导弹制导问题提供了新的方向[4-7]。但变结构制导律需要根据目标机动性大小来调节变结构项增益,增益过大会导致角速率抖振,不利于弹上机构的正常工作,同时制导精度下降[8];增益过小,则无法有效拦截目标。RBF神经网络结构简单,能够逼近任意非线性函数,且学习收敛速度快,具有实现复杂环境下实时控制的能力,可被用来调节变结构项的增益。
本文将变结构控制理论与RBF神经网络相结合,利用RBF神经网络来自适应调节变结构项的增益。同时考虑控制回路对系统的影响,主要是自动驾驶仪的影响。仿真结果表明:基于RBF神经网络增益调节的滑模制导律能有效削弱系统抖振,使脱靶量显著减小,对变结构控制理论在导弹拦截中的应用具有重要指导意义。
1 三维空间拦截模型
为方便讨论,首先建立三维空间拦截模型,如图1所示。M和VM为导弹及其速度;T和VT为目标及其速度;Oxyz为地面坐标系;Ox2y2z2为弹道坐标系;Ox4y4z4为视线坐标系;θM,φM,θT,φT分别为导弹和目标的弹道倾角和弹道偏角;qε,qβ分别为视线倾角和视线偏角。
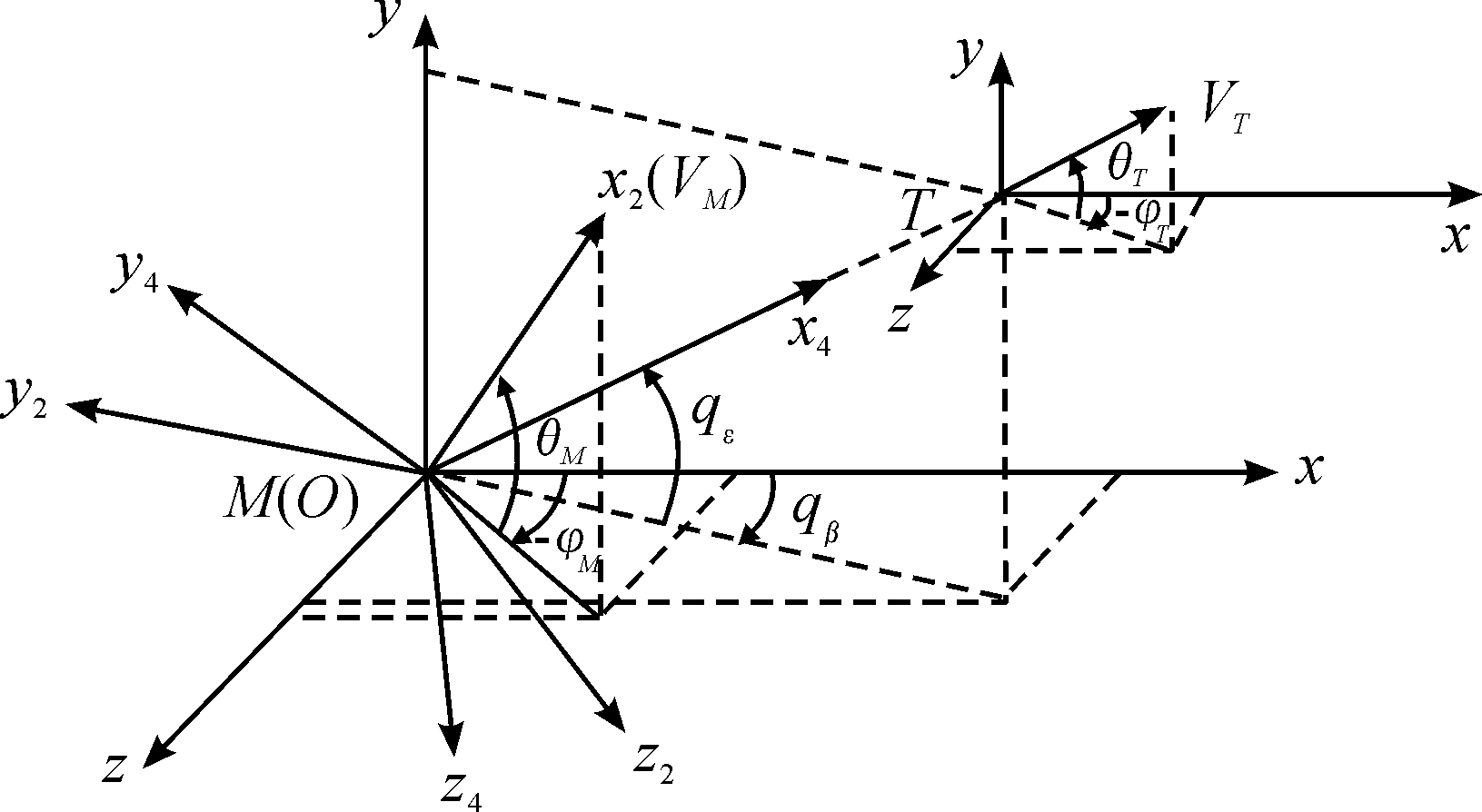
图1 三维空间拦截模型示意图
1.1 导弹的运动模型
在研究导弹运动特性中,把导弹运动分为质心运动和绕质心转动。本文中,将导弹视为可操纵的质点,不考虑其绕质心的转动,从而得到简化后的导弹三自由度运动模型[9]:
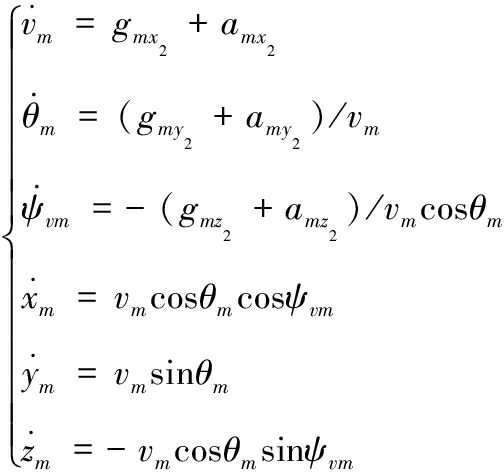
(1)
式(1)中:gmx2,gmy2,gmz2为重力加速度在弹道坐标系上的分量;amx2,amy2,amz2为导弹机动加速度在弹道坐标系上的分量;xm,ym,zm为导弹在地面坐标系中的位置。目标的运动模型和导弹类似。
1.2 导弹-目标相对运动模型
选取某一时间段Δt起始时刻的视线坐标系作为制导过程中导弹-目标相对运动的参考坐标系。在Δt内,此参考坐标系随弹体平动。于是整个制导过程中的相对运动可以解耦成纵向平面和侧向平面内的运动[10]。
在Δt时刻内,视线倾角和视线偏角的增量为![]() 则有:
则有:
(2)
当![]() 足够小时,则可以近似为:
足够小时,则可以近似为:
(3)
其中:![]() 分别为Δt内导弹和目标在Oy4,Oz4方向上的相对位移;R(t)为导弹与目标的相对距离;Rl(t)=R(t)cos qε。
分别为Δt内导弹和目标在Oy4,Oz4方向上的相对位移;R(t)为导弹与目标的相对距离;Rl(t)=R(t)cos qε。
将式(3)对时间进行两次微分,并取状态变量![]() 可得状态方程为
可得状态方程为
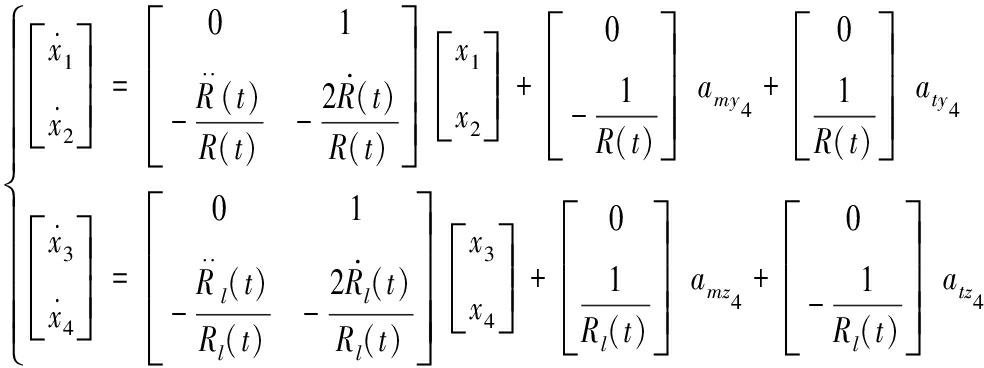
(4)
式(4)中:amy4(t),amz4(t),aty4(t),atz4(t)分别为导弹和目标机动加速度在Oy4和Oz4上的分量。
其中加速度指令由视线坐标系转化到弹道坐标系在的转换矩阵如下:
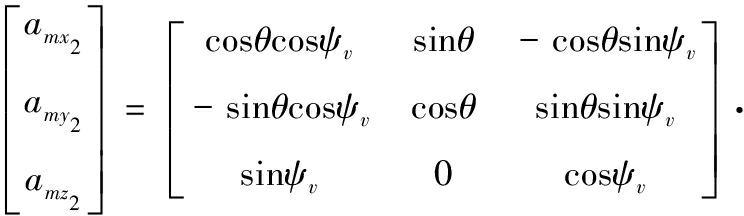

(5)
2 滑模变结构制导律
制导律的主要原则为准平行接近原则,即零化视线角速率,使![]() 趋于零。本文以纵向通道为例,选取滑动模态[10]为
趋于零。本文以纵向通道为例,选取滑动模态[10]为
(6)
为了保证能够良好地趋近滑模面,选取对导弹控制系统的时变性具有自适应能力的趋近律,即:
(7)
趋近律的物理意义在于当R较大时,趋近速率会适当放缓,当R→0时,趋近速率会迅速增加,避免视线角速率过早发散。当s→0时,趋近速率约为ε,可以保证在有限时间内到达滑模面。
将式(6)代入式(7)可得:
![]()
(8)
将![]() 移到等式右边,可得:
移到等式右边,可得:
(9)
把式(3)代入式(9),得到式(10):
![]()
(10)
由于目标机动加速度无法准确获得,可将其视为干扰量,可得:
![]()
(11)
取Lypunov函数为![]() 并对时间进行微分,由式(4)和式(11)可得:
并对时间进行微分,由式(4)和式(11)可得:
(12)
当k>1时,如果ε>|f|,那么![]() 根据Lypunov判据,V是正定的,
根据Lypunov判据,V是正定的,![]() 是负半定的,系统稳定于条件x2=0,可以保证视线角速率最后趋向于零。另外
是负半定的,系统稳定于条件x2=0,可以保证视线角速率最后趋向于零。另外![]() 变化较小,即
变化较小,即![]() 可得纵向平面的变结构制导律:
可得纵向平面的变结构制导律:
(13)
同理,侧向平面的变结构制导律为:
(14)
3 基于RBF神经网络的变结构项增益调节
由式(13)、式(14)可知,滑模变结构制导律是由比例导引项和变结构项组成。在导弹拦截目标时,目标机动和滑模制导律的变结构项均与视线角速率成正比。只有选取合适的ε,才能补偿目标机动造成的视线角速率变化,否则会造成脱靶。
RBF神经网络具有并行计算、分布式存储、容错能力强、快速学习、对任意非线性函数都具有良好的逼近能力、满足复杂动态环境下非线性实时控制的特点。利用RBF神经网络来自适应调节变结构项的增益,可达到削弱抖振和提高制导精度的目的,基于RBF神经网络增益调节的滑模制导律拦截原理方框图如图2。将滑模面及其导数作为RBF神经网络输入,输出作为变结构项增益。
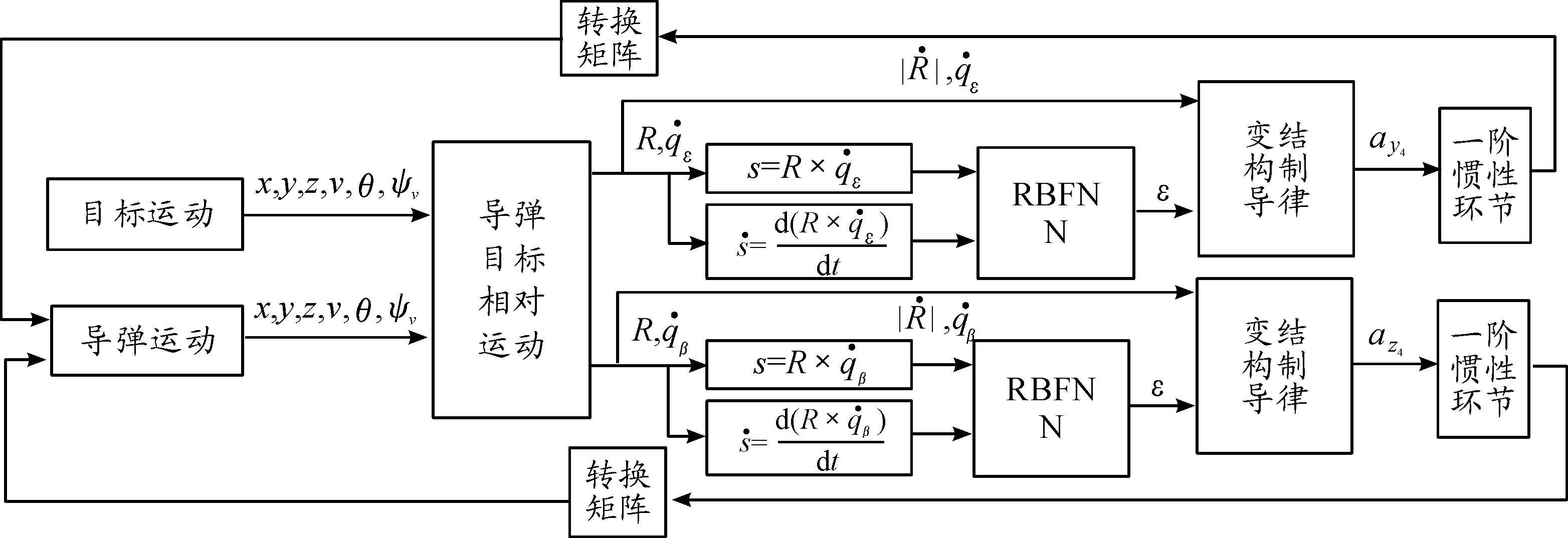
图2 基于RBFNN增益调节的滑模制导律拦截原理方框图
RBF神经网络的网络结构如下:
输入层:由信号源节点构成,仅起到数据信息的传递作用,对输入信息不做变换,本文中神经网络输入为![]()
隐含层:隐含层中神经元的激活函数即径向基函数是对中心点径向对称且衰减的非负非线性函数。对输入信息进行空间映射的变换,这里激活函数取高斯函数:
(15)
式(15)中,ci和bi分别是隐含层第i个神经元的中心点和基宽度。||·||表示欧式范数。
输出层:对输入模式进行响应。输出层神经元的作用函数为线性函数,对隐含层神经元输出进行线性加权后输出,作为整个神经网络的输出结果。本文中神经网络输出为变结构项增益ε=|WTh(x)|,其中W为网络权值向量。
RBF神经网络学习算法如下:
定义误差为![]() 为使导弹平行接近目标,令
为使导弹平行接近目标,令![]() 定义损失函数为
定义损失函数为![]() 采用梯度下降法更新参数。
采用梯度下降法更新参数。
输出层权重,隐含层单元中心及基宽度参数调整算法如下:

(16)
式中η∈(0,1)为学习速率。
4 仿真结果及分析
为了验证基于RBF神经网络增益调节的滑模制导律的有效性,利用Matlab进行仿真。初始仿真参数见表1。
表1 导弹-目标的初始仿真参数

V/(m·s-1)[θ,ψv][x,y,z]/mmissile1 000[30°,10°][0,0,0]target400[-10°,5°][5 000,10 000,200]
设目标在弹道坐标系中y轴分别有-7g,2g两种、z轴有![]() 的法向加速度机动。RBF神经网络学习速率η=0.9,权重初值为1,隐含层神经元个数为8,中心点ci和bi用K-means聚类算法初始化。考虑自动驾驶仪的动态延迟,取一阶惯性环节,时间常数τ=0.15 s;滑模变结构制导律比例导引项中k=3;将基于RBF神经网络增益调节的滑模制导律与固定增益滑模制导律
的法向加速度机动。RBF神经网络学习速率η=0.9,权重初值为1,隐含层神经元个数为8,中心点ci和bi用K-means聚类算法初始化。考虑自动驾驶仪的动态延迟,取一阶惯性环节,时间常数τ=0.15 s;滑模变结构制导律比例导引项中k=3;将基于RBF神经网络增益调节的滑模制导律与固定增益滑模制导律![]() (系数k=3,ε=100和ε=10)及比例导引法
(系数k=3,ε=100和ε=10)及比例导引法![]() 系数k=3)进行对比,结果如图3~图9所示。
系数k=3)进行对比,结果如图3~图9所示。
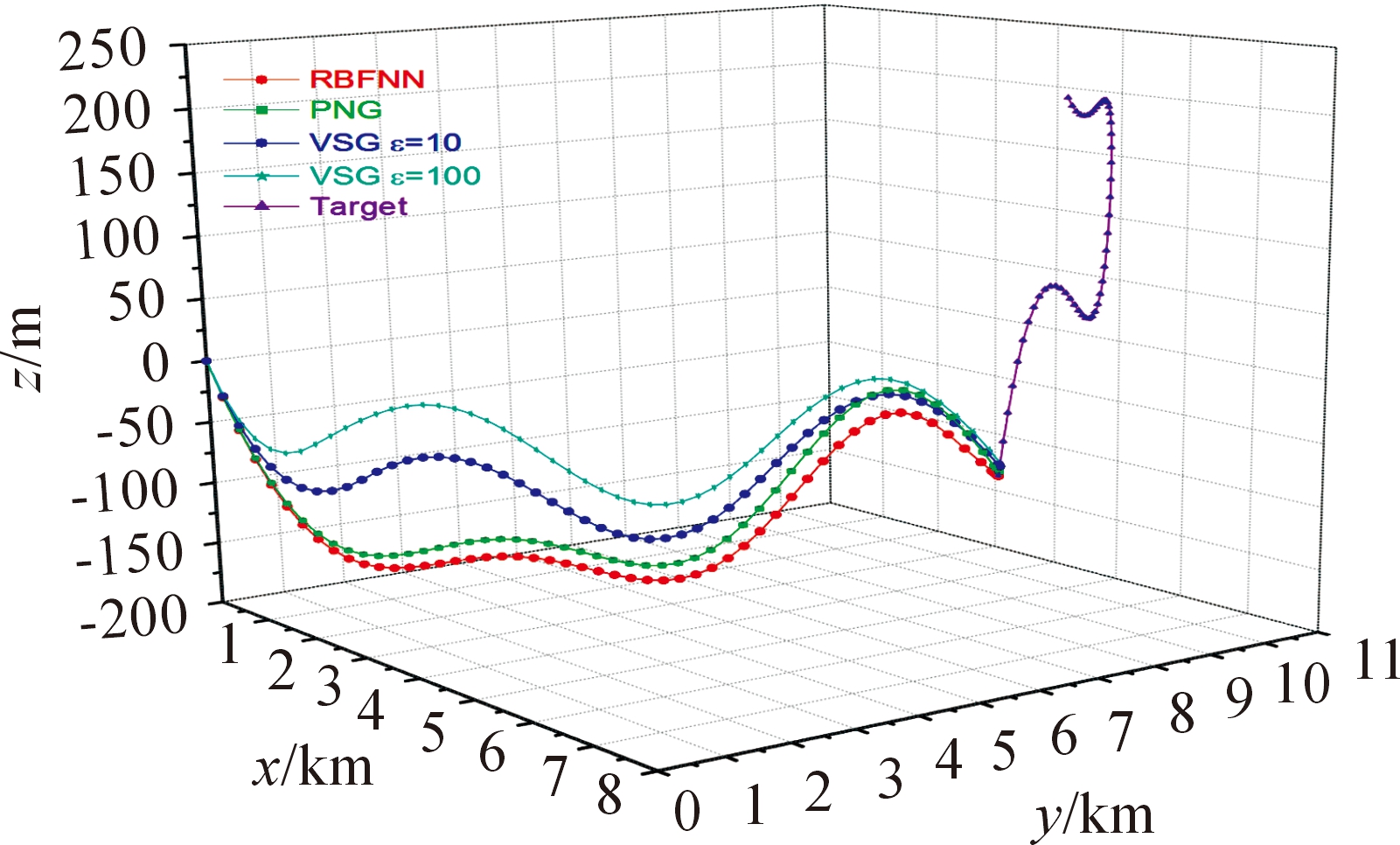
图3 aty2=-7g时导弹-目标运动轨迹
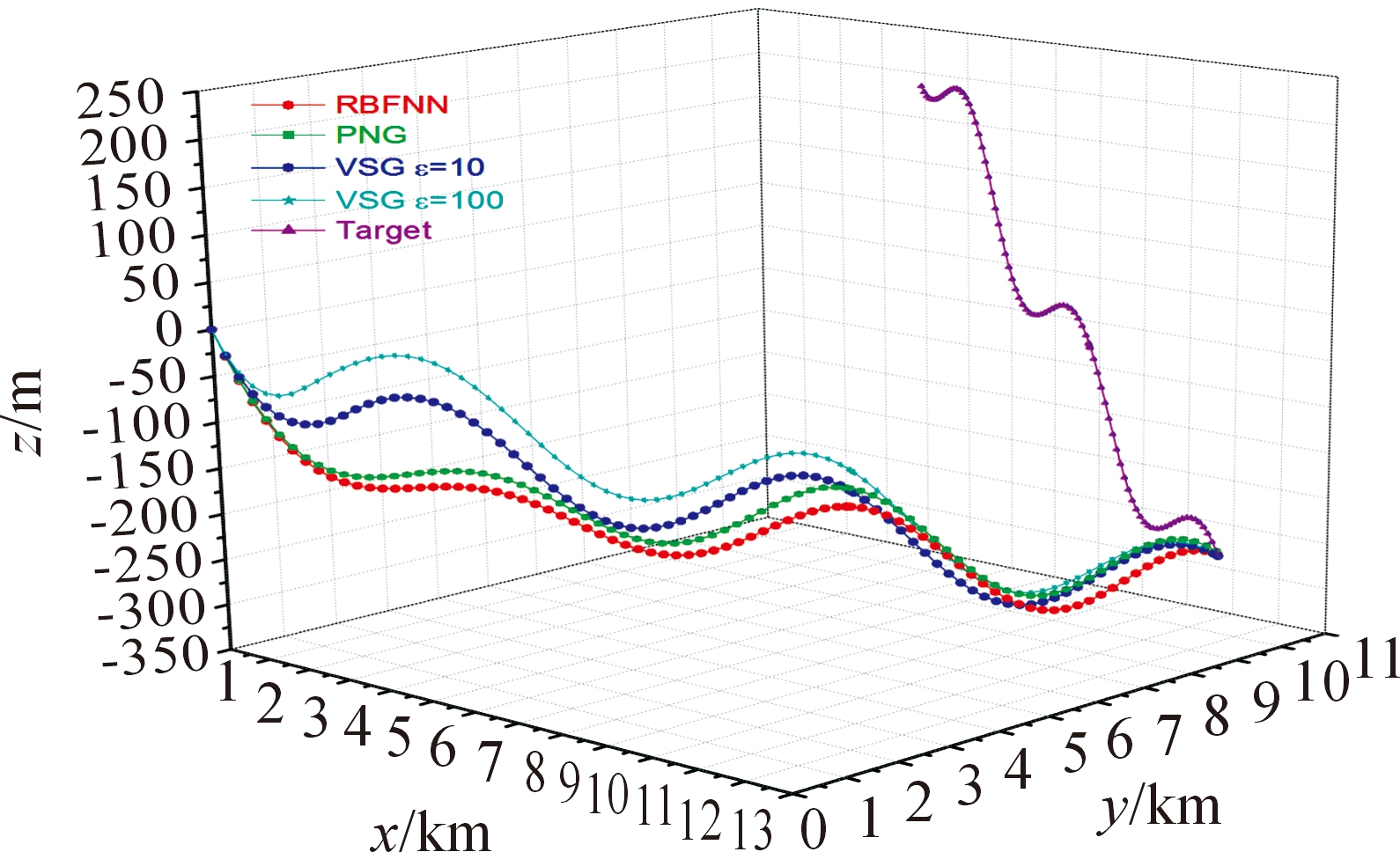
图4 aty2=2g时导弹-目标运动轨迹
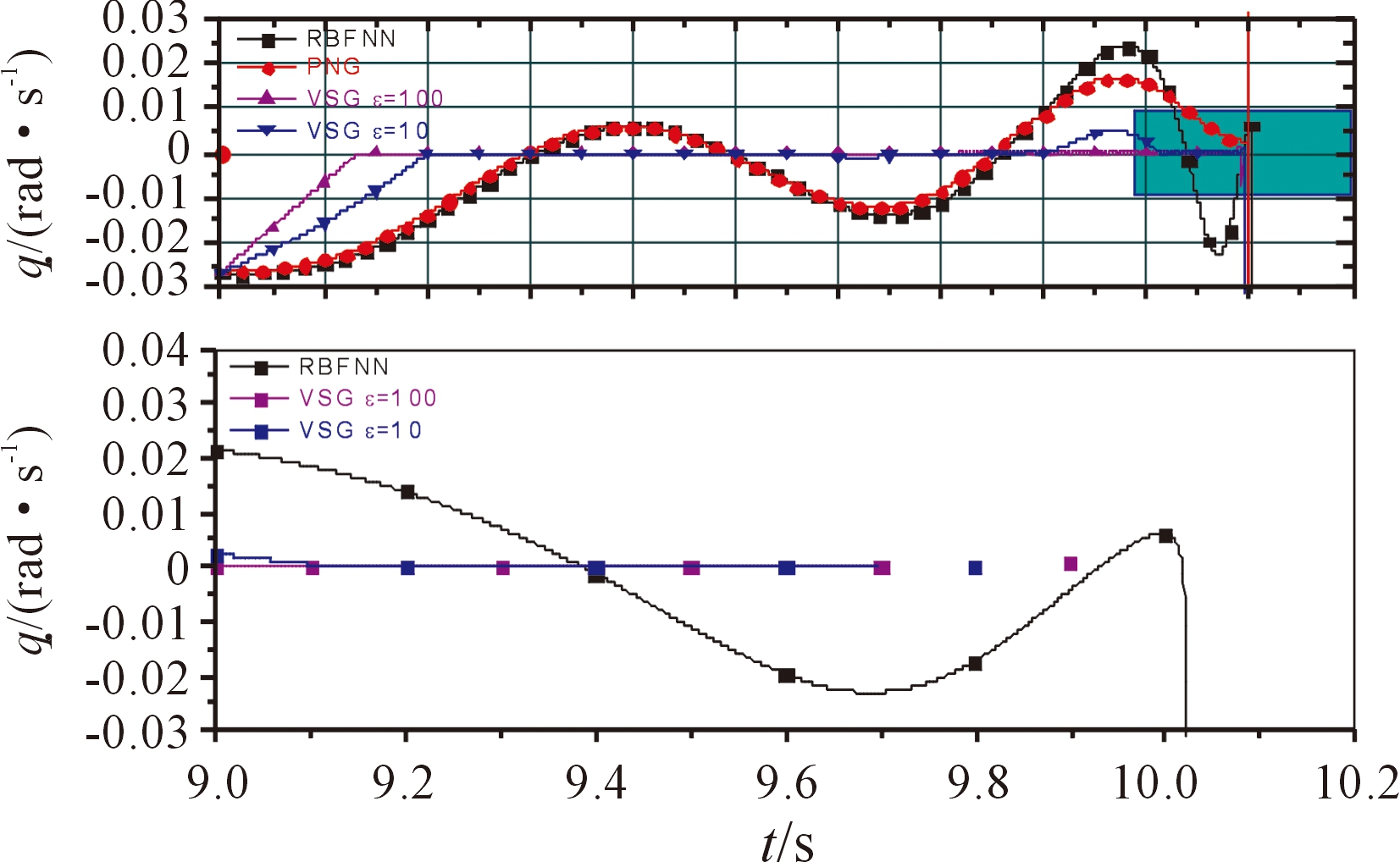
图5 aty2=-7g时的视线角速率变化

图6 aty2=2g时的视线角速率变化
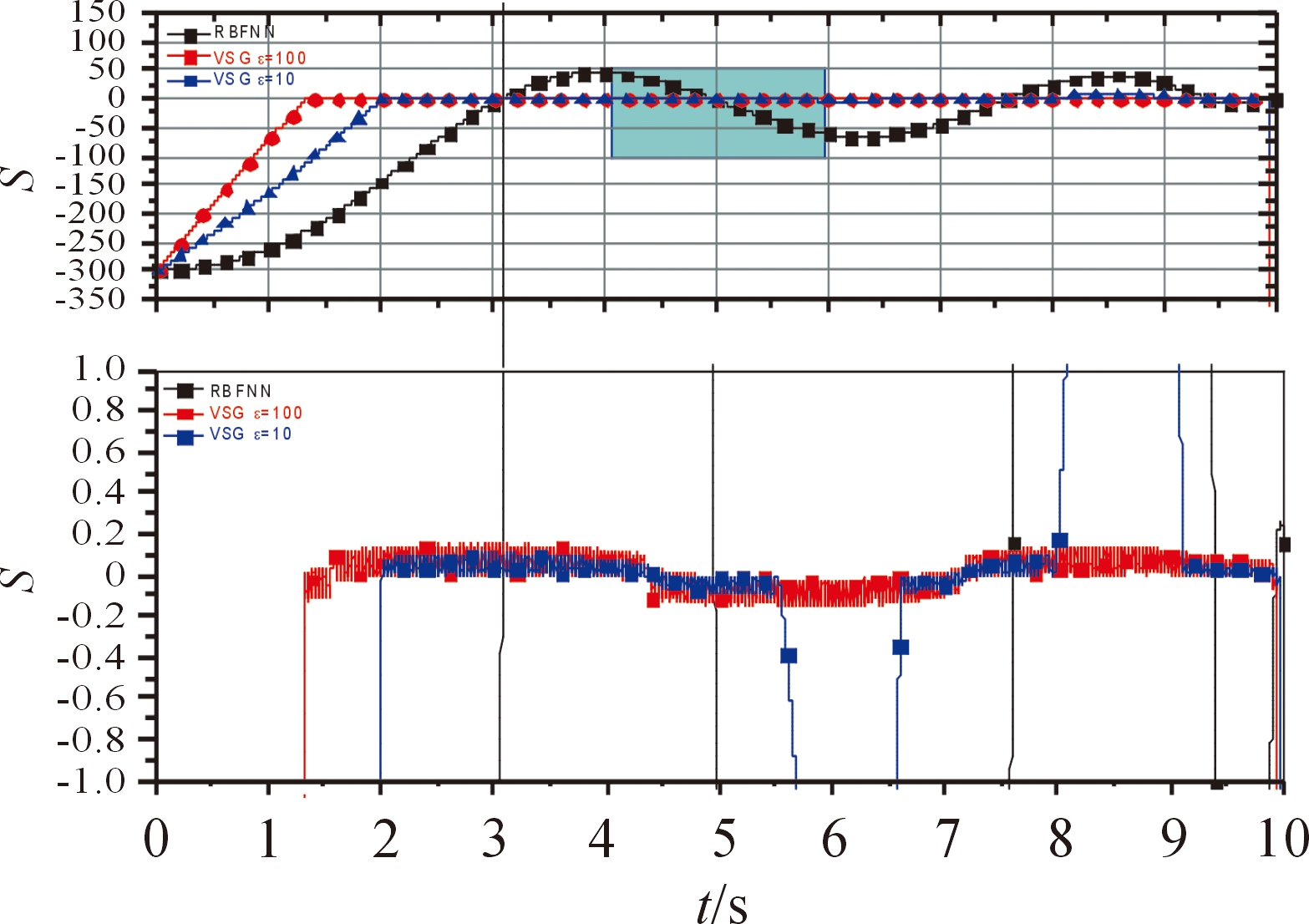
图7 aty2=-7g时S的变化
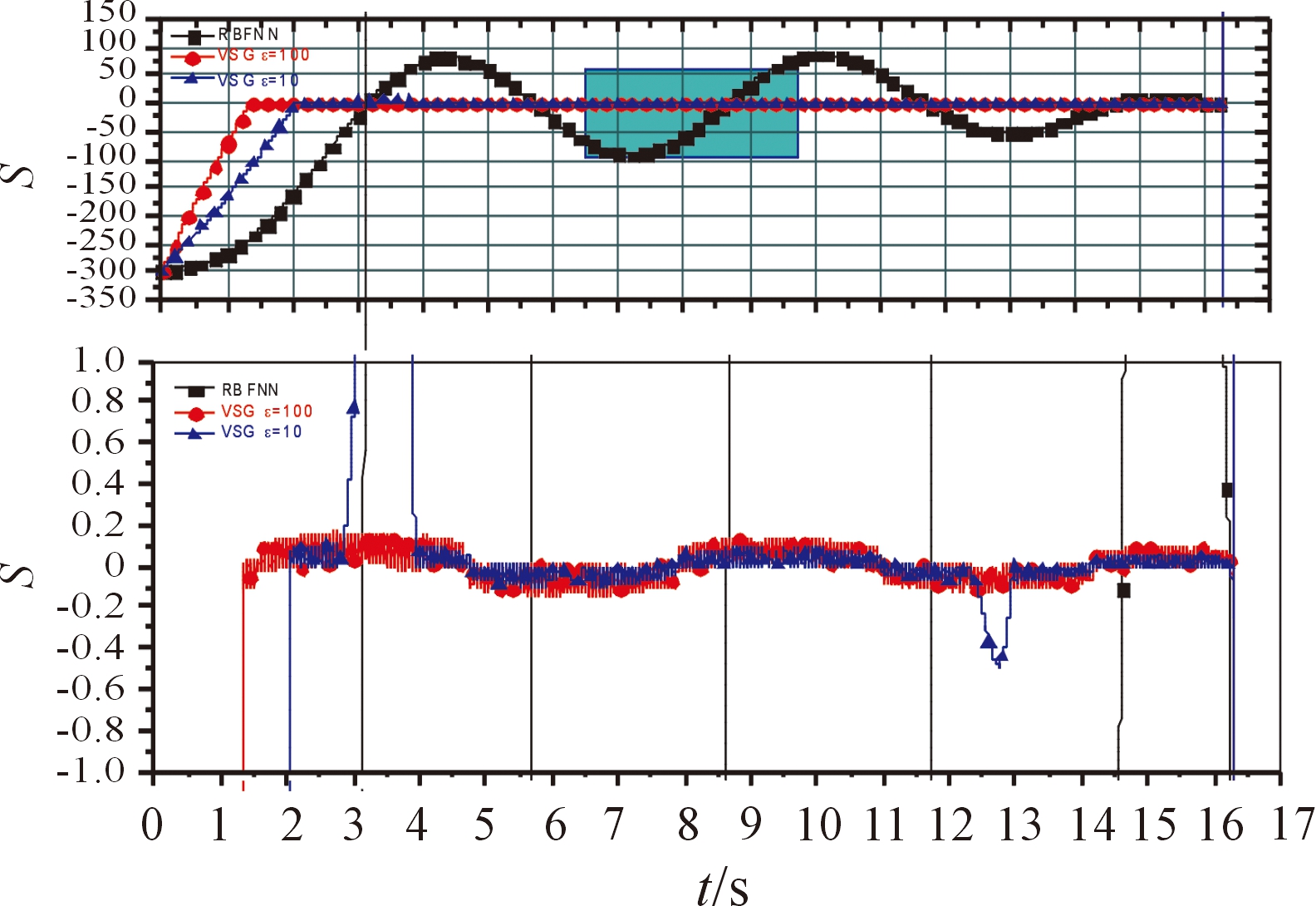
图8 aty2=2g时S的变化
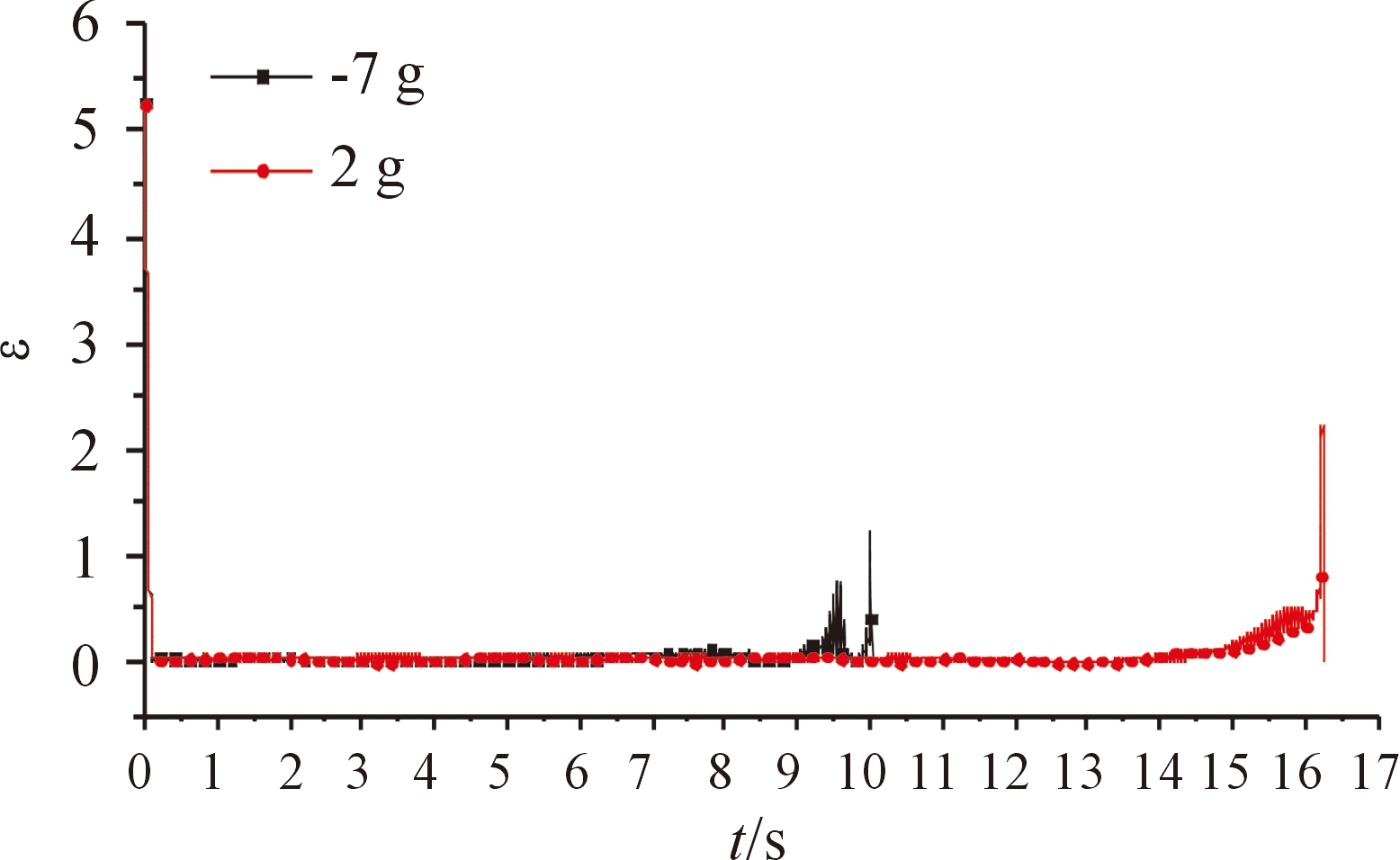
图9 aty2=-7g;2g时ε的变化
从图3、图4可知,基于RBF神经网络增益调节的滑模制导律在aty2=-7g,2g两种情况下都能命中目标。当![]() 时,RBF神经网络增益调节的滑模制导律的脱靶量为0.076 21 m,拦截时间为10.024 s;采用PNG的脱靶量为0.376 46 m,拦截时间为9.999 s;采用ε=10的VSG的脱靶量为0.202 65 m,拦截时间为9.962 0 s;采用ε=100的VSG的脱靶量为0.231 63 m,拦截时间为9.94 s。当
时,RBF神经网络增益调节的滑模制导律的脱靶量为0.076 21 m,拦截时间为10.024 s;采用PNG的脱靶量为0.376 46 m,拦截时间为9.999 s;采用ε=10的VSG的脱靶量为0.202 65 m,拦截时间为9.962 0 s;采用ε=100的VSG的脱靶量为0.231 63 m,拦截时间为9.94 s。当![]() 时,RBF神经网络增益调节的滑模制导律的脱靶量为0.095 35 m,拦截时间为16.24 s;采用PNG的脱靶量为0.325 59 m,拦截时间为16.177 s;采用ε=10的VSG的脱靶量为0.154 25 m,拦截时间为16.270 s;采用ε=100的VSG的脱靶量为0.230 86 m,拦截时间为16.281 s。与PNG和VSG相比,基于RBF神经网络增益调节的滑模制导律在精度方面都有所提升。此外,由图5~图8可知,与VSG相比,基于RBF神经网络增益调节的滑模制导律对增益项进行了自适应调节,很好地抵消了目标机动所带来的影响,全程视线偏角的角速率较为平滑,削弱了固定增益所带来的抖振问题,增强了系统的鲁棒性,有利于导弹拦截高速机动目标。由图9可知,在导弹末制导的初始时刻即R(t)较大时,变结构项增益减小来削弱抖振,趋向滑模面的速度较慢;在拦截时刻即R(t)较小时,变结构项增益会增大,保证有限时间内达到滑模面。
时,RBF神经网络增益调节的滑模制导律的脱靶量为0.095 35 m,拦截时间为16.24 s;采用PNG的脱靶量为0.325 59 m,拦截时间为16.177 s;采用ε=10的VSG的脱靶量为0.154 25 m,拦截时间为16.270 s;采用ε=100的VSG的脱靶量为0.230 86 m,拦截时间为16.281 s。与PNG和VSG相比,基于RBF神经网络增益调节的滑模制导律在精度方面都有所提升。此外,由图5~图8可知,与VSG相比,基于RBF神经网络增益调节的滑模制导律对增益项进行了自适应调节,很好地抵消了目标机动所带来的影响,全程视线偏角的角速率较为平滑,削弱了固定增益所带来的抖振问题,增强了系统的鲁棒性,有利于导弹拦截高速机动目标。由图9可知,在导弹末制导的初始时刻即R(t)较大时,变结构项增益减小来削弱抖振,趋向滑模面的速度较慢;在拦截时刻即R(t)较小时,变结构项增益会增大,保证有限时间内达到滑模面。
5 结论
1) 针对传统导引法无法有效拦截高速、大机动目标以及忽略自动驾驶仪动态特性等问题,结合变结构控制理论和神经网络,提出基于RBF神经网络增益调节的滑模制导律,利用RBF神经网络自适应调节变结构项增益。
2) 与比例导引法和固定增益滑模制导律相比,基于RBF神经网络增益调节的滑模制导律脱靶量有显著减小;同时,与固定增益滑模制导律相比,基于RBF神经网络增益调节的滑模制导律能有效削弱系统的抖振,对于目标的机动具有较强的鲁棒性。
[1] BABU K R.Switched bias proportional navigation for homing guidance against highly maneuvering targets[J].Journal of Guidance Control and Dynamics,1994,17(6):1357-1363.
[2] 杨丹.空间拦截变结构末制导律研究[D].上海:上海交通大学,2013.
[3] WANG X,HONG Y.Finite-time consensus for multi-agent networks with second-order agent dynamics[C]//Proceedings of the IFAC World Congress.Laxenburg:IFCA,2018:15185-15190.
[4] ABEDI M,BOLANDI H,SABERI F F.An adaptive RBF neural guidance law surface to air missile considering target and control loop uncertainties[C]//Industrial Electronics,ISIE 2007,IEEE International Symposium.USA:IEEE,2007:257-262.
[5] 李士勇,章钱.基于RBF网络增益自适应调节的滑模制导律[J].测试技术学报,2009,23(6):471-476.
[6] 孙胜,周荻.离散滑模导引律设计[J].航空学报,2008(6):1634-1639.
[7] 王华吉,简金蕾,雷虎民,等.带扩张观测器的新型滑模导引律[J].固体火箭技术,2015,38(5):622-627.
[8] 周德云,杨振,张堃.基于模糊RBF网络的自适应变结构制导律设计[J].飞行力学,2016,34(4):54-58.
[9] 钱杏芳,林瑞雄,赵亚男.导弹飞行力学[M].北京:北京理工大学出版社,2013:28-48.
[10]周荻.寻的导弹新型导引规律[M].北京:国防工业出版社,2002:5-14.