城市公共交通是在城市及其郊区范围内,为方便公众出行,用客运工具进行的旅客运输,对于完成战时交通运输任务以及保障和平时期经济建设具有举足轻重的作用。遵循战平结合原则,通过实施合理、经济的城市公共交通规划方案,可以优化城市用地布局,有效地提高交通效率、减少交通事故、降低环境污染,为居民提供迅速方便、安全高效、经济舒适、准点和低公害的交通条件,又能适应战争的需要。
作为城市客运交通主要方式之一的城市公共交通,发展水平直接关系到城市的整体发展水平;其服务水平与城市居民的居住水平密切联系,平时为经济服务,战时为战争服务,特别要满足军队重装备运输和短时间、高密度通过的需要。因此,寻求一种科学、客观、合理且量化的公交服务水平评价方法,是十分必要且必需的。
本文兼顾平时和战时公交发展水平影响因素建立公交评价指标体系,并根据现有的专家评论,利用模糊粗糙集的分类策略对城市公共交通服务水平进行综合评价,并通过两个实例,和KNN分类器做比较,验证了该方法的可行性和实用性。
1 相关工作
1.1 城市公共交通服务水平综合评价指标体系的建立
城市交通建设中的国防问题主要反映在以下几个方面:城市进出口道路问题;城市立交桥、高架桥问题;地下交通问题。这3个方面也是日常公共交通要关注和解决的焦点问题,属于城市公共交通基础设施。
反映公共交通系统服务水平优劣的指标多达数十种[1-4],我们对所有指标进行归类分析整理后,认为评价体系的指标可分为两大类。第1类为城市公共交通基础设施,它是决定公共交通系统服务水平的物质基础。它包括3个分指标,分别是公交车拥有率、公交线网密度和公交线路重叠系数。由于在战时公交车承担了运兵义务,这三大指标具有重大国防意义。公交车拥有率是城市总人口与公共交通车辆的保有量与城市总人口与之比,它可反映高峰时段公交车辆上乘客的拥挤情况,在考虑这个指标的规划时除了考虑平时市民的出行率,更要考虑战时增加的大量军人和后勤保障人员带来的出行压力。公共交通线路重叠系数是公共交通线路总长度与线路网长度之比,它反映了公交线路在城市主要道路上的密集程度;该指标在战时可能会由于部分路段戒严而低于平时水平,在早期规划时就要考虑足够的冗余。公共交通的线路网密度是指每平方公里城市用地面积上有公共交通线路经过的道路中心线长度,其值的大小反映了居民接近公交线路的程度。第2类指标为城市公共交通运输质量和效率,交通的拥堵不利于战时采取应急措施。共有如下3个分指标,公交车行车准点率、公交出行比例、公交车满载率,这3个指标决定了战时应急交通的效率。公交车行车准点率为运营公交车能够准点到达车站的比例,它是衡量顾客满意度的一个重要标准,在战时该指标也是指挥员预判运用公交工具运兵效率的重要参考。公交出行比例为公交车出行数量与全社会客车出行数量的比值,它反映了公共交通在城市客运中所起的作用,在战时指挥员通过该指标来权衡征用公交车辆还是社会车辆运兵之利弊。公交车辆的满载率为公交车辆实际的载客量与额定载客量之比或客运周转量与客位里程之比,它能反映公交车辆运行时车上的拥挤状况或车辆客位的利用程度,在战时该指标同样会因为大量战斗人员及后勤人员的加入引起与平时指标显著的增量,在规划时也要增加一定冗余量。城市公共交通服务水平评价指标如下:

将上述6项指标划分为高、中、低3级。指标分级标准以指标实际值的国家标准或国外城市达到平均水平为参考上限(高级),以国内城市现状平均水平为参考中间值(中级),其余内插或外推确定。具体分级情况参见表1。
表1 城市公共交通服务水平指标分级
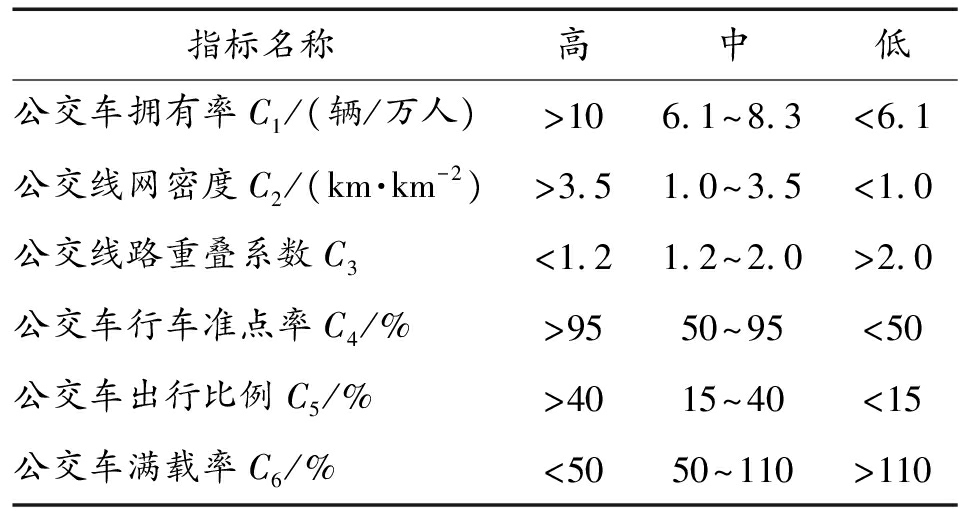
指标名称高中低公交车拥有率C1/(辆/万人)>106.1~8.3<6.1公交线网密度C2/(km·km-2)>3.51.0~3.5<1.0公交线路重叠系数C3<1.21.2~2.0>2.0公交车行车准点率C4/%>9550~95<50公交车出行比例C5/%>4015~40<15公交车满载率C6/%<5050~110>110
1.2 专家评价方法
首先,根据前述指标体系,把“公交车拥有率、公交线网密度、公交线路重叠系数”等 6 项作为高层主体指标,每个高层指标的分项作为低层主体指标。对上述高层主体指标、低层主体指标分别设计权重咨询表,由专家赋权,获得指标权重[5-7]。
对低层主体指标,再设计咨询表,由专家对每一项作出评价,评价以模糊评语的形式给出.咨询表的内容一般应包括:填表专家的权重(包括自评,如熟悉度、自信度等,以及他评,即各专家相互之间的评价) ;低层主体指标评分项;评分等级范围(即采用的是几级评价?每级评价以模糊评语方式给出) 以及其他附加项。咨询表的格式可以根据情况灵活设计,主要遵循简洁明了、便于专家评分的原则。
设计好咨询表以后,就要组织专家进行咨询。由于本方法本质上是专家决策方法,因此,专家的质量对决策结果影响很大,然而,由于战争、灾害、事故、政策变更造成客观情况的不确定因素,故本文根据已有的专家评价,运用模糊粗糙集的分类策略对城市公交服务水平进行综合评价。
2 模糊粗糙集分类策略
2.1 建立关系模型
为了运用模糊粗糙集的分类策略来进行服务水平的综合评价分类,首先需要建立关系数据模型。将各个评价指标视为条件属性,则条件属性集合C={C1,C2,…,Cn},将各专家根据每个评价指标打分后的最后综合分视为决策属性D,则可构建出一个二维决策信息表。
2.2 利用模糊粗糙集进行分类
给定一个决策系统DS,因为由决策属性d所描述样本的的属性值均为离散的,所以d用来表示样本的类别标记,鉴于此,利用决策属性d,可以构建出论域上的一个划分形如U/IND({d})={X1,X2,…, Xt},U/IND({d})表示U中的所有对象被分成t个不同的等价类,在粗糙集理论中,亦被称为一个决策类。除此之外,∀A⊆AT,可以根据条件属性集合A生成出一个模糊二元关系:

(1)
∀xi,xj∈U,r(xi,xj)∈[0,1]表示样本xi,xj之间的相似度[8-11]。相似度可以用距离的方式阐述,鉴于这一思想,Hu等[12]提出了利用高斯核函数来计算![]() 表示对象xi,xj之间的欧式距离,δ为高斯核函数的参数。
表示对象xi,xj之间的欧式距离,δ为高斯核函数的参数。
定义1 给定一决策系统DS=〈U, AT∪{d}〉,∀A⊆AT,∀Xk ∈ U/IND({d}),Xk的模糊粗糙下近似集、模糊粗糙上近似集分别记为![]() 和
和![]() 隶属于
隶属于![]() 和
和![]() 的程度为:
的程度为:
利用定义1所示的模糊粗糙下近似集,给定一个测试样本xt,可以得到如下所示的决策规则。
若![]() 则xt∈Xk。
则xt∈Xk。
上述规则说明了如果测试样本xt属于某一决策类的下近似集达到最大,那么该测试样本就被认定为是在这个决策类的范畴中的。这种决策规则实际上也可以被用来设计模糊粗糙分类器,其具体步骤为:① 计算测试样本与训练样本之间的高斯核相似度;② 利用高斯核相似度,计算测试样本属于每个决策类的模糊粗糙下近似隶属度;③ 选择模糊粗糙下近似隶属度最大值所所对应的决策类作为测试样本的类别。
3 实验分析
根据第二节的理论,本节通过两个实例,一个是已知多个专家对系统评分,另一个已知较少专家对系统评分。利用模糊粗糙集的分类策略,分析城市公共交通评价系统,并将此方法与KNN分类器进行了对比分析。
实例1 已知多个专家对系统评分
表2是6个专家对16个城市公共交通现状的给出的评分结果,评价标准是表1 的6个评价指标,分别为公交车拥有率(辆/万人),公交线网密度(km/km2),公交线路重叠系数,公交车行车准点率(%),公交出行比例(%)以及公交车满载率(%)。在表2中,前14个城市,专家已经给出了相应的评价,因此,可以视作训练样本,后两个城市,专家并未给出相应的评价,因此需要根据训练样本,判断这两个城市属于哪一类。
表2 已知多个专家对系统评分

城市专家1专家2专家3专家4专家5总评价18570858382227390898988338983898985348085818180257974808076167666777773177068787872189270909079298687878784310746879797811189768686853129675949482313957289898431492698989782
在表2中,根据总评价,可以得到由14个城市所构成的论域上的划分,即U/IND({d})={ X1, X2, X3}={{5,6,7,10},{1,4,8,14},{2,3,9,11,12,13}}。
1) KNN分类器。根据KNN分类器的思想,我们取k=5,通过计算可得,对于城市15,它的5个近邻分别为 5,6,2,9,11.故城市15被分为类别3。对于城市16,它的5个近邻分别为2,14,3,11,12.故城市16被分为类别3。可见分类不是太理想,这是由于KNN分类方法在分类时只考虑最近邻的样本点信息,而未考虑该样本点之间的联系。
2) 模糊粗糙集的分类策略。若高斯核参数δ设置为20,对于城市15来说,它属于第1类、第2类和第3类的下近似隶属度分别为![]() 0.197 5,因此,根据2.2节所示的决策规则,可以判定第15个城市在公共交通评价系统中应属于第2类。对于城市16来说,它属于第1类、第2类和第3类的下近似隶属度分别为
0.197 5,因此,根据2.2节所示的决策规则,可以判定第15个城市在公共交通评价系统中应属于第2类。对于城市16来说,它属于第1类、第2类和第3类的下近似隶属度分别为![]() 因此,根据2.2节所示的决策规则,可以判定第16个城市在公共交通评价系统中应属于第1类。
因此,根据2.2节所示的决策规则,可以判定第16个城市在公共交通评价系统中应属于第1类。
实例2 已知较少专家对系统评分
表3是6个专家对16个城市公共交通现状的给出的评分结果,评价标准是表1 的6个评价指标,分别为公交车拥有率(辆/万人),公交线网密度(km/km2),公交线路重叠系数,公交车行车准点率(%),公交出行比例(%)以及公交车满载率(%)。在表3中,前7个城市,专家已经给出了相应的评价,因此,可以视作训练样本,后9个城市,专家并未给出相应的评价,因此需要根据训练样本,判断这9个城市属于哪一类。
表3 已知较少专家对系统评分

专家1专家2专家3专家4专家5专家6总评价8570858382792739089898884389838989858738085818180812797480807682176667777737817068787872761
1) KNN分类器。根据KNN分类器的思想,我们取k=5,通过计算可得,城市8属于1类;城市9属于3类;城市10属于1类;城市11属于2类;城市12属于2类;城市13属于3类;城市14属于1类;城市15属于2类;城市16属于1类;
2) 模糊粗糙集的分类策略。若高斯核参数δ设置为20,对于城市8来说,它属于第1类、第2类和第3类的下近似隶属度分别为![]() 因此,根据2.2节所示的决策规则,可以判定第8个城市在公共交通评价系统中应属于第2类。对于城市9来说,它属于第1类、第2类和第3类的下近似隶属度分别为
因此,根据2.2节所示的决策规则,可以判定第8个城市在公共交通评价系统中应属于第2类。对于城市9来说,它属于第1类、第2类和第3类的下近似隶属度分别为![]() 因此,根据2.2节所示的决策规则,可以判定第15个城市在公共交通评价系统中应属于第3类。依次可计算出城市10属于1类;城市11属于2类;城市12属于3类;城市13属于3类;城市14属于2类;城市15属于2类;城市16属于1类;
因此,根据2.2节所示的决策规则,可以判定第15个城市在公共交通评价系统中应属于第3类。依次可计算出城市10属于1类;城市11属于2类;城市12属于3类;城市13属于3类;城市14属于2类;城市15属于2类;城市16属于1类;
实例2中的数据是来源实例1中的,对比发现,KNN分类器的分类准确率是没有模糊粗糙集分类策略的分类准确率高。由此说明了模糊粗糙集分类策略的可行性和实用性。
4 结论
模糊粗糙集综合评价法的基本原理是首先利用已有的专家评价进行训练,得到一个模糊粗糙分类器,然后再利用模糊粗糙分类器对新的专家还未评价的公共交通现状进行评价。相对于KNN分类方法,该方法计算简单,分类准确率高,且完全从数据中完成分析评价,不是单单考虑最近邻的样本点信息;不仅降低了评价成本,而且克服了一些专家评价方法的主观性,使综合评价更具客观性。
[1] 安晶,李香静,吴忠宜.面向公交优先绩效考核的城市公交发展水平评价指标体系研究[J].公路与汽运,2015(1):57-63.
[2] 王芹芹,王花兰.基于粗糙集理论的BRT运营服务水平可拓评价[J].兰州交通大学学报,2013,32(4):113-118.
[3] 徐以群,陈茜.城市公共交通服务水平的指标体系[J].城市交通,2006,4(6):42-46.
[4] 邓建任.城市公共交通服务水平评价指标体系研究——以西安市常规公交为例[D].西安:长安大学,2013:35-37.
[5] 刘维跃,曹溥晶,孔震.基于熵权的TOPSIS法的京津沪城市绿色交通发展对比研究[J].经济研究导刊2018,34(7):42-48.
[6] 谭将.城市公共交通线路调整评价方法研究与应用[D].北京:北京交通大学,2014:65-66.
[7] 张矢宇,韦金汛,仲超,等.基于PCA-DEA的武汉城市生态交通发展综合评价[J].公路与汽运,2018(6):22-27.
[8] 张文修,吴志伟,梁吉业,等.粗糙集理论与方法[M].北京:科学出版社,2001:76-77.
[9] 金保华,郭晓娟,张兴.模糊粗糙集在大学生综合素质测评中的研究及应用[J].现代计算机,2016,7(13):75-80.
[10]解难,孙龙,王玉伟.插电式混合动力汽车排放与能耗综合评价体系的构建[J].重庆理工大学学报(自然科学),2017,31(4):34-39.
[11]李京政,杨习贝,陈向坚.模糊粗糙集的稳定约简方法[J].南京理工大学学报,2018,42(1):68-75.
[12]HU Qinghua,ZHANG Lei,CHEN Degang,et al.Gaussian kernel based fuzzy rough sets:Model,uncertainty measures and applications[J].International Journal of Approximate Reasoning,2010 (4):117-119.