某小口径自动炮中的多股簧其主要作用是储存后坐动能、驱动后坐组件可靠地复进到前位,因此弹簧的加载、卸载响应特性决定着整个武器的射击速度和打击效能。由于多股簧主要承受周期性冲击载荷,多次循环使用后多股簧的损伤和性能退化必然会引起弹簧静、动态力学性能的改变,从而影响相关机构的动力学特性[1],因此开展多股簧性能退化特性研究对自动武器的科学使用和故障预测具有重要意义。
近年来许多学者对多股簧的摩擦、磨损机制和性能退化特性展开了相关研究。雷松[2]研究了多股簧的扭动微动磨损机制,认为随着扭动循环次数的增加,钢丝间的接触应力和剪切应力均会增大,其中剪切应力增大的更为明显,从而导致更大的簧丝磨损量;张明明[3]使用气锤对多股簧进行了连续冲击试验,发现连续冲击400次后多股簧加载后半段和卸载前半段的静态刚度分别增大了18%和28.2%;田志峰[4]对某35 mm高炮的复进簧进行了多轮射击考核试验,试验结束后发现该多股簧自由长度的平均缩短量为37.5 mm,静压至某高度时弹簧回弹力的平均衰退量为55.75 N。虽然以上研究取得了较好的成果,但当前并没有适用于多股簧性能变化的模型可用,迫切需要一种基于试验数据的性能计算模型或评估方法。
本文首先基于某小口径自动炮拨弹板簧和复进簧的测试数据,分析了多股簧使用之初和使用了2 000、4 000、6 000次后的动态响应特性,并提出多股簧性能退化的定义;然后采用反向差分演进算法对多股簧响应模型进行参数辨识,提出拨弹板簧和复进簧的性能退化模型;最后通过建立火炮自动机发射动力学有限元模型并将以上弹簧退化模型应用于自动机动力学仿真计算,本文分析了多股簧性能退化对自动机动力学特性的影响规律。
1 多股簧试验及试验结果分析
1.1 多股簧的自由长度
取两门自动炮的拨弹板簧和复进簧(共计四根弹簧)进行试验,二者的标准自由长度分别为600 mm和700 mm;虽然复进簧A的自由长度不足700 mm,但其预压后的静力学性能符合使用规定。每发射两千次之后立即检查多股簧簧丝的完整性并测量多股簧的自由长度,其结果如表1所示;从中可以看出随着循环使用次数的增加,多股簧出现了塑性变形,其自由长度和弹簧螺距均有所减小,拨弹板簧A和复进簧B的最大缩短量分别为10 mm、9 mm;由于在使用过程中出现了塑性硬化,N4000(4 000次发射,以此类推2 000次和6 000次用N2000和N6000表示)以后四根多股簧的自由长度不再有太多的改变。
表1 发射后的多股簧自由长度
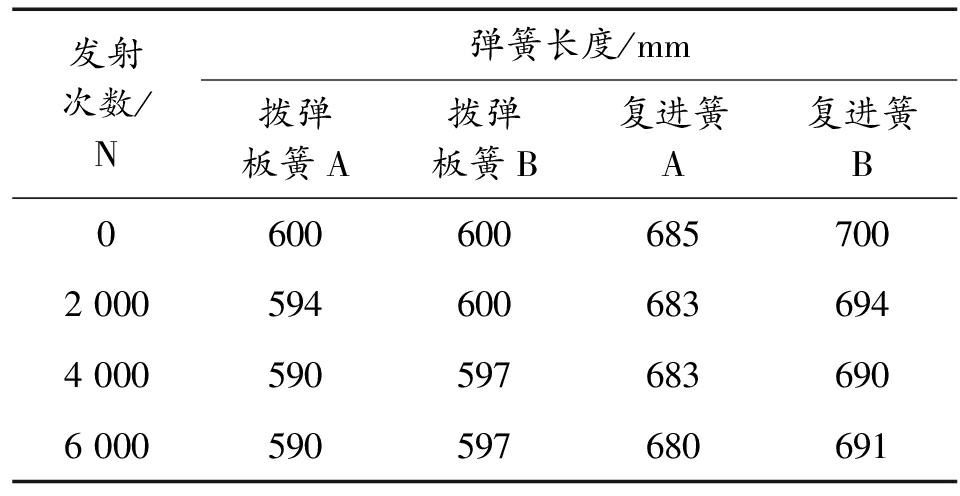
发射次数/N弹簧长度/mm拨弹板簧A拨弹板簧B复进簧A复进簧B06006006857002 0005946006836944 0005905976836906 000590597680691
1.2 多股簧动态试验及其结果分析
当前动力学试验装置为瑞士w+b公司生产的动态疲劳试验机,试验装置如图1所示。两根性质相同的多股簧被安装在上、下夹持件之间,并穿过各自的导杆以防止在加载过程中过度弯曲;下夹持件在试验过程中保持固定,上夹持件通过试验机夹头施加简谐激励信号x(t)=Asin(ωt)。多股簧的变形量为上夹头的位移,恢复力通过下夹头下的传感器测得。由于自动武器中的多股簧只能承受压缩变形,因此在试验之前对多股簧施加了一定的预压量并涂上润滑脂,从而保证多股簧在试验中一直处于压缩状态。图2即为加载频率为1 Hz时,当前动态试验装置输出的拨弹板簧和复进簧的力/位移响应曲线。

图1 多股簧动力学试验装置
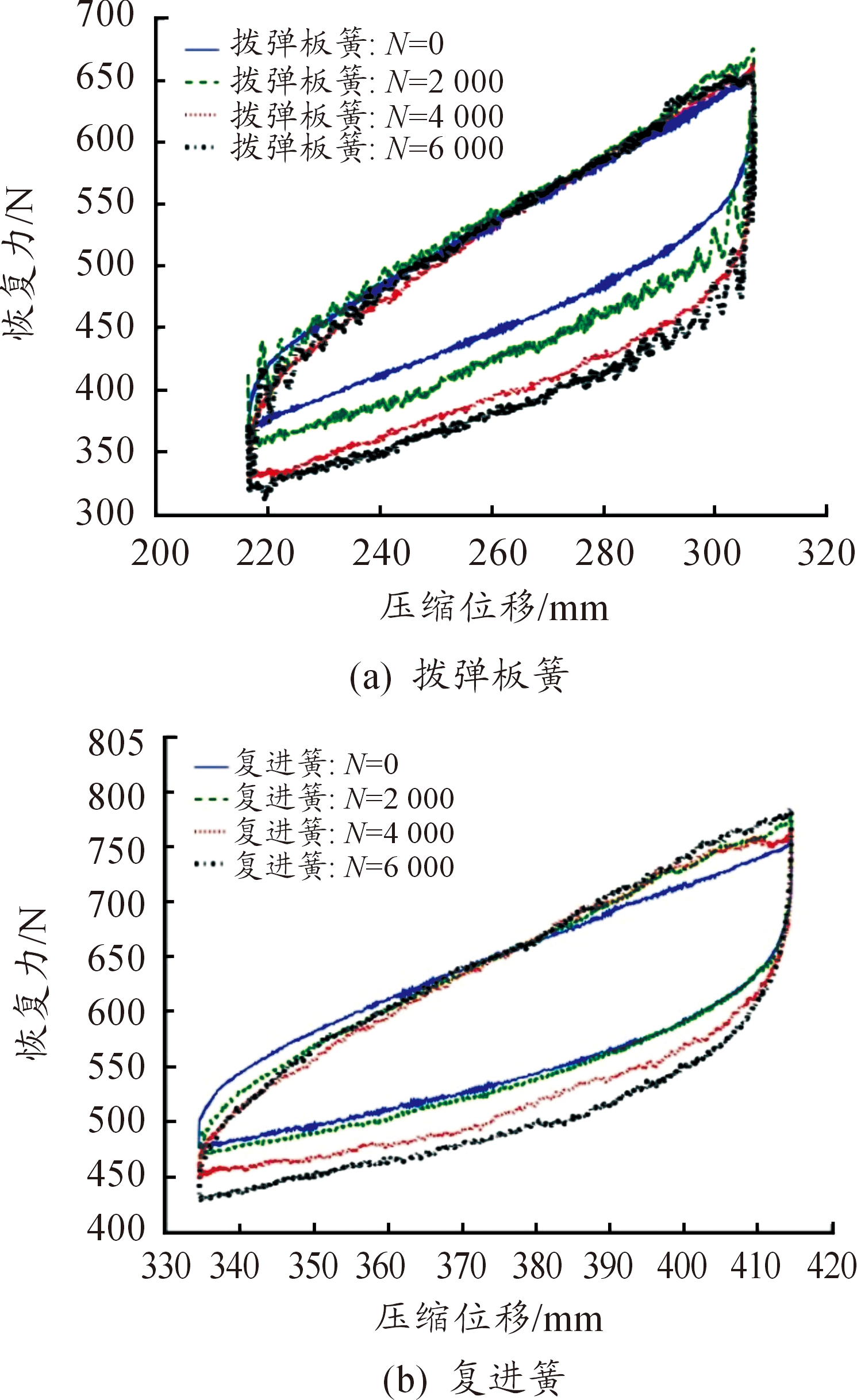
图2 实测的多股簧响应
从图2中可以看出,多次冲击循环使用后,多股簧的力/位移响应特性发生了较大的变化,现总结如下:第一,在相同的加载条件下,和无退化时的测试结果相比,多股簧响应曲线的光滑性逐渐变差,其原因可能是簧丝磨损使得原有的接触/摩擦特性发生较大改变;第二,加载初期多股簧的弹簧力变化不大,但随着加载位移的增大,多股簧的响应曲线有所上翘,线性刚度较最初使用阶段有所增大;第三,卸载时多股簧回弹力下降较大、响应曲线的迟滞耗能(包络面积)持续增加,但N4000以后多股簧迟滞耗能的增大量较使用前期均有所减小,这一规律和前述自由长度变化趋势类似。
基于以上试验结果的分析,本文拟定义多股簧的“性能退化”为,多次循环使用后,多股簧卸载时回弹力下降、弹簧迟滞耗能增大;同时拟定义多股簧“性能退化”的主要参数为迟滞耗能的增大比例,比如拨弹板簧的平均耗能量较使用之初分别增大了38.4%、67.9%、79.2%。
对多股簧的迟滞耗能量进行趋势拟合,其结果如图3所示。可以看出,若以迟滞耗能增大量来衡量多股簧的性能退化,则拨弹板簧的退化轨迹为凸形增长退化曲线,这说明随着射击次数的增加,退化量将缓慢增加;而复进簧的退化轨迹为凹形增长退化曲线,这说明随着射击次数的继续增加,退化量将逐渐增大;由于两种多股簧的几何参数不同,其中拨弹板簧簧圈直径较小、整体刚度较大,而复进簧簧圈直径较大、整体刚度较小,因此二者的性能退化量表现出不同的上升趋势。
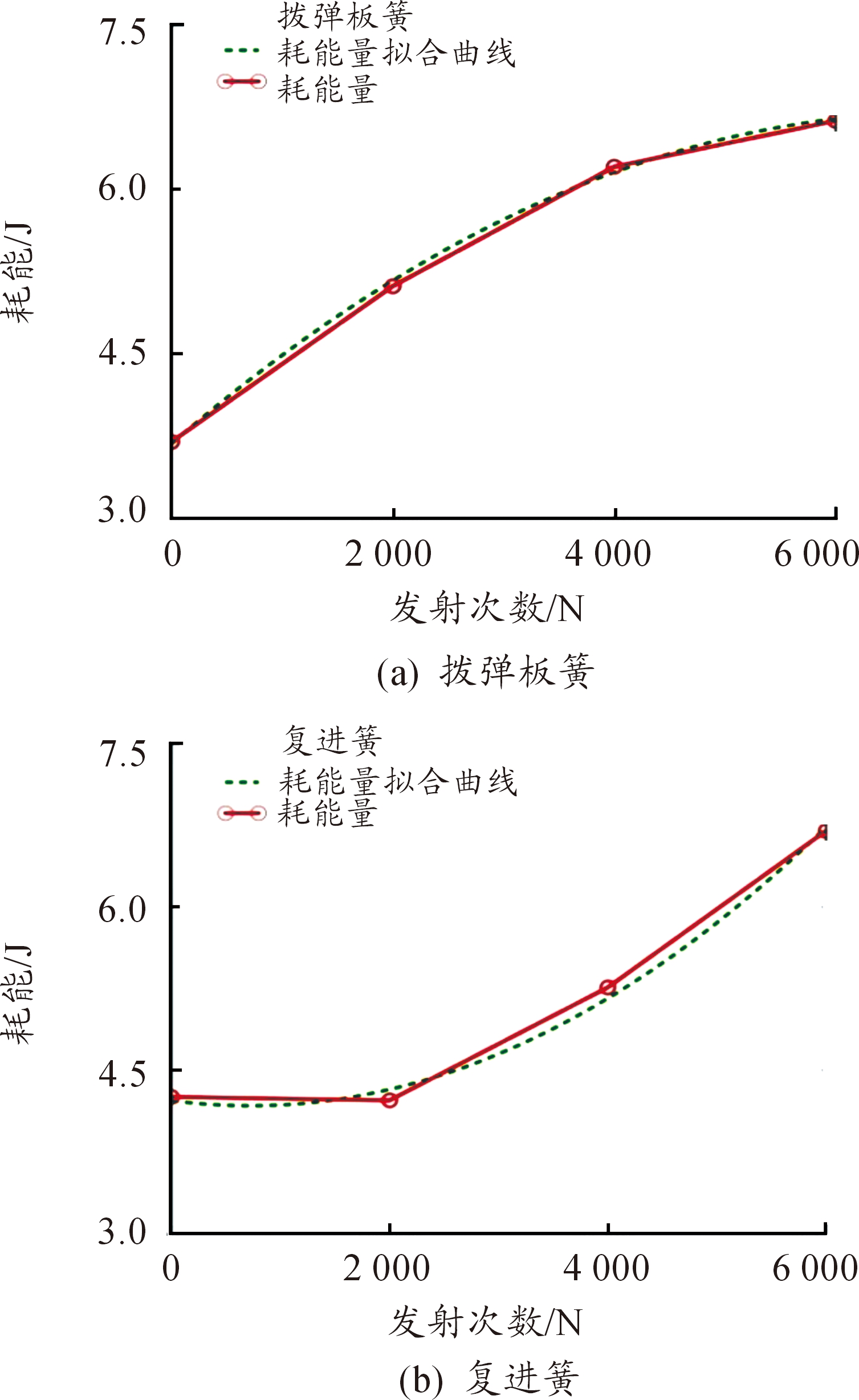
图3 多股簧的耗能趋势曲线
2 多股簧的非线性响应模型及其参数辨识
2.1 修正归一化Bouc-Wen模型(BW模型)
Zhao等[5]提出使用修正归一化BW模型来表示多股簧的力/位移响应特性。该模型作为非线性微分模型将弹性元件的恢复力分解为弹性部分和纯迟滞部分,并将迟滞量以微分方程解的形式给出。由于BW模型及其修正模型能够同时描述多股簧的刚度和迟滞阻尼效应,响应曲线比较光滑,因此能以较高的精度反映出多股簧的非线性动态特性并获得了广泛的应用。BW模型的表达式为:

式中:x、t分别为位移和时间;FE和FA分别是恢复力的非线性弹性部分和非线性放大部分;kEi和kAi分别是非线性刚度系数和非线性放大因子,N是多项式的阶数,一般取2阶或3阶;ω(t)为纯迟滞部分,对于任意的x和t,都有|ω(t)|≤1;ρ、σ、n为控制纯迟滞部分ω(t)曲线形状的迟滞三参数。Ikhouane等[6]进一步指出归一化BW模型只有在满足ρ>0、σ≥0.5时才有物理意义,而且在实际应用中,若n<1则会使微分方程的右端出现无限大的量,从而导致计算发散。
2.2 BW模型参数辨识算法
多股簧BW模型的参数识别问题可以归结为非线性优化问题,常见的求解方法有滤波算法[7]、粒子云算法[8]、差分演化算法[9]、最小二乘法[10]等。最小二乘法和滤波算法有着较高的求解效率,但求解前需要设置合适的参数初值,而粒子云和差分演进等进化类算法的抗噪声性能强,计算结果精度较高,但求解过程比较耗时。反向差分演进算法[11](ODE)作为差分演进算法的改进算法,具有较强的寻优能力和较高的求解效率,比较适合于当前中等维度的多股簧参数识别问题。
当多股簧系统采用三阶刚度系数时,BW模型待求解参数向量p为:
p=[kE0,kE1,kE2,kE3,kA0,kA1,kA2,kA3,ρ,σ,n]T
(2)
位移向量x(t)和速度向量![]() 为系统的已知输入,ω(t)可使用积分或者差分方法离散,多股簧系统的观测为恢复力向量F(t):
为系统的已知输入,ω(t)可使用积分或者差分方法离散,多股簧系统的观测为恢复力向量F(t):
F(t)=FE+ωFA=
(3)
设待求解的最小化问题(成本函数)为测量数据F和当前参数向量预测结果 ![]() 的归一化均方根误差(normalized mean square error,NMSE):
的归一化均方根误差(normalized mean square error,NMSE):
(4)
其中:![]() 为恢复力测量向量的方差,N为恢复力采样点的个数。Worden等[9]认为,当成本函数值小于5.0时,说明当前算法的优化精度较高,如果小于1.0,则可以认为当前参数即为模型的标准参数。
为恢复力测量向量的方差,N为恢复力采样点的个数。Worden等[9]认为,当成本函数值小于5.0时,说明当前算法的优化精度较高,如果小于1.0,则可以认为当前参数即为模型的标准参数。
设置种群大小为NP=5D,交叉率Cr=0.5,最大允许迭代次数Gmax=500,迭代终止条件为成本函数的最大最小值之差小于1.0e-6,算法框架采用Rahnamayan等[11]所介绍的抗噪声ODE框架,反向操作的跳转率Jr=0.3。
图4即为本文基于上述算法所预测的拨弹板簧、复进簧恢复力曲线。从图中可以看出,虽然部分测试结果噪声较强、且存在一定的波动,但使用抗噪声ODE算法依然可以获得较为光滑、合理的辨识结果。
2.3 参数辨识结果分析及多股簧退化模型
ODE算法所识别的复进簧参数如表2所示。对比其中数据可以发现,虽然NMSE随着发射次数的增加而持续增大,但其数值均小于5.0,这说明本文所获得的参数是比较精确的。纯迟滞部分参数ρ、σ、n的变化量较小,预示着多股簧耗能区间的光滑特性将不会发生较大变化;非线性刚度系数和非线性放大因子的改变量较大(为了表述的简洁性,表2已将kEi和kAi按照x的升幂写成向量形式kE和kA),这说明循环冲击载荷改变了多股簧加载和卸载时的非线性刚度(耗能)特性。
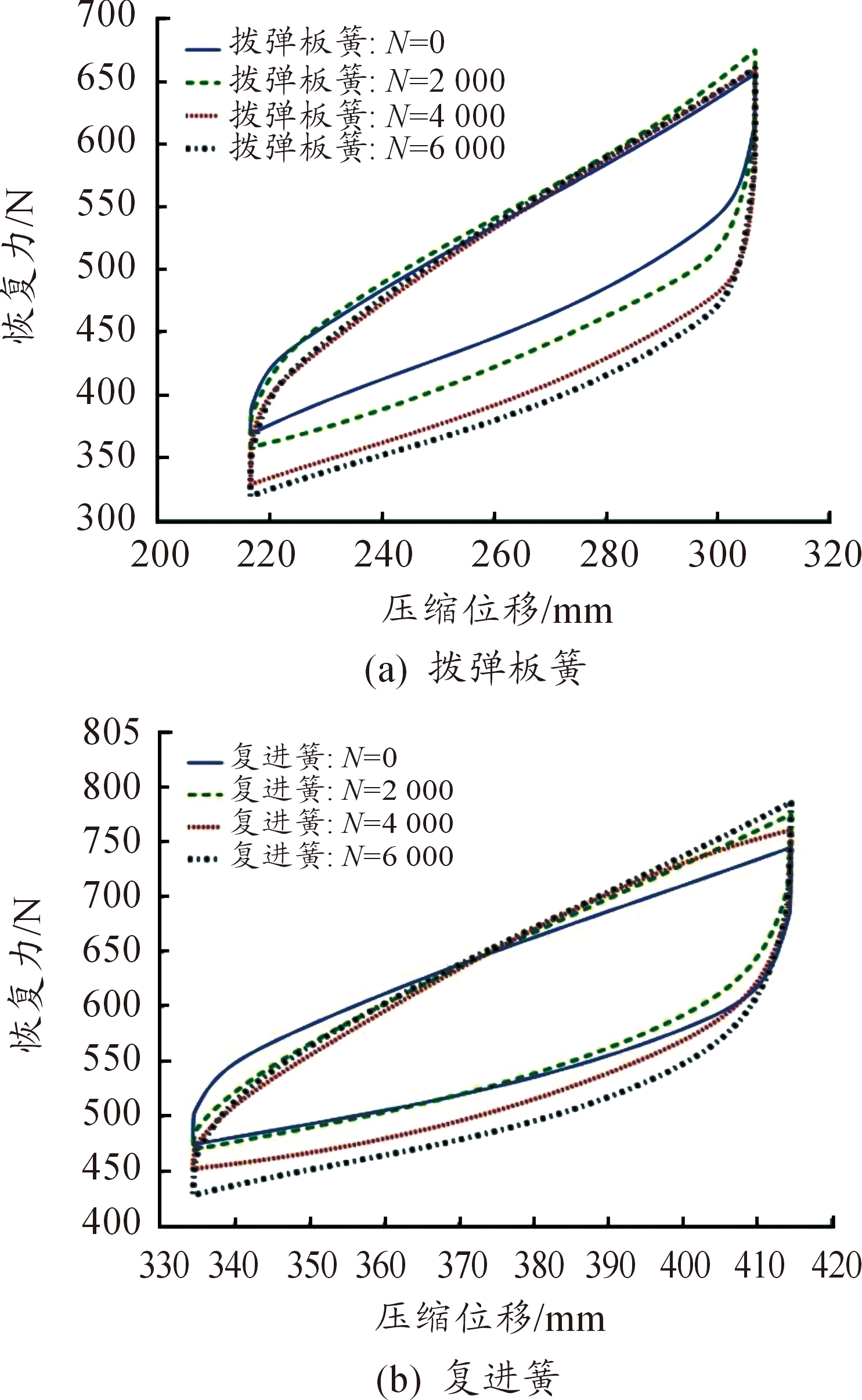
图4 预测的多股簧的动态响应曲线
表2 性能退化前后的复进簧BW模型参数

发射次数/NODEρσnkEkANMSE/N00.443 519.741 41.126 9[-62.028 7,2.026 8,0.004 3,1.5e-04][61.022 5,0.418 1,-0.010 3,-1.9e-05]1.821 02 0000.634 015.906 41.173 7[-60.959 1,2.535 0,0.005 7,1.5e-04][61.025 5,0.647 2,-0.012 3,-2.6e-05]2.028 84 0000.435 713.794 41.179 3[-72.541 8,2.783 1,0.002 4,-4.9e-05][73.165 9,0.831 8,-0.016 9,-1.2e-04]2.664 46 0000.373 816.251 91.174 5[-80.388 1,2.518 5,0.005 8,2.4e-04][83.659 1,0.848 3,-0.013 0,-8.5e-05]3.936 7
对复进簧kE和kA的各个参数进行趋势拟合,其结果如图5所示。观察曲线演化趋势发现,除前两阶系数变化趋势较为明显以外,二阶系数kE2、kA2变化量较小、拟合曲线的变化趋势不明显,而三阶系数kE3、kA3对整个多股簧响应力曲线的影响很小,部分文献[12]并不将其作为主要观察对象。传统观点[1]认为,多股簧疲劳后,弹簧的静态线性刚度(对应本文的一阶刚度系数kE1、kA1)将会显著下降,而本文的观察结果显示这种观点是值得推敲的。预压的多股簧在承受循环动态(冲击)载荷后,其一阶刚度将会有所提高,而在簧丝磨损、材料疲劳和塑性变形、簧丝之间的接触/摩擦特性恶化等退化因素的共同作用下,多股簧的回弹力将会下降、迟滞耗能量将会有所增大,这是多股簧性能退化的主要原因。
拨弹板簧模型参数的变化趋势和上述复进簧参数的变化过程基本一致,这里不再赘述,下面仍以复进簧为例构造多股簧的性能退化模型。由于多股簧BW模型中迟滞三参数变化较小,可以设为定值,且其他8个参数又可以通过曲线拟合获得相应的变化规律,因此本文基于BW模型构造以下复进簧性能退化模型:
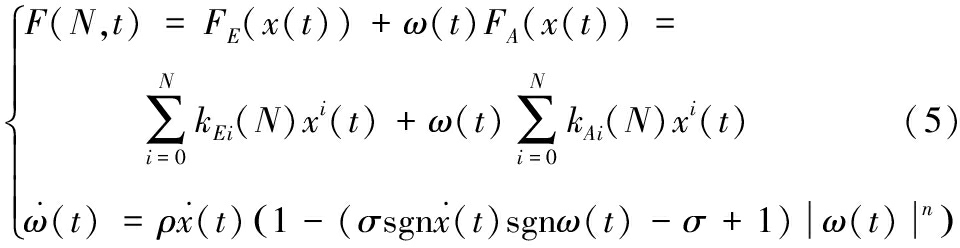
其中kE(N)和kA(N)的系数分别为:

(6)
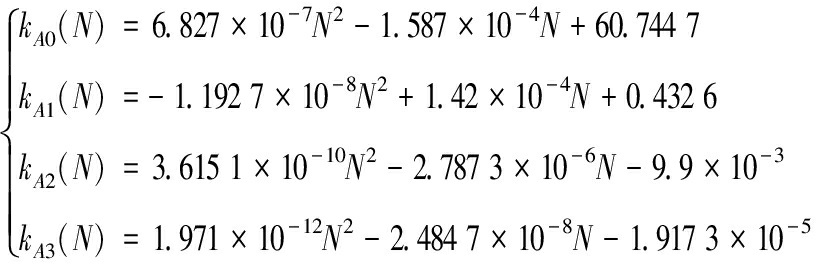
(7)
其中:N为发射次数(多股簧的循环使用次数)。
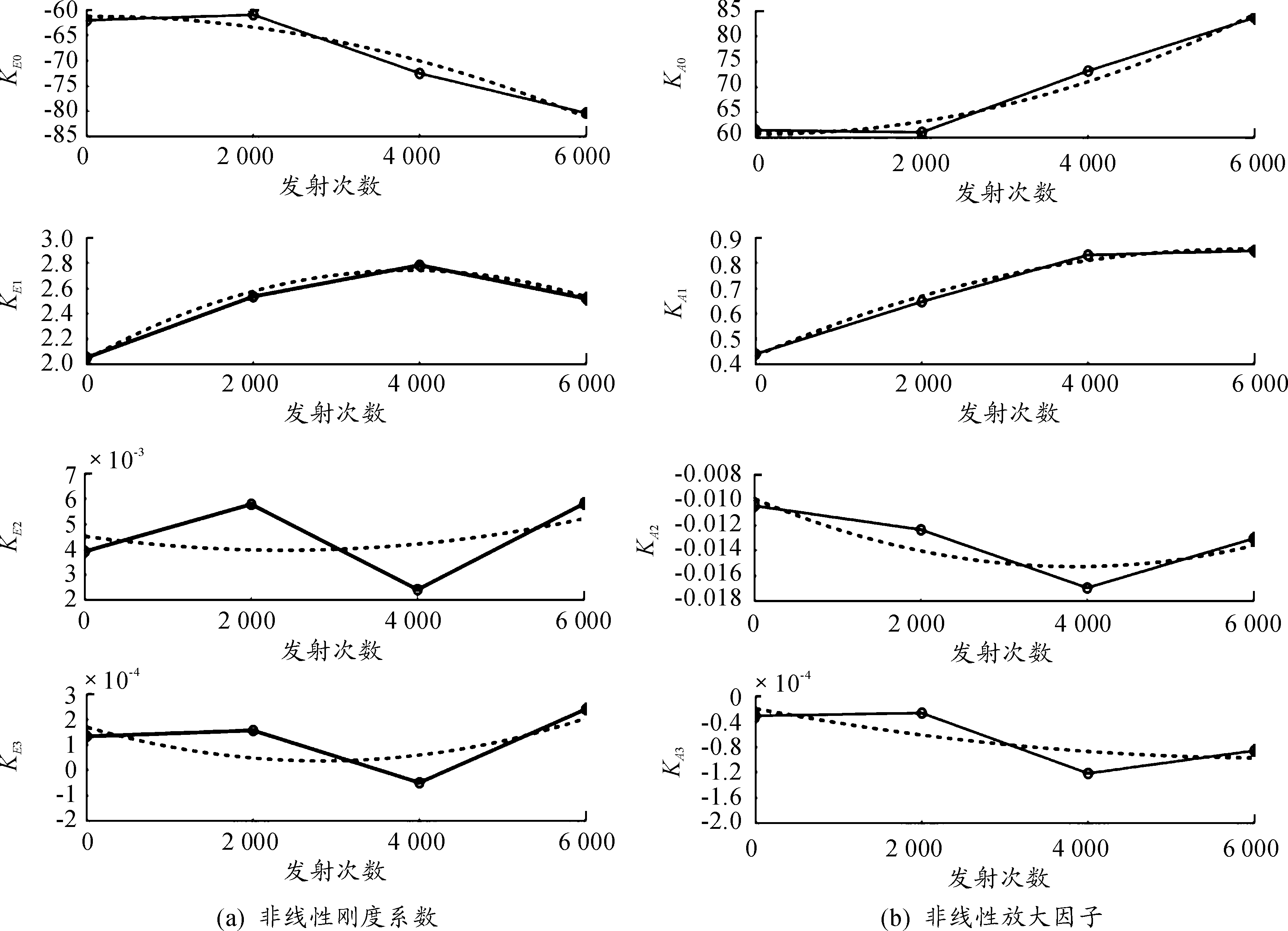
图5 非线性刚度系数和非线性放大因子的变化趋势曲线
3 多股簧性能退化对自动机运动性能的影响
在考察多股簧性能退化对导气式自动机运动性能的影响之前,本文首先建立内弹道耦合导气装置的变质量热力学计算模型,并编写VUAMP子程序将多股簧的弹簧力作为边界添加到自动机动力学仿真之中。
进行火炮自动机有限元建模时必须对模型进行简化。对于那些刚度大、变形小且对自动机运动影响较小的部件可以设定为刚体或者直接将其从计算模型中删去。炮箱作为一个比较复杂的部件,其内部有许多碰撞接触表面,在建模时需要精确处理;由于本文主要关注自动机运动情况,因此只建立药筒模型,并将膛底压力施加在药筒内部以计算抽壳力;推弹臂和加速臂之间、加速臂和传动框之间采用旋转铰单元建立铰接运动关系,并在这些单元上施加小质量和转动惯量以平衡计算;为了减少计算成本,将炮箱和加速座设定为刚体并将其固定在计算区域中;为方便弹簧力的施加,分别建立拨弹板簧和复进簧的施力耦合面,并将这些面耦合到弹簧力的施力点上。最终的计算模型共含有13个部件、409 108个实体单元,其中传动框部分的有限元模型如图6(b)所示。
3.1 导气室内火药气体压力计算和多股簧载荷施加
由于导气室内的气体压力变化规律与自动机传动框的往复运动有关,因此在计算导气室压力时需将传动框的运动和导气装置气流参数的变化规律耦合起来计算。导气式自动武器变质量热力学计算模型包括内弹道模型、导气装置模型和导气孔流量(耦合)方程。详细的内弹道方程和导气孔流量方程可以相关文献[13-14]。由于耦合模型中的传动框速度vh、位移xh可以通过ABAQUS的传感器接口向外输出,因此导气室气体参数方程不需要求解传动框的运动参数,于是简化后的导气装置动力学模型如下:
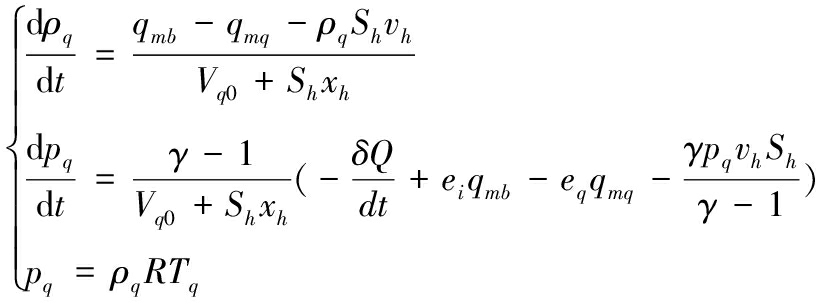
(8)
其中:ρq、pq、Tq分别为导气室内的气体密度、压力和温度; qmb、qmq、Vq0、Sh分别为流入导气室气体流量、导气室间隙的泄漏量、导气室初始容积、活塞的横截面积;γ、Q、R、ei、eq分别为绝热指数、导气室气体对外散热量、火药气体常数、导气室流入和流出单位质量气体所具有的能量。
计算时将内弹道程序输出的膛底压力施加在弹壳内部表面上,结合导气孔处的膛内火药气体压力和密度,将计算得到的导气室压力施加在活塞头端面上。至于复进簧和拨弹板簧的弹簧力,则需要在VUAMP子程序内部调用传动框的位移和速度信息、计算微分方程并将弹簧力施加在相应的耦合节点上;除了9.8 N/m2的重力场之外,以上所施加载荷均使用ABAQUS的VUAMP子程序进行施加,效果如图6(b)所示;模型中的其他载荷(如推弹臂推弹阻力、拨弹齿的弹链阻力)均采用均值的方式简化处理。构件之间的接触识别采用ABAQUS的通用接触算法(罚函数法);在有限元模型中设定计算时间为0.05 s,计算终止条件为,传动框撞击反跳锁后反弹速度为小于1.0e-6 m/s。

图6 传动框及其载荷
3.2 模型验证
本文首先使用无性能退化的多股簧模型来验证当前自动机计算模型的准确性。传动框的速度曲线如图7所示,后坐的初始阶段,在导气室压力的作用下,传动框的速度不断增大,并在加速臂撞击加速座之前达到了最大速度16.76 m/s。当前有限元模型所输出的传动框最大后坐速度较文献[15]给出的结果增大5.6%;使用当前模型获得的单次射击循环时间为41.102 ms,如果计入扣机打火时间和火药燃烧至弹丸启动时间,则单次射击循环时间为48.382 ms,对应理论速射为1 240.1 r/m,而该炮的理论速射不低于1 200 r/m。综上所述,可以认为当前所建立的导气式自动机动力学模型是准确的。
3.3 多股簧性能退化对自动机运动性能的影响
不同退化程度下的拨弹板簧恢复力曲线如图8所示,通过观察曲线变化趋势和恢复力的幅值,可以认为当前多股簧子程序的输出结果是正确的。N6000后的响应曲线包络面积最大,但此时耗能的增大趋势已经不再明显。传动框复进到0.1 m附近时,三个退化阶段拨弹板簧的恢复力分别为:509.5 N、474.0 N、459.1 N,较退化之初分别下降了6.9 %、13.4 %、16.1 %。
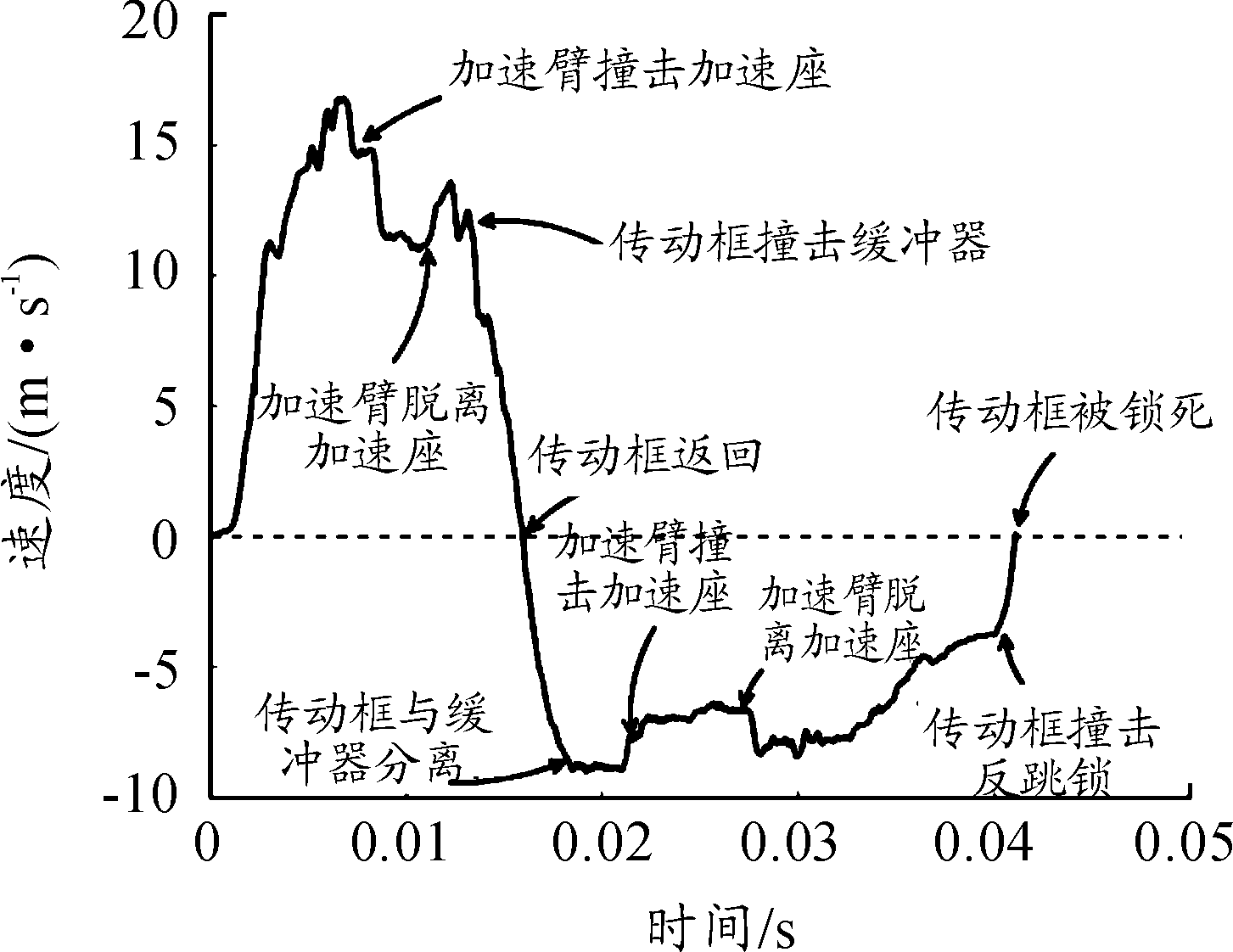
图7 传动框的运动速度曲线

图8 不同退化程度下拨弹板簧恢复力曲线
不同退化程度下的传动框速度和位移曲线如图9(a)、(b)所示。从图中可以看出,后坐时不同退化程度的传动框速度和位移曲线基本重叠,显示多股簧性能退化对传动框的后坐过程没有太大的影响。在复进的初始阶段,由于迟滞耗能过大,N6000的传动框速度和其他工况相比有所滞后;由于无退化模型计算出来的弹簧回弹力大于其他三种情况,因此在复进后期传动框复进的动力比较充足、复进速度较大,能够及时地使传动框复进到位,比如0.04 s时,无退化模型的传动框速度分别是N2000、N4000、N6000的1.53倍、2.99倍、2.89倍;同时由于N6000的迟滞耗能过大、输出的恢复力过小,导致传动框复进速度过低,在距离前位17 mm处,传动框的运动几乎陷入停滞。
多股簧不同退化程度下自动机传动框的最大后坐速度、位移、单次射击循环耗时和理论射速如表3所示。由于弹簧恢复力较大、复进动力较为充足,所以无退化模型的理论射速高于其他3种情况。文献[16]认为该武器的理论射速处于1 200~1 350 r/m之间,虽然N2000后的理论射速下降量不大(3.93%),但N4000和N6000后自动机射频的下降量分别为9.35%、10.07%;射频的下降势必会影响武器的打击效能,且当前的研究对象是导气式自动武器,如果计入内弹道性能退化对导气装置传动过程的影响,则射速的下降量会更大。
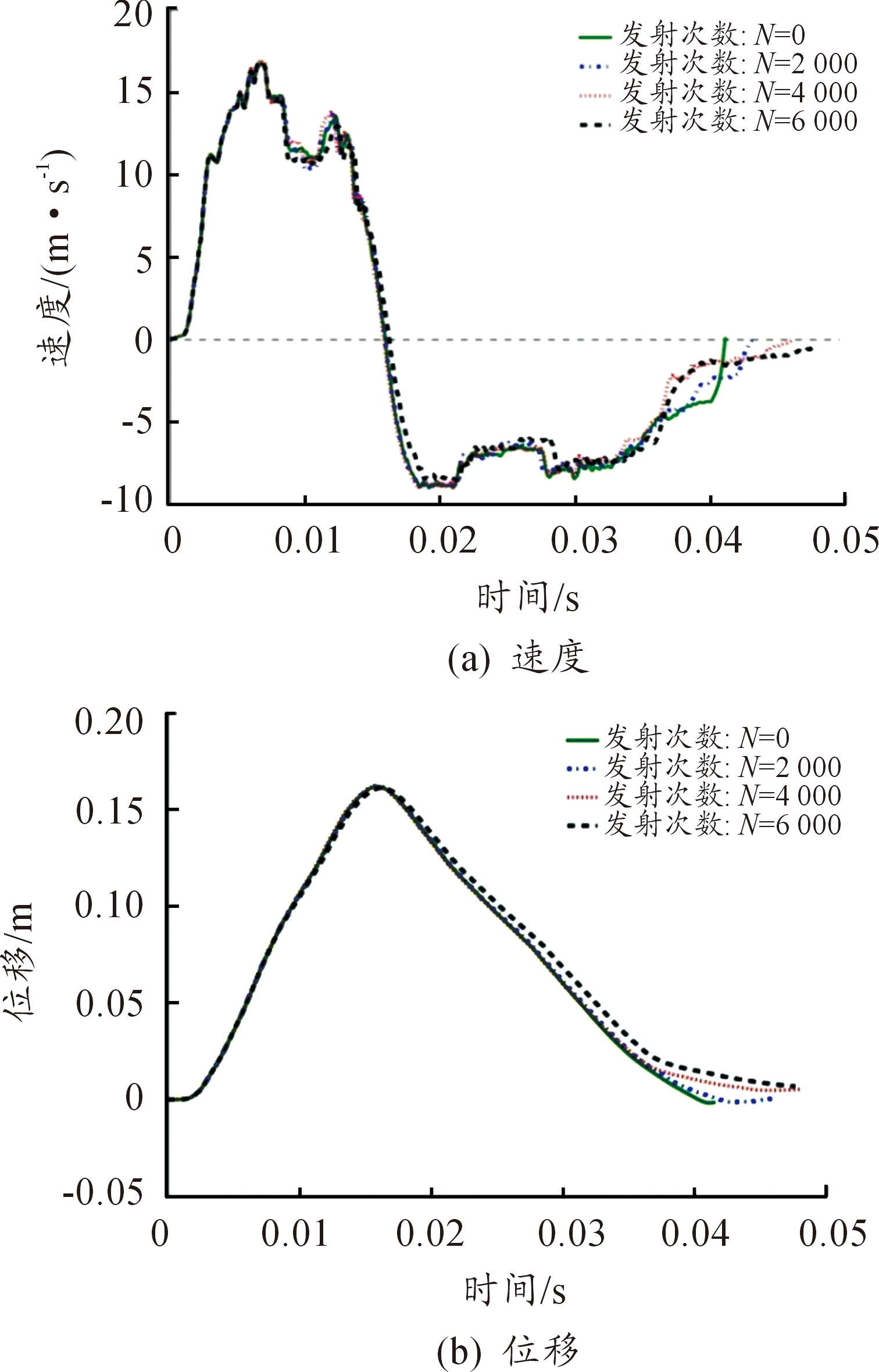
图9 多股簧不同退化程度下传动框的速度和位移曲线
表3 多股簧性能退化前后传动框的运动特性和理论射速

发射次数/N最大后坐速度/(m·s-1)最大后坐位移/mm射击循环耗时/ms理论射速/(r·m-1)0[15-16]15.69164.5<50.01 200~1 350016.765 6162.12448.3821 240.12 00016.732 2162.31450.3621 191.34 00017.008 3162.17553.3781 124.06 00016.659 4161.50254.8891 115.2
4 结论
1) 基于多股簧性能退化后的动态测试结果,定义多股簧性能退化后为多股簧卸载时的回弹力逐渐下降、弹簧迟滞耗能逐渐增大。
2) 多股簧性能退化后纯迟滞部分参数基本不变,而非线性刚度、非线性放大因子均有较大变化,分别影响多股簧响应曲线的光滑性和迟滞耗能量的大小。
3) 通过建立考虑身管和导气装置耦合过程的火炮自动机有限元模型、分析计算,证明当前所建立的内弹道耦合导气室计算模型、自动机仿真模型是准确的。6 000次使用后,多股簧性能退化将导致自动炮的理论射速降低约10%,如计及内弹道性能退化,该炮的射速改变量更大。
[1] 徐达,韩振飞,苏忠亭,等.小口径自动炮复进簧对发射过程动态特性影响仿真研究[J].装甲兵工程学院学报,2013,27(03):51-53.
[2] 雷松.多股簧冲击特性与损伤机理研究[D].重庆:重庆大学,2010:81-98.
[3] 张明明.多股簧动态参数检测技术及装备的研究[D].重庆:重庆大学,2011:42-53.
[4] 田志锋.特种多股螺旋弹簧检测与试验研究[D].重庆:重庆大学,2010:34-43.
[5] ZHAO Y,WANG S,ZHOU J,et al.Three-stage method for identifying the dynamic model parameters of stranded wire helical springs[J].Chinese Journal of Mechanical Engineering,2014,28(1):197-207.
[6] IKHOUANE F,GOMIS-BELLMUNT O.A limit cycle approach for the parametric identification of hysteretic systems[J].Systems & Control Letters,2008,57(8):663-669.
[7] WU M,SMYTH A.Real-time parameter estimation for degrading and pinching hysteretic models[J].International Journal of Non-Linear Mechanics,2008,43(9):822-833.
[8] ZHANG J,XIA P.An improved PSO algorithm for parameter identification of nonlinear dynamic hysteretic models[J].Journal of Sound and Vibration,2017,389:153-167.
[9] WORDEN K,MANSON G.On the identification of hysteretic systems.Part I:Fitness landscapes and evolutionary identification[J].Mechanical Systems and Signal Processing,2012,29:201-212.
[10]ZHU W,WANG D H.Non-symmetrical Bouc-Wen model for piezoelectric ceramic actuators[J].Sensors and Actuators A:Physical,2012,181:51-60.
[11]WANG H,WU Z,RAHNAMAYAN S.Enhancedopposition-based differential evolution for solving high-dimensional continuous optimization problems[J].Soft Computing,2011,15(11):2127-2140.
[12]程成.周期载荷下多股簧的动力学模型及响应特性研究[D].重庆:重庆大学,2014:30-44.
[13]冉景禄,徐诚,赵彦峻.导气式自动武器变质量热力学计算模型研究[J].兵工学报,2011,32(4):408-413.
[14]宋杰,廖振强,李佳圣,等.导气与枪管浮动混合式自动机动力学特性研究[J].兵工学报,2014,35(6):753-761.
[15]王娟.基于虚拟样机技术的航炮系统动力学仿真[D].西安:西北工业大学,2004:13-30.
[16]何志强,黄守仁,李载弘.航空自动武器设计手册[M].北京:国防工业出版社,1991:190-216.