桥吊作为一种常见的欠驱动设备,在工业生产中有广泛的应用。直观地讲,所谓欠驱动系统,是指系统的控制输入变量个数小于系统自由度的一类非线性系统,在生产实践中很多设备都具有欠驱动的形式,由于去掉系统部分驱动器,增加了系统自由度,提高了系统灵活性,使得欠驱动系统在节约能源、降低价格、增强系统适应性等方面都比全驱动系统优越。对于桥吊系统而言,其工作效率取决于负载的消摆时间,在桥吊系统中,由于非直接控制的摆动自由度的存在,使得其动力学特性与耦合性相比全驱动系统更为复杂,给系统的稳定控制带来了难度。桥吊负载的残余摆动一方面会延长操作时间,降低工作效率,另一方面会造成落吊困难。在一般情况下负载摆动呈现单摆特性,当吊钩质量相比负载质量不可忽略时负载相对吊钩会产生第二级摆动,此时桥吊系统呈现出双摆特性。
近年来,国内外学者针对桥吊系统的控制问题开展了很多研究工作,但大多针对单级摆动。主要控制模式分为开环和闭环控制,具体而言,主要控制方法有输入整形[1]、LQR[2]、PID[3]、部分反馈线性化[4]、输出反馈控制[5]、能量方法[6]、分级控制[7]以及智能控制[8]等等;当系统产生双摆效应时,桥吊系统会产生两个不同的固有频率,且与负载质量及重心配置等因素相关,使得摆动特性更为复杂。一方面传统针对单级摆的控制方法控制性能会大大下降。另一方面,以上控制方法在理想条件下均能够取得很好的控制效果,但是在工业生产中,由于大量的外界扰动、参数摄动以及风载荷、摩擦力的存在,采用传统的控制方法无法保证系统的稳定性以及对干扰的鲁棒性。滑模控制隶属于变结构控制(Variable Structure Control,VSC),滑模控制与其他控制方法最大的区别在于其系统结构具有时变的特点,处于动态过程的系统结构,根据当前的系统状态(如误差,误差变化率等)有目的地进行变化,迫使系统按照设计的“滑动模态”状态轨迹运动[9]。由于滑动模态可以根据控制目的进行设计且与对象参数以及外界扰动无关[10-11],使得滑模控制在系统稳定性、对干扰的鲁棒性等方面有独特的优势,广泛应用于非线性系统以及不确定系统的控制研究。
本文针对一类双摆吊车系统的消摆控制问题,采用耦合线性滑模控制方法(Coupling Conventional sliding mode control,CSMC);并改进等速趋近律得到一种非线性趋近规律,能够大大削弱抖振现象;针对不同工况条件进行了仿真分析;模拟外界干扰进行了鲁棒性测试。研究表明,本文基于非线性趋近律的耦合线性控制方法能够在干扰存在以及不同工况条件下取得良好的控制效果。
1 系统动力学模型建立
如图1所示为桥吊模型。在大多数工况下,“台车-吊绳-负载系统”质量集中于台车和负载之上,一方面吊钩远小于负载质量;另一方面二级吊绳长度一般忽略不计,此时系统便只会呈现单摆动力学特性。当实际工况的系统模型配置不满足以上假设条件时,系统会产生如图2所示双摆特性。考虑台车与轨道的摩擦力,根据欧拉-拉格朗日法建立双摆系统动力学模型[12]如下:
(1)
(2)
m3gl2Sθ=0
(3)
其中:m1,m2,m3为台车、吊钩、负载质量;l1,l2为一级、二级吊绳长度;φ, θ为吊绳相对铅垂方向的偏角;C,S代表余弦和正弦函数;b为摩擦阻力系数;U为控制输入。

图1 双摆桥吊模型
为方便进行仿真操作,将上式写成矩阵形式:
(4)
定义系统状态![]() 为广义坐标;U=[u,0,0]Τ为控制向量。系统矩阵如下所示:
为广义坐标;U=[u,0,0]Τ为控制向量。系统矩阵如下所示:
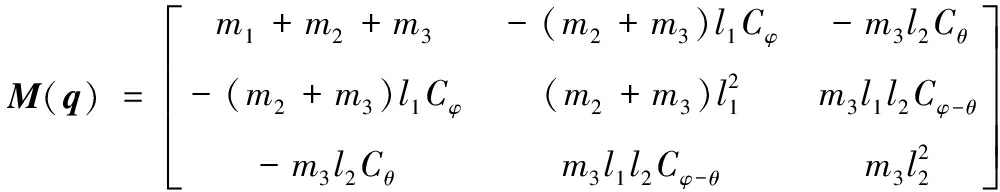


2 滑模控制器设计
针对式(1)~式(3)桥吊系统,取欠驱动系统的状态为q=[x,φ,θ]Τ,根据系统控制要求,得系统稳定状态为qd=[xd,0,0]Τ。定义位置误差:e=x-xd,设计双摆吊车系统耦合滑模面:
(5)
其中,λ,α,β为控制器参数。
求取系统滑模面函数导数:
(6)
设系统控制量为:
u=ueq+usw
(7)
利用等效控制原理,将式(1)代入式(6)得等效控制量:
(8)
为了获得整个系统的控制输入量,需要确定切换控制部分,且切换控制量usw的选取应使如下所示的滑模到达条件成立:
(9)
利用等速趋近律求解滑模控制器的切换控制量,即
(10)
其中,ε为严格正实数。
将式(1)、式(7)、式(8)代入式(10)得:
usw=-εsgn(S)
(11)
进而求得基于等速趋近律的传统滑模控制器总输入:
u=![]()
(12)
为进一步削弱系统状态高频切换引起的抖振现象,采用饱和函数代替符号函数:

(13)
其中,Δ为边界层厚度。
本文在文献[13]的基础上提出了式(14)所示非线性趋近律:
(14)
其中,k,ε为正实数,p为介于[0,1]区间的正实数,γ为正实数,χ为正整数。由式(14)求得:
(15)
其中,Q(S′)=p+(1-p)exp(-γ|S′|χ)>0。
式(15)表明滑模到达条件式(9)成立,因此整个控制系统处于稳定可控状态。此时系统控制输入为:
u=![]()
(16)
3 稳定性分析
定理 对于二维定绳长双摆吊车系统,若采用式(5)所示设计线性滑模面,并采用式(16)所示总滑模控制量,则整个桥式起重机系统的滑模面是渐进稳定的。
证明:构造Lyapunov能量函数
(17)
对上式求导得![]() 代入式(14)改进趋近律得
代入式(14)改进趋近律得
(18)
由式(14)可知,ε<ε/Q(S′)<ε/p,故式(18)可化简得
(19)
对式(19)积分运算可得
V(t)-V(0)≤![]() (-ε|S|-kS2)dΘ
(-ε|S|-kS2)dΘ
(20)
代入式(17)进而有
(21)
V(0)<∝
(22)
根据巴尔巴拉引理推论[14],由式(19)、式(21)可知![]() 由式(21)可知S∈L2,得到
由式(21)可知S∈L2,得到![]() 即系统总滑模面为渐进稳定,证毕。
即系统总滑模面为渐进稳定,证毕。
为进一步确定滑模控制器参数的取值范围,需将式(1)~式(3)双摆系统写成状态空间的形式。根据式(6)滑模到达充分条件得
(23)
将式(23)代入式(2)、式(3)得
(24)
(25)
双摆桥吊系统状态可记为
将式(23)~式(25)写成状态空间形式如下
![]()
(26)
其中,P(m),R(n),Q如下所示
P(m)=![]()
(27)
R(n)=![]()
(28)
Q=βu6+αu4+λu2
(29)
通过对平衡点附近的状态空间系统进行线性化,可以得到一个线性系统如式(29)所示,其雅可比矩阵如式(30)所示
(30)
根据李雅普诺夫稳定性定理,原系统渐进稳定的必要条件是线性化后的系统(29)是稳定的[15],即其系统矩阵H为Hurwitz矩阵,此时要求
λ>0,α>0, β<0
(31)
综上,采用式(16)所示滑模面,系统是渐进稳定的,且此时要求满足式(31)的参数要求。
4 仿真分析
为进一步分析本文桥吊防摆控制方法的有效性,本文采用Matlab/Simulink进行数值仿真试验验证。将本文控制方法与分层滑模控制方法对比分析收敛情况;分析各种控制方法到达滑模状态所需时间;最后对系统对干扰的鲁棒性进行试验分析。
仿真试验取台车预期位置为4 m,桥吊系统参数设置为:台车、吊钩、负载质量m1,m2,m3为30 kg,10 kg,2.5 kg,一二级吊绳l1,l2为3 m,0.3 m。控制器参数见表1、表2。
表1 改进趋近律参数

参数εkpχγ值3.50.550.118
表2 滑模控制器参数

参数μλαβΔ值550.4415.5-90.05
针对滑模控制器如图2(a)所示高频抖振问题,本文利用式(14)改进趋近率仿真结果如图2(b)所示,可见改进非线性趋近律能够有效削弱系统抖振现象,提高系统稳定性。
采用本文线性耦合滑模控制方法,对比分层滑模(Hierarchical sliding mode,HSMC),图3之桥吊系统响应曲线显示CSMC较HSMC方法系统状态波动范围小,不会造成负载发生大幅摆动,安全性较高;如图4相平面图仿真结果显示,两种控制方法均能够在有限时间内完成状态收敛;本文提出的线性滑模控制器能够在较短的时间内完成系统状态收敛,系统状态过度平缓,不会造成台车控制力矩突变或大幅切换的现象,系统平顺性较好;采用PID控制方法系统响应曲线如图5所示,该控制方法虽能够控制台车准确定位,但一级摆角收敛时间较长,无法消除二级摆残余摆动,实际工程运用效果欠佳。三种控制方法系统收敛时间见图6所示。
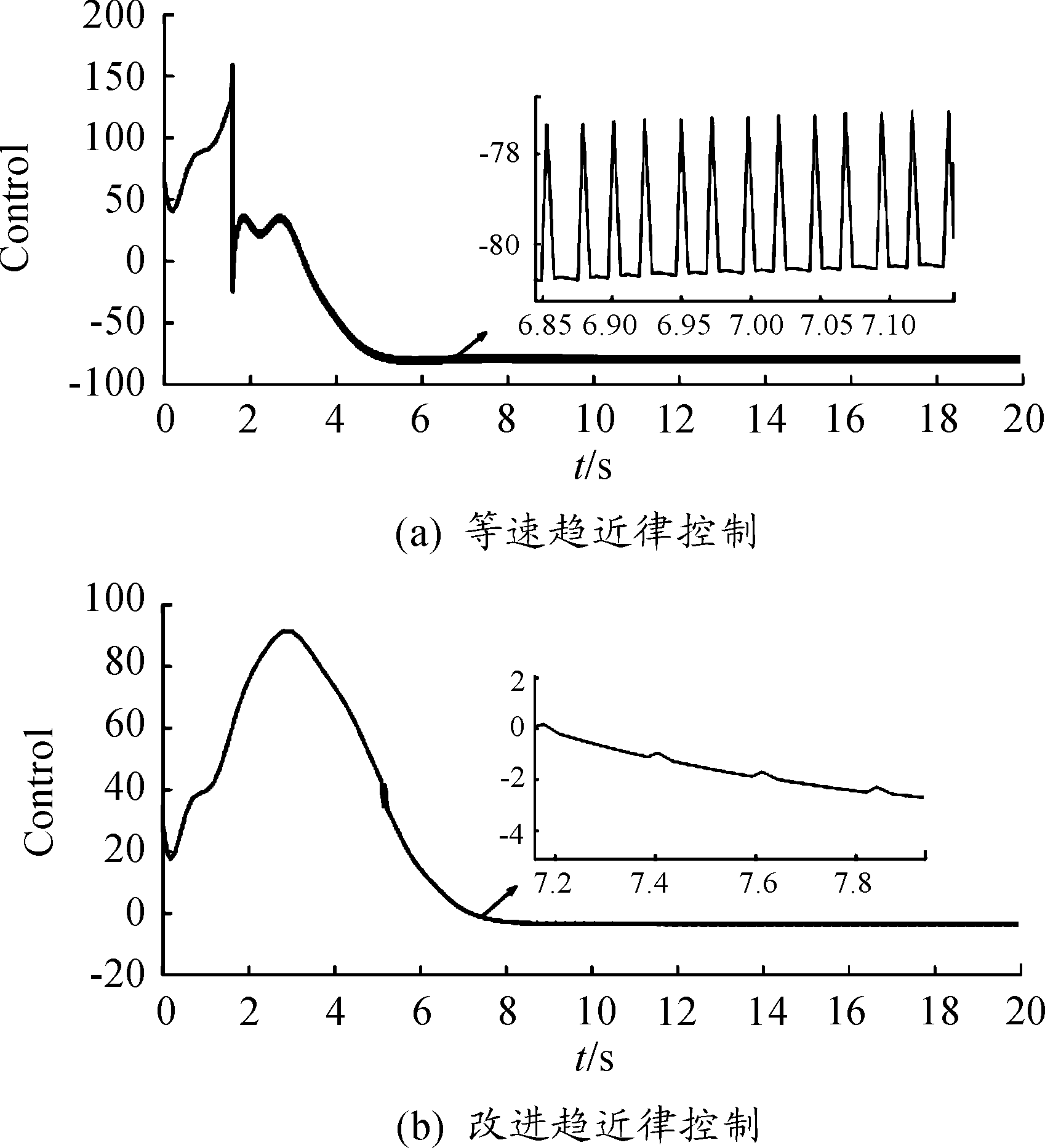
图2 滑模控制输入曲线
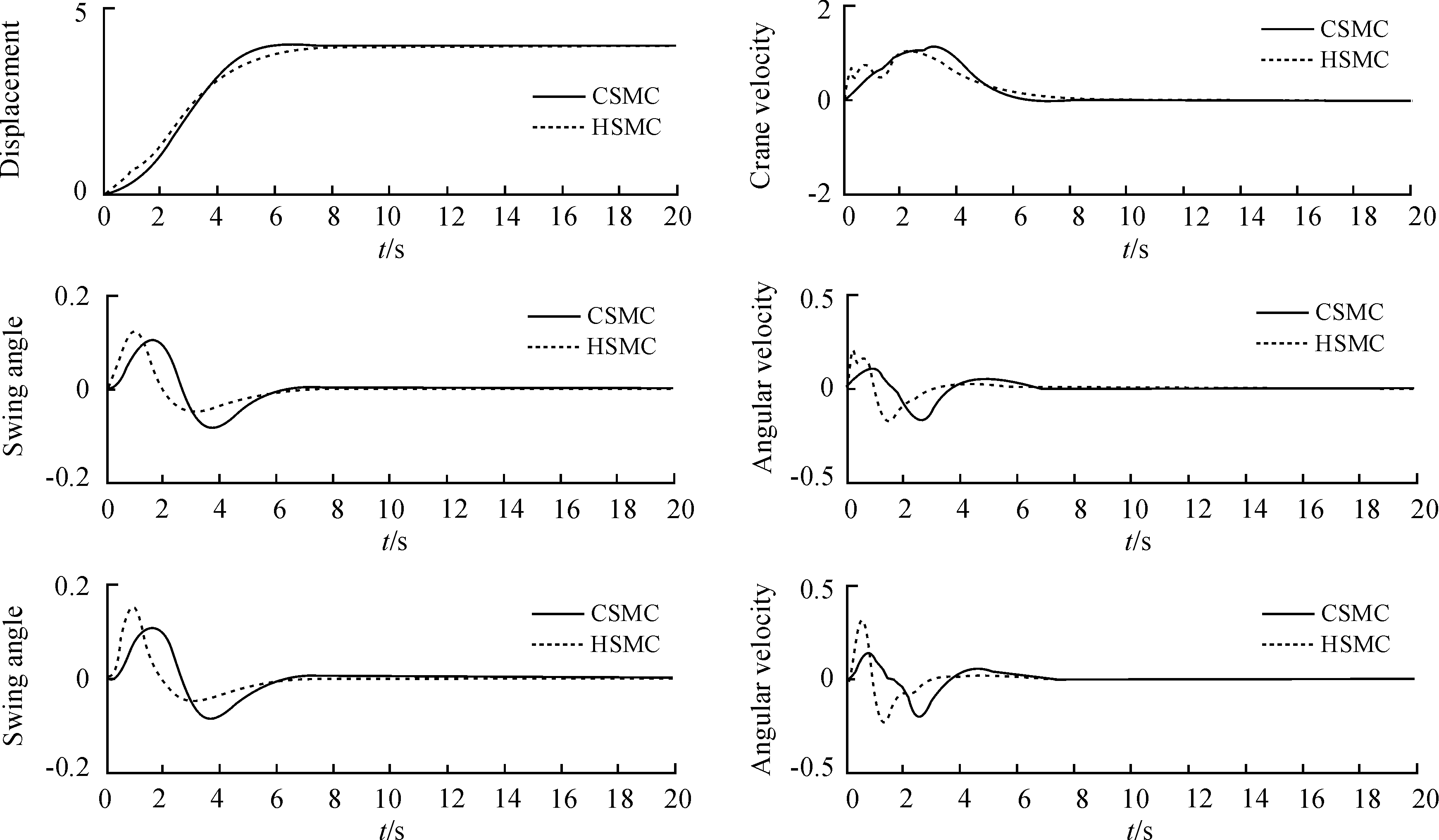
图3 桥吊系统响应曲线
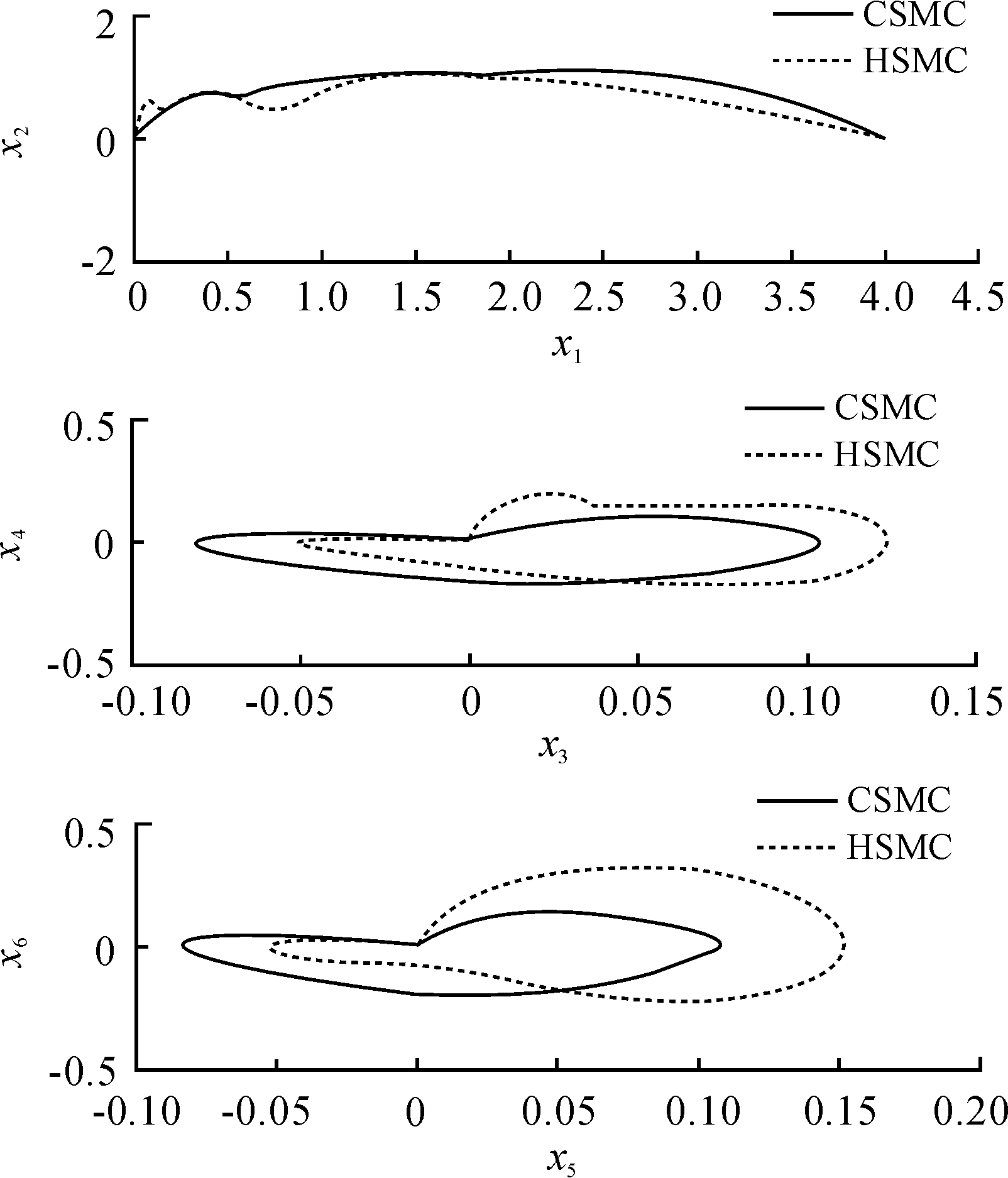
图4 系统状态相图

图5 基于PID控制桥吊系统响应曲线

图6 系统状态收敛时间
对两种滑模控制方法的滑模面进行仿真分析如图7所示,线性滑模面能够在2 s内到达滑模状态,且不会产生大幅抖振现象;分层滑模控制器第二层滑模面能够在0.2 s内到达滑模状态,但第一层滑模面仍处于趋近状态,且此时第二层滑模面有较为明显的抖振现象。
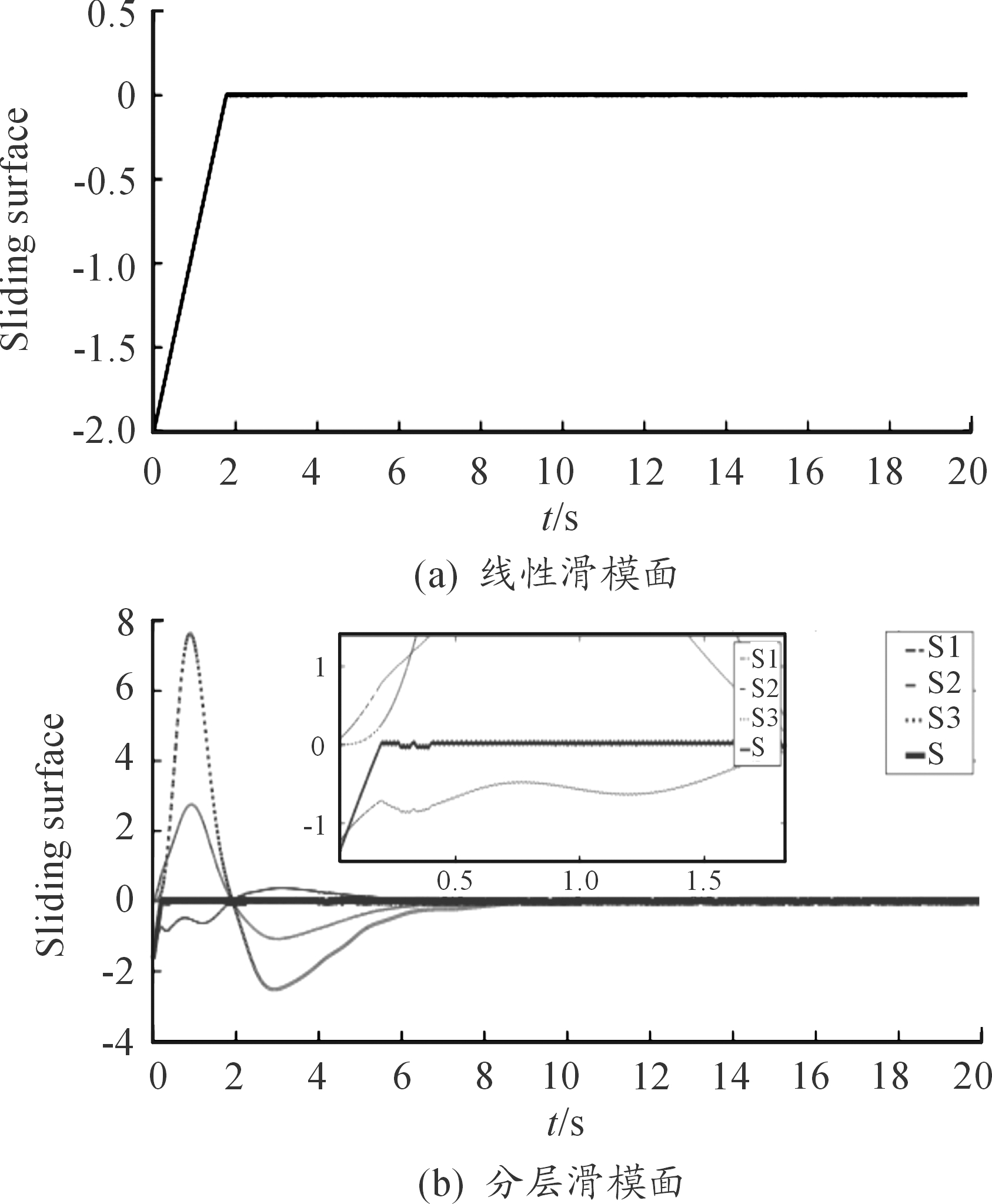
图7 控制器滑模面
对于不同工况条件下负载质量不一,第二级吊绳长度小范围变动的情况,进行仿真分析得到如图8所示,仿真结果表明本文控制方法对不确定系统同样适用,图8(a)、图8(b)仿真结果显示,在吊绳长度变化情况下以及负载质量不一的情况下,台车定位能力与消摆能力稳定且有极强的鲁棒性能。可见本文提出的线性滑模控制方法在不同工况条件下均有良好的适应性。
在大多数工业转运场合中,一级吊绳长度一般为定值,二级吊绳长度会因货物尺寸、外型而会产生较大变化。因此本文仅考虑二级吊绳的长度变化问题。
在系统鲁棒性测试中,对于桥式起重机复杂的工况条件,本文在11~12 s采用高斯噪声对台车运行状态进行干扰,模拟运行中出现的啃轨现象;在15~16 s对负载摆角采用正弦信号模拟短时强风的影响。两种干扰信号定义如下:
(32)
dt2=Bsin(t)
(33)
仿真试验取噪声信号幅值A=1.5,B=1.5,参数ci=11.5,bi=0.3,得到系统动态响应如图9所示。
仿真结果表明,本文线性滑模控制方法在解决欠驱动桥吊系统的防摆控制问题时,在短时间内让系统重回稳定状态,能够快速消除外界干扰和系统不确定性的影响,对外界各种形式的干扰有较强的鲁棒性。

图8 不同工况系统响应

图9 系统鲁棒性测试
5 结论
针对欠驱动桥吊系统的控制问题,分析了现有滑模控制方法存在的高频抖振问题,利用改进趋近规律的滑模控制方法削弱了系统抖振;利用线性滑模完成了欠驱动双摆吊车的消摆控制问题,与分层滑模以及PID控制对比分析,验证了本文控制方法的消摆快速性、系统稳定性以及控制安全性;在鲁棒性分析中通过模拟两种外界干扰信号,验证了系统对外界干扰的鲁棒性。
[1] RAMLI L,MOHAMED Z,ABDULLAHI A M,et al.Control strategies for crane systems:A comprehensive review[J].Mechanical Systems & Signal Processing,2017,95:1-23.
[2] ADELI M,ZARABADIPOUR H,ZARABADI S H,et al.Anti-swing control for a double-pendulum-type overhead crane via parallel distributed fuzzy LQR controller combined with genetic fuzzy rule set selection[C]//IEEE International Conference on Control System,Computing and Engineering.IEEE,2011:306-311.
[3] 杜文正,童国林,强宝民,等.基于模糊自适应PID控制器的桥式起重机定位与防摆控制研究[J].制造业自动化,2012,34(22):14-17.
[4] 张晓华,郭源博.基于嵌套饱和方法的吊车系统非线性控制[J].控制工程,2008,15(2):113-115.
[5] NING S,FANG Y,ZHANG X.Energy coupling output feedback control of 4-DOF underactuated cranes with saturated inputs[J].Automatica,2013,49(5):1318-1325.
[6] MA B,FANG Y,ZHANG X.Adaptive Tracking Control for an Overhead Crane System[J].IFAC Proceedings Volumes,2008,41(2):12194-12199.
[7] NING S,FANG Y,MA B.Motion planning for overhead cranes based on iterative strategy[C]//Control Conference.IEEE,2010:326-331.
[8] LEE L H,HUANG P H,SHIH Y C,et al.Parallel neural network combined with sliding mode control in overhead crane control system[J].Journal of Vibration & Control,2012,20(5):749-760.
[9] 刘金琨,孙富春.滑模变结构控制理论及其算法研究与进展[J].控制理论与应用,2007,24(3):407-418.
[10]康宇,奚宏生,季海波.有限时间快速收敛滑模变结构控制[J].控制理论与应用,2004,21(4):623-626.
[11]徐世许.不确定系统的终端滑模变结构控制[D].上海:复旦大学,2012.
[12]JAAFAR H I,MOHAMED Z,SHAMSUDIN M A,et al.Model re-ference command shaping for vibration control of multi-mode flexible systems with application to a double pendulum overhead crane[J].Mechanical Systems & Signal Processing,2019,115:677-695.
[13]FALLAHA C J,SAAD M,KANAAN H Y,et al.Sliding-Mode Robot Control With Exponential Reaching Law[J].IEEE Transactions on Industrial Electronics,2011,58(2):600-61.
[14]张运喜.有限时间收敛滑模制导律研究[D].天津:南开大学,2013.
[15]刘金琨.滑模变结构控制MATLAB仿真[M].北京:清华大学出版社,2012.