半球形炸药部件由HMX基PBX制成，该炸药部件在使用过程中，存在意外跌落的可能。半球形炸药部件意外跌落的情况下，其安全性，结构完整性，以及防止结构破坏的措施值得关注和研究。国内对于HMX基PBX的力学性能做了很多研究。温茂萍等[1]对等静压与模压HMX基PBX炸药的力学性能进行了比较研究，得到了两种工艺的炸药的力学性能,其中等静压制成的炸药在20℃下的压缩强度为48.23 MPa；颜熹琳等[2]在5 MPa轴向压应力条件下，对HMX基PBX炸药进行了温度循环试验，得到了炸药力学性能的变化规律，为本研究分析跌落过程中的应力提供了一定的依据。
对于炸药部件的安全性方面国内也做了相关研究。王晨、陈朗进行了JO-9159以及PBXCO3炸药的跌落响应数值模拟分析，对这两种炸药的起爆、点火、破碎三种响应情况进行了研究[3]；谢涛等[4]用LS-DYNA对某空空导弹在不同高度和角度条件下跌落进行了仿真分析，得出了导弹的跌落安全性结论。
虽然HMX基PBX安全性较高，其化学反应阈值可达1.4 GPa，点火阈值可达2.5 GPa，但是其结构强度不高，抗冲击能力不强。国内对炸药跌落的研究侧重点大多在安全性，对其结构完整性方面的研究较少。由于跌落试验时间短，危险性较高，试验成本高等原因，利用实物炸药进行跌落实验开展难度较大。本研究基于ANSYS WORKBENCH显示动力学模块，对半球形炸药部件在3种不同方式跌落时炸药部件的应力分布情况进行了仿真研究。通过仿真计算得到了炸药部件跌落条件下的安全性结论，并对炸药部件的结构完整性进行了深入分析，最后对缓冲垫层进行了设计研究。
1 跌落理论
1.1 跌落冲击原理
假设某物体质量为m，从高度为h处做自由落体运动，在不计空气阻力的情况下，根据能量守恒定律
可求得物体在落地前的瞬时速率为
从物体接触地面开始，由于物体受到地面的力的作用，速度开始减少直到0，假设此过程所经历的时间为t。根据动量定理时间t越小，物体受到的平均冲量就越大，因此物体的破坏程度也越大。时间t受物体的刚度(弹性模量、泊松比)的影响，物体的刚度越大t越小。
1.2 显式动力学原理
显示动力学模块Explicit Dynamics主要用于仿真短时间(几毫秒或更少)、非线性结构模型，如碰撞、冲击等[5-6]。在求解时，显示动力学模块通过动量守恒的偏微分方程建立加速度与应力张量之间的联系，其方程如下：
(1)
(2)
(3)
能量守恒方程如下：
(4)
通过输入相应的边界值，这些方程可对模型中的每个元素明确地求解。其中ρ为物体的密度，σ为应力，ε为应变，b为体力，e为能量。
2 建模与仿真
2.1 Solidworks/Ansys workbench 联合仿真平台
在利用ANSYS进行有限元仿真计算时，通常有两种建模途径。一是在相应的绘图软件中建立几何模型，再保存成相应的格式导入ANSYS，但是在导出和导入的过程中，模型的部分信息会丢失，或者出现数据不匹配等情况，给仿真带来不便。二是利用ANSYS自带的建模工具进行建模，但是ANSYS自带的建模工具操作十分复杂，界面十分不友好，对于复杂模型，建模的工作量十分巨大。CAD公司的建模软件Solidworks是一款十分强大的建模软件兼有操作简单、效率高等优点。本研究利用ANSYS的关联工具ANSYS CAD Configuration Manager 对Solidworks与ANSYS WORKBENCH 进行关联，从而可将Solidworks软件中建立的模型直接无缝对接到ANSYS WORKBENCH中，为仿真计算带来了极大的方便。同时，在Solidworks中对模型进行修改后，可直接在ANSYS中进行相应的更新[7]。
利用Solidworks对半球形炸药部件进行三维建模，以大端着地工况为例，其3D结构如图1所示。
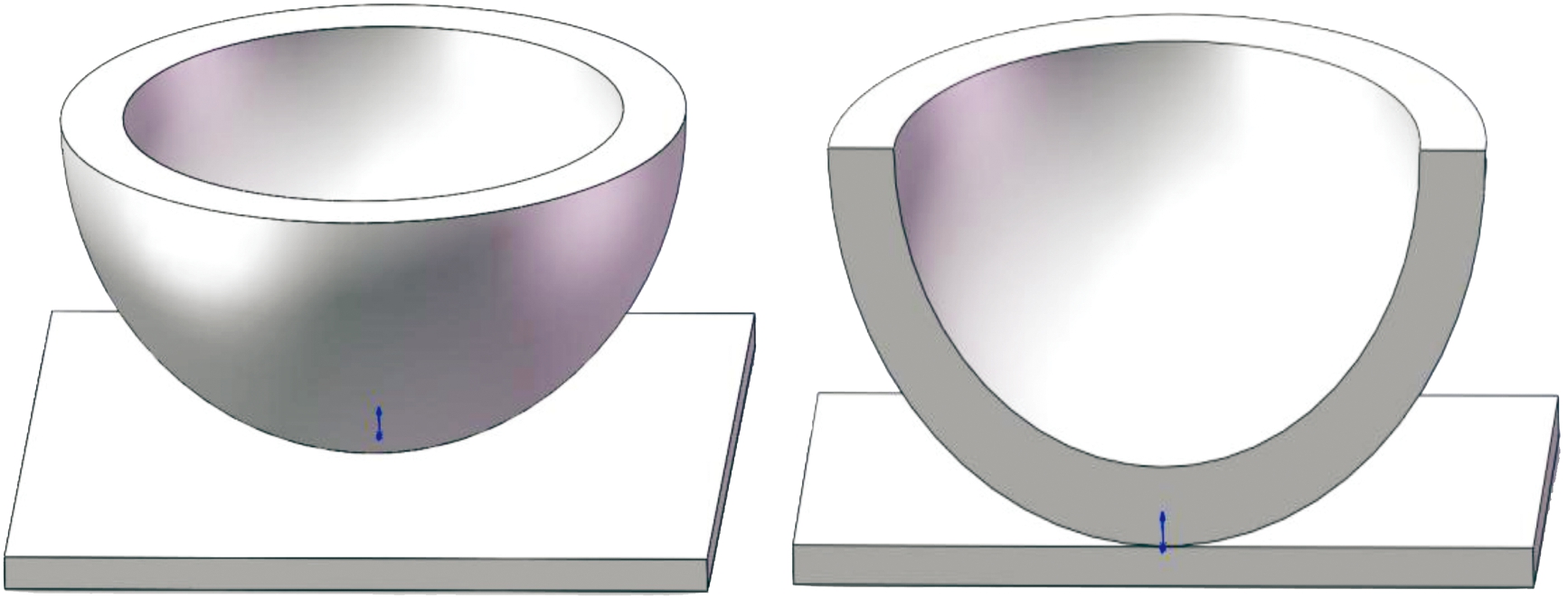
图1 炸药部件三维模型
将SolidWorks中绘制好的模型通过关联直接导入ANSYS workbench界面中。为保证计算精度同时减少计算量，网格单元尺寸选择5 mm，最终共得到 104 100个网格 120 614个节点。网格整体质量系数为0.904 8，网格质量较高，有限元模型如图2所示。由于炸药在不同温度下力学特性变化较大，本研究在温度为20 ℃的条件下进行跌落仿真实验，通过查阅相关资料得到HMX基PBX的材料属性[8]，如表1所示。
图2 炸药部件有限元模型
表1 材料参数
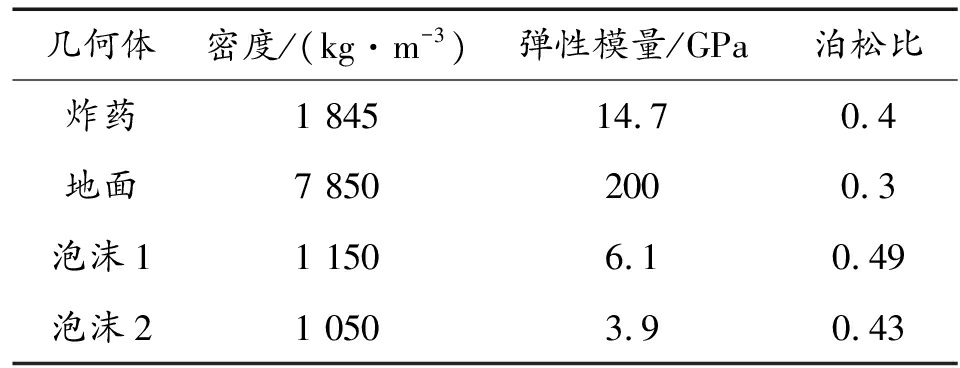
几何体密度/(kg·m-3)弹性模量/GPa泊松比炸药1 84514.70.4地面7 8502000.3泡沫11 1506.10.49泡沫21 0503.90.43
2.2 跌落姿态和边界条件设置
半球形炸药部件在装配过程中，工作台高度约为1 m，故本文以1 m为跌落高度进行仿真。为了减少计算量，直接计算得到炸药部件落地的速度，通过设置初始速的方法等效跌落高度。由于跌落姿态具有不确定性，本文选取最为典型的3种姿态进行仿真分析即炸药部件大端着地跌落、炸药部件小端着地跌落、炸药部件侧面着地跌落。
本文使用Ansys Workbench有限元分析软件中的Explicit Dynamic显示动力学模块进行仿真分析。将高度1 m代入公式计算后得到炸药部件在落地的瞬间速度为4 428.5 mm/s，在Initial Condition中选择velocity，选中炸药实体，并设置数值 4 428.5，设置方向为垂直地面。为保证计算精度，对炸药部件添加标准重力Standard Earth Gravity，加速度取值为9 806.6 mm/s2，方向垂直地面。在计算过程中地面需始终保持不动，故对地面的底面施加Fixed Support约束。在炸药部件侧面着地的情形中，炸药部件与地面之间有相对运动，故需考虑炸药部件与地面之间的滑动摩擦，摩擦因数设置为0.1。在确保炸药部件与地面充分碰撞的同时，为了减少计算量，将计算时间设置为1 ms。
3 炸药安全性分析
炸药部件小端着地时，其应力分布云图如图3所示，应力曲线如图4所示。在这种情况下，炸药与地面碰撞的瞬间接触面积小，故应力集中分布在与地面接触的点周围，并迅速向内扩散。碰撞过程历时约1 ms，最大应力出现在0.4 ms处，最大应力值为280.36 MPa，该应力值仍远小于炸药的爆炸极限应力值，故不会发生爆炸。
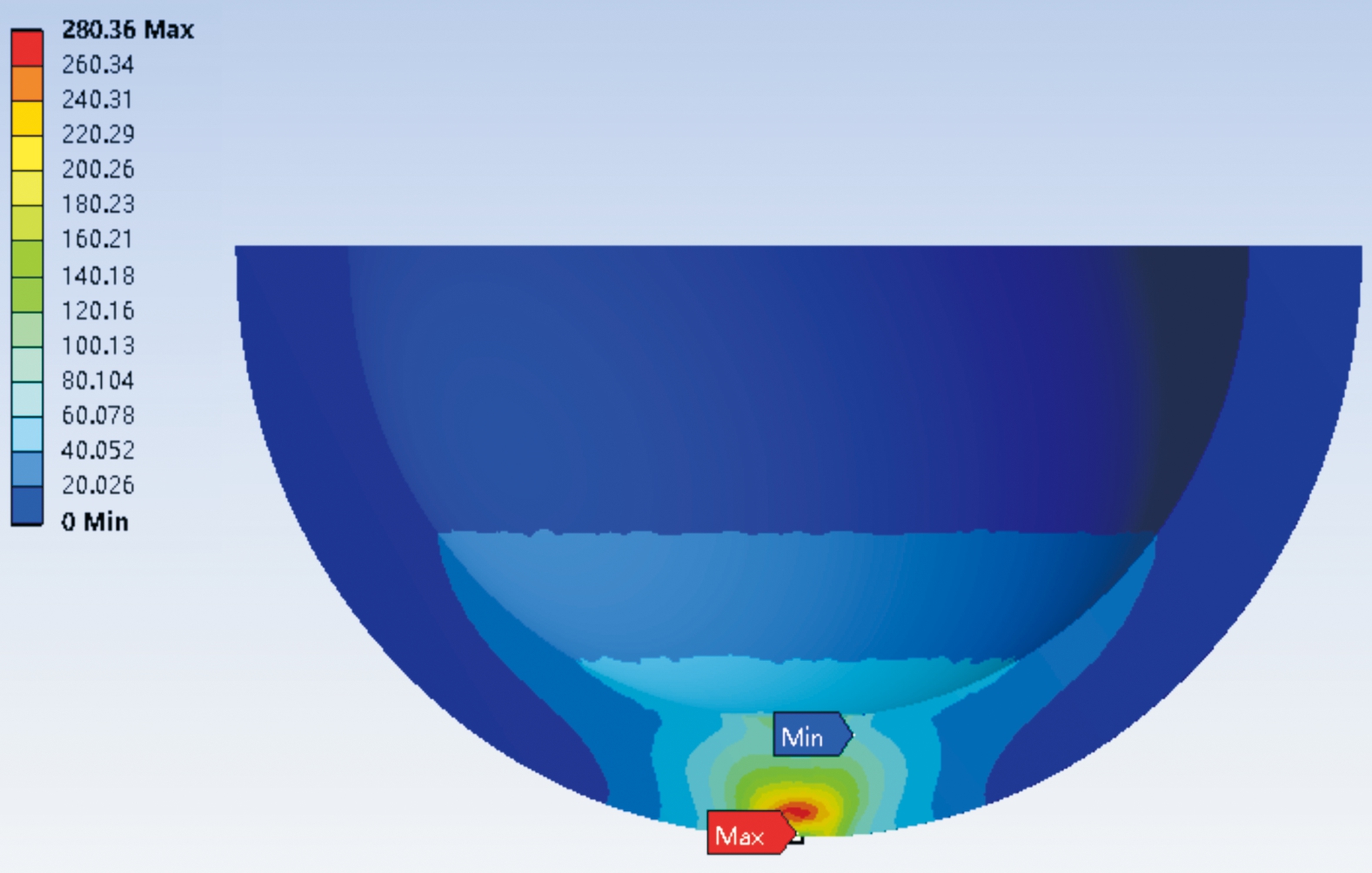
图3 炸药小端着地应力云图
图4 炸药小端着地应力曲线
炸药大端着地时，炸药部件与地面碰撞的瞬间接触面积相对较大，故炸药部件与地面接触的部分应力分布均匀，应力值较小，但是该部分的应力会沿着炸药部件向上传递到炸药上端，在炸药部件小端出现应力集中的情况。在炸药与地面接触之后，炸药部件的动能、弹性势能、内能便开始相互转化，因此炸药部件便会开始振荡，首次应力峰值出现在0.3 ms处，应力为78.647 MPa，第二次峰值出现在0.9 ms处，应力值为83.607 MPa。由此可判断，最大应力值仍远小于炸药的爆炸极限应力值，故不会发生爆炸。应力分布云图如图5所示，应力曲线如图6所示。
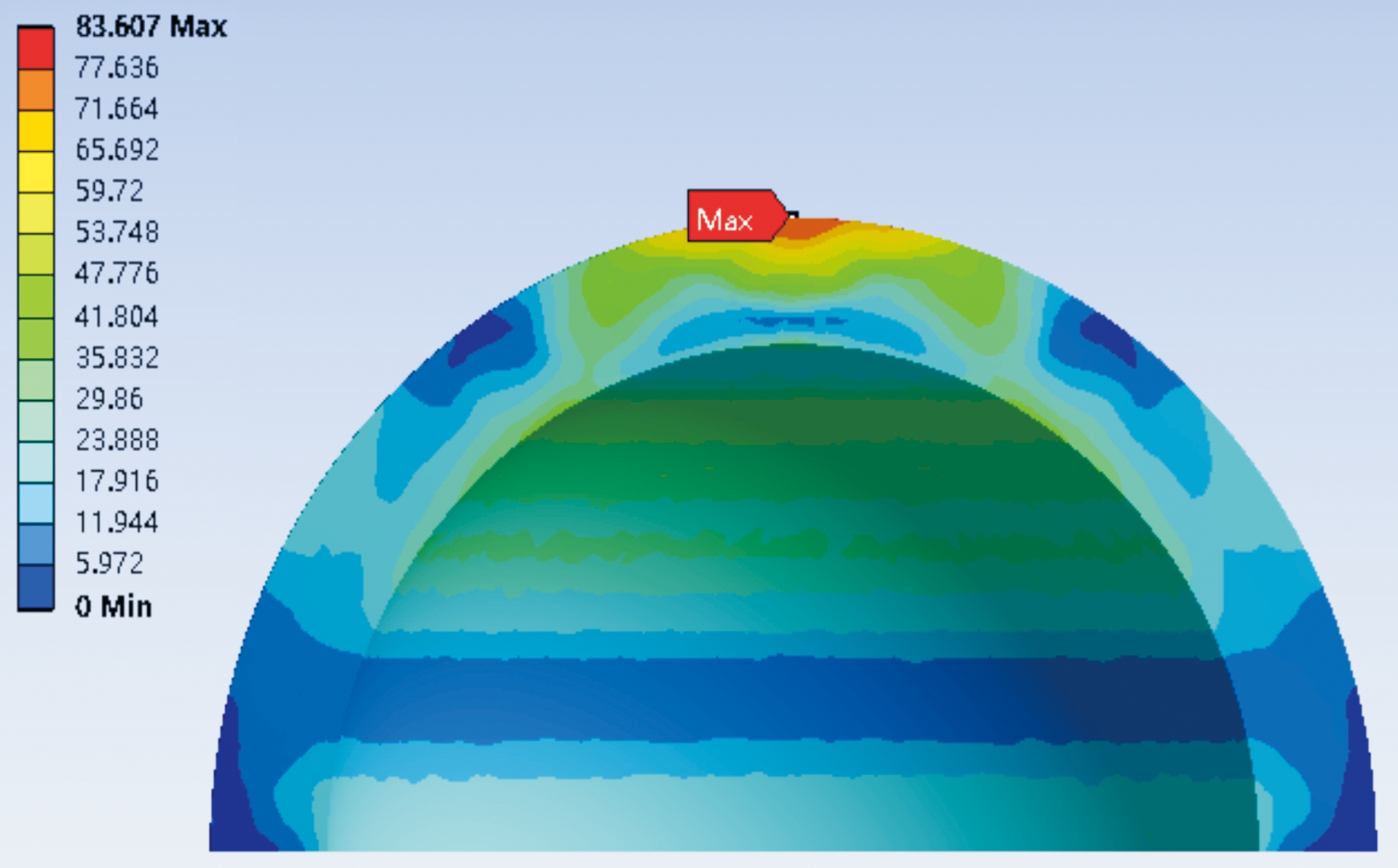
图5 炸药大端着地应力云图
图6 炸药大端着地应力曲线
炸药侧面着地时，其应力分布云图如图7所示，应力曲线如图8所示。在炸药着地0.05 ms内，炸药与地面间未发生相对位移，炸药与地面接触部分应力迅速增加到164.16 MPa。从0.05 ms至0.55 ms，炸药与地面之间开始发生相对滑动，但相对位移较小，炸药侧面应力最大值继续缓慢上升至227.71 MPa。从0.55 ms至1 ms，炸药部件与地面发生明显的相对位移，炸药侧面应力最大值开始迅速上升，最大应力达到337.18 MPa，该最大应力值仍远小于炸药的爆炸极限应力值，故不会发生爆炸。
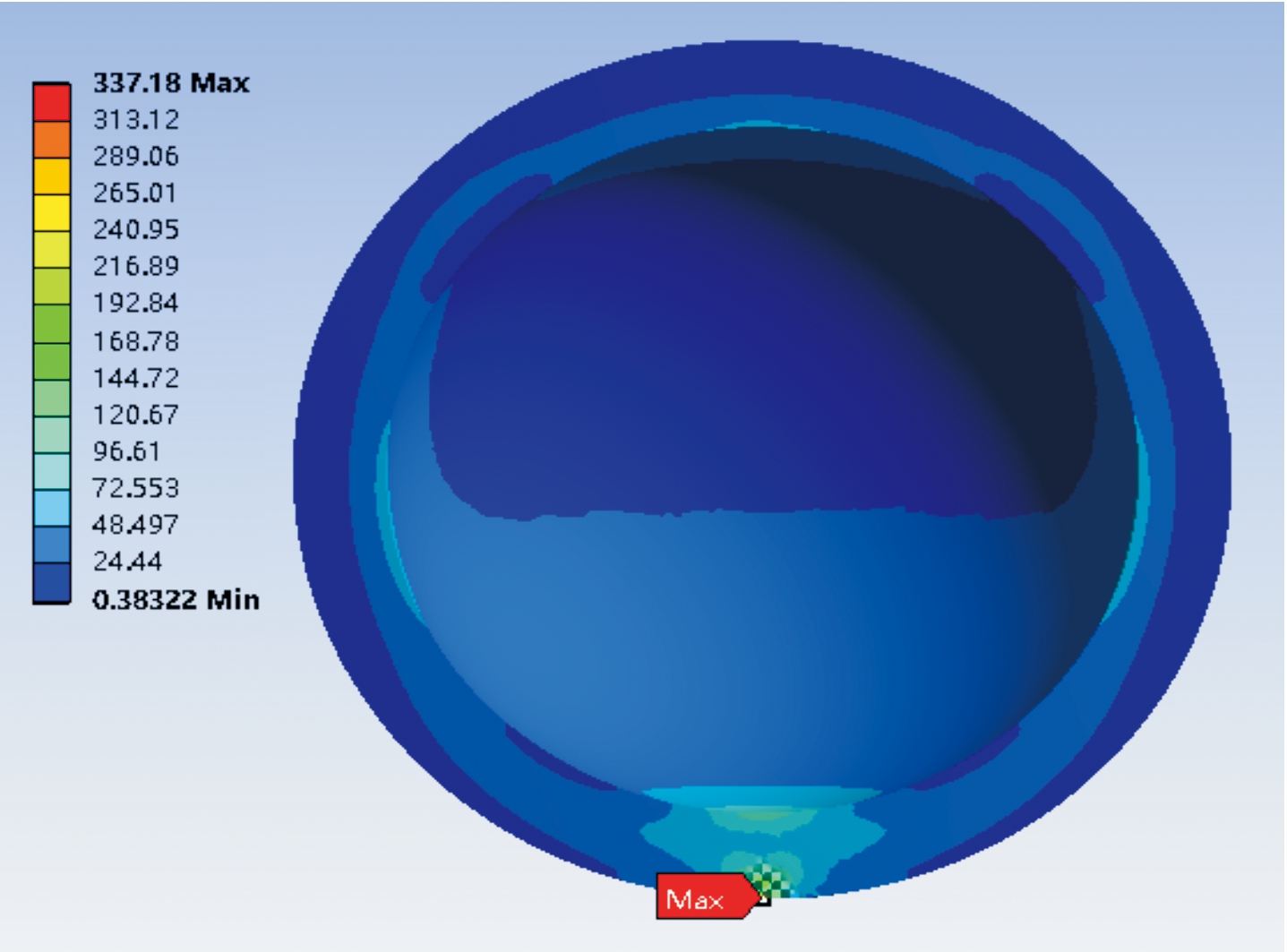
图7 炸药侧面着地应力云图
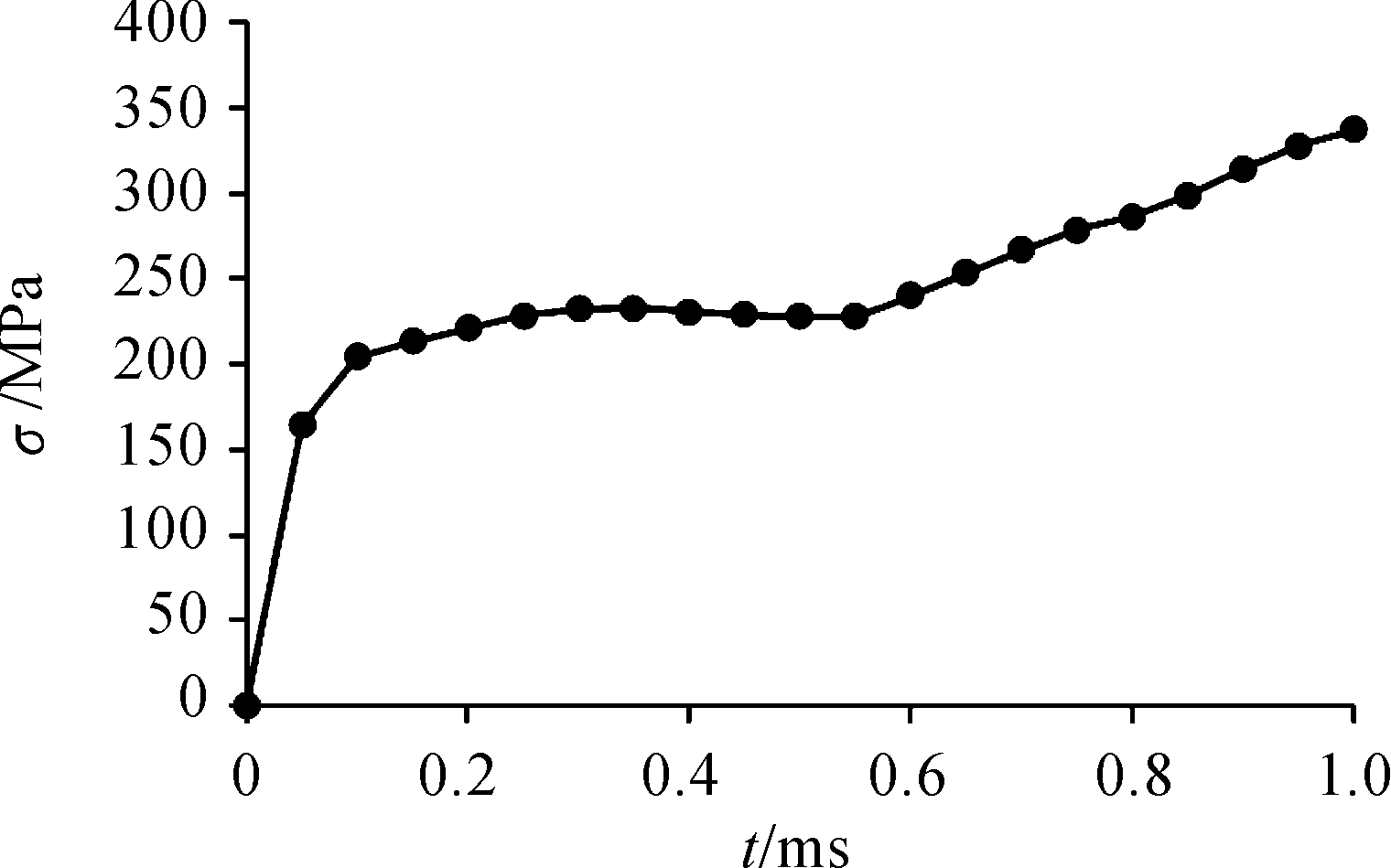
图8 炸药侧面着地应力曲线
4 炸药结构破坏分析
强度准则是判断炸药结构是否破坏的基础。由于炸药材料拉伸和压缩破坏性能有着明显的差异，故材料力学中常用的强度理论如最大拉应力理论、最大伸长应变理论、最大剪切理论等都不能很好地应用于炸药材料。唐维、李明等比较了4种强度准则在高聚物黏性炸药强度分析中的适用性，提出从精度看Mohr-Coulomb准则最优[9]。故本研究采用Mohr-Coulomb准则对该炸药部件的强度进行分析判断。Mohr-Coulomb准则表达式为：
F=τ13βσ13=C
(5)
式中，τij、σij、β的表达式如下：
(6)
其中：σi、σj为主应力；C为屈服极限； σt、σC分别为材料的单轴拉伸强度和单轴压缩强度。通过查阅相关资料可得到σt=6.47 MPa，σC=40.21 MPa，计算得到β=0.161。在唐维、李明等[9]的实验中，得到了在复杂应力条件下，HMX基PBX最先破坏处的三向主应力，并由此可计算得到HMX基PBX的Mohr-Coulomb屈服极限为C=29.0 MPa。因此本文认为，当炸药结构的Mohr-Coulomb应力值大于屈服极限为29.0 MPa时，炸药结构破坏。
在WORKBENCH后处理中选择user defined results,并输入=0.5×(s1-s3)+0.5×0.161×(s1+s3)可输出Mohr-Coulomb准则下的应力曲线及应力云图。3种姿态下Mohr-Coulomb应力曲线如图9。从图9中可以看出，以3种典型姿态从工作台上跌落时，炸药部件的Mohr-Coulomb应力都大于屈服极限，故炸药结构会破坏。
图9 Mohr-Coulomb条件下应力曲线
5 保护垫设计及仿真分析
结合炸药跌落冲击原理可知，当碰撞经历的时间t增大物体受到的平均冲量减少，因此物体的产生的应力也越小。在地面上增加一层缓冲垫层，对增大时间t减少炸药跌落冲击有关键作用[10]。本研究对两种不同软硬程度的泡沫垫层进行了仿真分析，当在地面上增加2 cm厚的常规泡沫垫层(泡沫1)时，仿真结果如图10、图11所示。
图10 2 cm常规泡沫垫层炸药着地应力云图
图11 2 cm常规泡沫垫层炸药着地应力曲线
从结果看出当使用2 cm厚的泡沫做垫层时，大端着地和小端着地时产生的应力值已小于屈服极限，此时跌落不会造成炸药部件结构破坏，但是以侧面着地姿态跌落时仍会产生较大应力值使其结构破坏。当采用4 cm厚更软的泡沫材料(泡沫2)时以侧面着地姿态跌落时产生的应力值小于屈服极限，此时以任意角度跌落炸药部件结构均不会破坏，应力曲线如图12。
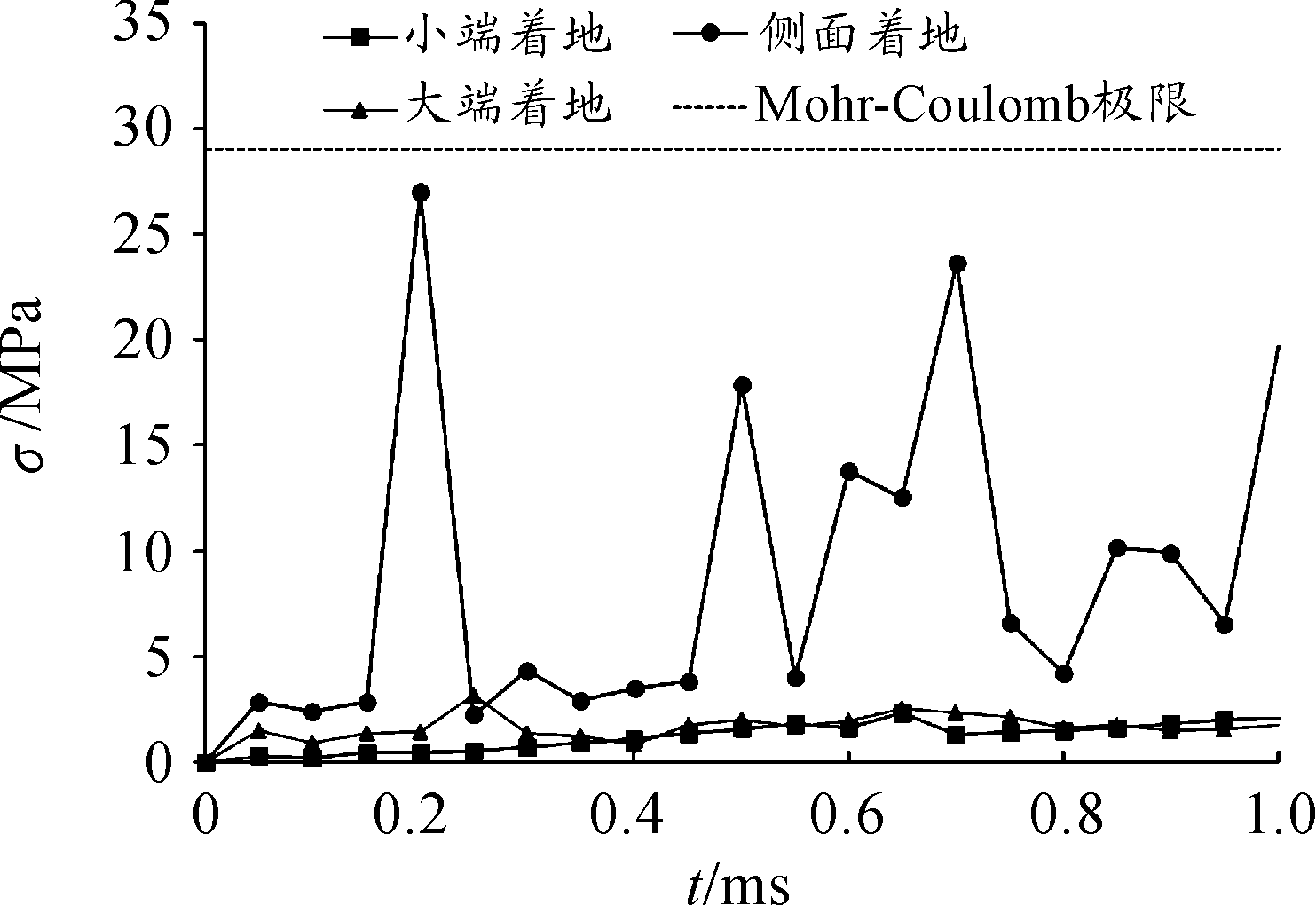
图12 4 cm软质泡沫垫层炸药着地应力曲线
6 结论
该炸药部件从1 m处跌落时，结构会被破坏，功能受损，但仍处于安全范围内，不会发生爆炸。当使用2 cm厚的常规泡沫垫层时，能防止炸药以大端着地和小端着地跌落时炸药结构被破坏，当使用4 cm厚的软质泡沫时，该炸药部件从1 m处以任意角度跌落结构均不会被破坏。
[1] 温茂萍，庞海燕.等静压与模压JOB-9003炸药力学性能比较[J].含能材料，2004，12(6):338-341.
[2] 颜熹琳，周阳.JOB-9003炸药的载荷环境实验[J].2009，32(1):36-39.
[3] 王晨，陈朗.炸药跌落响应数值模拟分析[J].含能材料，2012，19(6):748-753.
[4] 谢涛,吕红超.基于LS-DYNA的导弹战斗部跌落安全性分析[J].兵器装备工程学报，2018，39(8):26-29.
[5] 朱跃峰.基于ABAQUS的显示动力学分析方法研究[J].机械设计与制造，2015(3):107-113.
[6] PAWAR P，BALLAV R，KUMAR A.FEM Analysis of Different Materials Based on Explicit Dynamics ANSYS in Electrochemical Discharge Machine[M].2018.
[7] 唐崛，姬国勋.手机屏幕跌落安全性研究[J].包装工程，2018，39(11)：115-120.
[8] DANIEL D，WILLIAMSON D M.The mechanical response of PBX and binder:Combing results across the strain-rate and frequency domains[J].Journal of Physics D:Applied Physics，2010，43:1-7.
[9] 唐维，李明.四种强度准则在高聚物粘结炸药强度分析中的适应性[J].固体力学学报，2013，34(6):550-555.
[10]高德，卢富德.聚乙烯缓冲材料多自由度跌落包装系统优化设计[J].振动与冲击，2012，31(3):69-72.