锥状壳结构作为一种薄壁承载结构,在航天飞行器 、涡轮发动机、导弹壳体等领域中广泛应用。锥状壳结构内部通常设有敏感的电子元器件,当锥状壳结构周边产生爆炸冲击时,结构产生的径向形变将压缩内部设备的生存空间,目前装备装填系数不断提高,结构径向抗冲击能力的强弱直接关系到内部电子元器件的性能发挥[1],因此研究锥状壳结构径向抗冲击性能具有重要意义。
目前关于壳体抗冲击性能研究领域大多针对圆柱壳,如圆柱形防护壳抗冲击性能模拟[2]、双层壳结构抗冲击性能仿真研究[3]、典型爆炸载荷下柱壳结构的冲击响应和破坏研究[4]等,关于锥状壳抗冲击性能的研究较少。锥状壳同样作为一种被广泛应用的壳单元,研究其在爆炸载荷作用下的冲击响应,有助于深入了解锥状壳结构的失效规律和机理。壳体内部电子元器件的正常性能发挥受到多种因素影响,如温湿度、振动、碰撞等。选取由壳体变形对电子元器件产生的潜在碰撞挤压威胁进行研究,对于爆炸产生的振动、高温等因素暂不考虑。针对在开放空间下受爆炸冲击的锥状壳体,采用AUTODYN数值计算软件,以径向形变、冲击响应峰值为对象,研究内容主要包括径向冲击响应历时特点,径向形变历时特点,锥角与响应峰值及形变之间的相关性。
本研究关于锥状壳体方向,定义锥状壳体上测算点垂直指向轴线的方向为径向,与轴线平行方向为纵向,与径向、纵向构成平面垂直方向为横向。
1 材料参数
炸药属高能可燃材料,引爆后产生大量的高温高压气体。爆炸过程属于10-6 s量级,释放温度可达103 K量级,高压可产生1010 Pa量级的爆轰产物。炸药爆炸产生的冲击波超压是破坏时间最长,破坏区域最广,针对设备和防护设施最具有杀伤力的破坏效应。目前针对爆轰产物的状态方程有较多的成熟方程形式,比如BKW、LJD、JWL等方程,其中JWL方程作为一种常用的炸药爆轰产物状态方程能够精确描述爆轰产物膨胀过程,是典型的动力学状态方程,且不含有化学反应,因此,基本上所有的模拟计算爆炸问题的有限元软件材料库中炸药材料模型均采用了JWL状态方程。
本研究TNT炸药采用HIGH_EXPLOSIVE_BURN本构模型和JWL状态方程,JWL状态方程[6-9]如下:
(1)
式中:p为爆轰产物的压力;![]() 为爆轰产物的比容;E为单位体积炸药内能;A、B、R1、R2、ω表征炸药特性的参数,TNT炸药密度为1 630 kg/m3,爆速为6 930 m/s,压力PCJ为21 GPa, TNT材料参数如表1所示。
为爆轰产物的比容;E为单位体积炸药内能;A、B、R1、R2、ω表征炸药特性的参数,TNT炸药密度为1 630 kg/m3,爆速为6 930 m/s,压力PCJ为21 GPa, TNT材料参数如表1所示。
表1 TNT炸药模型材料参数

参数A/GPaB/GPaR1R2ωV0数值373.83.7474.150.90.351.0
在AUTODYN有限元计算程序中通常将空气假定为理想气体[10-12],理想气体状态方程为:
p=(γ-1)ρae+pshift
(2)
其中:p为气体压力;γ为多方指数;pshift为压力偏移量e为比热力学能;ρa为1.225 mg/cm3;e取为2.068×105。
壳体单元材料选择被广泛应用于飞机构件的2024-T4铝,密度ρ为2 785 kg/m3采用EOS_SHOCK状态方程与Steinberg Guinan本构模型。材料参数如表2所示。
表2 AL2024-T4材料参数

参数G/GPa初始屈服强度/GPa最大屈服强度/GPaC1S1数值28.60.260.765 3281.34
2 有限元建模
利用AUTODYN显式非线性动力学有限元差分软件,对壳模型的冲击响应进行计算。在模型建立过程中,流体材料(空气、炸药)采用欧拉网格,其他结构(壳体)采用拉格朗日网格,三者采用Solid185六面体网格单元。壳模型底部直径D=250 mm;锥顶进行钝化处理,提高顶点单元质量,使计算结果易于收敛。壳厚度d=10 mm;TNT当量W=10 kg;在分析锥角对锥状壳抗冲击性能产生的影响时,采取圆锥角θ=20°、24°、28°、32°、36° 5组角度为计算样本。在前处理过程中,对锥状壳底座进行固定约束,对空气施加Flow-out边界条件,采用测算点加速度描述法,对结构冲击响应值进行描述。有限元模型如图1。

图1 有限元模型
3 参数控制与精确度检验
3.1 比例距离控制和爆心与Gauge点控制
对于高爆炸药爆炸产生的入射冲击波的传播规律主要用冲击波压力、超压峰值、冲量、持续时间等参数来描述[10-11]。比例距离用来表述冲击波的各种参数,比例距离Z定义为:
Z=R/W1/3
(3)
式中:R为测点与爆心之间的距离(m);W为等效TNT药量(kg)。
TNT炸药采用中心起爆方式,通过多组模拟发现,在发生爆炸时,壳体主要变形区域集中在TNT炸药向壳体表面的投影区域,区域内与爆心处于同一水平高度的中心位置附近形变量最明显,如图6所示。因此选择壳体上爆心与锥状壳轴线构成的平面内且与爆心处于同一水平高度的点为Gauge点。在多组角度模拟中,保持Gauge点与爆心距离固定(即同时保持Gauge点与炸药最小距离固定)为634.39 mm,保持冲击因子Z=0.294不变,具体坐标参数如表3所示。
3.2 精确度检验
在有限元模型建立过程中,经过综合考虑计算量与计算精度,有限元模型参数如表4所示。
表3 Gauge点与爆心坐标参数

锥角Gauge点坐标爆心坐标20°(-140.10,-222.14,653.11)(494.29,-222.14,653.11)24°(-143.07,-222.14,653.11)(491.32,-222.14,653.11)28°(-146.48,-222.14,653.11)(487.91,-222.14,653.11)32°(-149.75,-222.14,653.11)(484.64,-222.14,653.11)36°(-152.57,-222.14,653.11)(481.82,-222.14,653.11)
表4 有限元模型参数

模型网格类型单元尺寸/mm单元数量壳体非均匀分布250万左右TNT均匀分布106000空气均匀分布1021万
根据Henrych提出的空气中冲击波的峰值超压(MPa)表达式[13]:
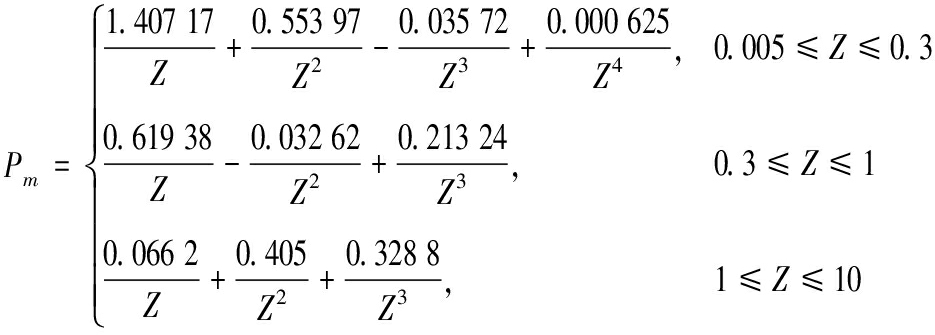
(4)
为了验证计算结果的可靠性,在炸药与空气的有限元模型中等距离选取3个测点,输出压力数据,提取出峰值超压并与Henrych公式的理论值如表5所示。结果显示:数值模拟结果与Henrych公式在0.05~0.3的比例距离内的理论值相近,比例距离越小(即测点与爆心距离减小)误差越大, 文中TNT爆炸产生的冲击波超压在Z=0.294处误差在3.665%以内。
表5 Gauge点冲击波超压

测点比例距离Z模拟超压/MPa理论超压/MPa误差/%Gauge10.289 79.71010.0783.665Gauge20.275 89.98010.8978.416Gauge30.261 910.27011.59711.443
总的来说数值模拟结果与Henrych公式计算结果相符,3.665%的冲击波超压误差在可接受范围内,Henrych公式也是当前被广泛应用的计算TNT爆炸峰值超压的公式。因此本研究采用的炸药参数、空气参数、单元尺寸等计算结果精确度较高。
4 结果分析
4.1 数值分析
4.1.1 Gauge点冲击响应分析
Gauge点5种锥角冲击响应历时曲线如图2,通过对5组曲线的分析可得,冲击响应历时曲线同时存在共性与特性。共性点:测算点加速度响应均为高频响应,冲击响应(加速度)在极短的时间内达到峰值,随后在反方向达到反向最大值;随着时间推移测算点冲击响应(加速度)振荡衰减且收敛至零。特性点:锥角改变,测算点冲击响应峰值随之产生变化;随着锥角变大,测算点在由过载衰减至零过程中的振荡幅度变大。
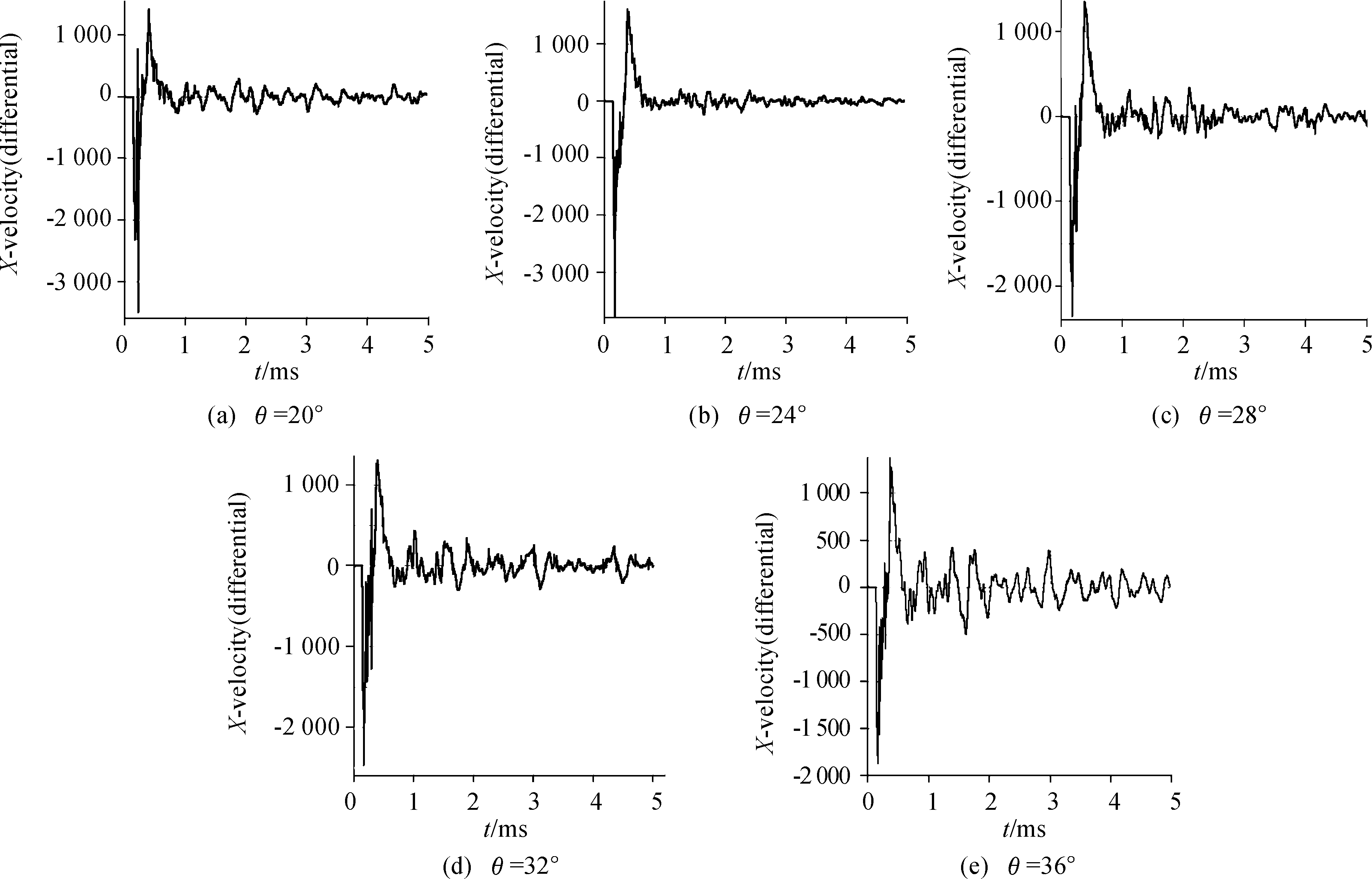
图2 测算点径向加速度历时曲线
4.1.2 Gauge点形变量分析
通过对Gauge点3个方向的形变量进行统计,由表6可知,当炸药位于锥状壳锥面一侧时,Gauge点的横向形变均小于1 mm,纵向形变约占径向形变的1/4到1/3左右,故径向形变是Gauge点的主要形变方向,对于壳体内部空间挤压程度最大。
Gauge点径向形变历时曲线如图3,通过五组曲线的对比分析可知,径向形变历时曲线共性:测算点的径向形变(测点径向位移量)在冲击波影响下瞬时接近峰值,随后在形变量峰值附近产生一定程度的振荡收敛。特性:随着锥角θ的增大,径向形变量逐渐减小;且收敛过程中振荡频率增大。
表6 Gauge点3个方向形变量

Gauge径向形变/mm纵向形变/mm横向形变/mm20°46.37213.4050.85124°43.77712.9570.80128°36.73510.7650.71232°32.49110.5790.59836°26.0329.1050.495
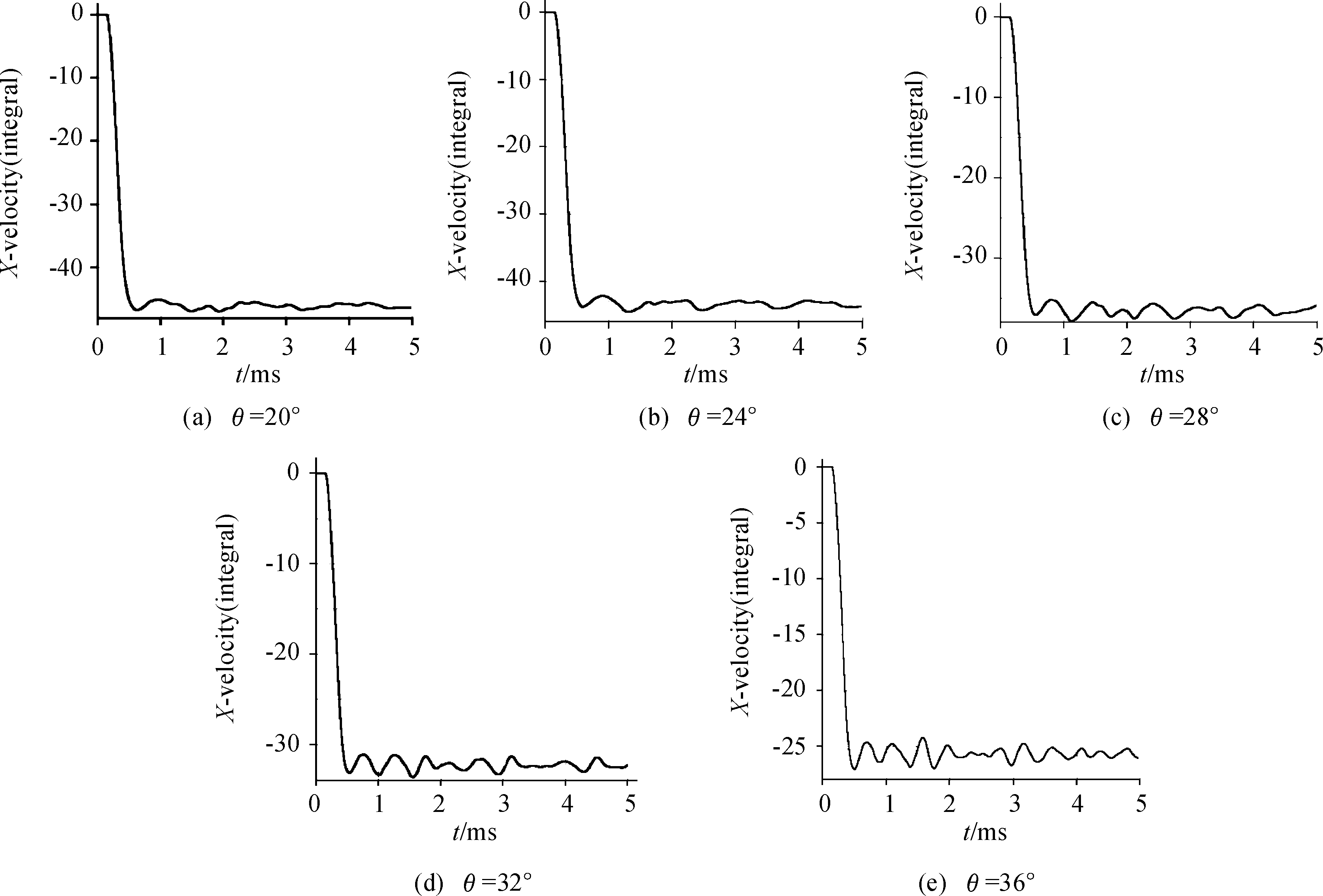
图3 测算点径向位移历时曲线
结果数值如表1所示,可知在5组锥角范围内,保持锥状壳底端尺寸、冲击因子Z等初始和边界条件不变的情况下:Gauge点径向冲击响应达到峰值的时刻随着锥角增大,没有明显的提前或延后的趋势,基本保持在10-4 s量级;Gauge点的径向冲击响应峰值随着锥角的增大,发生了不规则的变化,峰值不存在于5组数据的两端;随着锥角的增大,测算点的径向位移逐步减小。
随着锥角的增加,径向冲击响应峰值近在锥角24°附近达到最大值;随着锥角增大,Gauge点径向位移逐渐减小。锥角24°样本冲击响应峰值比20°样本大,但径向位移比之小。32°样本情况与24°样本情况相同。由此推断径向冲击响应峰值与径向位移不构成线性关系。
通过对Gauge点径向形变量与锥角进行线性拟合,获得回归直线方程:y=-1.317 2x+74.034,回归平方和R2=0.987,回归直线拟合优度较高,初步分析Gauge点径向形变量与锥角构成线性关系。
4.2 毁伤机理分析
以20°锥角情况为例,TNT炸药爆炸时产生的冲击波以球形向外传播,在约0.15 ms时传播到锥状壳体表面,传播过程如图4所示,冲击波到达壳体表面时,壳体未立即发生明显变形,结合图2和表7可知,在0.15~0.196 ms时间段,受冲击波影响,Gauge点冲击响应达到峰值,随后冲击响应在反方向达到峰值。0.15~0.196 ms时间段在自由空气中理想P-T曲线图5中,即Ta-Tc阶段。冲击波波阵面通过后超压值迅速下降,经过时间Td,超压指数衰减至0并继续下降直至出现负超压峰值,又在一定时间内回升至0。在负压阶段Gauge点径向冲击响应由达到反方向最大值。负压阶段结束,超压归零后,Gauge点径向冲击响应振荡衰减收敛至0[14]。
表7 计算结果数值统计
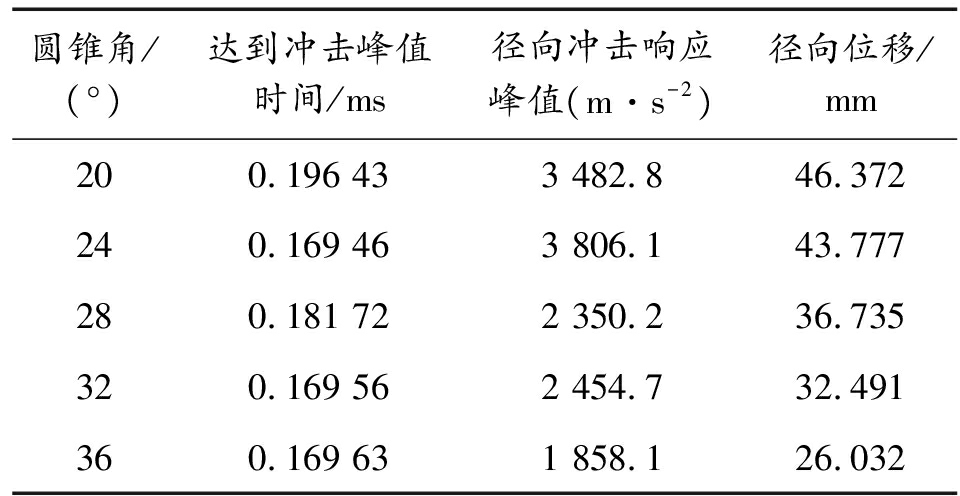
圆锥角/(°)达到冲击峰值时间/ms径向冲击响应峰值(m·s-2)径向位移/mm200.196 433 482.846.372240.169 463 806.143.777280.181 722 350.236.735320.169 562 454.732.491360.169 631 858.126.032

图4 冲击波传播过程云图
壳体受冲击波作用达到形变峰值。根据超压-冲量准则,锥状壳体结构受到破坏是由超压和冲量共同决定的。即结构受到的超压和冲量均超过了引起结构破坏的临界值,从而导致锥状壳产生径向塑性变形。
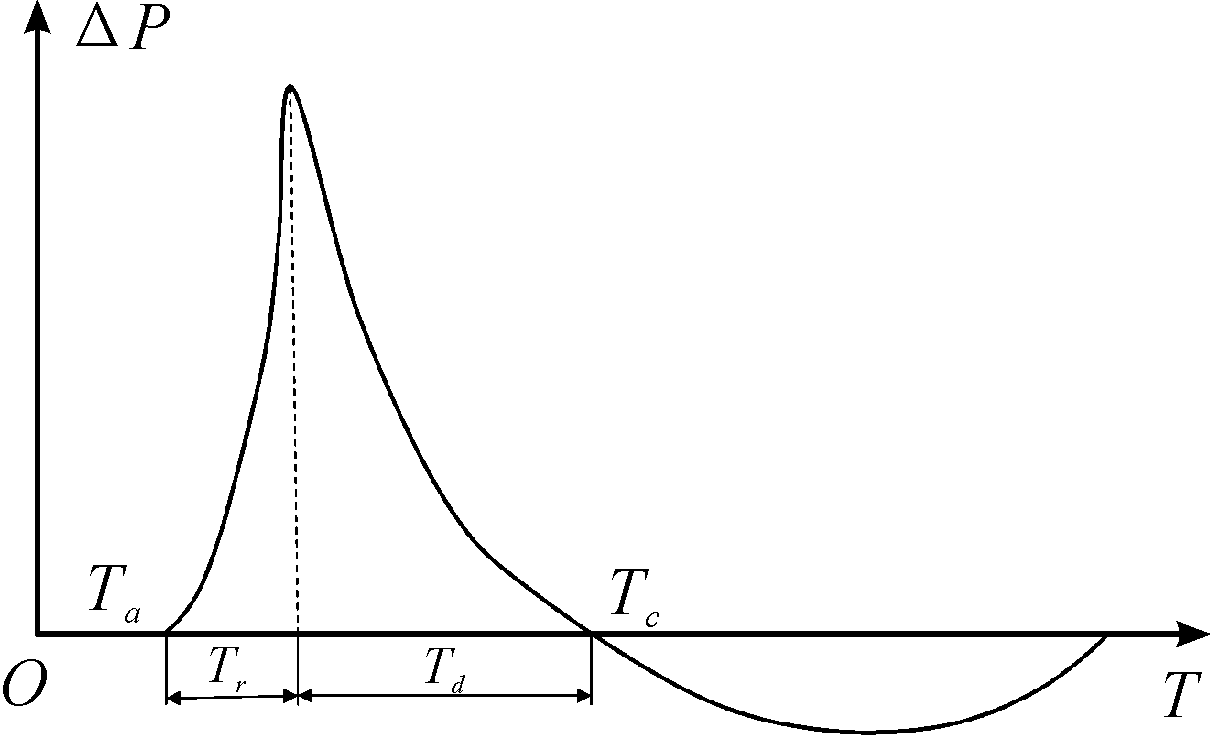
图5 自由空气中理想P-t曲线
图6为锥角20°时壳体形变云图,锥状壳靠近炸药一侧产生了较大的塑性变形,结构表面出现了明显凹陷,凹陷区域与TNT炸药向壳体表面投影区域大致相当,锥壳顶端以及背对TNT炸药一侧结构完整,没有产生明显的变形。Gauge点附近挠度最大,随着与Gauge点距离的增大,挠度逐渐减小。
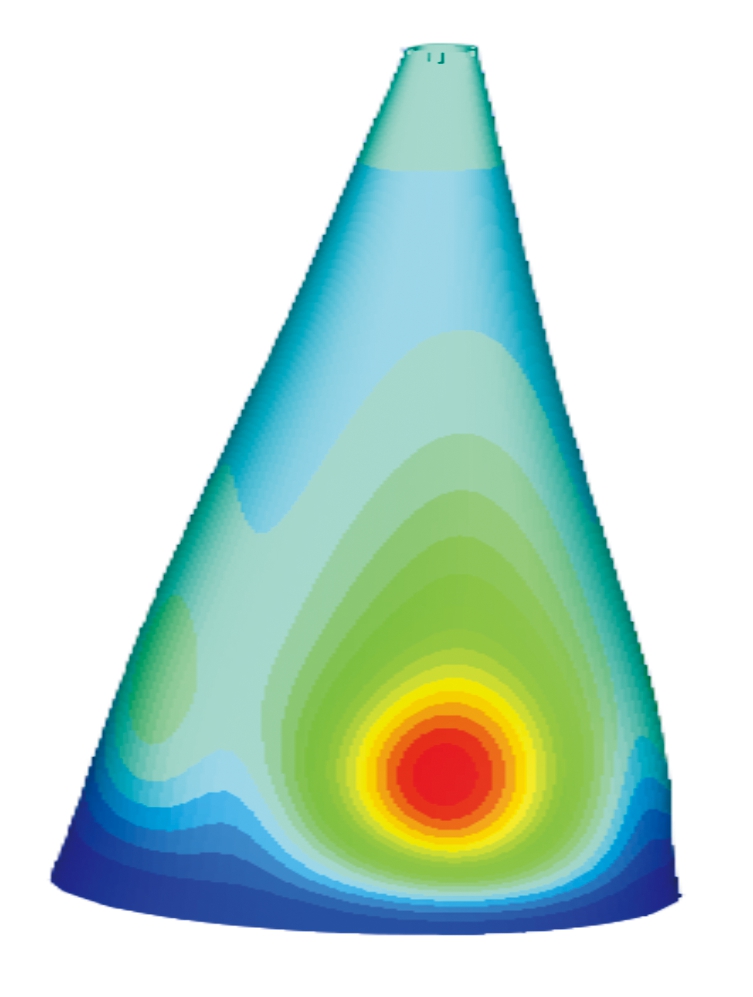
图6 结构径向形变云图
根据屈服准则,由于壳体受冲击波作用强度超过屈服强度,壳体发生塑性变形成对称状凹陷,凹陷区域内处在爆心与轴线平面两侧的对称点比例距离相同,结构对称,故凹陷处以爆心和轴线构成的平面为对称面。
锥状壳体Gauge点径向加速度积分获得径向速度,再次在时间上积分产生径向形变对于不同锥角的情况下,Gauge点受到的冲击波超压在径向的分量不同,随着锥角增大,冲击波超压在Gauge点径向分量减小,同时根据塑性失效准则,只有当壳壁整个厚度范围全部屈服时,壳体才能塑性失效,随着锥角的增大,导致Gauge点壳厚沿径向方向分量增大,从而在比例距离Z相同的情况下,Gauge点径向形变量随着角度增大而减小。
4 结论
1) 锥状壳在受到爆炸冲击时,主要受损伤部位与炸药位置、冲击因子等因素有关,冲击波作用时间在ms量级,测算点的加速度响应为高频响应,响应达到峰值后迅速衰减,衰减收敛过程中伴随剧烈振荡;径向位移收敛过程中同样存在一定程度振荡。
2) 冲击因子Z不变的情况下,随着锥角增大,测算点的径向冲击响应(加速度)峰值变化不规则。测算点径向加速度衰减收敛过程中,振荡幅度随着锥角的增大而增大。
3) 冲击因子Z不变的情况下,随着锥角逐渐增大,测算点的径向形变量逐渐减小,回归直线拟合优度较高;径向形变量收敛过程中,振荡频率随着锥角的增大而增大。
4) 在壳体受到爆炸冲击波作用过程中,受正超压作用超过屈服强度产生了塑性形变,正超压结束后,受负超压作用使塑性形变过程趋向结束,塑性形变量趋于稳定。
5)由于锥状壳体结构面对TNT爆炸冲击时与冲击波构成一定角度,通过改变壳厚改变沿径向分量,径向形变量也随之改变。
6)AUTODYN模拟空气中炸药爆炸问题时,距离爆心越近误差越大,通过控制比例距离,可以减少误差。
[1] 丁沛,刘文会,王佳南.航天电子设备在冲击环境下的失效问题研究[J].山西建筑,2019,45(5):40-41.
[2] 郭学敏,朱平.测试设备圆柱形防护壳体抗冲击性能的模拟和评估[J].兵器装备工程学报,2019,40(3):34-38.
[3] 姚熊亮,梁德利,许维军.双层壳结构抗冲击性能仿真研究[J].哈尔滨工程大学学报,2004,25(3):267-271.
[4] 范书群.典型爆炸载荷下柱壳结构的冲击响应和破坏研究[D].合肥:中国科学技术大学,2007.
[5] 孙承纬.应用爆轰物理[M].北京:国防工业出版社,2000.
[6] 陈华,周海兵,刘国昭,等.圆筒试验JWL状态方程参数的贝叶斯标定[J].爆炸与冲击,2017,37(4):585-590.
[7] 沈飞,王辉,袁建飞.一种确定JWL状态方程参数的简易算法[J].振动与冲击,2014,33(9):107-110.
[8] 贾则,陈高杰,高浩鹏,等.水下爆炸冲击波和气泡脉动载荷联合作用下舰船冲击响应研究[J].中国测试,2018,44(12):28-32.
[9] SHIN Y S.Ship shock modeling and simulation for far-field underwater explosion[J].Computers and Structures,2004,82(23/26):2211-2219.
[10]孔祥韶.爆炸载荷及复合多层防护结构响应特性研究[D].武汉:武汉理工大学,2013.
[11]华雨,于纪言,张庆,等.静爆冲击波在空气中的传播规律[J].兵器装备工程学报,2016,37(7):168-172.
[12]周杰,陶钢,潘保青.AUTO-DYN模拟炸药爆炸问题的分析[J].火炸药学报,2012,35(5):33-37.
[13]HENRYCH J.The dynamic of explosion and its use[M].Beijing:Science Press,1987.
[14]WU C,HAO H.Modeling of simultaneous ground shock and air blast pressure on nearby structures from surface explosions[J].Int J Impact Eng.,2005,31(6):699-717.