电磁发射是一项能够运用电磁力将负载加速至超高速的技术。它能够突破传统火药发射2 km/s的速度极限,通过控制激励脉冲电流从而实现速度的精确控制,是一项具有巨大潜力的发射技术[1-2]。四轨电磁发射器[3-5]是一种特殊的增强型电磁轨道发射装置,其四根轨道周向阵列使得轨道中心电枢位置产生的磁场相互抵消,为防止强电磁干扰实现精密仪器的电磁屏蔽提供了有效思路,促进了电磁发射技术在大载荷大口径导弹上的应用。
在四轨电磁发射器的设计中,电感梯度是一个重要的参数[2,5],它直接影响电枢的推进电磁力大小,关系到负载的出口速度大小,制约了整个发射器结构参数的设定,关系到发射效率。国内外学者对此进行了大量研究,对简单方形双轨发射器的电感梯度进行分析并提出了电感梯度的计算公式[5-7],但仍均具有或多或少的局限性。Grover提出了低频下矩形导轨电感梯度的计算公式[6];Kerrisk提出了高频电感梯度的计算公式[7];文献[8]对电感梯度进行了实验测量,但简化了实验模型。以上公式针对增强型多轨电磁轨道发射器并不适用,国内相关学者则对增强型电磁轨道炮进行了电感梯度的影响因素分析:武汉大学刘守豹[9]针对增强型轨道炮建立了二维电感梯度计算模型,分析了轨道尺寸对电感梯度的影响;中国科学院孙立强[10]分析了时电流频率对电感梯度的影响,表明实际发射过程中电流频率减小而导轨电感梯度增大;文献[11]中提出了计算电感梯度时有必要考虑电枢的影响。为了推进四轨电磁发射器的应用,本文通过三维有限元仿真准确地计算四轨发射器的电感梯度,分析电枢的位置、电流频率和轨道高度、厚度对电感梯度的影响。
1 电感梯度的计算方法
1.1 理论公式计算
简单方形导轨如图1所示,其电感梯度的公式国外研究专家已有归纳,文献[7]中所述是较为著名的Kerrisk L′,即为针对高频电流驱动下的电感梯度计算公式为:
L′=[A+BIn(F1)]In(F2)
(1)
式(1)中,
F1=1+A1(w/h)+A2(w/h)(s/h)
F2=B1+B2(s/h)+B3(w/h)+B4(w/h)(s/h)
其中,h为导轨高度,w为导轨厚度,s为导轨间距,Ai,Bi为常数。
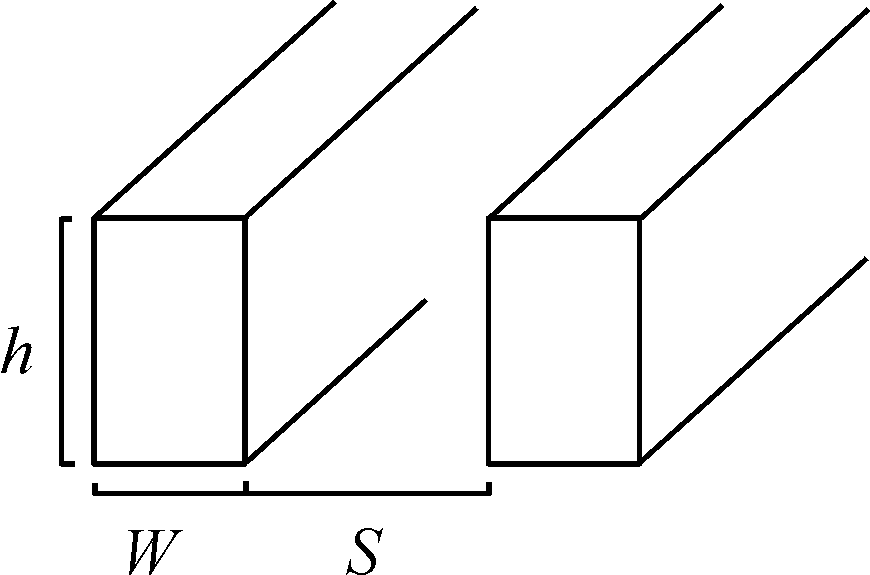
图1 导轨结构示意图
文献[8]中Grover所述针对低频电流驱动下的电感梯度的计算公式为:
L′=0.4[In((s+w)/(h+w))+1.5+Ink]
(2)
式(2)中:h为导轨高度;w为导轨厚度;s为导轨间距;Ink的值随着s/h和w/h的值变化,可通过查表获得。
对于具有多轨道的增强型电磁轨道发射器,整体电感由轨道的自感和轨道之间的互感两部分构成,针对四轨电磁发射装置,每根轨道均为主轨,需要考虑每两根轨道之间的互感,在不考虑电枢的情况下,其电感梯度计算公式可表示为:
L′=d(L+M)/dl
(3)
式(3)中,
L=L11+L22+L33+L44
M=2(M12+M13+M14+M23+M24+M34)
其中: Lii为第i根轨道的自感; Mij为第i根轨道和第j根轨道的互感,l为轨道长度。
1.2 仿真计算方法
有限元仿真软件Ansys Electronics中电磁场计算模型基于麦克斯韦方程组,可以方便计算复杂的多轨电磁轨道发射器的电感梯度。在此介绍两种计算方法:一是节点阻抗矩阵;二是从能量角度的虚功原理[12]。
以二阶节点阻抗矩阵的表达式为例,有:
![]()
(4)
在有限元软件中可以直接计算出轨道R和L的值,然后通过式(3)即可得出电感梯度值,但此方法适用于不考虑电枢的情况。
由虚功原理,假设电枢在电磁力作用下沿轨道轴向移动了dx,根据能量守恒可得关系式为:
dWi=dWh+dWo+dWa
(5)
式(5)中:dWk=Fdx,F=L′I2/2;Wi为输入发射器的总能量;Wh为磁场能量的增量;Wo为磁场外流失的能量(包含热效应等);Wa为传递给电枢的能量;F为电枢受到的电磁力;L′为发射器总电感梯度;I为通入的电流大小。由于dx非常小,近乎瞬时过程中可将输出的总能量视为全部作用于推动电枢做功,即公式简化为:
L′=2dWi/(I2dx)
(6)
由此可以计算,考虑电枢存在情况下瞬时的电感梯度,也可以计算理想情况下电枢移动一段距离的平均电感梯度。
2 仿真模型及仿真条件设定
四轨电磁发射器简易三维模型如图2所示,相邻的轨道通入电流方向相反,相对的轨道通入电流方向相同。相对轨道在电枢中心位置产生的磁场方向相反,起到了磁场屏蔽的作用。根据相关导弹武器发射口径需求以及轨道结构强度所需,本文中Solidworks三维建模数据为:轨道口径固定为800 mm×800 mm,轨道高度为200 mm,轨道厚度为100 mm,电枢轴向长度为400 mm,喉部厚度为150 mm。建模完成后导入Ansys Electronics,通过涡流求解器进行求解,设定铝电枢电导率为3.8×107 s/m,铜导轨电导率为5.8×107 s/m,进行计算的真空区域应能够准确计算而且节约计算时间,设定为500%,激励正弦电流幅值为1 MA,频率为1 kHz;考虑电流趋肤效应和临近效应,并采用趋肤网格进行划分,收敛时网格数量大约为24万。
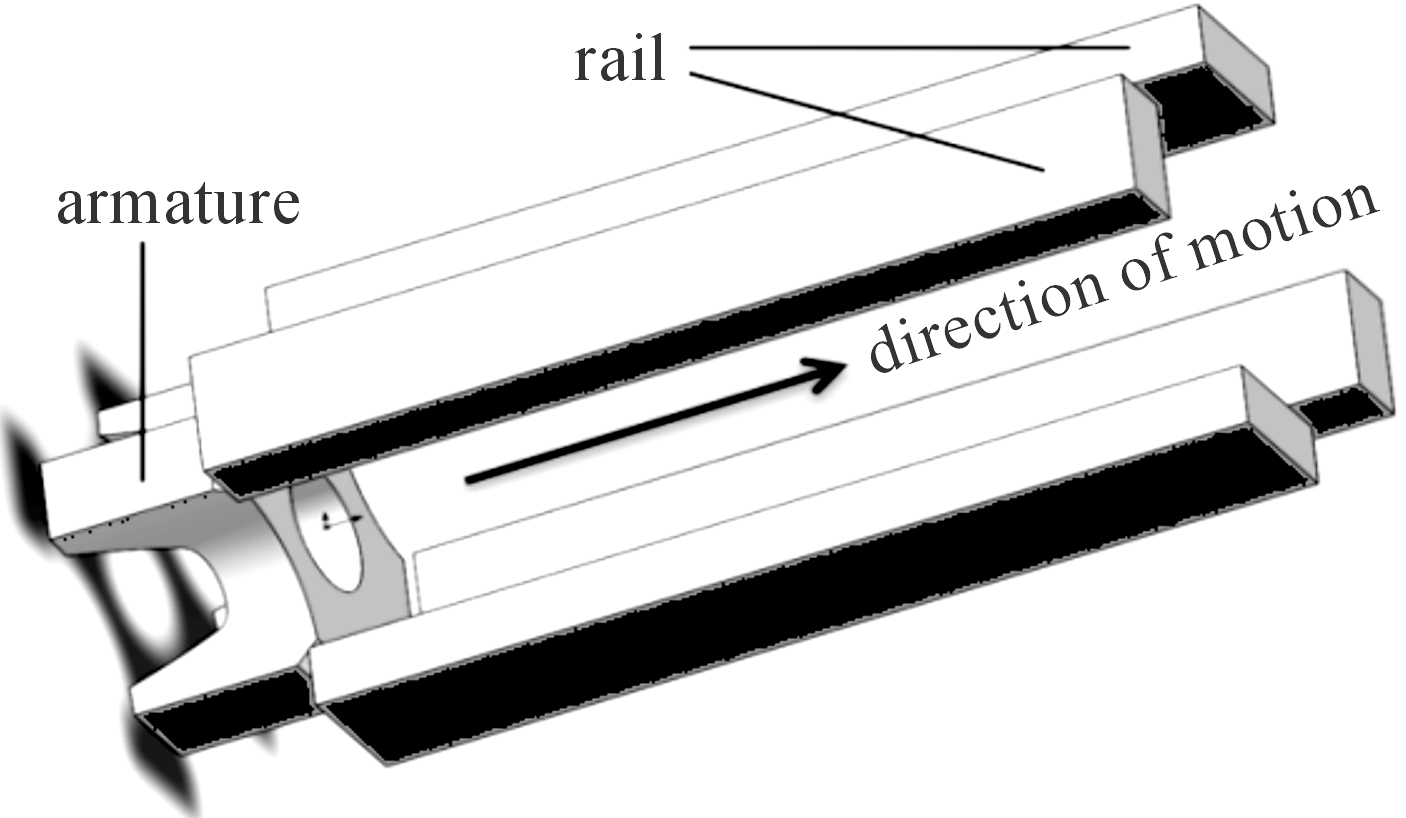
图2 四轨电磁发射器模型
3 电感梯度影响因素分析
3.1 电枢的有无及位置
在实际电磁发射中电流流经电枢形成闭合回路,尽管电枢长度相比于轨道长度很小,但由于趋肤和临近效应,在电枢和轨道接触面会产生较大的电流密度,而且电枢中电流也会影响整个回路的电感梯度,因此仿真将考虑有无电枢以及电枢在导轨中的位置对电感梯度的影响,位置定为电枢距导轨尾部1 000 mm、2 000 mm、3 000 mm、4 000 mm、5 000 mm 5个不同位置,如图3所示。
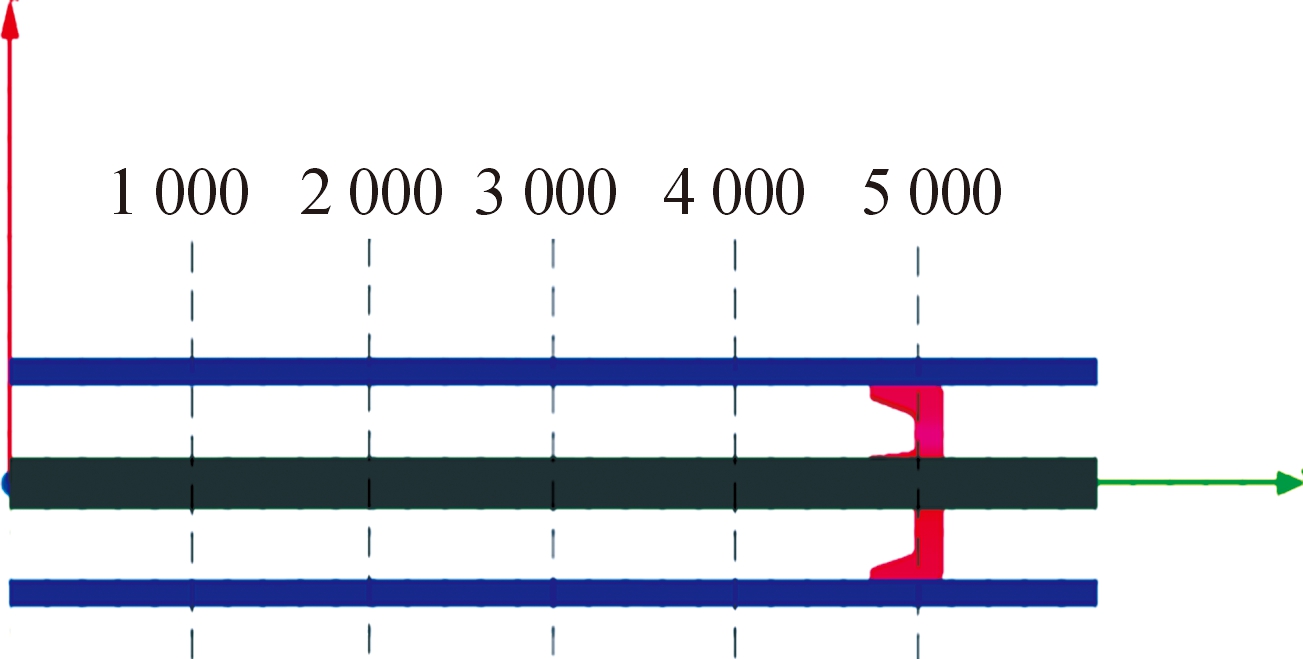
图3 电枢与导轨尾部距离
考虑无电枢情况,采用节点阻抗矩阵的方法进行计算,仿真结果如式(7)。矩阵中每个元素逗号前为阻抗,单位为Ω,后为感抗,单位为μH。每根轨道的自感系数大约5.10 μH/m,相邻轨道互感系数大约-2.67 μH/m,相对轨道互感系数大约2.28 μH/m,通过式(3)求得无电枢情况电感梯度为1.359 9 μH/m。
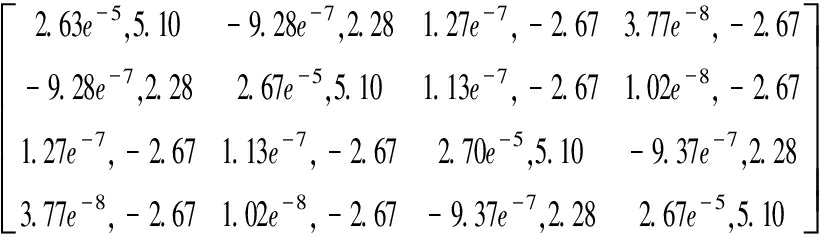
(7)
考虑有电枢情况,通过仿真计算电枢在5个位置处的能量总值,通过各个位置与零位置(能量为零)进行比较,根据式(6)计算电枢在后5个位置时轨道的平均电感梯度值,记录结果并计算如表1所示。
表1 电枢不同位置处电感梯度

电枢位置/mm1 0002 0003 0004 0005 000能量/106 J0.364 60.706 71.047 71.387 01.733 7电感梯度/(μH·m-1)1.458 41.413 41.396 91.387 01.386 9
通过表2可了解到,电枢越靠近轨道尾部,电感梯度越大,表明在较短的导电路径中,电枢对整体电感梯度的影响较大;当电枢离轨道尾部越远,电感梯度随之减小,并且减小幅度越来越小,此时电枢中电流对整体磁场影响已经很小,电感梯度值趋近于1.387 μH/m。相比无电枢电感梯度计算值,仍然增大了0.027 1 μH/m,占比约2%,为了更精确的计算电感梯度,从而设计满足要求的电磁发射器结构,有必要将电枢考虑进去,并取值于电枢在导轨中部时的电感梯度值,以下仿真均基于电枢在导轨中部3 000 mm处的模型。
3.2 电流频率
根据趋肤效应公式[13],电流频率越高,趋肤深度越小。电流集中在导体表面,导致实际电流路径发生变化从而影响电感梯度,此解释在小口径电磁轨道发射器上能较好体现。从微观理论上分析[14],磁性材料里的小磁畴随电流交变的频率不断变换极性,当频率升高以后,它跟不上电流的快速变化,体现出铜合金的逆磁性,磁导率下降,空间磁场能量降低,因而电感梯度下降。本文选取了5个不同电流频率对电感梯度进行仿真分析,记录如表2所示。
表2 不同电流频率对电感梯度影响

电流频率/Hz1005001 0002 0005 000能量/106 J1.058 71.058 01.057 51.056 61.056 3电感梯度/(μH·m-1)1.411 61.410 71.396 91.408 81.408 4
电流频率在实际发射过程中会因为脉冲电流波形的变化而变化,根据文献[10]中实验记录,发射过程中电流频率从1 000 Hz下降到100 Hz,在此过程中电感梯度呈上升趋势。在本文从100 Hz到5 000 Hz的仿真中,电感梯度下降0.23%,可见,在四轨电磁发射器中,频率对电感梯度的影响并不明显。在仿真中将材料磁导率设定为恒定值,改变电流频率主要影响了电流的趋肤深度,如图4所示。100 Hz时电流趋肤深度约为6.6 mm,1 000 Hz时约为2 mm,由于四轨发射器口径较大,而且轨道横截面积较大,导电路径的变化对电感梯度的影响不明显。
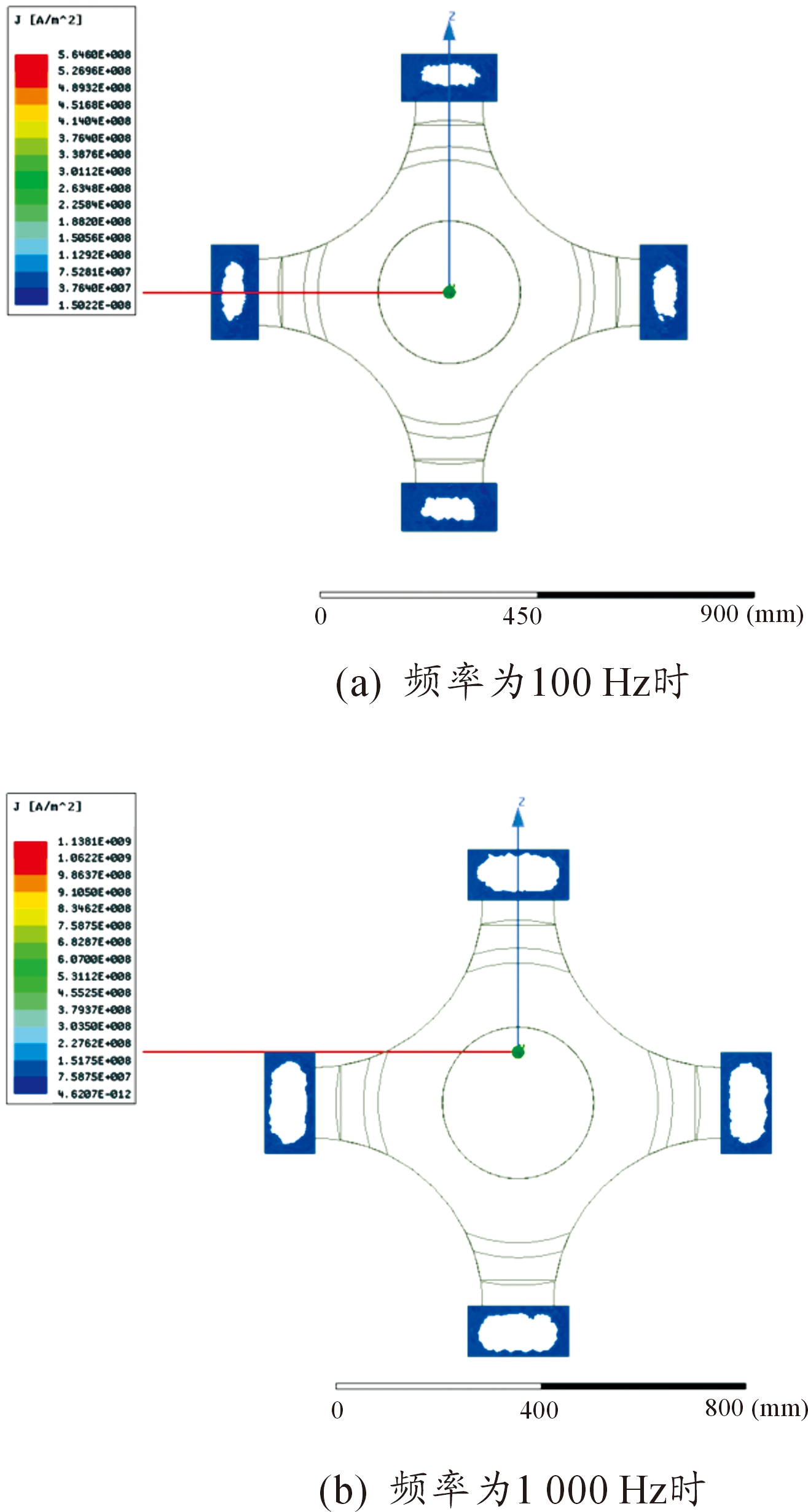
图4 同频率下电流趋肤深度
3.3 导轨高度和厚度
导轨的结构参数受到机械强度、导流能力等条件的制约,是设计电磁轨道发射器的关键,有必要分析导轨的结构参数对电感梯度的影响,从而设计出更为合理的结构。针对某一固定口径的负载,通过控制变量分别分析轨道高度和厚度对电感梯度的影响,仿真结果记录如表3、表4所示。
表3 不同轨道高度对电感梯度影响

轨道高度/mm160180200220240能量/106 J1.133 21.087 51.047 71.009 10.974 9电感梯度/(μH·m-1)1.510 91.450 01.396 91.345 51.299 9
表4 不同轨道厚度对电感梯度影响

轨道厚度/mm6080100120140能量/106 J1.120 51.082 81.047 71.020 10.994 3电感梯度/(μH·m-1)1.4941.443 71.396 91.360 11.325 7
由表3、表4可知,轨道高度和厚度越小,电感梯度均越大,大约可从1.3 μH/m增大至1.5 μH/m,增幅达15.4%,比较轨道高度,单位长度下轨道厚度变化对电感梯度影响稍敏感。在设计轨道时,由于还需要考虑枢轨之间配合、轨道的机械强度[15]以及防止电流过度集中[16]的问题,轨道的高度和厚度应在某一合适的范围内进行考量。
4 结论
1) 四轨电磁发射器口径较大,为准确计算出其电感梯度,需要考虑电枢的存在,并采用基于虚功原理的能量法;而且电枢越靠近轨道尾部,电感梯度越大,由本文建模数据,电感梯度可达1.458 μH/m。
2) 相比四轨电磁发射器的大口径,大截面尺寸,电流频率引起电流路径的改变较小,即不同电流频率对电感梯度的影响不明显。
3) 在导轨横截面积较大的情况下,导轨高度和厚度越小,电感梯度越大,可达1.5 μH/m;若需要增大四轨电磁发射器的电感梯度,提高发射效率,可着重从轨道截面尺寸上考虑。
[1] 马伟明,鲁军勇.电磁发射技术[J].国防科技大学学报,2016,38(6):1-5.
[2] MARSHALL R A,WANG Y.Railguns:their science and technology[M].Beijing:China Machine Press,2004.
[3] YANG Z Y,FENG G,XUE X P,et al.An electromagnetic rail launcher by quadrupole magnetic field for heavy intelligent projectiles[J].IEEE Transactions on Plasma Science,2017,45(7):1095-1100.
[4] 童思远,冯刚,杨志勇,等.导弹四级磁场电枢轨道过盈配合参数优化[J].强激光与离子束,2019,31(1):38-44.
[5] 王莹,肖锋.电炮原理[M].北京: 国防工业出版社,1995.
[6] GROVER F W.Inductance calculations:working formulas and tables[M].New York,USA:Dover Publications,1962:22-66.
[7] KERRISK J F.Current diffusion and inductance calculations for rail-gun conductors[R].USA:Los Alamos National Lab,1981.
[8] ELLIS R L,POYNOR J C,McGLASSON B T,et al.Influence of bore and rail geometry on an electromagnetic naval railgun system[J].IEEE Transaction on Magnetics,2005,41(1):182-187.
[9] 刘守豹,阮江军,张亚东,等.增强型轨道炮电感梯度及其影响因素[J].电工电能新技术,2009,28(2):50-53.
[10]孙立强,袁伟群,严萍.基于时频分析的电磁轨道发射电感梯度研究[J].电工电能新技术,2008,27(2):38-41.
[11]邢彦昌,吕庆敖,向红军,等.电磁轨道炮电感梯度影响因素分析[J].军械工程学院学报,2014,26(6):30-35.
[12]颜威利,杨庆新,汪友华.电气工程电磁场数值分析[M].北京:机械工业出版社,2005.
[13]倪光正.工程电磁场原理[M].北京:高等教育出版社,2009.
[14]段玉康.方舱电磁屏蔽技术研究[D].成都:电子科技大学,2009.
[15]张永胜,鲁军勇,谭赛,等.连续电磁发射过程中轨道受力分析[J].兵器装备工程学报,2018,39(3):618-624.
[16]贺景瑞,李小将,齐跃.电磁轨道发射装置轨道几何参数对电流分布的影响[J].兵器装备工程学报,2017,38(2):186-190.