中子扩散方程的求解最常见的算法是有限差分法[1],即通过对中子输运方程的各种简化处理得到扩散方程,再通过内迭代外迭代划分网格等得到最终的收敛解。随着时代的发展,近年来,研究者开发了许多其他的用于求解中子扩散方程解法,如节块法[2],现在已成为压水堆设计中最为常用的方法。同时,国内外有学者提出对中子扩散方程进行改造扩展,引入两个分别与中子吸收和中子扩散有关的修正因子以弥补经典中子扩散方程的不足,从而可以有效计算多变量下的中子截面以及不均匀结构间的中子通量密度分布[3-4]。除此之外,国外又发展出了中子扩散方程的线性扩展方法,利用这种方程得到的结果与半解析法得到的基准数据吻合的很好,从而证明了扩散方程线性扩展的可行性[5]。作为中子扩散方程的经典解法,有限差分法至今仍有着很重要的地位,本文采用有限差分法数值模拟堆芯中子通量分布。
1 堆芯差分方程
1.1 边界条件
在堆芯中子通量密度计算中,需要应用到两类边界条件。首先因为是对1/4堆芯进行计算,这样在对称分界面部分需要应用全反射边界条件,此类边界条件较简单在此不赘述。另一类边界条件即反照率边界条件,而反照率本身带有很多经验因子,无法精确得到其解析解,Segev[6]和M.Itagaki[7]分别提出应用有限差分和边界元数值法直接数值地产生边界条件。由于相关文献的报道很少,本文直接采用应用于节块法的一种边界条件,如表1所示。
表1中界面AB等按照图1对应,其中,BCA,BCB分别为利用第一种和第二种方法得到的反照率数值解。
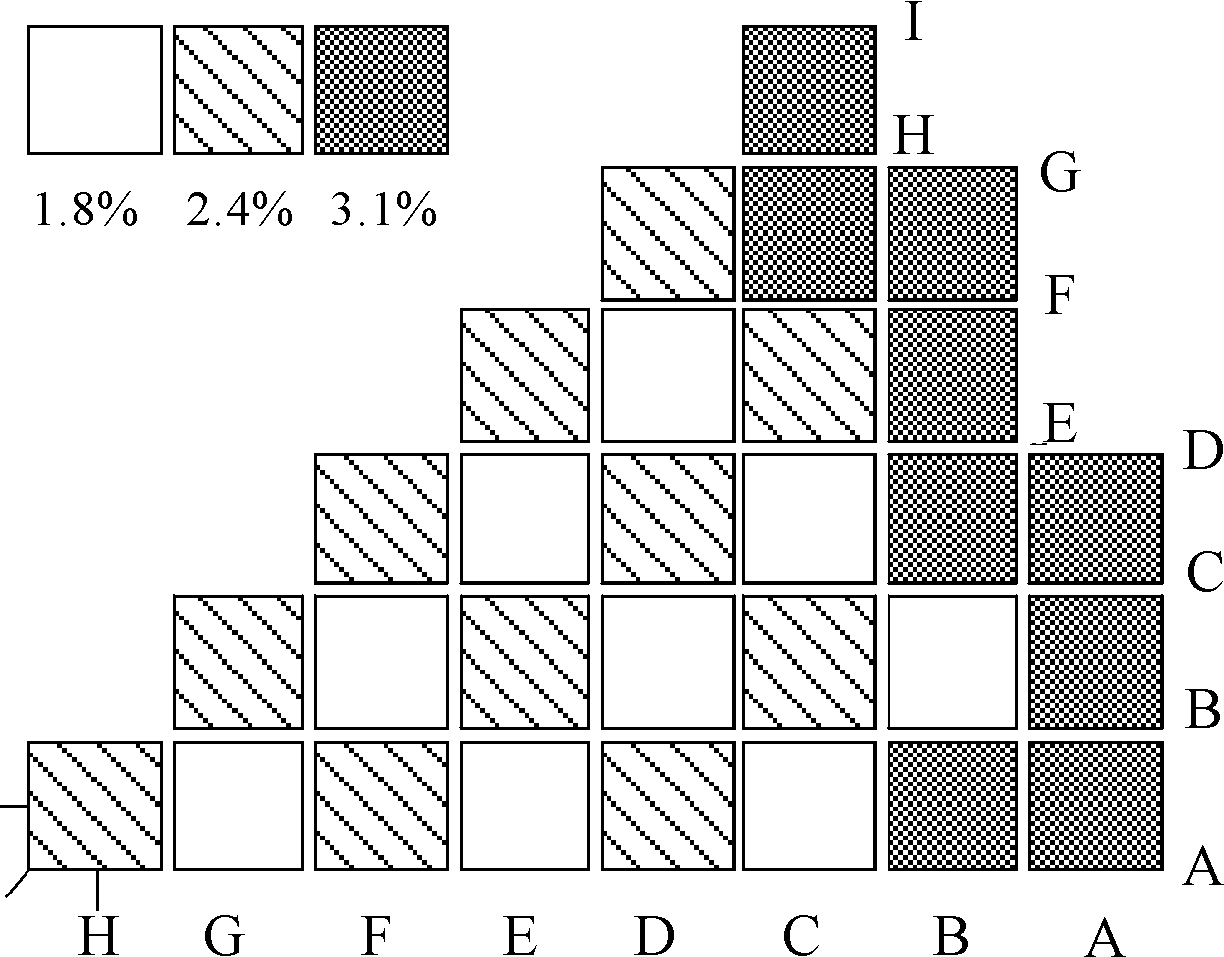
图1 反应堆堆芯燃料组件分布及边界
表1 IAEA问题的反照率数值解[8]
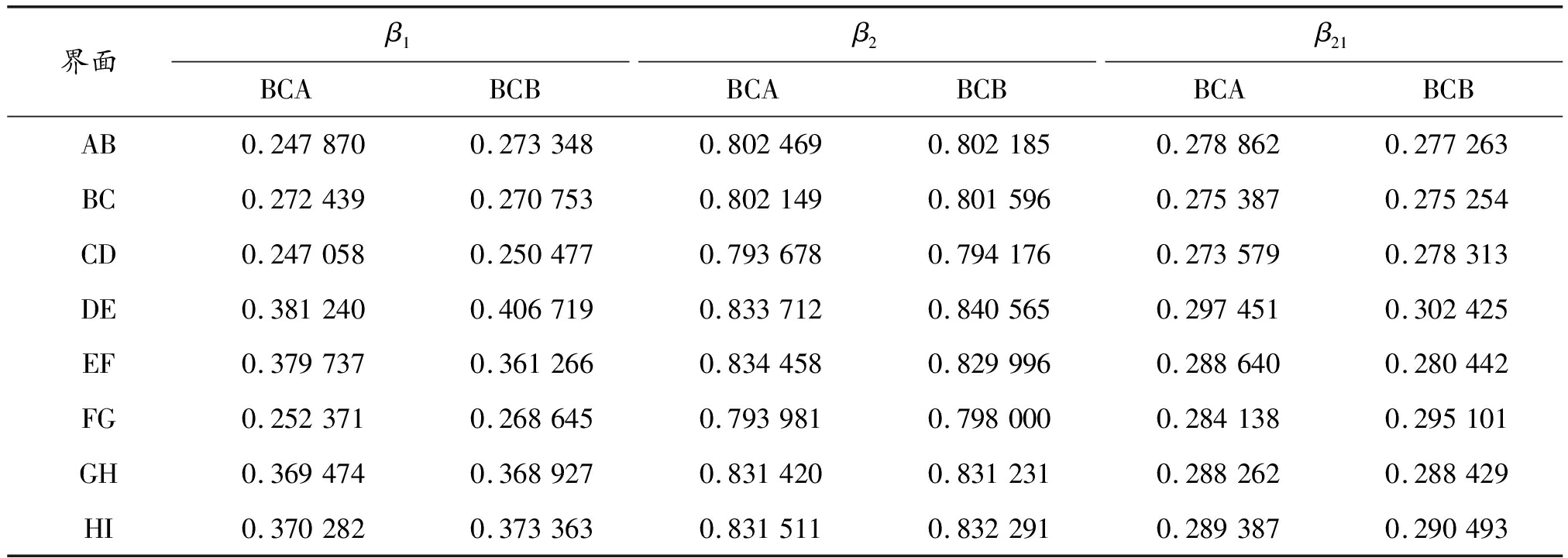
界面β1BCABCBβ2BCABCBβ21BCABCBAB0.2478700.2733480.8024690.8021850.2788620.277263BC0.2724390.2707530.8021490.8015960.2753870.275254CD0.2470580.2504770.7936780.7941760.2735790.278313DE0.3812400.4067190.8337120.8405650.2974510.302425EF0.3797370.3612660.8344580.8299960.2886400.280442FG0.2523710.2686450.7939810.7980000.2841380.295101GH0.3694740.3689270.8314200.8312310.2882620.288429HI0.3702820.3733630.8315110.8322910.2893870.290493
在编制计算程序的过程中,对反照率边界条件进行进一步简化,综合考虑补充边界节点代数方程的方法和附加源项法[9],假设在反射层中与堆芯紧邻处添加节点,且该节块内的系数与堆芯相同,同时假设其中子通量密度Φr与该紧邻堆芯节块内中子通量密度Φr关系为:
Φr=β*Φc
(1)
1.2 堆芯差分方程形式
式(2)为堆芯中子扩散方程:
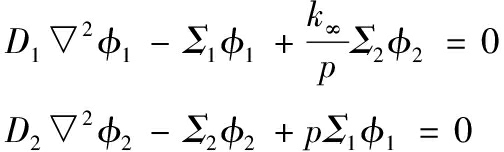
(2)
对于1/4堆芯组件,其节块中子扩散方程需要分为13种(如图2所示),首先分析元胞1节块扩散方程形式及规律。需要说明的是,本文的计算以组件均匀化系数为准。假设现在已经获得堆芯组件扩散系数1×47矩阵X,以及堆芯组件的移出截面数据1×47矩阵Y(编号以图2为准)。
ai-1, jΦi-1, j+ai, j-1Φi, j-1+ai, jΦi, j+
ai, j+1Φi, j+1+ai+1, jΦi+1, j=Si, j
(3)
式(3)为普遍情况下节块的差分方程。对于元胞1,即1~8号组件第1层节块,上表面需要考虑全反射边界条件,第150个节块即(1,150)号节块,则还要考虑反照率边界条件。
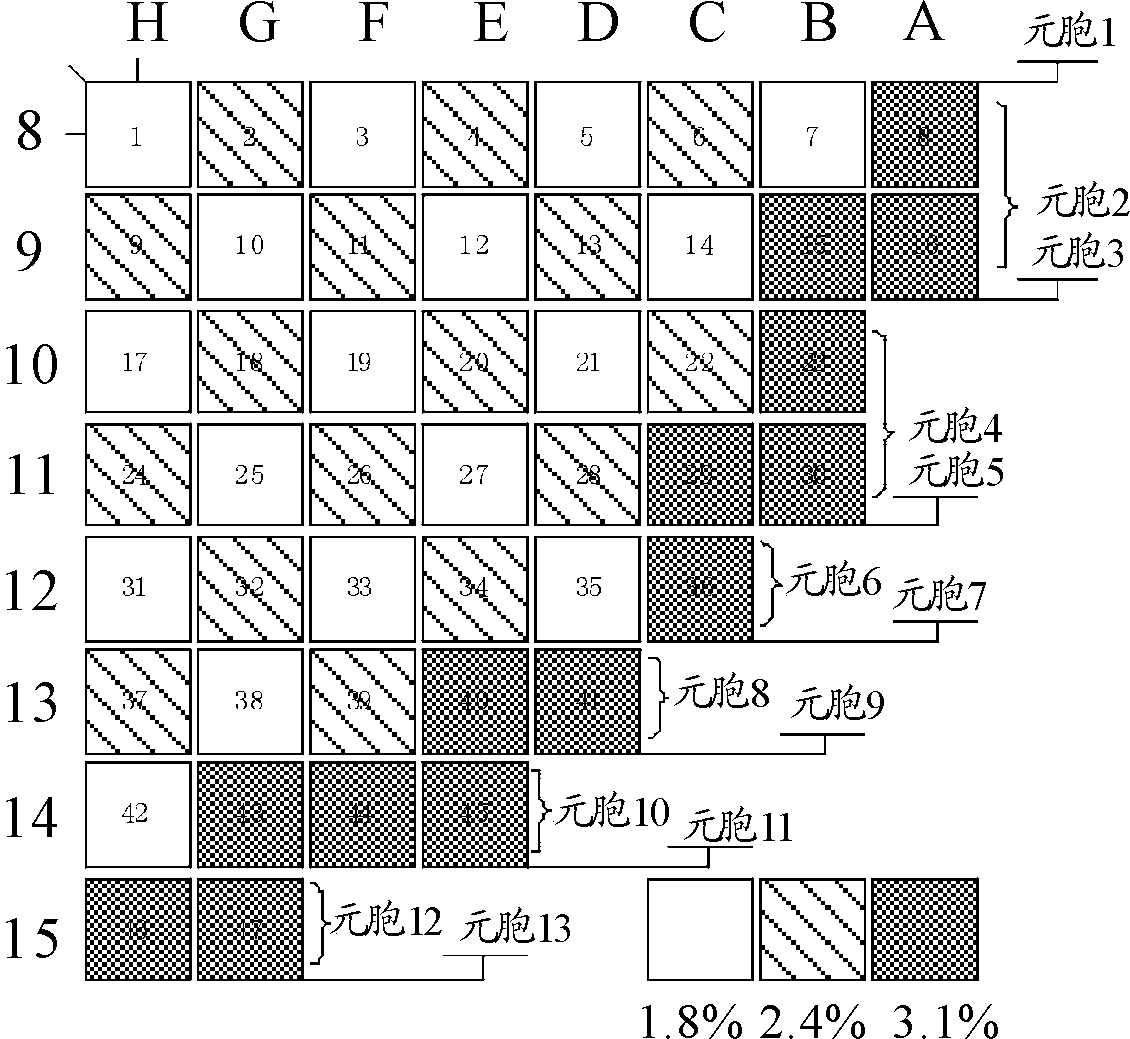
图2 1/4反应堆堆芯组件图
式(3)中各项系数如下所示:
ai+1, j=-2Di+1, jDi, j/Δl2(Di+1, j+Di, j)
ai-1, j=-2Di-1, jDi, j/Δl2(Di-1, j+Di, j)
ai, j-1=-2Di, j-1Di, j/Δl2(Di, j-1+Di, j)
ai, j+1=-2Di, j+1Di, j/Δl2(Di, j+1+Di, j)
ai, j=ΣR,i, j-ai-1, j-ai, j-1-ai, j+1-ai+1, j
(4)
元胞1的1号节块,即整体的(1,1)节块,考虑全反射边界条件差分方程形式为(5)形式
ai, jΦi, j+ai, j+1Φi, j+1+ai+1, jΦi+1, j=Si, j
(5)
各项系数只有ai, j发生变化为
ai, j=ΣR,i, j-ai, j+1-ai+1, j
(6)
对于元胞1的第2~149号节块即总体(1,2)~(1,149)号节块,考虑全反射边界条件差分方程形式为
ai, j-1Φi, j-1+ai, jΦi, j+ai, j+1Φi, j+1+ai+1, jΦi+1, j=Si, j
(7)
各项系数只有ai, j发生变化为
ai, j=ΣR,i, j-ai, j-1-ai, j+1-ai+1, j
(8)
对于元胞1的第150号节块即总体第(1,150)节块,考虑全反射及反照率边界条件差分方程形式为
ai, j-1Φi, j-1+ai, jΦi, j+ai+1, jΦi+1, j=Si, j
(9)
各项系数只有ai, j发生变化为
(10)
其余元胞各类节块差分方程的推导方法可根据元胞1类推。
1.3 中子扩散方程方程组系数矩阵
对此矩阵进行稀疏处理,系数矩阵构造如图3所示,M代表非零数字,其余位置皆为0。图3给出了系数矩阵的具体构成,由图可见每一个括号表示一类元胞,共有13类元胞。
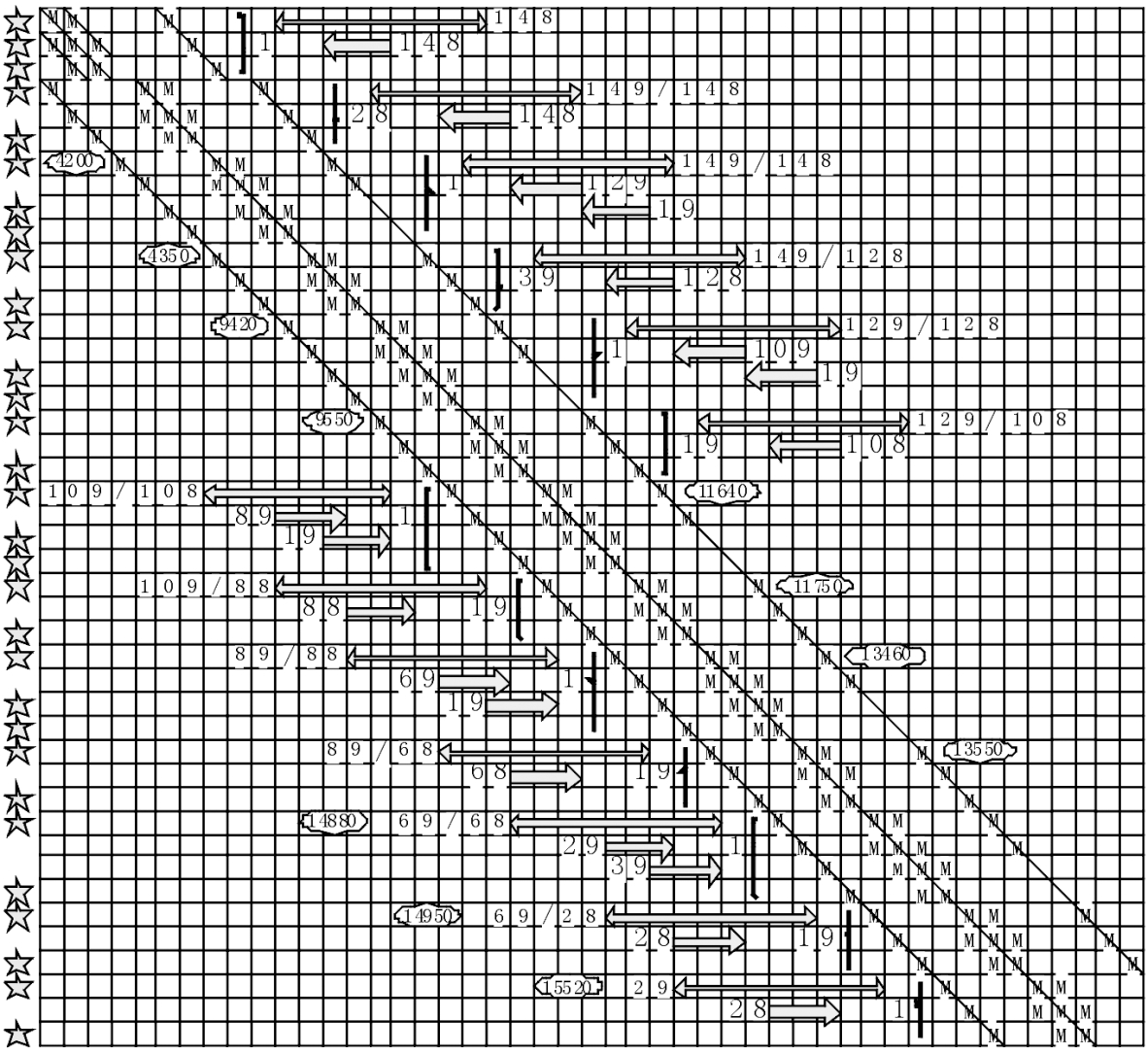
图3 系数矩阵构造
图3中,括号旁边的标注数字为此类元胞包含的行数。单向箭头所在行即大部分节块共用差分方程行,其标注数字为可用此方程代表的结块数目。无单向箭头的行即只代表一个节块。双向箭头位于每一类元胞的第一行,表示这类元胞方程有系数项之间空隙包含的0位数目。椭圆圈住数字就是说明在此类元胞第一行方程的第一个非零系数前有多少个0空位。
考虑到系数矩阵方程组数目较多且均为手工编程组建,不可避免的会有错误。在一切正确的前提下,该系数矩阵是一个严格对角占优阵,在迭代算法中,严格对角占优阵有很好的收敛特性。因此额外编写检查矩阵的对角占优性程序以检查系数矩阵对角占优性。
2 二群中子扩散方程数值算法
本文采用SOR内迭代算法,其基本算法流程如下:
1)取初始点Φ(0),松弛因子w,置k=0,精度要求ε和最大迭代次数N;其中最佳松弛因子
(11)
ρ(BJ)为Jacobi迭代阵谱半径,利用改进乘幂法计算。
2)利用迭代式计算Φ(k+1);SOR迭代式为
Φ(k+1)=BwΦ(k)+fw
(12)
其中,Bw=(D-wL)-1[(1-w)D+wU],fw=w(D-wL)-1b。
3)若||Φ(k)-Φ(k-1)||∞≤ε或者达到最大迭代次数,计算终止,返回Φ(k)。
4)否则,k=k+1,转(2)。
很明显,由于A是严格对角占优阵,其Jacobi迭代一定收敛也就是说其Jacobi迭代阵谱半径一定小于1,由式(11)可知w一定小于2,因此,SOR迭代阵谱半径一定小于1,则必收敛。
模拟过程的源迭代收敛准则为:
(13)
3 计算结果及分析
3.1 计算所需数据确定
在中子扩散方程数值解法的程序中,需要利用的核参数主要有:
1)三区散射系数D,用于差分方程系数的计算;
2)三区移出截面ΣR,用于差分方程对角系数的计算;
3)反照率β,选取方法和相应数值见1.1;
4)节块长度Δl,作为划分网格的主要依据;
5)三区裂变截面Σf,用于在源迭代中计算新的裂变源项;
6)三区平均裂变中子数ν,用于在源迭代中计算新的源项;
7)三区快群到热群的转移截面Σs,1→2,用于热群中子扩散方程差分方程组的解。
8)三区中子裂变能谱χ,用于二群扩散方程差分方程组的解。
本文采用MOX七群核燃料核数据[10],处理得到二群核数据见表2与表3。表格中数据从左往右依次为扩散系数、移出截面、裂变截面。
表2 快群核数据
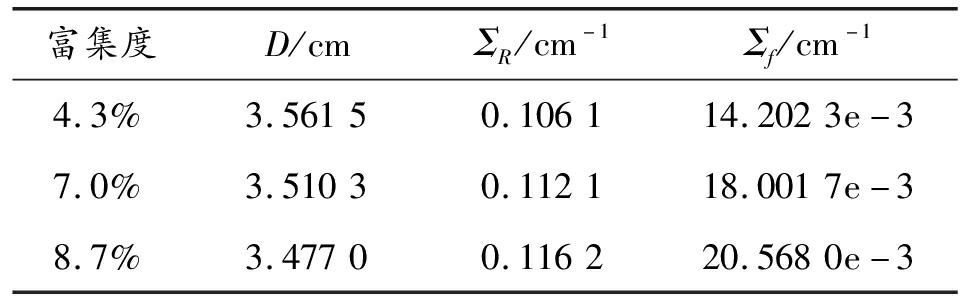
富集度D/cmΣR/cm-1Σf/cm-14.3%3.56150.106114.2023e-37.0%3.51030.112118.0017e-38.7%3.47700.116220.5680e-3
表3 热群核数据
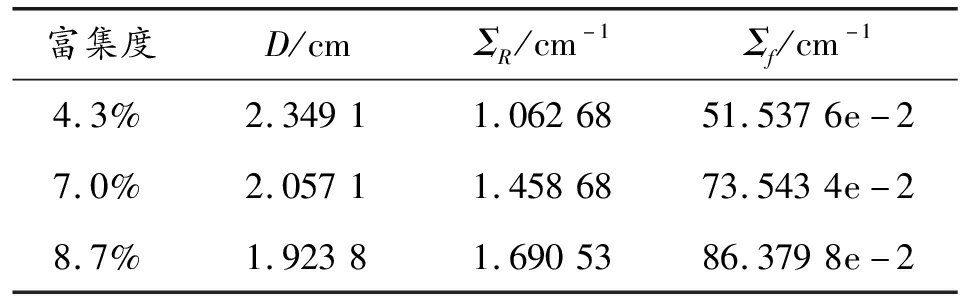
富集度D/cmΣR/cm-1Σf/cm-14.3%2.34911.0626851.5376e-27.0%2.05711.4586873.5434e-28.7%1.92381.6905386.3798e-2
对于节块长度即网格的边长Δl,考虑到一般不能大于中子扩散长度的0.5~1倍,中子扩散长度约为1.8 cm,以及燃料组件边长为21.504 cm,确定节块边长为1.075 2 cm。
对于反照率β值,其取值过程1.1中已经详细介绍,在此不赘述。
对于裂变能谱χ,具体数值为χ1=1-1.176 1e-7,χ2=1.176 1e-7。
对于转移截面Σs,1→2,1~3区的Σs,1→2分别为2.614 20e-3,2.533 10e-3,2.474 90e-3,单位为cm-1。
对于平均裂变中子数ν,三种富集度下分别对其去平均值为2.863 6,2.877 3,2.883 5,进一步简化取ν的三区平均值为2.874 8。
3.2 计算结果及分析
表4给出了6次运行时的运算特征数据,分别为运算时间t/s,源迭代次数i_k,快群热群SOR最佳松弛因子w1、w2,快群热群Jacobi迭代阵最大特征值lamat_1、lamat_2,快群热群乘幂法迭代次数i_lamat_1、i_lamat_2。
表4 运行特征数据
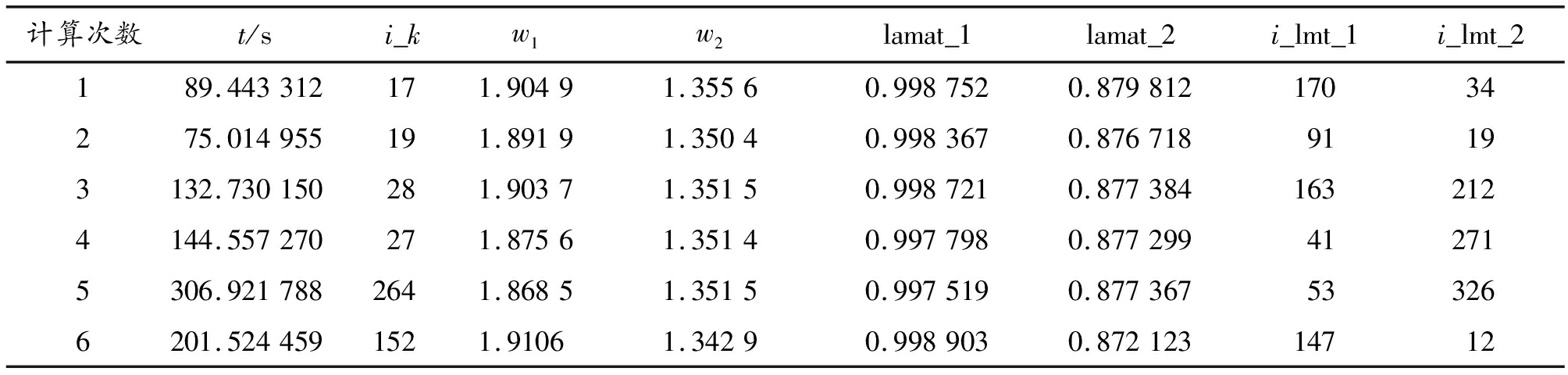
计算次数t/si_kw1w2lamat_1lamat_2i_lmt_1i_lmt_2189.443312171.90491.35560.9987520.87981217034275.014955191.89191.35040.9983670.87671891193132.730150281.90371.35150.9987210.8773841632124144.557270271.87561.35140.9977980.877299412715306.9217882641.86851.35150.9975190.877367533266201.5244591521.91061.34290.9989030.87212314712
快群、热群内迭代以及源迭代的收敛精度分别取10-4,10-4,10-4;10-5,10-5,10-5;10-5,10-6,10-6。选取第6次数值模拟结果,如图4与图5所示。发现中子通量密度分布相对于实际峰因子很大,分析认为是因为本程序采取了各种简化手段,如认为反射层中无中子慢化,将反射层物理参数与堆芯归一化处理,在反射层应用添加结块边界处理方法,认为堆芯内无外中子源等。为简化问题,计算核数据只是MOX燃料棒的核数据,没有考虑水以及其他材料的慢化作用。
由图6与图7中的曲线可见快群中子内迭代次数随源迭代次数的增加减小。这是因为随着源迭代次数增加快中子分布越来越精确,所以每后一次内迭代的初始数据都要比前一次精确。
热群中子内迭代过程只需几次源迭代就可以得到比较精确的分布,其内迭代次数在首次源迭代时相比较快群中子小很多,且可以发现热群中子分布基本上就是快群中子分布按照富集度增加或减少得到的,这一现象通过其surf图表现的很明显。
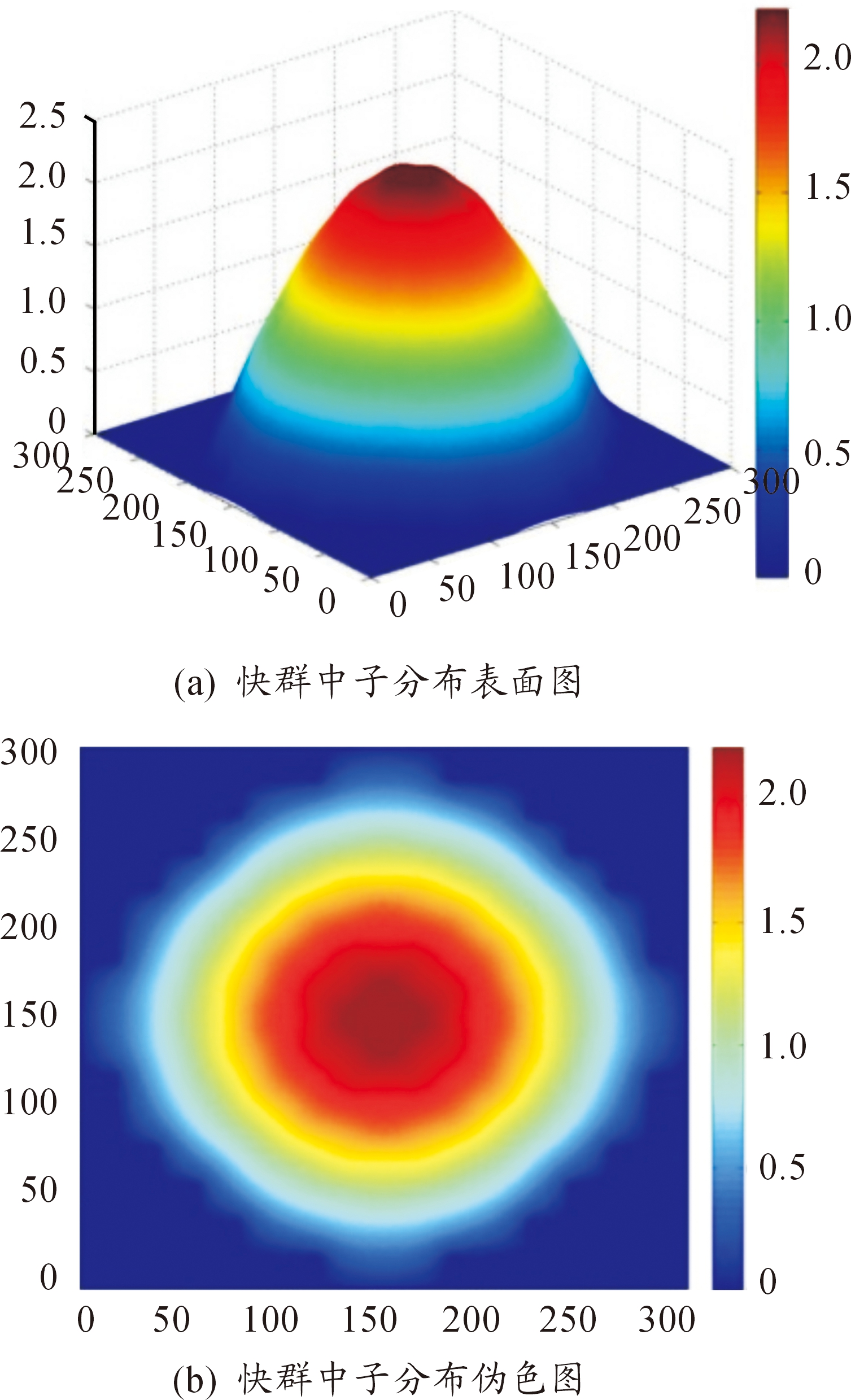
图4 第6次快群中子分布数值模拟结果
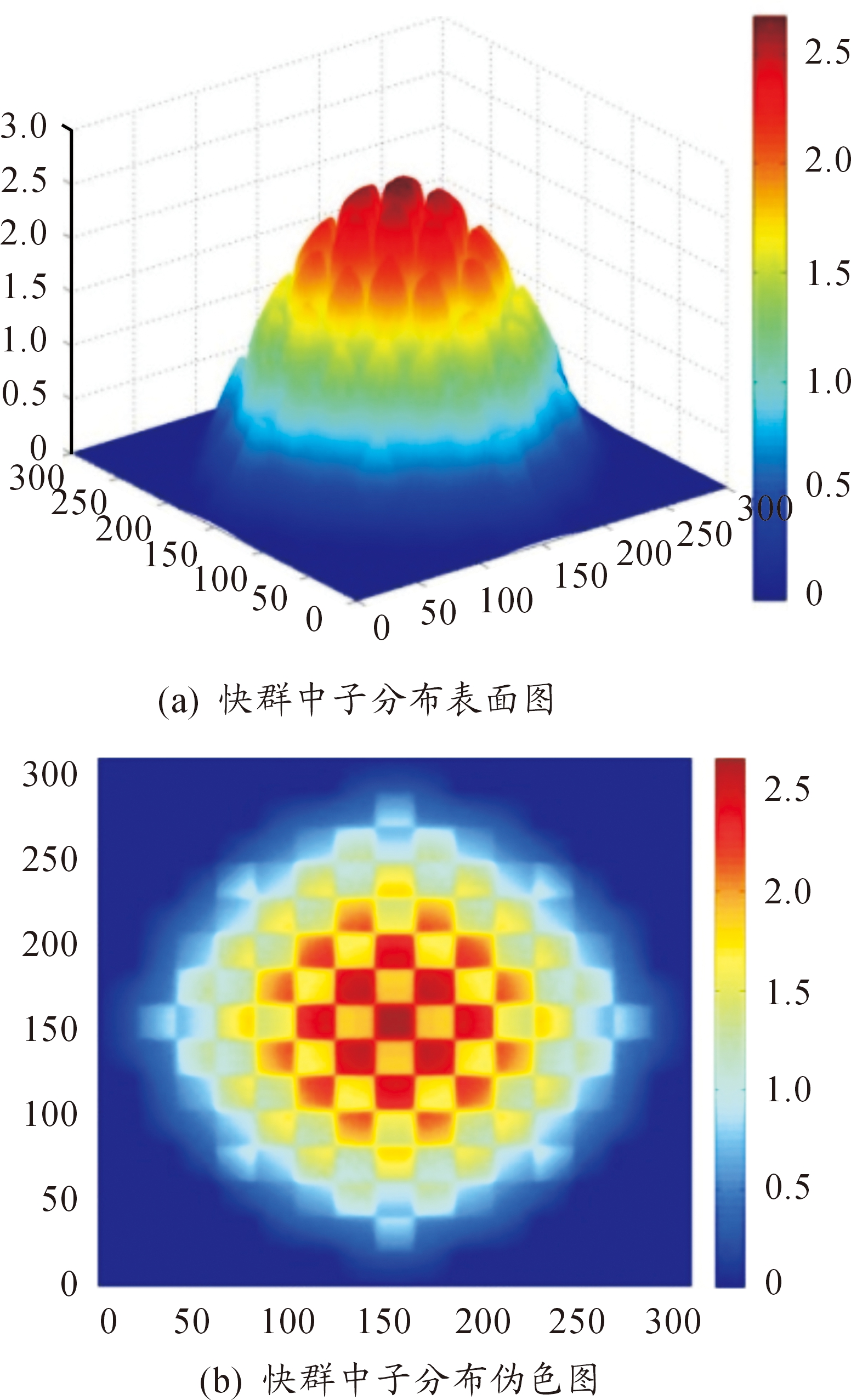
图5 第6次热群中子分布数值模拟结果

图6 第3次计算内迭代次数变化曲线
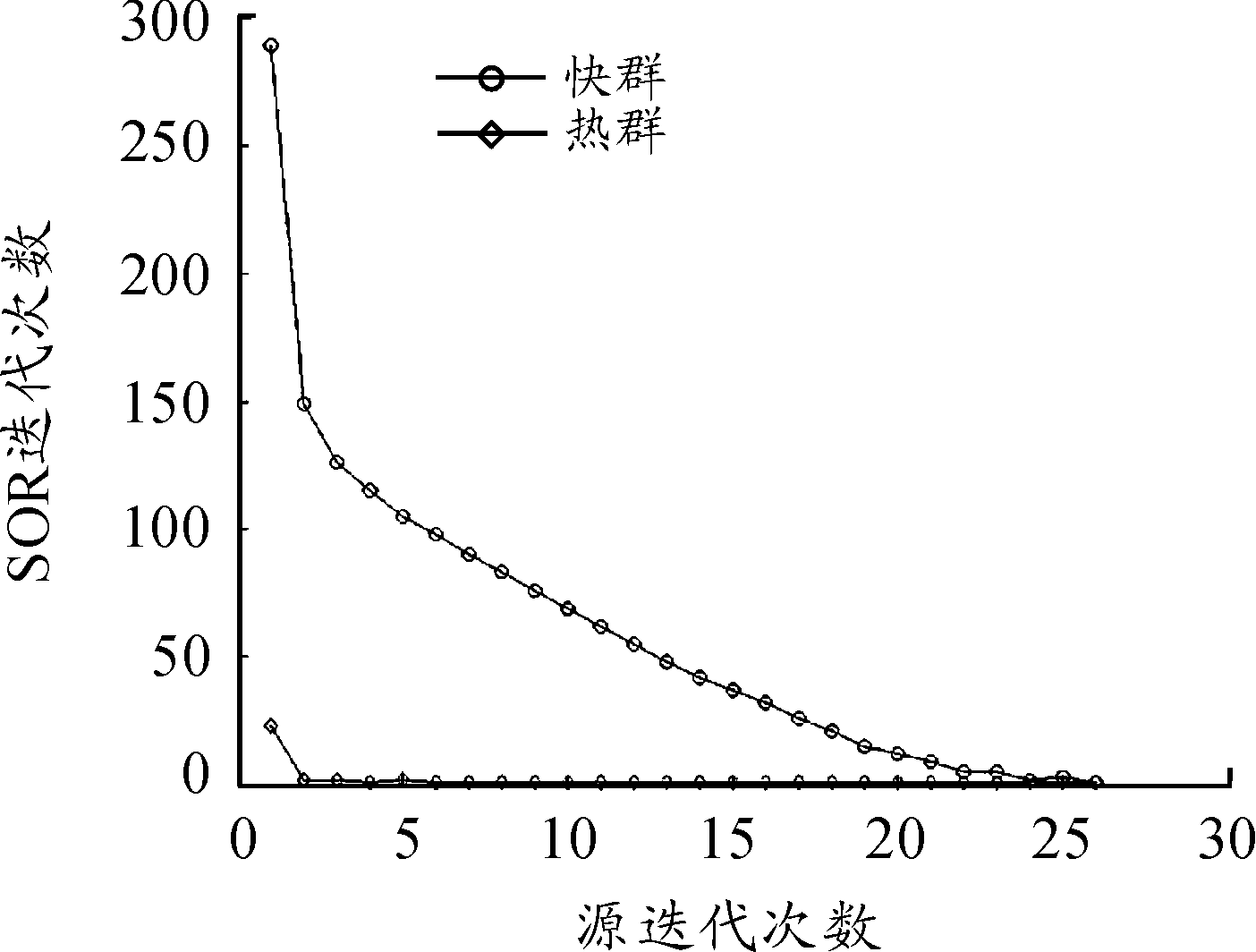
图7 第4次计算内迭代次数变化曲线
热群中子扩散方程的迭代式右端项b2=(xita2/keff(i_k))*S_origin+xigema_s_12.*Fi_1。其中xigema_s_12.*Fi_1的贡献要明显大于(xita2/keff(i_k))*S_origin项。这是因为源项多为快中子,体现在xita2值非常小,本程序取值为xita2=1.7161e-7,几近为0。这又反过来说明了内迭代的初始迭代次数一定是很小且收敛速度一定是很快的。如此也很好的说明了快热中子surf图中分布形状几近相同这一情况。正是考虑到了热群中子收敛很快这一现象故将其收敛精度由0.000 01调整至0.000 001。
由图8与图9中的曲线可以看出,有效增殖因数基本收敛到0.43左右,可以获得稳定源分布。
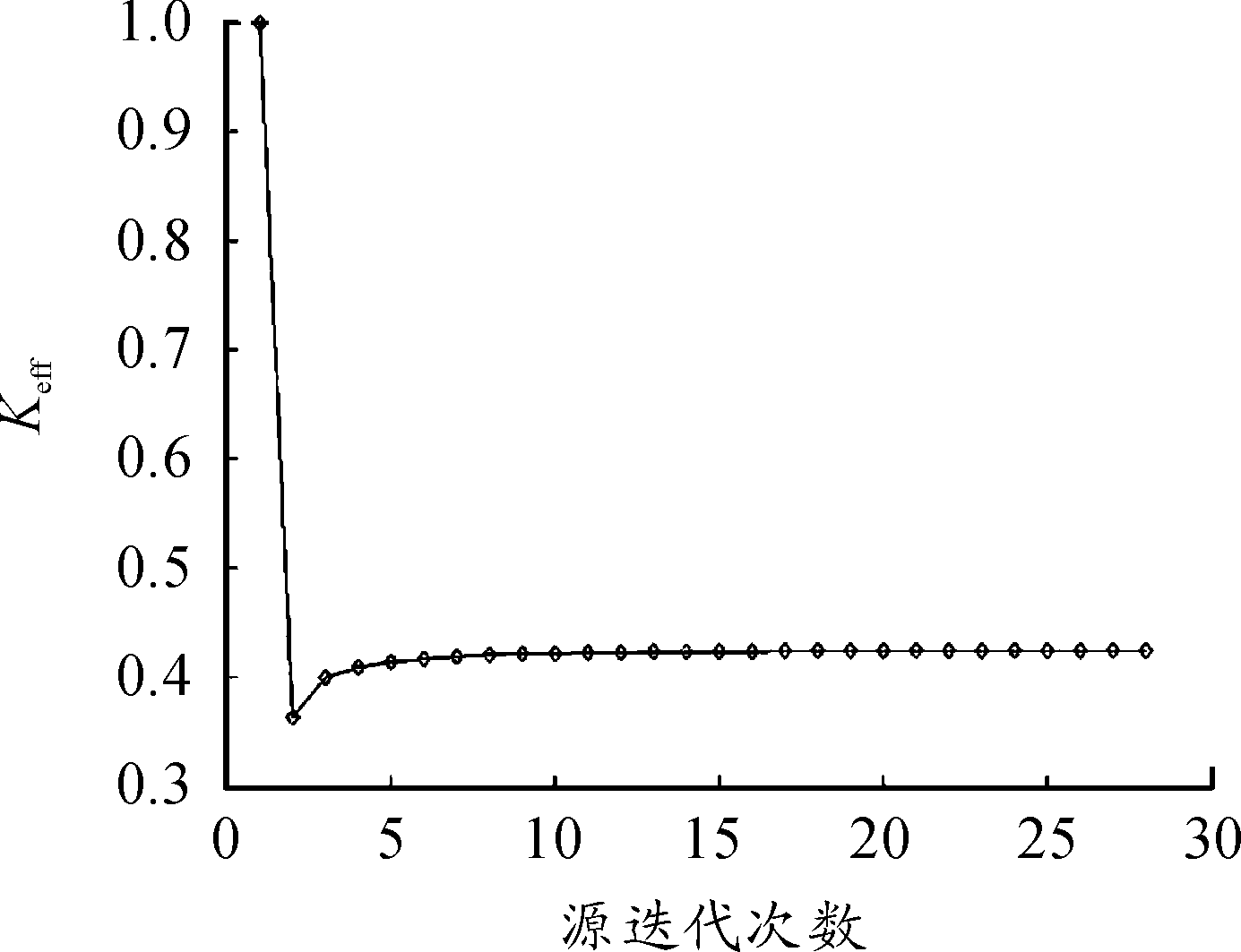
图8 第3次计算Keff收敛过程
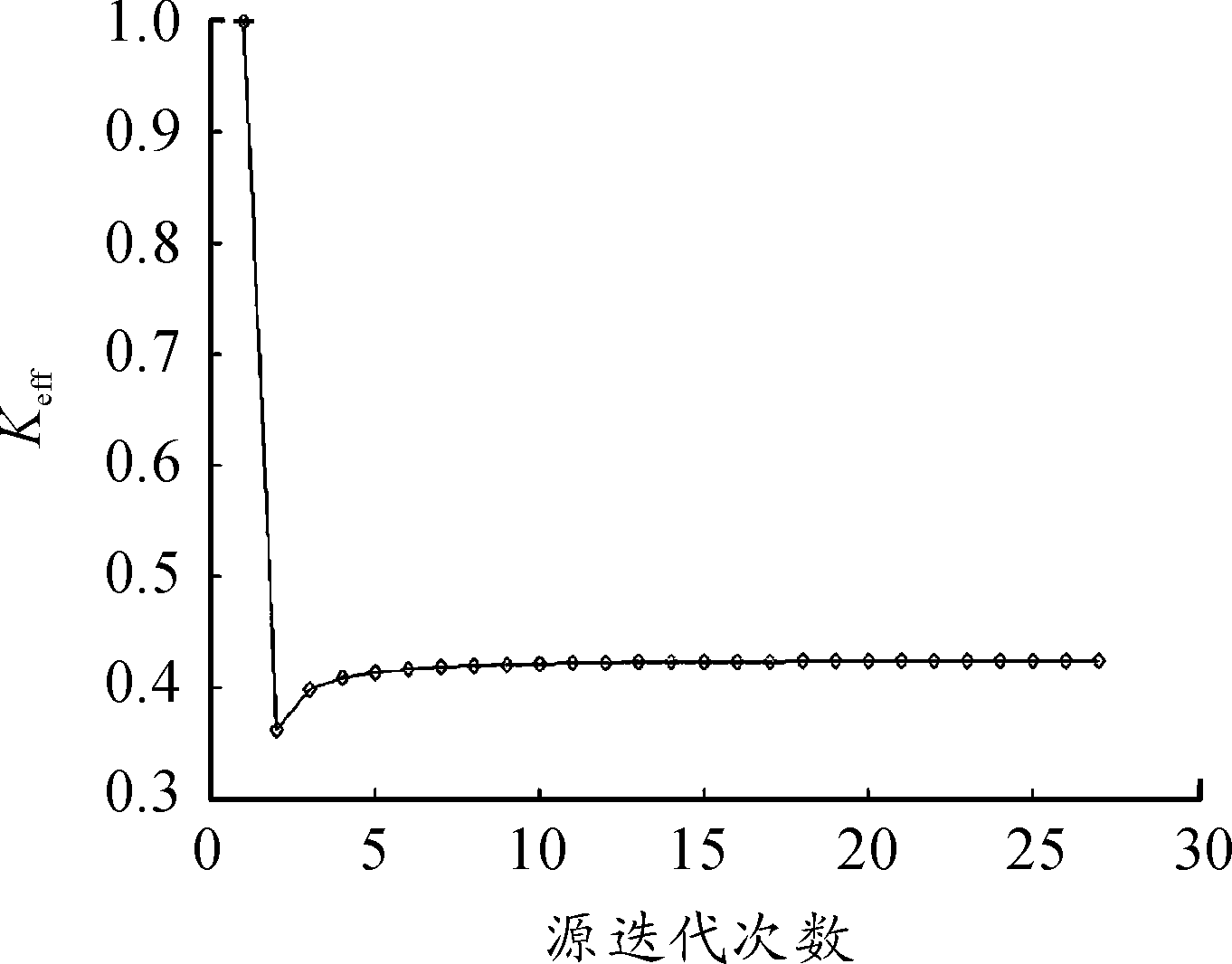
图9 第4次计算Keff收敛过程
4 结论
本文数值模拟了反应堆堆芯快群中子以及热群中子分布情况,认为相对于实际情况峰因子过大是因为反照率边界条件应用不当,不同富集度组件中子分布差异剧烈是因为截面数据选取不当。
通过编程获得了有效增殖因数、Jacobi迭代阵谱半径、快热群内迭代次数的收敛曲线,本数值计算程序具有较快的收敛速度,计算结果合理。
[1] 杨应辉,杨质,孙建嵩,等.二维少群反应堆中子扩散方程的数值计算[J].原子能科学技术,1979(1):32-39.
[2] 谢仲生.压水堆核电厂堆芯燃料管理计算及优化[M].北京.原子能出版社,2001.
[3] VAZQUEZ-RODRIGUEZ R,ESPINOSA-PAREDES G,MORALES-SANDOVAL J B,et al.Averaging the neutron diffusion equation[J].Progress in Nuclear Energy,2009,51(3):474-484.
[4] 谢明亮,于雷,陈玉清.AP1000核反应堆控制棒价值特性的MC模拟[J].兵器装备工程学报,2016(3):121-125.
[5] ESPINOSA-PAREDES G,VAZQUEZ-RODRIGUEZ R.Application of Linear-extended Neutron Diffusion Equation in a Semi-infinite Homogeneous Medium[J].Annals of Nuclear Energy,2011,38(2/3):713-719.
[6] SAGEV M.Application of Light Water Reactor Core/Reflector Boundary Conditions[J].Nuclear Science and Engineering,1985,90(2):221-230.
[7] ITAGAKI M,BREBBIA C A.Space-Dependent Core/Reflector Boundary Conditions Generated by Boundary Element Method for Pressurized Water Reactors[J].Nuclear Science and Engineering,1991,107(3):246-264.
[8] 谢仲生,成红武,梁薇.反应堆节块计算中一种数值求解边界反照率的方法[J].核科学与工程,1997,17(3):220-226.
[9] 陶文栓.数值传热学[M].2版.西安:西安交通大学出版社,2001:92-98.
[10] 汤春桃.中子输运方程特征线解法及嵌入式组件均匀化方法的研究[D].上海:上海交通大学,2009.