随着串联攻坚战斗部技术的发展,常规随进子弹已经越来越满足不了工程人员的实际需要,而在钻地弹领域取得一定研究成果的刻槽弹丸结构随之进入人们的视野。关于常规随进弹丸侵深的计算国内外已有不少研究,而对于刻槽随进弹丸侵彻深度的工程计算研究见刊的并不多。少数研究学者主要就其理论模型进行了公式推算并做了部分试验验证工作,但纯理论公式所需数据量大,工程人员实际使用不便。因此本文就此研究内容提出了对随进弹丸侵彻公式的推广和改进,以适用不同刻槽弹丸对于预开孔径目标的侵深计算。基本随进弹丸侵彻公式采用王静、王成[1]提出的修正Teland模型[2],参考了邓佳杰[3]、王震宇[4]对随进子弹的研究成果,并借鉴了陈小伟[5-6]、武海军[7]、Mehmet Erengil、Steve Kornguth [8]等人的研究方式及思路。
1 物理模型和数值仿真模型
本文以串联攻坚战斗部前级杆式射流开孔预破坏后的混凝土为目标模型,靶板开孔简化为直壁圆筒通道,见图1。

图1 基本物理模型
采用LS-DYNA软件进行三维建模及数值模拟计算。具体弹靶模型网格划分见图2。
数值模拟中使用靶板为圆柱预开孔混凝土半无限靶,厚度400 mm,考虑靶板建模尺寸及边界效应。混凝土开孔孔径20 mm,深色预损伤靶板材料区域为孔径3倍。
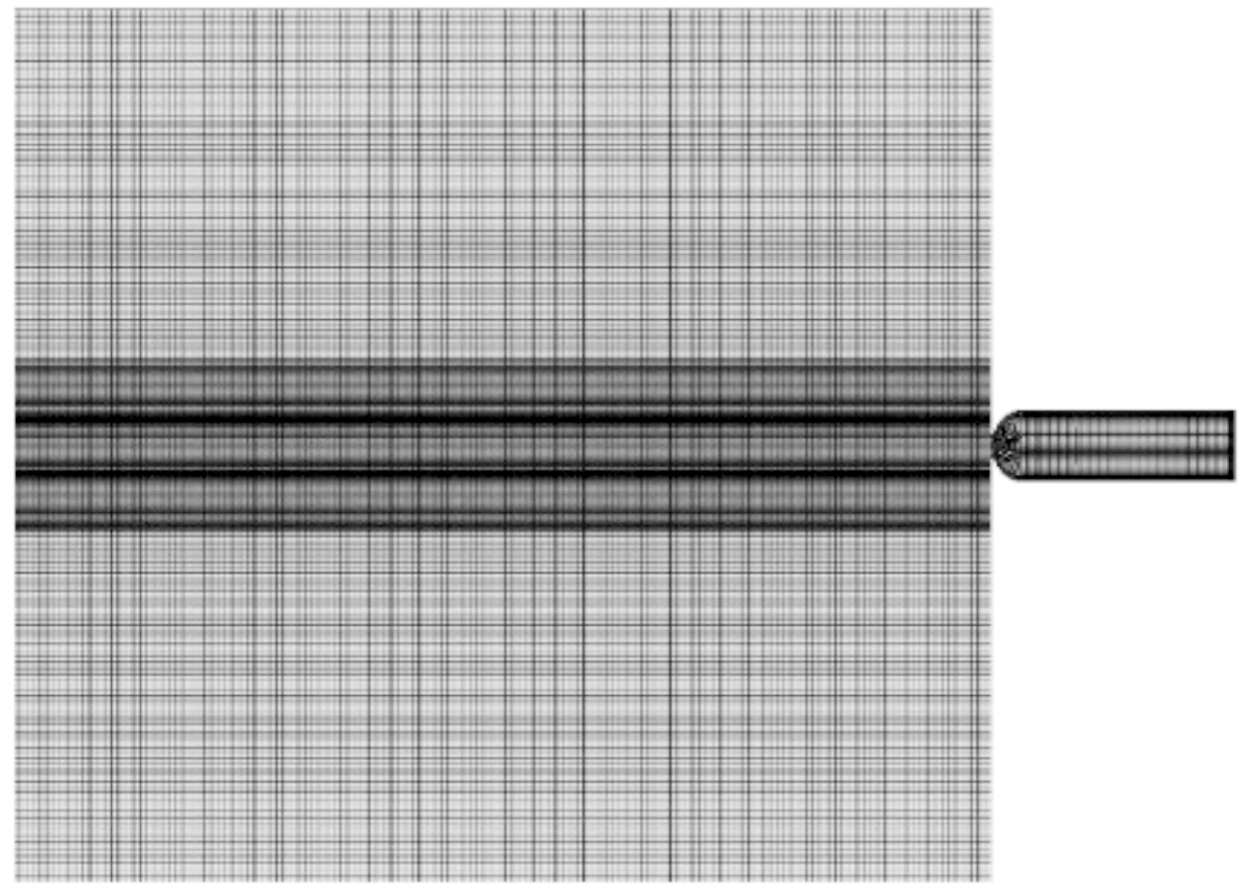
图2 模型网格划分
本文所涉及弹丸的弹型有4种,其主要技术参数见表1。
表1 弹丸结构尺寸主要技术参数
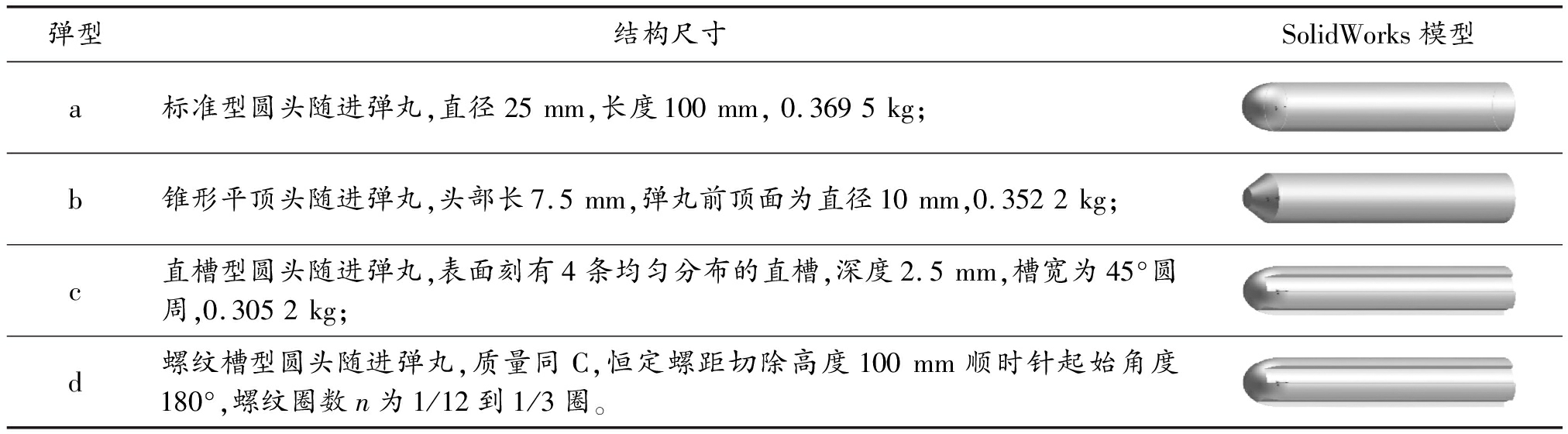
弹型结构尺寸SolidWorks模型a标准型圆头随进弹丸,直径25mm,长度100mm,0.3695kg;b锥形平顶头随进弹丸,头部长7.5mm,弹丸前顶面为直径10mm,0.3522kg;c直槽型圆头随进弹丸,表面刻有4条均匀分布的直槽,深度2.5mm,槽宽为45°圆周,0.3052kg;d螺纹槽型圆头随进弹丸,质量同C,恒定螺距切除高度100mm顺时针起始角度180°,螺纹圈数n为1/12到1/3圈。
弹丸及靶板预损伤混凝土主要参数见表2、表3。
表2 弹体材料主要参数

RO/(g·cm-2)E/GPaPRSIGY/GPa7.852.0700.31.800E-02
表3 预损伤状态混凝土主要参数

RO/(g·cm-2)G/GPaFT/GPaFC/GPa2.560.2680.004250.012
本文理论计算公式是基于王静等[1]提出的修正Teland模型,如下:
![]()
(1)
而根据文献[3-4]的研究,可以认为仿真模型状态下弹丸速度、倾角均符合公式基本假设条件。原公式基本参数不再赘述,其结果在下文中统一表述为P,则本文a、b型弹丸侵彻混凝土靶数值仿真与公式计算结果如图3、图4。
图3中最大误差为7.9%,图4中最大误差为9.5%,排除公式误差造成的影响,弹丸侵彻能力增加的趋势基本一致。

图3 a型弹丸仿真结果与计算结果
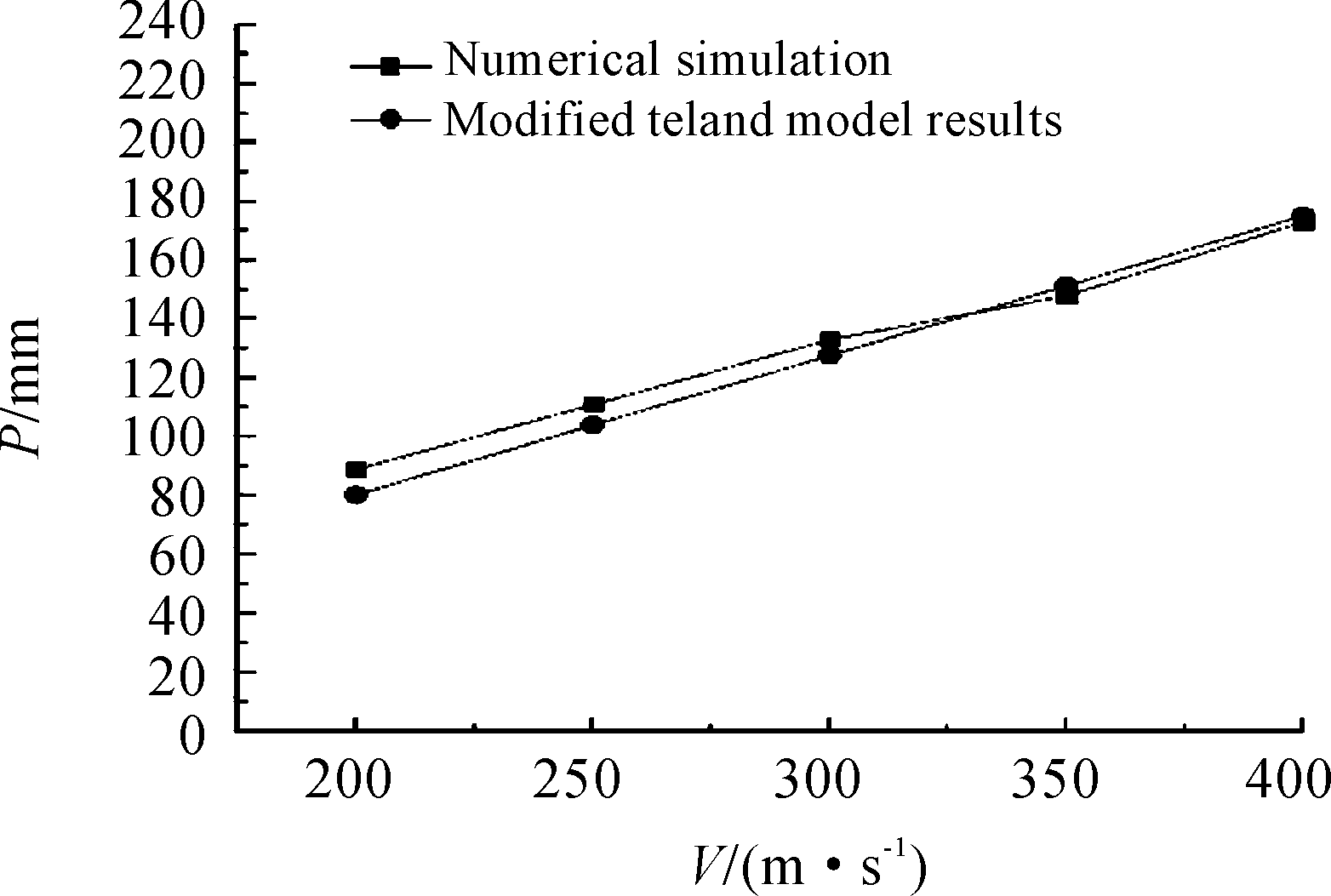
图4 b型弹丸仿真结果与计算结果
2 刻槽随进弹丸侵彻过程分析
.对于刻槽随进弹丸侵彻开孔预破坏混凝土靶过程,有部分动能钻地弹的研究试验可以借鉴。陈小伟[5-6]、武海军[7]及Mehmet Erengil等[6]分别就刻槽弹体侵彻混凝土靶的过程展开了研究并得到结论:初速1 000 m/s范围内,侵彻过程中,弹体凸起部分参与空腔膨胀,凹陷部分不参与空腔膨胀,只受摩擦力作用。而根据Forrestal在1988年进行的一项研究表明[9],杆身部的摩擦力影响非常小故忽略。
2.1 直槽随进弹丸侵深的工程计算参数
基于文献[10]对于空腔膨胀理论的研究,对于a、c型弹丸,其轴向总阻力理论值分别为:
(2)
V为着靶速度,其余参见文献[8]。引入理论刻槽阻力系数KF:
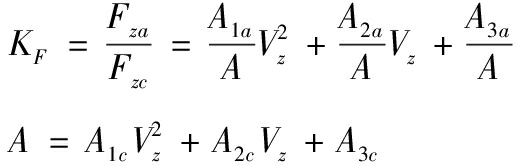
(3)
系数KF表征原弹丸a型及在此基础上的直槽弹丸c型侵彻深度比例关系,但实践计算中所涉及的混凝土参数过多,工程实际难以得到合理的曲线。而在本文2节看到,同一预设条件、材料下的模拟仿真计算具有一定计算精度且用于比例关系中也可以一定程度上削减其条件带来的误差影响。因此引入一个等效阻力系数Kf:
(4)
实践中,KF公式中各系数在单组试验弹丸初速基本一致的状况下跳动不大,因此工程计算可采用系数Kf进行估算(Kf由仿真拟合得出,故不对仿真与计算结果做比对)。图5所示为基于c型弹丸计算的KF和Kf在速度200~400 m/s时的等效结果曲线,可见采用固定系数其误差是可以接受的。
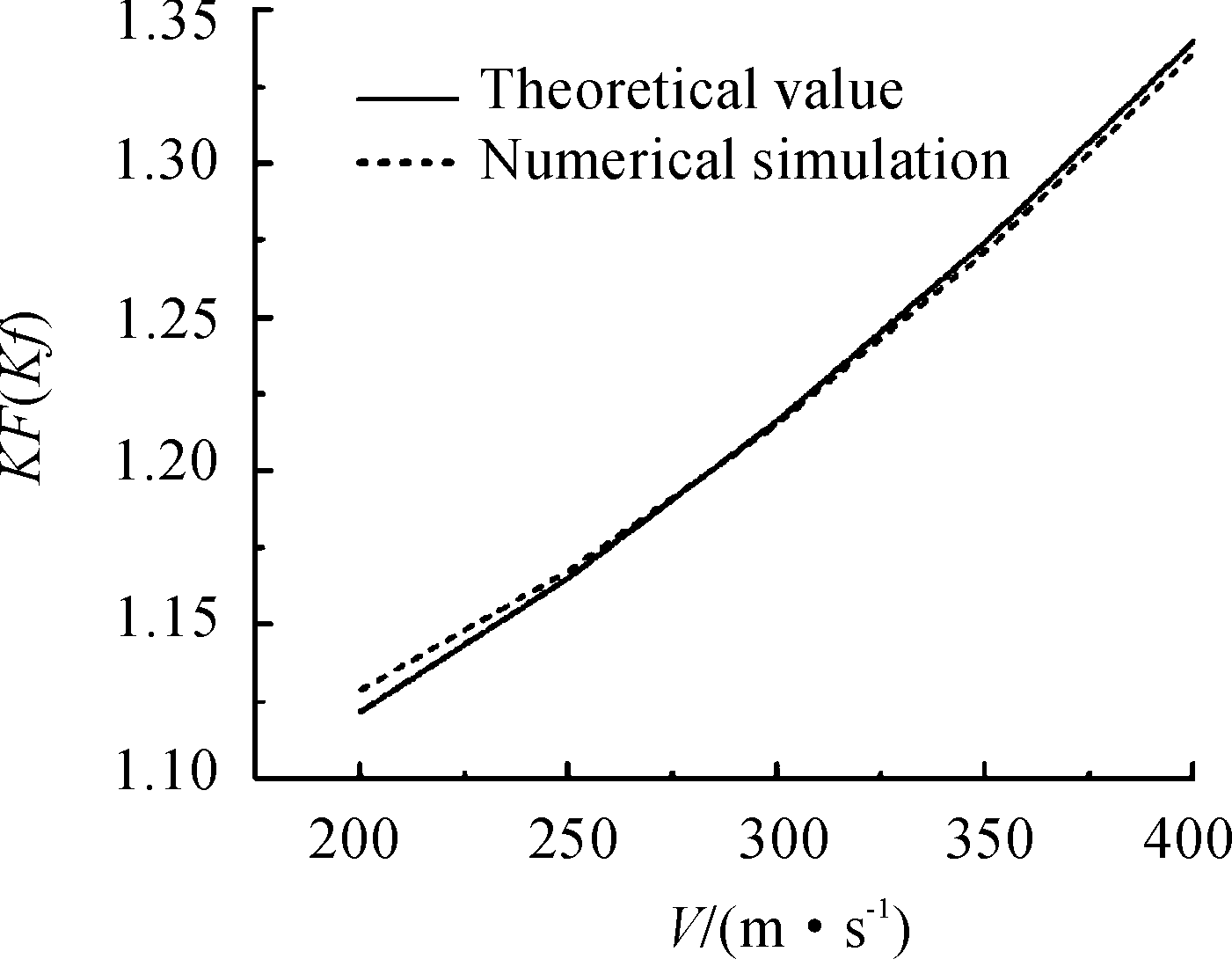
图5 KF与Kf等效结果曲线
2.2 螺旋槽随进弹丸侵深的工程计算参数
本文对于4种不同螺纹数n的螺纹槽随进弹丸侵彻目标过程进行了仿真,结果如下:
对于螺旋槽随进弹丸D型,由图6可以得出,不同圈数螺纹结构侵彻过程中其槽内所受应力区域不同故而等效阻力面也不同,由参数Kx定义:
Kx=45/(45+0.03×360n)
(5)
Kx表征螺旋刻槽弹丸等效截面面积与直槽弹丸截面面积的比值。而运动过程中弹体速度分解为垂直于槽壁的速度和平行与槽壁的速度,因此螺纹刻槽圈数不仅影响头部等效阻力面,也会通过槽壁受力影起弹丸转动,进而进一步转化为沿槽壁方向的侵彻效果。通过运动分析,对螺旋刻槽结构引入系数:
(6)
Ku表征侵彻过程中螺纹对于轴向、径向受力的影响,ln为螺纹长度,a为槽深。进一步提出螺旋系数Kq,由下式定义:
Kq=Kx·Ku(刻槽);Kq=1(非刻槽);
(7)
此时:
P+=P·Kq·Kf
(8)
其中P为原随进弹丸公式计算数据。各参数参见前文,表4列出初速250 m/s不同n值螺纹槽弹丸侵彻值。

图6 不同圈数螺纹结构侵彻700 μs应力云图
表4 D型弹丸的侵彻值

n模拟仿真值/mm公式计算值/mm1/12123116.57601/6119113.74571/4118110.65681/3116107.3508
最终计算值与仿真值误差分别为5.5%、4.6%、6.6%、8.1%,而根据本文2.4节分析,原始公式与本文仿真模型误差最大值为9.5%,可见本文公式推广具有较好的准确性和一致性。
3 结论
1)提出了新的刻槽随进弹丸计算参数方法具有较好的计算精度,适合工程人员实际设计使用;
2)螺纹槽弹丸在不加转速的前提下侵彻阻力大于直槽弹丸。
[1] 王静,王成.修正的卵形弹丸侵彻带有预制孔混凝土靶板的理论模型与数值模拟研究[J].计算力学学报,2009,26(4):558-561.
[2] TELAND J A.Cavity expansion theory applied to penetration of targets with pre-drillde cavities[C]//19th International Symposium of Ballistics,2001:1329-1336.
[3] 王震宇,陈江,张镇锋,等.一种串联子弹随进故障分析研究[J].兵器装备工程学报,2017,38(7):42-45,56.
[4] 邓佳杰,张先锋,陈东东,等.串联随进弹侵彻预开孔靶弹道轨迹的数值模拟[J].兵工学报,2016,37(5):808-816.
[5] 何丽灵,陈小伟.高速侵彻先进钻地弹缩比弹质量损失的实验研究[C]//第十届全国冲击动力学讨论会论文集.中国力学学会爆炸力学专业委员会冲击动力学专业组,太原:2011:1-7.
[6] 梁斌,陈小伟,姬永强,等.先进钻地弹概念弹的次口径高速深侵彻实验研究[J].爆炸与冲击,2008,28(1):1-9.
[7] WANG Y N,WU H J,HUANG F L.Penetration concrete targets experiments with non-ideal & high velocity between 800 and 1100m/s[J].International Journal of Modern Physics,B.Condensed Matter Physics,Statistical Physics,Applied Physics,2008,22(9/11 Pt.1):1087-1093.
[8] ERENGIL M E,CARGILE D J.Advanced projectile concept for high speed penetration of concrete targets[C].The 20th International Symposium on Ballistics.Florida:National Defense Industrial.Association,2002.
[9] ZVI R,EREZ D.Terminal Ballistics[M].北京:国防工业出版社,2014:86-86.
[10] 张欣欣.刻槽弹体高速侵彻混凝土响应特性研究[D].北京:北京理工大学,2016.