制退机是控制火炮后坐时的受力和运动规律的关键部件,起到消耗后坐能量、平稳后坐的作用。制退机常见结构形式主要有节制杆式、沟槽式、筒壁沟槽式等[1],同时也不断有新兴结构的制退机涌现出来。制退机的液压阻力系数是非常关键的一个参数,它与流道结构特征和流速密切相关,对制退机理论计算和结构设计有着重要意义。针对新设计的制退机,通常根据经验按相似结构类比的方法确定,再结合试验进行反复修正,实际结果一般与初定值偏差不大。若所研究的制退机不是采用那些已经发展的较为成熟的结构形式时,类比取值的方法将不再适用。
近几年计算流体力学(CFD)开始广泛应用于复杂流场问题的研究中。范永等[2]通过流体力学仿真软件对制退机内部三维流场进行了数值模拟,将制退机内部流场分布规律较为准确的显示出来,同时根据计算得到了火炮后坐时制退机内部液体流动时的液压阻力系数。张晓东等[3]研究分析了标准k-ε模型、Realizable k-ε模型和RNG k-ε模型对模拟计算制退机内部各腔室产生的不同影响结果,得出了标准k-ε模型效果最优的结论。潘孝斌等[4]针对某筒壁沟槽式制退机,为了确定合理的液压阻力系数K的取值范围,以及其影响参数、变化规律等,通过筒壁沟槽式制退机主流流道特征进行分析,并以某成熟制退机为例进行了方法验证。上述相关方法与湍流模型的选取都为后续研究提供了很好的借鉴作用,本文通过数值模拟仿真的方式对一种新型阀控式制退机的液压阻力系数与流场情况进行分析研究,为之后的相关试验提供一定的数据参考。
1 新型阀控式制退机工作原理与试验背景
新型阀控式制退机的结构原理示意图如图1,它的主体结构依然是由活塞、制退杆与外筒组成,不过与传统制退机的区别在于其活塞分为动、静两部分,静活塞与制退杆一体,开有8个圆形流液孔;动活塞通过电机、减速机控制,经由止推轴承作用与静活塞实现相对旋转运动,其表面同样开有8个完全相同的圆形流液孔。当外力作用制退机工作时,制退杆与活塞整体进行轴向运动,动活塞通过周向旋转不同的角度,使初始的圆形流液孔形成错位,改变流道面积,从而产生不同大小的液压阻力。
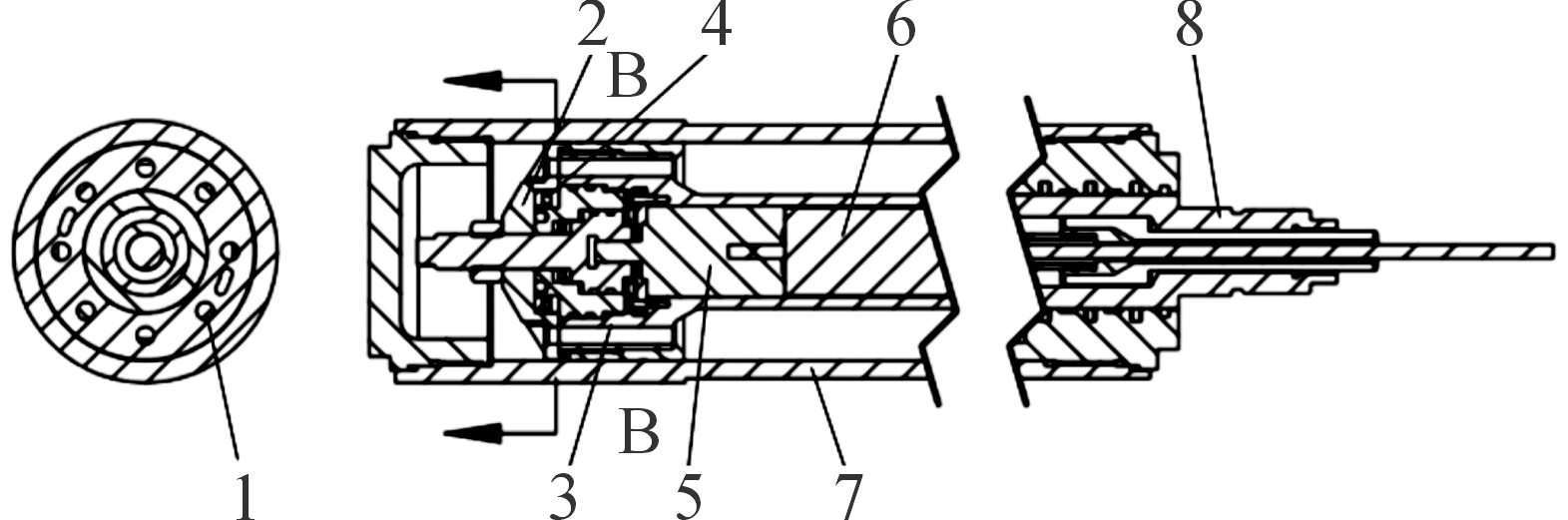
1.流液孔;2.动活塞;3.静活塞;4.止推轴承;5.减速机;6.电机;7.外筒;8.制退杆
图1 新型阀控式制退机结构原理示意图
新型阀控式制退机应用在火炮实弹射击前,为了降低风险,需要先进行台架试验,以验证其对冲击载荷的缓冲作用。
试验台架结构示意图如图2,顶端悬挂重物,制退机主体部分固定于试验台架底部,重物与制退机之间通过滑轮组件与绳索相连。重物先进行自由落体运动产生一个初速度,来近似模拟火炮发射时产生的冲击力,随后绳索收紧,制退杆开始被拉出,同时由电机与减速机所控制的动活塞进行周向旋转改变流液孔的大小,二者所产生的后坐阻力将对重物下落过程进行缓冲,最终使重物能够在工作行程中平稳缓冲。
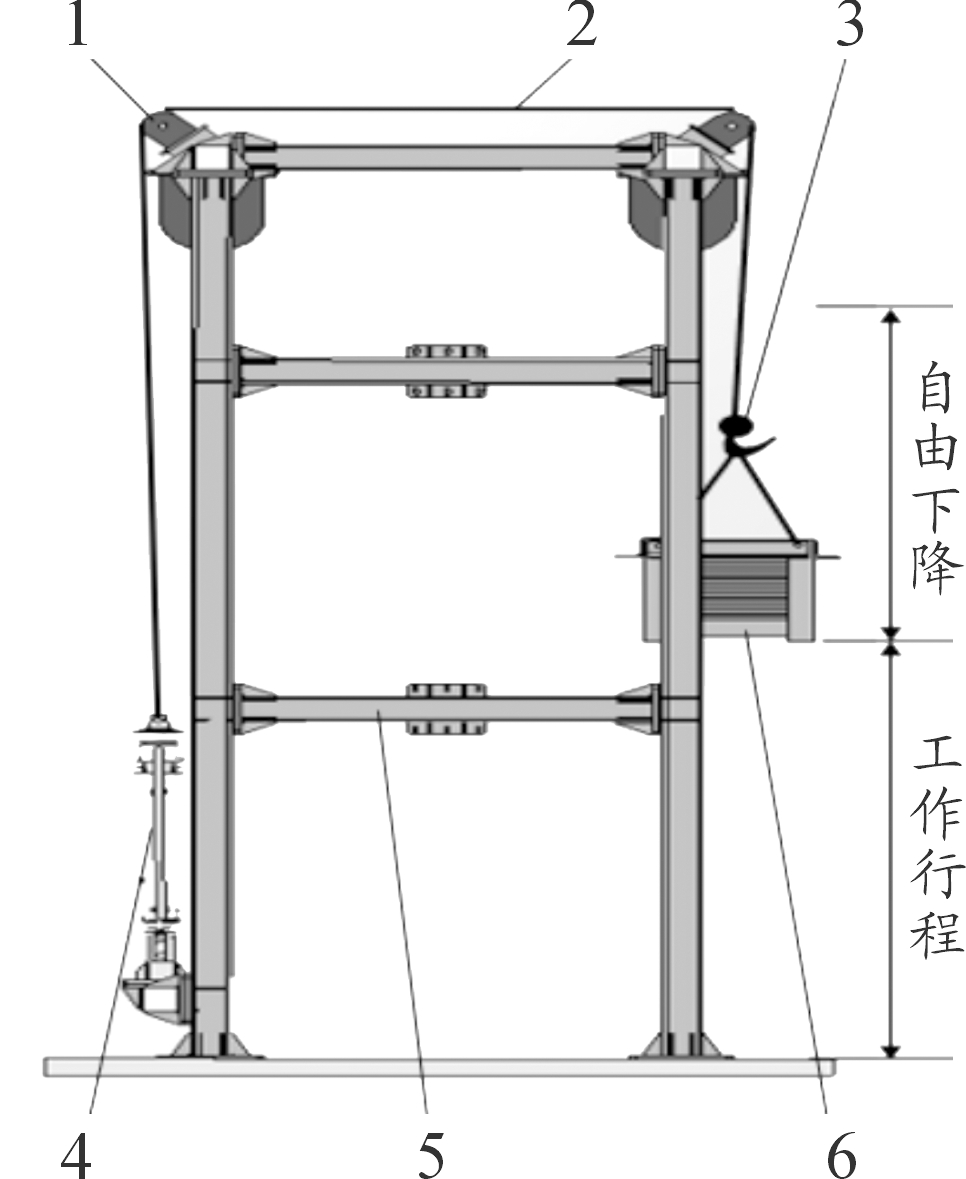
1.滑轮组件;2.绳索;3.挂钩;4.阀控式新型制退机;5.台架主体;6.重物
图2 试验台架结构示意图
分析可得制退机台架试验中的动力学方程为
(1)
式中:M为重物的质量,X为工作行程,即制退机的后坐行程,g为重力加速,Fr为缓冲时的后坐阻力,Ff为制退机中结构因素产生的阻力。
2 流场建模与仿真
2.1 模型分析
由于动、静活塞位置交错而产生的流液孔面积形状是不规则的,流场中的阻力损失不适合用流体力学给出的公式进行计算。可通过流场仿真[5-8],模拟制退机工作时的内部流动,根据流场结果反推,确定液压阻力系数K。
为了便于研究分析制退机工作时的流场情况,可以将模型进行简化,如图3。
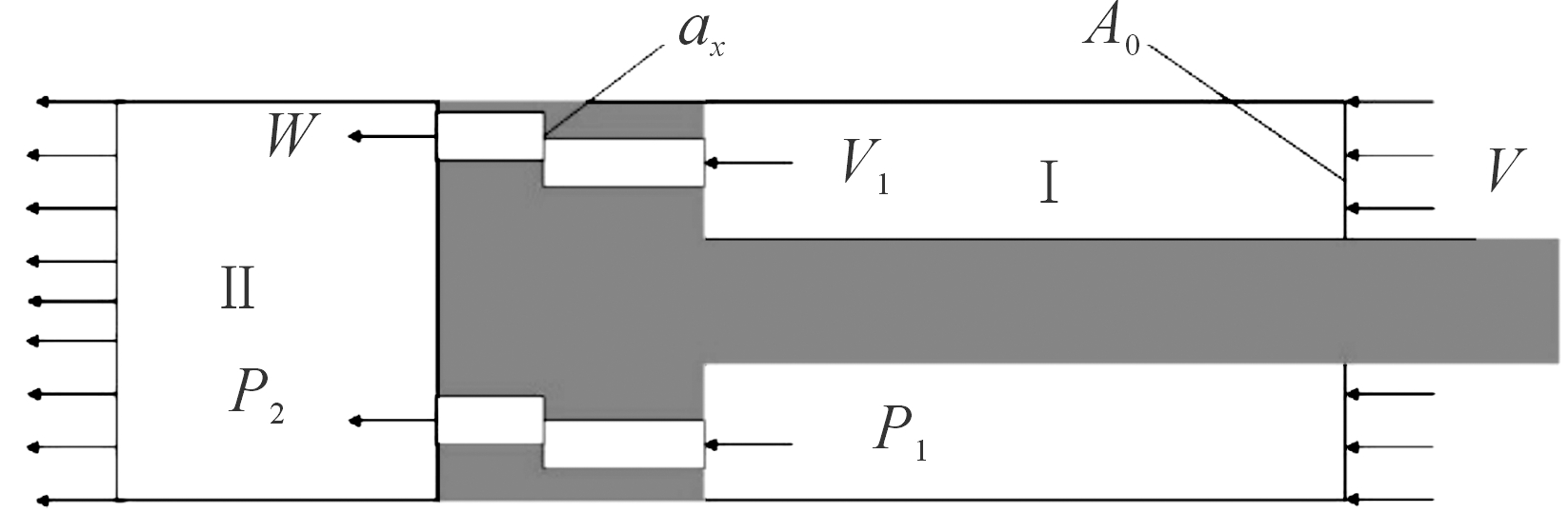
图3 制退机流体流动简化模型
简化模型中将活塞与外筒固定,通过设置入口的边界条件实现了等效流动。活塞将制退机内腔分为Ⅰ和Ⅱ两部分,取Ⅰ腔中的断面压力为p1,即为活塞工作面所受到的平均圧力;Ⅱ腔中的断面压力为p2,由于制退机在实际工作过程中会在Ⅱ腔形成真空区域,故p2可以忽略不计,即p2=0。入流速度为V,制退机工作时,液体从Ⅰ腔通过动、静活塞产生的流液孔流向Ⅱ腔,其在Ⅰ和Ⅱ腔中的速度分别为V1与ω,其中V1=V。A0为入流断面面积,ax为动静活塞错位产生的流液孔面积。由此模型可以得到液压阻力的计算公式为
Fr=p1A1-p2A2=p1A0
(2)
式中:A1为活塞的工作面面积,且A1=A0;A2为活塞的非工作面面积。
同样,根据该模型可以引入伯努利方程如式(3)所示
(3)
式中:z1、z2为流体的位置高度,在简化模型中可认为z1=z2;ρ为液体密度;![]() 和
和![]() 分别为液体在Ⅰ腔与Ⅱ腔的比动能,V2=ω;Hγ为流动能量损失,它与比动能成正比,如下式所示
分别为液体在Ⅰ腔与Ⅱ腔的比动能,V2=ω;Hγ为流动能量损失,它与比动能成正比,如下式所示
(4)
式中:ξ为液流损失系数。
同样,由流体的连续方程可得液体流动速度与液流截面积的关系如下
(5)
联立式(3)(4)(5)并化简得
(6)
工程实践中会将1+ξ用修正系数K来代替,即为制退机的液压阻力系数,故可得其计算公式为
![]()
(7)
由于![]() 是一个极小的值,因此可将上述公式简化为
是一个极小的值,因此可将上述公式简化为
(8)
在实际情况中,活塞工作时的轴向运动速度,即后坐速度V′与简化模型的入流速度V有如下关系
(9)
因此,在已知其他条件的情况下,设定不同的入流速度V进行流场仿真,就可由以上公式计算得到制退机的液压阻力系数。
2.2 液压阻力系数研究方法验证
本文拟采用流场数值仿真方法对新型阀控式制退机进行仿真分析,对其液压阻力系数的取值范围进行研究。为了确保流场数值仿真分析的可信度与可行性,本文先以较为成熟的某105 mm火炮节制杆式制退机进行分析[4]。其工作原理简图如图4。
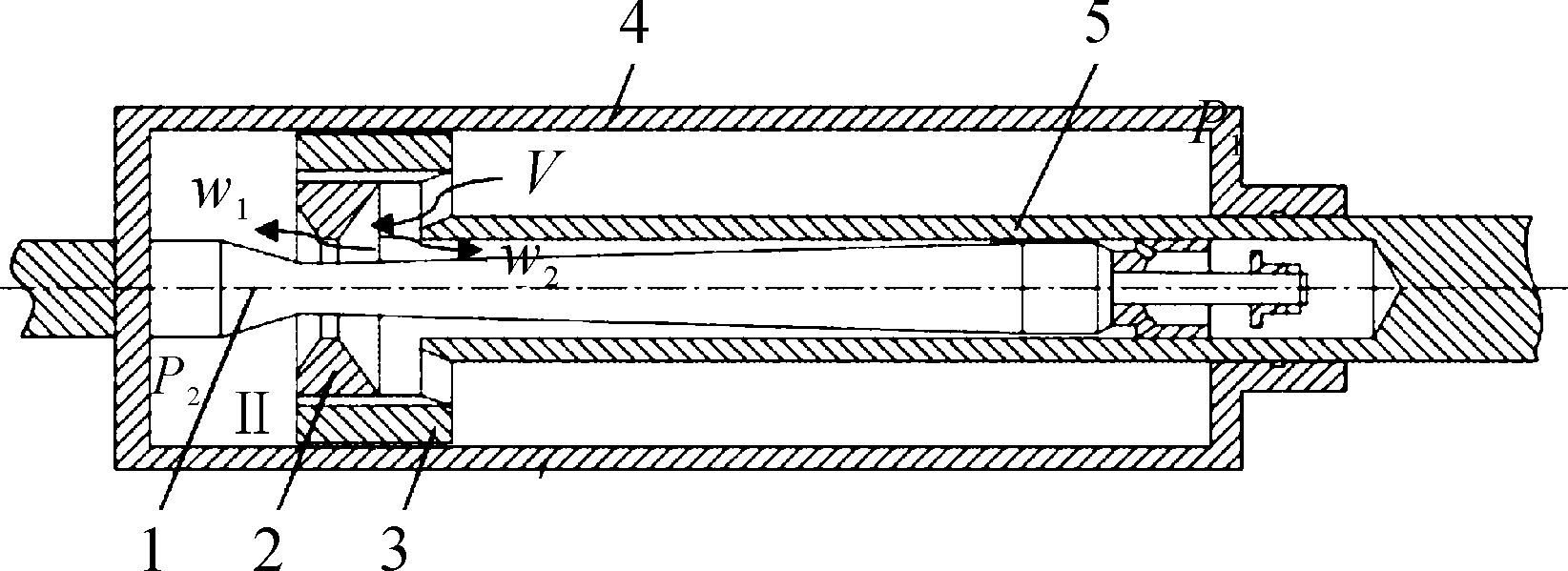
1.变直径节制杆;2.节制环;3.活塞主体;4.外筒;5.制退杆
图4 节制杆式制退机工作原理简图
由图4可知,其结构与图3类似。节制杆式制退机内腔主要分为Ⅰ和Ⅱ两部分,Ⅰ腔中的断面压力为p1,Ⅱ腔中的断面压力为p2。制退机工作时,会在Ⅱ腔形成真空区域,即p2=0。液体从Ⅰ腔以速度V流入后,经过变直径节制杆与节制环形成的流液孔ax以速度ω1流入Ⅱ腔,它是产生制退机液压阻力的主要部分,称为主流。本节主要针对节制杆式制退机的主流进行研究验证。
为了后续便于描述,本文将该制退机命名为A制退机。由于之后所研究的新型阀控式制退机的流液孔是通过动静活塞错位产生的,因此不太适合取二分之一的轴对称模型进行仿真分析,为了保证模型结构的一致性,A制退机也采用整个模型。针对该特性,建立的流场仿真计算模型如图5。
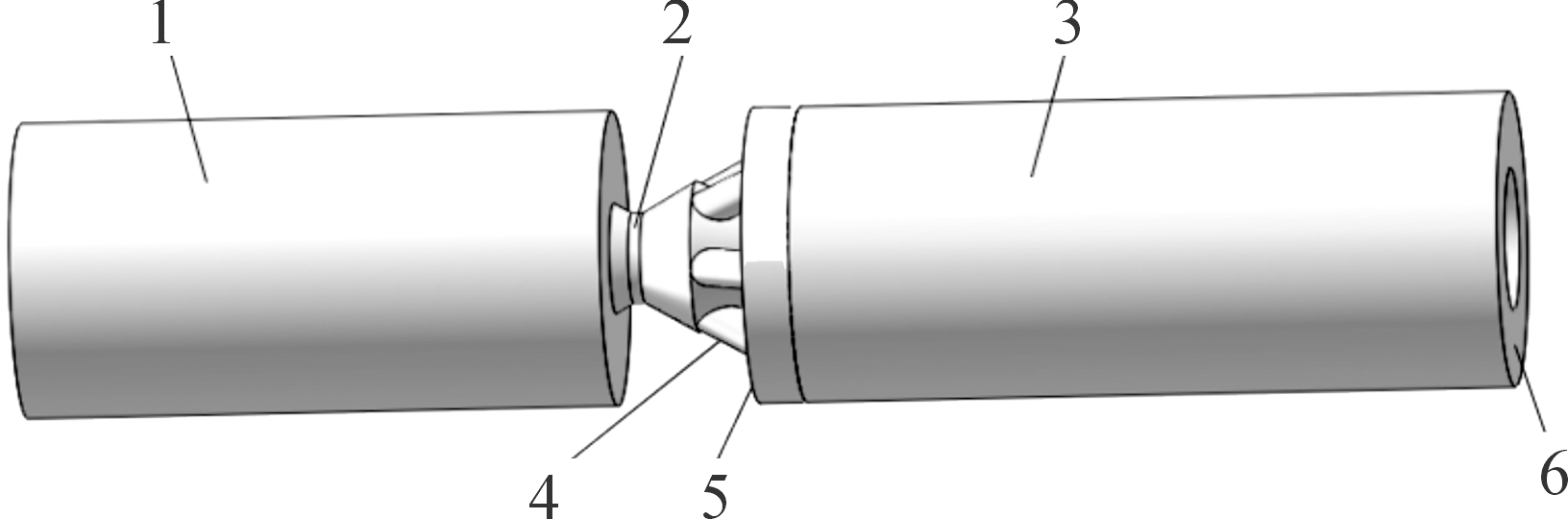
1.非工作腔;2.节制环;3.工作腔;4.流液通道;5.活塞壁面;6.液体入流处
图5 A制退机的流场仿真计算模型
对A制退机的流场仿真,采用标准k-ε湍流模型,非耦合方法、一阶迎风差分格式进行求解,制退液为不可压缩三维粘性流动,密度为1 100 kg/m2,动力粘度为0.001 kg/m·s。分别设定不同的入流速度V用来模拟制退机实际工作时的后坐速度V′,通过软件中的积分计算得到工作面受到的后坐阻力Fr,再带入到式(8)中求得相应的液压阻力系数K的值。
结合A制退机在实际工作过程中后坐速度的情况,通过式(9)的换算,取入流速度V的范围为1~12 m/s,间隔为1 m/s。图6为A制退机在入流速度V=12 m/s时内部流场的速度分布图,其中活塞工作面所受到的压力为320.1 kN。图中节制环处的液体流动速度与入流速度满足式(5)的流体连续方程,验证了理论上流场速度分布的规律。
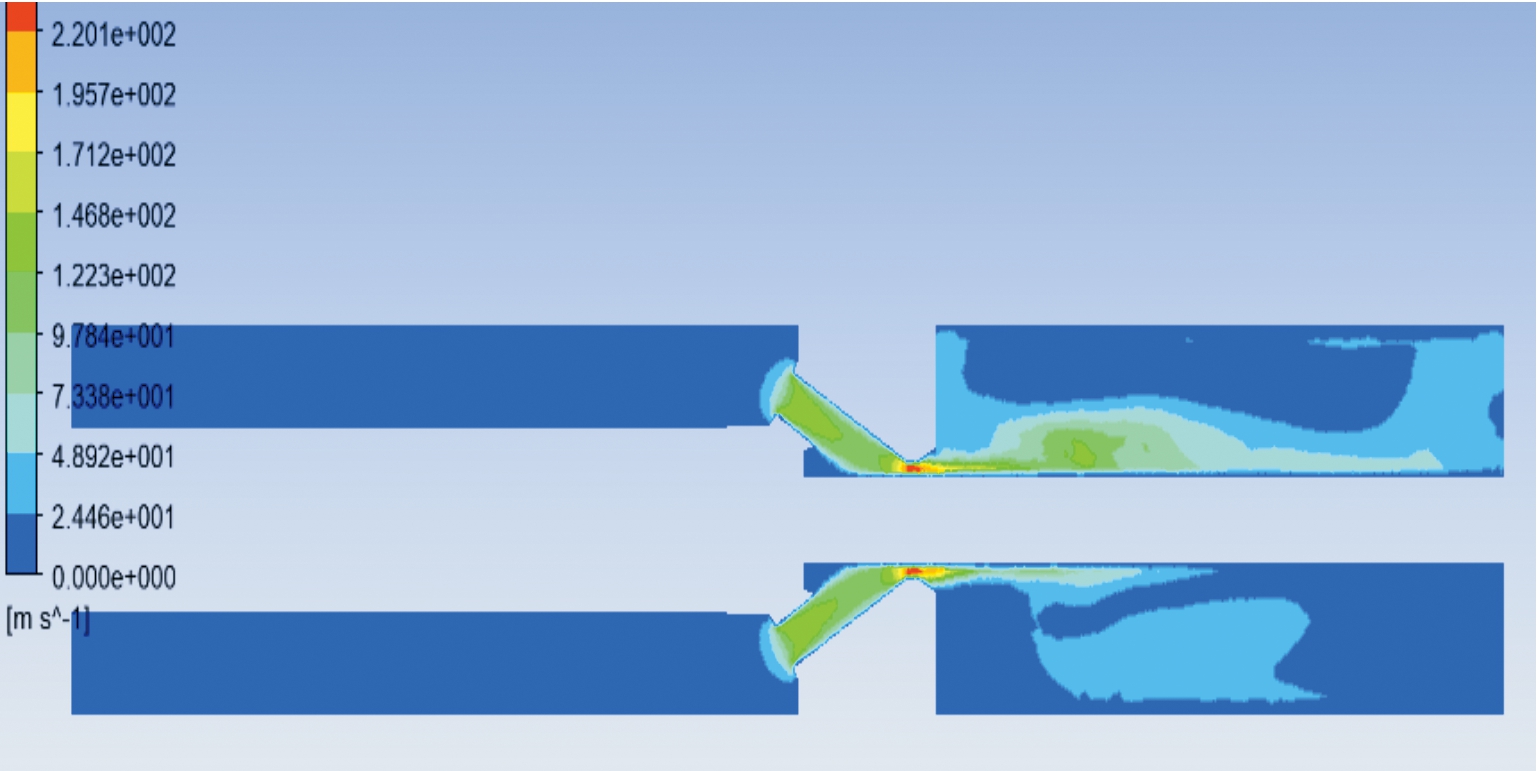
图6 A制退机的流场速度分布图
对不同入流速度情况下的流场模型进行仿真分析后,将得到的结果通过式(9)换算成后坐速度V′与液压阻力系数K的关系,拟合后的曲线如图7所示。
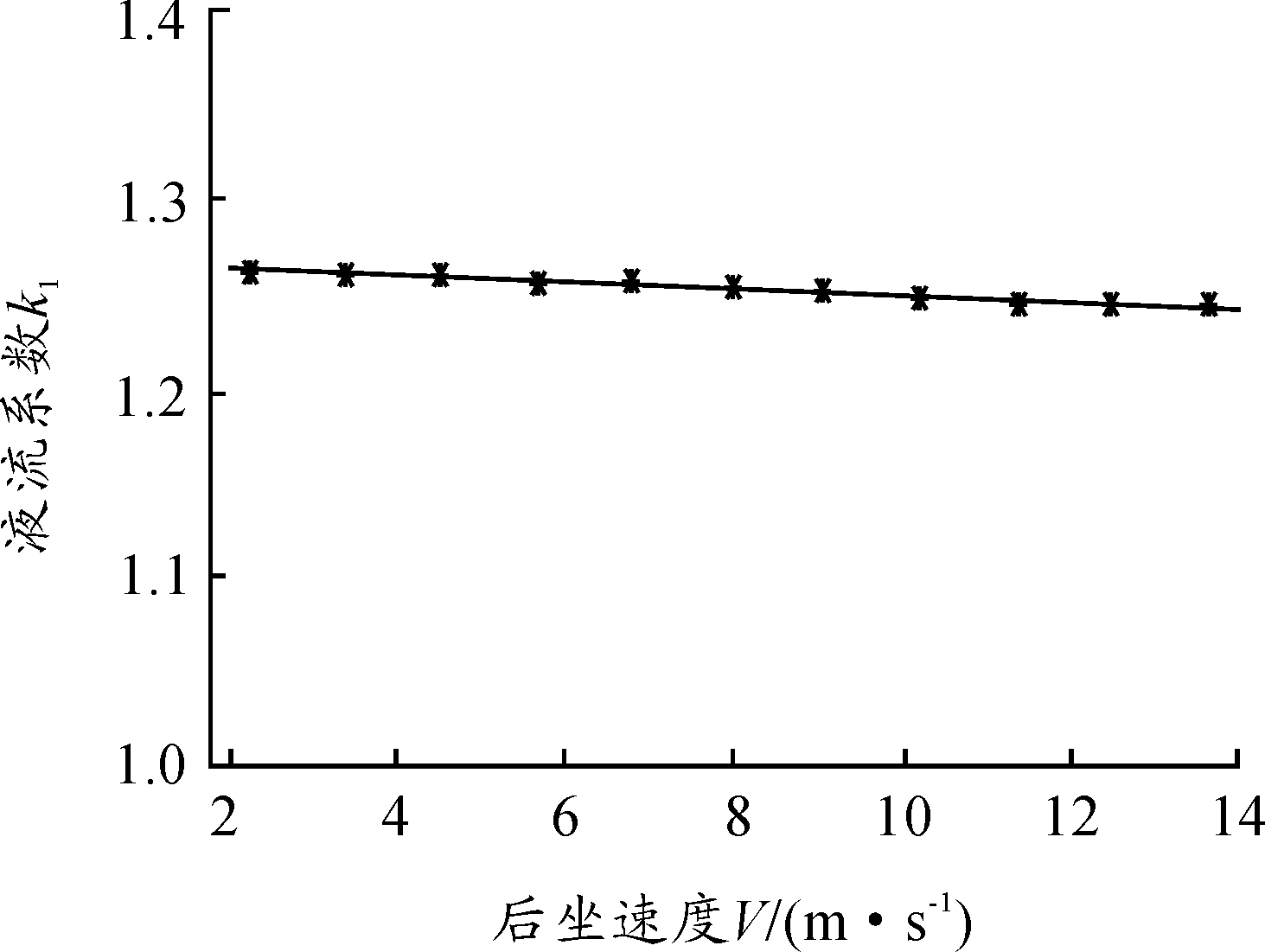
图7 A制退机的K值与后坐速度V′的仿真结果拟合曲线
根据图7的仿真结果拟合曲线可知,A制退机的液压阻力系数K的理论取值范围为1.2~1.4。查阅得到产品设计计算书中的取值K=1.27,该值在此范围内,同时也符合文献[1]中提供的取值范围,说明运用数值模拟仿真来研究分析新型制退机液压阻力系数K的方法是具有可信度与可行性的。
2.2 阀控式新型制退机液压阻力系数分析
影响新型阀控式制退机内部流场变化的因素除了结构特征和后坐速度以外,还与流液孔面积有关。而流液孔面积又由动活塞偏转角度决定。其中,制退机的结构特征已经给定,因此在工作过程中的变量主要为活塞整体的轴向后坐速度与动活塞周向旋转的角度变化。故在研究新型阀控式制退机的液压阻力系数时需要考虑这两个变量对它的影响。同样为了后续描述方便,本文将新型阀控式制退机命名为B制退机。根据初步设计的结构参数与图3的简化模型构建了B制退机用于流场仿真分析的模型,如图8所示。
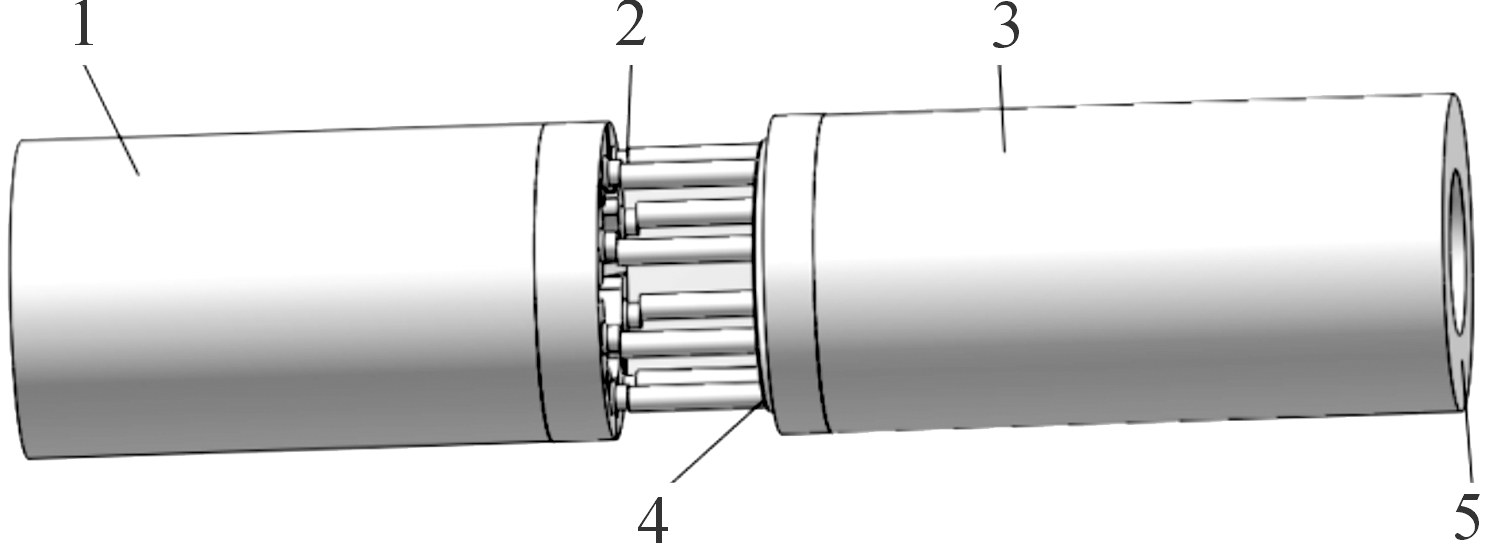
1.非工作腔;2.流液孔;3.工作腔;4.活塞壁面;5.液体入流处
图8 B制退机流场计算模型
同理,在流场仿真时,结合B制退机在台架试验中后坐速度的实际情况,通过式(9)的换算,取入流速度V的范围为1~6 m/s,动活塞的转角范围取0~11.8°。为了简化研究过程,本文取2~8°代表转动过程的前、中、后期进行仿真分析,间隔为1°,其对应的流液孔面积由大到小,取值范围在494.88~135.92 mm2。运用与前一节同样的计算模型、方法、差分格式以及制退液材料进行流场仿真分析。图9为入流速度V=6 m/s,动活塞转角为2°时B制退机的流场分布图,其中活塞工作面所受到的压力为64.7 kN。同样,图中流液孔处的液体流动速度与入流速度满足式(5)的流体连续方程,再次验证了理论上流场速度分布的规律。

图9 B制退机的流场速度分布图
运用上述计算方法,对不同入流速度和转角情况下的流场模型进行仿真分析,得到的结果通过式(9)换算成不同大小的流液孔ax所对应的后坐速度V′与液压阻力系数K的关系,拟合曲线如图10。
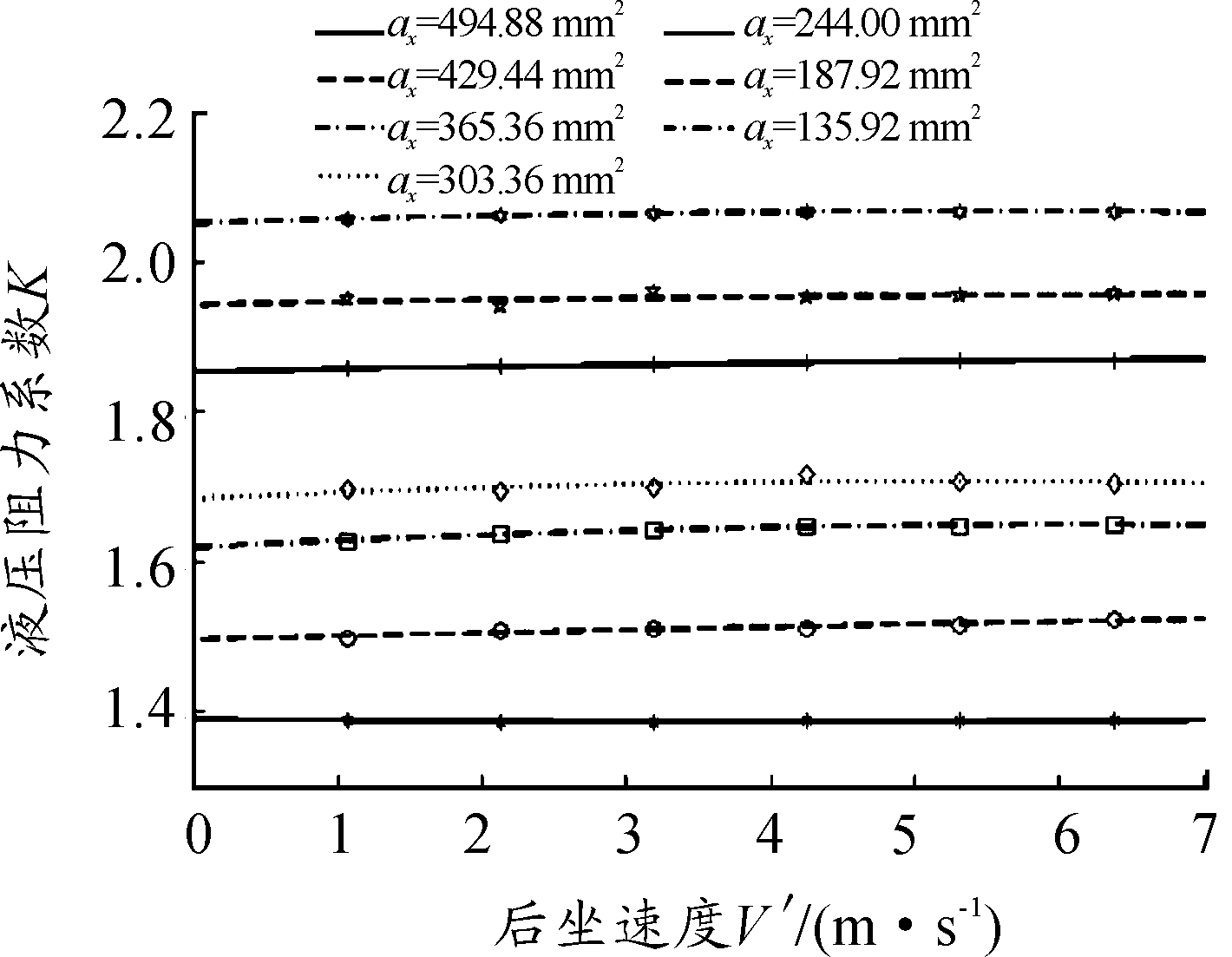
图10 B制退机的K值与后坐速度V′的仿真结果拟合曲线
从图10中的仿真结果拟合曲线可以看出,随着流液孔面积ax的减小,K值增大,但后坐速度V′的改变对K值的影响很小。同时得出B制退机的液压阻力系数K的取值范围为1.39~2.05,与A制退机相比,B制退机的K值较大,这是由两者不同的流场结构特征决定的,局部流动损失越大,液压阻力系数的值就越大。本次研究得到的结果,为今后新设计的阀控式制退机液压阻力系数K初值的设定,提供了必要的参考依据。
3 仿真结果的应用与验证
结合上述的试验背景与流场简化模型,可以进一步研究分析B制退机在连续工作过程中的状态,同时也为了验证K值范围的合理性,本文运用Matlab/Simulink软件建立运动仿真模型进行分析[9]。
由之前的流场仿真分析可知,K的取值与流液孔面积ax变化相关,后坐速度V′对K值的影响可以忽略,而流液孔面积又受到动活塞偏转角度的影响。故将图10数据进行插值,得到转角在2~8°时K值关于动活塞偏转角度θ的变化曲线 f(θ);而在8~11.8°采用工程实际中近似取固定值的方法将K值取为2.05,插值曲线如图11所示,该规律将应用于运动仿真模型中的计算[10]。
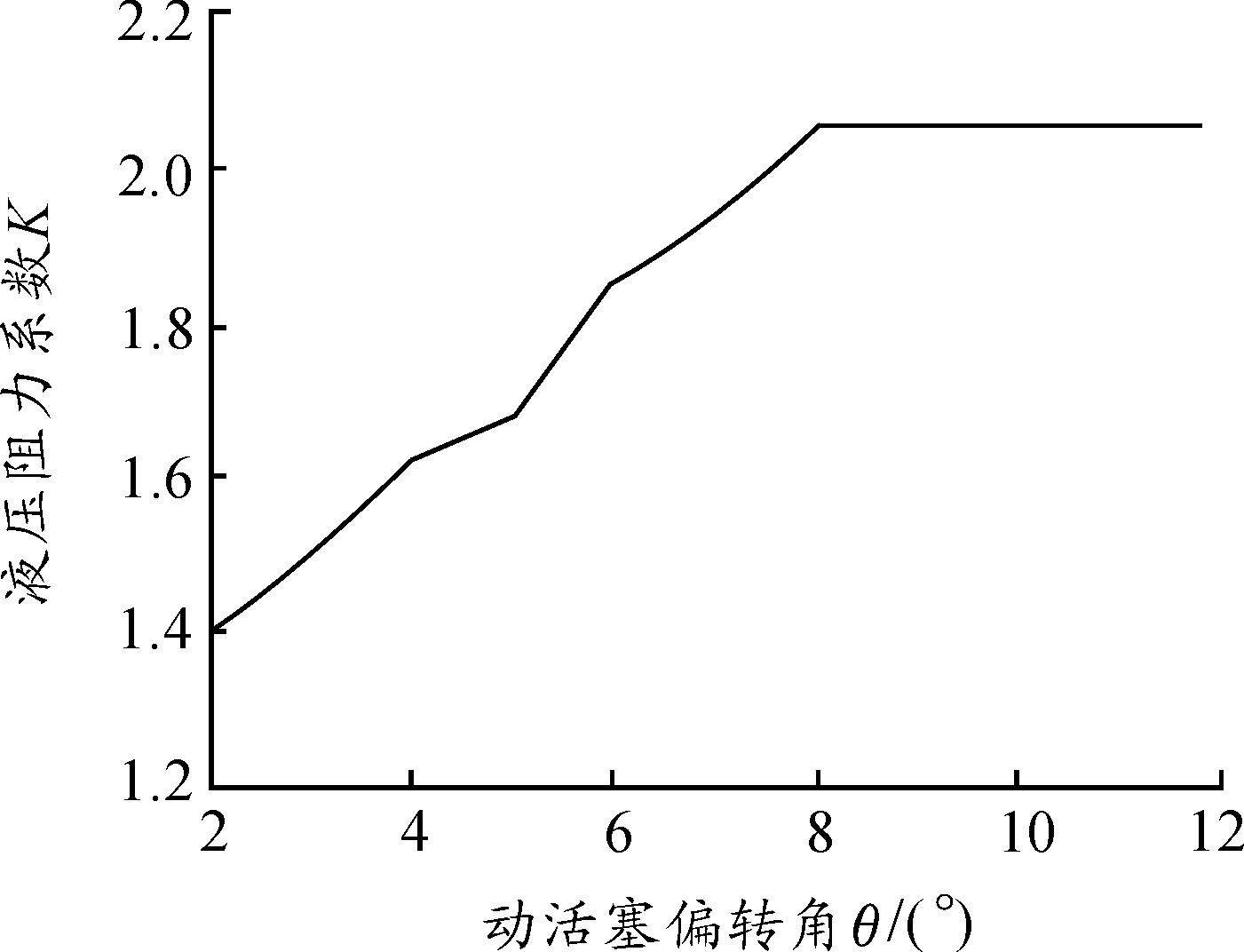
图11 液压阻力系数K的插值曲线
在实际工作过程中,后坐速度V′是不断变化的。在图3构建的简化模型中,由换算关系可知入流速度V也对应着这种变化,因此可以得到后坐行程X与入流速度V的关系如下
(10)
式中:t为缓冲过程所需的时间。
入流断面面积A0为已知量,流液孔面积ax的取值受到动活塞偏转角度θ的影响,根据几何关系可以得到流液孔面积的计算公式为
(11)
综上所述,将所有公式联立可得方程组如下
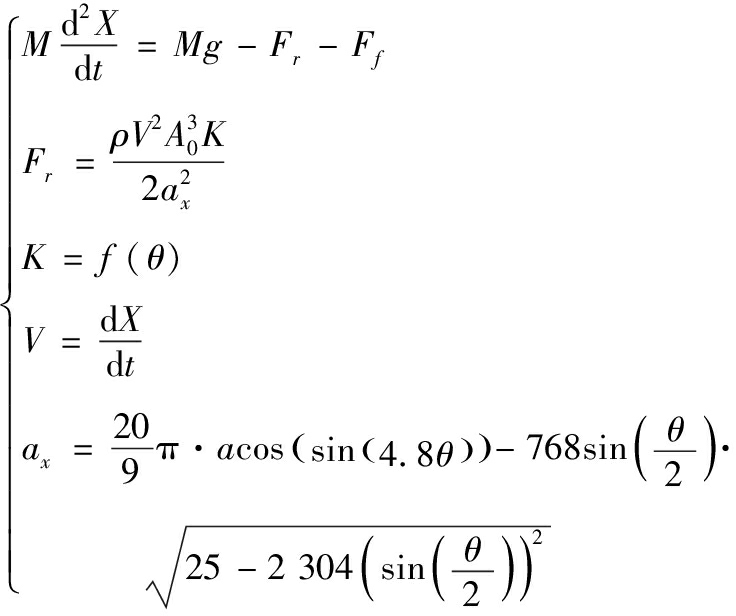
(12)
根据方程组(12)建立B制退机的运动仿真模型。仿真时,重物加速过程耗时为0.005 s,速度峰值为6 m/s,动活塞偏转角度起始为2°;进入缓冲过程后,动活塞偏转角度开始按照图12所示的规律进行变化,该变化规律是为了得到较为理想的后坐阻力曲线,通过反复修正和调整后最终确定的;由于在实际工况中,B制退机的工作行程最大为0.6 m,因此整个试验过程中的后坐行程不得超过此范围。
按照上述设置参数进行仿真后,得到了B制退机后坐阻力与后坐行程之间的关系曲线如图13所示。
由图13可知,曲线反映了B制退机的动态特性,最大后坐行程为0.463 9 m,满足台架试验所允许的最大后坐行程范围。在加速过程中,由于外部巨大的冲击载荷作用,后坐阻力先是讯速增大,达到一定值后,增加幅度慢慢趋于平稳;在缓冲过程前期,曲线平缓,后坐阻力变化较为稳定,当到达缓冲过程末期时,由于速度基本减小为零,使得后坐阻力急剧下降。该曲线所包含的图形面积即为B制退机所吸收的能量,图形形状类似于矩形,说明缓冲效果好[11]。因此,可以认为流场仿真所得到的液压阻力系数K的取值范围是合理的,同时该结果也为之后台架试验的相关研究提供了指导与借鉴作用。
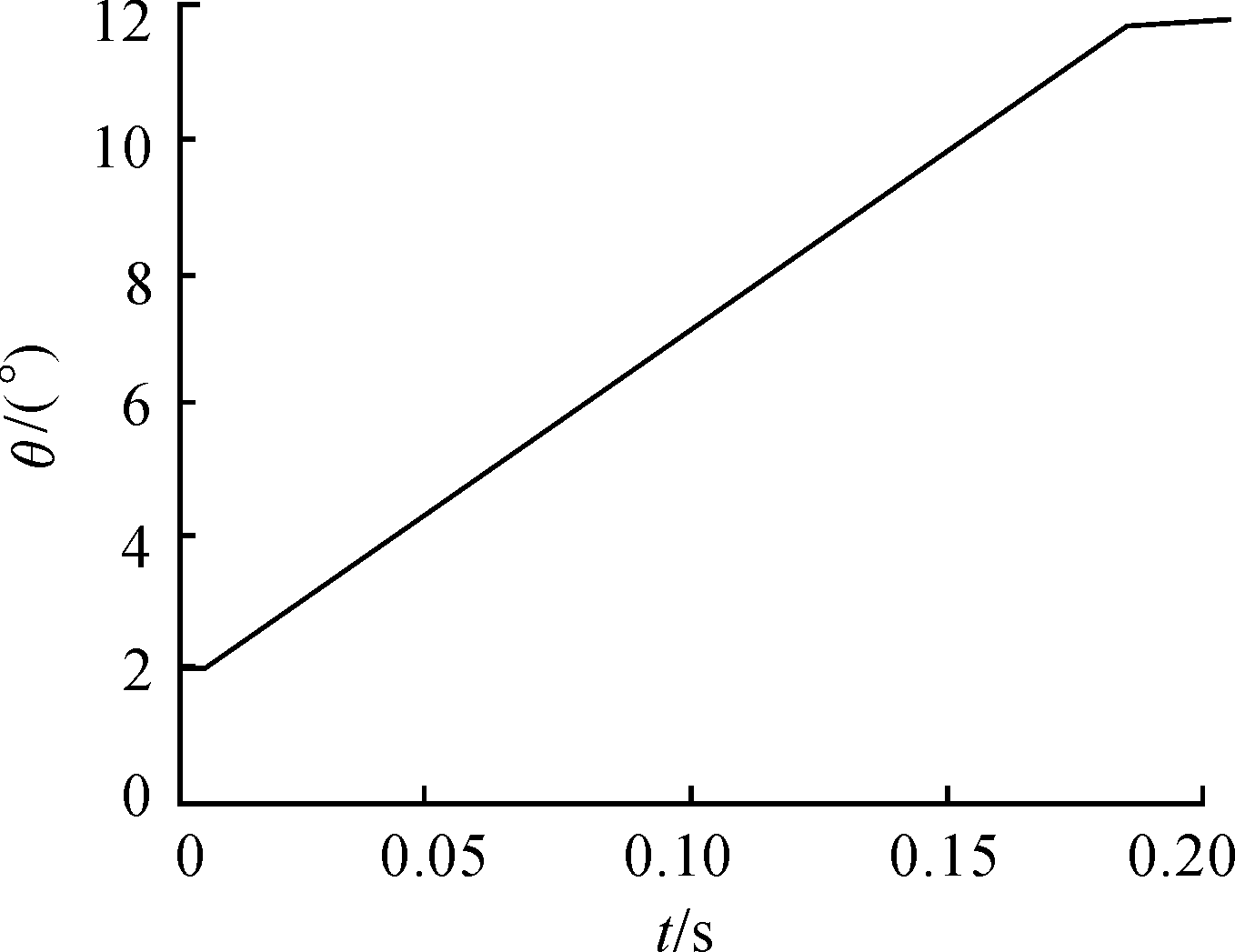
图12 动活塞偏转角度变化曲线

图13 后坐阻力与后坐行程之间的关系曲线
4 结论
1)通过等效简化了两种制退机的流场模型,采用流场仿真分析确定了两者液压阻力系数的取值范围。对某105 mm火炮节制杆式制退机的研究结果验证了流场仿真的可行性与可信度,运用同样分析方法确定新型阀控式制退机液压阻力系数值为1.39~2.05。
2)新型阀控式制退机的液压阻力系数K随流液孔面积ax的减小而增大,而后坐速度V′的变化对K值的影响很小,可以忽略不计。
3)运用Matlab/Simulink软件分析得到新型阀控式制退机在连续工作过程中的后坐阻力与行程的关系曲线,验证了流场仿真中所确定K值的合理性,可为之后的台架试验提供借鉴,为类似制退机结构的设计工程提供参考。
[1] 高树兹,陈运生,张月林,等.火炮反后坐装置设计[M].北京:兵器工业出版社,1995.
[2] 范永,刘树华,曹广群.基于动网格的某驻退机三维流场数值模拟与分析[J].火炮发射与控制学报,2010(4):63-65.
[3] 张晓东,张培林,傅建平,等.k-ε双方程湍流模型对制退机内流场计算的适用性分析[J].爆炸与冲击,2011,31(5):516-520.
[4] 潘孝斌,宋彦明,谈乐斌.筒壁沟槽式制退机主流液压阻力系数分析[J].振动与冲击,2016,35(17):146-150.
[5] WREN G P,RAY S E.Simulation of flow problems with moving mechanical components,fluid-structure interactions and two-fluid interactions and two-fluid interfaces[J].International Journal for Numerical Methods in Fluids,1997(24):1443-1448.
[6] 朱锐,郭保全,于斌.火炮制退机流场分析及节制环磨损机理研究[J].火炮发射与控制学报,2015,36(2):12-15.
[7] 谢立峰,郑建国,陈传君,等.考虑空化效应的制退机流场数值模拟[J].机械制造与自动化,2014,43(6):129-132.
[8] 狄长春,顾赵强.基于空化效应的某驻退机液压阻力仿真研究[J].润滑与密封,2016(2):114-117.
[9] 黄景峰,董楠,刘圣杰.基于Simulink的液压缓冲器动态特性分析[J].机床与液压,2015,43(13):145-148.
[10] 郝保臣,孙卫国,潘孝斌.某火炮液压缓冲器缓冲特性研究[J].兵器装备工程学报,2018,39(9):54-58.
[11] 马星国,鲁江,尤小梅,等.渐变式液压缓冲器的设计与仿真研究[J].机床与液压,2016,44(13):148-153