冲击波超压是武器弹药最主要的毁伤元,对绝大部分目标起主要毁伤作用,冲击波效应一般以冲击波超压峰值、正压持续时间和比冲量进行表征,通常关注的是冲击波各项参数中的某一项,而冲击波的整体波形往往被忽略。但事实上,冲击波波形对毁伤过程的研究具有重要作用,其直接与毁伤威力大小紧密相关。并且在对冲击波仿真计算分析时,为简化计算,往往将冲击波脉冲等效为三角波或矩形波,冲击波波形也是压力简化参数设置的重要依据[1]。对爆炸冲击波进行数值模拟时,有限元网格尺寸对数值仿真的精度具有很大的影响[2-5]。目前,已有部分学者提出或研究过爆炸波模拟中的网格尺寸效应。崔莹等通过开展钢管混泥土柱爆炸试验,分析不同空气和炸药网格尺寸对冲击波传播及数值分析结果的影响,最终确定网格尺寸为20 mm符合折合距离不超过1.1 m·kg-1/3试验条件下的爆炸数值模拟要求[6];Luccioni等[7]研究了利用流体力学软件模拟预测爆炸荷载时的网格尺寸效应,认为100 mm的网格尺寸就可以较为精确的模拟爆炸荷载的传播规律,而较粗的网格尺寸则仅仅可以用来定性的模拟爆炸荷载在城市复杂环境中的传播规律;石磊等[8]研究了与炸药当量相关的网格划分方法,并应用有限元软件LS-DYNA进行了计算对比,结果表明按照3/80倍炸药体边长进行网格划分在计算精度与计算效率上取得了很好的平衡;可见,不同研究者在研究中使用的网格尺寸有较大差别且只关注冲击波的个别参数信息,对冲击波的波形关注不够,模拟结果的精度不够。已有文献对网格尺寸效应的研究往往针对某一特定情况,故提出的网格尺寸的使用有较大的局限性。而且,由于爆炸问题的复杂性,多数爆炸冲击波的网格效应的研究均集中在理论分析和数值模拟的对比上,缺乏有效的实验验证。
本研究运用ANSYS/LS-DYNA软件对炸药在空气中的爆炸进行模拟,对比分析不同网格尺寸对冲击波波形的影响,得出与经验计算误差小于5%,并且计算时间合理的最佳网格划分尺寸。并进行爆炸实验,用本文得出的网格尺寸对实验进行模拟,与实验结果进行比较,模拟结果与实验结果的误差小于5%,证明本文结果的正确性与适用性。
1 爆炸冲击波及其经验计算方法
自由空气中的理想冲击波超压曲线,如图1所示。在冲击波到达之前,该处的压力等于大气压力P0,压力经过时间Tc由大气压力突跃至最大值。压力最大值与P0的差值,通常称为入射超压峰值P∞。波阵面通过后压力即迅速下降,经过时间Td,压力经指数衰减到大气压力并继续下降,直至出现负超压峰值,在一定时间内又逐渐地回升到大气压力[9]。

图1 理想冲击波超压曲线
目前常用的方法,是用比例距离表达冲击波的各种参数。比例距离为Z=R/W1/3。其中,R为测点与爆心之间的距离,W为等效TNT药量[10-13]。参照文献[8]和文献[9],选取以下经验公式。
Henrych根据实验提出冲击波的超压峰值(MPa)表达式为:

(1)
Henrych根据实验提出冲击波超压峰值(MPa)的表达式为:
0.05≤Z≤3
(2)
Chengqing Wu和Hong Hao给出了冲击波超压上升段(从大气压上升到峰值)持续时间的表达式为:
TC=0.001 9Z0.13C
(3)
萨多夫斯基建议爆炸冲击波超压持续时间为:
(4)
2 单元网格尺寸对爆炸冲击波波形的影响
分别取0.84 kg,13.12 kg,105 kg炸药作为计算模型,利用计算模型的对称性取1 /8模型进行计算,对称面采用对称边界,非对称面采用透射边界,炸药和空气均采用LS-DYNA Explicit 3D SOLID164模型,炸药边长为d,d分别取80 mm,200 mm,400 mm,模型如图2。当比例距离小于1.3时,网格尺寸对冲击波波形计算结果影响较大,这里计算并比较了比例距离小于1.3时的冲击波结果。

图2 计算模型
2.1 材料的状态方程和参数
空气采用*MAT_NULL材料模型,压力P用线性多项式状态方程*EOS_LINEAR_POLYNOMIAL来描述[14]。
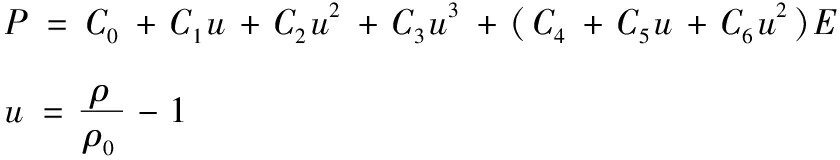
(6)
式中:E为单位初始体积内能;ρ为空气质量密度;ρ0为参考质量密度;线性多项式状态方程描述空气时遵守γ定律;V为初始相对体积;C0、C1、C2、C3、C4、C5、C6为实常数。材料参数如表1所示。
炸药采用ANSYS/LS-DYNA中的*MAT_HIGH_EXPLOSIVE_BURN材料模型,定义压力P为相对体积初始能量E的函数[15]。
(7)
式中: V为相对体积;E为单位体积内能;A、B、R1、R2、ω为表征炸药材料特性的常数。JWL状态方程参数及炸药参数如表2所示。
通过对爆炸冲击波已有研究成果进行对比分析,参照文献[6-8]和文献[11-13],发现当冲击波超压峰值的误差较小时,网格划分在炸药体边长的1/8至炸药体边长的3/80之间。所以,本文模拟时的单元划分尺寸w分别采用1/4、1/8、1/16、1/32倍炸药体边长(d)。
表1 空气参数
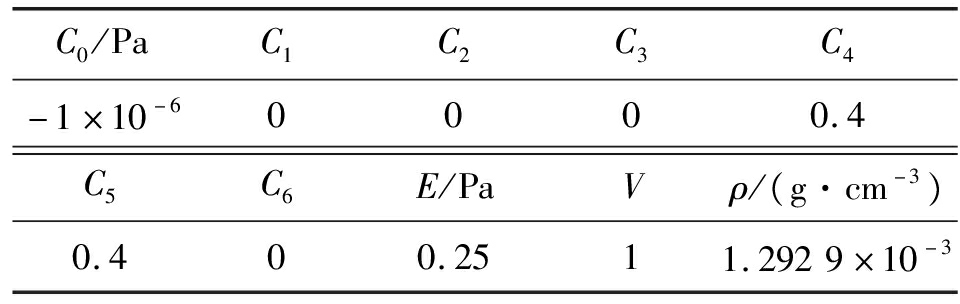
C0/PaC1C2C3C4-1×10-60000.4C5C6E/PaVρ/(g·cm-3)0.400.2511.2929×10-3
表2 炸药参数
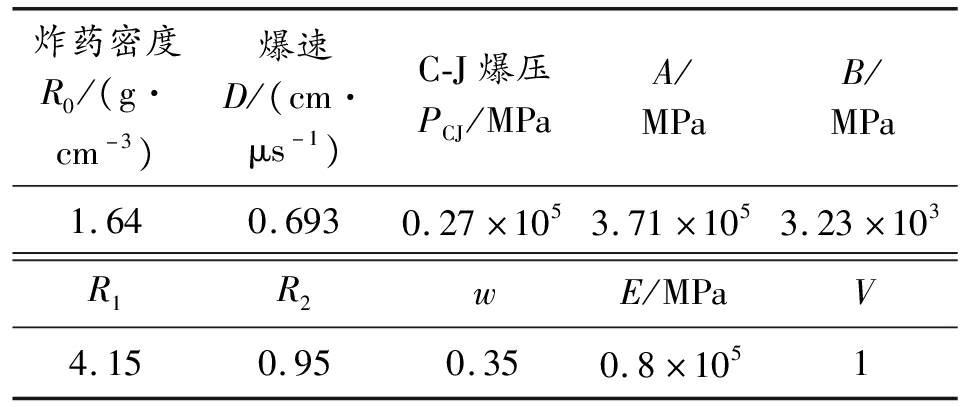
炸药密度R0/(g·cm-3)爆速D/(cm·μs-1)C-J爆压PCJ/MPaA/MPaB/MPa1.640.6930.27×1053.71×1053.23×103R1R2wE/MPaV4.150.950.350.8×1051
2.2 模拟结果及分析
图3(a),图3(b),图3(c)分别是d=80 mm,200 mm,400 mm时,分别按照1/4、1/8、1/16、1/32倍炸药体边长d进行单元划分的超压峰值曲线,图4、图5分别为图3相对应的正压时间曲线和超压上升时间曲线。可以看出:① 随着比例距离的增大,超压峰值的模拟结果与式(1)之间的相对误差越来越小;② 相同网格划分时,炸药的当量越大,在相同的比例距离,模拟结果的超压峰值相同,而超压上升时间和正压时间与式(3)和式(4)的误差越大;③ 爆炸冲击波的超压峰值,正压时间和超压上升时间随着单元尺寸的减小而越来越接近经验公式值,冲击波的从平滑曲线变为上升和下降明显的三角形曲线;④ 在比例距离为0.1~0.2时,网格划分为1/16d的冲击波各项参数的误差都大于5%,发现当进一步划分网格至1/32d时,0.1-0.2比例距离的冲击波各项参数很接近经验公式,误差小于5%。导致这种情况的主要原因可能是当网格划分的单元比较大时,提取点距爆心的比例距离小于0.1,这导致了计算数值提取点与相应比例距离的偏差,而在0.1~0.2比例距离内冲击波高频分量作用显著,受爆心距影响非常明显,这种微小的偏差足以导致计算结果的巨大差异。当网格划分的单元比较小时,这种偏差也就减小了,计算结果将更为精确。
进一步探究网格划分对冲击波结果的影响,对比分析不同网格划分对冲击波模拟结果和经验公式的误差,确定准确的单元网格划分方法。图6为比例距离为0.2时,炸药体边长d分别为80 mm,200 mm,400 mm时,不同网格划分的冲击波超压峰值和式(1)的误差曲线。在网格划分小于1/27d以后,误差均小于5%,认为是符合模拟的精度要求的。图7为比例距离为0.3时,d分别为80 mm,200 mm,400 mm时,不同网格划分的正压时间模拟结果和式(4)的误差曲线。在网格划分小于1/29d以后,误差均小于5%符合模拟精度要求。

图3 不同当量炸药不同网格尺寸的超压峰值曲线
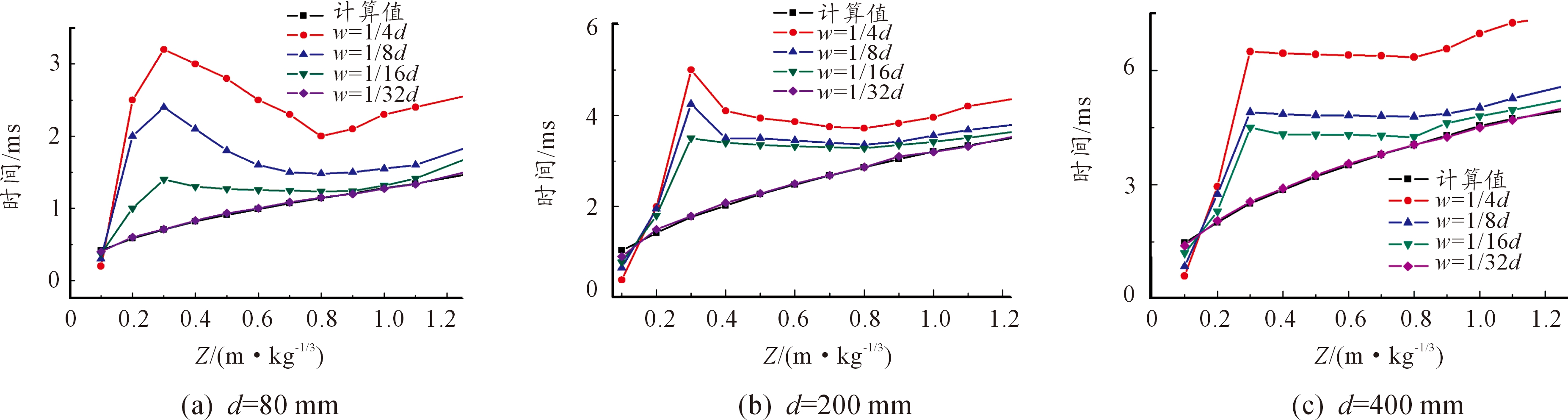
图4 不同当量炸药不同网格尺寸的正压时间曲线
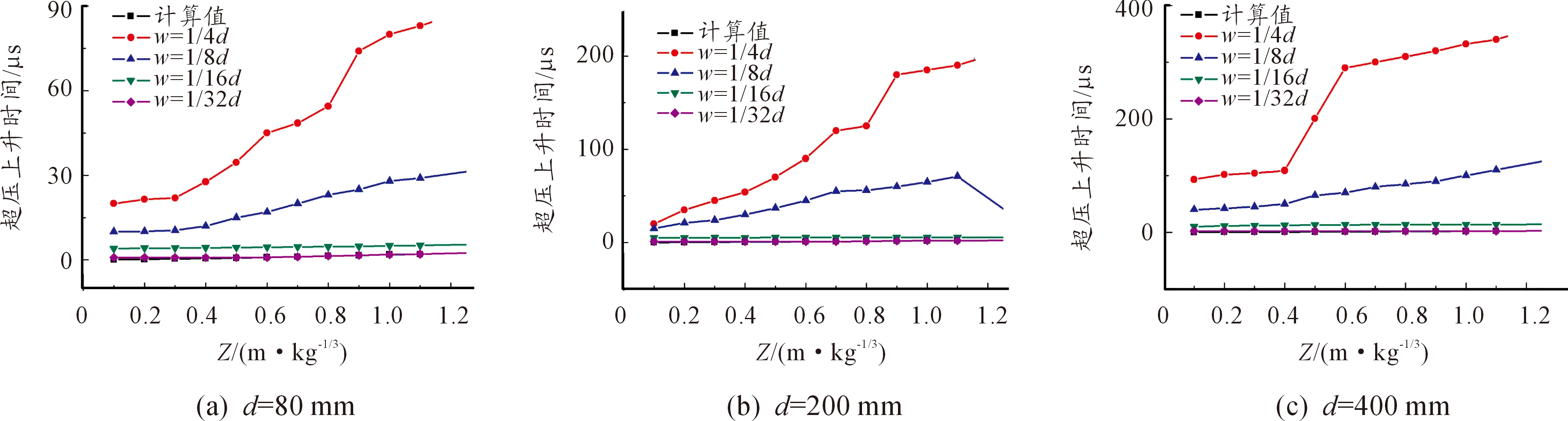
图5 不同当量炸药不同网格尺寸的超压上升时间曲线
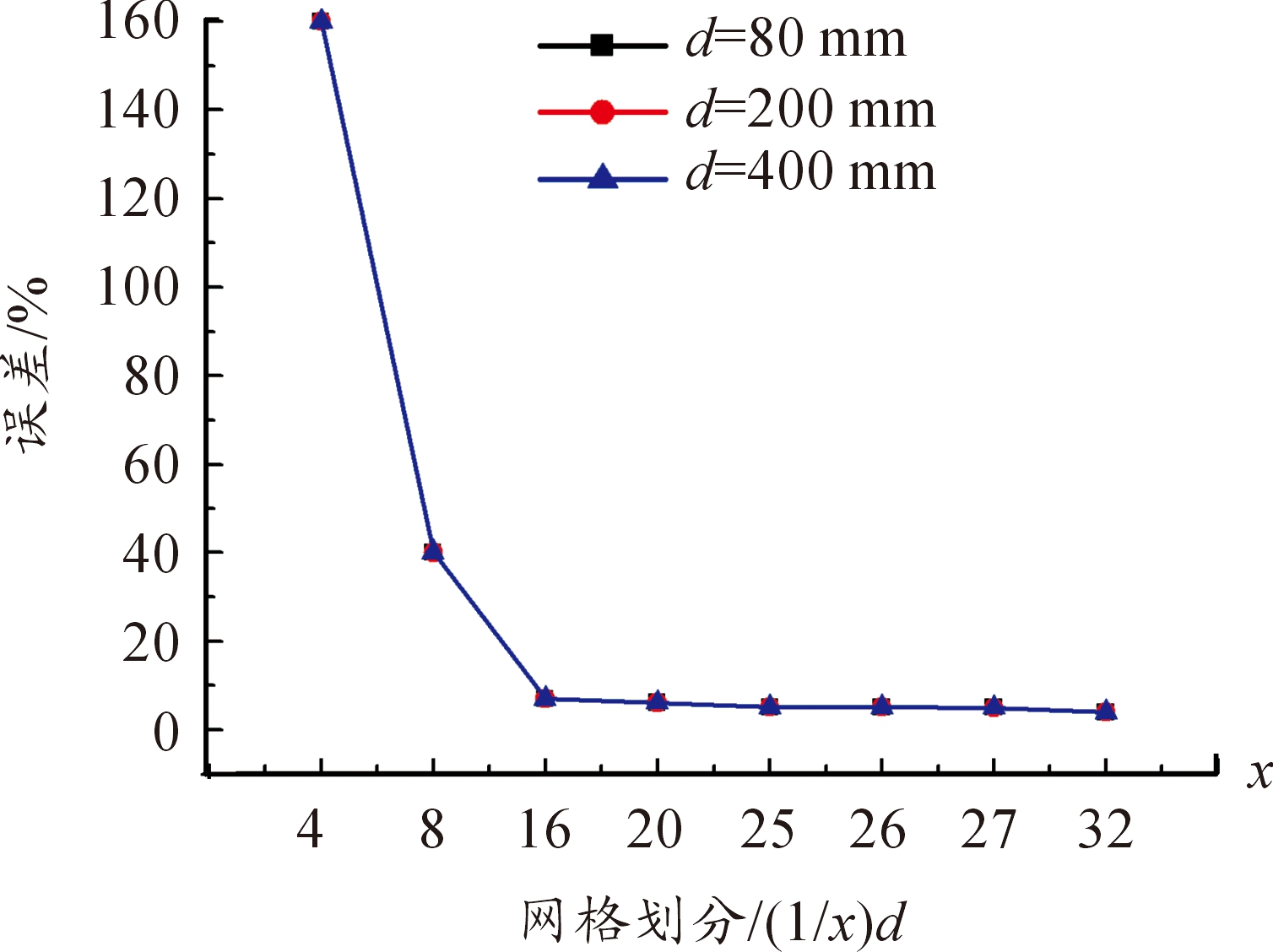
图6 不同网格划分的超压峰值和经验公式的误差曲线
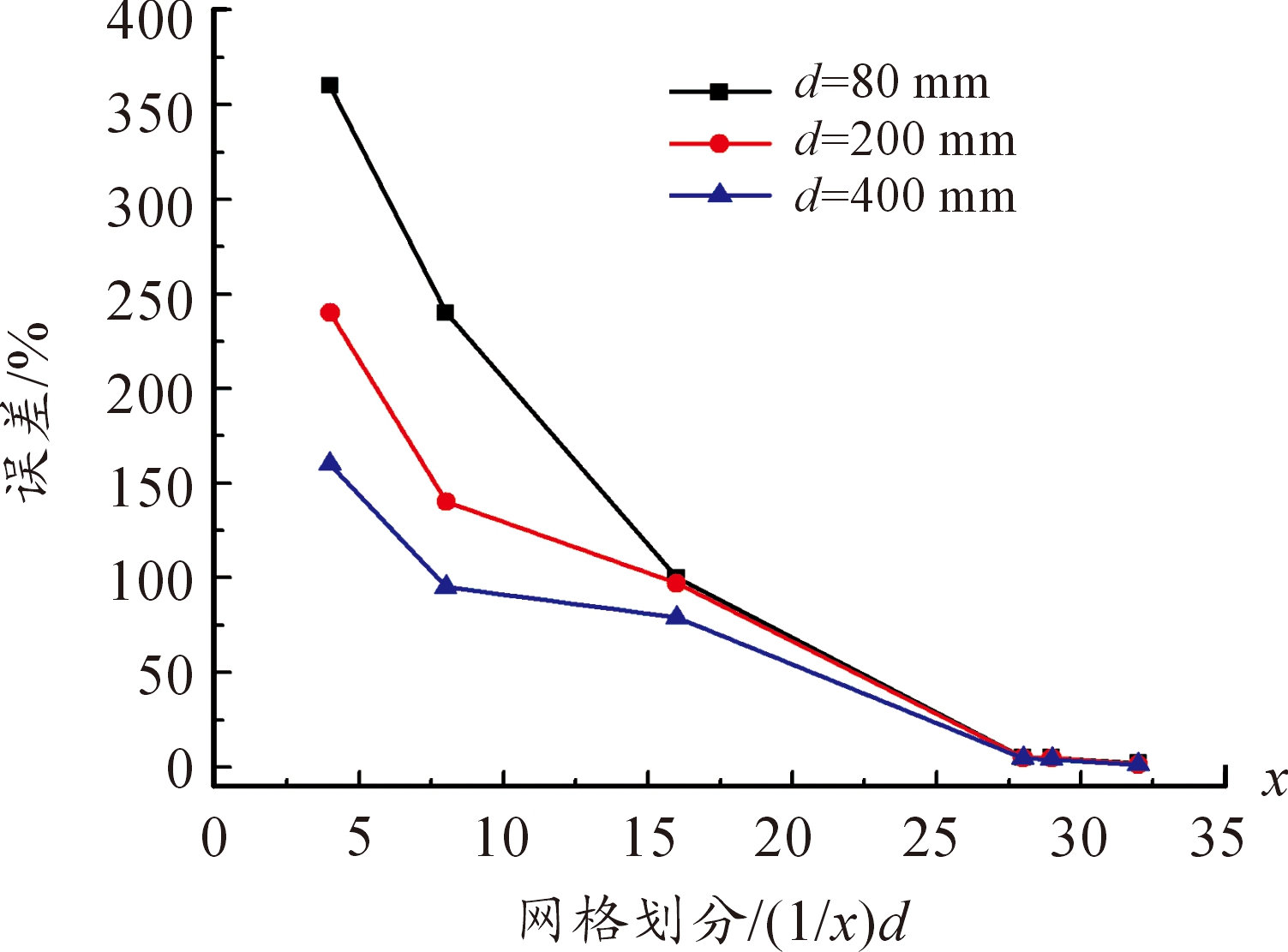
图7 不同网格划分的正压时间和经验公式的误差曲线
随着炸药当量的增大,相同网格划分的正压时间模拟结果和经验公式的误差逐渐减小。导致这种情况的主要原因可能是当炸药当量比较大时,相同比例距离的位置距离炸药的实际距离较远,当单元比较小时,计算数值提取点与相应比例距离的偏差减小了,计算结果将更为精确。
图8为比例距离为0.2时,d分别为80 mm,200 mm,400 mm时,不同网格划分的超压上升时间曲线和式(3)的误差曲线。在网格划分小于1/30d以后,误差均小于5%,符合模拟的精度要求。但随着炸药当量的增大,相同网格划分的超压上升时间的模拟结果和经验公式的误差逐渐增大。于是进一步研究网格划分为炸药体边长的1/32时,不同炸药当量对模拟结果的影响,冲击波超压上升时间的模拟结果和式(3)的误差曲线如图9所示。可以得出:炸药质量在1 000 kg以内,网格划分为炸药体边长的1/32时,模拟得到的冲击波各项参数都符合精度要求,冲击波的波形也符合精度要求。
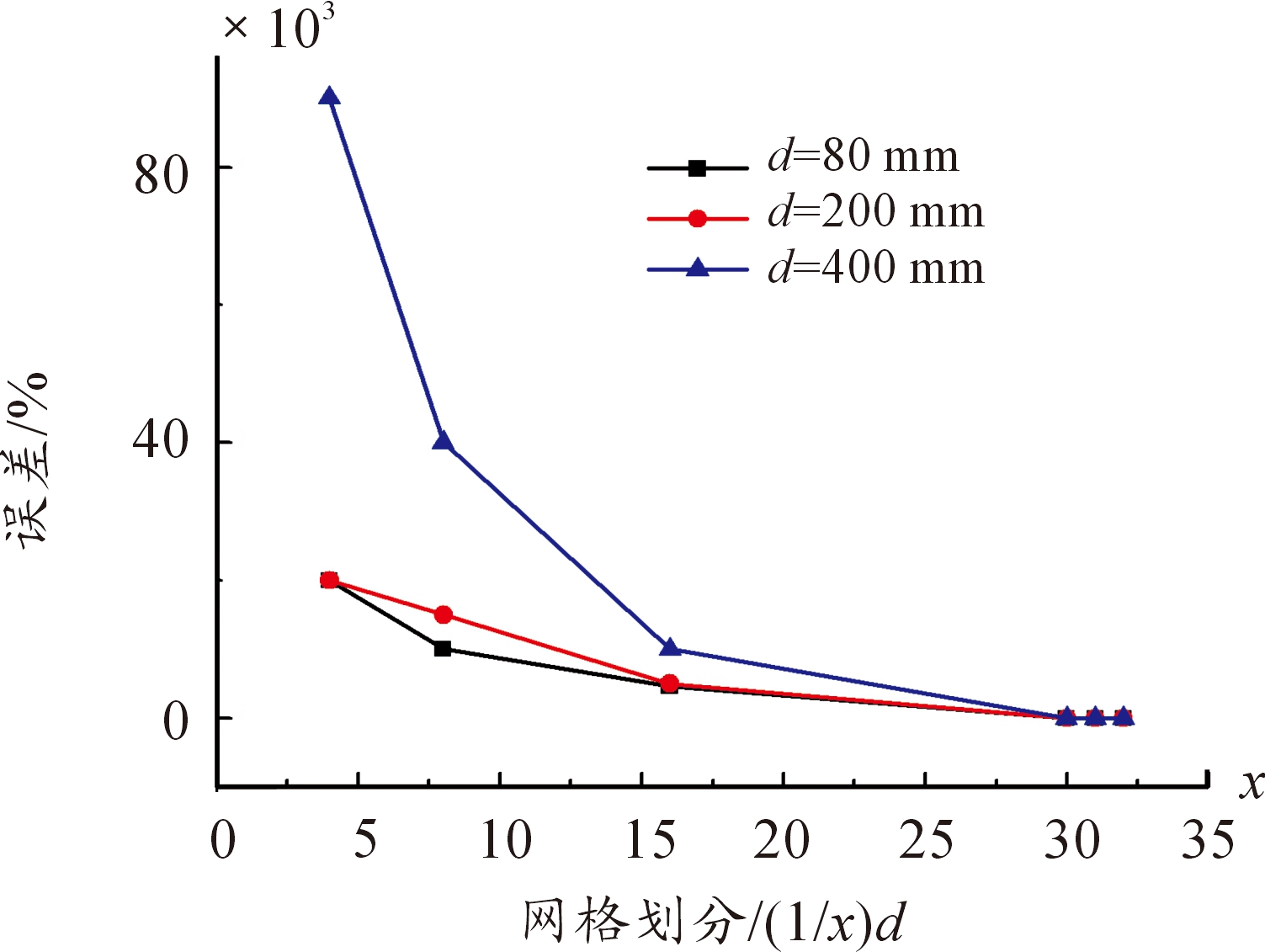
图8 不同网格划分的超压上升时间和经验公式的误差曲线
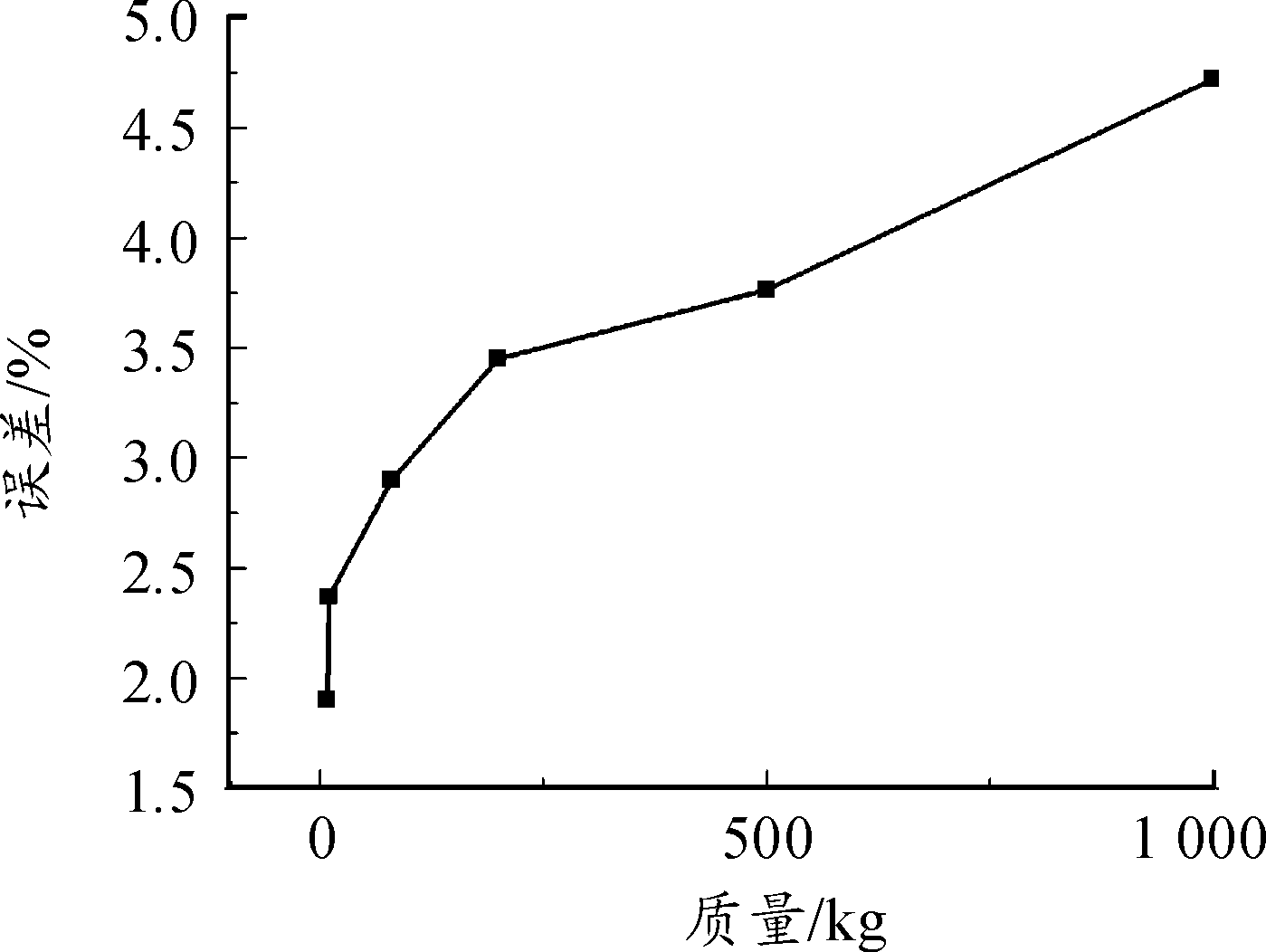
图9 不同炸药当量对模拟结果和经验公式的误差曲线
3 爆炸实验及对实验的模拟
3.1 实验样品和靶场布置
实验采用弹体进行试验,由于冲击波正压时间一般在从几毫秒到数十毫秒,上升前沿仅为数微秒,测试装置采用高频响测试系统,主要由压力传感器和瞬态数据采集仪组成。传感器选用美国PCB公司的压电式传感器113 A。实验样品为弹药,等效TNT药量m为515 kg,装药密度为1.64 g·cm-3,装药长径比为1∶1。传爆药为JH-14,质量为30 g,为减小冲击波能量对地作用损耗,采用8号铜雷管从装药底端起爆。
实验时,将弹药放在距地面3 m的支架上,以装药在地面上的垂直投影点为爆心,在爆心区周围200 m内无建筑物、较开阔的地面上布置地面传感器,如图10所示。压力传感器安装在Φ200 mm的钢质基础上,传感器敏感面与基准地面平齐安装并用土夯实进行防护,防止热及冲击振动干扰。实验现场布置如图11所示。

图10 传感器
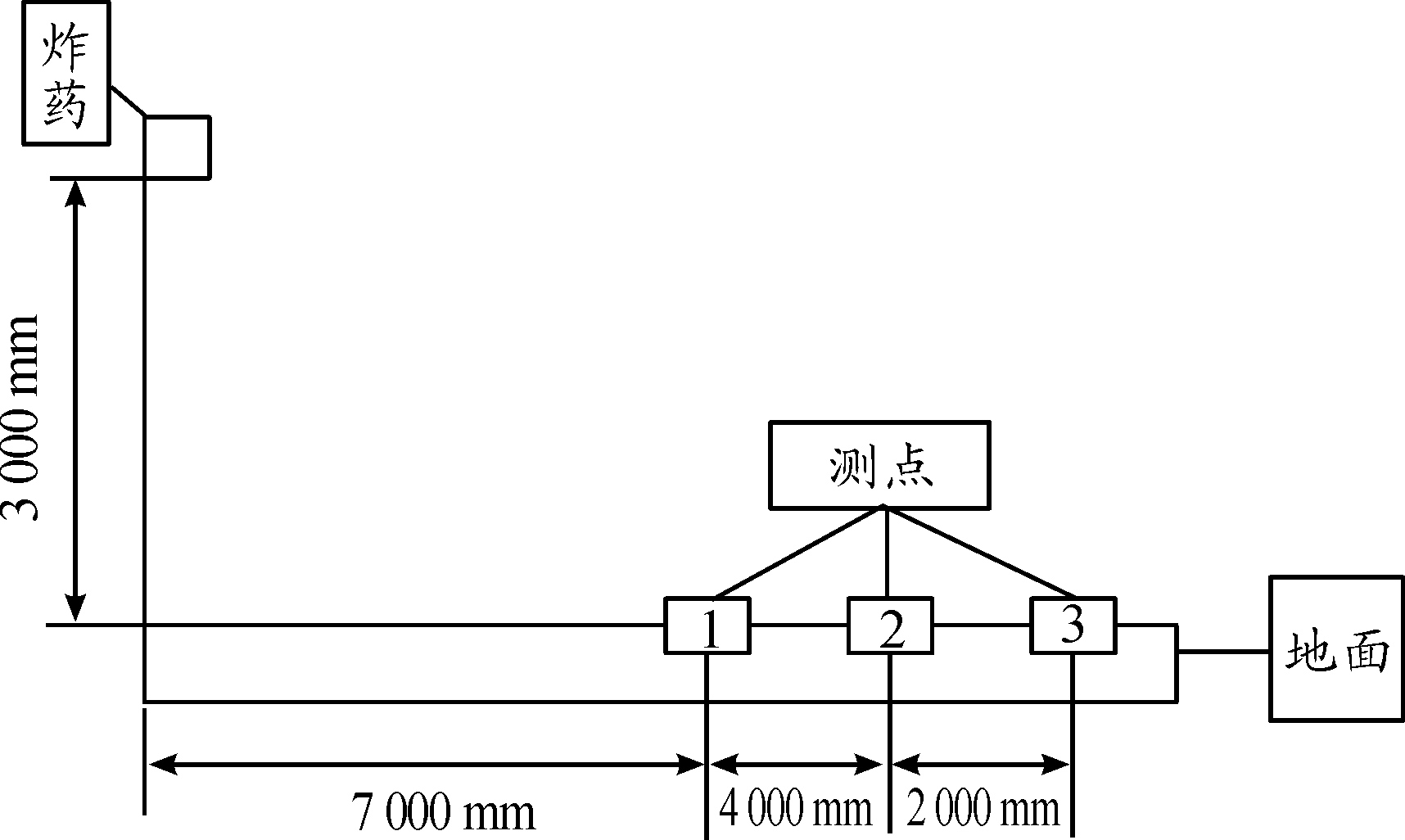
图11 实验现场布置示意图
3.2 对实验的模拟
土选取SOIL_AND_FOAM_FAILURE材料模型,该模型在某些方面具有流体性质,其应用于土或泡沫被限制在结构中或有几何边界存在的情况下。压力是正压缩,在负压缩情况下,体积应变是相对体积的自然对数,相对体积是计算开始时当前体积与初始体积之比。其塑性屈服极限函数φ根据应力偏量第二不变量J2描述[16]。
φ=J2-(a0+a1p+a2p)
(8)
式中:J2=SijSij/2,a0,a1,a2为常数;p为压力。主要材料参数参见表3。
表3 主要材料参数

ρG/GPaBa0/GPaa1/GPaa2/GPaPe/GPaCVCR1εpe21.86.385×10-40.33.4×10-137.033×10-70.3-6.9×10-80-0.104εpe3εpe4εpe5εpe6εpe7εpe8εpe9εpe10-0.016-0.192-0.22-0.246-0.271-0.283-0.29-0.4P3/GPaP4/GPaP5/GPaP6/GPaP7/GPaP8/GPaP9/GPaP10/GPa4×10-46×10-31.2×10-32×10-34×10-36×10-38×10-34×10-2
取515 kg炸药作为计算模型,利用计算模型的对称性取1/8模型进行计算,对称面采用对称边界,非对称面采用透射边界。炸药和空气均采用LS-DYNA Explicit 3DSOLID164模型,炸药边长为680 mm,炸药离地3 m,利用模型的对称性取1/8模型进行计算,网格划分为炸药体边长d的1/32,模型如图12。

图12 实验的模拟模型
3.3 模拟结果分析
爆炸实验的测点1处的实验结果如图13所示,图14为对应的模拟结果,表4列出了本次实验3个测点处冲击波的实验值,模拟值和计算值。
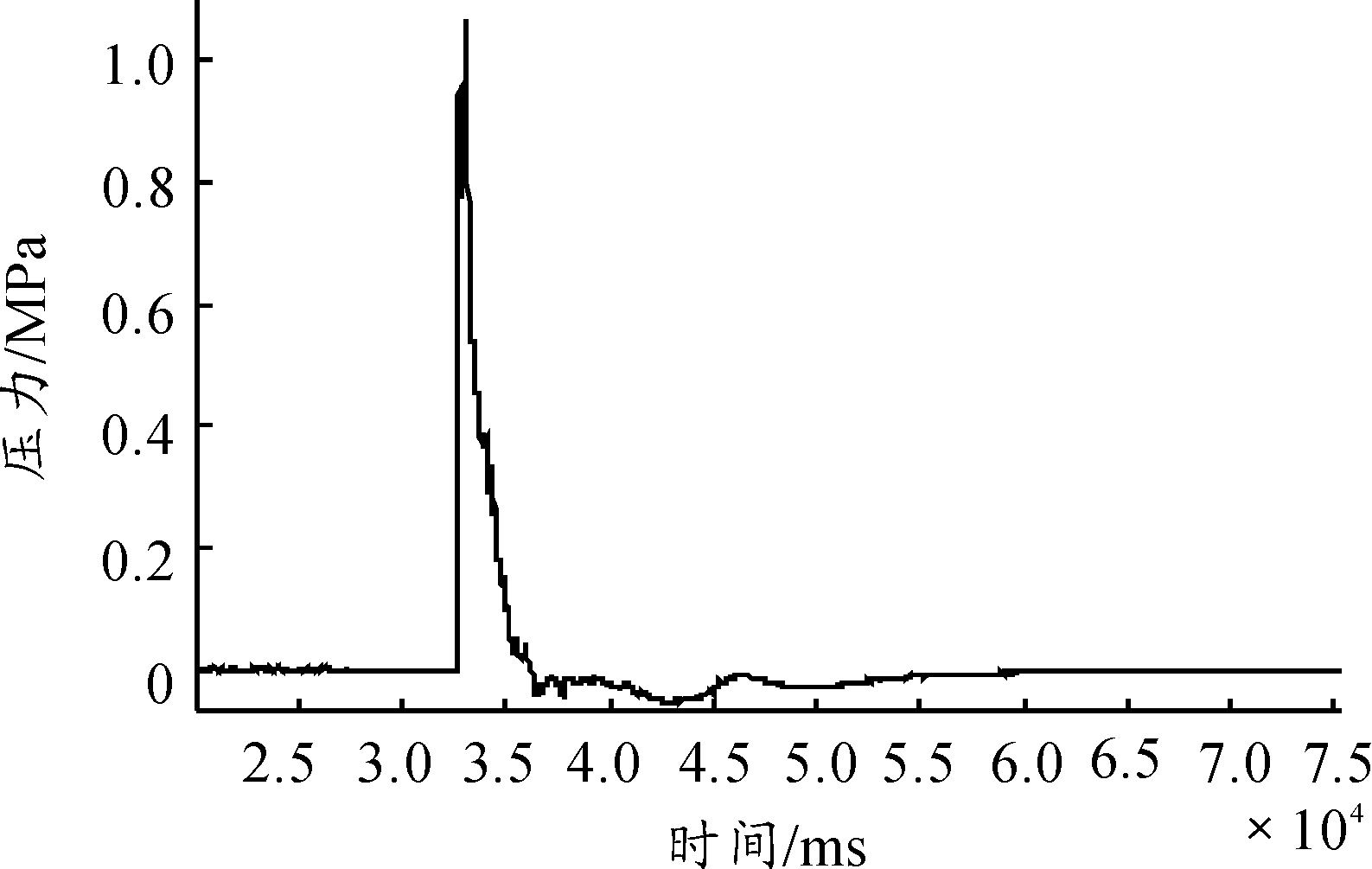
图13 实验结果
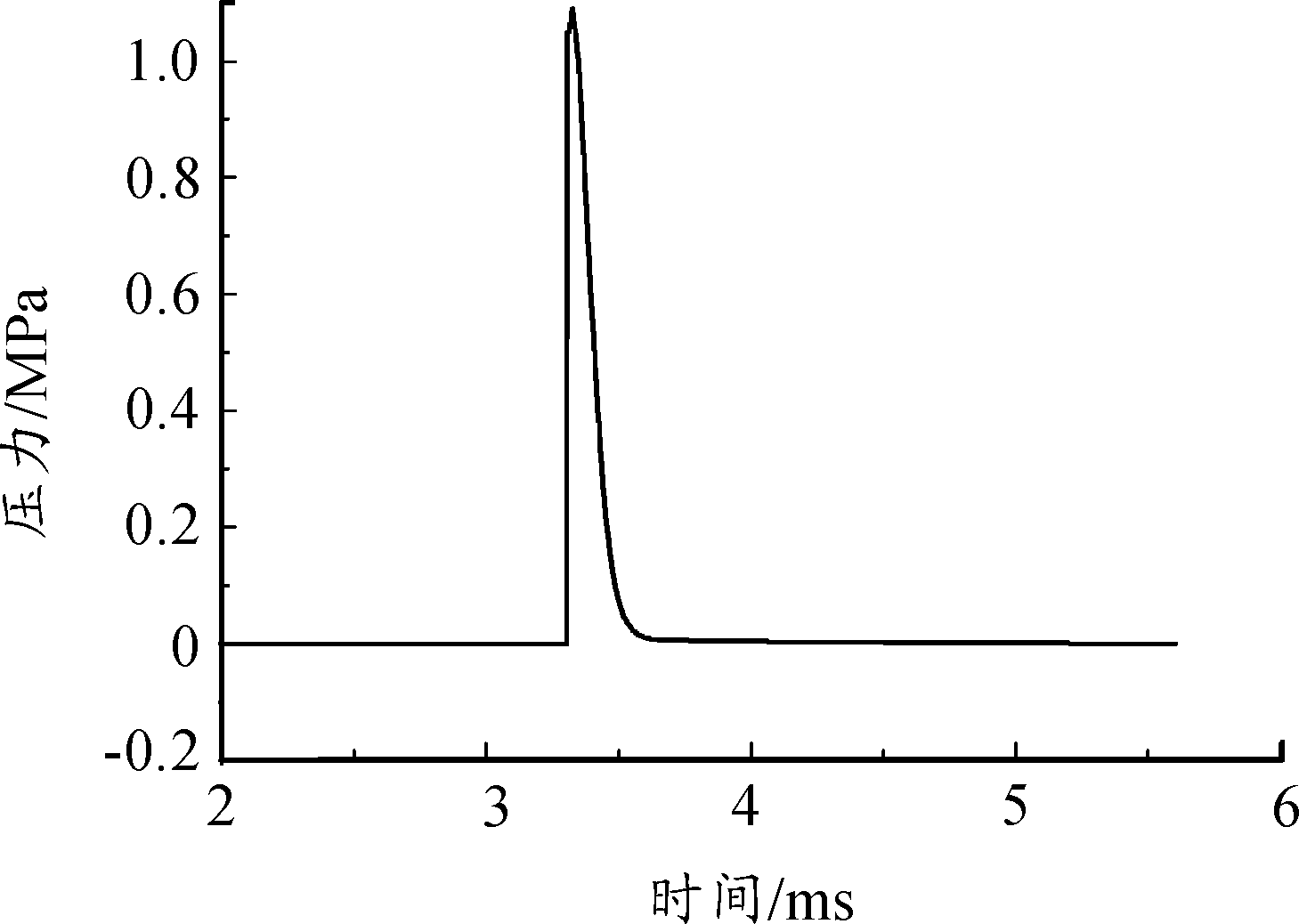
图14 模拟结果
表4 冲击波的实验值,模拟值和计算值的偏差分析

测点超压峰值/MPa正压时间/ms超压上升时间/μs测点1经验计算值1.0861.5881.800实验值1.0711.6001.860模拟值1.0901.5961.820实验和计算误差/%1.3811.2473.330实验和模拟误差/%1.8000.2322.150测点2经验计算值0.4001.9283.020实验值0.4051.9503.100模拟值0.4071.9563.130实验和计算误差/%1.2351.1282.580实验和模拟误差/%1.7200.3070.968测点3经验计算值0.2762.0883.750实验值0.2752.0203.860模拟值0.27902.9403.800实验和计算误差/%0.3643.2502.93实验和模拟误差/%1.4503.5301.58
从表4可以看出,网格划分为炸药体边长d的1/32时,模拟结果的各项参数对实验值和计算值的误差都小于5%,实验结果和模拟结果的冲击波波形基本一致,能够满足模拟的精度要求。
4 结论
不同网格尺寸对冲击波波形有影响。网格尺寸过大时,压力小于真实值,随着网格的不断减小,超压峰值逐渐增大,接近真实值。在网格尺寸小于炸药体边长的1/27后,超压峰值符合精度要求。网格尺寸越小,正压时间越小,越符合真实值。在网格尺寸小于炸药体边长的1/29后,正压时间符合精度要求。网格尺寸越小,超压上升时间越小,越符合真实值。在网格尺寸小于炸药体边长的1/32后,超压上升时间符合精度要求。数值模拟与实验值和理论值的误差随着网格的减小而不断减小,冲击波波形从平缓曲线变为上升段和下降段明显的三角形曲线。实验结果表明,在炸药小于1 000 kg,单元网格划分小于炸药体边长的1/32时,模拟结果与计算结果,模拟结果和实验结果的各项参数误差都小于5%。
[1] 姬建荣,苏健军,张玉磊,等.不同量级TNT爆炸冲击波正压时间的试验研究[J].科学技术与工程,2018,18(5):202-206.
[2] HASHEMI S K,BRADFORD M A.Numerical Simulation of Free-Air Explosion Using LS-DYNA[J].Applied Mechanics and Materials,2014,553(2014):780-785.
[3] YANCHAO S,ZHANGXIAN L I,HONG H.Mesh size effect in numerical simulation of blast wave propagation and interaction with structures[J].Transactions of Tianjin University,2008,14(6):396-402.
[4] 高轩能,刘颖,王书鹏.基于LS-DYNA的大空间柱壳结构爆炸波压力场分析[J].振动与冲击,2011,30(9):70-75.
[5] 任朋飞,王显会,张进成,等.刚性地面爆炸冲击场仿真与试验研究[J].科学技术与工程,2017,17(21):30-36.
[6] 崔莹,赵均海,张常光,等.基于爆炸试验的冲击波传播网格划分效应研究[EB/OL].[2013-10-31].http://www.paper.edu.cn/releasepaper/content/201310-435.
[7] LUCCIONI B,AMBROSINI D,DANESI R.Blast load assessment using hydrocodes[J].Engineering Structures,2006,28(12):1736-1744.
[8] 石磊,杜修力,樊鑫.爆炸冲击波数值计算网格划分方法研究[J].北京工业大学学报,2010,36(11):1465-1466.
[9] 杨鑫,石少卿,程鹏飞,等.爆炸冲击波在空气中传播规律的经验公式对比及数值模拟[J].四川建筑,2007,27(5):71-73.
[10] 杨坤,陈朗,伍俊英,等.计算网格与人工粘性系数对炸药水中爆炸数值模拟计算的影响分析[J].兵工学报,2014(s2):237-243.
[11] 张社荣,李宏璧,王高辉,等.水下爆炸冲击波数值模拟的网格尺寸确定方法[J].振动与冲击,2015,34(8):93-100.
[12] 胡兆颖,唐德高.空气中TNT爆炸的数值模拟[J].爆破,2014,31(4):41-45.
[13] 娄浩然,胡晶,梁向前,等.超重力场下球形炸药水下爆炸实验及数值模拟[J].工程爆破,2017,23(3):15-21.
[14] 杜欣新,毛毳.网格划分影响二维爆炸冲击波数值模拟精度的研究[J].天津城建大学学报,2013(4):277-279.
[15] 仲倩,王伯良,黄菊,等.TNT空中爆炸超压的相似律[J].火炸药学报,2010,33(4):32-35.
[16] 李顺波,东兆星,齐燕军,等.爆炸冲击波在不同介质中传播衰减规律的数值模拟[J].振动与冲击,2009,28(7):115-117.