防护工程是针对武器杀伤破坏作用,按预定防护要求修建的军事或民用设施,通常作为首脑指挥、战略武器等重要作战力量生存的依托,绝大多数埋设于地下,是我国积极防御战略的重要基石[1]。针对防护工程的攻防对抗是现代战争中的一个重要环节,其基本流程为:
通过全面的勘测与评估,防护方按照一定原则与战技指标进行工程设计与建设;运用间谍渗透、卫星侦察等方式,进攻方采集目标工程防护信息,制定打击方案;进攻方进行攻击,造成防护工程毁伤;防护方对工程毁伤状态进行评估,制定方案,针对毁伤特点改进工程设计策略。
防护方与进攻方是带有对抗性质的两方。进攻方通过优化火力配置、改进武器装备等对目标工程进行有效打击,使目标工程损失最大;综合防护方通过改进防护效能对武器毁伤方进行防御和反击,使武器毁伤效果最差。攻防双方博弈的最终目标都是利用最小的代价获取最大的收益。
目前进行防护效能设计时,往往预设一定的战技指标,利用可靠度理论等方法进行防护设计,在确定打击条件下对己方设施进行优化。然而战争是双方博弈的行为,如果单凭传统经验或己方决策的单方面优化进行防护设计,一方面容易被对方洞悉设计方法,另一方面在对方改变攻击策略时难以做出有益的防护选择。因此,利用博弈论将防护策略从单方面发展为双边,更加符合实战,决策结果也更加科学。本研究利用博弈论对武器打击下的工程防护设计策略进行研究,对博弈论在防护工程建设发展中应用进行探讨。
1 博弈类型与假设
攻防双方的目标都是追求自身利益的最大化,不可能达成合作意向,且收益信息不固定,双方收益和不为零。军事对抗决策环境具有天然的不确定性,不可能完全了解对方的策略集与收益函数,对于博弈双方来说,信息都是不确定的。
攻防双方的对抗不同于一般军事对抗,不是一种同时选择行为,防护工程作为不动体,其防护策略的选择必然在打击策略之前。因此,该博弈模型为非合作、非零和的动态贝叶斯博弈[2]。
从经济学的角度来看,收益大于成本的预期是人类理性行为的基本原则[3]。不管是进攻还是防护,都必须考虑其费效比。本研究以攻守双方均为理性的决策主体为前提,给出以下相关假设:
假设1:进攻方明确可选的攻击方式和进攻手段,对未知的工程防护策略具有预期,带有明确的偏好,在经过一系列优化后慎重选择行动;防护方明确可选的防护策略,对对手进攻策略具有预期。双方对对方策略的了解程度取决于各自有效信息的获取以及对真实信息的判断。
假设2:在攻防博弈中,进攻方与防护方都希望通过最优策略来最大化收益。在进攻获得收益相同的情况下,理性的武器打击方会考虑攻击成本,选择具有低成本的进攻策略;理性的防护方同样也会采取成本尽量低廉的防护策略,来获得足够的防护效能。
在以上两条合理假设的基础上,可以将攻防矛盾冲突关系描述的更为具体。此假设建立的矛盾冲突明确了攻防双方策略集与收益的博弈模型,通过计算该博弈模型的精炼贝叶斯纳什均衡获得攻击意图和最优的防护策略[4]。
2 博弈模型的建立
2.1 框架构建
该博弈模型为一个四元组,即W={P,A,S,U}[5],其中:P=(Pa,Pd)为参与者集合,Pa表示进攻方,Pd表示防护方。在对抗过程中,攻防双方是策略选择的主体和制定者。
A=(Aa,Ad)为攻防动作集,Aa为进攻动作集,Ad为防护动作集。其中Aa=(a1,a2,…,au),子元素a代表进攻方时采取的单个进攻动作u为进攻方动作总数; Ad=(d1,d2,…,dv),子元素d代表综合防护方防守时选用的单个防护策略,v为综合防护方动作总数。
S=(Sa,Sd)为攻防策略集。进攻方(防护方)选择的理性可行的行动方案称为进攻(防护)策略,攻防策略集是全部策略的集合。进攻策略集Sa=(sa1,sa2,…,sam),m为可选进攻策略总数;同理,防护策略集Sd=(sd1,sd2,…,sdn),n为可选防护策略总数。攻防双方以概率形式选取可用的攻防策略,此时攻防策略也被称之为混合策略,如果攻防策略唯一,此攻防策略被称之为纯策略[3]。
U=(Ua,Ud)分别为攻防双方收益函数。该函数表达了攻防双方从博弈中能够得到的收益水平,它是攻防双方真正关心的参数。
2.2 参与方
1)参与方的类型
一般进攻方进攻的目的性很强,常表现为对某种功能毁伤的偏好,因此其类型主要取决于选取的进攻策略,如采用大当量动能侵彻导弹等主要是造成内部设备与人员的毁伤,而采用导电纤维战斗部、EMP战斗部等的导弹主要针对工程内部电子设备[6]。定义武器打击方类型θa,其内容与进攻策略sa一一对应,进攻策略数便是武器打击方类型数。
综合防护方必须拥有所有防护功能才能正常工作,因此其功能类型不可能像进攻方一样只偏向某种或几种功能,而是要全面考虑与决策。定义防护方工程设计类型θd,不同类型的防护工程其功能性大相径庭,在设计与决策时的侧重点也不同,部分类型如表1[7]。
表1 防护工程部分功能类型

编码防护工程功能类型θd1指挥通信工程θd2飞机洞库θd3潜(舰)艇洞库θd4导弹发射井θd5人员掩蔽工程θd6后方物资(火工品)仓库θd7人防指挥工程θd8人防专业队工程
建立攻防双方类型向量,通过海萨尼转换[4],可以将动态贝叶斯博弈转化为完全但不完美信息的动态博弈。通过虚拟的“自然”博弈方Pn选择攻守双方的策略类型,既可以将攻防双方收益区分开,也便于推断对手后续策略。
2)参与方的信息知识集
定义攻防双方各自的信息知识集分别为Ia和Id,攻防双方信息集包含的信息来自于采取卫星侦察、间谍渗透等措施收集信息做出的判断。定义信息知识集帮助博弈双方对对方的类型可能性进行推测,即经过理性地判断,将信息集归结到攻守双方对对方类型的先验信念fa(θd)和fd(θa)上。运用加权模糊产生式规则将双方的信息知识集转化为对对方类型的先验信念值,该方法是模糊产生式规则的扩展[8]。如下面这条推理:
规则R:
If {fa(θd1)+=0.05, fa(θd2)+=0.1
Then fa(θd3)+=0.2, LwI, Gw(R)}
该规则表示,当信息知识集Ia等于X时,进攻方对防护方类型θd1、θd2、θd3的先验信念分别增加0.05、0.1、0.2。其中,LwI,Gw(R)分别表示规则前置条件“Ia=X”的局权和规则R的全权,其定义域均为(0,1]。通过罗列规则并设置权值,对攻防双方获得的信息逐条推理,推理完毕后,对结果归一化处理得出对方各类型的先验信念。
通过分析不难发现,双方得到的信息知识集越大,对对方类型的先验信念值越高,进攻或防护策略的制定也会更加准确。因此,在现代战争攻防对抗中,通过一定方法获取对手有效信息对战争打赢有着十分重要的意义与价值,知己知彼百战不殆的战法理念得到了很好的体现。
3)参与方的行动顺序
定义参与方行动顺序:自然博弈方Pn对参与方博弈类型进行定义,防护方Pd根据类型选取策略进行防护工程设计与建设,然后进攻方Pa根据侦测到的动作从进攻策略集中选取合适策略进行打击,计算双方收益。博弈树如图1。
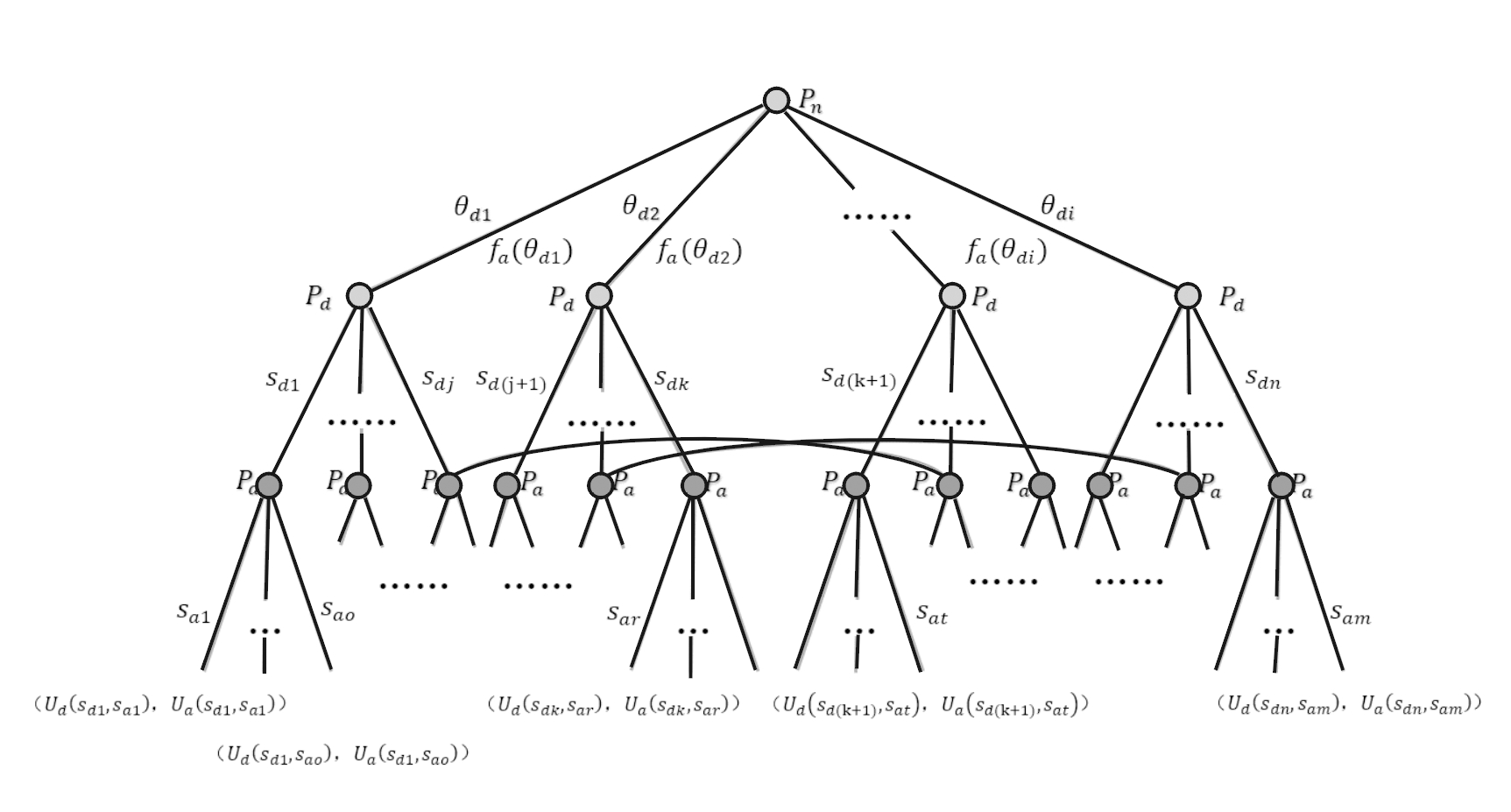
图1 攻防博弈树
2.3 博弈双方的收益
博弈中,进攻方收益Ua由进攻获利及进攻成本组成,防护方收益Ud由防护工程损失工程自身功能损失、防护目标功能损失及防护成本组成。
1)进攻获利与防护损失
进攻获利较为复杂,分为直接获利和间接获利,有对防护工程的破坏、对防护方心理上的威慑等,也可能通过打击重要经济目标在信息、能源等方面占据优势。这些主观或延伸的获利很难量化,然而不管何种获利其根源都是防护方工程的损失,因此以防护工程功能损失代表进攻方的进攻获利。
防护损失由工程自身功能损失和防护目标功能损失两方面组成。工程自身功能损失是指防护工程设计功能的削弱或丧失,如指挥防护工程在打击过后由设备损坏造成的通信功能损失;防护目标功能损失是防护效能失效后工程防护目标的功能损失,如飞机掩蔽库内被毁伤战斗机的功能损失、人防设施内被杀伤平民的价值损失。
因此,定义防护方损失(亦即进攻方获利)
L(sd,sa,θd)=Ve×De(sd,sa)+Lt(sd,sa)
(1)
其中,Ve为使用Sd策略建造的θd类型防护工程的功能价值,由工程抗力等级、规模等指标综合评估确定;De(sd,sa)为攻防策略为Sa、Sd时,工程自身功能的平均毁伤程度,Lt(sd,sa)为攻防策略为Sa、Sd时,防护目标毁伤后的功能损失值。
2)功能毁伤评估方法
在计算防护方损失时,求解工程自身与内部防护目标的功能毁伤程度十分关键,是模型计算时需重点解决的问题。本模型采用降阶态易损性分析方法(DSVM),对防护工程与内部防护目标的功能毁伤进行探究。此方法作为武器装备的重要分析方法之一,主要优点是层次分明,对工程内部各级部件状态了解更加直观,对毁伤状态的战术响应更加及时[9]。
在确定攻防策略后,在武器毁伤效应库内搜索最优算法进行弹目交汇模拟,设定相应参数,计算工程自身与防护目标的部件级物理毁伤,然后根据这些部件级物理毁伤状态进行功能毁伤评估。
对于工程自身,先对工程的功能因素φ进行梳理,如表2为指挥防护工程功能因素[10-12]。然后从部件级物理毁伤状态出发,运用演绎法,将工程内部关键部件(位)的毁伤作为基础事件,将工程功能因素作为顶事件,按照一定逻辑关系构造毁伤树[9],由下至上逐级评估,运用降阶态理论判断各功能因素毁伤的程度dφ。如一定当量的低阻式爆破弹以堵口爆炸方式打击目标工程[6],造成防护门、防护密闭门、扩散室等完全毁伤,防爆波活门、消波室等部分毁伤,根据毁伤树逐级向上推演,可定量判断出爆炸冲击、生化毒害等功能因素的毁伤程度。根据防护工程类型定义各功能因素权重∂,则:
(2)
其中we为工程功能因素总数。
表2 指挥防护工程功能因素

编码功能因素编码功能因素φ1指挥通信功能φ5防燃烧高温功能φ2生活保障功能φ6防电磁毁伤功能φ3出入通行功能φ7防辐射沾染功能φ4防爆炸冲击功能φ8防生化毒害功能
对于防护目标,将其分为人员与装备两类。人员按实现价值能力VHu分类,根据模拟出的物理毁伤状态判断不同VHu的人员伤亡占比dHu,计算打击后的人员价值损失。装备方面,不管是大型装备(战机、舰船等),还是小型装备(单兵装备、弹药等),选取合适单元将其分类(如10枚MK-82低阻航弹)并定义每个单元的功能价值VEq,根据物理毁伤状态通过降阶态理论判断每个单元的毁伤程度dEq,计算打击后装备功能损失。
故防护目标毁伤后的功能损失值
(3)
其中,δHu、δEq为二进制系数,值为1时表示有人员装备毁伤,为0时表示无人员装备毁伤。wHu、wEq分别为人员与装备的分类总数。
综上所述,防护方损失(进攻方获利)
(4)
3)攻防成本
在博弈过程中,攻防支出成本也是双方收益的重要组成部分。然而,如果简单将消耗实际金钱数额表示攻防成本,一方面攻防双方选取策略的效率与价值不能很好体现,另一方面实际消耗金钱数额与工程功能损失值量纲并不统一,最终收益无法计算。因此,需要将攻防成本与工程功能损失价值货币统一化并体现选取策略支出的效率。
对于确定类型θd的防护工程,搜集大量工程实测数据可以计算出该类型工程的单位功能价值消耗期望QdAVG与标准差σd。使用sd策略建造的消耗为Md的防护工程的单位功能价值消耗
![]()
(5)
因此,通过z-score标准化方法[13]定义综合防护方选用sd策略的防护成本
(6)
αθ为防护成本修正系数,定义域为(0,1),由大量样本数据统计归纳求得,在战时作战效能越高的工程值越小。
陆军工程大学爆炸冲击防灾减灾国家重点实验室搜集国内外最新武器数据,建立了较为完整的武器毁伤效应库,同时也掌握大量实测防护工程数据。依托实验室现有资源,进行多源数据融合处理,构建确定类型θ与对应功能价值Ve的标准防护工程BIM(Building Information Modeling)模型,运用相关算法进行多次模拟,确定造成相同功能毁伤程度De(sd,sa)时的打击消耗期望MaAVG与标准差σa。
通过z-score标准化方法定义武器打击方选用sa策略打击θd类型工程的进攻成本
(7)
βθ为进攻成本修正系数,定义域为(0,1),其值与武器类型、打击方式和目标类型相关;Ma为选用sa策略进攻实际消耗。式(6)、式(7)统一了攻防成本与工程功能损失价值的量纲,也将攻防实际消耗与攻防效率结合起来,结果更加符合实际,与攻防获利的比较也更加客观。
4)攻防收益
确定防护损失与成本后,博弈中防护方的收益为防护损失的相反数与防护支出之差,即:
Ud(sd,sa)=-L(sd,sa,θd)-costd(sd,θd)
(8)
同样地,进攻方收益为进攻获利与进攻成本之差,即:
Ua(sd,sa)=L(sd,sa,θd)-costa(sa,θd)
(9)
将式(4)、式(6)、式(7)代入即可求解。
3 博弈模型的精炼贝叶斯纳什均衡
随着卫星等侦测手段的高速发展,进攻方可以了解防护工程的毁伤情况。本研究假定博弈过程是完美的,即进攻方对防护方的防护动作是了解的,因此进攻方对防护方类型的信念可以通过探测到的防护策略而做出调整,形成后验信念。
已知攻防双方对对方类型的先验信念为fa(θd)和fd(θa)。根据贝叶斯定理,进攻方对防护方类型的后验信念
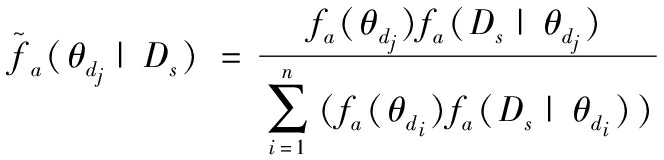
(10)
式(10)表示进攻方侦测到工程毁伤情况Ds后对防护类型信念的调整,其中fa(Ds|θdi)为在防护方类型为θdi时,针对进攻策略sak进行设计的概率,一般由统计获得。
获得攻守双方对对方类型的信念后,经过序列理性和均衡策略的判断后[2],该不完全信息博弈可转换为完美贝叶斯均衡![]() 其攻防双方最优策略:
其攻防双方最优策略:
(11)
(12)
其中,![]() 和
和![]() 分别为攻防双方在博弈中的最优均衡策略。将式(8)、式(9)中攻防收益代入即可求得该模型的完美贝叶斯均衡。
分别为攻防双方在博弈中的最优均衡策略。将式(8)、式(9)中攻防收益代入即可求得该模型的完美贝叶斯均衡。
根据纳什均衡的存在条件[2]:任意有限策略型博弈至少存在一个混合策略纳什均衡。由于攻守双方的动作数目有限,博弈模型的扩展型博弈和对应的策略型博弈均是有限的,因此至少存在一个混合策略纳什均衡。又因博弈过程是完美的,根据“完美信息的有限扩展型博弈存在纯策略纳什均衡[14]”这个定理,该模型至少存在一个纯策略纳什均衡。
关于均衡的精炼,根据完美贝叶斯均衡法则[2],在所有后续动态贝叶斯博弈上也达成贝叶斯均衡,即对于进攻方的任意一个策略,均需满足式(11),在计算后加以验证。
在完成贝叶斯精炼计算后,该模型求解出的均衡策略仍然有可能大于一个。采用预设策略的方式进行指导,根据设计经验以及防护工程类型,制定工程设计预方案,在解得的均衡策略中选择更接近其经验预案的策略。
4 算例分析
下面通过简单算例介绍模型分析过程,并分析结果。防护方设计建造防护工程用于特定功能,进攻方针对需求进行战略打击,本文列举部分攻防博弈策略进行简要计算说明。
攻防策略由攻防动作集中不同动作组合而成,进攻策略包含动作与实际消耗见表3,防护策略包含动作与实际消耗见表4所示。表4中每种设计布局均代表一种设计样式,如样式5-1中,5代表该布局的功能类型,1代表该样式的编号。
根据工程抗力、规模等指标综合评估确定防护工程价值,不仅要考虑工程自身的价值,也要考虑防护目标的价值。表中工程主防护目标均为人员,无储存装备损伤,为保证对工程功能的完全评估,在计算毁伤程度时考虑防护目标满编状态,将人员按职能划分平均分配到各个功能房间,该房间完全毁伤则造成分配人员伤亡。各策略建造防护工程的详细指标见表5。利用上述数据进行部件级物理毁伤模拟,固定交汇速度与弹着角,引入弹着点圆概率偏差(CEP),运用空气冲击波、侵彻、爆炸等相关算法与蒙特卡洛方法计算打击造成各节点(部件)平均物理毁伤参数,编写Matlab程序与设计抗力指标进行比较,进而判断物理毁伤程度。运用降阶态易损性分析方法,构建各级功能毁伤树,由下到上逐级推演,计算工程平均功能毁伤程度De(sd,sa),见表6所示。已知工程部件级毁伤状态,可根据式(3)与表5,计算出工程内部人员价值损失Lt(sd,sa),见表7。通过大量攻防样本数据比对,修正攻防支出带来的价值偏差,确定攻防成本修正系数。其中,防护成本修正系数αθ1=0.652,αθ5=0.829,进攻成本修正系数βθ见表8所示。在衡量进攻支出的均值时,提前构造多种类型的样本工程BIM模型,通过改变弹体型号、战斗部型号、装药量等数据进行蒙特卡洛模拟,计算出造成相同功能毁伤De(sd,sa)时的打击消耗期望MaAVG与标准差σa,储存在数据库中,使用时直接调用。
表3 进攻方进攻策略与消耗
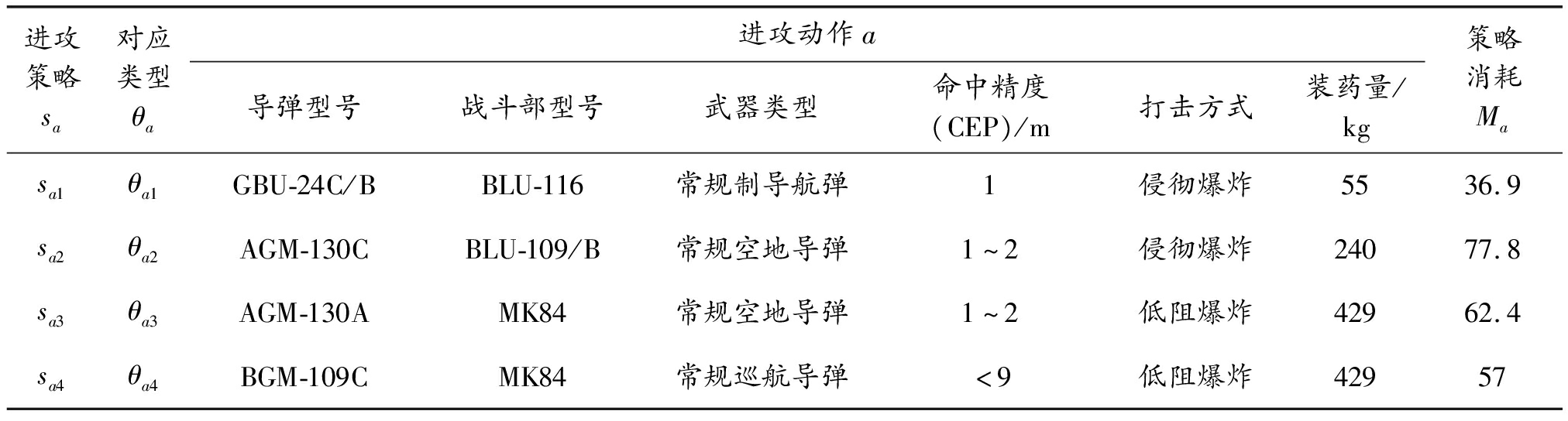
进攻策略sa对应类型θa进攻动作a导弹型号战斗部型号武器类型命中精度(CEP)/m打击方式装药量/kg策略消耗Masa1θa1GBU-24C/BBLU-116常规制导航弹1侵彻爆炸5536.9sa2θa2AGM-130CBLU-109/B常规空地导弹1~2侵彻爆炸24077.8sa3θa3AGM-130AMK84常规空地导弹1~2低阻爆炸42962.4sa4θa4BGM-109CMK84常规巡航导弹<9低阻爆炸42957
表4 防护方防护策略与消耗

防护策略sd对应类型θd防护动作d设计布局结构常规武器抗力等级伪装防护分级人员隔震分级电磁脉冲防护分级防化防护分级策略消耗Mdsd1θd1样式1-1X22221432.7sd2θd1样式1-2X+122221245.6sd3θd5样式5-1X2122 853.4sd4θd5样式5-1X+13222 683.1sd5θd5样式5-2X+12122 762.2
表5 防护方建造防护工程的详细指标
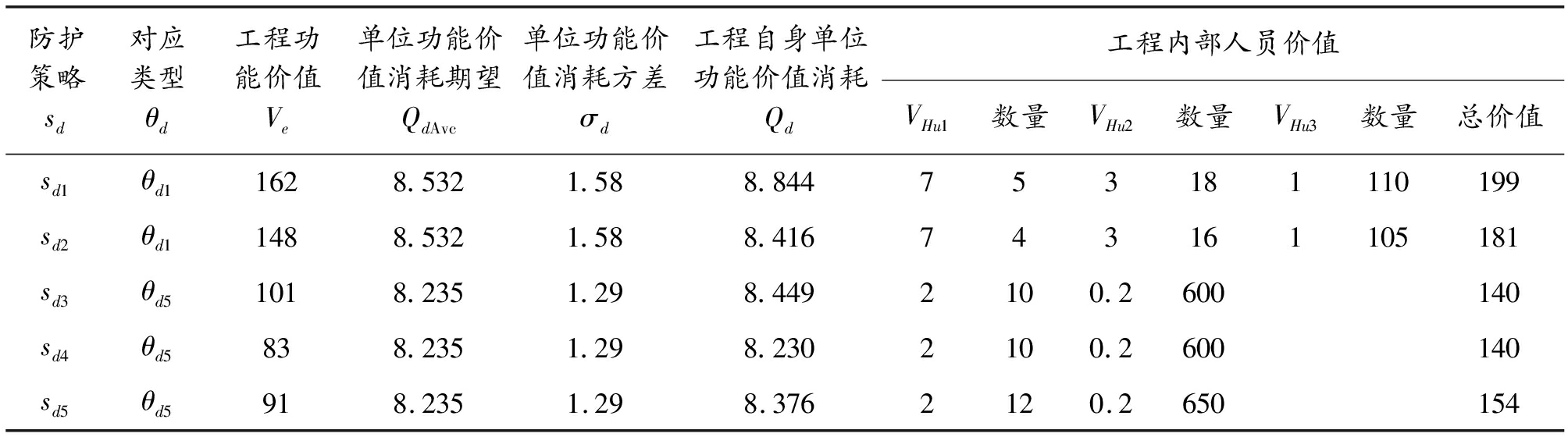
防护策略sd对应类型θd工程功能价值Ve单位功能价值消耗期望QdAvc单位功能价值消耗方差σd工程自身单位功能价值消耗Qd工程内部人员价值VHu1数量VHu2数量VHu3数量总价值sd1θd11628.5321.588.844753181110199sd2θd11488.5321.588.416743161105181sd3θd51018.2351.298.4492100.2600140sd4θd5838.2351.298.2302100.2600140sd5θd5918.2351.298.3762120.2650154
表6 工程平均功能毁伤程度
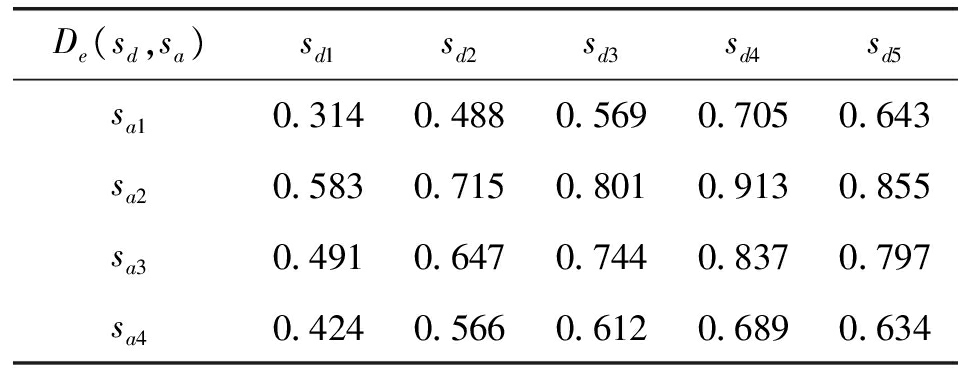
De(sd,sa)sd1sd2sd3sd4sd5sa10.3140.4880.5690.7050.643sa20.5830.7150.8010.9130.855sa30.4910.6470.7440.8370.797sa40.4240.5660.6120.6890.634
表7 内部人员价值损失
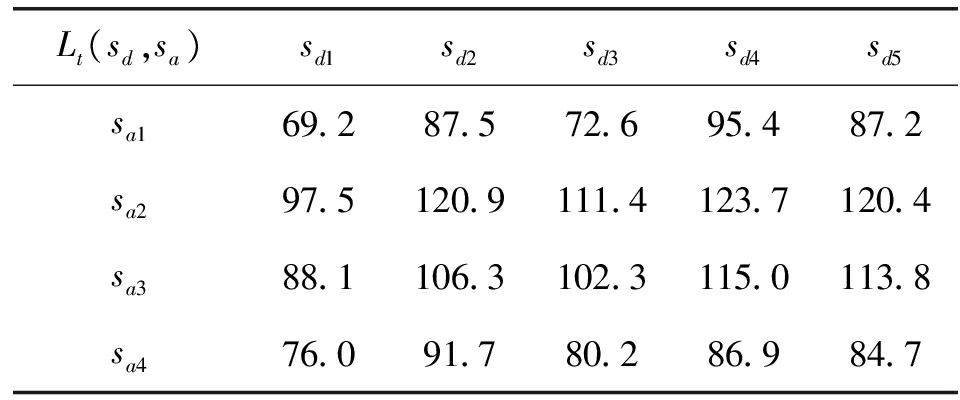
Lt(sd,sa)sd1sd2sd3sd4sd5sa169.287.572.695.487.2sa297.5120.9111.4123.7120.4sa388.1106.3102.3115.0113.8sa476.091.780.286.984.7
表8 进攻成本修正系数

βθθa1θa2θa3θa4θd10.8030.5820.6740.639θd50.9150.5530.7490.717
将上述数据代入式(11)、式(12),得到攻防双方收益。进攻方收益见表9,防护方收益见表10所示。
根据获得的信息集Ia和Id,攻守双方推理出对对方策略的先验信念。打击后,进攻方对防护方类型信念进行调整,形成后验信念。代入式(10),得出进攻方对防护方类型的后验概率。
将上述数据代入式(11)、式(12)中进行运算,如表11所示,得到完美贝叶斯均衡解![]() 因此,sd4策略为最优设计策略,攻防双方完美贝叶斯均解的收益为99.4和-91.2。将该均衡进行精炼,发现后续均衡过程均与攻防双方预期(即信念概率)吻合,符合精炼贝叶斯纳什均衡条件。此时无论哪一方单方面改变策略,其收益一定受损,在后续博弈中也会与自身信念不符。
因此,sd4策略为最优设计策略,攻防双方完美贝叶斯均解的收益为99.4和-91.2。将该均衡进行精炼,发现后续均衡过程均与攻防双方预期(即信念概率)吻合,符合精炼贝叶斯纳什均衡条件。此时无论哪一方单方面改变策略,其收益一定受损,在后续博弈中也会与自身信念不符。
表9 进攻方收益
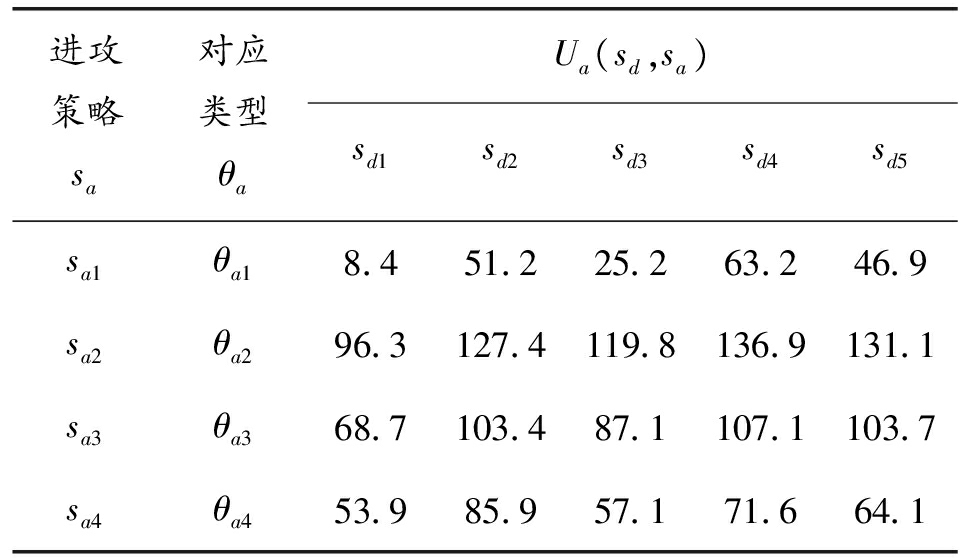
进攻策略sa对应类型θaUa(sd,sa)sd1sd2sd3sd4sd5sa1θa18.451.225.263.246.9sa2θa296.3127.4119.8136.9131.1sa3θa368.7103.487.1107.1103.7sa4θa453.985.957.171.664.1
表10 防护方收益
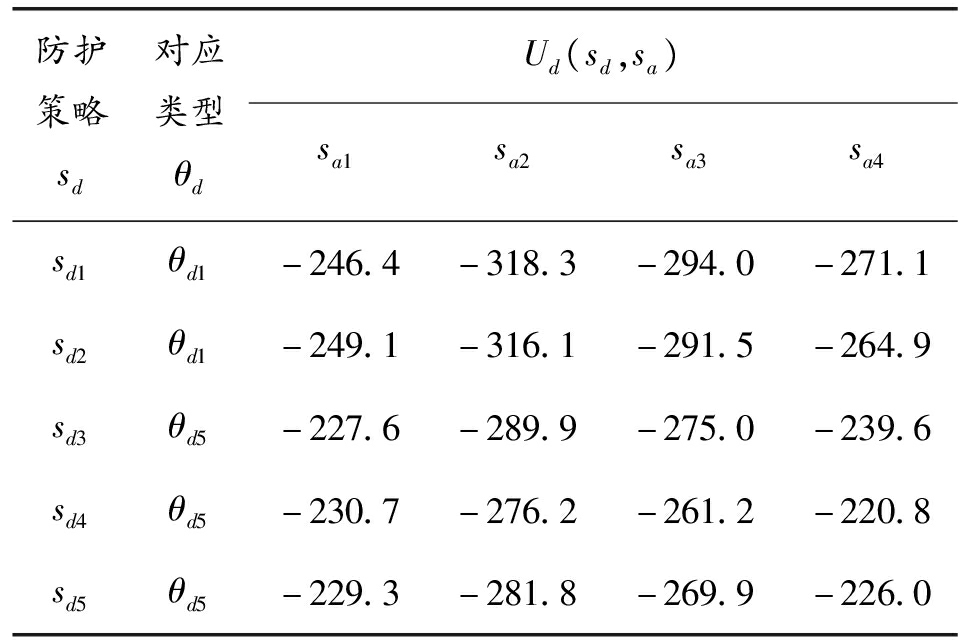
防护策略sd对应类型θdUd(sd,sa)sa1sa2sa3sa4sd1θd1-246.4-318.3-294.0-271.1sd2θd1-249.1-316.1-291.5-264.9sd3θd5-227.6-289.9-275.0-239.6sd4θd5-230.7-276.2-261.2-220.8sd5θd5-229.3-281.8-269.9-226.0
在该算例中,如果仅从单方面考虑,防护方会选择平均收益较高的sd5策略,此时其最佳收益为-40.7。而进攻方会通过判断选择对自己有利的(sa2,sd5)组合,攻防收益变为73.7和-93.0。由此可知,如果仅从单方面判断最优策略是不稳定的,模型充分考虑了双方可能的策略变化与收益,计算结果的准确性更高、稳定性更强。
表11 攻防双方博弈收益矩阵

Payoffsa1sa2sa3sa4sd1(4.9,-61.6)(61.9,-105.1)(29.6,-70.6)(24.6,-48.8)sd2(26.3,-62.3)(76.3,-104.3)(55.5,-71.0)(49.2,-47.7)sd3(16.2,-56.9)(68.8,-95.7)(45.6,-66.0)(31.3,-43.1)sd4(46.5,-57.7)(99.4,-91.2)(91.8,-62.7)(58.3,-39.8)sd5(32.0,-57.3)(73.7,-93.0)(70.4,-64.8)(37.8,-40.7)
5 结论
本研究以博弈论为基础建立攻防收益模型,充分考虑攻防双方收益以及策略的变化因素,计算出双方最优策略集。由式(11)、式(12)易得,所求解出的最优防护策略,是针对进攻方所有可能的进攻策略选出的最优决策。它充分考虑了攻防双方的收益,与单向考虑模型相比,其结果更加稳定、可靠。计算中考虑攻防双方类型的偏好,体现了双方攻防博弈时的意图与目的,同时也巧妙解决了攻防获利与成本支出无法统一货币单位的问题,收益的计算更加准确。
攻防收益的计算以功能毁伤程度为基准,严格考虑博弈中功能的损失,实现了功能价值的量化,比只从物理毁伤角度分析更加符合实战,也便于非工程专业的指挥人员了解实况并进行后续战术部署。在计算中不可避免地使用了少量人工指定参数(如工程功能价值等),在下步工作中,要严格规范这些参数的评价标准,进而提高模型的准确性。另外,本文以攻防双方行为均为理性的前提建立模型,在实际战斗条件下双方很难做到完全理性,在决策过程中难免会出现纰漏,可从进化博弈角度完善模型,解决防护工程遭受再打击的难题。
[1] 钱七虎.钱七虎院士论文选集[M].北京:科学出版社,2007.
[2] OSBORNE M J,RUBINSTEIN A,AUMANN R,et al.A Course in Game Theory[M].2nd ed.Cambridge:The MIT Press,1994.
[3] 姜伟.基于攻防博弈模型的主动防御关键技术研究[D].哈尔滨:哈尔滨工业大学,2010.
[4] 谢识予.经济博弈论[M].上海:复旦大学出版社,2002.
[5] 陈永强,付钰,吴晓平.基于非零和攻防博弈模型的主动防御策略选取方法[J].计算机应用,2013,33(5):1347-1349,1352.
[6] 周旭.导弹毁伤效能试验与评估[M].北京:国防工业出版社,2014.
[7] 方秦,柳锦春.地下防护结构[M].北京:中国水利水电出版社,2010.
[8] 王熙照,安素芳.基于极大模糊熵原理的模糊产生式规则中的权重获取方法研究[J].计算机研究与发展,2006(4):673-678.
[9] 耿昊,卢浩,邱艳宇.指挥防护工程体系功能毁伤降阶态易损性分析方法研究[J].防护工程,2018,40(3):31-37.
[10] 陈小青,王可定.防护工程综合防护多目标优化的进化算法模型[J].解放军理工大学学报(自然科学版),2004,5(4):85-89.
[11] 邬建华,夏志成,龚华栋.防护工程综合防护效能评价[J].解放军理工大学学报(自然科学版),2003(2):52-55.
[12] 总参工程兵国防工程研究设计所.防护工程毁伤判据与综合防护能力评估模型[R].北京:总参工程兵国防工程研究设计所,1993.
[13] 刘竞妍,张可,王桂华.综合评价中数据标准化方法比较研究[J].数字技术与应用,2018,36(6):84-85.
[14] KUHN H,TUCKER A.Extensive games and the problem of information[C]//Contributions to the Theory of Games II,Annals of Mathematics Studies No.28,Princeton,1953.