现代武器装备日趋功能多样,结构复杂,但就其设计实现来说,无处不体现出层次性的特点。装备的层次设计具有其现实意义,既便于现实中的设计、使用、维护,又便于思维逻辑上的理解,这种层次划分的现象在自然界、认识领域、人类社会等方方面面普遍存在。目前,层次分析法作为一种认识和处理层次问题的主要方法,受到广泛关注,许多学者进行了深入研究。论文主要针对层次分析法中判断矩阵的不一致性问题展开研究,提出了改进的算法。
1 层次分析法简述
层次分析法是为了解决多目标或多措施决策问题而提出的,最早由Saaty于1977年提出,1980年其专著问世[1-2],表示这种理论方法已具有系统性。
其实现过程可分为4步,见图1。
1)根据系统分析结果,构建整体的递阶层次结构。
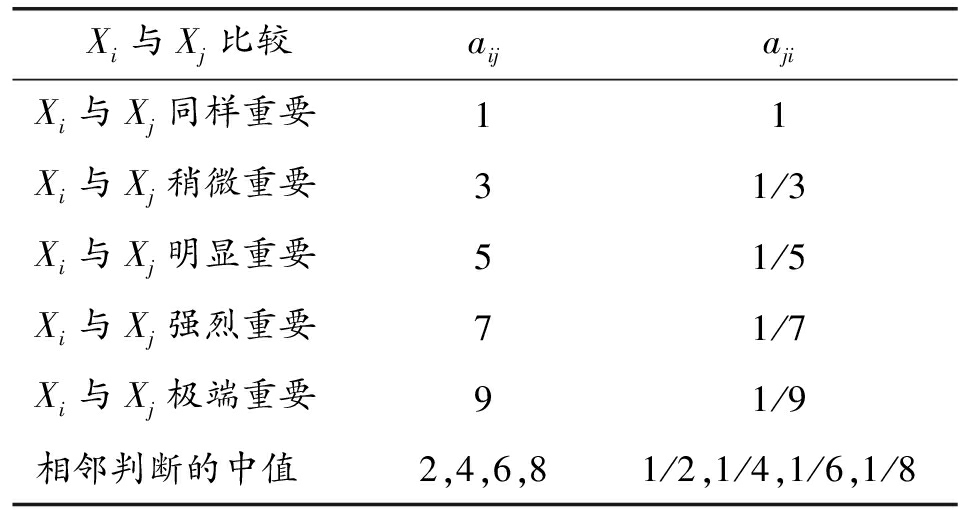
2)根据经验或专家评比,由比例标度给出元素值,构造各层次的判断矩阵。根据Saaty的研究建议,将比例标度按照重要程度分为1~9级,见表1。
Xi、Xj分别表示同一层次中两个因素,aij、aji分别表示Xi与Xj的比较标度值。
3)计算矩阵的最大特征值和特征向量,特征向量归一化后即为相对权重,并进行一致性检验,得出每一层次相对于上一层次的单排序[3]。
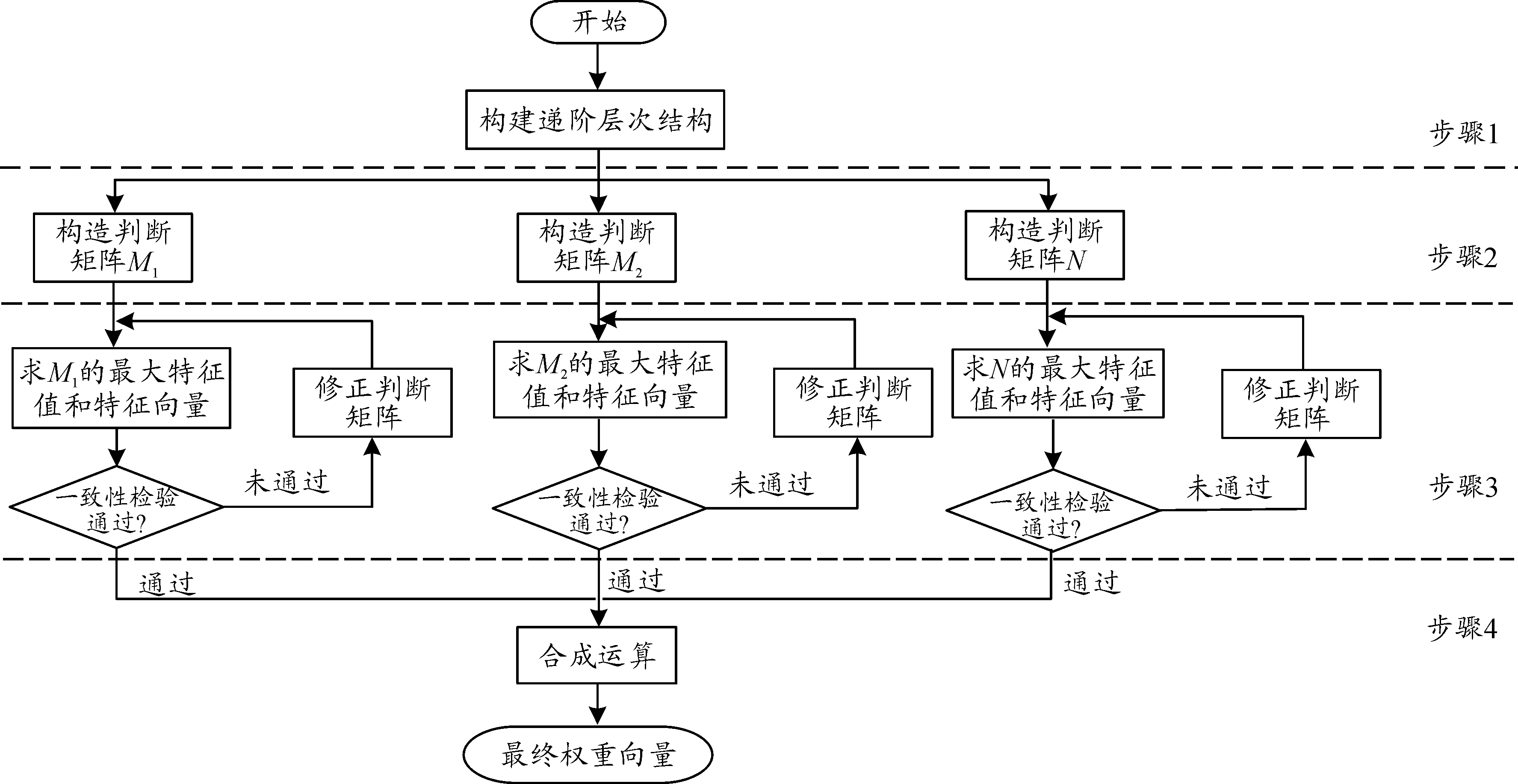
图1 层次分析法基本步骤框图
(a)计算一致性指标CI:
(1)
(b)查找平均随机一致性指标RI。
其计算方法为[4]:随机的构造500个样本矩阵,样本值从1~9及其倒数中选取,计算最大特征根的均值![]() 则
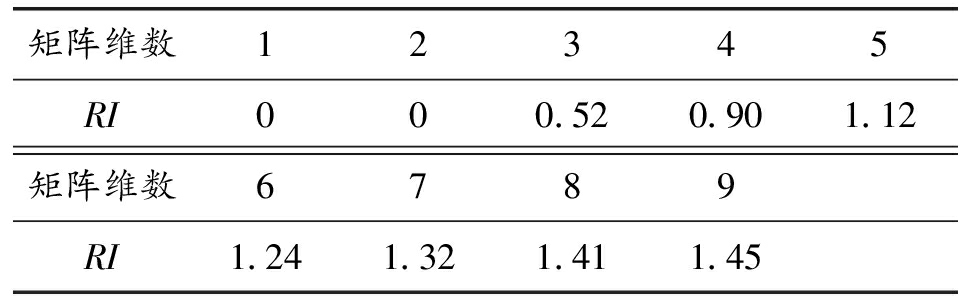
则![]() 其取值见表2。
其取值见表2。
表1 九标度表示法
Xi与Xj比较aijajiXi与Xj同样重要11Xi与Xj稍微重要31/3Xi与Xj明显重要51/5Xi与Xj强烈重要71/7Xi与Xj极端重要91/9相邻判断的中值2,4,6,81/2,1/4,1/6,1/8
表2 平均随机一致性指标
矩阵维数12345RI000.520.901.12矩阵维数6789RI1.241.321.411.45
(c)计算满意一致性比例CR:
(2)
一般认为当CR<0.1时,矩阵满足一致性要求,一般为满足顺序一致性要求。
4)相邻两层进行合成运算,最终得到底层元素相对于顶层的总权重,以用于决策判断。
2 判断矩阵不一致性问题
研究表明,当同一层次内元素数n>9时,很容易造成判断矩阵逻辑混乱,导致判断矩阵元素值不一致现象发生。导致判断矩阵不一致的因素有[5]:
1)模糊关系的累加。两个因素的重要性比较是专家的一种模糊比较,“同样重要”和“稍微重要”的区别本身不明显,经过多次比较后这种模糊性往往会表现为不一致。
2)缺乏统一的标准进行系统的度量。对于两个因素的相对重要性,专家往往能够给出一个明确的判断结果,但对于多个因素整体而言,往往会出现判断标准的前后不一致性,造成最终判断矩阵的不一致。
为了解决这个问题,许多研究学者进行了研究。① 文献[6]介绍了经验调整的方法,通过观察发现矩阵中的元素不满足顺序一致性的要求,人为修改相关的元素值使其满足顺序一致性。② 文献[7]的思路是采用次序一致性和绝对一致性对判断矩阵进行检验,检验不通过时采用极差标准对相关元素进行修正,而后再次检验,最终满意一致性指标CR低于设定阈值时,算法结束;文献[8]在文献[7]的基础上,改进了绝对一致性矩阵的构建算法,采用最大偏离距离作为调整标准,降低运算复杂度,能够支持快速运算。③ 文献[6,9-11]则采用的是一种拟优一致矩阵的概念,为了避免进行一致性检验的繁琐过程,将判断矩阵直接转换为拟优一致矩阵,在此基础上计算权重向量作为原判断矩阵的权重向量。④ 文献[12]将判断矩阵看做一致性矩阵和扰动矩阵的组合,并利用区间模糊数的方法调整扰动矩阵中最大的值,经过反复调整,使矩阵满足满意一致性指标。
3 判断矩阵调整方法实现
文献[6-12]从不同的角度研究了判断矩阵不一致性的调整方法,但仍存在一些不足:凭借观察进行调整,方法移植性差,不便于计算实现;使用拟优一致矩阵替换判断矩阵,会大量丢失专家判断信息;使用区间模糊数调整判断矩阵元素值,会使九标度条件下的平均随机一致性指标不再适用。针对这些问题,本文使用扰动矩阵[8]的概念,按照扰动值由大到小的顺序对元素值进行调整,最终达到满意一致性指标,调整结束。
3.1 调整方法
一般来说,只需要考虑aij>1的情况,其相对应的|dij|必在排序结果的前列。对于aij<1的情况,在实际应用中调整的可能性很小,可以不用考虑。
调整的原则是每个元素值aij最多调整一个标度,调整的目标是使扰动值dij趋于0。
这样调整的目的是最大可能保留专家的判断结果,同时满足九标度法的要求,能够使用满意一致性原则进行一致性评判。
3.2 实现步骤
步骤1 计算判断矩阵的最大特征值,并计算满意一致性指标CR,与满意性阈值M进行比较,若CR(A)≤M,不需要进行调整,直接转到步骤5;否则,转到步骤2。
步骤2 采用几何平均法[13]计算特征向量。
构造一致性矩阵W:
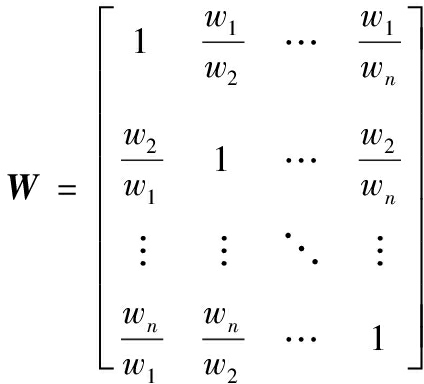
计算扰动矩阵D:

即![]()
对非对角线元素的绝对值|dij|由大到小进行排序,得到排序结果{l1,l2,…,ln2-n}。
步骤3 调整ls对应的元素值aij,其中![]()
1)若aij>1且dij>0,则将aij降低1个标度值,即aij-1,若aij=2,则不进行调整;
2)若aij>1且dij<0,则将aij提高1个标度值,即aij+1,若aij=9,则不进行调整;
当aij做出调整后,其对称位置元素aji做相应调整,使调整后的矩阵仍然是互反矩阵。
步骤4 将调整后的矩阵标记为As(s表示调整的次数),计算其满意一致性指标CR(As),如果CR(As)≤M,转到步骤5,否则转到步骤3。
步骤5 计算最终调整后的矩阵As的最大特征值和特征向量,特征向量归一化后即为各因素的权重。
4 算例分析
为了说明算法的实际操作,使用一个实例进行说明。岳女士需要购买一件衣服,在仅考虑款式的条件下,其对4件备选服装给出了如下的判断矩阵:
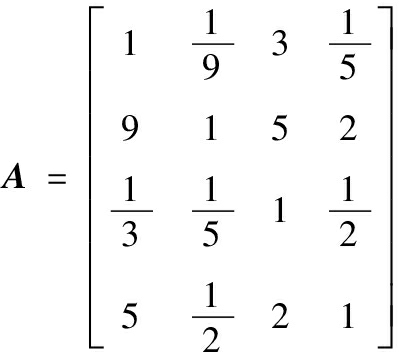
1)计算最大特征值为λmax=4.464 4,计算其满意一致性指标为CR(A)=0.172,设定满意性阈值为M=0.1,显然,矩阵A不满足一致性指标,需要进行调整。
2)计算矩阵A的权重向量为[0.092 2 0.558 9 0.077 5 0.271 3]T,构造W矩阵为

计算扰动矩阵D为
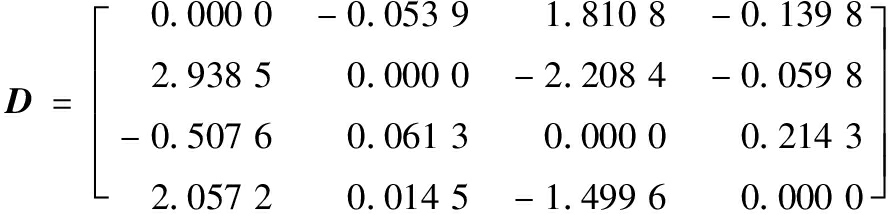
对矩阵D非对角线元素绝对值进行排序得到:
{2.938 5 -2.208 4 2.057 2 1.810 8 -1.499 6 …}
3)D矩阵元素2.938 5对应的A矩阵元素值为a21=9,符合第一个条件,将其调整为8,调整后的矩阵为
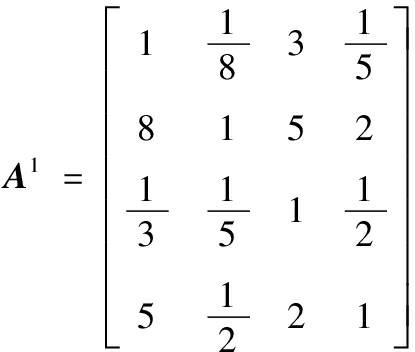
计算其最大特征值为λmax=4.440 9,其满意一致性指标为CR(A1)=0.163 3>0.1仍不满足一致性条件,继续调整。
4)D矩阵元素-2.208 4对应的A矩阵元素值为a23=5,符合第二个条件,将其调整为6,调整后的矩阵为

计算其最大特征值为λmax=4.412 3,其满意一致性指标为CR(A2)=0.152 7>0.1仍不满足一致性条件,继续调整。
5)D矩阵元素2.057 2对应的A矩阵元素值为a41=5,符合第一个条件,将其调整为4,调整后的矩阵为

计算其最大特征值为λmax=4.348 2,其满意一致性指标为CR(A3)=0.129 0>0.1仍不满足一致性条件,继续调整。
6)D矩阵元素1.810 8对应的A矩阵元素值为a13=3,符合第一个条件,将其调整为2,调整后的矩阵为
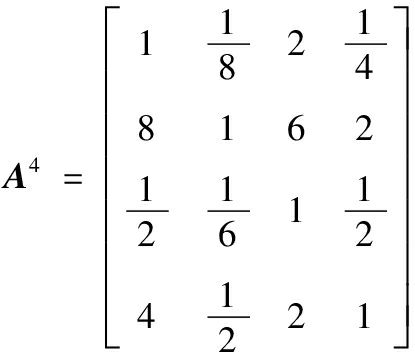
计算其最大特征值为λmax=4.196 4,其满意一致性指标为CR(A4)=0.072 7<0.1满足一致性条件。
计算其权重向量为[0.091 0 0.569 5 0.082 2 0.257 3]。
若采用拟优一致性矩阵替换判断矩阵,计算拟优一致性矩阵为

计算权重向量为[0.092 2 0.558 9 0.077 5 0.271 3]。
对比可以看出,拟优一致性矩阵对每个元素值进行了调整,调整幅度明显大于本文,说明其过多的舍弃了专家的判断信息。
5 结论
针对判断矩阵的不一致性问题,通过构造扰动矩阵、排序扰动值、按次序调整扰动元素等步骤调整判断矩阵,既保留了专家的判断信息,又符合满意一致性指标的使用条件。与拟优一致矩阵对比表明,本文的方法能够更多的保留专家判断信息。
[1] SATTY L T.The Analytic Hierarchy Process[M].New York:McGraw-Hill,1980.
[2] VENKADASALAM S.An Analytic Hierarchy Process(AHP)Approach to Training Typology Selection Based on Student Perspective[J].Asia-Pacific Journal of Business Administration,2015,7(2):140.
[3] 姜帆.模糊层次分析法不一致性问题研究[D].保定:华北电力大学,2015.
[4] 宋花玉.基于判断矩阵行一致信息的指标权重均值算法[J].现代电子技术,2015,38(17):114-116.
[5] 王中胜,李敏强,寇纪淞.层次分析法判断矩阵不一致性的形成机理和一种修正方法[J].系统工程理论与实践,1995,15(9):36-43.
[6] 梁樑,盛昭翰,徐南荣.一种改进的层次分析法[J].系统工程,1989(3):5-7.
[7] 杨永清.层次分析法中判断矩阵不一致性调整方法研究[J].运筹与管理,1999(3):12-16.
[8] 严世华,田效.基于层次分析法的判断矩阵一致性调整方法[J].兵工自动化,2008,27(4):8-9.
[9] 钱虹,马萃萃.基于改进层次分析法的核电站故障诊断方法[J].电力科学与技术学报,2017,32(2):105-110.
[10] 张艳丰,李贺,彭丽徽,等.基于语义隶属度模糊推理的网络舆情监测预警实证研究[J].情报理论与实践,2017,40(9):86-93.
[11] 张华丽,徐雪娇,金鑫,等.基于改进层次分析法的高校综合奖学金评定[J].科技广场,2017(9):181-185.
[12] 江文奇.一种判断矩阵的不一致性调整方法[J].系统工程与电子技术,2009,31(9):2129-2132.
[13] 董君.层次分析法权重计算方法分析及其应用研究[J].科技资讯,2015(29):218.