刚柔耦合柔性并联机构的弹性动力学建模及振动主动控制一直是机构学研究热点[1-3]。由于其动态性能好、操作灵巧、能耗低,可以实现高速、高加速度运动,广泛应用在高端电子芯片制造、精密加工、细胞操作等领域。最近几十年来,通过众多学者持续不断的努力,动力学建模理论已取得了许多有意义的成果[4-6]。然而,高速、高加速度柔性并联机构由于其刚度较小,容易产生弹性振动,其残余振动严重影响其重复定位精度,因此,必须对其弹性振动进行有效的控制。目前,柔性机构的振动控制方式主要有被动(如添加阻尼材料、增大系统刚度)和主动两种[7],其中基于压电陶瓷传感器和致动器的主动控制方式是近年来研究热点[7-9],但控制对象主要集中在柔性毂-梁机构、两连杆柔性机构、多连杆简单柔性机构(如四杆机构、链等)[10-12]。对复杂的柔性并联机构,相关研究成果较少[8,13-16],控制方法主要集中在应变速率反馈控制、应变与应变速率反馈控制、最优状态反馈控制等。但这些控制没有考虑模态截断引起的观测和控制“溢出”问题,鲁棒性较差,而滑模变结构控制具有良好的抗外部干扰和参数扰动性能,鲁棒性好,因此,本研究将对一类高速柔性并联机构进行研究,着重探讨滑模变结构控制在柔性并联机构残余振动主动控制方面的可行性和优越性,提高其重复定位精度,为高速精密定位平台提供理论基础。
1 柔性并联机构弹性振动控制方程
为了建立该柔性并联机构的动力学控制方程,采有限元法对柔性连杆进行梁单元划分,考虑压电陶瓷传感器和致动器的正逆压电效应,基于拉格朗日方程建立了智能梁单元的弹性动力学方程,假设整个系统有个致动器和个传感器,考虑单元间的约束关系可建立系统总的弹性动力学方程[4,16],
(1)
其中: U为系统的广义坐标列阵;C为阻尼矩阵;Q为广义力矩阵,包括广义外力,哥式力和离心力等,![]() 为输入矩阵,Vin=[Vae1,Vae2,…,Vaem]T为p维输入向量,Vs=[Vse1,Vse2,…,Vsem]T为q维输出向量,Cs为q×n阶输出矩阵。
为输入矩阵,Vin=[Vae1,Vae2,…,Vaem]T为p维输入向量,Vs=[Vse1,Vse2,…,Vsem]T为q维输出向量,Cs为q×n阶输出矩阵。
本研究的目标是抑制柔性构件的残余振动,以使动平台快速、精确地稳定在目标位置。残余振动是机构在名义运动结束后由于负载和自身的惯性和伺服电机的耦合作用而引起的柔性构件的振动。因此,式(1)的系数矩阵中与名义运动速度和加速度相关的量都为零。从而, 质量矩阵M为对称正定常数矩阵,刚度矩阵K为对称定常矩阵,外力矩阵Q为零矩阵。根据模态理论,系统的弹性振动主要由其低阶模态决定。采用实模态方法,把物理空间描述的动力学方程变换到模态空间上,并取其前r阶低阶模态进行控制。因此,系统的控制模型可以简化为:
![]()
(2)
式中: ηr为系统前r阶低阶模态;Cr为模态阻尼矩阵;Kr为模态刚度矩阵;![]() 为输入、输出系数矩阵。
为输入、输出系数矩阵。
把式(2)写成状态空间的形式,得
![]()
(3)
其中![]()
2 滑模变结构控制器设计
设状态变量为Xc(t),理想的状态Xcd(t)=0,因此系统跟踪误差及其导数为:
![]()
(4)
则切换函数矩阵s(x)可表示为:
s(t)=He(t)
(5)
其中H为m×2r阶矩阵。
本研究采用指数趋近律迫使系统从任意初始状态趋向切换面,直到到达切换面,即
(6)
可以证明该指数趋近律可以保证系统的稳定性,设Lyapunov函数为![]() 可得
可得
![]()
![]()
s(t)T(-diag(εi)sgns(t)-diag(ki)s(t))≤
![]()
(7)
解不等式(7),可得[17]:
(8)
由不等式(8)可知,系统状态方程V(t)指数收敛至零。收敛速度取决于![]()
根据式(3)和指数趋近律式(6),可求得控制函数:
Vin=(HBc)+(-diag(εi)sgns(t)-diag(ki)s(t)-HAcXc)
(9)
3 仿真与实验
如图1所示,以一平面完全对称的3-RRR柔性并联机构为例,对上述滑模变结构控制器进行数值仿真分析,验证该控制器可以有效地抑制柔性连杆的残余弹性振动。

图1 平面3-RRR柔性并联机构示意图
假设动平台中心点的运动轨迹为:

(10)
主动连杆、被动连杆及动平台的材料都是铝合金,主动连杆是刚性的,被动连杆是柔性的。假设连杆两端的集中质量为0.2 kg,集中转动惯量为0.000 5 kg·m2.每根柔性杆被划分为3个单元,2对PZT致动器对称地粘贴在每根被动柔性杆的第一、三单元的中间位置,PZT传感器粘贴在第二单元中间位置,杆件参数和PZT致动器和传感器参数见表1。取系统前三阶模态作为被控模态[12],取矩阵H=[2*I I],diag(εi)=0.000 03*I, diag(ki)=15*I,I为3×3的单位矩阵。
表1 构件参数

主动杆从动杆(PZT致动器/PZT传感器)长/mm25425250宽/mm252525高/mm1032弹性模量/MPa0.7102×1050.6×105密度/(kg·m-3)2及712~压电常数~1.86×10-10
首先,动平台按照式(10)给定的轨迹做圆周运动,运动一个周期后名义运动停止,开始施加控制。图2是3根主动连杆与相应的被动柔性连杆在X方向的最大弹性位移随时间的变化情况;图3是3根主动连杆与相应的被动柔性连杆在Y方向的最大弹性位移随时间的变化情况,从图3、图4可知,被动柔性连杆的最大弹性位移比相应的主动连杆大,这符合本文的主动连杆是刚性的假设。图4、图5、图6分别是在没有控制和滑模变结构控制下动平台在X方向、Y方向的弹性位移以及弹性转角随时间的变化情况;从图4、图5、图6可知,柔性连杆和动平台的弹性振动呈衰减振荡趋势。
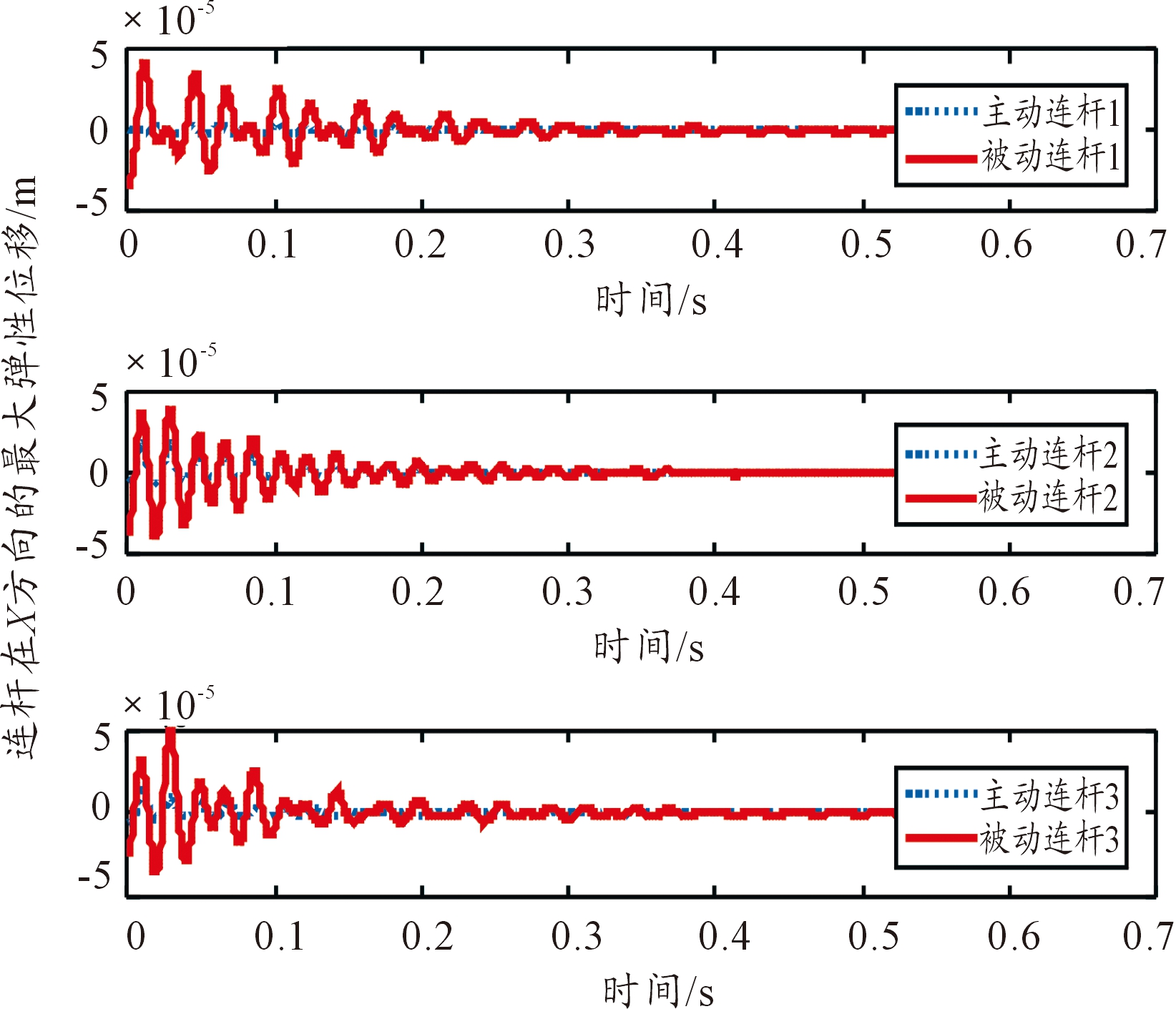
图2 所有主动连杆与相应的被动连杆在X方向的最大弹性位移随时间的变化情况

图3 所有主动连杆与相应的被动连杆在Y方向的最大弹性位移随时间的变化情况
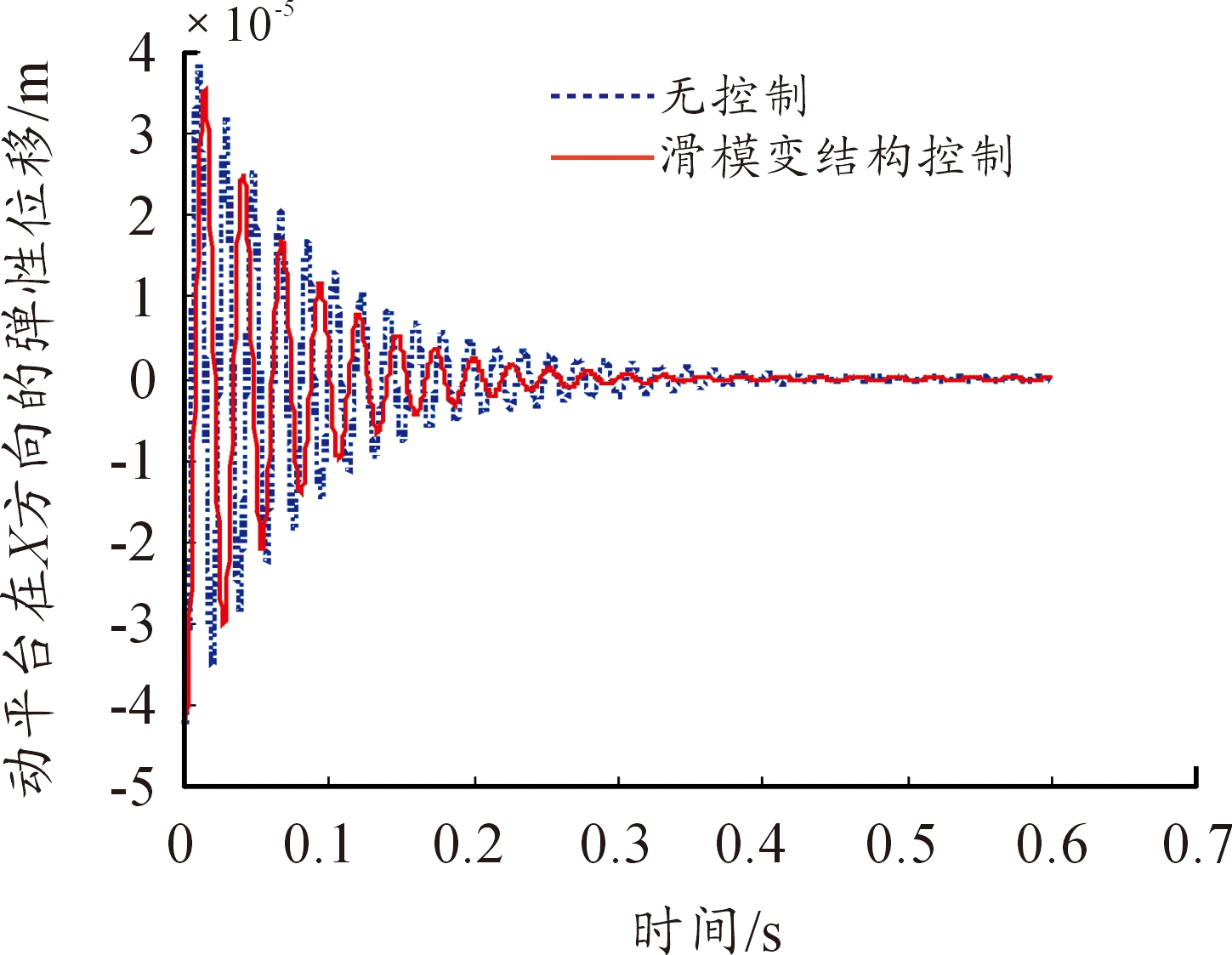
图4 在没有控制和滑模变结构控制下动平台在X方向的弹性位移随时间的变化情况
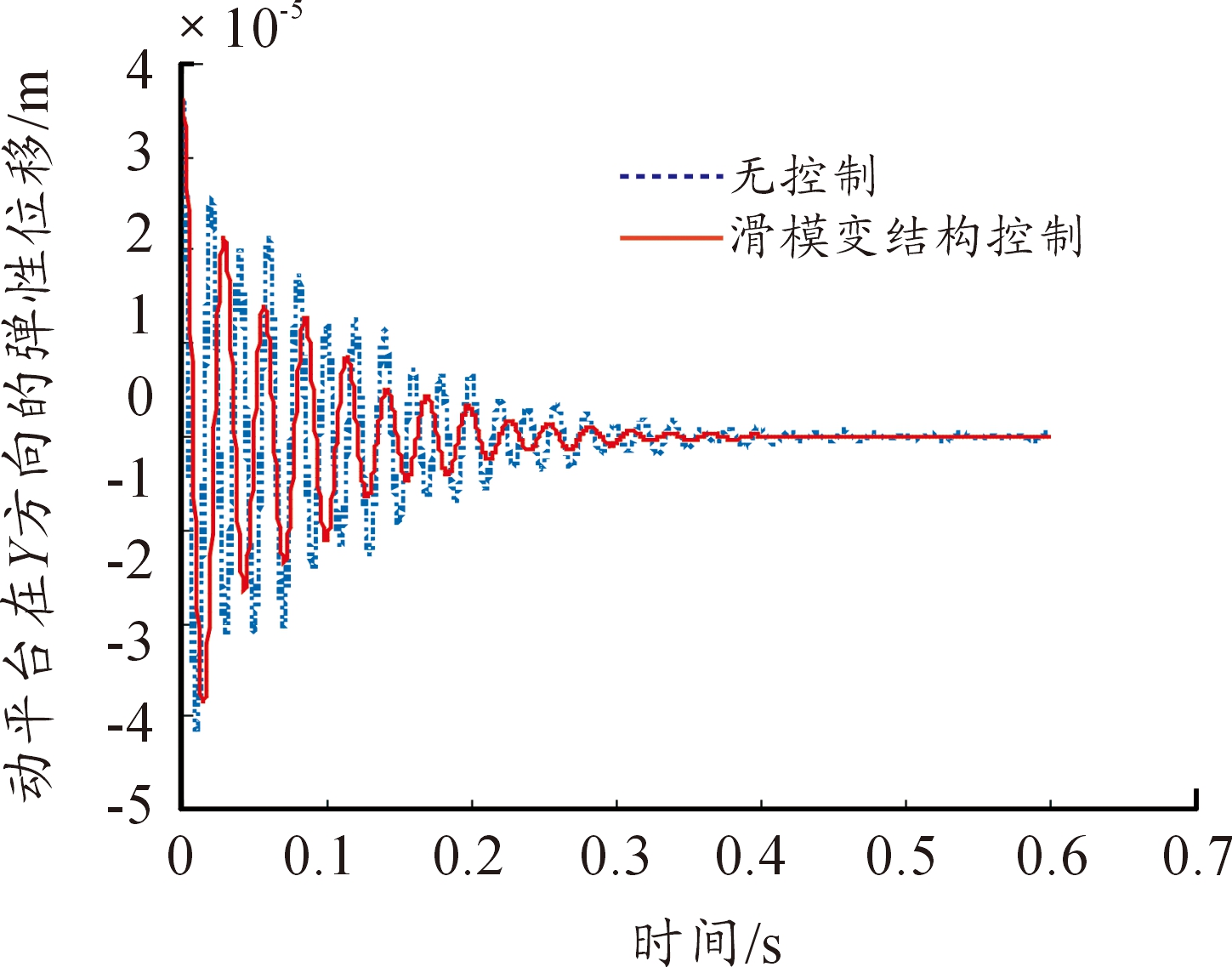
图5 在没有控制和滑模变结构控制下动平台在Y方向的弹性位移随时间的变化情况

图6 在没有控制和滑模变结构控制下动平台的弹性转角随时间的变化情况
在滑模变结构控制下,振动迅速趋于0,且没有“抖振”现象发生,因此,基于指数趋近律的滑模变结构控制可以有效地抑制动平台的残余弹性振动,进而提高动平台的重复定位精度。
图7、图8、图9分别是施加在三根柔性梁致动器片上的控制电压,通过PZT致动器正压电效应。抑制柔性连杆的弹性振动,进而抑制动平台的弹性振动。从图7、图8、图9可知,最大控制电压在被动柔性连杆1的PZT致动器对上,大小为270.5 V,大部分时间的控制电压限制在以内。被动柔性连杆3上的PZT致动器对所需的电压信号最小,同时,控制电压随着柔性连杆弹性振动的减小而减小。

图7 被动柔性连杆1上PZT致动器上所施加到电压随时间的变化情况

图8 被动柔性连杆2上PZT致动器所施加到电压随时间的变化情况

图9 被动柔性连杆3上PZT致动器所施加到电压随时间的变化情况
为验证滑模变结构控制算法的有效性,搭建了一套实验系统,实验系统如图10所示,主要由平面3-RRR柔性并联机构、压电陶瓷传感器和致动器、电荷放大器、压电陶瓷驱动电源、半物理仿真控制系统dSPACE-DS1103等组成。其中3根被动连杆为柔性,尺寸参数为:252 mm×25 mm×3 mm;主动连杆为刚性,尺寸参数为:254 mm×25 mm×10 mm,主、被动杆、动平台以及旋转关节材料均为铝合金,为使杆件表面绝缘,对其进行氧化处理。为方便电机的安装和良好的隔振,静平台由大理石、钢架结构和长方形钢板组成。压电陶瓷片有两种规格,一种尺寸为:50 mm×25 mm×2 mm,用作致动器;另一种尺寸为:30 mm×15 mm×1 mm,用作传感器。由保定宏声科技有限公司提供。

图10 实验系统
振动控制实验过程如图11所示,PZT传感器测量柔性连杆的弹性振动位移信号,经电荷放大器放大后传递给dSPACE控制器,通过上位机控制算法计算出所需的控制量,再通过dSPACE的DAC口传递给压电陶瓷驱动电源,放大的电压信号再施加给PZT致动器对,进而抑制柔性连杆的弹性振动,最终实现动平台的快速镇定。
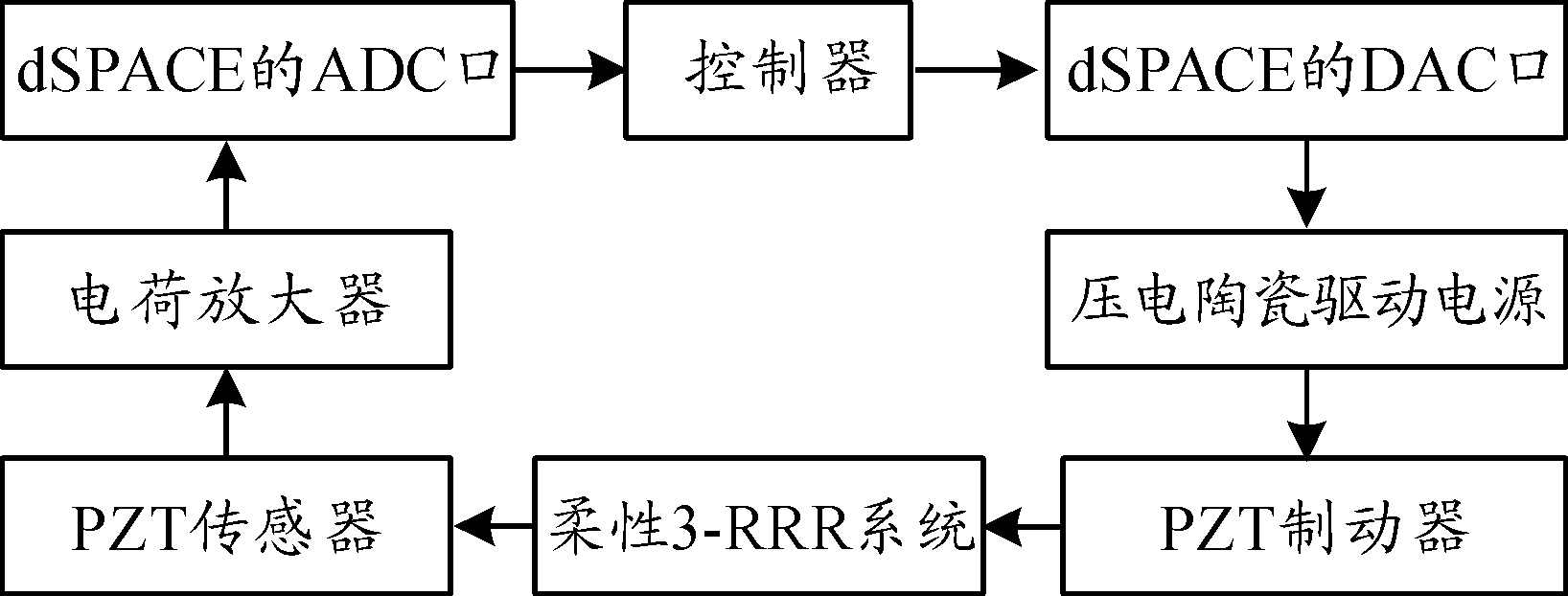
图11 振动控制过程框图
实验过程如下:动平台按给定轨迹运动一个周期[16]然后停止。PZT传感器片采集的振动信号反馈给同一杆上的两对PZT致动器。因此整个系统有3个PZT传感器,6对PZT致动器。取动平台名义运动停止后2.7 s内的数据进行分析,在Matlab/Simulation中设置采样频率为0.1 ms,即从每路传感器各提取了2.7万个数据。图12至图14分别是3片PZT传感器在控制和未控制时测得的柔性连杆1、2、3的振动信号曲线。从传感器测得的振动信号可知:本文设计的滑模变结构控制器可有效地抑制柔性连杆的残余弹性振动。
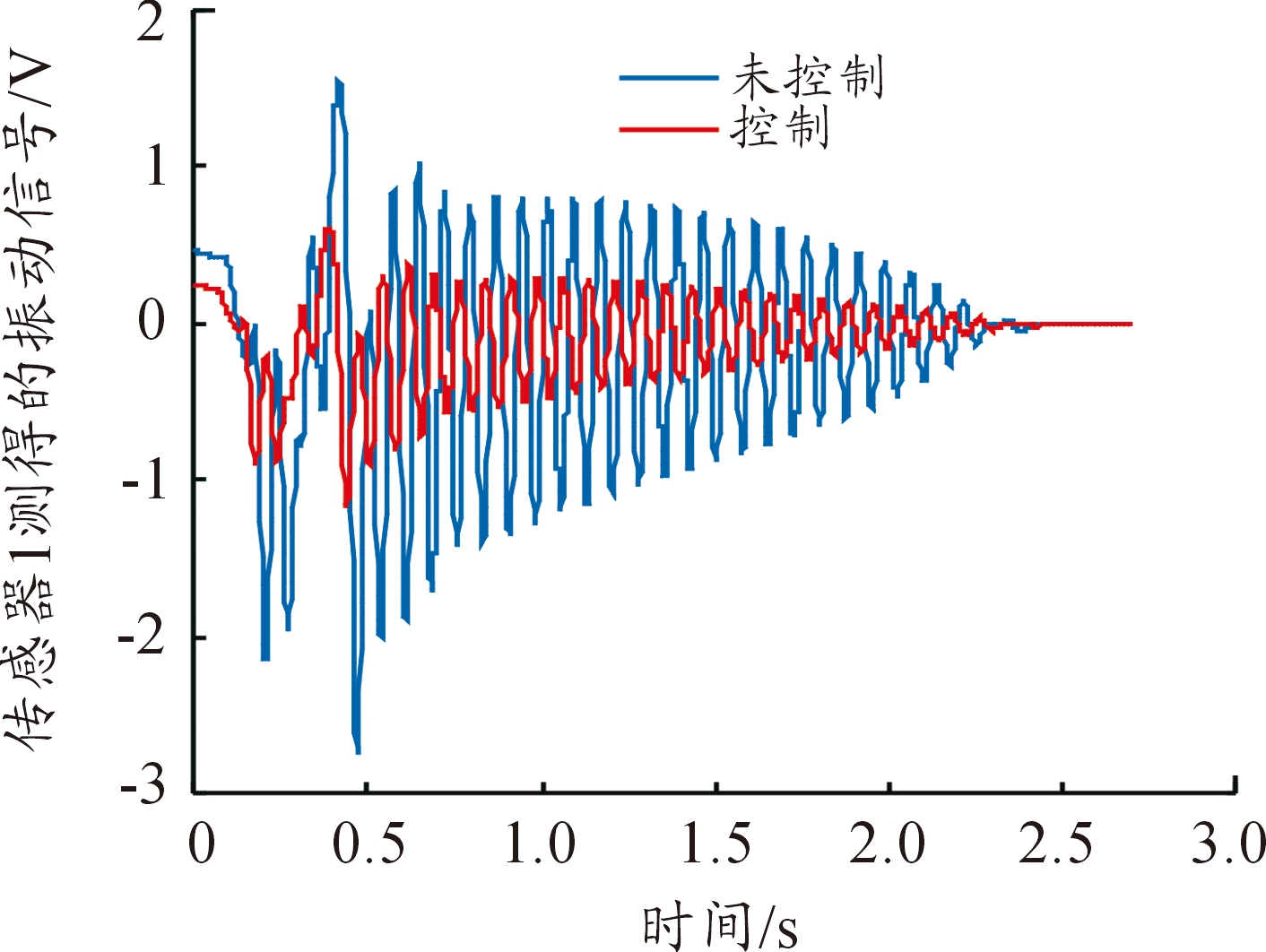
图12 传感器1测得的振动信号
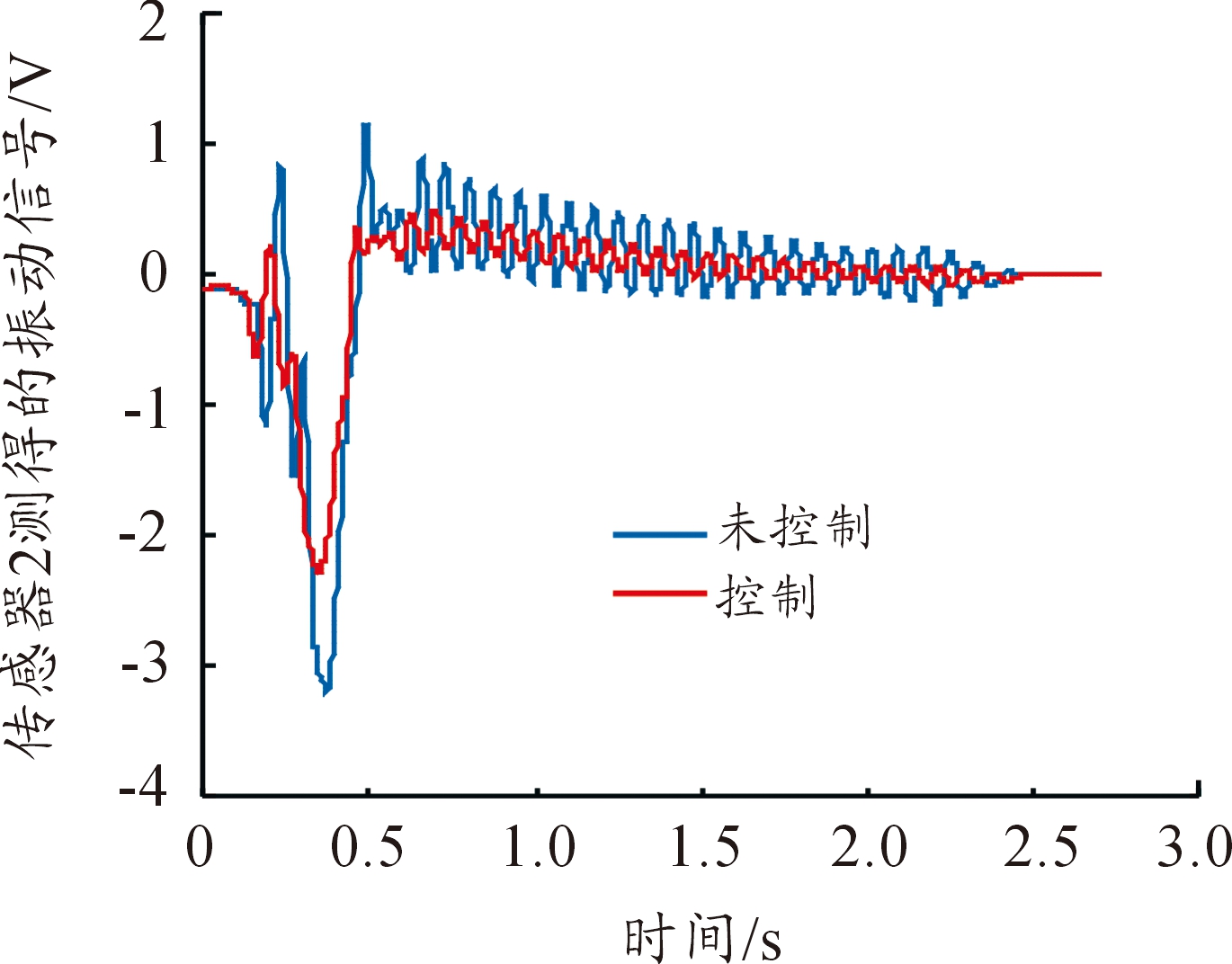
图13 传感器2测得的振动信号

图14 传感器3测得的振动信号
图15是柔性连杆3在未控制、应变率反馈控制[16]、滑模变结构控制三种情况下的第一阶模态(第一阶固有频率是12.5 Hz)的功率密度谱,在应变率反馈控制下第一阶模态功率密度谱下降了42.30%,在滑模变结构控制下第一阶模态功率密度谱下降了68.90%,对比应变率反馈控制,滑模变结构控制能获得了更好的控制效果,具体数据见表2所示。

图15 功率密度谱
表2 三种情况下柔性连杆3的第一阶固频的功率密度谱 dB

控制方式未控制应变率反馈控制滑模变结构控制第一阶固频的功率密度谱(柔性杆3)17.9210.34(-42.30%)[15]5.573(-68.90%)
4 结论
本研究基于已建立的柔性并联机器人机构的弹性动力学方程,采用模态截断理论,把高维弹性动力学方程化为r阶解耦方程。基于Lyapunov稳定性理论,采用指数趋近律函数,设计了多维滑模变结构控制器。验证了该控制器能有效地抑制并联机器人机构柔性连杆的弹性振动,进而可提高系统动平台的定位精度,通过与应变率反馈控制方法进行比较,得出滑模变结构控制在较低的控制电压下能取得更好的控制效果,其第一阶模态的功率密度谱下降68.90%,好于已有的控制结果[15-16]。
[1] BENSOMAN M,VEY G L.Control of flexible manipulators:A survey[J].Robotica,2004,22(5):533-545.
[2] DWIVEDY S K,EBERHARD P.Dynamic analysis of flexible manipulators,a literature review[J].Mechanism and Machine Theory,2006,41(7):749-777.
[3] 刘辛军,于靖军,王国彪,等.机器人研究进展与科学挑战[J].中国科学基金,2016(5):425-431.
[4] 张清华,张宪民.平面3-RRR柔性并联机器人动力学建模与分析[J].振动工程学报,2013,26(2):239-245.
[5] 杜兆才,余跃庆,张绪平.平面柔性并联机器人动力学建模[J].机械工程学报,2007,43(9):96-101.
[6] 毕富国,何广平.微型扑翼飞行器动力学模型参数的灵敏度分析[J].兵器装备工程学报,2019,40(8):94-99.
[7] ZHANG X M,SHAO C J,LI S,et al.Robust H∞ Vibration Control for Flexible Linkage Mechanism System with Piezoelectric Sensors and Actuators[J].Journal of Sound and Vibration,2001,243(1),145-155.
[8] ZHANG X P,WANG X Y,MILLS J K,et al.Experimental Implementation on Vibration Mode Control of a Moving 3-PRR Flexible Parallel Manipulator with Multiple PZT Transducers[J].Journal of Vibration and Control,2010,16(13):2035-2054.
[9] ZHANG Q,LI C,ZHANG J,et al.Active Vibration Control and Coupled Vibration Analysis of a Parallel Manipulator with Multiple Flexible Links[J].Shock and Vibration,2016,2016(2):1-19.
[10] 邱志成,许燕飞.基于自适应RBF模糊神经网络的旋转柔性铰接梁的振动控制[J].振动与冲击,2016,35(7):89-95.
[11] CHU Z Y,CUI J.Experiment on vibration control of a two-link flexible manipulator using an input shaper and adaptive positive position feedback[J].Advances in Mechanical Engineering,2015,7(10).
[12] 于潇雁,陈力.漂浮基柔性两杆空间机械臂基于状态观测器的鲁棒控制及振动控制[J].机械工程学报,2016,52(15):28-35.
[13] 张清华,张宪民.平面3-RRR柔性并联机器人残余振动主动控制[J].农业机械学报,2013,44(2):232-237.
[14] ZHANG X,MILLS J K,CLEGHORN W L.Vibration control of elastodynamic response of a 3-PRR flexible parallel manipulator using PZT transducers[J].Robotica,2008,26(5),655-665.
[15] ZHANG Q,JIN J M,ZHANG J H,et al.Active Vibration Suppression of a 3-DOF Flexible Parallel Manipulator Using Efficient Modal Control[J].Shock and Vibration,2014:953694.
[16] ZHANG Q,ZHANG X,WEI J.Experimental Study of Active Vibration Control of Planar 3-RRR Flexible Parallel Robots Mechanism[J].Shock and Vibration,2016:4780181.
[17] 刘金琨.滑模变结构控制MATLAB仿真(第3版):基本理论与设计方法[M].北京:清华大学出版社,2015.