空域划设问题直接关系到空域使用效率和安全,从而影响作战效能和经济效益,不论在军航还是民航都是研究的热点。目前,空域划设主要有两种思路[1]:一是从上向下划设,以基于最优化理论的“排样”法为典型代表。该算法将空域划设问题抽象为一个多维“下料”问题,结合最优化算法,得到空域划设方案。二是从下向上划设,以网格“生长”算法[2-3]最为突出。该算法是在空域离散化的基础上,从初始生长点,按照一定的信息素条件进行临近生长,直至实现空域的完全划分。两种思路各有其特点。近年来,网格“生长”算法由于更贴近划设实际、算法过程明晰等特点,得到了更广泛应用和研究。
一般的“生长”算法[4-5],网格选择任意,缺乏实际意义,不能与地图相匹配,信息素收集困难;且生长网格没有嵌套效应,需专门设计边缘平滑算法。弧度制全球网格系统,用等弧度划分替代等角度划分,用十进制代替六十进制,采用单一尺度均匀划设而非多尺度划设,形成了以网格为单元的全新地理空间计算和管理框架,极大地简化了空间计算。基于弧度制网格剖分的改进“生长”算法,信息素收集方便,使用算法嵌套平滑边缘,能极大提升空域划设效率。
1 弧度制全球网格
全球网格参考网格系统是一种科学的、简明的、全球统一的刚性定位网格参照系统,比较常见的是MGRS和GARS[6-7]。MGRS与GARS网格系统,在目标定位和区域协同方面各有其优势,但存在共同缺陷:① 采用角度制,计算复杂。角度制是一种六十进制的计数方法,与日常生活的十进制区别较大,带来计算和认知麻烦;② 划分具有多尺度效应。两种网格都是等度、等分、等秒划设,但间隔尺度不一。如在GARS中,划分为30′、15′和5′的3个层级[8-10],实现网格向下 “四等分”和“九等分”,这种尺度差异给跨网格(空域)组合和拆分带来极大的困难。弧度制网格参考系统,采用弧度制和“百等分”方法,将角度和距离统一起来,并实现十进制计算,克服了MGRS与GARS网格系统的不足。
1.1 弧度制网格构建
弧度制网格系统,按照“确定地图基础和坐标系——确定划分规则,进行全球划分——确定编码规则,对剖分进行编码”的步骤进行网格系统构建[11,12]。
1.1.1 确定地图基础和坐标系
以经纬度坐标体系为依据,采用圆柱投影中的横轴墨卡托投影,按照西经180°经线展开形成平面地图为划分基础,它的坐标范围为:西经180°至东经180°;南纬90°至北纬90°,将其转换为弧度制为:经线(-π,π);纬线(-π/2,π/2)。若以180°W90°N(南极点)为原点,180°W经线方向为y轴,垂直于180°W经线方向为x轴,建立平面直角坐标系,则相应的坐标范围变为:x轴方向(0,2π);y轴方向为(0,π),如图1所示。由于π值近似等于3.14,因此坐标范围又可描述为:x轴方向(0,6.29);y轴方向为(0,3.15)。
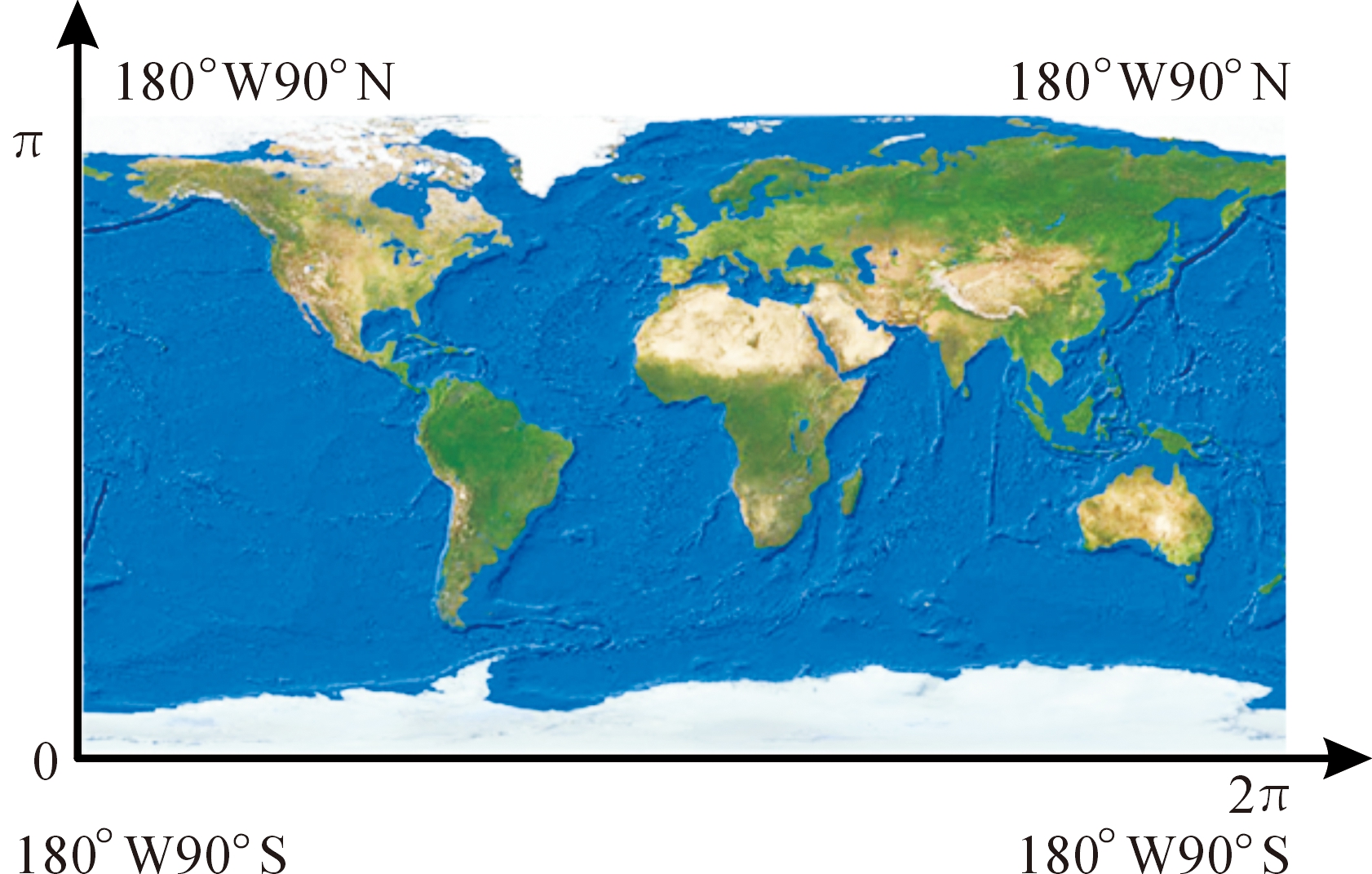
图1 弧度制坐标系统
1.1.2 确定划分规则,进行全球划分
弧度制网格剖分,以原点为起点,向东和向北,按照0.01 rad×0.01 rad进行划分,形成628×314个一级网格,网格大小为64 km×64 km。依次对上一级网格进行10×10等分,形成第二、三、四、五、六级网格(见图2),后一级网格尺寸是上一级尺寸的1/10,面积为1/100,维持十进制关系。弧度制能使角的集合与实数集合R存在一一对应关系,一个完整的圆的弧度是2π,即2π rad=360°,因此1 rad=57.3°。弧度制不仅能将角度和距离度量统一到十进制,而且能够极大的简化弧长(距离)的计算:L=α(弧度)×R(半径)。
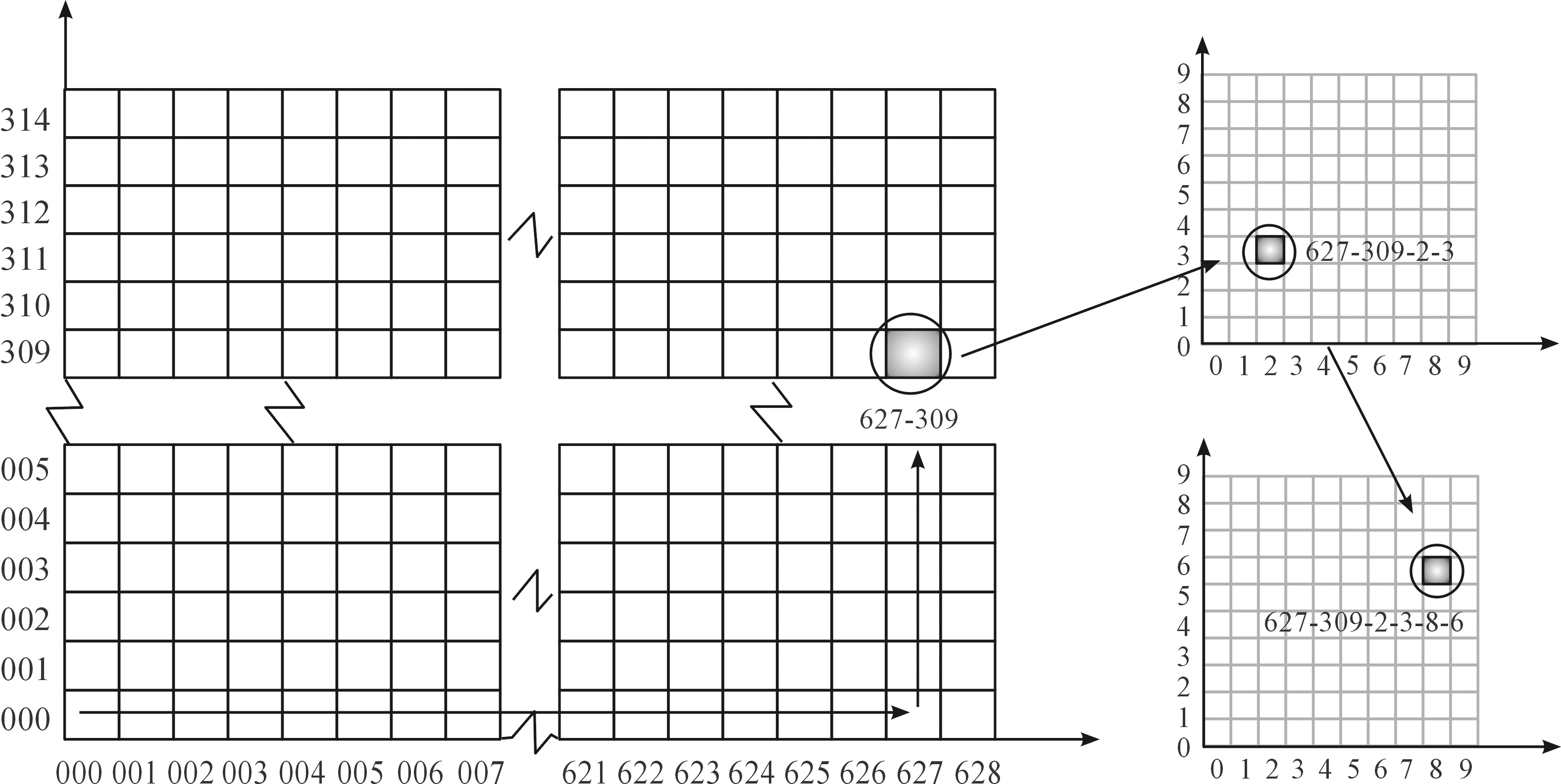
图2 RGRS剖分及编码示意图
1.1.3 确定编码规则,对网格进行编码
按照弧度制网格剖分规则,全球可划设628×314个一级网格。一级网格编码按照“序号不足三位补足三位数”的编码规则,构成XXX-YYY的结构,则网格坐标轴范围为:纬线方向000~628;经线方向000~314。如图2中阴影部分的一级网格的编码为“627-309”,二级至六级编码,按照“10×10”坐标点的方式进行“分层—交叉”编码,图2中的二级编码为“2-3”,三级编码为“8-6”,则一个完整的精确到三级网格的编码为“627-309-2-3-8-6”,亦可简写为“627-309-23-86”。
1.2 网格信息素矩阵
地球是一个椭球体,两极稍扁,赤道略鼓,半径长度均值约为6 400 km,由此可得弧度制全球网格系统基础网格层级及精度,见表1。一个完整的网格编码长度等于“4+2×级数”,第六级网格的完整编码有16位,通常划分到三级(10位),区域精度为“640 m×640 m”,已经能够满足绝大多数区域定位和协调需求。
表1 RGRS基础网格层级及精度
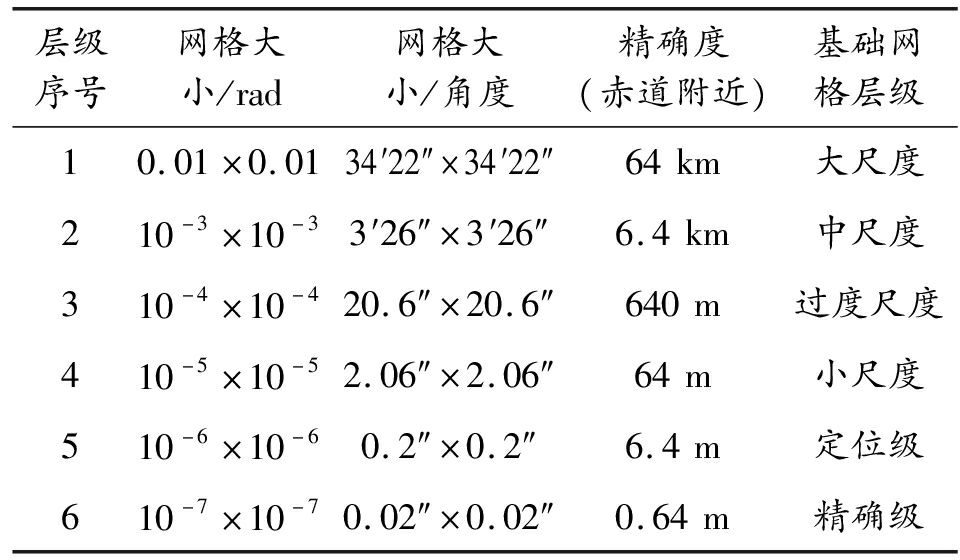
层级序号网格大小/rad网格大小/角度精确度(赤道附近)基础网格层级10.01×0.0134′22″×34′22″64km大尺度210-3×10-33′26″×3′26″6.4km中尺度310-4×10-420.6″×20.6″640m过度尺度410-5×10-52.06″×2.06″64m小尺度510-6×10-60.2″×0.2″6.4m定位级610-7×10-70.02″×0.02″0.64m精确级
以不同精度的弧度网格作为存储空间数据的“抽屉”,把多源异构数据规则地放置到“抽屉”中,不同数据之间通过网格编码有机地关联在一起,由此可实现多源异构数据在空间特征上的关联整合,这些“抽屉”和信息数据共同构成了网格信息素矩阵。在图2中,弧度制全球网格参考系统的一级网格,构成了一个628×314的信息素矩阵A;二级网格构成了一个6 280×3 140的信息素矩阵B;三级网格构成了一个62 800×31 400的信息素矩阵C。


显然,上一级网格是下一级网格的矩阵分块。用元包数组对信息素矩阵进行存储,一个精确到三级的弧度网格可表示为A=cell(cell(cell(·)10×10)10×10)618×314。定义某个区块Bij的信息素大小为![]() 则各网格之间信息素的传递关系为:
则各网格之间信息素的传递关系为:
(1)
式(1)中:∀i∈[1,618];∀j∈[1,314]; ∀k, l∈[1,10];sum+(·)算子表示信息素矩阵所有元素值求和。利用多颗粒度的信息素矩阵,能够实现区域定位和数据的存储计算。
2 弧度制网格空域划设
区域生长算法[2-3],是一种经典的基于区域的图像分割方法,是一种根据事前定义的准则将像素或子区域聚合成更大区域的过程,其实质就是按照一定的规则(如性质相似)把像素连通起来,从而最终构成分割区域。本文中将区域生长算法应用到空域划设,将弧度网格单元统计数据(信息素)作为“像素值”。
2.1 空域划设数学模型
空域生长算法是从初始点网格出发,向四周不断的生长合并其他网格,最终实现对区域网格的完全划分。划分的过程中始终坚持各划分区域之间信息素均衡。由此可得,基于弧度网格的空域划设数学模型为:
MIN=VAR(Zi)
s.t.
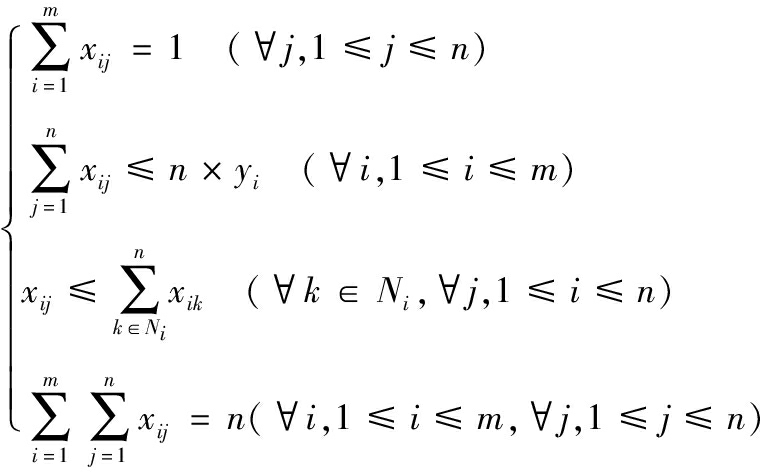
(2)
式(2)中:i表示优化划分的第i个区域;j表示空域内第j个网格单元;n表示空域内的所有网格单元个数;m表示区域划分总数;Ni表示与网格单元j相邻的网格单元集合;xij∈{0,1}表示网格单元j是否属于区域i;yi∈{0,1}表示存在第i区域输出时为1,否则为0;Zi表示第i个划分区总信息素。
目标函数表示各划分区块信息素应当均匀;约束条件1确保了每个空域网格单元只能归属于一个分区,即反映了分区不能交叉重叠,也不能留有空隙的约束;约束条件2确保所划分的分区大小和形状合理;约束条件3确保扇区内所有网格单元是相连的,满足了分区连续性约束;约束条件4保证所有网格单元被划分出去,不会有剩余网格存在。
2.2 改进区域生长算法
区域生长算法是建立在区域网格化的基础之上,有三个关键步骤[4-5]:
1)种子点的选取。选择一组能正确反映所需区域特征的点。一是种子点的数目m,即空域划设的数目;二是种子点的位置,该问题可选择航迹点密度最大的前m个网格作为种子点或者随机选择。
2)生长准则的确定。确定在生长过程中将相邻网格包括进来的条件。对于航迹来说,采用被划分区域中航迹总密度最小原则进行生长,即![]() 其中π(·)表示求区域或者网格信息素。
其中π(·)表示求区域或者网格信息素。
3)确定区域生长的终止原则。所有的网格都分配完毕。
以基于航迹点密度的空域分割为例,改进生长算法的具体步骤为:
步骤1 根据划设区域范围,建立划设区一级网格坐标系统;根据划设精度,确定弧度网格最终等级Num;
步骤2 统计当前等级网格系统中,每个网格的信息素,确定划设分区数目及相应初始生长点;
步骤3 从每个初始点所在单元网格出发,搜索相邻单元网格中信息素最小的网格,并将其信息素与相应生长点的信息素相加,形成待生长区;
步骤4 比较各待生长区总信息素,找到其中信息素最小的待生长区,合并其网格及信息素,作为下一轮生长的初始生长点,释放其余待生长区;
步骤5 重复步骤3、步骤4,直至找不到还未分配网格,完成该级网格划分;
步骤6 判断网格等级是否达到Num;若没有达到网格等级要求,则根据该级网格划分确定的划分边界,依次对每一个边界网格10×10剖分,形成下一级网格坐标系统,选出该系统中最靠近相应分区的点作为新的生长点,转到步骤2;若达到网格等级要求,转到步骤7。
步骤7 对网格边沿进行平滑,完成空域划设。
假设任意网格单元为Bij,共N个;分为M个区块;每个区块的种子单元为Zijk, k∈[1,M];第k个区块集合为Qk,显然Zijk⊂Qk;第k个区块的临近区块集合为Lk={与k区块相邻且未分配的Bij},Bijk表示集合Lk中信息素最小的网格,则一个层级网格的算法流程如图3所示。
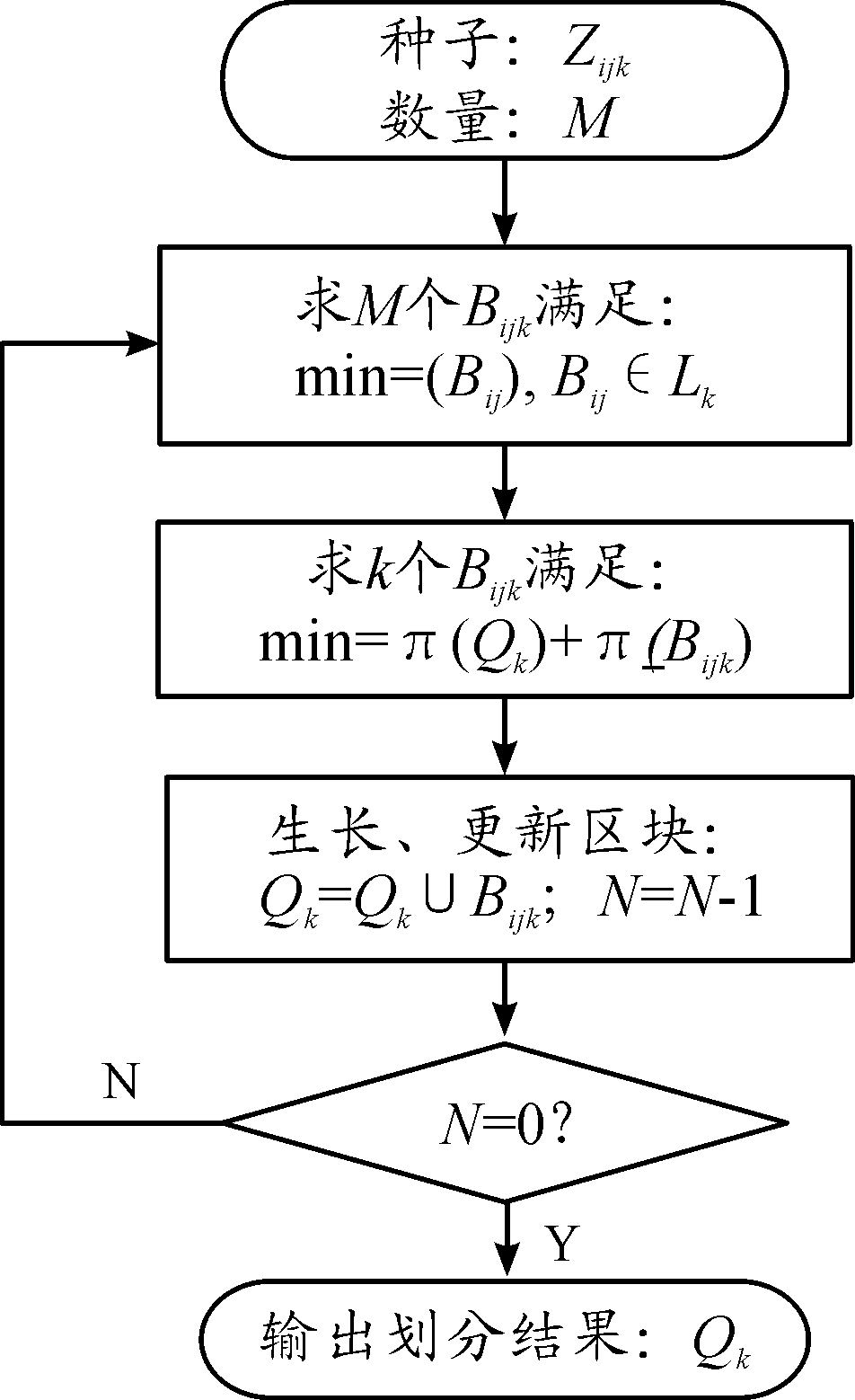
图3 改进生长算法流程
由算法步骤和流程图,得到改进生长算法与原生长算法[2-3],见表2。
表2 改进生长算法与原算法

算法名称RGRS生长算法原生长算法网格构建1.基于RGRS的全球网格,网格具有刚性,不随问题的改变而改变;2.网格具有多级效应,能够适应多种尺度的问题;3.能够适应动态变化的问题。1.网格临时确定,网格的大小,依据问题的尺度不同;2.网格尺度唯一;3.不能应对动态问题。信息收集1.信息收集能够立足于平时,存储于多级信息素矩阵;2.能与区域其他信息相交互。1.信息收集只能针对固定问题专门进行;2.不能与区域其他信息相联系。生长方式采用层次生长方式,从宏观到微观,多尺度划设,不仅能满足多分辨率的要求,还能很大程度提升划设效率。采用一次生长方式,划设效率较低。边缘平滑边缘嵌套生长,实现平滑需设计专门的平滑算法
3 空域划设仿真
以某地区空战场管制空域划设为例,该空战场覆盖的区域是一个由A1~A5(顺时针)五个顶点构成的多边形区域,各顶点的经纬度坐标已知,则按照弧度制网格编码规则能够计算出对应的网格编码,见表3。
表3 区域顶点坐标及所在网格编码
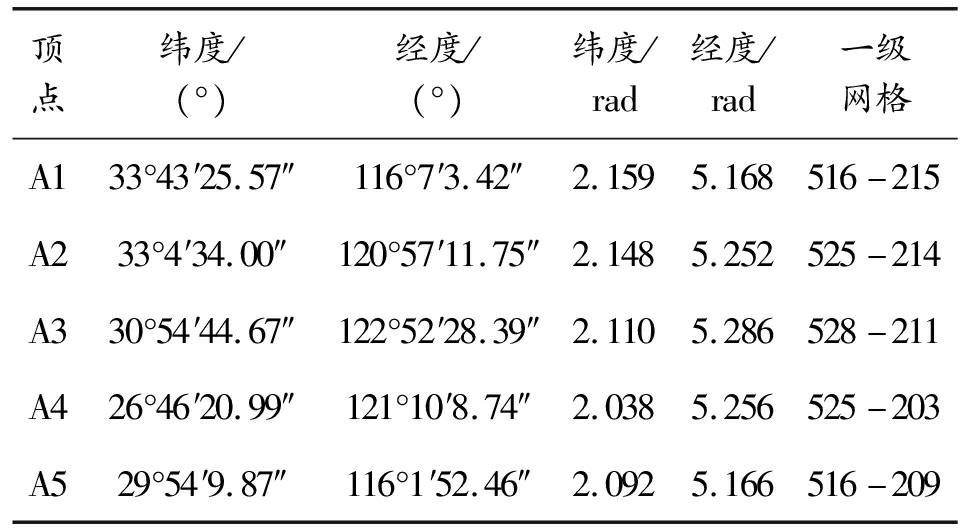
顶点纬度/(°)经度/(°)纬度/rad经度/rad一级网格A133°43′25.57″116°7′3.42″2.1595.168516-215A233°4′34.00″120°57′11.75″2.1485.252525-214A330°54′44.67″122°52′28.39″2.1105.286528-211A426°46′20.99″121°10′8.74″2.0385.256525-203A529°54′9.87″116°1′52.46″2.0925.166516-209
按照弧度制剖分规则,进一步将待划设的对多边形区域进行栅格化,形成13×13个一级网格组成的栅格化区域,精确度为64 km×64 km,如图4所示。
根据作战计划,特别是航迹规划信息,可以得到航迹点统计数据,由于保密原因,以随即产生一组信息素矩阵A为条件进行仿真实验,表4为一组随机信息素矩阵A数据。
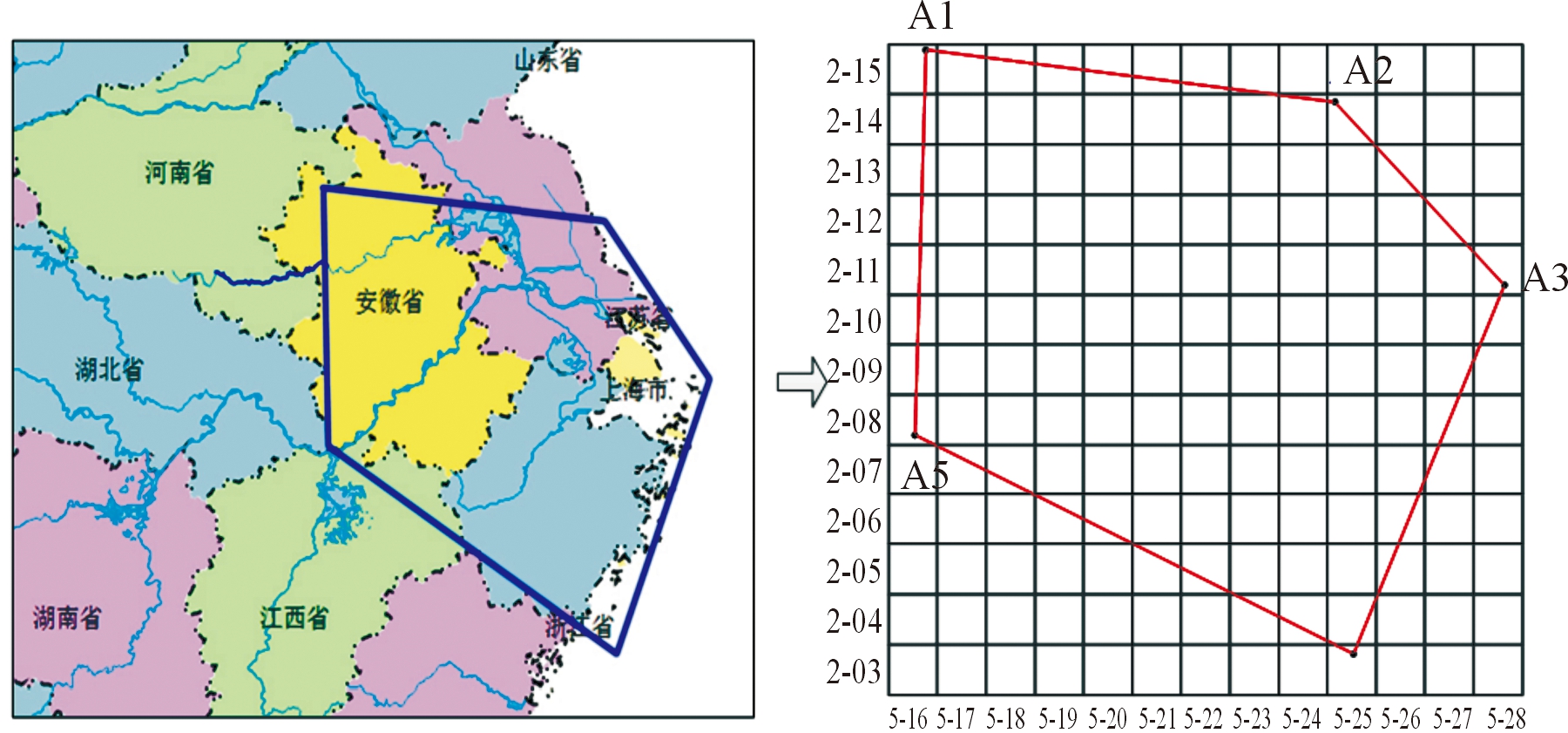
图4 多边形区域及栅格化
表4 信息素矩阵A13×13

A13×1352336851327499113386488358035913933757773987137726468220721418362282441459685543036772471798403793040535024753605776274757167478892196227682848451543798135182168550589310092777553632840296787953365212471433554669827888171345971213458381580975154945846133584278524710794769498738128721773315548835727679138207192936941839639583632
随机选择A(3,4)(对应弧度网格519-213)、A(6,11)(对应弧度网格526-210)、A(8,9)(对应弧度网格524-208)三个点,作为初始生长点(表3中被框选的位置),按照2.2节的改进生长算法进行空域分割。
经过一次空域生长,得到了一个大体的分区划设结果,如图5所示。显然,该结果并不能满足分区空域满足凸约束的条件,因此需要对其边缘进行调整。将三部分空域区块的边缘部分网格进行向下一级剖分,每个网格重新形成10×10个二级网格,精确度为6.4 km×6.4 km,然后按照2.2节的改进生长算法对每个边缘网格再进行一次空域分割,并进行边缘平滑,得到最终的分区划设结果,如图6所示。
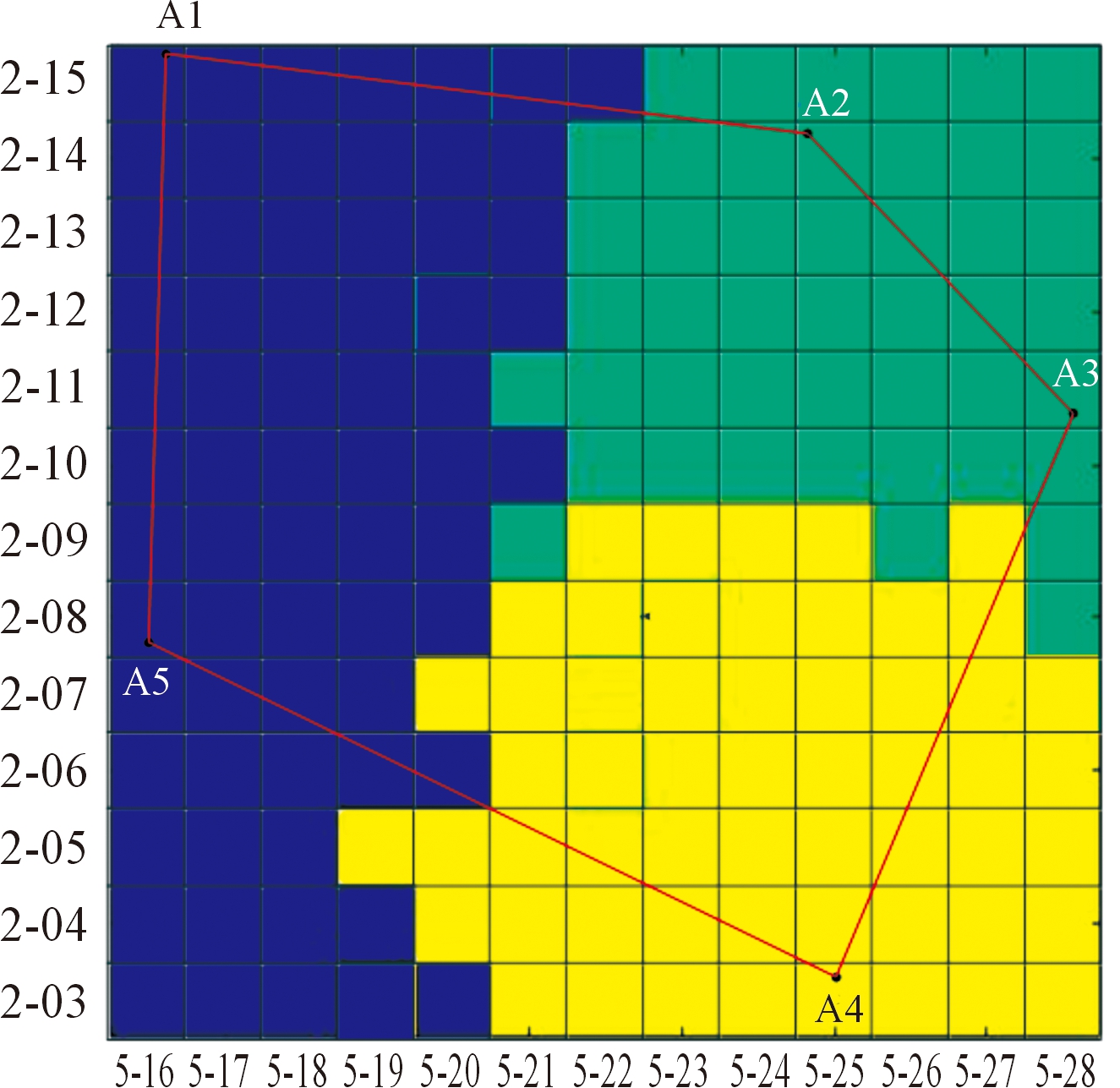
图5 一级网格尺度下空域分区划设结果

图6 边缘平滑及最终分区
由生长算法的流程可以看出,算法复杂度和对于系统资源的消耗主要集中在本文2.2节步骤3(改进算法与原算法共有):搜索生长区边界最小信息素单元网格。以按照四个方向生长为例,可以归纳统计出边界单元网格数目n边与区域内部网格数目n内的关系,如表5所示。
由表5可以得到:n边≥2n内,当n内较大时n边≈2n内。从初始生长点生长到n内网格点的区域的过程中,需要进行的边缘搜索的总次数为:S=n内(n内+1)。若待生长区域总网格数为n,区域划分块数为N,每个区块所包含的网格数为n/N,则区域划设总边缘搜索总次数为:n2/N+n,对于一个固定的问题N为定值,则该算法的复杂度由n2/N决定。因此,对于本文空域划设问题,提升效率的计算方法如下:
(3)
式(3)中:ρ表示提升的划设效率;λ内表示多边形内网格数量;λ边表示多边形内部各分区之间的边界所包含的网格数量;乘数100表示将当前网格划分为100个次一级网格。在该问题中划设效率大概提升了90.4%,效果明显。
表5 边缘网格数目计算

4 结论
本文提出了基于弧度制的全球网格系统,并将其应用于空战场管制空域划设。利用弧度制网格参考系统的全球剖分、十进制和多颗粒度特性,对空域划设生长算法进行了改进。仿真实验表明,该方法信息素收集方便,嵌套平滑边缘,能够极大的提升空域划设的效率。
[1] 马嘉呈,姚登凯,赵顾颢.战术训练空域规划优化仿真研究[J].计算机仿真,2017,34(2):75-80.
[2] 潘家辉,朱玲利,鲍苏苏.基于区域生长算法的CT序列图像分割[J].洛阳师范学院学报,2015,34(5):64-67.
[3] 刘雅静,邓楠,宋丙新.基于区域生长算法激光深熔焊监测图像处理研究[J].机械科学与技术,2015,34(11):89-93.
[4] 刘振宇,汪淼.改进区域生长算法在视杯图像分割中的应用[J].辽宁大学学报(自然科学版),2017,42(2):15-23.
[5] 戴福青,王丹.基于改进区域生长算法的终端区扇区优化[J].中国民航飞行学院学报,2017,28(3):16-20.
[6] 程承旗,吴飞龙,王嵘,等.地球空间参考网格系统建设初探[J].北京大学学报(自然科学版),2016,52(6):1041-1049.
[7] SCAPARROTTI C M.the joint Chiefs of Staff.Geospatial intelligence in joint operations[EB/OL].http://www.dtic.mil/ doctrine/new_pubs/jp2_03.pdf.
[8] Headquarters,Department of the Army.Grids and grid references[R].Washington:US Government Printing Office,1967.
[9] NGA Office of GEOINT Sciences.The universal grid system[EB/OL].[2012-03-17].http://earth-info.nga.Mil /GandG/coordsys/images/utm_mgrs_images/utm_basics_20070319.doc/.
[10] NAULT L.NGA introduces global area reference system[J].Pathfinder,2006,11:19-21.
[11] 宋树华,董芳,万元鬼,等.几种地球剖分网格分析与初探[J].测绘学报,2016,45(s1):48-55.
[12] 宋树华,董芳,陈东,等.基于GeoSOT剖分编码的不动产单元统一标识模型研究[J].测绘学报,2016.45(S1):99-105.
[13] 赵学胜,贲进,孙文彬,等.地球剖分格网研究进展综述[J].测绘学报,2016.45(S1):1-14.
[14] 李献,萧文贺.军用地形图识别与使用[M].北京:军事宜文出版社,1994:76-80.
[15] 吕晓华,万刚,宗传孟,等.美国军事网格参考系统及其启示[J].测绘科学与工程,2008.28(4):69-73.
[16] 孙天驰,姚登凯,赵顾籁,等.基于联合火力的改进杀伤盒建模与仿真[J].火力与指打控制,2018.43(2):143-146.
[17] 何建新.基于UTM网格坐标的地形基准数据库技术[J].现代导航,2013(4):246-251.
[18] Joint Publication 3-52,Joint Airspace Control[S].
[19] 戴福青,王丹.基于改进区域生长算法的终端区扇区优化[J].中国民航飞行学院学报,2017,28(3):14-18.
[20] 岳源,屈高敏.分布式多无人机协同侦察目标分配研究[J].兵器装备工程学报,2018,39(3):57-61.
[21] 邓青,薛青,陈琳,等.一种混合路径规划方法在装甲车辆CGF中的应用[J].兵器装备工程学报,2018,39(7):120-122.