JOHNSON_HOLMQUIST_CONCRETE模型,简称HJC模型。以材料压缩损伤演化为主,较好地考虑了压缩强度的压力相关性、应变率效应和损伤软化效应,适用于大应变、高应变率和高压作用下的混凝土的损伤破坏情况[1],被广泛应用于预测动能弹侵彻混凝土的侵深及弹体的剩余速度。目前针对该模型中参数的确定方法主要有:借鉴前人(或他人)的数据,一般是套用模型提供的原始数据或在其基础上作适当调整[2-3];利用经验公式近似获得部分参数[4];通过实验的方法近似获得部分参数[5-6]。但是由于混凝土HJC本构模型形式较复杂,要求参数较多,并且混凝土是非线性、非均匀材料,因此其参数确定比较困难,并部分带有主观性和不确定性,参数普适性较差,一定程度上影响了数值模拟的应用。
针对上述问题,国内外部分研究人员开展了部分研究工作。陈星明等[7]应用LS-DYNA数值模拟方法进行HJC本构模型抗侵彻性能的参数敏感性研究,通过大量数值模拟得出HJC模型的抗侵彻敏感参数,主要是针对混凝土抗压强度响应得出的敏感性参数,且部分参数在敏感性分析中取值不尽合理。凌天龙等[8]通过相关静力学实验,获得岩石的弹性模量、泊松比、单轴抗压强度以及抗拉强度等参数。应用三轴压缩实验和单轴SHPB 冲击实验,分别得到了该砂岩极限面参数、应变率效应参数、压力参数和损伤模型参数的取值,但获取参数不全。任根茂等[9]基于已有普通混凝土(单轴抗压强度≤60 MPa)的准静态单轴压缩实验、三轴围压实验、一维SHPB 实验和一维平面应变Hugoniot 冲击压缩实验数据,确定了一组适用于不同强度普通混凝土材料HJC 本构模型的强度参数、率效应参数和状态方程参数取值。通过数值模拟验证将研究得到的参数应用于动能弹侵彻钢筋混凝土时,其侵彻毁伤效应结果离散性较大,偏差也较大。
本研究基于前人的研究成果,确定一组较为合理的基准参数,并分类给定参数的调试范围,采用多学科优化平台HyperStudy联合LS-DYNA软件进行DOE分析,得到参数中对侵彻效应的余速影响较大的参数,在动能弹高速侵彻钢筋混凝土仿真计算时结合试验结果或精度较高的经验公式重点确定敏感参数的取值,获取一套HJC模型具有一定适用范围且稳定的参数,以达到模型具有一定的普适性。
1 HJC模型介绍
HJC本构模型主要包括三方面:强度方程、状态方程以及损伤演化方程,下面分别对各部分作简要介绍和分析[10]。
1.1 强度方程
HJC模型本构关系见图1所示,其屈服面强度方程可表示为:
(1)
式中:σ*=σ/fc定义为标准化的等效应力(σ为实际等效应力,fc为材料准静态单轴抗压强度);D为损伤系数![]() 为标准化静水压力(P为实际压力);
为标准化静水压力(P为实际压力);![]() 为无量纲应变率
为无量纲应变率![]() 为真实应变率,
为真实应变率,![]() 为参考应变率);A为归一化内聚强度系数;B为归一化压力硬化系数;N为压力硬化指数;C为应变率系数。
为参考应变率);A为归一化内聚强度系数;B为归一化压力硬化系数;N为压力硬化指数;C为应变率系数。
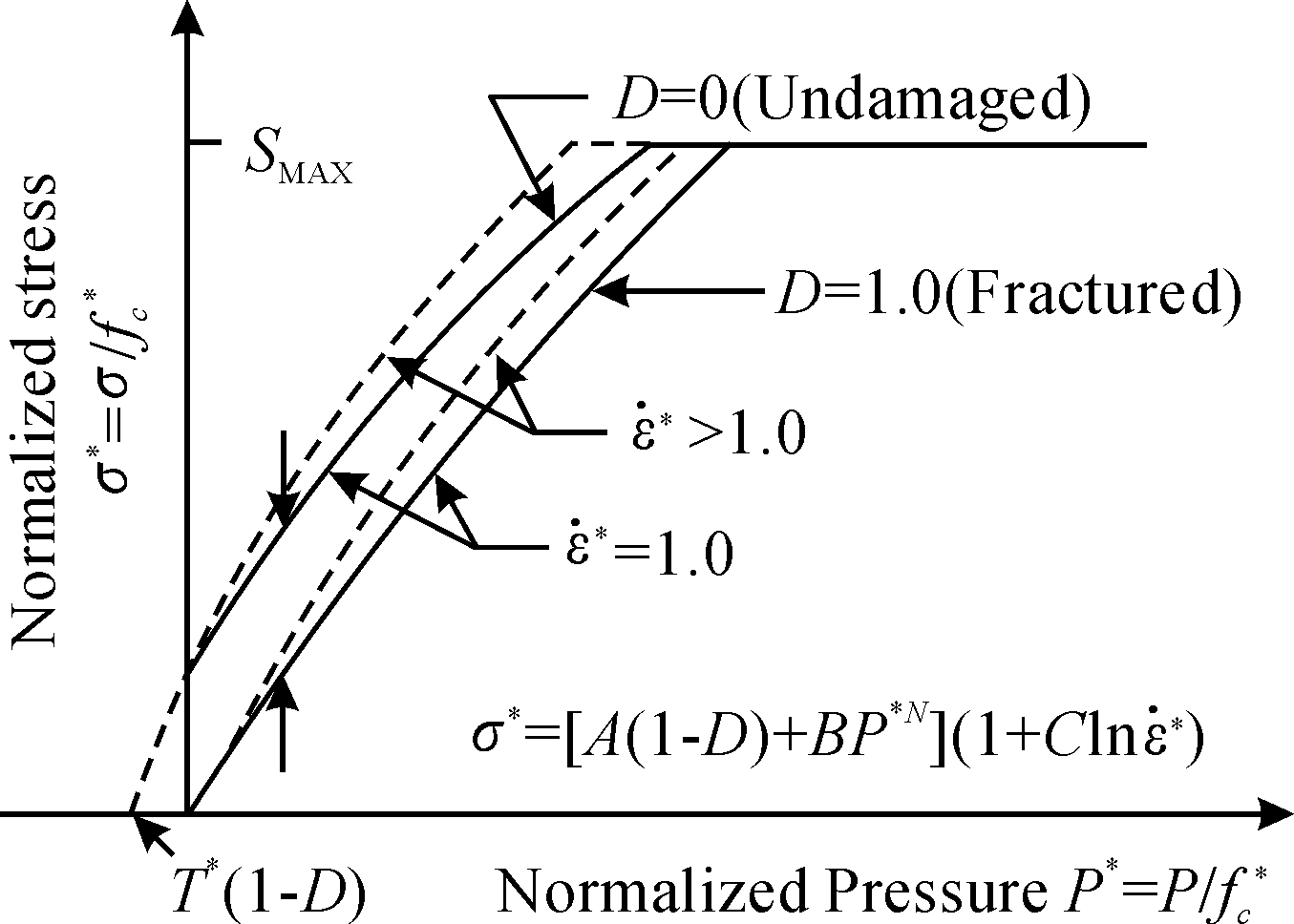
图1 混凝土HJC本构关系
1.2 状态方程
材料所受压力P与相应的应变μ的关系曲线如图2所示。
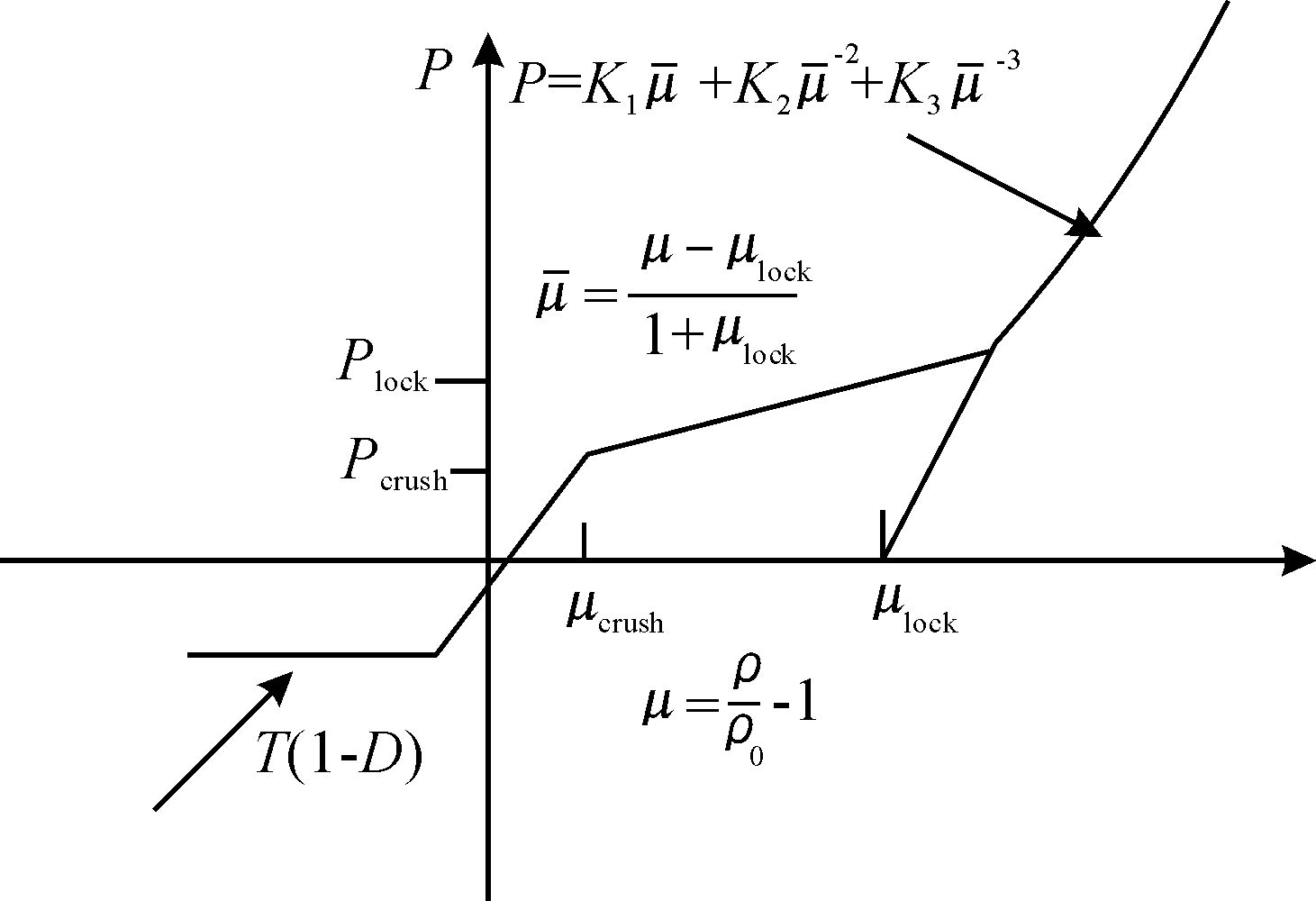
图2 HJC材料模型状态方程
1)拉伸状态方程
① 线弹性阶段
P=Kμ
(2)
式中:K为材料的体积弹性模量,K=Pcash/μcrash;Pcrash为材料空隙开始闭合时的临界压力;μcrash为对应的体应变;μ=(ρ/ρ0)-1为单元的体积应变;ρ和ρ0分别表示单元的实时密度和初始密度。
② 裂缝贯通断裂阶段
P=T(1-D)
(3)
式中:T是材料最大拉伸截止静水压力;D是材料的损伤程度。从图2中可知即使此时拉应力不再变化然而应变却依旧缓慢增大,即可以看出该本构模型在拉伸失效描述与现实混凝土拉伸失效相比过于简单。
2)压缩状态方程
在该材料本构模型的压缩阶段又分为:线弹性阶段、过渡阶段和压实阶段。
① 线弹性阶段(0<P<Pcrush)
P=Kμ,同拉伸状态的线性阶段一样。
② 过渡阶段(Pcrush≤P≤Plock)
这一阶段是指混凝土内部的气泡开始破裂,混凝土结构受到损伤,并开始产生破碎性裂纹,但混凝土结构还没有完全破碎。
P=Pcrash+Kcrash(μ-μcrash)
(4)
式中:Kcrush=(Plock-Pcrush)/(μlock-μcrush),Plock为材料空隙全部闭合时的临界压力,μlock为对应的体积应变。
③ 压实阶段(P≻Plock)
当压力达到Plock,混凝土内部气孔被完全压碎。关系式常用三次多项式表示:
(5)
式中:![]() 为修正体积应变;K1,K2和K3为状态方程参数由Hugoniot确定的数据可以查知。
为修正体积应变;K1,K2和K3为状态方程参数由Hugoniot确定的数据可以查知。
1.3 损伤演化方程
HJC损伤模型如图3所示。模型损伤由塑性应变累积而成,其中塑性应变包括了等效塑性应变和塑性体积应变。其损伤演化方程为:
(6)
式中:![]() 分别表示当前积分步下等效塑性应变增量和塑性体积应变增量,P为实际压力,D1、D2为材料损伤因子,EFmin为材料的最小破碎应变,
分别表示当前积分步下等效塑性应变增量和塑性体积应变增量,P为实际压力,D1、D2为材料损伤因子,EFmin为材料的最小破碎应变,![]() 为混凝土最大抗拉强度;
为混凝土最大抗拉强度;![]() 为常压P作用下材料发生断裂时的塑性应变。
为常压P作用下材料发生断裂时的塑性应变。

图3 HJC材料损伤模型
2 模型基准参数的确定
2.1 参数及其一般确定方法
目前HJC模型中参数的确定方法主要是:借鉴前人(或他人)的数据,一般是套用模型提供的原始数据或在其基础上作适当调整;利用经验公式近似获得部分参数;通过实验的方法近似获得部分参数。但是由于混凝土HJC本构模型形式较复杂,参数较多,并且混凝土是非线性、非均匀材料,因此其参数确定比较困难,并部分带有主观性和不确定性。获得的参数离散性较大,不具有普适应,本文拟采用多学科优化平台HyperStudy联合LS-DYNA软件进行DOE分析,得到参数中对侵彻效应的余速影响较大的参数,然后在动能弹侵彻混凝土数值模拟中重点确定影响度较大的参数,以获取一组稳定的具有普适应的HJC模型参数。在进行DOE分析之前,首先需要确定一组相对合理的基准参数以及计算浮动范围,以确保最终获取的参数的合理性。
2.2 HJC模型参数的归类及确定方法
LS-DYNA软件中HJC模型关键字可以分为以下类型:
1)基本力学参数(4个)
ρ(密度)、G(剪切模量)、fc(准静态单轴抗压强度)、T(单轴抗拉强度)。该类参数可依据试验数据取值,当试验数据不全时,按照剪切模量G=E/2(1+υ)(其中普通混凝土泊松比υ一般取0.2)。弹性模量E和抗拉强度T可由美国混凝土协会(American Concrete Institute,ACI)[11] 提出计算公式得到:![]() (静水压力下抗拉强度T可由混凝土劈裂抗拉试验)。
(静水压力下抗拉强度T可由混凝土劈裂抗拉试验)。
2)强度参数(5个)
A(归一化黏聚强度系数)、B(归一化压力硬化系数)、C(应变率影响系数)、N(压力硬化指数)、SFmax(归一化最大强度);其中,对于特征化黏聚强度A,由于缺少实验数据,Holmquist等通过假设准静态下![]() 黏聚强度为0.75fc,推导得出A;熊益波等[12]基于塑性曲面理论,依据A与三轴围压与围压线性关系的斜率K的关系
黏聚强度为0.75fc,推导得出A;熊益波等[12]基于塑性曲面理论,依据A与三轴围压与围压线性关系的斜率K的关系![]() 推导得出。在不考虑损伤和应变率效应的影响下依据HJC本构模型的屈服面方程以及P*-σ*关系拟合得到B和N。为了消除静水压力的影响,按照Holmquist等提出的方法,基于混凝土的SHPB试验确定应变率效应参数C。
推导得出。在不考虑损伤和应变率效应的影响下依据HJC本构模型的屈服面方程以及P*-σ*关系拟合得到B和N。为了消除静水压力的影响,按照Holmquist等提出的方法,基于混凝土的SHPB试验确定应变率效应参数C。
3)压力参数(7个)
pcrush(压碎压力)、μcrash(压碎体应变)、plock(压实压力)、μlock(压实体应变)、K1(压实后P-V曲线系数)、K2(压实后P-V曲线系数)、K3(压实后P-V曲线系数)。其中,HJC模型状态方程的第二段和第三阶段参数,可采用GRADY等[13-14]开展的飞片撞击实验数据来确定,对于pcrush=fc/3,μcrash=pcrush/K,K为体积模量,可通过式K=E/3(1-2υ)进行计算;第三阶段K1、K2、K3可由冲击Hugoniot数据确定或直接采用手册中[15]给定的数值;对于plock、μlock可通过实验数据联合第二阶段和第三阶段进行拟合得到。
4)损伤参数(3个)
D1(损伤常数)、D2(损伤常数)、EFmin(最小断裂应变);该类参数一般通过混凝土圆柱体试件循环加载试验得到,由于缺少已有试验数据,且Holmquist等假定损伤参数与混凝土强度无关,通常取原始文献值。
5)软件参数(2个)
EPs0(参考应变率)、FS(失效类型),该类参数取软件推荐值。
2.3 基准参数及调试范围的取值
将影响较大的基础参数 fc,取值离散性较大的参数A、B、N、SFmax、plock、μlock、K1、K2、K3共10项参数,取参考值的±40%进行参数影响度的调试;对于可通过试验测试、参数间相互关系推导、数值拟合以及文献中取值离散性较小的参数:G、T、C、pcrush、μcrash、D1、D2、EFmin8项参数,考虑到试验及数据拟合等因素的偏差,取参考值的±20%进行参数影响度的调试;而对于剩下的可精确测试的ρ(密度)和EPs0(参考应变率)2项参数无需进行参数影响度的调试。最终确定的基准参数及DOE分析调试值见表1所示。
3 DOE分析参数灵敏度
3.1 数值模型的建立
在确定了合理的基准参数后,利用LS-DYNA软件针对一种典型尖卵形弹体结构撞击混凝土靶板进行DOE分析,分析各参数的变化对侵彻毁伤效应(本研究主要考虑弹体的剩余速度响应)的稳定性,以此来判断混凝土HJC本构模型中参数的灵敏度。其弹体模型为:长度L=825 mm,直径Φ=150 mm,头形系数CRH(Caliber Radius Head)为3,密度7 850 kg/m3,质量m=66.5 kg;靶体模型为:厚度2 m,密度2 400 kg/m3,单轴抗压强度 fc=48 MPa;弹体撞击初始速度为2Ma;数值模拟中弹体采用 J-C模型。通过HyperMesh软件建立的有限元模型见图4所示。
表1 HJC模型基准参数及调试值

参数ρ0/(g·cm-3)G/GPaABCnfc/MPa参考值2.414.860.551.60.0070.648调试范围—11.89~17.830.33~0.770.96~2.040.0056~0.00840.36~0.8428.8~67.2参数T/MPaEFminSFmaxPc/MPaμcPl/MPaμl参考值40.0110160.00110000.10调试范围3.2~4.80.008~0.0126~1412.8~19.20.0008~0.0012600~14000.06~0.14参数D1D2K1/GPaK2/GPaK3/GPaFS参考值0.041.085-1712080.5调试范围0.032~0.0480.8~1.251~119-103~239125~2880.3~0.7

图4 DOE分析有限元模型
3.2 DOE分析方法简介
DOE(Design of Experiment)分析,又称试验设计[16],通常是要发现关于一个特定过程或系统的某些特性。一个设计的试验是一个或一系列试验。它对一个过程或系统的输入变量做一些有目的的改变,以便识别出引起输出响应变化的原因。进行试验设计的主要目的在于确定哪些输入变量对输出响应影响最大,确定将有影响的可控输入变量设置为何值,使输出响应接近于所希望的额定值,使输出响应的变化较小,使系统的不可控参量对输出响应的影响最小,用以构建近似模型来代替计算量非常大的实际模型进行求解等。
HyperStudy软件进行试验设计的方法主要有全因子设计、部分因子设计、中心复合设计、BOX-Behnken设计、用户自定义设计等9种方法,但大部分方法要么计算规模过于庞大,要么采样覆盖面不全,不适用于参量(变量)较多的试验设计。本次分析采用用户自定义设计方法允许使用自己的设计方案进行参数研究。HyperStudy将用户自定义试验设计方案输入,并使用与其他试验设计方法相同的形式调用。该方法最大优势在于可以结合特殊的工程需求来构建不同的试验设计方案。在用户自定义设计时,必须在矩阵的第一列给出本次设计的试验次数(行数)和因子数(列数)。本次DOE分析中总计19个参量,每个参量取3个水平因子,总计需分析57次。
3.3 DOE分析
利用以上建立的算法及选取的材料参数范围,基于HyperStudy软件的DOE分析平台,通过调用LS-DYNA软件对侵彻结构体以2Ma速度侵彻2 m混凝土进行DOE分析。在进行DOE分析之前,首先应定义各参数设计变量进行一次基本的分析计算,然后提取弹体余速为响应变量进行DOE分析,本次DOE分析暂未考虑参数间的相互影响,如果考虑多参数之间的相互影响,计算结果的不确定性增加,因此只考虑各单一因素在表1所取值范围内变化对弹体余速的影响,具体分析流程见图5所示。
通过DOE分析得到参数主效应图,即各参数对于速度的响应灵敏度情况如图6所示。通过分析知对余速影响程度依次为Pl、fc、μl、A、B、n、D1、K1、T、C、EFmin、G、μc、Pc、D2、K2、K3、SFmax、Fs。各材料参数对余速影响大小及排序见表2所示。
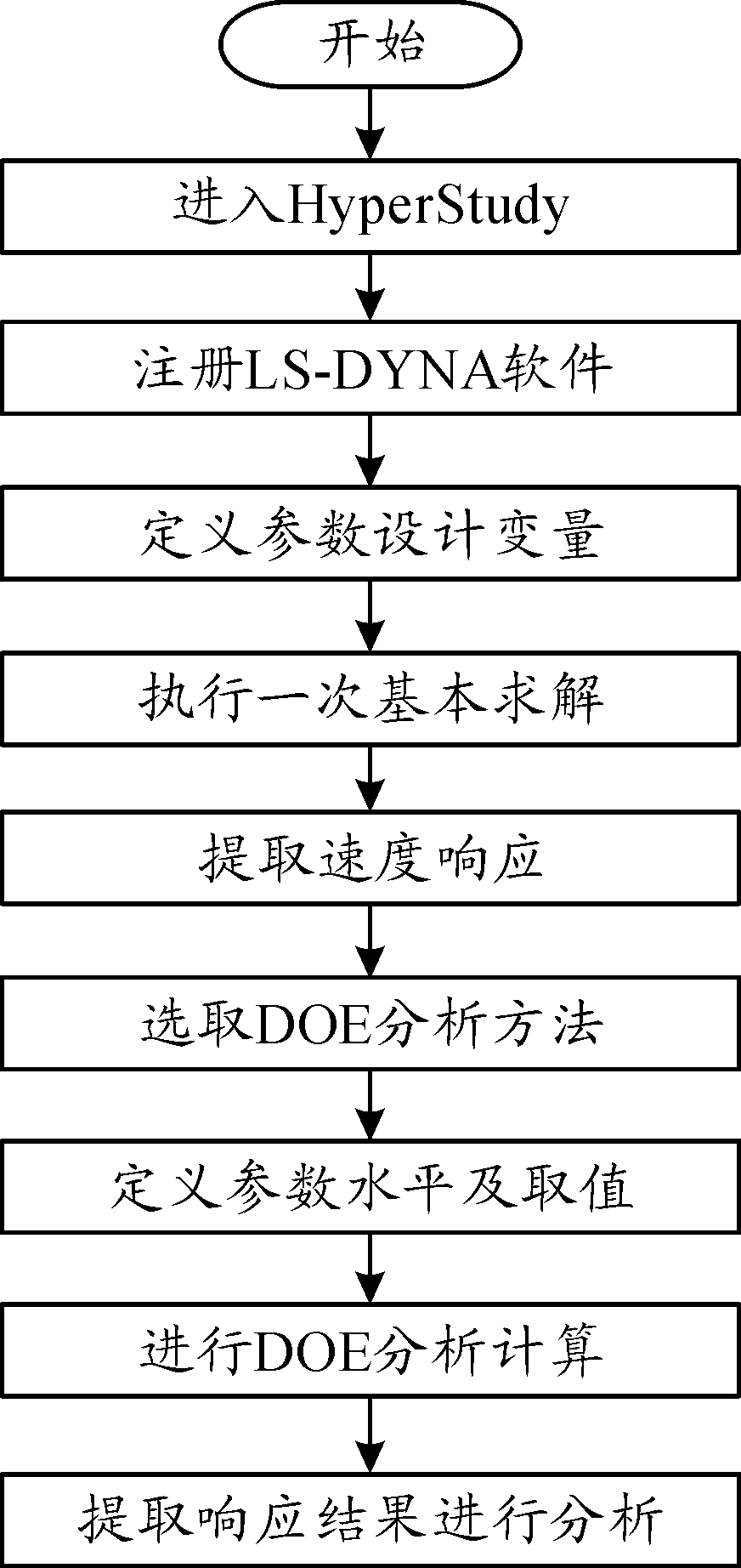
图5 DOE分析详细流程
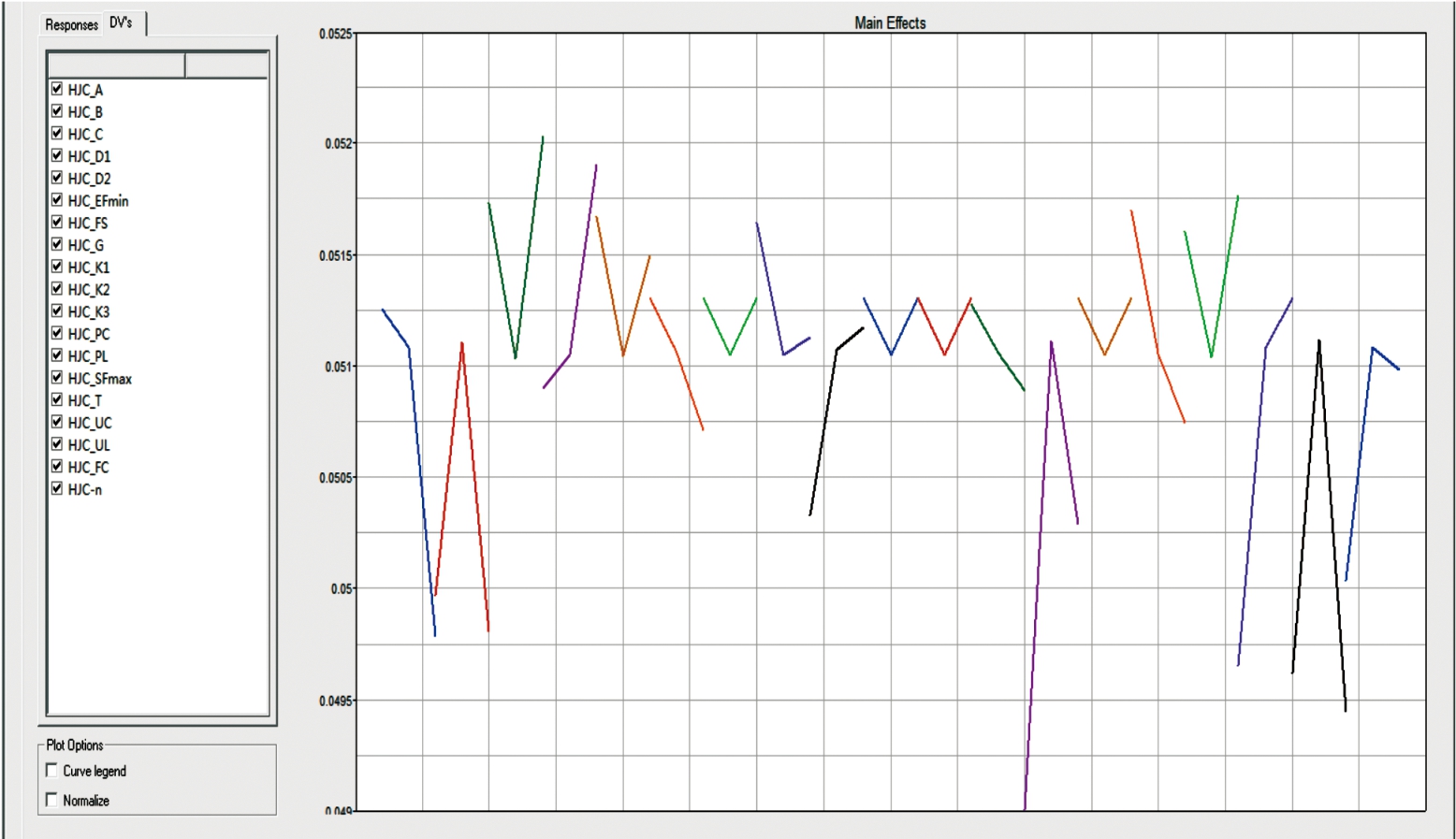
图6 参数主效应响应图
表2 2Ma速度对余速影响大小及排序
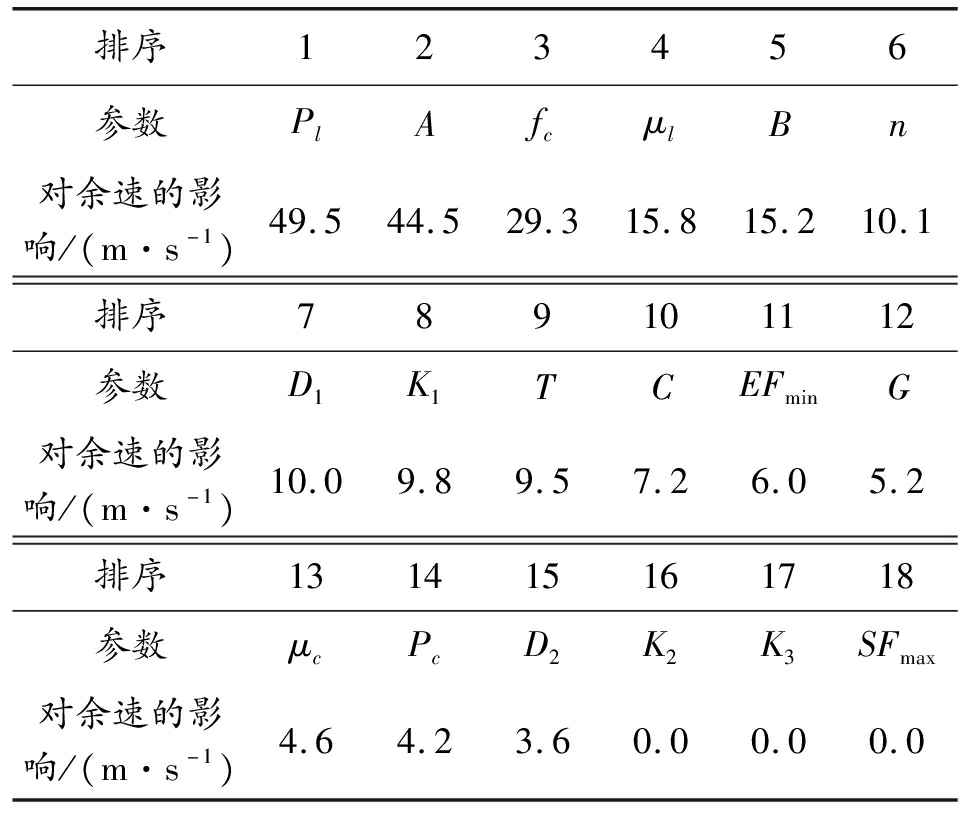
排序123456参数PlAfcμlBn对余速的影响/(m·s-1)49.544.529.315.815.210.1排序789101112参数D1K1TCEFminG对余速的影响/(m·s-1)10.09.89.57.26.05.2排序131415161718参数μcPcD2K2K3SFmax对余速的影响/(m·s-1)4.64.23.60.00.00.0
注:对余速的影响(m/s)是指高(或低)水平参数相对于中间水平参数余速的变化大小。
通过图6和表2可以看出,弹体以2Ma速度侵彻2 m混凝土对余速影响较大的参数是压实压力Pl、归一化黏聚强度系数A、准静态单轴抗压强度fc、压实体应变μl、归一化压力硬化系数B等5个参数,对余速的影响超过15 m/s,在动能弹侵彻混凝土仿真时可重点调试这5个参数,其余参数对余速的影响均小于10 m/s,可忽略不计。
通过取参数Pl=1 200±200(MPa),fc=48±19.2(MPa),μl=0.1±0.04,A=0.55±0.22,B=1.60±0.64针对图4所示的模型进行单因素变化的数值分析可知,压实压力Pl和归一化黏聚强度系数A两个参数对余速的影响度超过10%,影响最大;而剩下3个参数对余速的影响度在3.5%~7%左右;且各参数增大或较小相对参考值而言,余速均有增大的趋势。
4 结论
1)首先基于前人的研究成果,总结分析了HJC模型及参数确定方法,确定了一组较为合理的基准参数,并分类给定参数的调试范围;
2)基于多学科优化平台HyperStudy联合LS-DYNA软件对文中模型进行DOE分析,得到HJC模型参数中对侵彻混凝土中余速影响较大参数为Pl、A、fc、μl、B。
3)Pl和A两个参数对余速的影响度超过10%,影响最大;而fc、μl和B三个参数对余速的影响在3.5%~7%左右;各参数增大或较小相对参考值而言,余速均有增大的趋势。
[1] LSTC.LS-DYNA keyword user’s manual[M].California:LSTC,2013.
[2] HOLMQUIST T J,JOHNSON G R.A compulational constitutive model for concrete subjected to large strains,high strain rates,and high pressures[C]//14 th International Symposium on Balllistics.Quebec,1993:591-600.
[3] JOHNSON G R,BEISSEL S R,HOLMQUIST T J,et al.Computed radial stresses in a concrete target penetrated by a steel projectile[C]//5th Structures under shock and Impact.Aristotle University of Thessaloniki,Greece:Computaional Mechnics Publications,1998.
[4] 张凤国,李恩征.混凝土撞击损伤模型参数的确定方法[J].弹道学报,2001,13(4):12-17.
[5] 崔伟峰.动能弹丸侵彻混凝土的数值模拟研究[D].长沙:国防科学技术大学,2003.
[6] 陈建林,李旭东,刘凯欣.素混凝土本构模型参数的实验研究[J].北京大学学报(自然科学版),2008,44(5):689-694.
[7] 陈星明,刘彤,肖正学.混凝土HJC模型抗侵彻参数敏感性数值模拟研究[J].高压物理学报,2012,26(3):313-317.
[8] 凌天龙,吴帅峰,刘殿书,等.砂岩Holmquist-Johnson-Cook 模型参数确定[J].煤炭学报,2018,43(8):2211-2216.
[9] 任根茂,吴昊,方秦,等.普通混凝土HJC 本构模型参数确定[J].振动与冲击,2016,35(18):9-15.
[10] 林琛,徐建军,杨晋伟,等.基于HJC模型的钢筋混凝土侵彻仿真失效准则与参数[J].探测与控制学报,2017,39(2):100-105.
[11] ACI Committee 318,Building code requirements for reinforced concrete:(ACI 318—1989)and commentary(318R—1989)[S].
[12] 熊益波,胡永乐,徐进,等.基于Mohr-Coulomb准则和高压三轴试验的混凝土JH模型极限面参数[C]//第九届全国冲击动力学学术会议论文集(下册).2009.
[13] RADYDE G.Dynamic decompression properties of concrete from Hugoniot states 3 to 25 GPa[R].Sandia National Laboratories,USA,1996.
[14] RADYDE G.Shock equation of state properties of concrete[C]//International Conference on Structures under Shock and Impact.Udine,Italy,1996.
[15] MARSH S P.LASL Shock Hugoniot Data[M].California:University of California Press,1980.
[16] 洪清泉,赵康,张攀,等.OptiStruct & HyperStudy理论基础与工程应用[M].北京:机械工业出版社,2012.