开关电源技术广泛应用于汽车、航天、军工等诸多领域,一般可分为非隔离与隔离两种形式,非隔离式包括Buck、Boost、Buck-Boost等电路;隔离式按结构可分为正激式和反激式两大类[1]。其中反激变换器拓扑具有不需要输出滤波电感、体积小、成本低等优点,得到了广泛的应用。例如一些引信系统中,会使用这种方式实现高压点火电源[2],不仅工作时间短、点火完成后即关闭高压输出,对负载和输入电压的适应性也较低。
反激变换器是一个离散的非线性时变闭环系统[3],多数元器件在一个工作周期内会处于不同的工作状态,因此经典分析方法如根轨迹法、频率响应法[4]等并不适用。而平均法的物理概念明确,表达式相对简单,是开关变换器中一个重要的建模方法,对于设计有很大的指导意义[5]。国内外已出现较多的对直流变换器小信号的分析方法,例如状态空间平均法、开关元件平均模型法等,为分析系统的特性提供了理论基础。在反激变换器相关研究中,连续导通模式(CCM)的建模研究较多[6-7],不连续导通模式(DCM)原边励磁电感较小、响应快、输出电压增益高,同时可应对一定的输入电压波动和负载突变,但过程相对复杂,有关建模仿真研究较CCM略少[8]。因此在高压电源的研究中,有必要以应用更广的DCM为环境建立反激式电源的动态响应过程。
本研究应反激变换器输出电压的需求,采用开关网络平均模型法对一定条件下的单端反激变换器进行建模,详述过程,通过Matlab软件进行计算仿真,对比实验结果分析,验证其可行性。并以建模为基础,对实际应用环境下的反激变换器进行参数调整和输出预测,进一步验证其指导意义。
1 工作状态分析与建模
单端反激变换器的电路图一般可表示为图1,用开关网络平均模型法建模重点在于将变换器中的所有开关元件作为整体来分析其中的变量,使反激变换器电路抽象为一个二端口网络,研究端口各变量关系来分析受控电压源和受控电流源等组成的等效电路[9]。
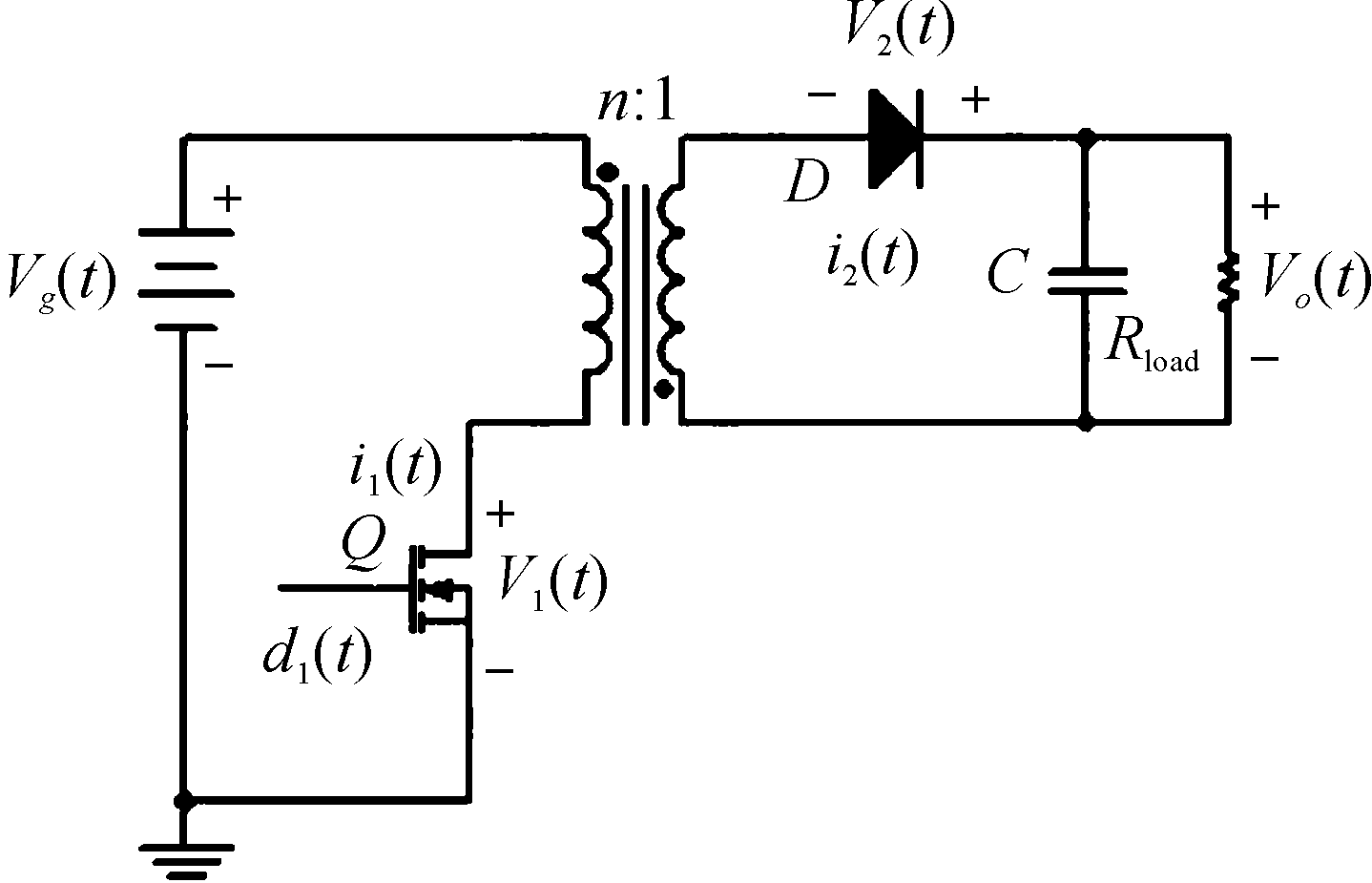
图1 单端反激变换器电路图
以升压为主要目的反激变换器常选择不连续导通模式(DCM),在此模式下,将工作状态分为3个阶段:
状态1:任一开关周期,在(0,d1Ts)时间段内,开关Q导通,电源向变压器原边侧绕组充电,电流线性增加,使变压器磁芯磁通增大[10]。此时副边二极管D反向截止,无电流通过,能量储存在原边侧绕组电感。有:

(1)
状态2:任一开关周期,在(d1Ts,d2Ts)时间段内,开关Q关断,副边二极管D导通,副边侧电感感应电压向电容充电,并给负载供电。原边储存能量传递至副边得到释放,此时副边侧相当于电感,电流线性下降,在开关管导通前下降至零。有:
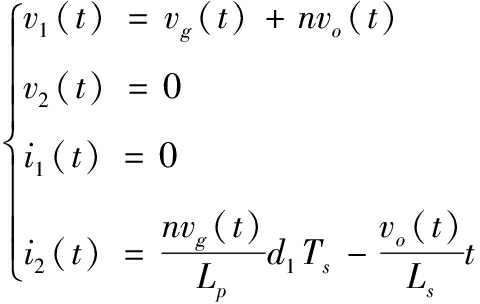
(2)
状态3:任一开关周期,在(d2Ts,Ts)时间段内,开关Q关断,副边二极管D关断,变压器磁通降为零,输出电容对负载供电。至开关管再次导通时,电容给负载供电,变压器原边侧重新储能,再次循环。有:

(3)
1.1 平均变量等效电路
平均法首要思路是平均变量以消除纹波的影响,有利于响应过程的清晰表达。在低频、小纹波和小信号基本假设条件下,提取开关网络建模如图2。同时根据上述3个工作状态写出相应变量的平均变量关系式,其中变量加符号〈 〉Ts表示一个周期内的平均值,Ts表示工作周期,d1(t)表示开关占空比。
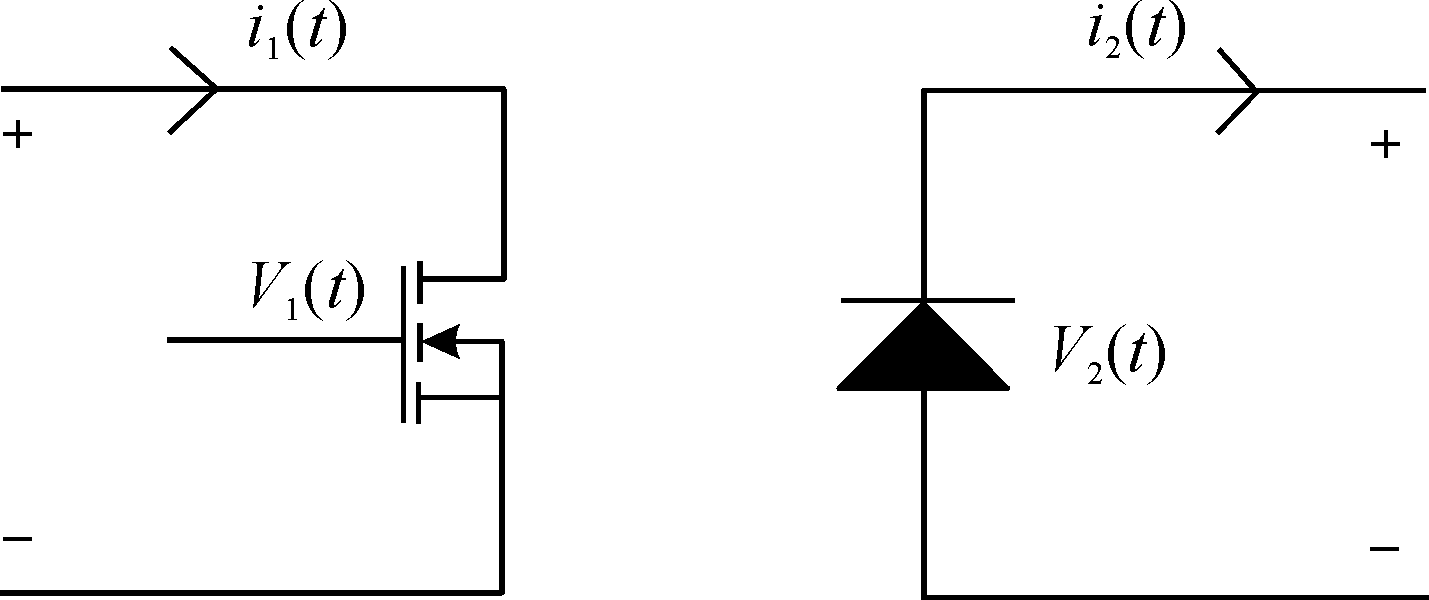
图2 开关网络模型
(4)
(5)
d1(t)+d2(t)+d3(t)=1
(6)
〈v1(t)〉Ts=nd2(t)〈vo(t)〉Ts+(1-d1(t))〈vg(t)〉Ts
(7)
(8)
(9)
![]()
(10)
其中d2(t)在建立稳态的过程中是变化的,为消去它建立辅助方程,需要对变压器进行一定的简化处理。磁芯磁导率不是无限大,可理解为存在励磁电感(约为初级电感)在变压器中工作;初级线圈和次级线圈不是全耦合,有很小的漏感串联于初级线圈;导线有电阻损耗,线圈间有寄生电容,基本可以忽略。而对于理想的变压器,初级绕组电感Lp和次级绕组电感Ls存在Lp=n2Ls,n为变比,代入式(5)可得:
![]()
(11)
整理代入式(7)~式(10)可得:
〈v1(t)〉Ts=〈vg(t)〉Ts
(12)
〈v2(t)〉Ts=〈vo(t)〉Ts
(13)
(14)
(15)
对式(14),电流〈i1(t)〉Ts与电压〈v1(t)〉Ts成正比,类似于电阻特性,可设Re(d1)为等效电阻,则有:
(16)
对式(15),用符号〈p(t)〉Ts表示平均功率,则等式变为:
![]()
(17)
表明受控功率源的输出等于Re(d1)吸收的平均功率〈p(t)〉Ts,将开关管用等效电阻代换,将副边二极管用受控功率源代换,建立开关网络平均变量等效电路图如图3所示,替换反激变换器中的开关网络得到平均变量等效电路图如图4所示。

图3 开关网络平均变量等效电路图
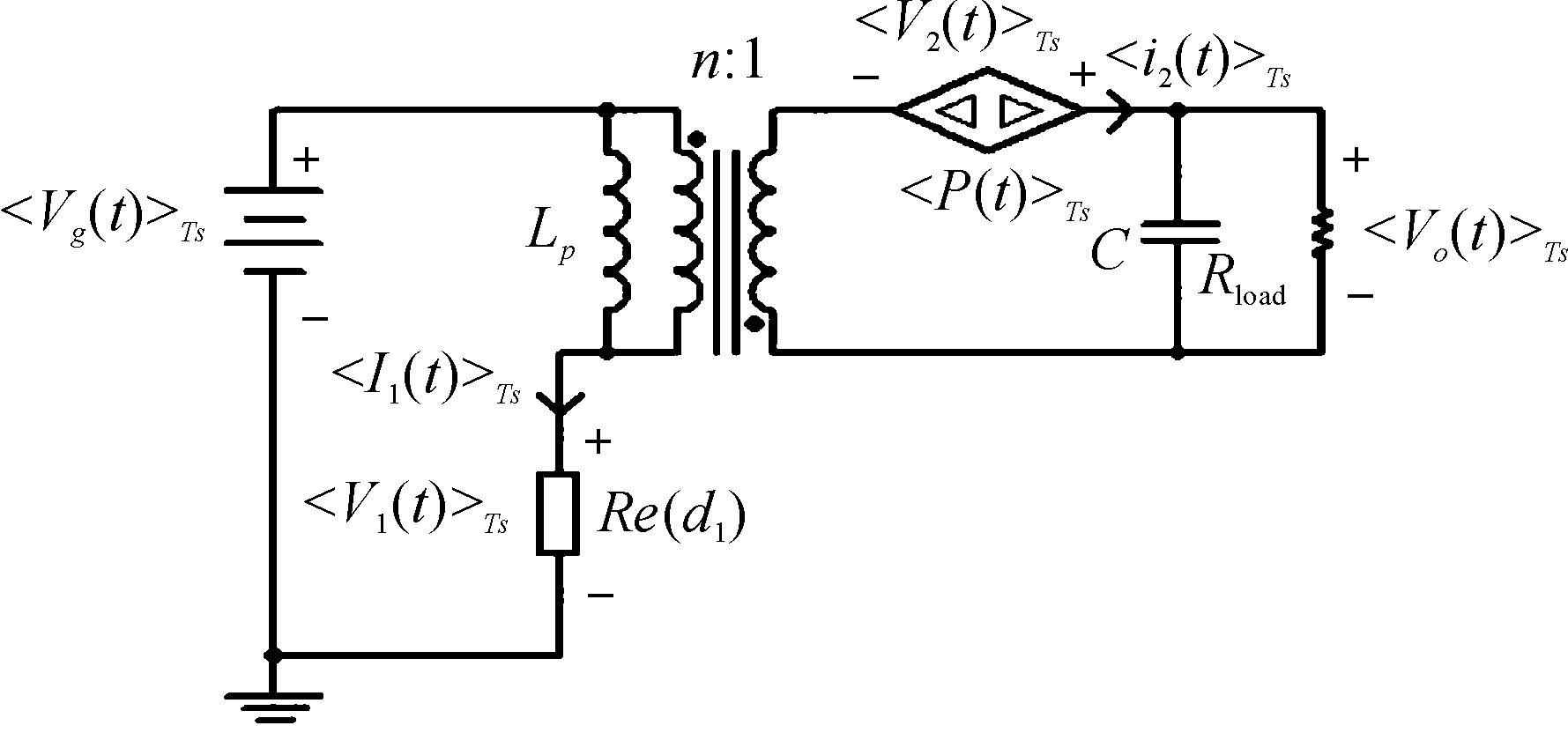
图4 平均变量等效电路图
1.2 直流等效电路
直流工作表达了电路的稳定终点状态,需建立响应等效电路。在平均变量等效电路中,令电路中各平均变量等于其对应的直流量,占空比d1(t)=D1,并使电感短路,电容开路,可得直流等效电路如图图5所示。

图5 直流等效电路图
根据直流等效电路,计算变换器的直流工作点,如下:
V1=Vg
(18)
V2=Vo
(19)
(20)
![]()
(21)
![]()
(22)
(23)
1.3 交流小信号等效电路
继续求解小信号等效电路,以反映电路动态响应建立过程。对平均变量进行分解以分析交流小信号在静态工作点的工作状况,分解为直流分量与交流小信号分量之和,如下:
![]()
(24)
(25)
![]()
(26)
![]()
(27)
(28)
对各平均变量分离扰动,并消去等式中的直流量,再消去高阶的交流量乘积项使其线性化,整理后可得:
(29)
(30)
简化系数表示,式(30)可表达为:
(31)
(32)
由此可得开关网络交流小信号等效电路图,如图6所示。
用开关网络交流小信号等效电路替换反激变换器中的开关网络平均变量等效电路,可得DCM反激变换器交流小信号等效电路。而DCM反激变换器中,理想变压器满足伏秒平衡,初级电感电流断续,因而初级电感电压平均值〈VL(t)〉Ts=0,即相应交流分量为0,同理处理次级电感,则等效电路中可将变压器初级和次级电感短路而进一步化简电路图,如图7所示。

图6 开关网络交流小信号等效电路图

图7 DCM反激变换器交流小信号等效电路图
由此分析交流小信号模型,通过各等效电路参数,可得输出电压对开关管占空比的传递函数与输出电压对输入电压的传递函数,如下:
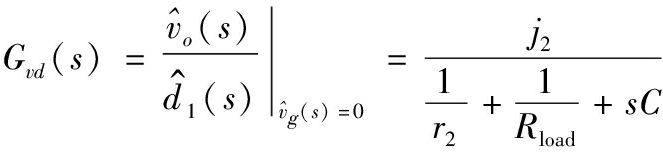
(33)

(34)
针对模型的杂散参数[11],Lk为漏感串联于原边,初级寄生电阻主要包括励磁电感Lm等效串联电阻Rm、MOS管导通电阻Ron1、线路电阻Rp,输出电容等效串联电阻Rc,次级寄生电阻主要包括次级电感等效串联电阻n2Rm(由初级折算)、二极管导通电阻Ron2、线路电阻Rs。反映到模型中,状态1中的电感Lp由(Lm+Lk)代替,状态2中电感由励磁电感Lm代替,副边Ls由Lm折算。实测初级次级寄生电阻均在1 Ω以内,Lk为μH级别,远小于励磁电感。考虑加入杂散参数后模型过于复杂,忽略部分,可改写传递函数(33)与传递函数(34)为:
(35)
(36)
2 仿真与实验分析
2.1 仿真验证
根据实际引信的应用和指导[12],设计初始实验的单端反激变换器,其主要电路参数为:电源Vg=12 V,变比n=0.05,实际匝数比20∶400,原边电感Lp=0.15 mH,输出电容C=0.22 μF,负载Rload=100 MΩ,工作频率 fs=55.9 k,开关MOS管占空比静态工作点D1=0.22。使用Matlab中的Simulink工具根据式(33)、式(34)建立单端反激变换器电路的小信号开关网络平均模型法仿真模型如图8所示,为便于后文对比,得到输出电压Vo的10倍衰减仿真波形如图9所示。

图8 小信号开关网络平均模型法Simulink模型
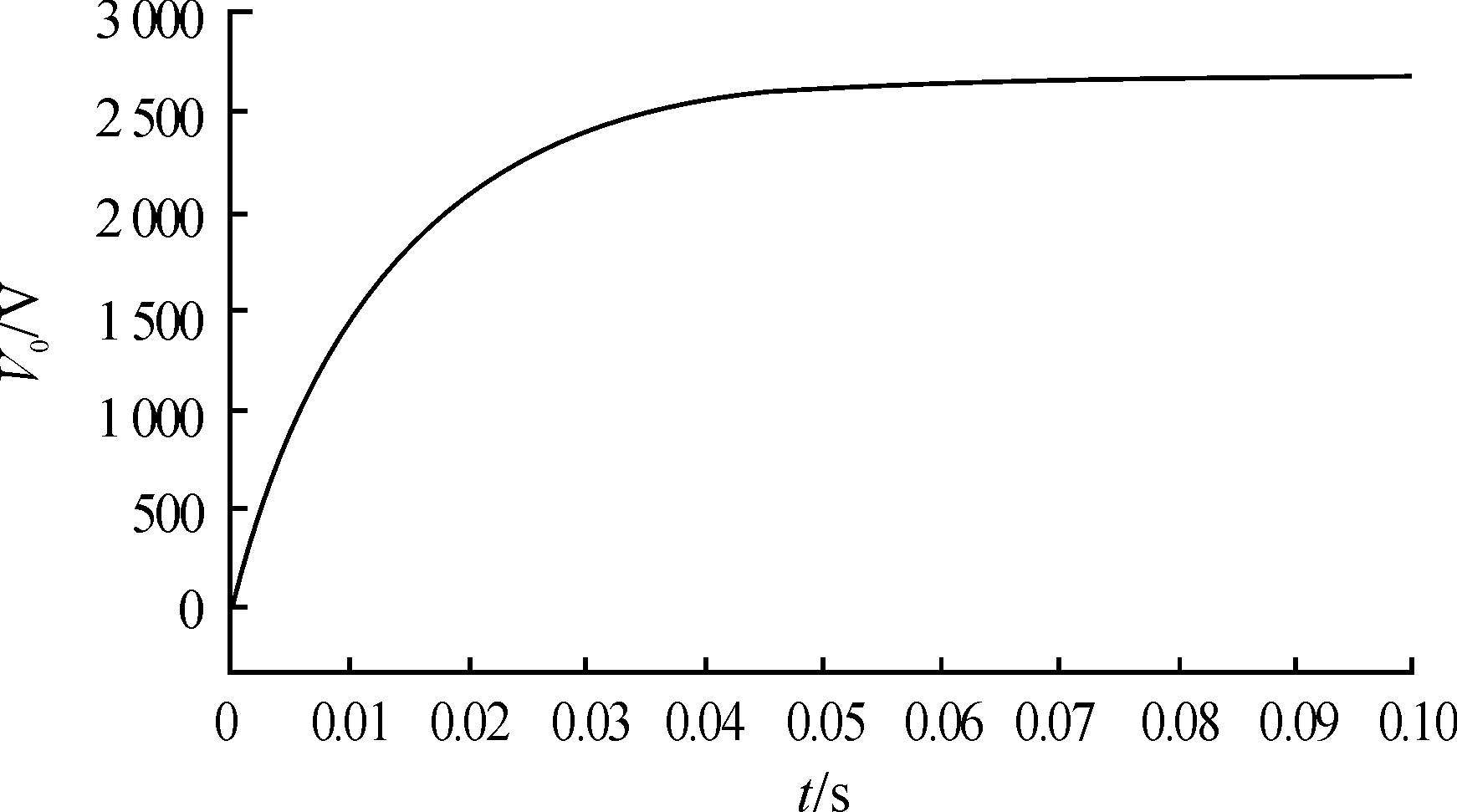
图9 Simulink模型仿真波形
观察发现,输出电压升压过程先快后慢,是由于建立稳态的过程中随着输出电压升高,每周期所能传输的电压值也越来越小,最终达到稳定。在经过60 ms左右的时间后,电压达到稳态值约2 660 V,较好地反映了单端反激变换器的输出特性,所建立的模型效果良好。实际电路达到稳态后,输出电压在每周期仍然有升压和降压,即含有纹波[13]。由平均法的建模思路,会对变量进行平均,近似将变量在周期内维持恒定,即消除了开关纹波的影响,一定程度上忽略了交流分量,从而直观反映了直流变换的趋势。
2.2 实验
测试设计的初始单端反激变换器电路,用示波器观察输出波形的变化。考虑输出的高电压,使用1 000倍高压探头衰减10倍测量,示波器显示结果为实际结果的1/10 000,为便于观察纵坐标设为0.1倍输出。调整时间轴,输入12 V的输入电压,开关脉冲波高电平约为12 V,负载输出电压变化曲线导出处理后与仿真对比如图10所示。观察实验结果,与仿真波形基本趋势一致,稳态值在2 380 V左右,约为仿真值的90%。主要影响输出原因包括前面讨论的杂散参数,及变压器铁损、分布电容等直接影响功率输出的因素。综合考虑可将其整体反映在输出的效率上,由式(17)知,输出电压会较理想情况有小幅降低。将实验电路的效率理解为80%,通过一定的折算,即可使用小信号建模方法建立实际反激变换器模型,以便研究系统的稳定性和其他性质。

图10 实验输出电压与仿真对比
3 算例设计与验证
由杂散参数分析,器件选型方面选用特殊金属薄膜电容作为输出电容,其ESR很小,很大程度上减小了Rc对传递函数的影响,同时鉴于对安全性的考虑,此类电容耐高压性能好,稳定性强。鉴于电源模块已选定,输入电压不做改变,同时保持负载不变,以提高输出电压为方向,其他参数考虑调整周期和占空比。由仿真模型做出占空比0.22条件下周期17~27 μs区间的曲线族如图11所示,周期20 μs条件下占空比0.2~0.25区间的曲线族如图12所示。

图11 D1=0.22周期17~27 μs(间隔1 μs)曲线族
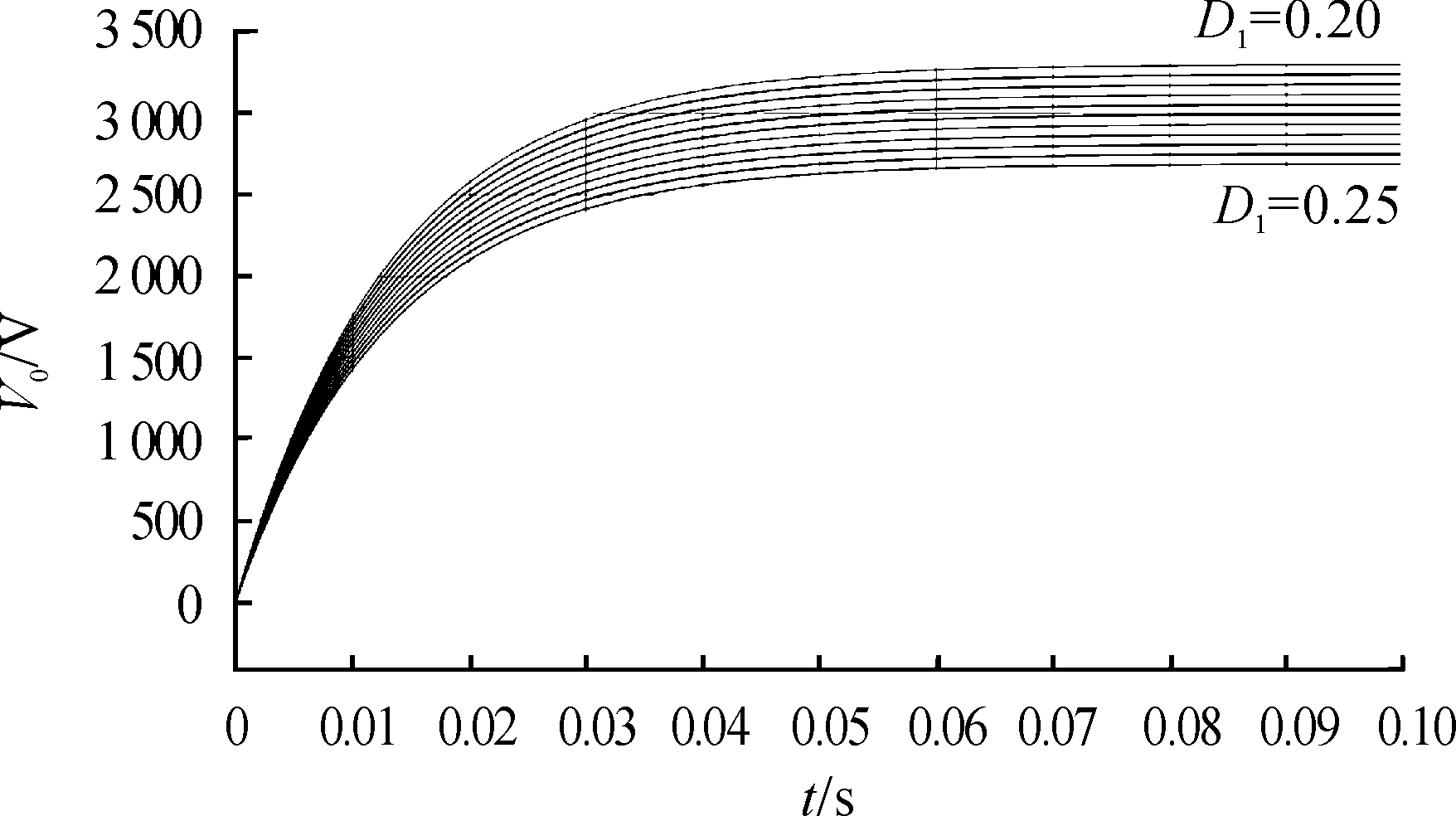
图12 Ts=20 μs占空比0.2~0.25(间隔0.005)曲线族
对不同的参数条件,设计部分仿真与实验结果对比的算例如图14与图15所示,对终点效率的估算分别约为80%与78%。
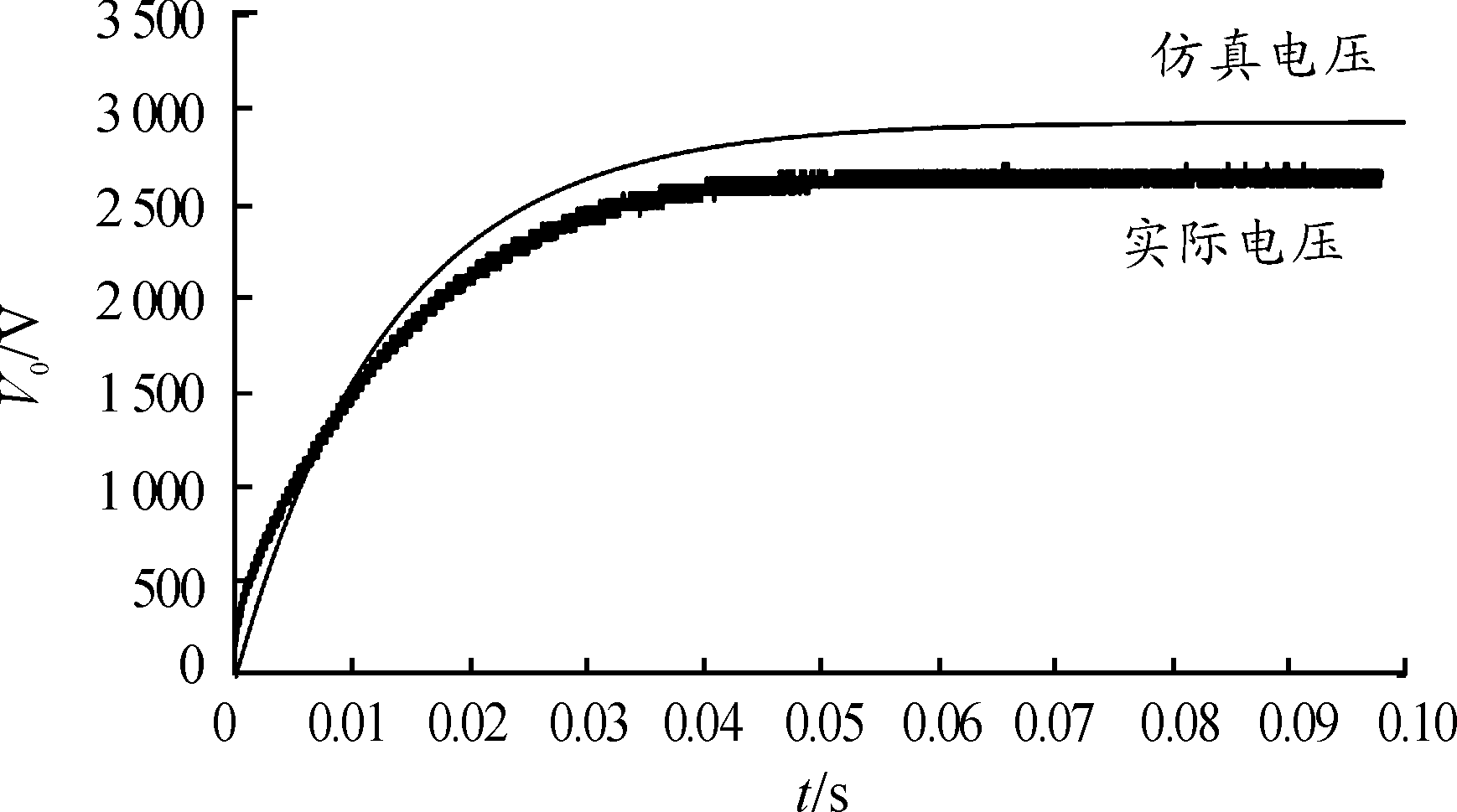
图13 Ts=19 μs, D1=0.22实验与仿真预测对比

图14 Ts=20 μs, D1=0.34实验与仿真预测对比
假定欲获得2 650 V稳态输出电压,以上节对电路效率的估值80%计,仿真稳态电压会在2 940 V左右。由此在两组算例基础上,可取值D1=0.22,Ts=20 μs,分别进行仿真与实验测试,比较实际输出波形和仿真输出波形如图15所示。仿真稳态值约为2 935 V,对应条件下实测电压约为2 660 V,满足要求,实验结果基本与仿真的预测基本一致,验证了模型的准确性和可行性。
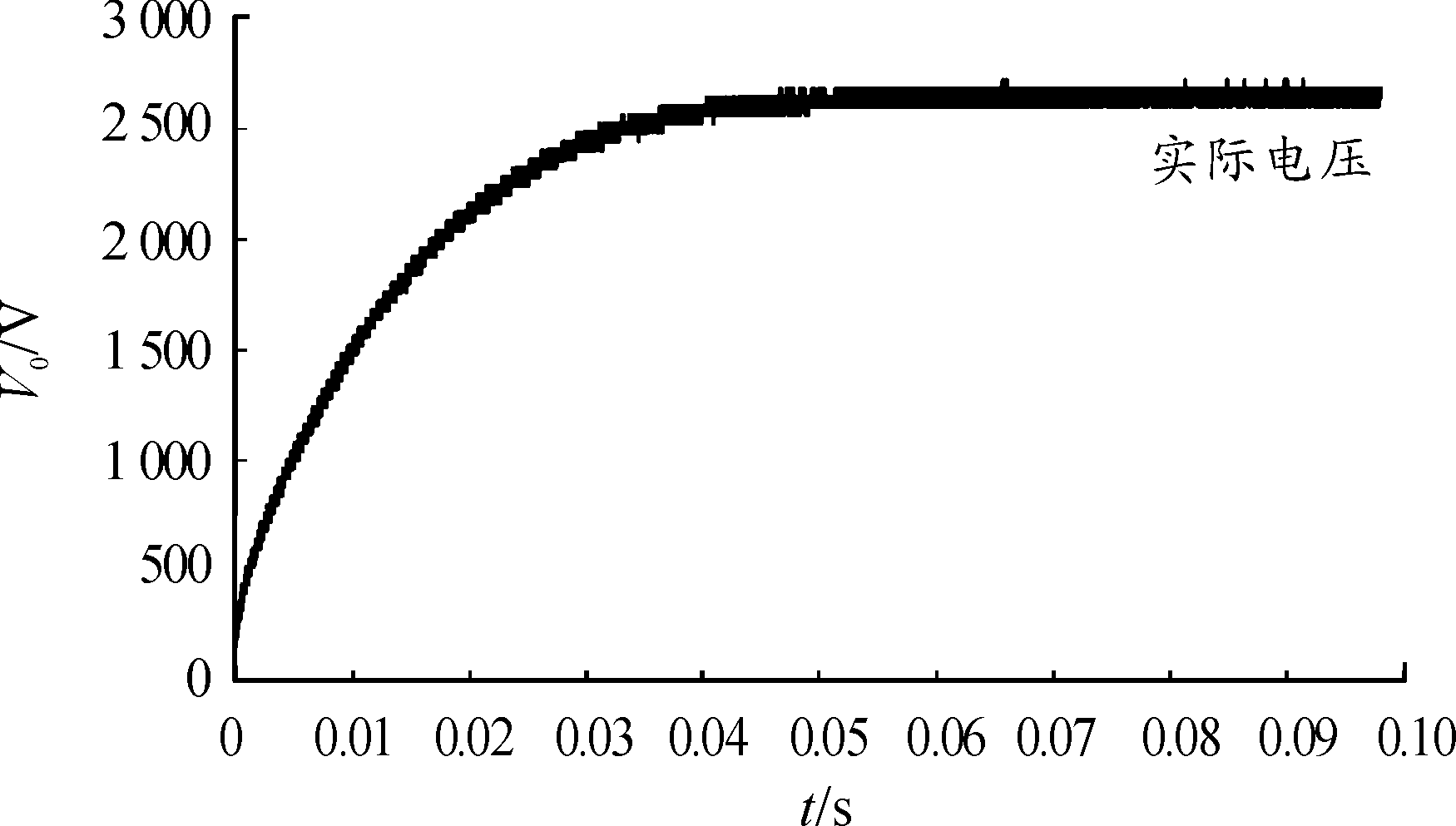
图15 提升周期后实验与仿真预测对比
4 结论
提出一种以电路平均法为主要思路的建模方法,并由此推导出其时域稳态建立模型,设计相应的反激变换器为主体的高压电源电路并进行测试,该建模与相关分析方法能清晰地反映直流高压输出的稳态建立过程与终点状态,对相关设计具有指导意义和参考价值,可为高压电源相关研究提供理论支撑。
[1] SANJAYA M.Switching Power Supplies A-Z[M].2E.北京:人民邮电出版社,2015.
[2] 李晓峰,王亚斌,吴碧.侵彻弹药引信技术[M].北京:国防工业出版社,2016.
[3] TSE C K,DI BERNARDO M.Complex behavior in switching power converters[J].Proceedings of the IEEE,2002,90(5):768-781.
[4] 王传芳.开关电源的建模与仿真研究[D].西安:西北工业大学,2007.
[5] 李昊.原边反馈反激变换器建模与动态优化[D].南京:东南大学,2015.
[6] 王建华,张方华,龚春英,等.开关变换器两端口网络建模,分析与设计[J].电子测量与仪器学报,2009(1):212-218.
[7] 黄荣赓.非理想反激变换器连续工作模式建模分析[J].宜宾学院学报,2013,13(6):65-67.
[8] SUN J,MITCHELL D M,GREUEL M F,et al.Average modeling of PWM converters operating in discontinuous conduction mode[J].IEEE Transactions on Power Electronics,2001,16(4):482-492.
[9] 冯丹,任宏滨,宁飞,等.开关电源变换器的小信号建模设计[J].计算机仿真,2015,32(11):141-145.
[10] 祖金龙.基于原边反馈控制的反激变换器设计与分析[D].哈尔滨:哈尔滨工业大学,2015.
[11] 侯庆会,岳奥飞,汪洋,等.一种磁隔离非理想反激变换器的建模与设计[J].电力电子技术,2018,52(11):47-50.
[12] ABRAHAM I P,KEITH B,TAYLOR M.开关电源设计[M].3版.北京:电子工业出版社,2010.
[13] CHRISTOPHE P B.Switch-Mode Power Supplies SPICE Simulations and Practical Designs[M].北京:电子工业出版社,2009.