钢丝绳隔振器作为被动隔振技术[1]的一种代表，其具有异于其他非线性器材的优良性能，如固有频率低，对低频和高频干扰[2]均有良好的隔振作用；在冲击载荷作用下刚度软化，能够有效隔离冲击；此外，还具有耐高、低温等优点，被广泛的运用到建筑设备、高压设备、气体绝缘变电站、抗震改造断路器、地震隔离设备、卫星运载、舰载等电子、机械设备与仪器仪表的隔振缓冲中[3-4]。国内外学者对钢丝绳隔振器进行了大量的试验研究，获得了钢丝绳隔振器直径、股数、缠绕方式和尺寸对钢丝绳隔振器刚度和阻尼特性的影响。由于钢丝绳隔振器具有突出的结构非线性、几何非线性、材料非线性等因素[5]，以及明显的迟滞效应，因此，对其非线性的理论分析是研究的重点。
本文从钢丝绳隔振器的结构上介绍了现在常用的五种钢丝绳隔振器，在非线性动力学中重点分析了四种常用的力-位移迟滞模型，在此基础上，通过准静态、振动和冲击试验研究钢丝绳隔振器的力学特性，以期在保证钢丝绳隔振器隔振能力的基础上，提高其隔冲能力，并对待进一步解决的问题以及将来的研究方向进行了讨论与展望。
1 钢丝绳隔振器的分类
1)T型钢丝绳隔振器
T型结构的钢丝绳隔振器也称为条形钢丝绳隔振器，主要是由一根钢丝绳缠绕固定在夹板之间，目前应用最多。但此种结构的钢丝绳隔振器在侧挂时容易产生较大变形影响其隔振性能。T型钢丝绳隔振器隔振性能主要由钢丝绳直径、线圈数目、缠绕螺旋倾斜角决定，其结构参数对刚度、阻尼特性有很大影响[6]。常见的T型钢丝绳隔振器结构如图1所示：其中图1(a)是常用的的T型钢丝绳隔振器，图1(b)具有限位装置，适用于有位移要求的设备。
图1 T型钢丝绳隔振器
2)G型钢丝绳隔振器
G型钢丝绳隔振器由于隔振器呈拱形结构，故又称之为拱形钢丝绳隔振器。与T型钢丝绳隔振器相比，其横向、纵向、垂向的刚度比接近1∶1∶1，拱形结构稳定性更优，G型钢丝绳隔振器如图2。
图2 G型钢丝绳隔振器
3)Q型钢丝绳隔振器
Q型钢丝绳隔振器其钢丝绳缠绕在两圆形夹板之间，由于整个隔振器呈球形结构，故称之为球形钢丝绳隔振器。如图3所示：该隔振器夹板为圆形，比T型隔振器稳定性好。
4)D型钢丝绳隔振器
D型钢丝绳隔振器又称碟型钢丝绳隔振器，其结构简单，重量轻、体积小，上下单孔安装，安装使用中通过多种设置方法可以吸收上下、左右、前后三维的振动和冲击，适用于飞行器、摄像设备减振，如图4所示。
图3 Q型钢丝绳隔振器 图4 D型钢丝绳隔振器
5)环形单元钢丝绳隔振器
环形单元钢丝绳隔振器的弹性阻尼元件是多个相互独立的钢丝绳圈[7]，通过选用一定个数的绳圈组成如图5所示的环形钢丝绳隔振器。该隔振器绳圈安装便捷，通过改变线圈数目调整隔振器的刚度和阻尼。环形钢丝绳弹性元件可以由不同直径的钢丝绳做成，相同尺寸的绳圈可以组合安装。由于多个线圈并联安装，因此研究几何参数对单个钢丝绳圈性能的影响就可以得到整个钢丝绳隔振器的刚度特性[8]。
图5 环形单元钢丝绳隔振器
除了以上5种主要形式外，还有其他结构形式的钢丝绳隔振器，比如钢丝绳管道阻尼隔振器、柱形钢丝绳隔振器以及与橡胶复合的钢丝绳隔振器等。
在实际应用中钢丝绳隔振器会产生失效现象，如图6所示，研究发现钢丝绳隔振器多是拉伸断裂，压缩时隔振隔冲性能较好，可以通过设计一种新型的可双向压缩钢丝绳隔振器改善其拉伸性能。
图6 钢丝绳隔振器失效图
2 钢丝绳隔振器的非线性力学特性
钢丝绳隔振器作为优异的非线性隔振器材，其隔振原理是钢丝绳丝与丝、股与股之间相对滑移从而产生干摩擦并消耗大量的能量。基于干摩擦的产生过程，建立钢丝绳隔振器的力学模型。通过对钢丝绳隔振器的力-位移曲线进行研究，发现钢丝绳隔振器有明显的迟滞现象，用数学方程建立钢丝绳隔振器迟滞力学模型。
2.1 干摩擦阻尼的性质
机械系统中的摩擦主要有库伦摩擦、粘性摩擦和stribeck摩擦。库伦摩擦切向力正比于法向力，其摩擦系数与接触面积无关[9]。白亮亮对机械系统进行无量纲化处理发现激励频率影响振幅，轨迹的形态与摩擦力有一定的关系[10]。激励频率变大钢丝绳隔振器的共振值反而减小，能够明显的改善隔振性能。研究发现干摩擦力滞后于钢丝绳丝与丝、股与股之间的相对滑移，随着位移的增加，干摩擦力逐渐增大。钢丝绳隔振器的力与位移所围成的封闭曲线代表了所消耗的能量。
李守昆将[11]干摩擦阻尼展开成傅立叶级数，将迟滞部分的阻尼和等效阻尼中的弹性力部分分开表达，从而建立了干摩擦阻尼的迟滞模型。
2.2 钢丝绳隔振器的动态迟滞力学模型
钢丝绳隔振器的结构多种多样，但其力学特性可以通过迟滞特性力学模型来描述。钢丝绳隔振器的力学性能主要包括刚度和阻尼性能，它们反映了力与位移、力与速度之间的关系，对于线性隔振器，作用力和位移呈线性关系，其刚度特性和阻尼特性比较简单，用试验即可测定，可得到较准确的数学模型；而非线性隔振器作用力和位移关系不可以用简单的线性函数来表示，其刚度和阻尼特性呈非线性，对其迟滞特性力学模型的建立是动力学研究领域研究的重点[12]。学者们从理论和试验两个方面探究非线性隔振器的数学模型。
钢丝绳隔振器是一种非常实用的隔振器材，其非线性迟滞特性决定了它的隔振性能，其迟滞回线与非线性软弹簧系统有很大不同，其模型主要为Bouc-Wen模型、双线性模型、迹法模型和多项式模型[13]。
1)Bouc-Wen模型
Bouc-Wen模型最初是由Bouc在研究迟滞系统的周期运动的时候提出的，后由Wen等学者不断改进而最终形成[14]，其数学描述如式：
(1)
其中：z(t)表示迟滞恢复力; α、β、γ和n是迟滞环参数，它们控制迟滞环的形状和大小；α，β和n是正实数；γ是实数。Bouc-Wen模型中包括四个参数，他们对迟滞环的形状有很大的影响。
Bouc-Wen模型的力—位移关系通过一阶线性方程来描述，迟滞环的切线即为钢丝绳隔振器的刚度，迟滞环的切线表达式即为刚度的表达式，改进的Bouc-Wen模型[15]更适合非线性的表达。
2)双线性模型
Bouc等提出的有非线性微分方程控制的光滑滞回模型通过设置不同的模型参数来描述不同的非线性隔振器的力学特性。在实际应用中，可以采用与实际情况更符合的双线性迟滞模型[16]来描述，双线性迟滞模型可以更好的表达非线性性能。双线性迟滞模型如图7所示。
图7 双线性迟滞模型
图7中，K1为隔振器在临界滑移力之前的刚度，K2为钢丝绳在临界滑移力之后的刚度，Py为临界滑移力。这种特性表明，当承载小于Py时，它有较大的刚度K1，这时钢丝绳股间没有滑动，整个钢丝绳构成完整的弹性体；当承载大于Py时，钢丝相对滑动而软化，因此刚度降低为K2，载荷降低时刚度又增大为K1，加载和卸载迟滞曲线为一密闭曲线，从而耗能并产生了迟滞阻尼。
双线性模型通过临界滑移力对迟滞曲线进行两阶段处理，考虑了钢丝绳隔振器的压缩刚度软化特性，但滞回曲线表明隔振器拉伸时刚度硬化，双线性模型不能准确描述钢丝绳隔振器拉伸和压缩方向不对称的迟滞特性。
3)迹法模型
Badrakhan在Bouc-Wen模型的基础上建立了迹法模型[17]，其数学表达式为：
(2)
迹法模型运用的主要理论为平均原理和等效原理[18]，其模型表达方式很多。迟滞恢复力F为非线性弹性恢复力Fe与阻尼力Fc之和，振幅和频率是决定力大小的两个因素，其表达式为：F=Fe+Fc
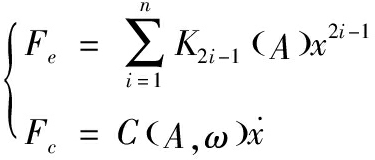(n为正整数)
(3)
其中: K为非线性隔振器的刚度；C为阻尼系数；x是隔振器的变形大小；
是隔振器的速度；A为输入信号振幅；ω为输入信号的频率。
迹法模型根据不同的研究对象有不同的表达式。Cutchins[19]等通过振动试验，运用多库仑阻尼模型来分析钢丝绳隔振器的刚度和阻尼特性。Tinker[20]等提出用与速度相关的多次方粘滞阻尼描述，实验表明，速度对隔振器的迟滞特性影响较小。付永辉[21]通过多项式描述迹法模型恢复力，小振幅时拟合度较好，振幅较大时不能准确描述其迟滞特性。
4)多项式模型
龚宪生等用与振幅和频率相关的多项式模型来体现钢丝绳隔振器的刚度和阻尼特性[22]。将钢丝绳隔振器的迟滞曲线分别用刚度曲线和多项式阻尼曲线来描述，刚度函数、多项式阻尼函数和与阻尼相关的函数改变迟滞回线的形状。此种方法能识别出阻尼成分中的粘性阻尼、干摩擦阻尼和高阶阻尼的比值。闻邦椿院士称之为“多项式模型”[23]，该模型适用于描述对称的力-位移曲线，不能准确描述钢丝绳隔振器拉压时的非对称力-位移曲线。
当前应用最广泛的是Bouc-Wen模型和双线性模型，这两种模型相比迹法模型和多项式模型能够较准确描述钢丝绳隔振器的力-位移曲线。Bouc-Wen模型和双线性模型现多用于描述钢丝绳隔振器准静态和振动时的力学特性，冲击时的力学特性与准静态和振动的力学特性之间的关系还需进一步的研究。同时，钢丝绳隔振器拉伸时刚度硬化，压缩时刚度软化，应将拉伸和压缩分开考虑，建立更符合实际的迟滞力学模型。
3 钢丝绳隔振器的力学性能试验研究
钢丝绳隔振器以其结构简单、安装方便、重量轻等特点，以及优越的隔振性能，已经越来越广泛的被应用到机械、交通、航空、船舶和建筑领域。随着技术的发展，对于钢丝绳隔振器的非线性性能的研究和模拟分析的技术也在不断的深入和发展，一些学者们进行了大量的试验研究，包括静态试验、振动试验和冲击试验。
1)在静态试验中，刘广璞[24]对钢丝绳隔振器进行加载和卸载变形试验，结果表明迟滞曲线面积大较线性元件能够吸收更多的冲击能量。班书昊[25]对钢丝绳隔振器的静态加载试验表明压缩状态下垂向呈软化特性，横向和纵向呈硬非线性特性，并且近似满足线性刚度之比k横向∶k纵向∶k垂向=1∶1∶3，但没有研究拉伸时钢丝绳隔振器迟滞特性。其垂向拉压试验表明压缩时刚度软化，拉伸时刚度硬化。压缩刚度的软化是由于钢丝之间出现较大滑移所致;拉伸时向直钢丝绳拉伸状态过渡刚度有渐硬趋势。万叶青[26]通过电液伺服液压试验台测得钢丝绳隔振器的迟滞曲线、摩擦阻力、隔振器刚度和阻尼曲线，通过多项式的拟合获取钢丝绳隔振器动力方程的有关参数，为动态分析及振动响应模拟做准备。通过准静态试验学者们发现钢丝绳直径、线圈数目和位移等几何参数对钢丝绳隔振器垂直和水平方向准静态载荷下滞回性能有很大的影响，能量损失比和有效刚度是评价不同钢丝绳隔振器滞回性能的两个重要参数[27]。Bo Cen通过对螺旋绳建立一个简化的有限元模型[28]，采用数值模拟方法，将1+16+12单线简化为一根单线，研究了简化有限元模型对垂向静刚度的影响，有限元分析得到的WRI载荷-位移关系与实验结果的对比如图8所示。
研究发现，不同的加载速度、预加载位移和幅值对钢丝绳隔振器滞回性能也会产生影响。Rashidi[29]提出了一种人工神经网络模型能够较好的预测钢丝绳隔振器的迟滞行为。Vaiana[30]对四种钢丝绳隔振器分别进行小、大、较大位移的实验，在每次静态试验中，水平位移以0.5 mm/s的速度线性增加，结果表明在大位移时，静动有效刚度比趋于1。在刚度较低且位移较大的最佳荷载挠度时，刚度可以用三次硬化行为来表示。王红霞[31]提出一种环形单元钢丝绳隔振器，采用多个并联的线圈作为耗能元件，研究了线圈数目、钢丝绳直径、绳环参数、绳环的水平倾斜角度、激励振幅和频率对钢丝绳隔振器在剪切、横滚和拉压承载方向上迟滞特性的影响规律。钢丝绳隔振器的几何参数影响其力学特性，同时钢丝绳的性能也影响着隔振器的力学性能。钢丝绳股内应力和载荷分布对钢丝绳性能有很大影响[32-33]。王晓宇对钢丝绳进行参数化建模[34]，对其空间模型进行有限元分析，提出了新的钢丝绳设计流程方法。许光鹏根据悬索的斜抛物线长度计算公式，从理论上推导挠度对钢丝绳弹性模量影响的计算公式[35]。用纵向连续均匀假设和纵向同性假设对钢丝绳弹性模量进行研究。
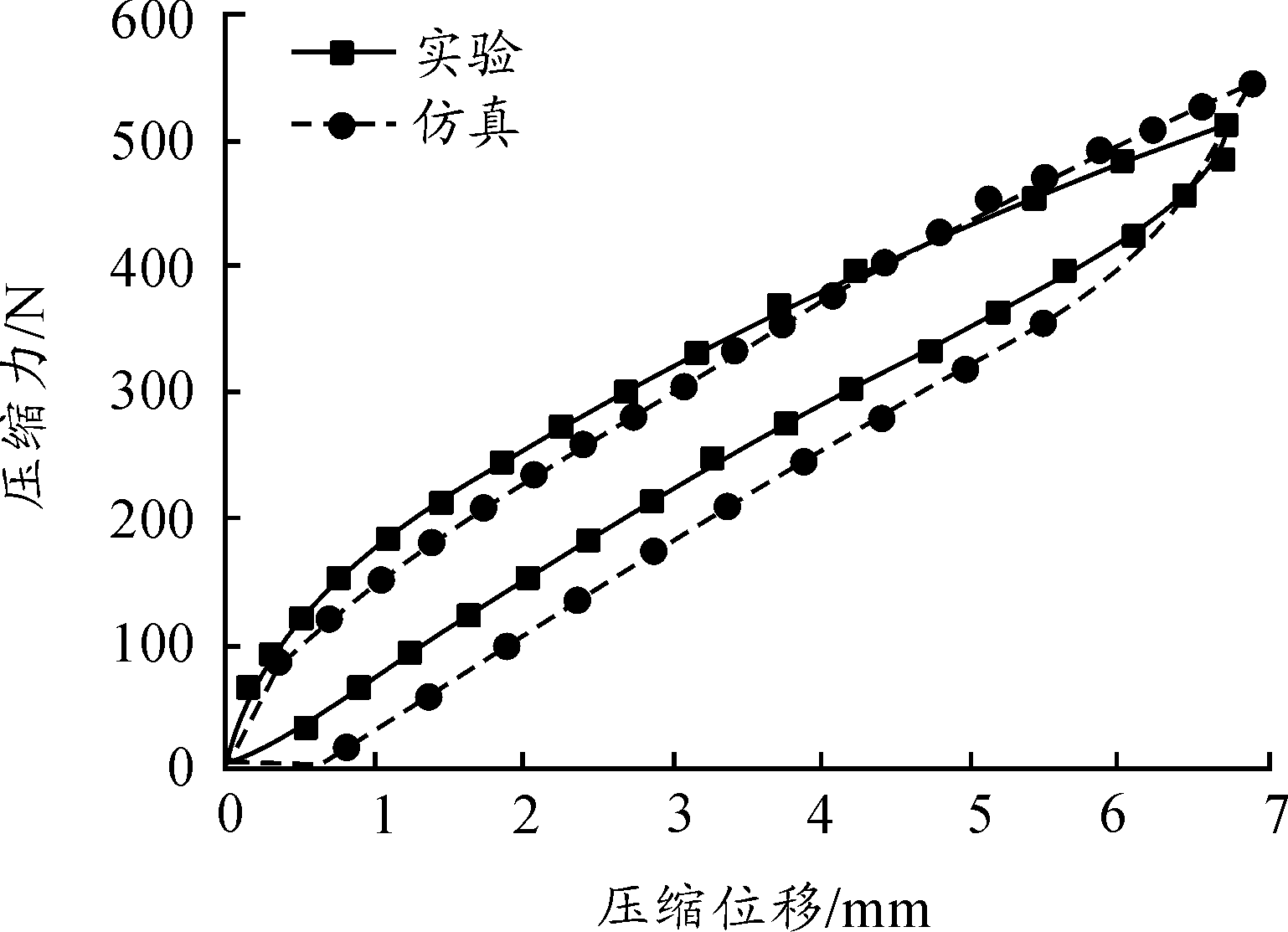
图8 有限元分析得到的WRI载荷-位移关系与实验结果
2)在振动试验中，班书昊45°安装钢丝绳隔振器[25]，引入频率软化系数，结果表明有频率软化系数的模型比传统的线性动力学模型更加符合实际情况。通过对钢丝绳隔离系统施加不同幅值的扫频正弦激励，结果表明钢丝绳隔振器在较宽的频带内(2～30)Hz，振动加速度衰减明显，隔振效率高。朱海潮[36]将三个已成熟的HGGS-1200型钢丝绳隔振器组成一个隔振单元，整机用10个隔振单元用于重为40t的船舶主机隔振。用功率流传递谱从振动能量传递的观点来研究隔振问题[37-38]，功率流估算与实测的振级落差总的趋势一致，验证了钢丝绳隔振器用于船舶柴油机主机隔振的可行性。其研究不同预加载和不同振幅条件下钢丝绳隔振器的固有频率、动刚度和阻尼时发现了不同于粘性阻尼和库仑阻尼的对振动速度更加敏感的“高阶阻尼”[39]。王江涛[40]分别研究负载质量、激励幅值和橡胶材料对橡胶钢丝绳复合隔振器传递率的影响，复合隔振器在共振时的滞回环包围的面积大于钢丝绳隔振器，说明了复合隔振器在共振时的隔振效率要强于钢丝绳隔振器，橡胶钢丝绳复合隔振器如图9所示。
Pablo[41]在冲击试验的基础上提出了一种考虑三次平稳性的杜芬振子数学模型的建立方法，同时提出一种考虑滞回特性的改进模型，在周期加载和参数识别过程中能够进行滞回环的测量。Vaiana[30]设计了一种特殊的试验装置用于研究位移幅值、频率、垂直载荷、几何特性和钢丝绳直径对钢丝绳隔振器在水平方向上即横滚和剪切方向的动力学行为，建立的一维非线性指数模型较好的吻合试验得到的滞回环。Buzea[42]研究表明，人工神经网络模型能够准确的预测钢丝绳隔振器在各种加载条件下的行为，可用于滞回环的预测。
图9 橡胶钢丝绳复合隔振器
3)在冲击试验中，王勇[43]用锤击法对小型钢丝绳隔振器进行空载和有预载的冲击特性试验，适当加载后隔振器的抗冲击性能可以提高，然而锤击法并不能真实模拟冲击信号。与锤击法相比，气缸式冲击模拟台所产生的冲击环境与舰船设备所处的冲击环境相比比较相似，冲击试验表明，钢丝绳隔振器表现出明显的冲击软化现象[44]。
Pablo[41]用不同脉冲持续时间对钢丝绳隔振器进行冲击试验，在试验的基础上，提出一种考虑三次平稳性的Duffing振子数学模型[45-46]，使用谐波平衡法[47-49]来求解，建立了冲击响应的数学模型。现有的冲击考核方法主要有锤击法跌落试验台和冲击机，与前两种方法相比，冲击机所产生的正负双波更能模拟真实的冲击环境。
钢丝绳隔振器的试验研究主要集中在静态和振动试验，冲击试验和冲击时的力学特性数学模型还有所欠缺。
4 结论
1)前人的研究主要集中在静态和动态特性研究，冲击时钢丝绳隔振器的刚度特性、阻尼特性和迟滞力学模型的建立是值得关注和研究的重点。
2)现有的钢丝绳隔振器动态迟滞特性力学模型描述拉压时为对称的迟滞特性。然而静态和动态试验迟滞曲线表明，钢丝绳隔振器在拉压方向为非对称迟滞特性，在拉伸和压缩时运用同伦分析方法，能够更准确的描述其迟滞特性。
3)由于钢丝绳隔振器非线性较强，对于其有限元实体模型的建立较困难。运用等效的方法将1+6+12钢丝等效成单根钢丝，建立其本构模型，从而建立准确的钢丝绳隔振器有限元模型，运用有限元分析的方法研究几何参数对其性能的影响。
4)对于冲击响应的数学模型以杜芬振荡器为原型提出具有三次弹性分量的数学模型，此模型局限于拉压方向，没有考虑到横滚和剪切方向，可对冲击响应模型进行进一步的改进。
[1] 龚宪生,骆意,王红霞.钢丝绳隔振器弹性元件空间曲线模型分析[J].重庆大学学报,2014,37(2):7-13,21.
[2] RAOULT J,BLAIN A,DORIDANT A,et al.Interference Signal Effects on a High-Frequency Monolithic Voltage-Controlled Oscillator:Experiments and Simulations[J].IEEE+9 Transactions on Electromagnetic Compatibility,2014,56(1):51-59.
[3] SPIZZUOCOM,QUAGLINI V,CALABRESE A,et al.Study of wire rope devices for improving the re-centering capability of base isolated buildings:Study of Wire Rope Devices for Improving the Re-Centering Capability[J].Structural Control and Health Monitoring,2016,24(6).
[4] 曹晓政,姜文涛,李倩,唐贵基.车载电子设备隔振的随机振动分析[J].云南电力技术,2018,46(6):68-71.
[5] BALAJI P S,LEBLOUBA M,RAHMAN M E,et al.Static lateral stiffness of wire rope isolators[J].Mechanics Based Design of Structures and Machines,2016，44(4),462-475.
[6] ZHANG W,WU C,YAN C,et al.The structure design and performance analysis for damping system of the airborne equipment[C].Proceedings of SPIE-The International Society for Optical Engineering,2015,9255.
[7] 王红霞,龚宪生,刘巍,潘飞.环形钢丝绳隔振器动态特性建模与参数识别[J].振动与冲击,2014,33(23):53-57.
[8] FRANCISCO LEDEZMA-RAMIREZ D,FERGUSON N S,BRENNAN M J,et al.An experimental nonlinear low dynamic stiffness device for shock isolation[J].Journal of Sound and Vibration,2015,347:1-13.
[9] 李喜晟.干摩擦中的多尺度动力学问题研究[C]第十届全国多体动力学与控制暨第五届全国航天动力学与控制学术会议论文摘要集，北京：中国力学学会,2017:1.
[10] 白亮亮.非线性机械振动系统的动力学研究[D].兰州：兰州交通大学,2016.
[11] 李守昆.基于钢丝绳隔振器的非线性隔振系统动力学特性研究[D].济南：山东大学,2012.
[12] VALEEVA,ZOTOV A,KHARISOV S.Designing of Compact Low Frequency Vibration Isolator with Quasi-Zero-Stiffness[J].Low Frequency Noise,Vibration and Active Control,2015,34(4):459-474.
[13] 丁旭杰.非线性隔振抗冲器的设计与建模研究[D].上海：上海交通大学,2008.
[14] PENG Z,ZHOU C.Research on modeling of nonlinear vibration isolation system based on Bouc-Wen model[J].Defense Technology,2014，10(4):371-374.
[15] 李宗京,舒赣平.正则化Bouc-Wen模型的参数研究及其在金属阻尼器中的应用[J].振动与冲击,2018,37(22):128-135.
[16] 李韶华,杨绍普.滞后非线性模型的研究进展[J].动力学与控制学报,2006(1):8-15.
[17] BADRAKHAN F.Rational study of hysteretic systems under stationary random excitation[J].Nonlinear Mechanics,1987,22(4):312-315.
[18] XU Wenjing,XU Wei,ZHANG Shuo.The averaging principle for stochastic differential equations with Caputo fractional derivative[J].Applied Mathematics Letters,2019,93.
[19] CUTCHINS M A,COCHRAN J E,GUEST S,et al.An investigation of the damping phenomena in wire rope isolators[C].Proceedings of the 1987 ASME Design Technology Conference,Boston,Massachussets,1987,5:197-204.
[20] TINKER M L,CUTCHINS M A.Damping phenomena in a wire rope vibration isolation system[J].Journal of Sound and Vibration,1992,157(1):7-18.
[21] 付永辉.金属丝网阻尼器建模及其减振应用研究[D].西安:西北工业大学,2007.
[22] 龚宪生,唐一科.一类迟滞非线性振动系统建模新方法[J].机械工程学报,1999,35(4):11-14.
[23] 闻邦椿,李以农,徐培民，等.工程非线性振动[M].北京,科学出版社,2007.
[24] 刘广璞,王福明,樊文欣.钢丝绳隔振器动态特性试验研究[J].华北工学院测试技术学报,1999,13(3):180-184.
[25] 班书昊,李晓艳,蒋学东,等.钢丝绳隔振器的非线性动力学模型[J].力学与实践，2012,34(1):66-69.
[26] 万叶青,范立民,齐煜.钢丝绳隔振器非线性特性分析[J].振动与冲击,2007,26(7)：46-49.
[27] 贡金鑫,王莹.基于有效刚度的空间框架结构几何非线性分析[J].大连理工大学学报,2015,55(2):157-164.
[28] CEN B,LU X,ZHU X.Research of numerical simulation method on vertical stiffness of polycal wire rope isolator[J].Journal of Mechanical Science and Technology,2018，32(6):2541-2549.
[29] RASHIDI S,ZIAEI-RAD S.Experimental and numerical vibration analysis of wire rope isolators under quasi-static and dynamic loadings[J].Engineering Structures,2017,148:328-339.
[30] VAIANA N,SPIZZUOCO M, SERINO G.Wire rope isolators for seismically base-isolated lightweight structures:Experimental characterization and mathematical modeling[J].Engineering Structures,2017，140:498-514.
[31] 王红霞.O型钢丝绳隔振器特性研究[D].重庆：重庆大学,2015.
[32] 陈原培.钢丝绳股力学与摩擦磨损性能研究[D].重庆：重庆大学,2016.
[33] 刘玉辉,寇子明,吴娟,等.单捻钢丝绳股内钢丝应力分布研究[J].矿山机械,2014,42(2):45-48.
[34] 王晓宇.钢丝绳参数化建模及力学特性分析[D].长春：吉林大学,2017.
[35] 许光鹏,张伟明,徐洋.挠度对钢丝绳弹性模量的影响[J].后勤工程学院学报,2005(4):57-59.
[36] 朱海潮,何琳,霍睿,等.钢丝绳隔振器用于船舶主机隔振[J].中国造船,2003(2):35-40.
[37] DEMETRIADES G F,CONSTANTINOU M C,REINHORN A M.Study of wire rope systems for seismic protection of equipment in buildings[J].Engineering Structures,1993,15(5):321-334.
[38] XI J,FENG Z,WANG G,et al.Vibration and noise source identification methods for a diesel engine[J].Journal of Mechanical Science and Technology,2015，29(1),181-189.doi:10.1007/s12206-014-1225-9
[39] LEDEZMA-RAMIREZ D F,FERGUSON N S,BRENNAN M J.An experimental switchable stiffness device for shock isolation[J].Journal of Sound and Vibration,2012,331(23):4987-5001.
[40] 王江涛.橡胶钢丝绳复合隔振器的试验研究[D].大连：大连理工大学,2010.
[41] LIU L,THOMAS J P,DOWELL E H,et al.A comparison of classical and high dimensional harmonic balance approaches for a Duffing oscillator[J].Journal of Computational Physics,2006，215(1):298-320.
[42] BUZEA D,IACOB A,SOIMARU C,et al.Vibration Behavior Analysis of Wire Rope Isolators Under Traction and Compression Load[J].Applied Mechanics and Materials,2013,332:357-362.
[43] 王勇,黄映云.锤击法测评小型钢丝绳隔振器冲击特性[J].船舶工程,2007,29(4):79-81.
[44] 黄映云,秦俊明,吴善跃.钢丝绳隔振器冲击特性试验研究[J].海军工程大学学报,2007,19(1):23-26.
[45] LIU L,THOMAS J P,DOWELL E H,et al.A comparison of classical and high dimensional harmonic balance approaches for a Duffing oscillator[J].Journal of Computational Physics，2006，215(1),298-320.
[46] FANG T,DOWELL E H.Numerical simulations of jump phenomena in stable Duffingsystems[J].International Journal of Non-Linear Mechanics,1987,22(3):267-274.
[47] BRENNAN M J,KOVACIC I,CARRELLA A,et al.On the jump-up and jump-down frequencies of the Duffing oscillator[J].Journal of Sound and Vibration,2008，318(4/5),1250-1261.
[48] HU H,TANG J H.Solution of a Duffing-harmonic oscillator by the method of harmonic balance[J].Journal of Sound and Vibration,2006,294(3):637-639.
[49] HA-MDAN M N,BURTON T D.On the Steady State Response and Stability of Non-Linear Oscillators Using Harmonic Balance[J].Journal of Sound and Vibration,1993,166(2):255-266.