土壤通常由各种不同尺寸的离散微粒组成,成分较为复杂,物理参数各异。绝大多数土壤具有不均匀的物理特性且各向异性,在受到撞击时颗粒之间发生强烈的挤压和摩擦,往往会表现出较大的流动性[1]。土壤是一种非平衡态的能量耗散体系,具有很好的缓冲性能,可以用来作为弹丸的回收介质,成本低廉且易于实现。侵彻土壤过程的研究在军事和民用领域都有着重要的意义。例如军事上钻地武器的研制和掩体的设计,试验装置回收等,民用上打桩过程分析和民防工程等。
目前还未出现成熟的理论可以精确描述土壤的动力学行为,一般只能使用经验公式法、试验研究和数值仿真来对弹丸侵彻土壤的过程进行分析[2-3]。随着计算机性能的提高和算法的不断优化,使用数值仿真分析侵彻过程成为一种方便有效的途径。在侵彻问题的数值仿真方法中,使用最多的是FEM有限元法,但是FEM法在模拟大变形时网格会发生畸变影响计算精度[4-5],任保祥等[2]利用FEM方法对弹丸侵彻自然土的弹道进行了模拟并与试验结果进行了对比;周燕[6]同样使用了FEM方法对钻地弹土中弹道的影响因素进行了对比。可以看出使用FEM法虽然可以较为准确的模拟出弹丸的弹道,却不能准确表现出土壤受冲击过程土粒飞溅及土壤变形的过程。近年来逐渐兴起的光滑粒子流体动力算法(Smoothed Particle Hydrodynamic,简称SPH)作为一种无网格拉格朗日算法,由于其不依赖于网格,不用考虑网格大变形带来的计算失败,对于处理土壤大变形和失稳问题非常适合。SPH方法不使用单元,而是具有一定质量的粒子,该方法使用一个近似函数来表征粒子运动的信息,在任意时刻求解这些粒子的速度和能量。目前已经有很多国内外学者利用SPH方法对土壤材料的性质进行模拟,并应用在山体滑坡等大变形的工程实际中,获得了较好的结果[7-9]。本文使用土壤作为弹丸回收箱内的回收介质。为了保证弹丸的安全回收,防止弹丸击穿土壤甚至发生事故,并尽可能的减小回收箱的大小,需要选择合适的结构尺寸。使用SPH法来对弹丸在预定速度下侵彻土壤的过程和侵彻深度进行数值模拟,并研究撞击面大小对侵深的影响,为回收箱设计提供参考。
1 试验背景及建模
本文所述土壤回收箱是用于抗过载试验中弹丸的回收,发射系统可以选择使用火药或者高压气体作为能源,弹丸射入回收箱内的土壤中停止并进行回收。回收箱三维模型如图1所示,箱内充满土壤,箱体上表面由多个钢板拼接,方便找到射入的弹丸。撞击表面上安装有薄板,该薄板可以防止土壤塌陷,射击时弹丸击穿薄板后射入土壤中进行回收。
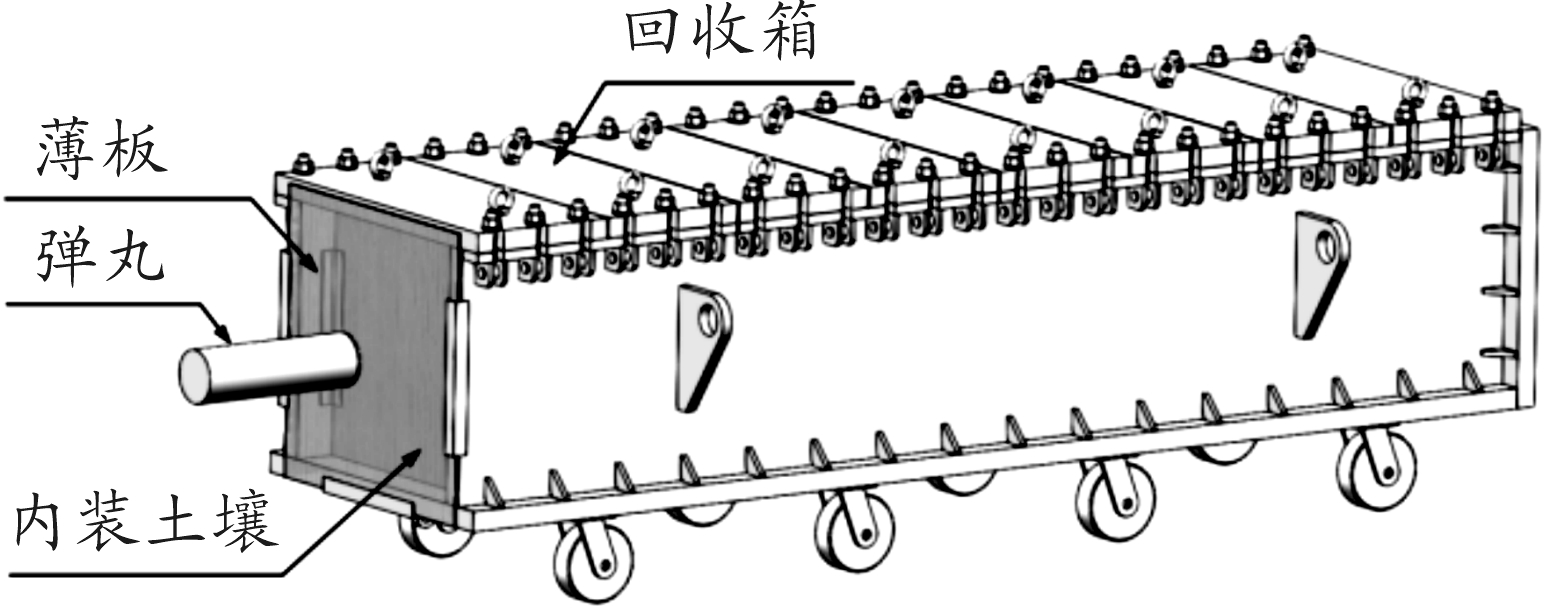
图1 回收箱三维模型
弹丸为直径105 mm、长度350 mm的平头试验弹,内部中空用来安装试验装置,质量为4 kg。考虑到试验弹在撞击土壤过程中不应产生大的变形,将其设置为刚体来节省计算时间,其材质为钢,密度为7.85 g/cm3。土壤为一长宽各为500 mm、深度为2 400 mm的长方体。考虑到弹丸在侵彻土壤过程中可能会发生不同方向的偏移,为了准确观察弹丸在土壤中偏移和翻转情况,采用全尺寸土壤分析模型。
弹丸采用实体SOLID164单元,采用拉格朗日算法描述,利用ANSYS Workbench建立三维模型并进行网格划分,有限元模型共 5 690个单元、1 884个节点。土壤采用SPH粒子进行模拟,利用LS-PrePost建立模型,长度和宽度方向各50个粒子、深度方向240个,共计 600 000个粒子。回收箱仿真模型如图2。
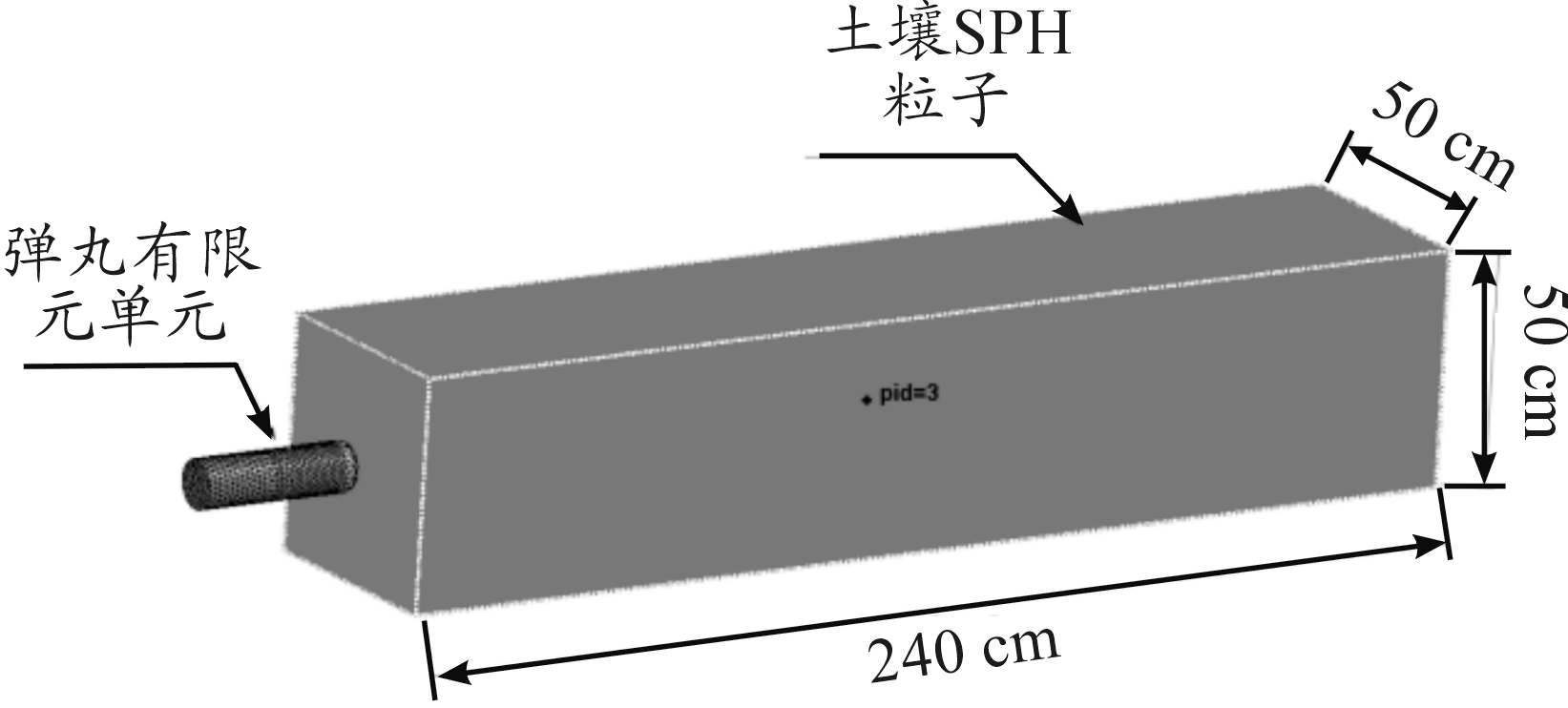
图2 回收箱仿真模型
弹丸使用LS-DYNA材料库中的MAT020材料模型,关键字*MAT_RIGID,材料参数如表1所示。
表1 弹丸材料参数

参数密度/(g·cm-3)弹性模量/GPa泊松比值7.852100.3
土壤采用带失效的土壤和可压缩泡沫模型,该模型由Krieg[10]提出,LS-DYNA关键字为*MAT_SOIL_AND_ FORM_FAILURE。这种材料适用于土壤和可压缩泡沫的模拟,该模型中的理想塑性屈服函数φ与压力p有关:
![]()
(1)
式中: φ为理想塑性屈服函数;Sij为偏应力分量;a0、a1和a2均为常数,由用户自己定义;p为压力。如果a1和a2为非零值,则塑性流动是非关联的;如果a1和a2为零,则![]() 类似于von Mises屈服函数。屈服极限为:
类似于von Mises屈服函数。屈服极限为:
(2)
σy仅和压力p有关,卸载时p=Kuεv,Ku为卸载体积模量;加载时p=f(εv),体积应变-压力关系曲线如图3所示,该曲线数值点使用表格形式由用户输入,土壤模型参数和曲线数值点分别如表2和表3所示[6]。

图3 SOIL_AND_FORM体积应变-压力关系曲线
表2 土壤模型参数
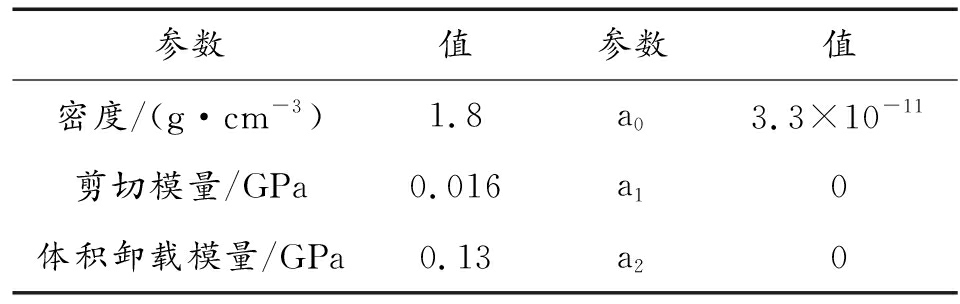
参数值参数值密度/(g·cm-3)1.8a03.3×10-11剪切模量/GPa0.016a10体积卸载模量/GPa0.13a20
表3 土壤模型体积应变-压力曲线数值点
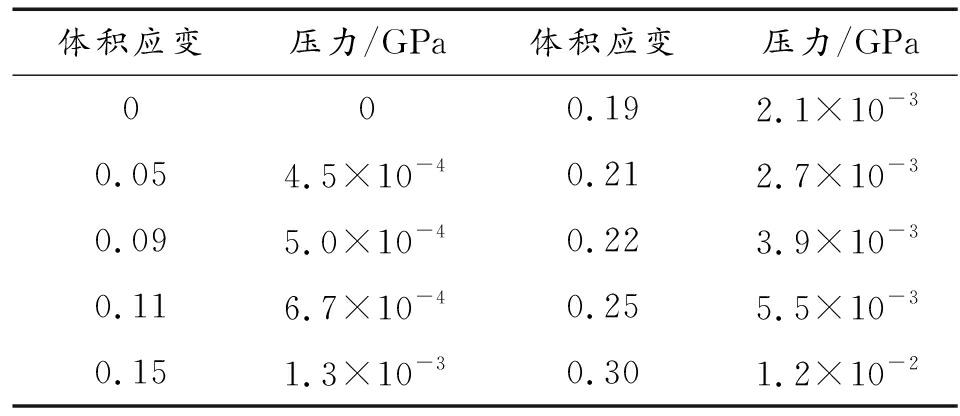
体积应变压力/GPa体积应变压力/GPa000.192.1×10-30.054.5×10-40.212.7×10-30.095.0×10-40.223.9×10-30.116.7×10-40.255.5×10-30.151.3×10-30.301.2×10-2
设置弹丸初速垂直于撞击表面且并不约束其任何方向平移和转动,通过关键字*BOUNDARY_SPC_SET对SPH粒子边界进行完全约束;弹丸与土壤之间的接触采用关键字*CONTACT_ERODING_NODES_TO_SURFACE侵蚀接触,并使用软约束选项;仿真采用cm-g-μs单位制,计算时间25 000 μs,每200 μs输出一个结果。
2 结果分析
对上述模型在弹丸初速500 m/s的条件下进行仿真,得到弹丸在土壤中运动情况和弹丸的速度位移时程曲线,并观察土壤粒子的位移情况。
弹丸土中运动情况如图4所示。弹丸侵入土壤后,先推开弹头两侧的土壤,使得两侧的土壤冲击边界,但由于边界被限制,只能撞击表面上未被限制的土壤。弹丸运动过程中不断压缩前方的土壤,最终按照近似直线的弹道前进,其x、y方向速度如图5所示。可以看到弹丸在垂直于速度方向上有小幅度的摆动,但最终都在土壤中运动。弹丸的总速度时程曲线如图6所示,在撞击的最初两个毫秒内速度从500 m/s迅速下降到176 m/s。随着弹丸速度的降低,速度下降的速率减缓,说明土壤对弹丸的阻力与弹丸冲击土壤的速度正相关。

图4 弹丸土中运动情况
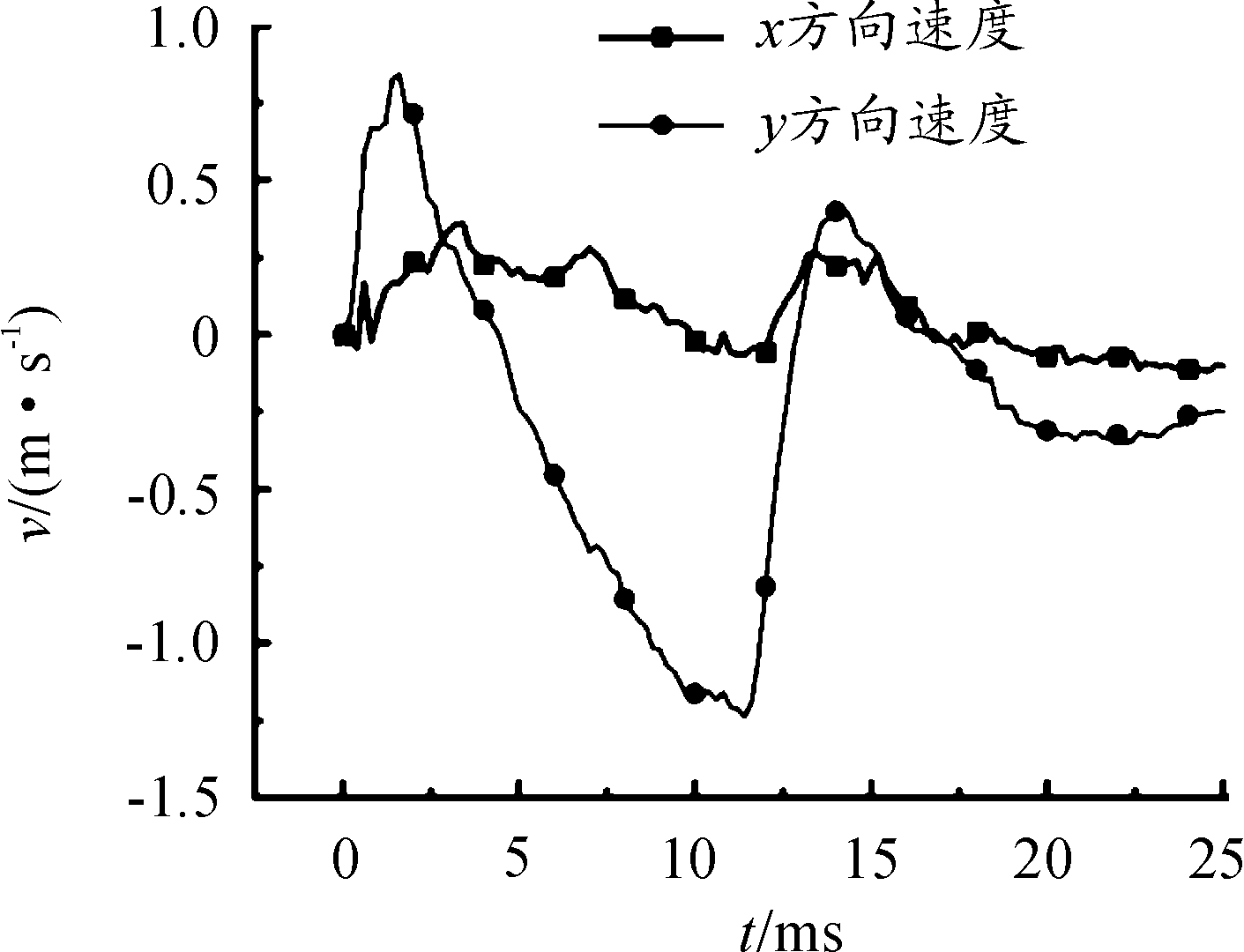
图5 弹丸x、y方向速度曲线
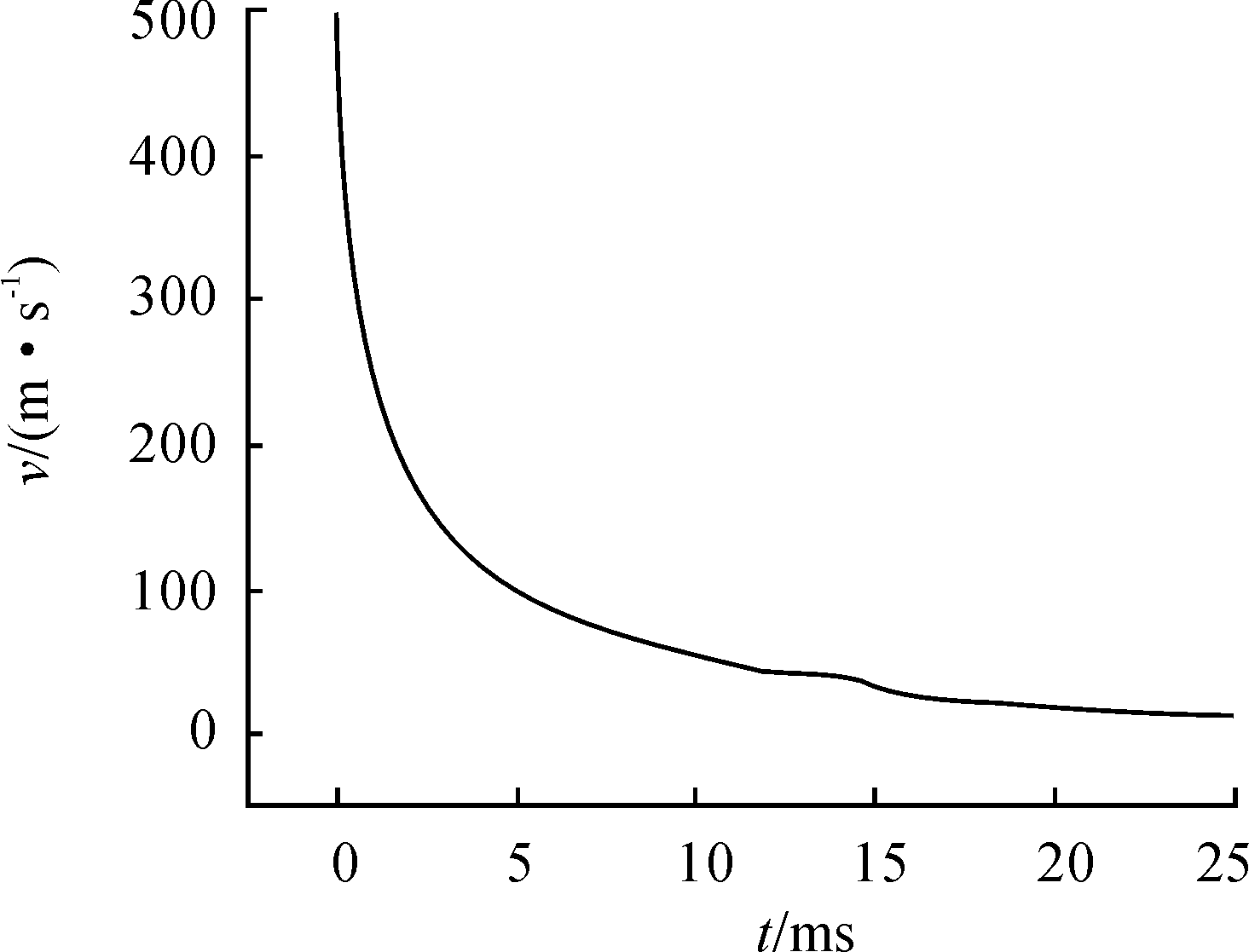
图6 弹丸总速度时程曲线
土壤粒子的位移情况如图7所示。观察在侵彻过程中土壤的形状可以看出弹丸刚开始撞击土壤时,其附近的土壤被推开,距离弹丸越远的土壤其位移越小,在撞击表面上出现形似漏斗的坑。这是因为土壤材料的拉伸强度远低于压缩强度,在反射拉伸波的作用下,土壤由外及内逐渐发生拉伸破坏,在土壤内部形成了空腔,且随着弹丸前进其速度不断减小,空腔的直径越来越小。弹丸前部的部分土壤粒子在获得了弹丸的撞击能量后,速度会大于弹丸的速度,这些粒子在一定程度上会帮助弹丸推开前方的土壤,减小弹丸前进的阻力。弹丸的位移时程曲线如图8所示。
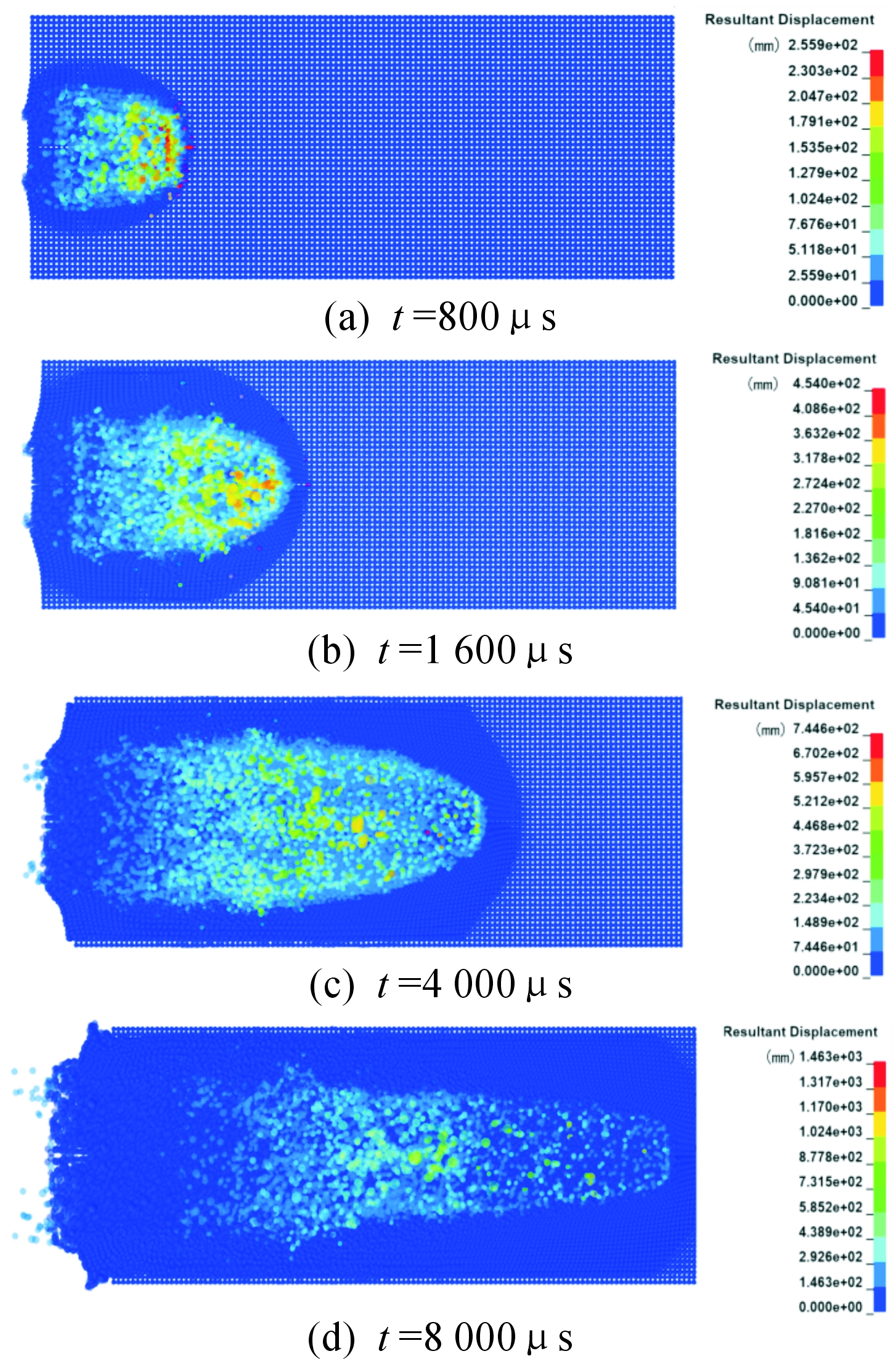
图7 土壤粒子位移云图
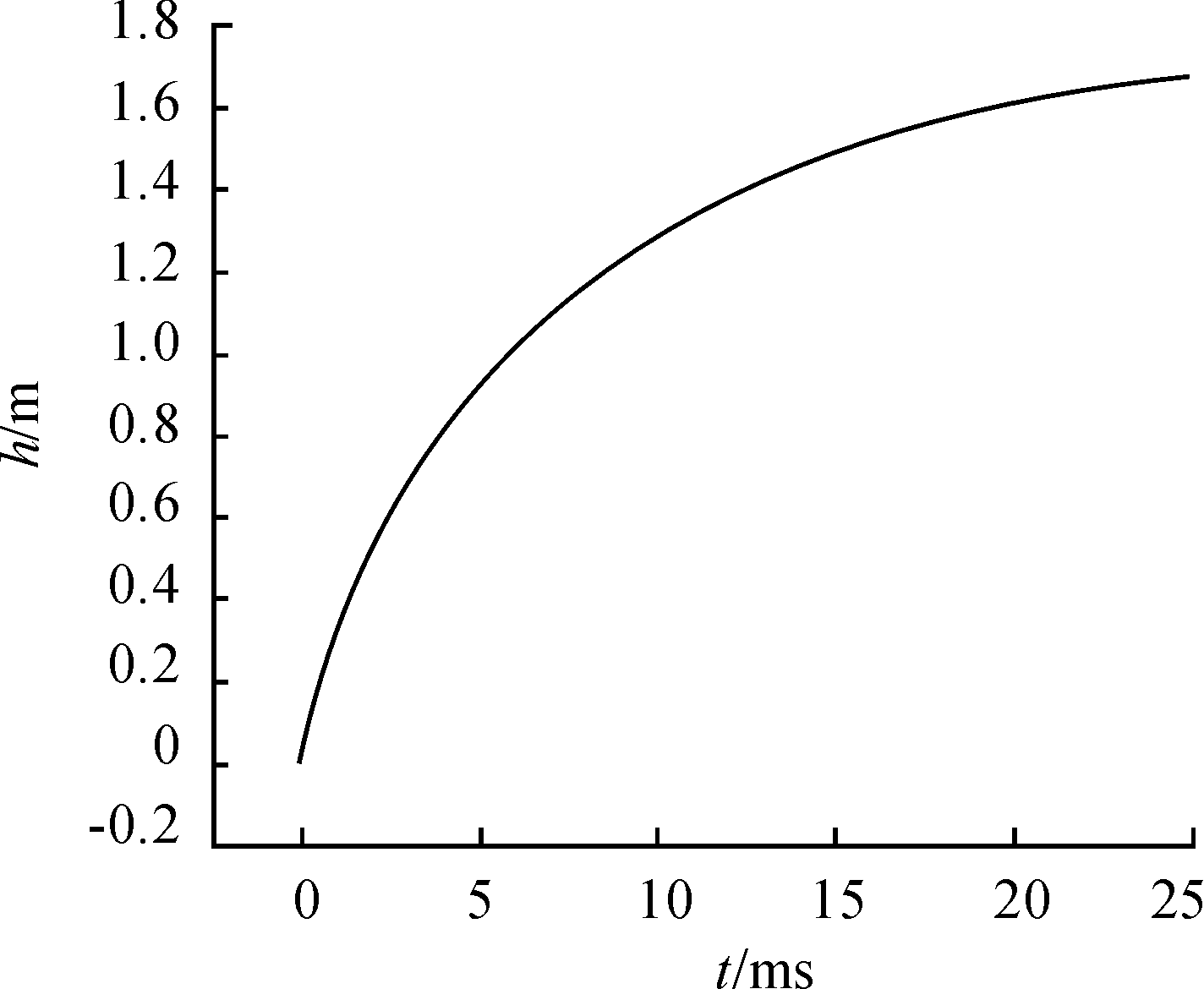
图8 弹丸位移时程曲线
3 侵彻深度分析
3.1 与Young公式对比
目前针对土质、岩石、混凝土等侵彻深度的计算公式有几十种,其中Young公式是在工程中应用较好的一种。Young公式是用于弹丸侵彻土、岩石、混凝土计算侵深的经典公式,目前在土介质的侵彻方面仍具有广泛的应用。用于土介质的SI单位制的Young侵彻公式如下:
![]()
(3)
式中:P为侵彻深度;m为弹丸质量;A为弹丸截面积;v为撞击速度;S为可侵彻性指标;N为弹头形状系数[11];对于本文平头弹丸,N取0.58。
Young公式的适用条件中指出,当弹丸质量较小时,公式右侧必须乘以K项:
K=0.274 5m0.4
(4)
由于土壤种类和成分的复杂性,使得确定其S值变得困难。董永香等[12]提出了由所研究不同软硬度土介质统计平均压缩模量,得到了S值的近似表达式:
S=20.1-4Es/3
(5)
式中:Es为土介质的压缩模量(MPa)。通过上式可近似估算不同土壤在低速条件下的可侵彻性指标S值。
土介质的压缩模量Es是在侧限条件下应力与应变的比值,可以通过室内试验获取。土壤的压缩模量差别巨大,往往软土的压缩模量随着其所受载荷增加而增加[13]。并且S值与土壤的深度有关,在土壤深度超过15 m时,极少数的土壤其S值会小于15,而对于普通的土壤其S值很少会大于5,除非材料是粘合的[14]。试验使用的是中等密度到松散的沙土,相对于更加坚硬的粘土,松散的沙土往往更加难以侵彻。本文使用中硬土压缩模量统计平均值9 MPa作为试验土壤的压缩模量,根据Young公式应用参考,取可侵彻性指标S=9。分别使用SPH法仿真、Young公式计算弹丸初速为400 m/s、500 m/s、600 m/s时侵彻深度,两种结果如表4所示。
表4 不同弹丸初速下的侵彻深度
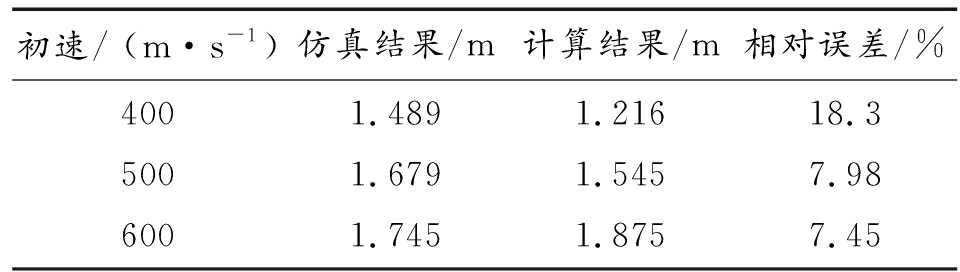
初速/ (m·s-1)仿真结果/m计算结果/m相对误差/%4005006001.4891.6791.7451.2161.5451.87518.37.987.45
通过对比发现,仿真结果与计算结果在弹丸速度400、500、600 m/s时的相对误差分别为18.3%、7.9%、7.4%,两者结果比较接近。说明使用SPH方法得到的弹丸侵彻回收箱土壤深度具有一定可信度,可以参考仿真结果来确定回收箱的尺寸。仿真结果与计算结果产生误差的原因主要在于:1) 弹丸的撞击表面较小,撞击过程中两侧的土壤很快接触到回收箱壁,导致形成的空腔比无限空间情况下小,增加了弹丸前进的阻力,这种阻力在弹丸速度较低时不明显,随着弹丸速度的增加,弹丸周围土壤粒子获得的速度也增大,这部分土壤挤压到回收箱壁上使得产生的空腔变小;2) 该模型不适合于弹丸在极低速度下的仿真,弹丸速度下降到10 m/s左右时,可以发现其减速度几乎为零,导致在低速情况下侵深增加,与实际情况不符,其数理模型有待进一步的分析研究;3) SPH粒子分布密度会对结果精度产生影响,为了在获得满意的计算精度的同时提高计算效率,本文未使用很高的粒子密度;4) SPH算法中忽略了粒子之间的摩擦滑移。
3.2 撞击面土壤面积的影响
通过弹丸在不同速度下侵深与Young公式计算结果对比,发现在弹丸速度600 m/s时,侵彻深度反而小于公式计算结果,相同模型在低速情况下的侵深均大于Young公式。为了研究不同撞击面土壤面积在弹丸高速情况下对侵深的影响,修改撞击表面的边长l重新进行仿真。为了防止粒子密度对结果的影响,这里4种情况采用相同的粒子密度,同时为了降低弹丸在低速情况下产生较大误差,只对侵彻过程的前半程进行仿真。撞击表面的大小示意图如图9所示,仿真的结果如图10所示。
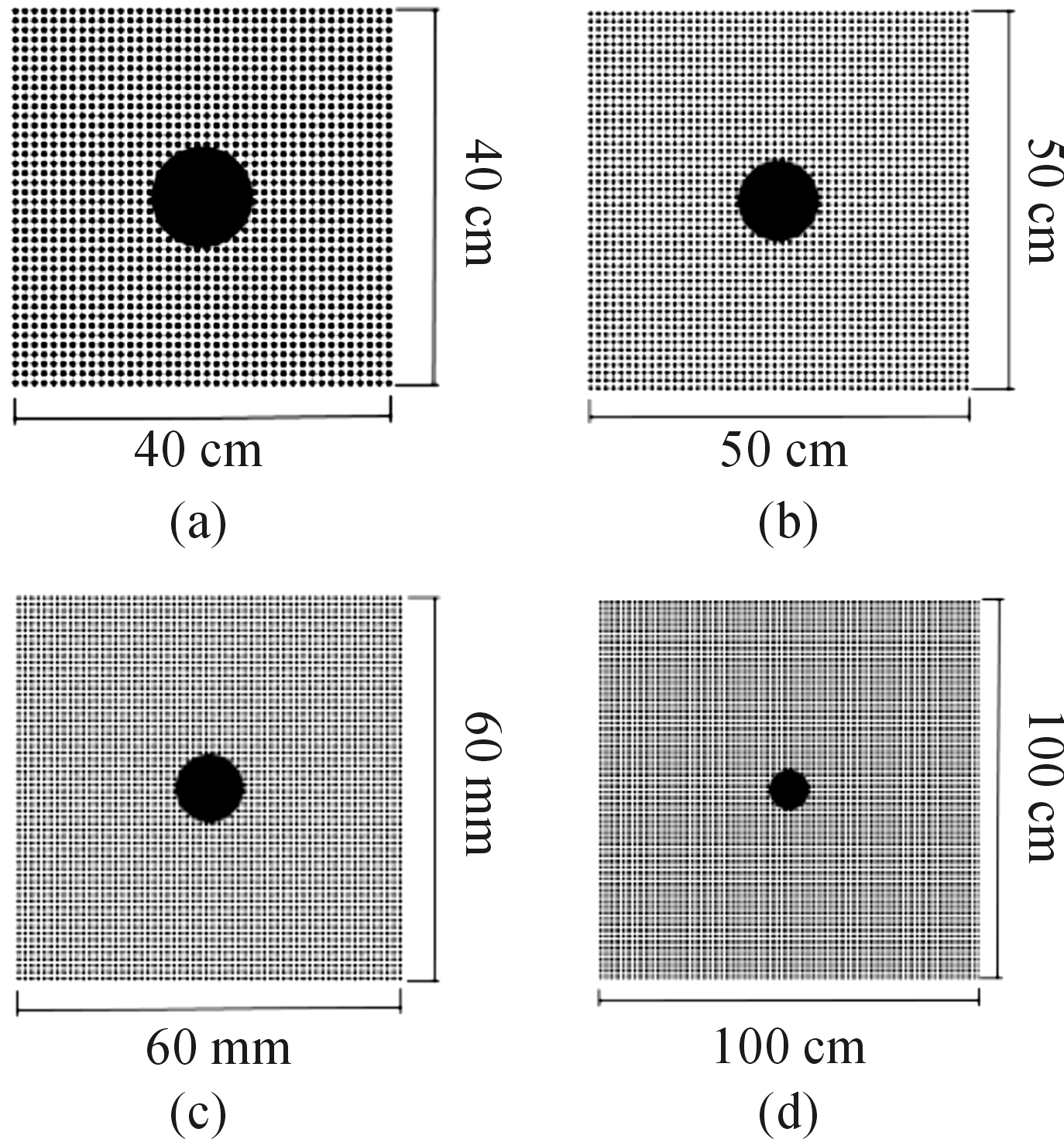
图9 不同大小的撞击表面示意图

图10 仿真得到的不同撞击面大小时的侵深
可以发现,弹丸在600 m/s下对于不同撞击面积的土壤区域获得的侵彻深度不同,撞击面尺寸越大侵深越大,但这种变化是非线性的,当撞击面尺寸增加到一定程度后,侵深的增加可以忽略。因此对于弹丸回收箱而言,为了防止弹丸击穿土壤撞击在回收箱后壁上,可以适当减小撞击面的尺寸,但是因为实际土壤密度存在较大的不均匀性,考虑到弹丸可能会在侵彻过程中发生偏移撞击在侧板上,撞击面的尺寸不能过小。
4 结论
1) 使用SPH方法可以很好的再现弹丸撞击土壤粒子的弹道和土壤变形的整个过程。
2) 仿真获得的侵彻深度与Young公式很好的吻合,说明使用此仿真获得的侵深数据可以用来作为设计弹丸回收箱尺寸的参考。
3) 该方法在弹丸极低速度下仿真结果偏差较大,故弹丸低速下侵彻的数理模型有待进一步研究。
4) 回收箱撞击表面土壤面积的大小会影响弹丸高速撞击时的侵彻深度,在一定范围内面积越小侵彻深度越小。
[1] 罗杰,肖建春,马克俭,等.半球壳冲击土壤的SPH-FEM耦合分析方法[J].振动与冲击,2017,36(17):195-199,230.
[2] 张学伦,刘宗伟,张团,等.弹丸侵彻运动钢板的数值模拟[J].兵器装备工程学报,2017,38(04):32-36.
[3] 任保祥,陶钢.弹丸侵彻自然土弹道的试验研究与数值模拟[J].科学技术与工程,2018,18(1):28-33.
[4] 罗伟铭,石少卿,田镇华,等.基于FEM-SPH算法的弹丸侵彻土体数值模拟[J].后勤工程学院学报,2014,30(2):13-17.
[5] 陈鹏,何勇,沈培辉,等.复合杆侵彻半无限靶的数值模拟分析[J].兵器装备工程学报,2019,40(3):25-30.
[6] 周燕.钻地弹土中弹道影响因素的数值模拟研究[D].南京:南京理工大学,2009.
[7] GORDON R.JOHNSON,ROBERT A.Stryk,Stephen R.Beissel.SPH for high velocity impact computations[J].Comput.Methods Appl.Mech.Engrg,139(1996):347-37.
[8] NIROUMAND H,MEHRIZI M E M,SAALY M.Application of SPH Method in simulation of Failure of Soil and Rocks Exposed to Great Pressure[J].Soil Mechanics and Foundation Engineering,2017,54(4):216-223.
[9] 徐兵,崔思婕,徐敏婕.基于SPH方法的弹丸侵彻仿真分析[J].大学物理试验,2016,29(6):108-110.
[10] KRIEG R D.A Simple Constitutive Description for Soils and Crushable Foams[J].SC-DR-72-0883,Sandia Laboratories,Albuquerque,New Mexico,1972.
[11] 宋梅利,王晓鸣,李文彬,等.弹头形状对高速侵彻效应的影响[J].弹道学报,2014,26(3):66-71.
[12] 董永香,冯顺山,李砚东,等.土介质对低速弹丸的抗侵彻性能试验研究[J].高压物理学报,2007,21(4):419-424.
[13] 闫小庆,周翠英,房营光,等.载荷作用下软土压缩模量与孔隙结构关系研究[J].中山大学学报(自然科学版),2018,57(5):57-63.
[14] YOUNG C W.Penetration Equations:SAND 97-2426[R].Albuquerque:Sandia National Labs,1997.