工程实践研究表明,加工误差造成的身管壁厚差对发射弹丸炮口扰动影响很大。由于身管存在壁厚差,身管在承受火药燃气压力和温度时,内部应力、传热等不均匀,导致身管发生弯曲,从而使得弹丸产生炮口扰动,最终影响射击精度。目前国内外学者从身管结构、弹炮耦合等多个角度对火炮身管开展了深入的研究,其中多数研究为简化模型将身管视为理想几何体。部分学者对火炮身管壁厚差的测量进行了研究[1-3],有待进一步对身管壁厚差及其对身管弯曲的影响建立理论模型进行深入研究。
传统的研究主要考虑身管承受火药燃气高压,重点对身管结构刚强度进行分析。火炮发射内弹道过程中,身管承受火药燃气产生的高温高压,这一过程中温度场、压力场等多场耦合,仅考虑火药燃气高压将使得研究结果与实际情况存在差异。由于射击过程中多场耦合情况较为复杂,使得建立与实际完全吻合的身管多物理场耦合理论模型较为困难。随着计算技术的发展,基于各类有限元仿真软件建立火炮发射有限元模型进行仿真分析是目前的一种主流方法。许多国内外学者针对身管多场耦合问题,通过合理的假设简化模型,然后仿真分析取得了一定的成果。赵天涛[4]对身管内多物理场耦合进行了分析,总结了多场耦合计算理论,借助MpCCI多物理场耦合计算平台联合ABAQUS和Fluent对机枪身管进行了流-固-热多物理场耦合分析,计算得到了身管内部温度、应力场分布;武峰等[5]对大口径火炮多发连射炮管热力耦合进行了分析,分析20发连射时炮管的热结构耦合场,得到某155 mm火炮药室部温度场和瞬态热应力场分布规律;陈龙淼等[6]对复合材料身管热-结构耦合进行了分析,得到了复合材料身管二维瞬态温度场和应力场分布;姚建军等[7]分析了速射武器身管的热-应力耦合场,结果表明射击过程中,由热冲击引起的身管应力变化比膛压引起的身管应力变化要大得多,连续射击时身管径向各点的温度呈脉冲式上升。Abdullah Sentürk等[8]从试验研究、数值分析和理论分析的角度,对7.62 mm枪管热力耦合问题进行了研究,结果表明身管内的温升是必须考虑的重要影响因素之一。李强等[9]对身管内膛镀层进行了热压耦合分析,针对计算和试验结果分析了镀层失效的原因,并提出了两种身管镀层方案。徐亚东等[10]建立了以复合材料身管质量最轻为优化目标、复合材料身管结构刚强度为约束的优化模型,对各层材料厚度和复合材料缠绕角进行了优化设计。Chung等[11]用40 mm火炮身管内部热传导情况作为预测身管侵蚀的依据,推导了新的侵蚀经验方程,能够得到精确的火炮身管侵蚀速率,这也为大口径火炮侵蚀速率的计算提供了参考。
上述研究均将身管视为理想几何体,忽略了由于加工造成的身管壁厚差。因此,建立考虑身管壁厚差的身管几何模型,基于身管热力耦合有限元模型,分析火炮发射内弹道过程中身管弯曲变形情况。综合考虑不同壁厚差身管射击时的弯曲情况和实际加工成本,提出合理的壁厚差控制范围,对提高火炮射击精度及指导工程实践具有重要意义。
1 考虑壁厚差分布的身管几何建模
图1为某火炮身管设计示意图。根据工程实际生产经验,由于身管长径比大,加工后的身管主要存在轴向形状误差,其截面形状误差及表面分布相比之下可忽略不计。此外,由于火炮射击过程中,身管内表面是主要工作表面。为了满足要求,身管内表面的加工采用了多种措施以保证其精度,可将身管内孔视为理想直孔。因此,身管壁厚差主要为外壁的轴向形状误差导致。根据生产经验,外壁轴向形状误差主要表现为身管外壁的弯曲,由于身管外壁的弯曲导致身管壁厚差在身管中间截面处最大,在身管两端很小。
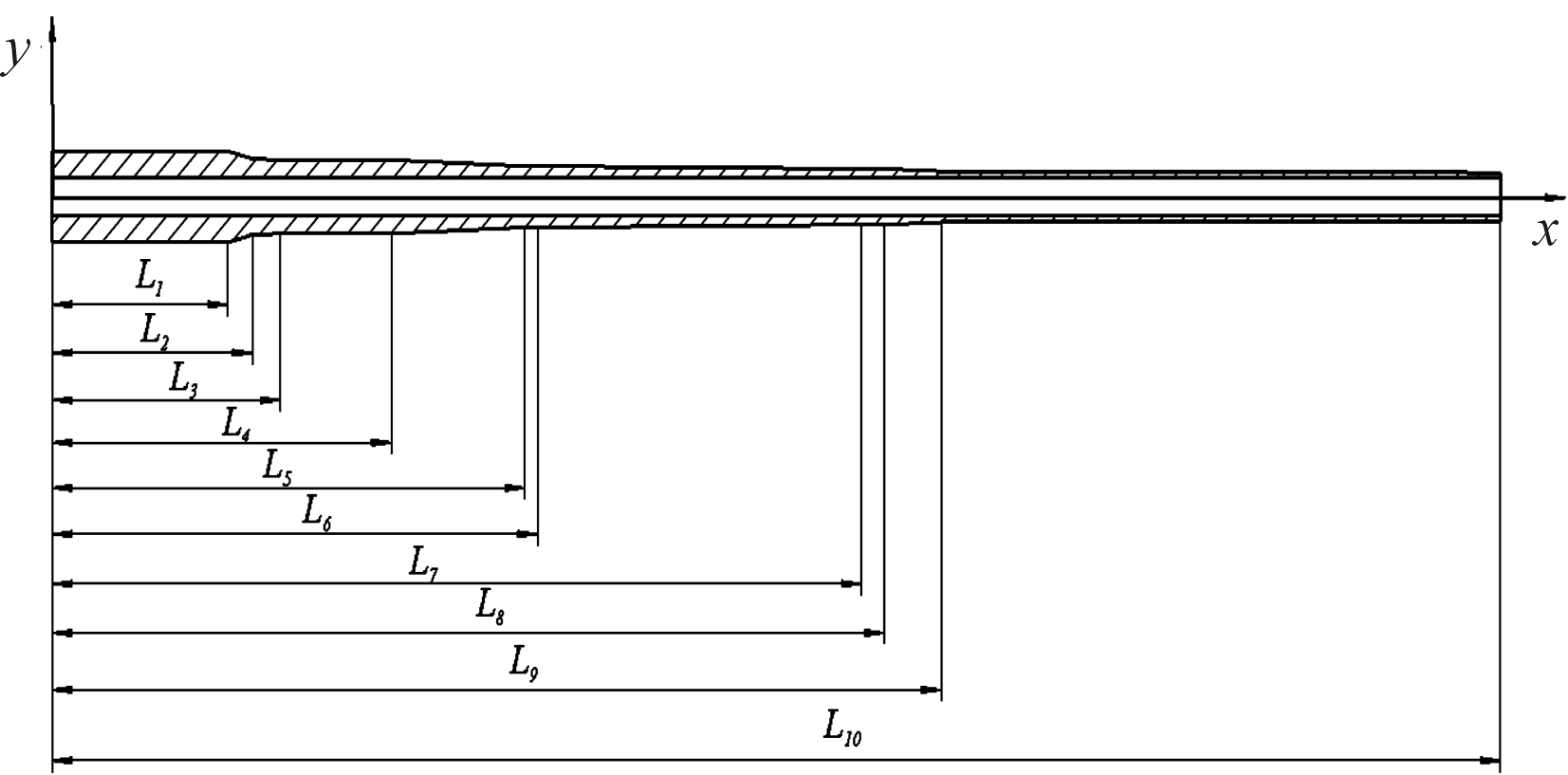
图1 身管设计示意图
根据上述实际生产经验,对身管壁厚差几何模型做如下假设:
1) 忽略身管各截面形状误差及表面分布,即身管各截面的内、外边界均为圆;
2) 身管内孔轴线为直线,即身管内孔为直孔;
3) 身管外壁轴线呈抛物线分布,在身管两端外壁圆心与内孔圆心重合,即壁厚差为零;在身管中间截面外壁圆心偏离内孔圆心最大,即壁厚差最大。对于最大壁厚差为Δd的身管,取y轴与内膛轴线重合,x轴过身管起始端截面中心且垂直于内膛轴线指向外壁弯曲方向,其外壁轴线方程为:
![]()
(1)
式中:L10对应图1中身管总长。图2为存在壁厚差分布的身管内孔及外壁轴线示意图。
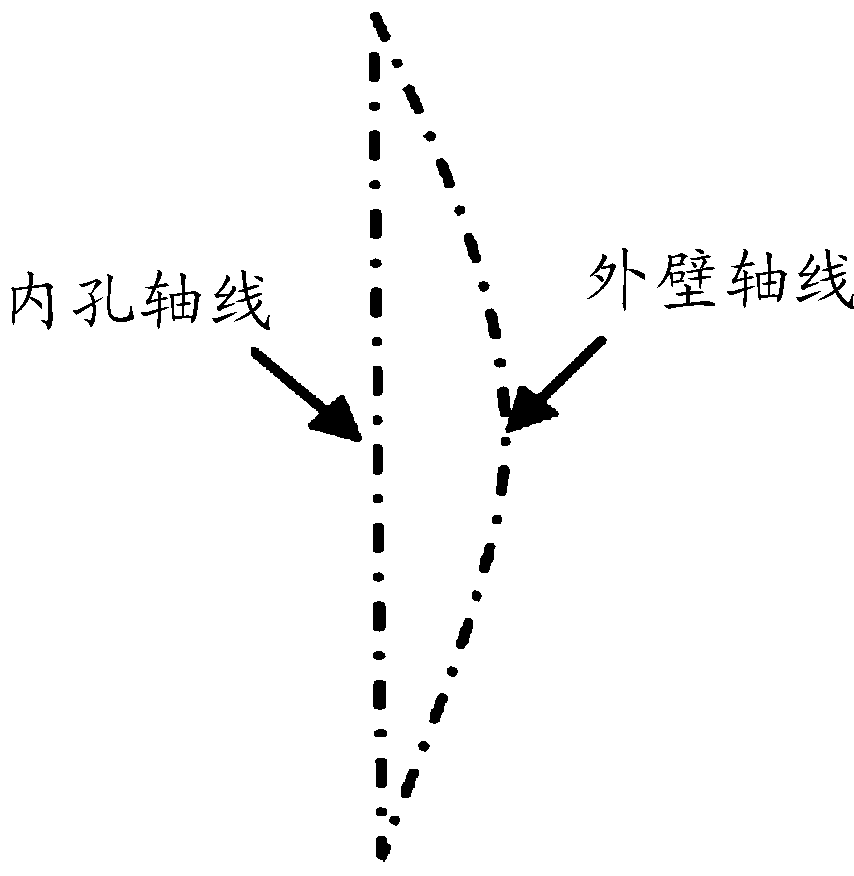
图2 身管内孔及外壁轴线示意图
由式(1)知,对于一定的身管,给定其最大壁厚差,则能确定身管壁厚差的整体分布,因此本文中以身管最大壁厚差来代表身管壁厚差的整体分布。图3为2 mm壁厚差身管三维几何模型剖视图。
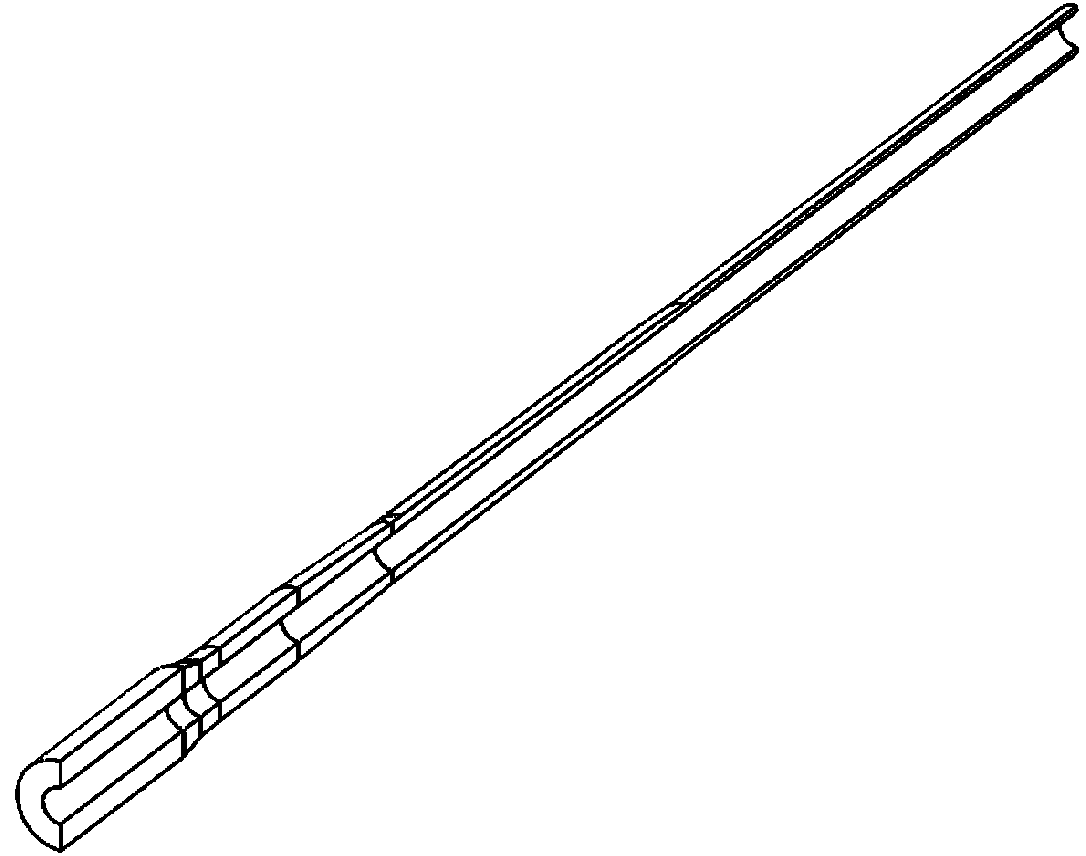
图3 2 mm壁厚差身管三维几何模型剖视图
2 身管热力耦合建模
火炮发射时,火药燃气产生的高压直接作用在身管内壁,同时高温气体也与身管发生强热相互对流。火药燃气的高压及高温均能使身管产生应力,应力分布不均导致身管发生变形。为建立火炮发射过程身管热力耦合模型,做如下基本假设:
1) 为单独分析身管在火药燃气作用下的变形,不考虑弹丸及其与身管的相互作用;
2) 身管自身重力对身管变形的影响相比于火药燃气的影响可忽略不计,不予考虑;
3) 不考虑火药燃气压力在同一截面的分布,仅考虑火药燃气压力沿身管轴向的分布,满足经典内弹道中弹后气体压力沿轴线呈抛物线分布;
4) 火焰燃气在弹后空间温度相同,由于火药燃气的作用时间短,文献[12]在分析身管热应力时将火药燃气与身管热相互作用的对流换热系数视为常数,本文也做相同处理。
2.1 火药燃气压力及温度分析
根据经典内弹道理论,得到内弹道方程组数值求解模型[13]:
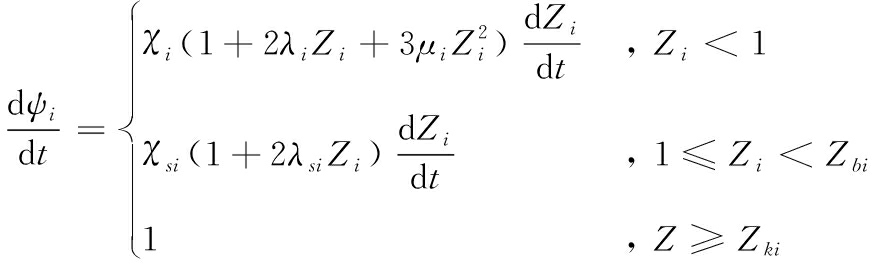
(2)
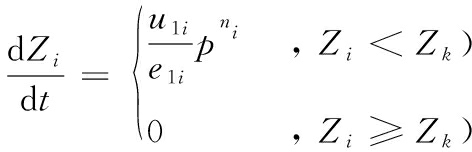
(3)
(4)
![]()
(5)
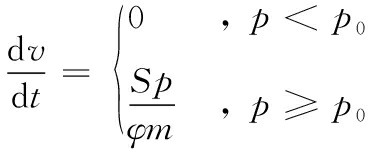
(6)
其中:
(7)
(8)
式中:m为弹丸质量;v为弹丸速度;l为弹丸行程;p为平均膛压;p0=30 MPa为挤进压力;S为内膛截面积;V0为药室容积;φ为次要功系数;ψi、Zi分别表示第i种火药燃烧百分比和相对厚度;χi、λi、μi、χsi、λsi、Zbi、Zki、e1i分别为与第i种火药形状相关的参数;u1i、n1i分别为第i种火药燃烧系数和燃烧指数;ωi、Δi、ρi、αi、fi分别为第i种火药装填质量、装填密度、密度、余容和火药力。
任意时刻弹后火药气体压力及温度分布分别为[13]:
(9)
![]()
(10)
式中: φ1为阻力系数; θ=k-1,k为绝热指数;Tbw为火药燃气爆温,约为2 800 K。
在Matlab软件中用四阶Runge-Kutta法对经典内弹道方程组求解,求得火药燃气平均压力分别随时间和弹丸行程变化曲线如图4,火药燃气温度随时间变化曲线如图5。
为了验证内弹道求解正确性,表1给出了部分内弹道特征量的求解值与试验测试值。由表可知,特征量的求解值与试验值基本吻合,说明内弹道求解结果具有参考价值。
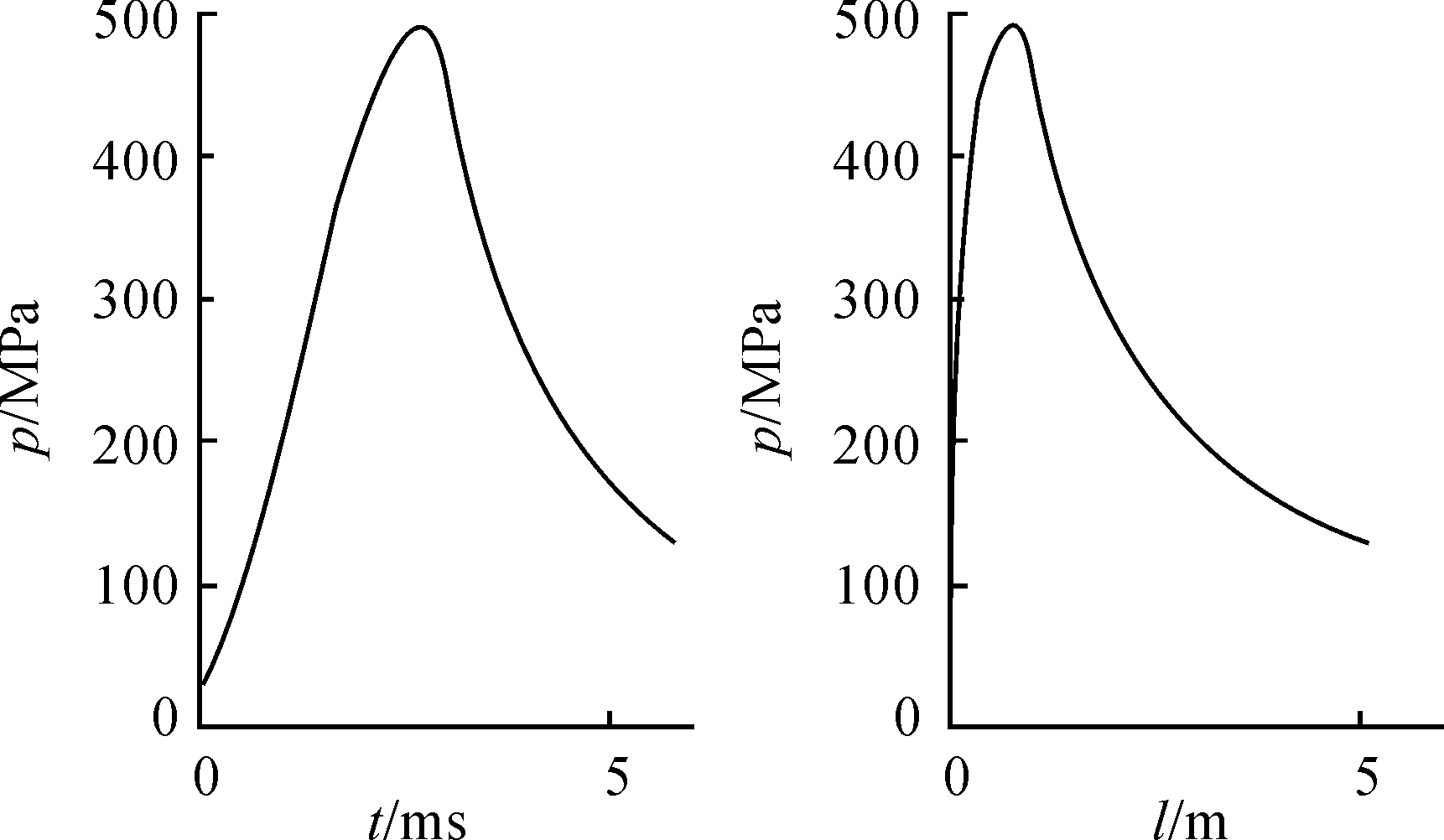
图4 平均膛压分别与时间和弹丸行程关系曲线
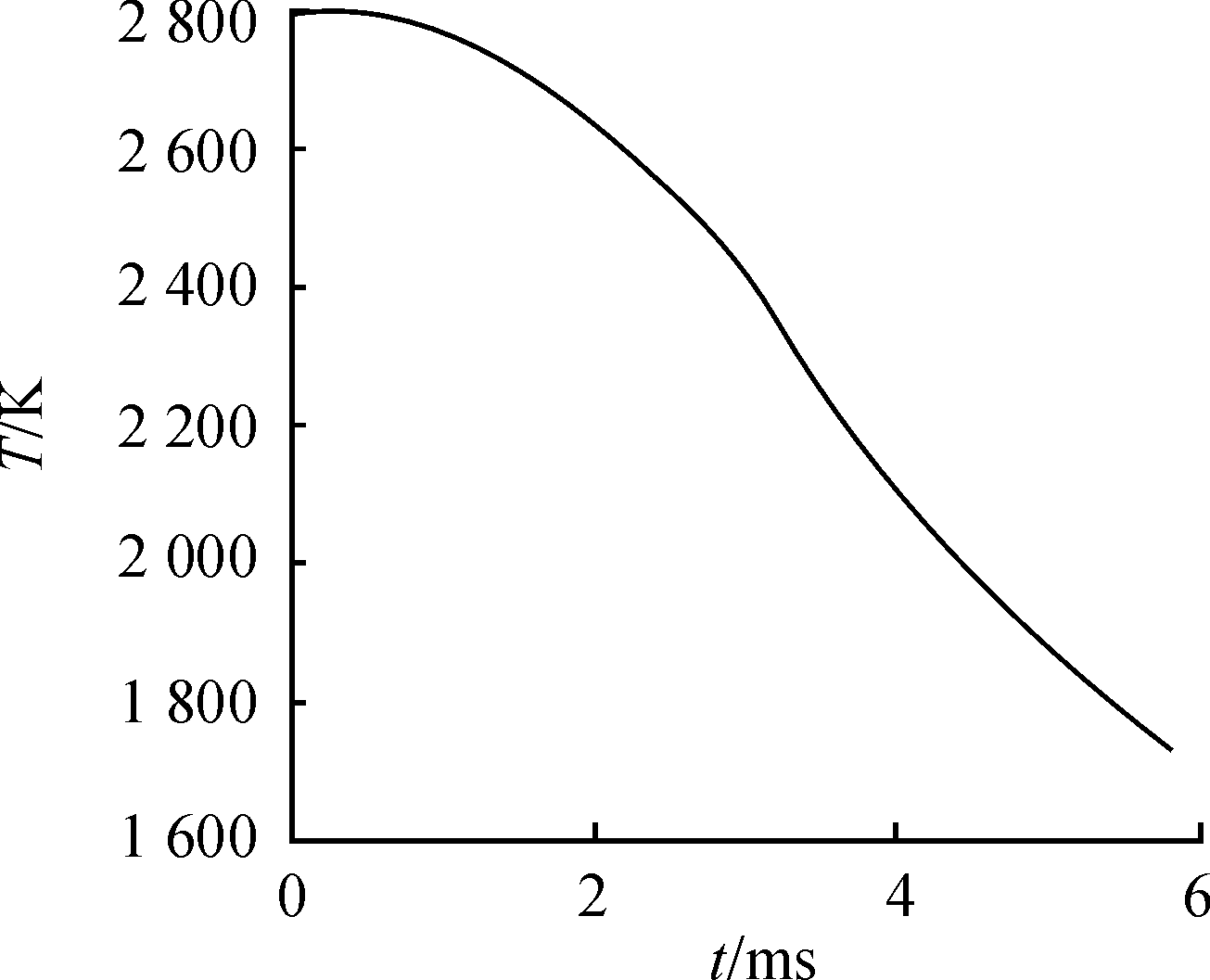
图5 火药燃气温度随时间变化曲线
表1 内弹道特征量求解值与试验测试值

弹丸出炮口速度/(m·s-1)最大平均膛压/MPa最大膛压对应行程/m求解量1 748.94880.787参考值1 733.64650.765相对误差/%0.884.943.01
2.2 身管热传导分析
火炮发射过程中除了火药燃气压力作用,还伴随燃气与身管的热交换及身管内热传导。直角坐标系下热传导微分方程表达式的一般形式为[4]:
(11)
式中:c为物质比热容; ρ为物质密度;Q为热源强度;kx、ky、kz分别为三个方向热传导系数。对于各向同性物质稳态热传导,其微分方程形式为:
(12)
为了求解上述偏微分方程,还需要一定的定解条件,对于身管,初始条件可认为身管的温度等于室温,即:
T|t=0=T0
(13)
式中: T0=295 K为室温。
身管边界条件为第三类边界条件,即身管内壁和外壁分别与火药燃气和空气发生热对流:
![]()
(14)
(15)
式中: TR为火药燃气温度,随空间和时间变化;T0为室温;hin 、hout分别为身管内壁与燃气、身管外壁与环境对流换热系数,在本章中根据假设(4)将身管外壁与环境的对流换热系数视为常数。
2.3 身管热力耦合有限元模型
将考虑壁厚差分布的身管三维模型导入Abaqus,在Abaqus中建立热力耦合分析步。热力耦合分析过程中身管内部温度会发生变化,温度的变化会导致身管的材料属性发生变化,表2为身管材料参数与温度T的关系[4]。
表2 身管材料参数随温度变化关系

材料参数取值密度/10-12(t·mm-3)7 833弹性模量/103 MPa929×T-0.263泊松比0.249 18+3.365 17×10-5T+4.523 51×10-8T2热导率/(mW·(mm·K)-1)298×T-0.331热膨胀系数(1/K)1.3×10-5比热容/106(mJ·((t·K)-1)808.228 5-333.373 4×e-T1 374.962
将火药燃气压力作为载荷施加在身管内壁,将火药燃气温度作为边界条件,与身管内壁发生热交换。注意到任意时刻,火药燃气仅在弹后空间与身管发生相互作用。对于这种随空间和时间变化的复杂载荷及边界条件在Abaqus中直接加载会比较困难。考虑调用Abaqus子程序,通过Fortran语言编写相应程序的方法定义火药燃气压力和火药燃气温度。在Abaqus中通过DLOAD子程序施加载荷,通过FLIM子程序定义火药燃气温度。对于每一个时间步,Abaqus主程序调用子程序,判断积分点坐标y是否满足:
y≤l(t)
(16)
式中:l(t)为t时刻弹丸行程。如果满足则施加相应的压力和温度,如果不满足,则视为常温常压。
将身管进行网格离散,设置单元为C3D8T(六面体热力耦合8节点)单元。内弹道弹丸运动总时长约为5.83 ms,因此有限元分析时长设为5.83 ms。
3 结果分析
3.1 理想身管单发射击结果分析
图6给出了理想身管在1.071 5 ms、2.013 4 ms、2.736 8 ms、4.282 5 ms、5.055 3 ms、5.830 0 ms时刻的温度分布云图。由图可知,随着弹丸的轴向运动,身管内壁的热交换面积增大。虽然内弹道过程中火药燃气的温度降低,但是一直向身管内壁传递热量,使得身管内壁各处的温度一直增高,直至弹丸出炮口,身管内壁各处温度达到最高。由于药室部与火药燃气接触时间最长,故药室部位温度最高。弹丸出炮口时,最高温度出现在药室部,约929.9 K。由于整个内弹道时间较短,身管内壁获得的热量还来不及传导,因此身管内壁的径向传热并不明显。
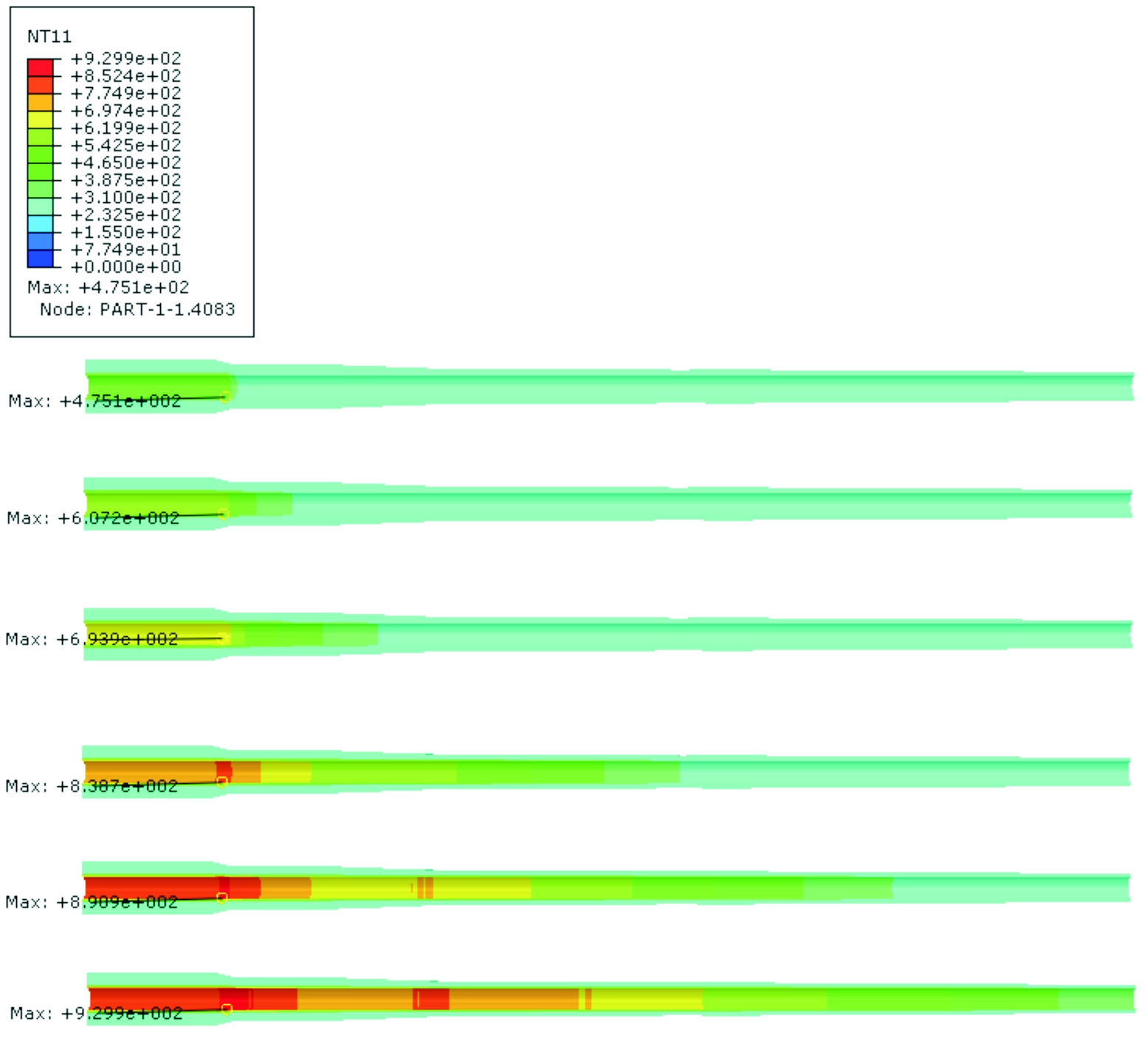
图6 0 mm壁厚差身管不同时刻温度分布云图
图7分别给出了与图6相同时刻的理想身管等效应力分布云图。由图可知,随着弹丸轴向运动,身管内壁受力面积增大。身管最大应力有先增大后减小再增大的趋势,在约2.736 8 ms出现极大值,4.282 5 ms出现极小值,最大应力出现在药室部不同位置。整个内弹道时期内,在2.736 8 ms时刻身管最大应力达到极大值,为870.2 MPa。
事实上,身管的应力是由火药燃气压力和温度产生的热应力共同造成的。内弹道膛压曲线随时间先增后减,因此由火药燃气压力造成的身管应力也有先增后减的趋势。而身管内壁温度一直在升高,因此由热应力造成的身管应力也会一直增加。初始一段时间由于温度较低,火药燃气压力起主要作用,因此身管应力会有类似于火药燃气压力先增后减的趋势,身管应力达到极大值的时间2.736 8 ms与内弹道膛压最大值时间2.6 ms基本一致。之后由于膛压下降,温度继续升高,热应力起主要作用,因此身管应力达到一个极小值之后又会继续增大。
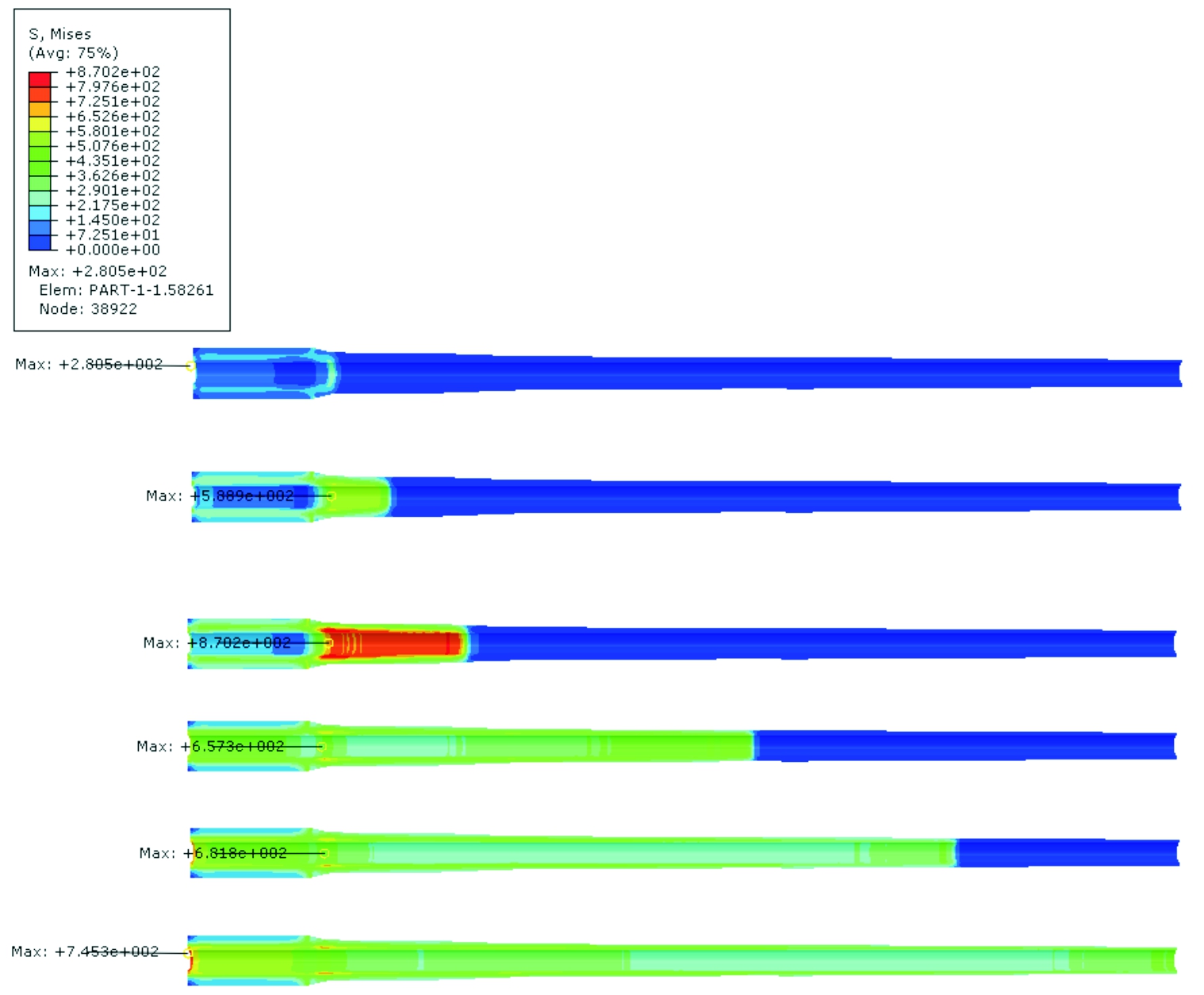
图7 0 mm壁厚差身管不同时刻应力分布云图
图8给出了无壁厚差分布身管的变形云图(以身管各点位移表示),由于无壁厚差分布身管的几何形状及受载荷等均为轴对称,因此其变形只会发生径向膨胀及轴向伸长,不会发生弯曲。

图8 0 mm壁厚差身管变形云图
3.2 不同壁厚差分布身管单发射击结果分析
为了比较不同壁厚差分布对身管弯曲的影响,进一步分析计算了壁厚差分别为0.5 mm、1 mm和2 mm时的结果。当身管存在壁厚差时,其温度和应力变化趋势与理想身管类似,仅温度和应力极大值存在差异。此外,由于壁厚差的存在,引起应力和应变沿周向分布的变化,导致身管发生弯曲变形,除了径向膨胀和轴向伸长,身管还会发生弯曲。
图9分别给出了0.5 mm、1 mm、2 mm壁厚差身管在弹丸出炮口时的温度分布云图,此时身管温度均达到最大。由图可知,随着身管壁厚差增大,身管最大温度值也增大。注意到由于壁厚差的存在,身管内部沿周向出现温度分布不均的现象,这是造成身管弯曲的主要原因之一。
图10~图12分别给出了不同壁厚差身管在应力出现极大值时刻与弹丸出炮口时刻(5.83 ms)的应力分布云图,0.5 mm、1 mm、2 mm壁厚差身管的身管应力极大值分别出现在2.678 7 ms、2.657 9 ms、2.724 9 ms。由图可知,随着壁厚差增大,身管最大应力值有增大趋势,且注意到随着壁厚差的增大,身管最大应力会出现在弹丸出炮口时刻。为了避免火炮射击过程中身管强度失效,应控制身管壁厚差不能过大,一般壁厚差的绝对值与口径有关。
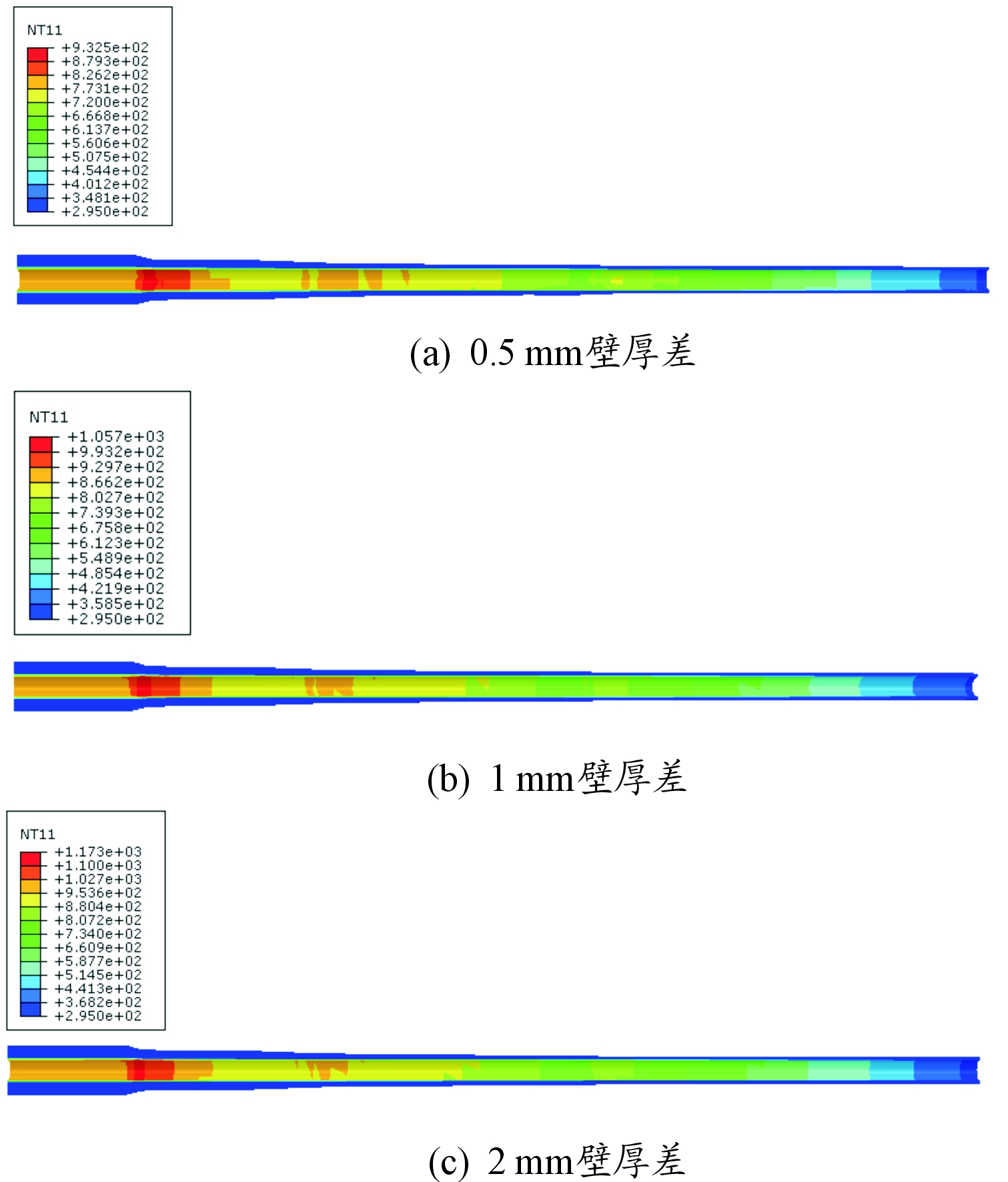
图9 不同壁厚差分布身管温度分布云图(0.58 ms)

图10 0.5 mm壁厚差身管不同时刻应力分布云图
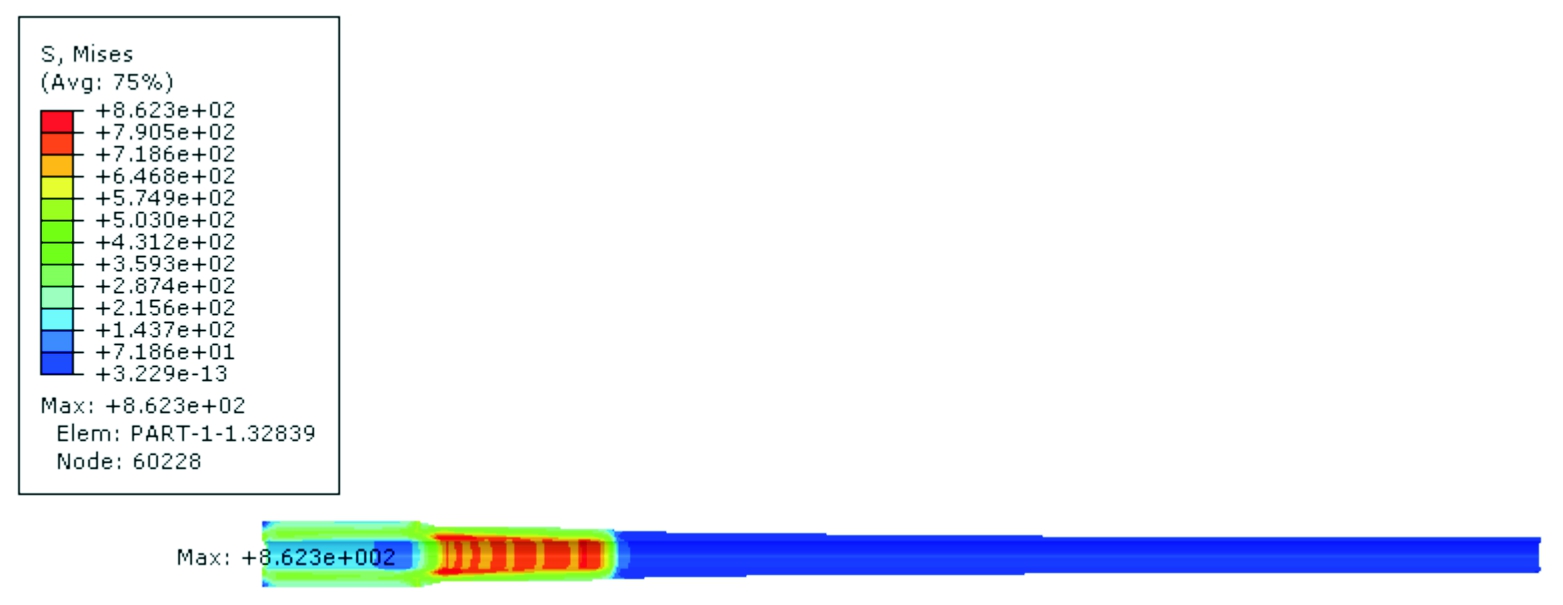
图11 1 mm壁厚差身管不同时刻应力分布云图
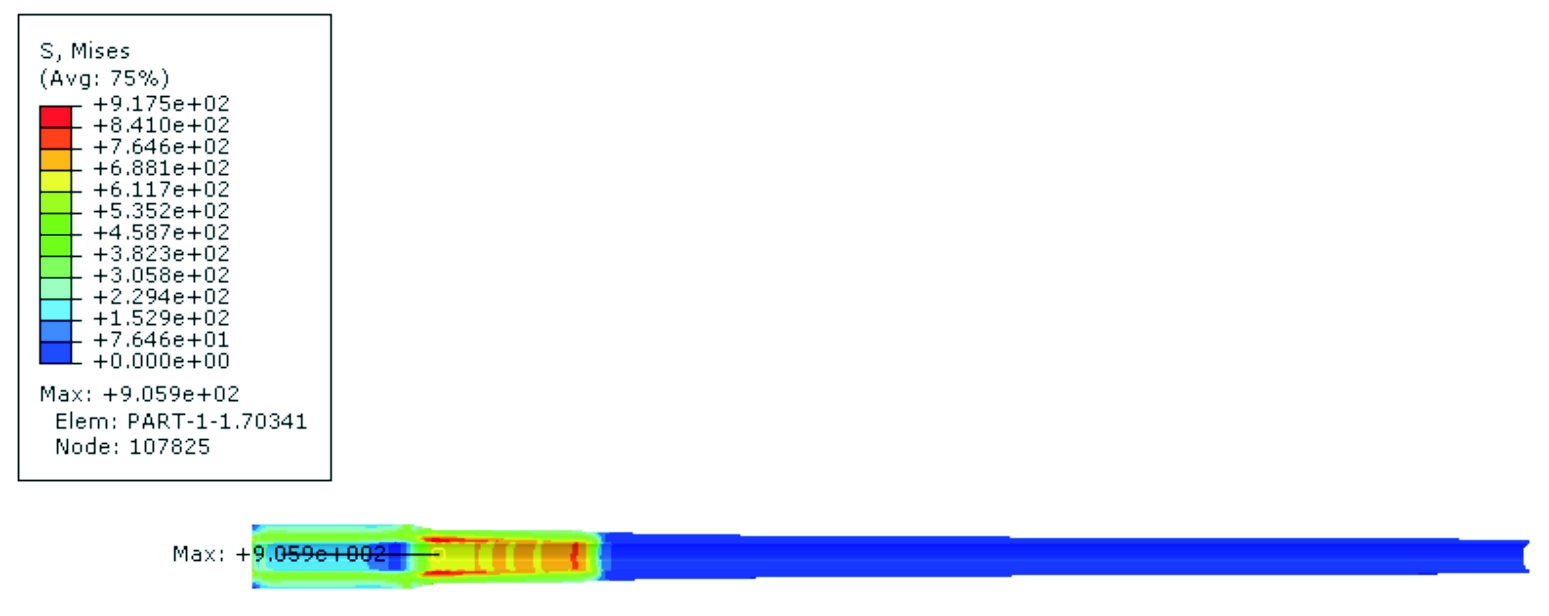
图12 2 mm壁厚差身管不同时刻应力分布云图
存在壁厚差分布的身管在受到火药燃气的高温高压作用时,由于结构不对称,会发生弯曲,这是造成炮口扰动的主要原因之一。图13分别给出了0.5 mm、1 mm、2 mm壁厚差身管在弹丸出炮口时的弯曲变形(放大100倍)示意图,图14为射击过程中不同壁厚差身管在x方向位移曲线。
由图13可知,存在壁厚差分布的身管在火炮发射内弹道过程中会向壁厚较厚一侧弯曲,这是因为身管内壁受到火药燃气热传递时,壁厚较薄的一方温度梯度大,壁厚较厚一方温度梯度小,使得身管向壁厚较厚一方发生弯曲,这与文献[14]中描述的情况一致。
由图14可知,壁厚差越大,身管弯曲越大,对弹丸出炮口状态的影响越大。注意到当身管壁厚差为2mm时,身管在x方向最大位移为0.902 6 mm。当壁厚差减小到1 mm时,身管在x方向最大位移有较明显的减小,为0.563 7 mm。继续减小壁厚差到0.5 mm时,身管在x方向最大位移为0.447 6 mm,无明显减小。但是将壁厚差从1 mm减小到0.5 mm,需要较大的加工成本。综上分析,将身管壁厚差控制在1 mm左右较为合理。

图13 不同壁厚差身管弯曲变形云图
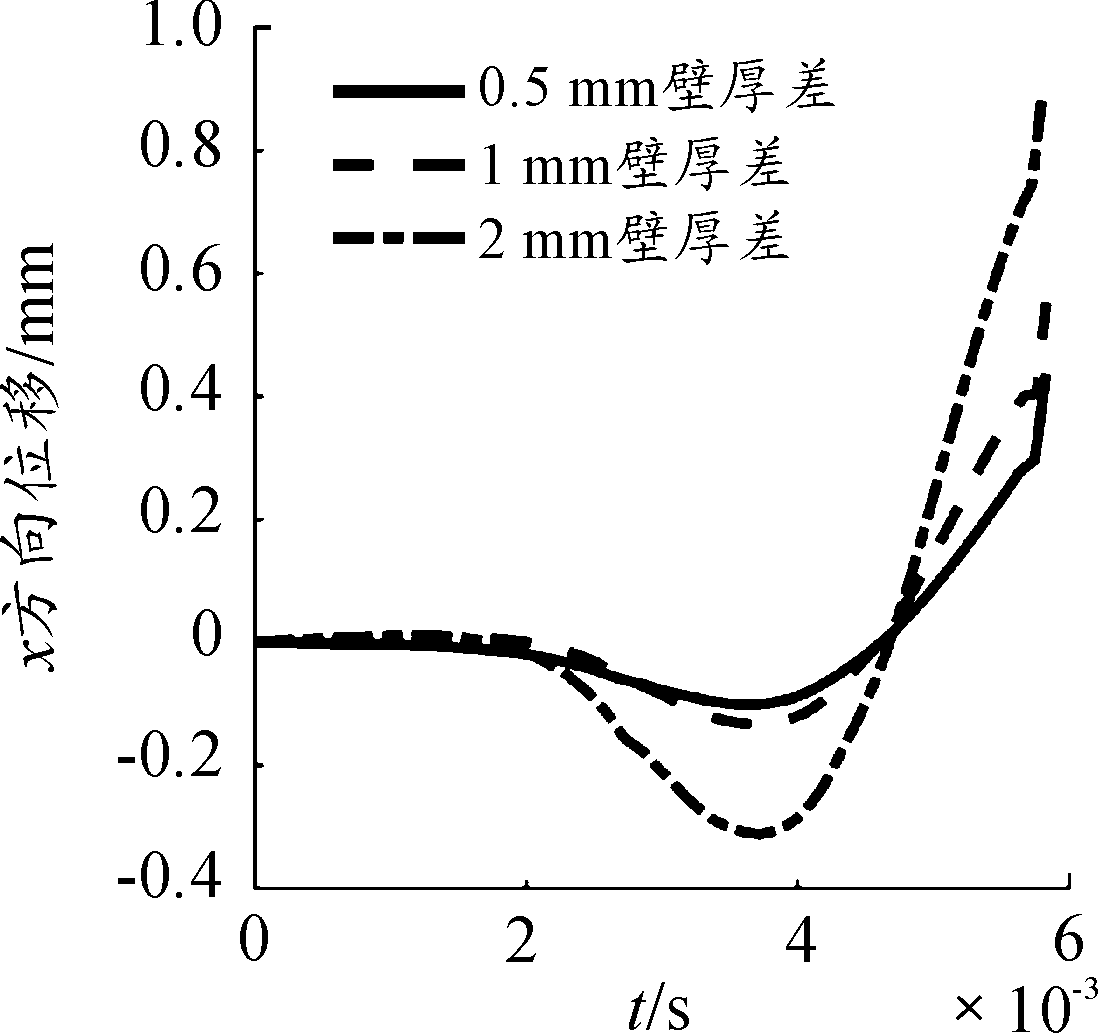
图14 射击过程不同壁厚差身管炮口
x方向位移曲线
4 结论
1) 壁厚差的存在,会使射击过程中身管内部应力和温度分布发生改变,随着壁厚差的增大,射击过程中应力和温度的最大值均会增大,应防止壁厚差过大导致射击过程中身管强度失效;
2) 由于身管内壁受到火药燃气高温时,壁厚较薄一方温度梯度大于壁厚较厚一方,因此存在壁厚差分布的身管在射击过程中最终会向壁厚较厚一方弯曲,且随着壁厚差的增大弯曲越明显。以本文研究的火炮对象为例,为了尽可能减小身管弯曲从而减小炮口扰动,同时控制加工成本要求,应将壁厚差控制在1 mm左右。
[1] 徐春广,陈磊,周世圆,等.火炮身管壁厚差超声测量中的误差源分析[J].传感器技术,2005(09):35-36,42.
[2] 谢杰涛,马威,吴娟,等.火炮身管指向测试方法研究[J].火力与指挥控制,2018,43(12):170-175.
[3] 张荔萍,任绍卿,张建国.线膛火炮身管壁厚差测量的不确定度评定[J].内蒙古科技与经济,2017(23):100,102.
[4] 赵天涛.身管内多物理场耦合分析[D].兰州:兰州理工大学,2016.
[5] 武锋,郑祖华,吴圣川,等.大口径火炮多发连射炮管热力耦合分析[J].中国机械工程,2012,23(09):1056-1059.
[6] 陈龙淼,钱林方,徐亚栋.纤维增强复合材料身管瞬态热弹性耦合分析[J].玻璃钢/复合材料,2008(06):11-16.
[7] 姚建军,徐诚,郭凯.速射武器身管的热-应力耦合场分析[J].火炮发射与控制学报,2001(02):36-39.
[8] SENTÜRK A,ISLK H,EVCI C.Thermo-mechanically coupled thermal and stress analysis of interior ballistics problem[J].International Journal of Thermal Sciences,2016(104):39-53.
[9] 李强,谭庆.身管内膛镀层热压耦合分析研究[J].火炮发射与控制学报,2017,38(04):6-11.
[10] 徐亚栋,钱林方.复合材料身管热-结构耦合分析与优化[J].弹道学报,2006(02):31-35.
[11] CHUNG D Y,SHIN N,OH M,et al.Prediction of erosion from heat transfer measurements of 40 mm gun tubes[J].Wear,2007,263(1-6),246-250.
[12] 罗来科,宣益民,韩玉阁.坦克炮管温度场的有限元计算[J].兵工学报,2005(01):6-9.
[13] 钱林方.火炮弹道学[M].北京:北京理工大学出版社,2016.157-159.
[14] 拉尔曼.炮身构造与设计[M].王天槐,等译.北京:国防工业出版社,1982:188-242.