传统的筒弹装填是利用吊机及吊索在操作人员的辅助下完成,此方法费时费力,影响备战效率。在改进过程中引入自动装填的概念。在已知障碍物的空间信息后,对装填车上起始位置及发射车上目标装填位置进行路径规划,得出一条最优的路径,供吊机和吊具执行筒弹装填操作。近年来,路径规划逐渐成为国内外智能机器研究中的一项关键内容[1]。机器根据已知的局部环境信息,在不碰到障碍物的要求下,规划出一条从起点到目标点并满足特定要求的最优或次最优路径,以供机器执行下一步操作。
目前解决路径规划的方法很多,有人工势场法[2]、遗传算法[3]、模糊算法[4]、神经网络算法[5]、蚁群算法[6]等。其中人工势场法因其原理简单、规划路径时间短、效率高等特点,被广泛应用于智能机器的各种路径规划中。但同时,传统的人工势场法存在陷入局部极小值点导致目标点不可达、靠近障碍物时出现抖动等问题。针对这些问题,许多研究者提出了有效的改进方法。彭艳等[7]利用切点法对人工势场法进行优化,以切点为施力点进行路径规划,解决了震荡和目标点不可达问题;张鹏彬等[8]设置中间目标点,有效地使机器人脱离局部极小值点;韩伟等[9]借助专家经验进行模糊决策[10],对机器合力的大小和方向做出调整,使得机器人准确地到达目标点;师五喜等[11]提出了双层递阶模糊系统的方法,一阶系统调整斥力增益系数,二阶系统对合力的信息进行改变,有效地避免抖动并达到优化路径的目的;梁献霞等[12]提出设置虚拟障碍物的方法,改变机器人的运动方向,从而顺利到达目标点;邓青等[13]提出一种混合路径规划的方法,使得装甲车能够在虚拟战场环境里根据地形信息选择机动路线,实现良好的路径规划。
现有研究中,大多都是针对移动机器人、车辆、机械臂和无人机进行路径规划,而筒弹自动装填条件下的路径规划鲜有研究。尤其是在考虑三维障碍物模型时,实际情况中车上障碍物区域多为矩形,但大多数研究都只将障碍物简化成球体,并未考虑障碍物的边角等矩形区域。此外在优化增益系数时,多数研究者都只单独对斥力增益系数进行优化,并未同时考虑引力增益系数和斥力增益系数对三维路径的影响。对此,本文以某筒弹自动装填车和发射车为研究对象,建立装填车和发射车上的矩形障碍物模型。在改进势场函数的基础上,利用最优化方法同时对引力增益系数和斥力增益系数进行优化,以实现避开局部极小值点和优化路径的目的。文中所提到的最优路径即为长度最短的路径。
1 人工势场法
1.1 传统人工势场法
1986年,Khatib[14]首次提出人工势场法,其基本原理是把运动体在某环境中的运动看作是在虚拟势场中受到势场力引导下的运动。虚拟势场包含目标点处产生的引力场和障碍物处产生的斥力场,两个力场的合成方向则决定了运动体的运动方向。因此,人工势场可以定义为:
U=Ua+Ur
(1)
式中: Ua为目标点处的引力场;Ur为障碍物处的斥力场,定义两个力场的负梯度分别为引力和斥力。
结合空间动力学和拉格朗日方程,合成的人工势场对运动体的作用力F为:
F=Fa+Fr
(2)
式中: Fa为目标点对运动体的引力; Fr为障碍物对运动体的排斥力。
在二维平面中,运动点在未达到目标点前,目标点对其会持续存在吸引趋势,且该引力与距离成正比。故将引力势场函数定义为:
(3)
式中: g为引力增益系数;X为运动点的当前位置;Xg为目标点的位置;(X-Xg)为当前运动点与目标点之间的距离。对引力势场函数求负梯度得出引力Fa为:
Fa=-▽(Ua)=g(X-Xg)
(4)
障碍物附近斥力场的处理和引力场相似。假设障碍物自身存在一定的影响范围,当运动点与障碍物之间的最短距离大于影响范围时,运动点不受斥力的作用;当最短距离小于或等于影响范围时,运动点受到斥力的作用,且该斥力与最短距离成反比。故将斥力场函数定义为:

(5)
式中: m为斥力增益系数; ρ为运动点到障碍物之间的最短距离; w为障碍物自身的影响范围。对斥力场函数求负梯度得出斥力Fr为:

(6)
运动点在引力和斥力的合力作用下运动时,其受力情况如图1所示。
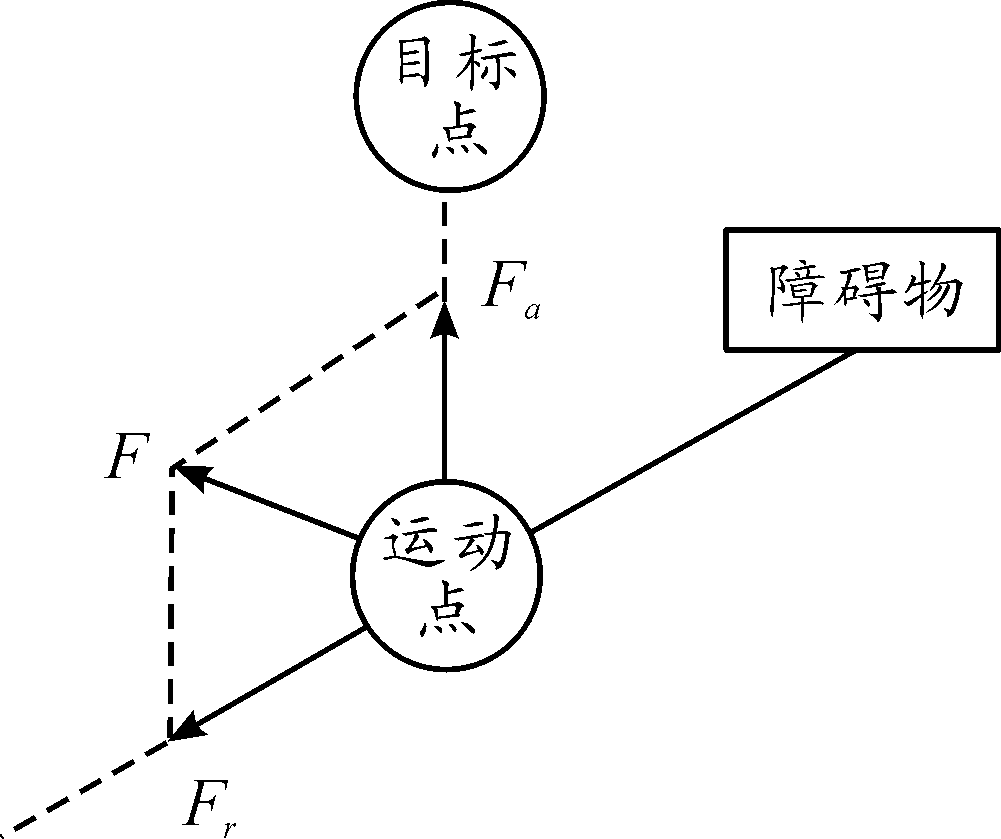
图1 运动点的受力情况
传统的人工势场法主要存在如下两点缺陷:
1) 陷入极小值点。当运动点在运动过程中受到的引力和斥力的大小相等且方向相反时,运动点将误以为已到达目标点,无法确定下一步的运动方向,即陷入极小值点,从而停止运动。
2) 目标点不可达。当目标点在障碍物的影响范围内时,运动点受到的斥力大于引力,从而导致运动点一直在目标点附近徘徊,无法到达目标点。
1.2 改进人工势场法
针对上述人工势场法的缺陷,引入相对距离的概念。即在计算斥力场的同时考虑运动点与目标点间的相对距离,通过改进斥力场函数[15]来解决目标点不可达问题。
当目标点在障碍物的作用范围内时,整个势场的最小点并不是目标点,原因在于运动点在靠近目标点的同时,障碍物的势场也在迅速增大,从而运动点到达不了目标点。若运动点在靠近目标点时,障碍物的势场趋向于零,则目标点将是该势场环境下的最小点。因此在定义斥力场函数时,需要将运动点与目标点间的相对距离考虑在内。修改后的斥力场函数如下:
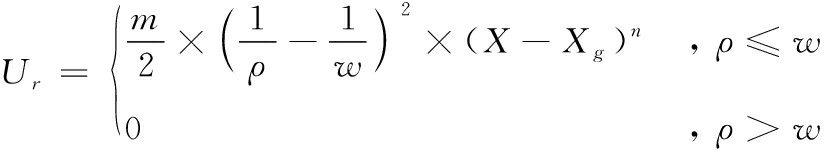
(7)
其中增加了调节项(X-Xg)n,n为大于零的实数。此调节项可确保斥力场在目标点处最小。相应的斥力函数修改为:
![]()
(8)
式中: Fr1和Fr2为Fr的两个分力; Fr1的方向为从障碍物指向运动点; Fr2的方向为从运动点指向目标点,分别表达如下:
(9)
![]()
(10)
2 模型建立
在野外作战环境下实施筒弹自动装填前,发射车和装填车按要求停车到位,如图2所示。经调平后,两车相对空间位置固定,图中所示圆为吊机携带吊具所能到达的吊装范围。在筒弹装填前,需将装填空间内的障碍物区域信息提前录入主控计算机内进行路径解算。发射车和装填车上的障碍物主要有光电装置、雷达、转塔、油机电站等,这些设备作为障碍物所构成的区域大多为矩形区域。但很多研究者仅仅将三维障碍物区域简化扩展成球体进行建模计算。本文综合考虑实际障碍物区域和斥力计算方法,采用矩形障碍物模型对实际筒弹装填进行数值仿真。
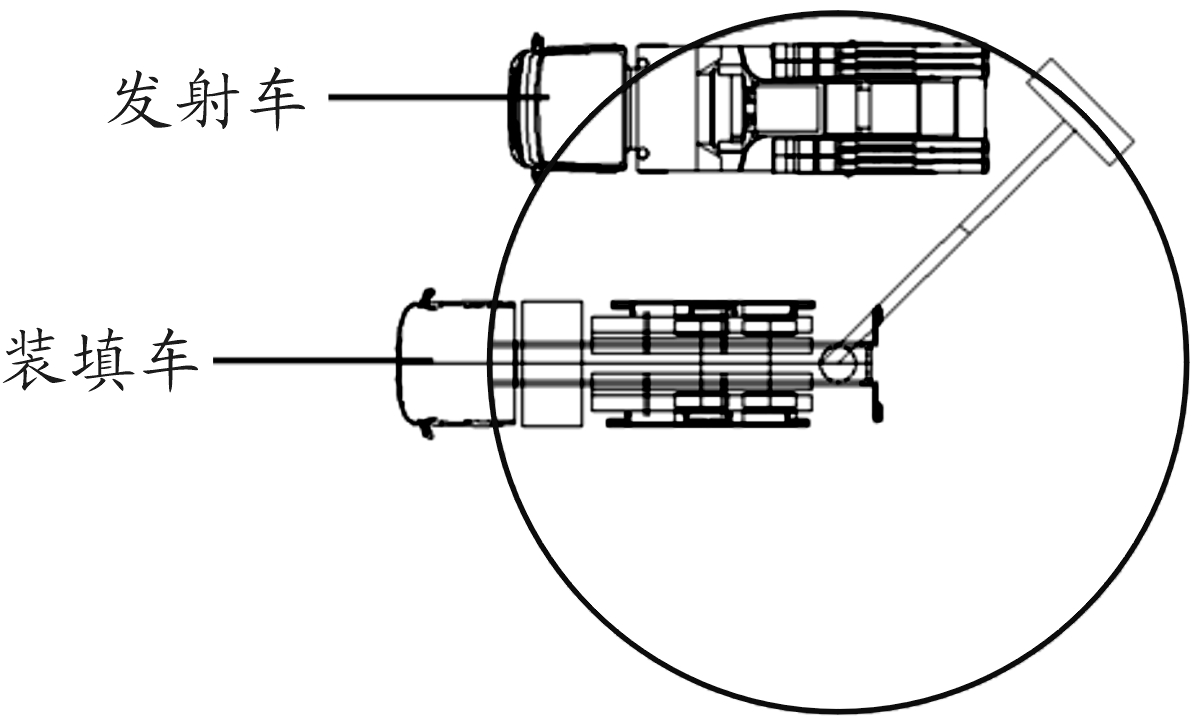
图2 装填车与发射车的相对位置示意图
为了仿真不同障碍物区域的效果,建立矩形障碍物模型如图3所示,球体障碍物模型如图4所示。图3中,黑色部分代表发射车和装填车的车体平面,白色部分代表筒弹联装架。并将每个长方体离散成若干个点,便于后续计算距离ρ。装填车上筒弹联装架起吊的起始点简化为起点(50,30,65),发射车上装填位上方点简化为目标点(242.5,90,73),障碍物的起点分别为(25,40,50)、(25,50,60)、(200,40,50)、(200,50,60),长宽高分别为(50,100,10)、(15,80,5)、(50,100,10)、(15,80,5)。图4中起点与目标点的位置与图3中相同,球体障碍物的中心点为(50,65,50)和(235,65,50),半径为25(高度方向上的包络值)。

图3 矩形障碍物模型
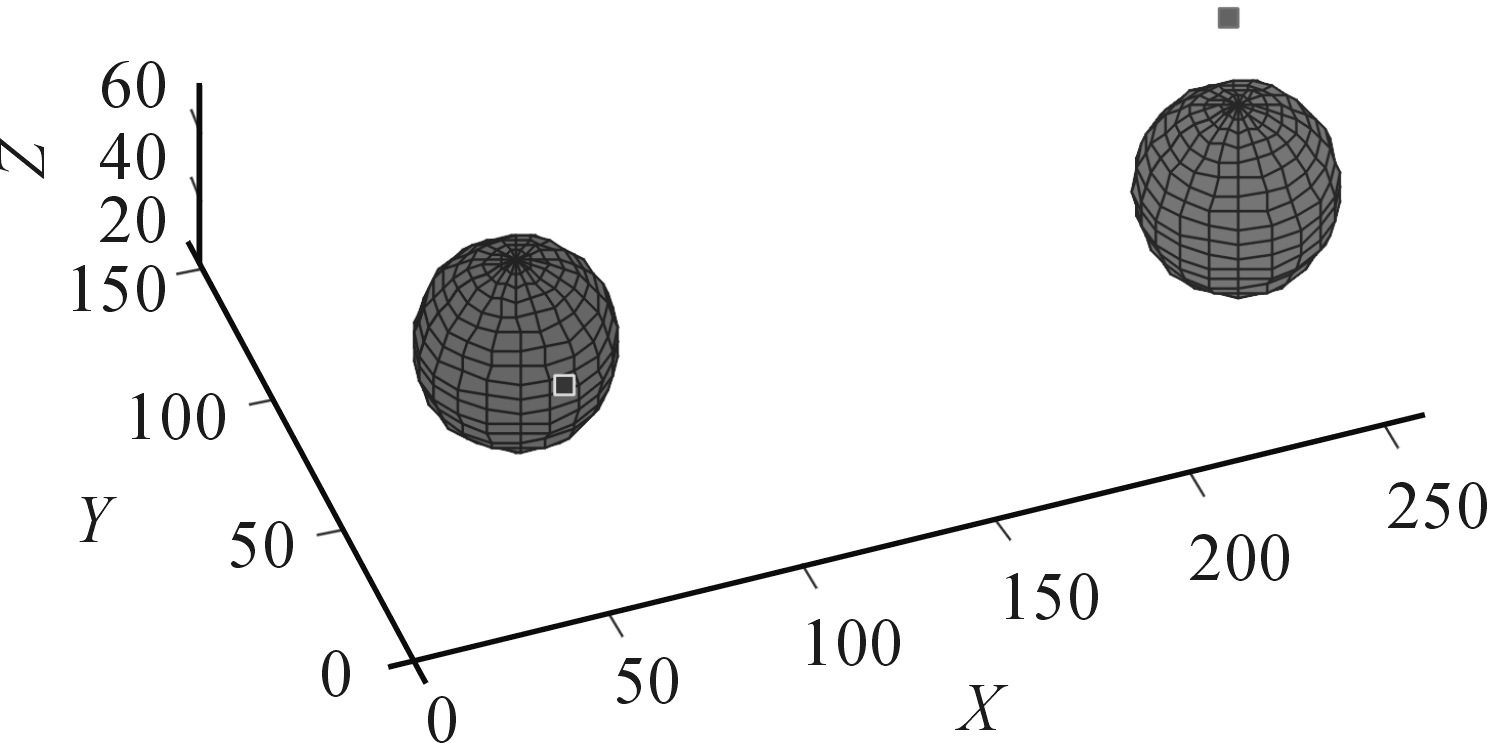
图4 球体障碍物模型
3 仿真计算
运动点的运动计算流程如图5所示。运动点从起点出发,按照运动点指向目标点的方向运动;每走一步,计算当前运动点与矩形障碍物中每个点的距离ρ,并比较该距离与障碍物的影响范围w。若ρ>w,则按运动点原来的运动方向继续运动;若ρ≤w,则计算虚拟力在每个方向上分力的大小,从而更新上一步运动点的坐标,改变方向继续运动。
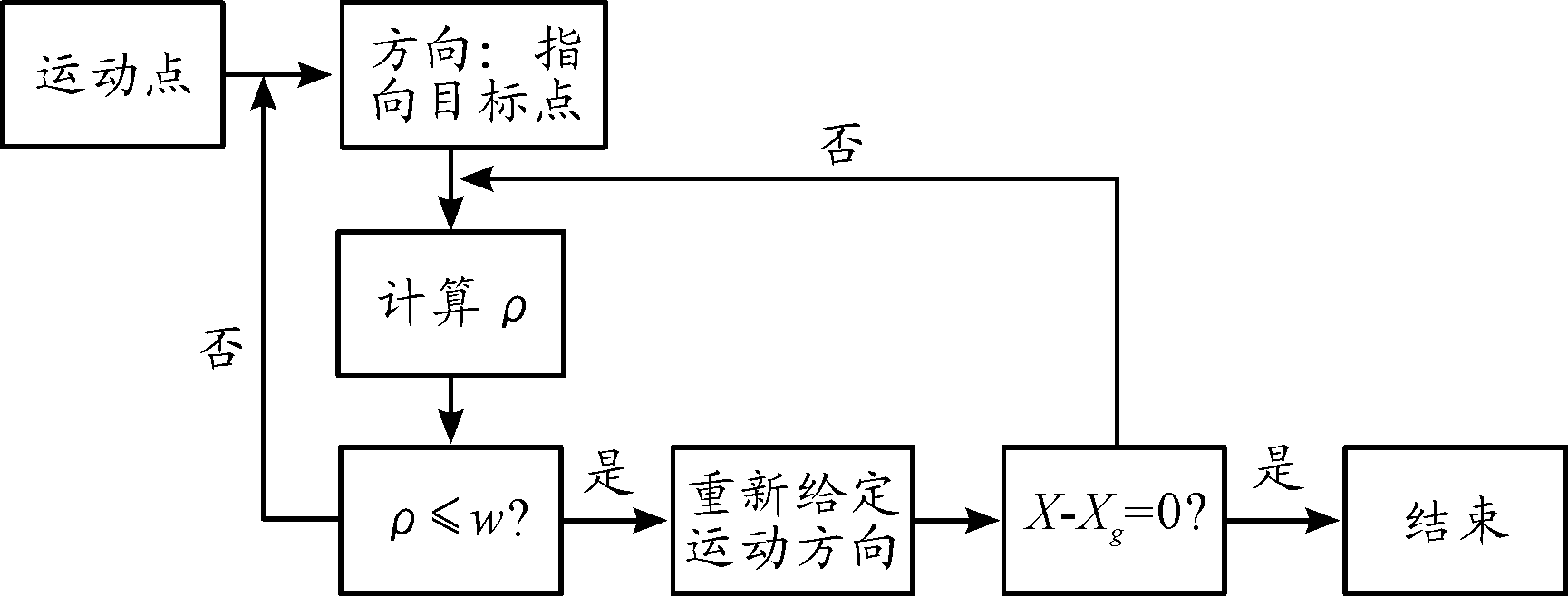
图5 运动点的计算流程框图
3.1 球体与矩形障碍物对比
首先利用传统的人工势场法分别对球体和矩形障碍物进行仿真分析,式(2)为人工势场对运动体的作用力。取引力增益系数g=5,斥力增益系数m=1,障碍物影响范围w=1。仿真结果如图6所示。
图6(a)中,黑线表示运动点在球体障碍物区域下规划的路径,仿真得出该路径的长度L为201.8;图6(b)中,黑线表示运动点在矩形障碍物区域下规划的路径,运动点运动到(194,74,71)该位置时,陷入局部极小值点并停止运动,无法到达目标点。
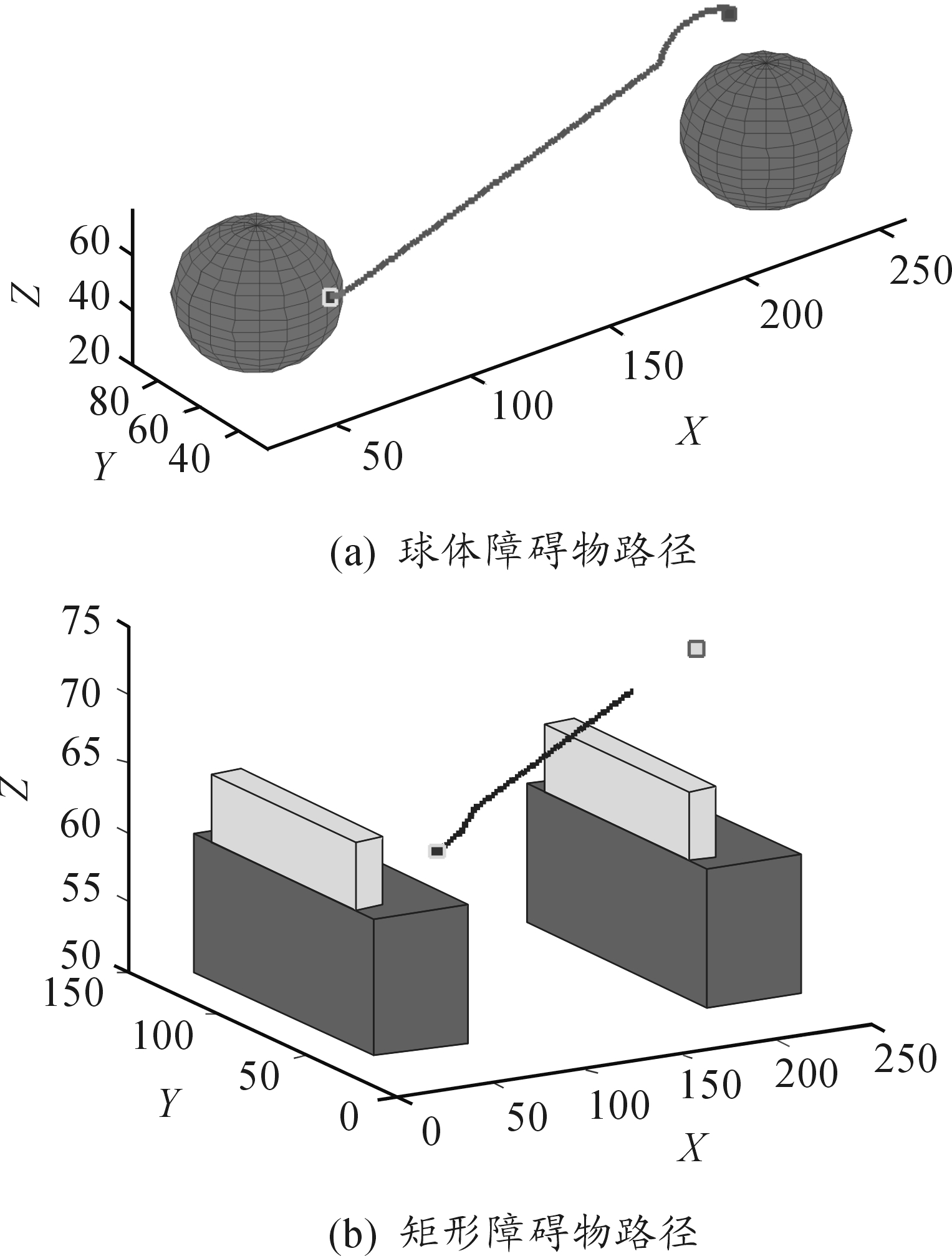
图6 传统人工势场法规划的路径
3.2 传统与改进人工势场法对比
针对传统人工势场法下出现的如图6(b)所示极小值点情况,采用公式(7)对斥力场函数进行改进。取n=2,在其余参数不变的情况下进行仿真,结果如图7所示。改进后运动点能够在该特殊位置下,改变极小值点处的运动方向,顺利绕过障碍物到达目标点。仿真得出该路径的长度L为197.6。
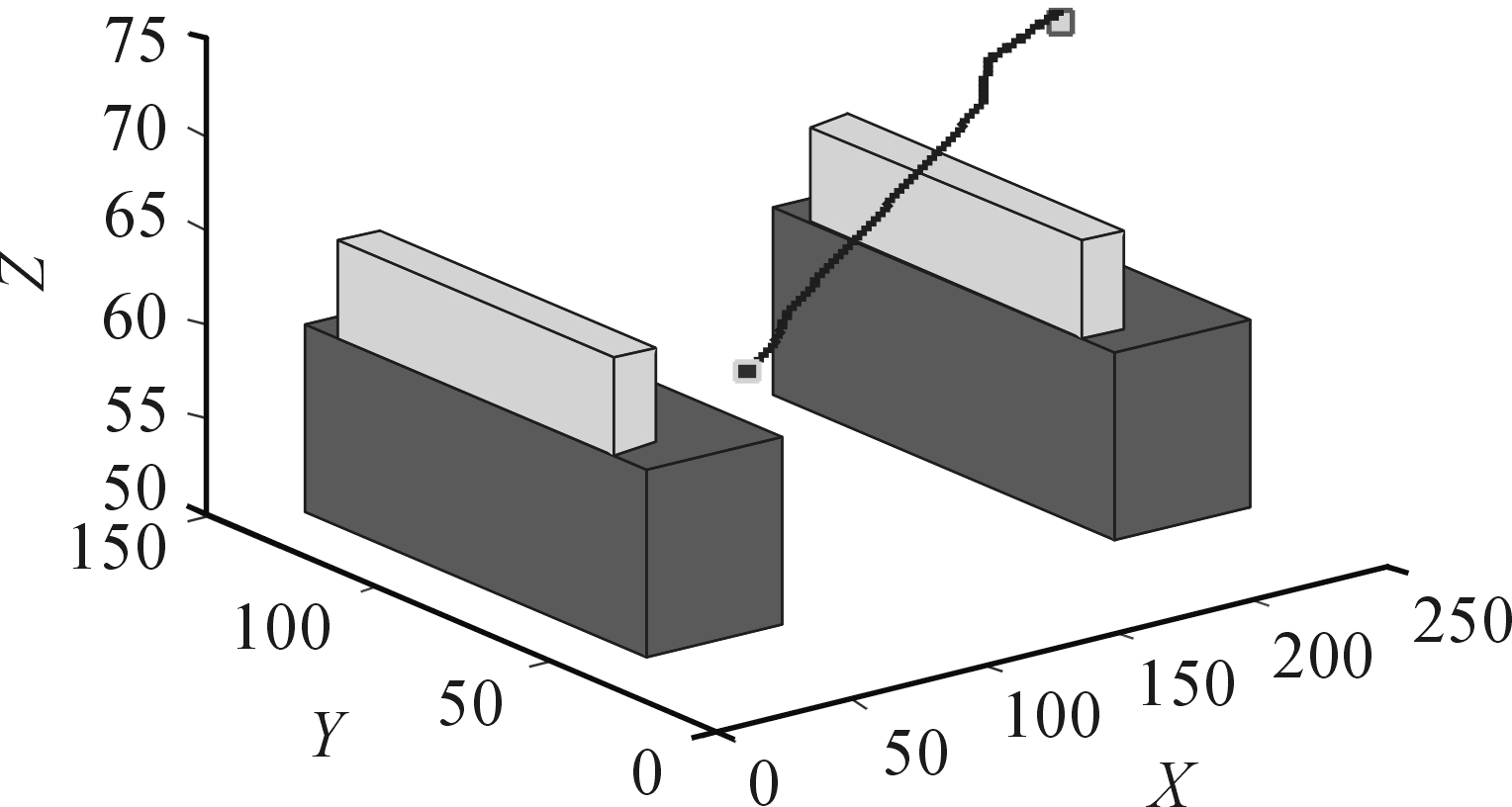
图7 改进人工势场法规划的路径
对比图6和图7可知:如图6(a),采用传统的人工势场法,障碍物为球体时,规划路径的长度L=201.8;如图6(b),障碍物为矩形时,传统人工势场法存在陷入局部极小值点、目标不可达问题,无法进行完整的路径规划;而在图7中,改进后的人工势场法使得矩形障碍物解决了原有问题,并成功规划出一条优于球体障碍物的更短路径L=197.6。因此,矩形障碍物模型是合理的。矩形障碍物模型比球体障碍物模型规划的路径更优,且矩形障碍物模型更接近真实场景。
3.3 增益系数的影响
采用改进后的人工势场法,在矩形障碍物模型的基础上,考虑增益系数的影响。整个势场函数中存在两个增益系数,为引力增益系数g和斥力增益系数m,它们分别对引力和斥力进行调节。研究中发现,增益系数的变化影响特定环境下的最优路径。若要单独对某一增益系数进行优化时,需在给定区间内利用最优化方法进行求解,从而得到最优路径;若要同时对两个增益系数进行优化,则需给定两个增益系数分别对应的区间,并对应相应的路径长度;再结合最优化方法,对区间内的增益系数进行调整,并寻找其中的最优解,以使得路径最优,从而实现路径优化。
最优化方法[16]是求一个多元函数在某个给定集合上的极值,可用如下数学模型描述:
min L=f(m,g)
s.t. m∈K1, g∈K2
(11)
其中:K1、K2为给定的集合; L=f(m,g)为定义在集合K1、K2上的路径实值函数;m、g为两增益系数。
分析不同的引力增益系数和斥力增益系数对路径的影响,采用改进后的势场函数进行仿真,路径的长度为L,结果如图8、图9所示。
由仿真结果可以看出,在斥力增益系数及其他参数相同的情况下,改变引力增益系数,路径的长度会随之改变;同样,在引力增益系数相同的情况下,改变斥力增益系数,路径也会随之变化。因此以引力增益系数和斥力增益系数为自变量,以路径长度为目标,构建多元函数,并利用最优化函数即式(11)对其进行优化,所得结果如图10所示。
由图10可知,两增益系数共同影响路径长度L。当引力增益系数g在(1,5)、斥力增益系数m在(5,15)组成的平面内时,路径的长度L变化幅度非常小。因此在取增益系数时,只要两增益系数落在上述区间内,都能得到最优路径,其取值L=195。
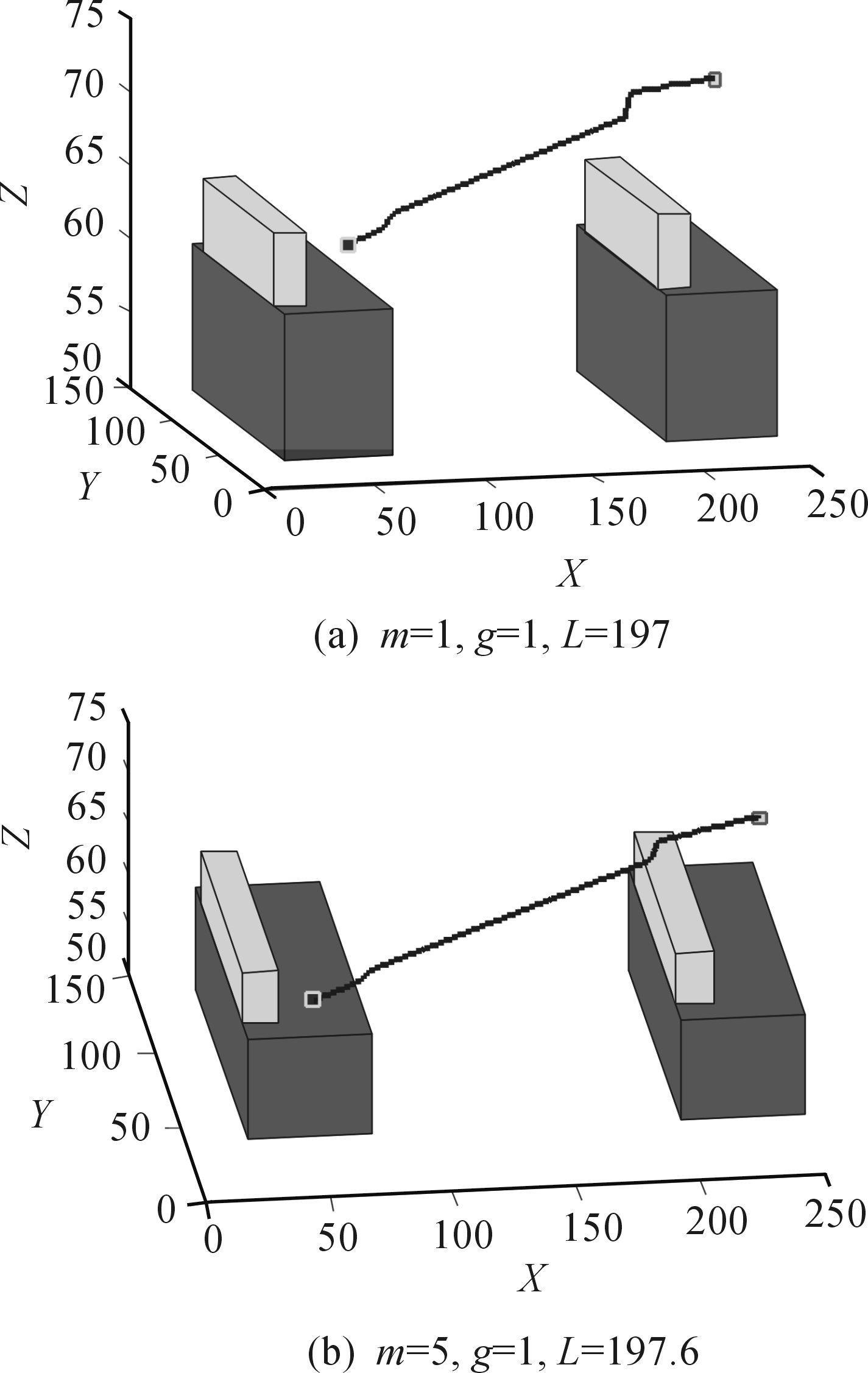
图8 相同斥力增益系数,不同引力增益系数下的路径
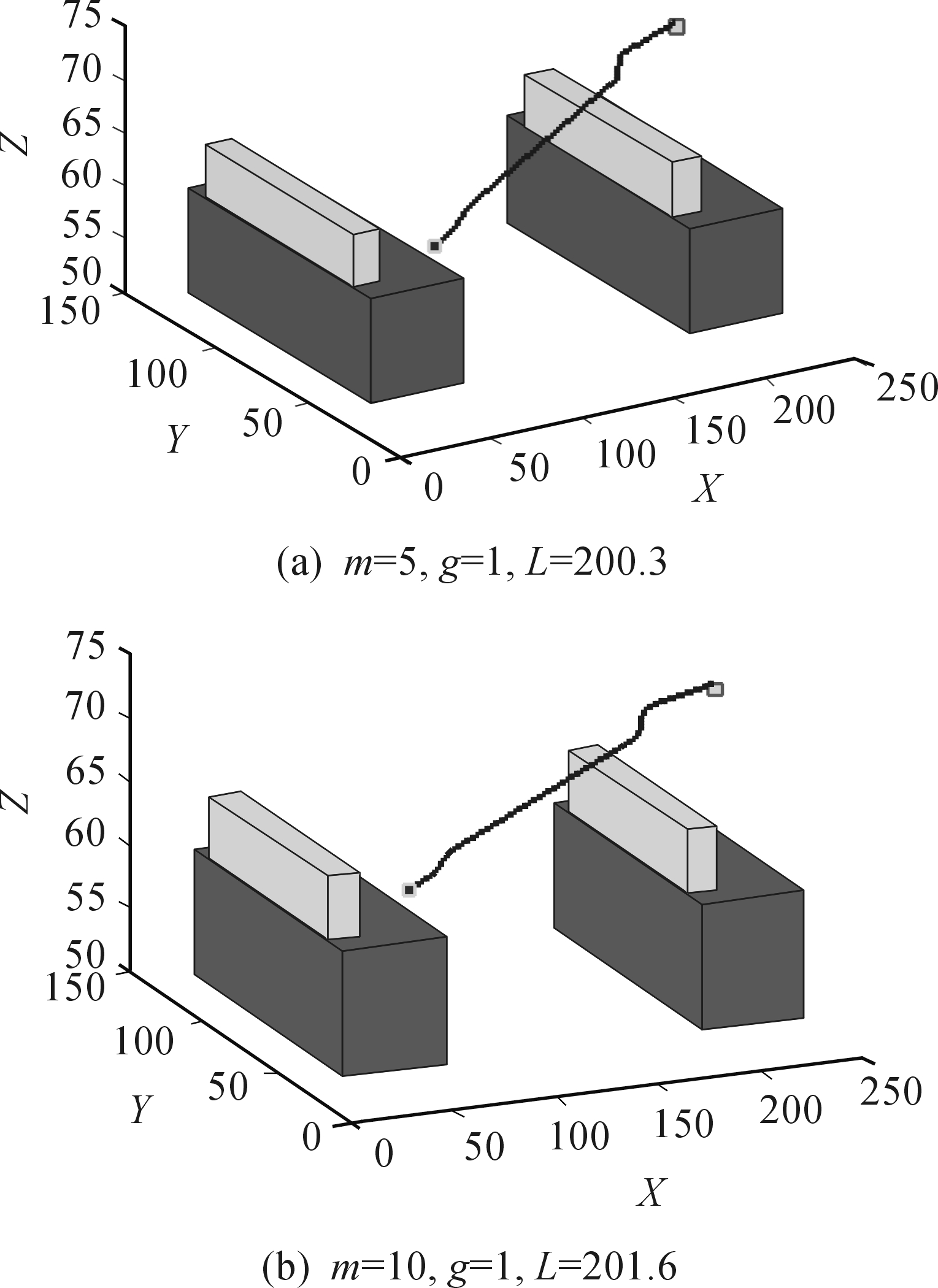
图9 相同引力增益系数,不同斥力增益系数下的路径
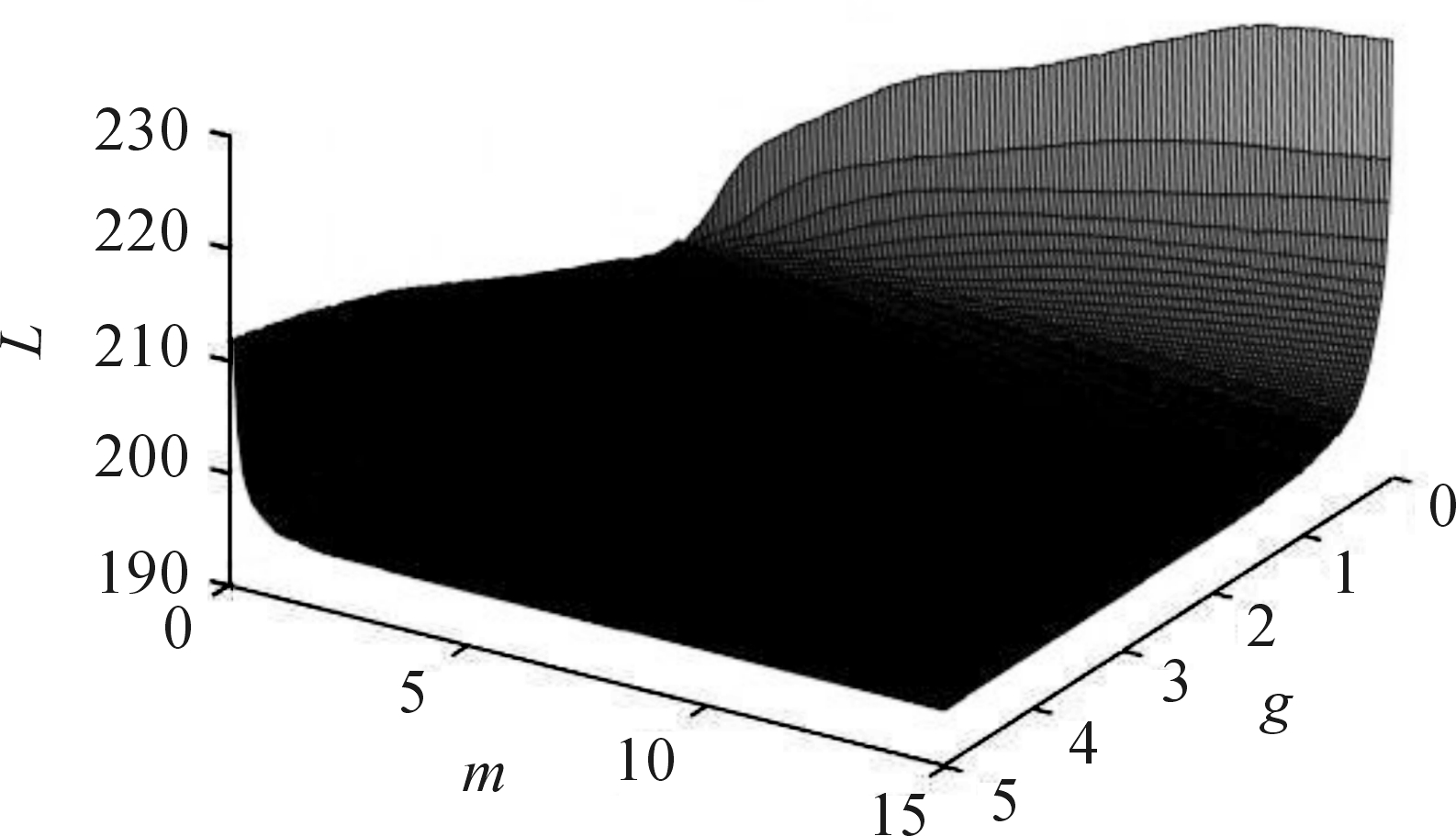
图10 优化后的路径长度随增益系数的变化
4 结论
1) 较之球体障碍物模型,矩形障碍物模型能更真实地模拟车上障碍物的实际区域,并且矩形障碍物下的路径规划更优。
2) 对斥力场函数进行改进后的人工势场法,能够使运动点成功脱离局部极小值点到达目标点。
3) 同时对引力增益系数和斥力增益系数进行优化时,给定系数一定范围内,能够寻找到特定增益系数,使得该增益系数下的路径为最优。
[1] 杨兴.室内自主导航移动机器人路径规划研究[D].太原:中北大学,2016.
[2] 朱毅,张涛,宋靖雁.非完整移动机器人的人工势场法路径规划[J].控制理论与应用,2010,27(2):152-158.
[3] 李志海,付宜利.基于遗传算法的仿生双足爬壁机器人越障运动规划[J].机器人,2012,34(6):751-757.
[4] WEN S H,ZHENG W,ZHU J H,et al.Elman Fuzzy Adaptive Control for Obstacle Avoidance of Mobile Robots Using Hybrid Force/Position Incorporation[J].IEEE Transaction on Systems,Man and Cybernetics(C) (S1083-4427),2012,42(4):603-608.
[5] SINGH M K,PARHI D R.Path optimization of a mobile robot using an artificial neural network controller[J].International Journal of Systems Science(S2077-7721),2011,42(1):107-120.
[6] 邓高峰,张雪萍,刘彦萍.一种障碍环境下机器人路径规划的蚁群粒子算法[J].控制理论与应用,2009,26(8):879-883.
[7] 彭艳,国文青,刘梅,等.基于切点优化人工势场法的三维避障规划[J].系统仿真学报,2014,26(8):1758-1762.
[8] 张鹏彬,曾钰培.改进人工势场法的移动机器人路径规划[J].技术应用,2018(3):27-29.
[9] 韩伟,孙凯彪.基于模糊人工势场法的智能全向车路径规划[J].计算机工程与应用,2018,54(6):105-109.
[10] MASMOUDI M S,KRICHEN N,MASMOUDI M,et al.Fuzzy Logic Controllers Design for Omnidirectionnal Mobile Robot Navigation[J].Applied Soft Computing,2016:S1568494616304598.
[11] 师五喜,李福荣,常绍平,等.基于递阶模糊系统的人工势场法机器人路径规划[J].天津工业大学学报,2014,33(6):45-50.
[12] 梁献霞,刘朝英,宋雪玲,等.改进人工势场法的移动机器人路径规划研究[J].计算机仿真,2018,35(4):291-295.
[13] 邓青,薛青,陈琳,等.一种混合路径规划方法在装甲车CGF中的应用[J].兵器装备工程学报,2018,39(7):120-122,150.
[14] 王肖青,王奇志.传统人工势场法的改进[J].计算机技术与发展,2006,16(4):96-98.
[15] 王会丽,傅卫平,方宗德,等.基于改进的势场函数的移动机器人路径规划[J].机床与液压,2002,6:67-68.
[16] 马昌凤.最优化方法及其Matlab程序设计[M].北京:科学出版社,2010.