大口径舰炮供弹系统主要完成运弹、扬弹、摆弹、转弹、输弹和退弹六个动作,摆弹机作为自动供弹系统的重要组成部分,将扬弹末端垂直摆放的弹药快速、准确地摆送至转弹机工作位置。进行摆弹机运动特性研究与误差分析对改进自动机设计,提高机构可靠性对提升装备性能有着重要意义。
国内已有学者对满足现代化海战要求的含摆弹机构的舰炮自动供弹系统展开了研究[1-12]。在常见的摆弹机构研究中,普遍基于有限元法和虚拟样机技术。文献[6-7]采用笛卡尔坐标分量和弧坐标分量来共同描述柔性摆弹臂的弹性变形及运动关系。文献[9]中考虑摆弹臂的柔性变形及参数的随机分布,以有限元模型为基础,综合运用支持向量回归机与蒙特卡洛法分析动作可靠性。文献[10]中建立了考虑弹药质量、质心位置等为随即变量的摆弹机构数学模型。唐文献[13]应用ANSYS软件的FE-SAFE疲劳分析模块,探讨了零件表面粗糙度对中腹摆弹臂的疲劳寿命及安全系数的影响。李渊明[14]运用含间隙机构的分析方法,对摆弹机构进行了运动学和动力学特性分析,并以此对机构的关键部件进行了静力分析和结构改进。
在以上研究的基础上,本研究基于ADAMS虚拟样机技术,研究了转动副不同间隙大小、摆臂柔性、摆弹过程中弹体滑移以及弹药质量偏差对摆弹运动特性的影响并分析其误差的成因。
1 摆弹机简化模型与工作机理
摆弹机构主要由动力原件、齿轮齿条组件、摆弹臂3部分组成(如图1所示),其中齿轮轴受支承转动约束。摆弹机构在竖直位置时抱弹装置抱住扬弹末端的弹药,动力源对齿条施加拉力,齿条开始向后运动,啮合齿轮逆时针转动并带动摆弹臂摆动,使得摆弹臂上的弹药运动到转弹机交接位置,摆弹过程如图2所示。
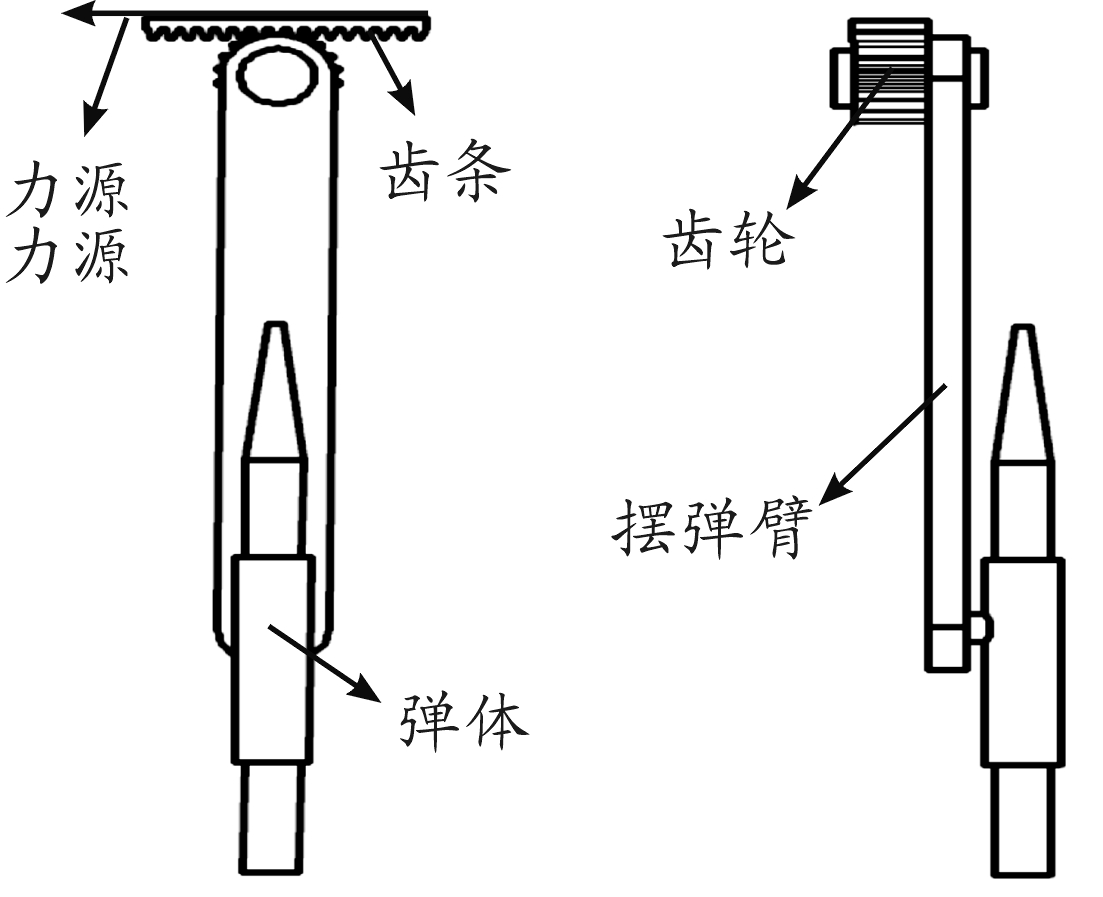
图1 摆弹机结构
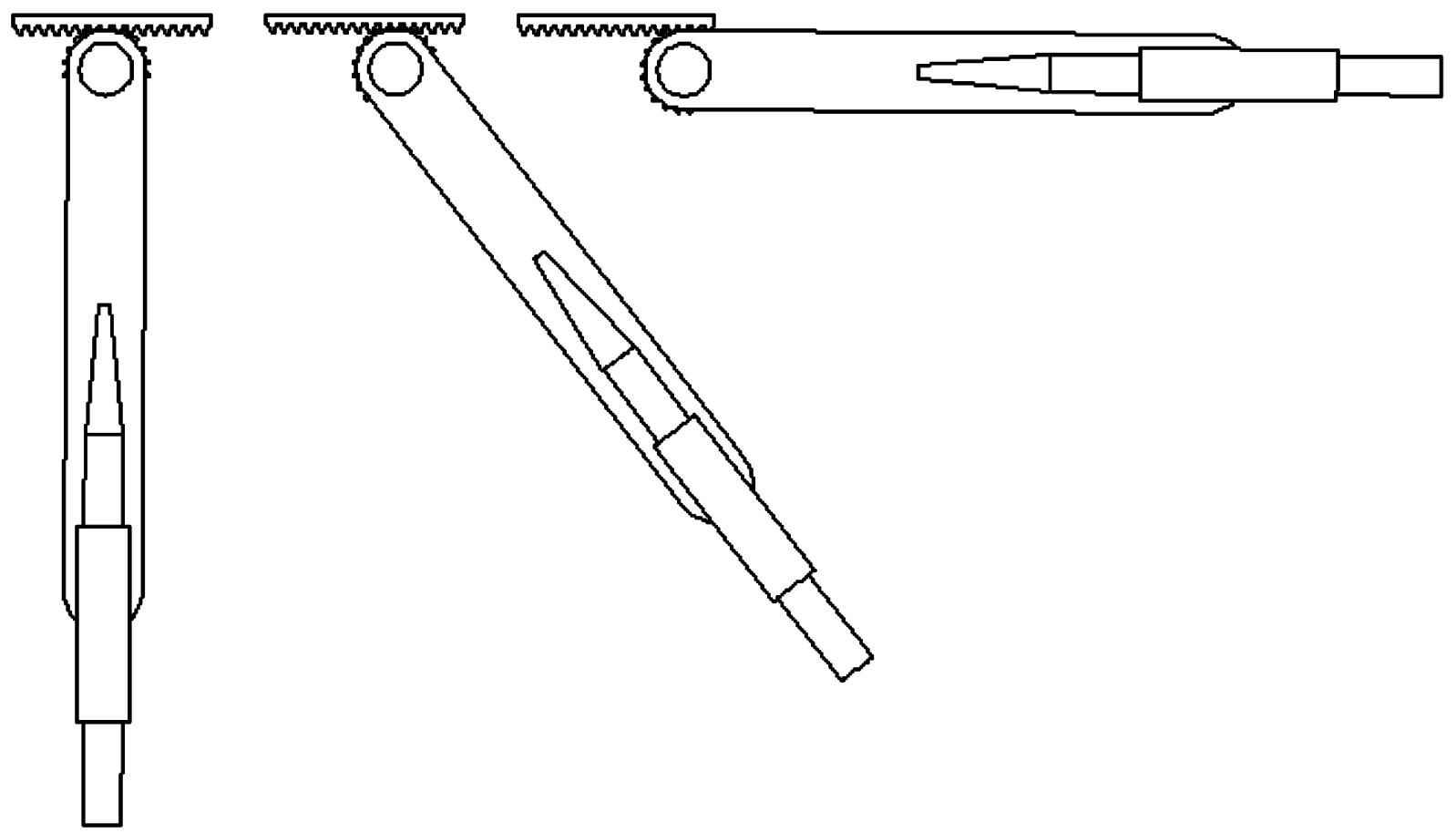
图2 摆弹运动过程
2 摆弹机构的力学模型
摆弹机摆动过程的受力模型如图3所示,其中O、Ob、Od分别是齿轮转轴轴心、摆臂与抱弹装置的质心、弹体质心;Gb、Gd表示质心Ob、Od处的重力;Lb、Ld是质心Ob、Od到齿轮轴心O的垂直距离;θ表示摆弹臂的转角;rp是齿轮的分度圆半径;F是驱动力,与转角θ关联。
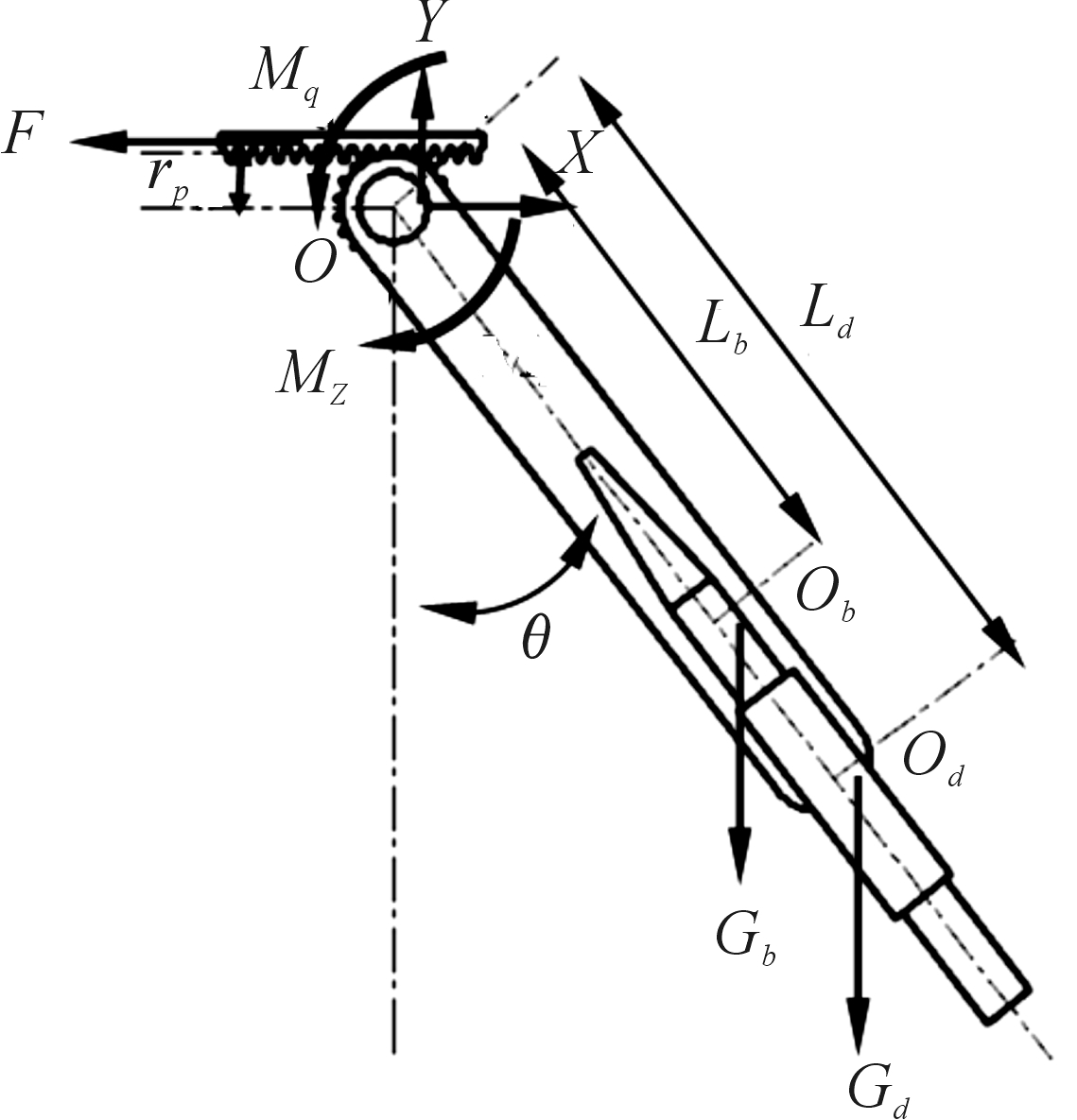
图3 摆弹机受力模型
弹体在摆弹运动过程中受力如图4所示,其中FN是重力作用下抱弹装置给的支撑力;Fj是抱弹装置给弹体的紧箍力。
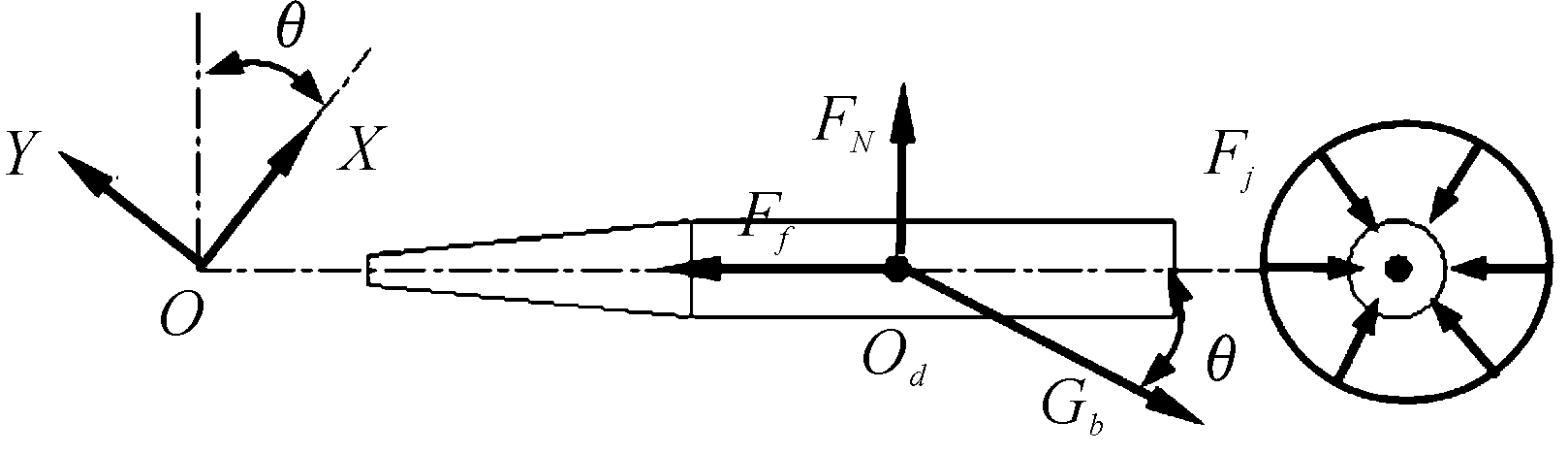
图4 弹体受力示意图
3 摆弹机构摆弹运动仿真分析
3.1 转动副间隙对摆弹运动的影响
两个相对运动构件动配合时普遍存在间隙,间隙的存在会增加系统的自由度,导致机构运动精度降低和恶化运动稳定性。在摆弹机构中齿轮轴与支承的转动副间存在间隙,如图5所示,研究间隙的存在和间隙大小对摆弹运动的影响是研究摆弹机运动的重要内容。
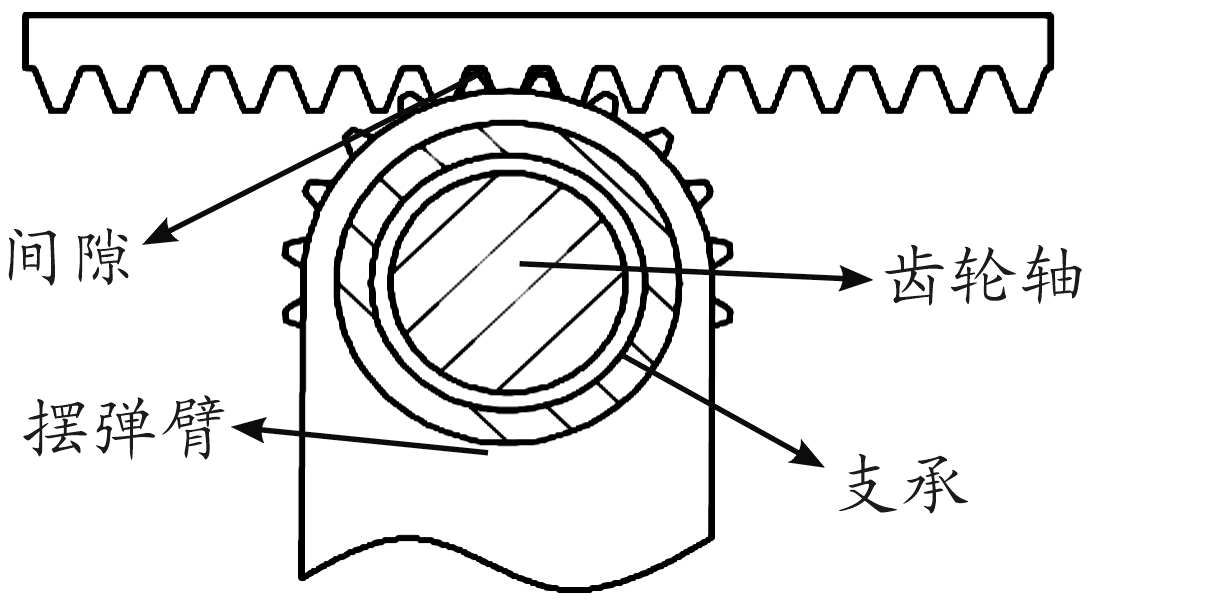
图5 含间隙转动副示意图
在不考虑润滑条件下,分析含间隙转动副的碰撞与摩擦常用的接触力模型[15]是法向非线性滞后阻尼单侧接触力模型与切向Coulomb摩擦力模型[16]。
法相接触力:
(1)
切向摩擦力:
Ft=-μFNsgn(vt)
(2)
式中:K和D分别为等效接触刚度和阻尼系数;n为非线性指数,金属材料通常取1.5; μ为摩擦因数;νt相对切向速度;FN为支撑力。
通过SolidWorks三维建模后将模型导入Adams,对各部件施加相应约束,在不同间隙值δ=0.1 mm、δ=0.3 mm和δ=0.5 mm时分别对齿轮轴与支承间创建接触力,利用Adams和Matlab联合仿真分析得到不同大小间隙存在时的摆弹转角与时间的关系曲线,如图6所示。
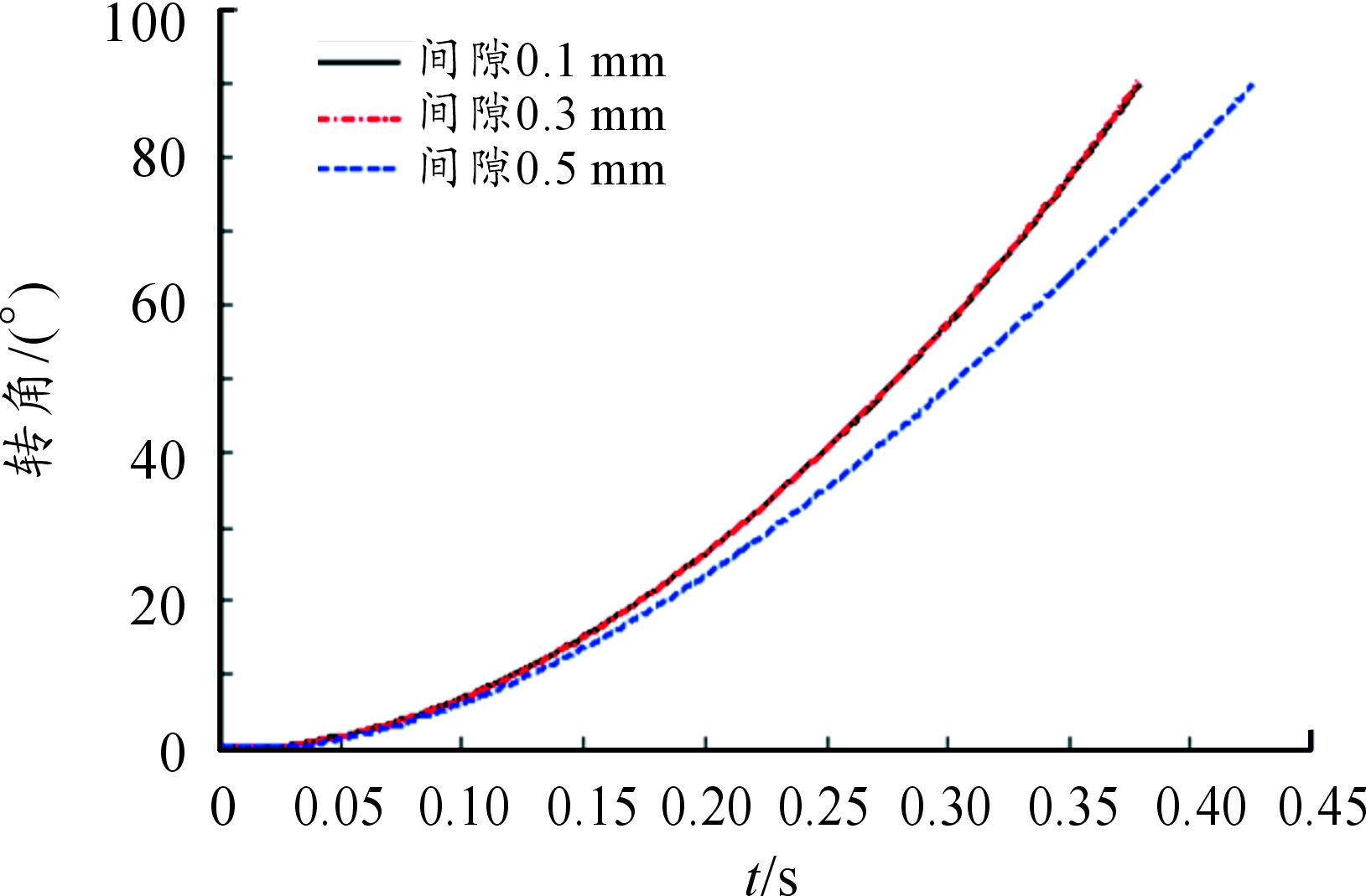
图6 不同间隙时转角与时间的关系曲线
由图6可知,在转动副间隙值为δ=0.1 mm、δ=0.3 mm和δ=0.5 mm时分别对应的摆弹截止时间t为0.379 2 s、0.378 6 s和0.426 3 s,间隙造成摆弹过程产生误差,间隙的大小与控制是减小摆弹误差的方法。
3.2 摆臂柔性对摆弹运动的影响
在摆弹过程中摆弹臂会产生弹性变形,研究摆臂柔性对摆弹运动的影响,有利于提高摆弹动作的可靠性。利用ANSYS对摆弹臂进行柔化处理,如图7所示,生成mnf中性文件,导入Adams建立刚柔耦合模型进行仿真分析,仿真结果如图8所示。

图7 摆弹臂柔化处理示意图
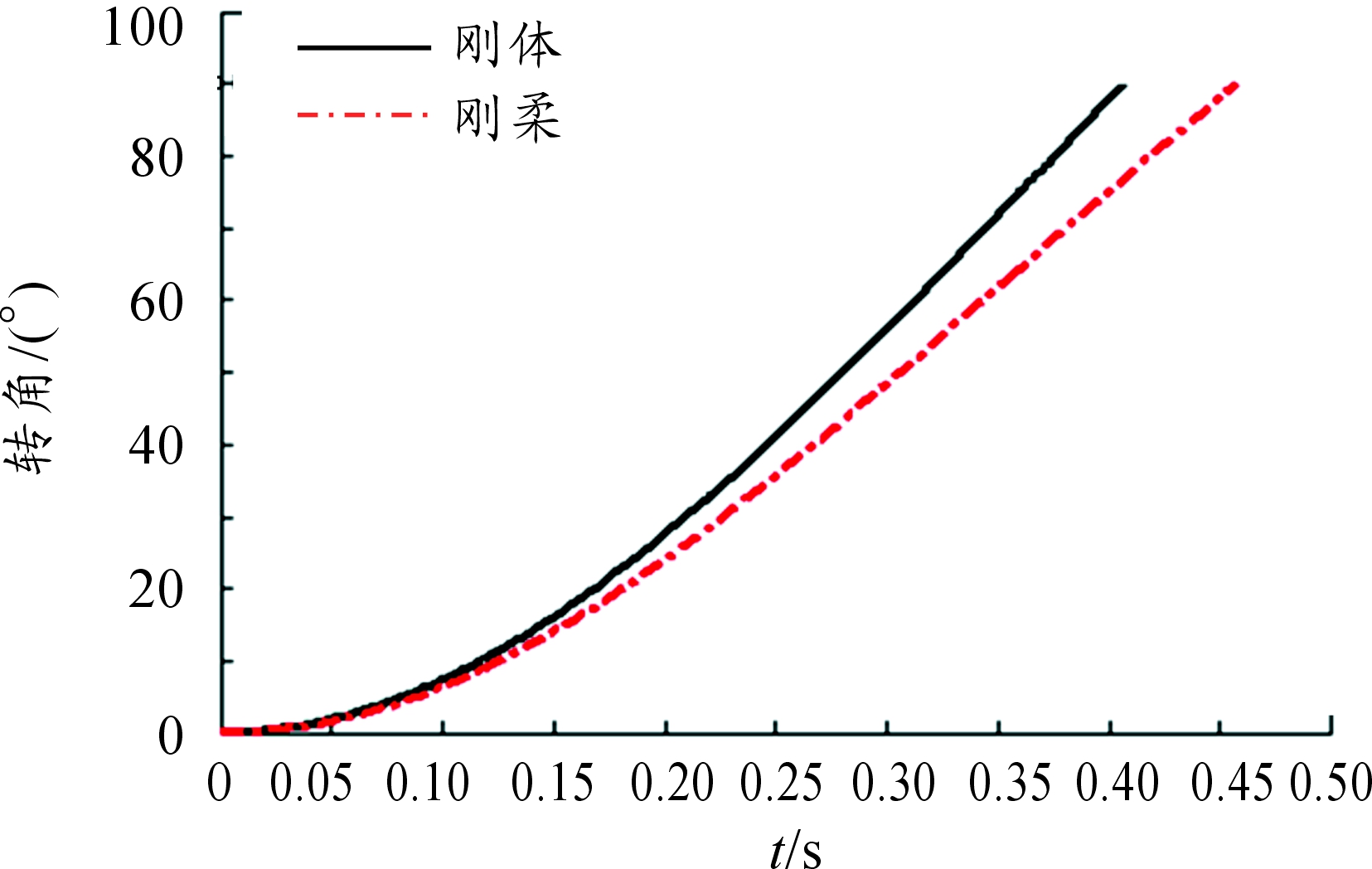
图8 刚体/刚柔时转角与时间的关系曲线
由图8可知刚体模型摆弹截止时间是t=0.406 5 s刚柔耦合模型截止时间是t=0.457 8 s,摆杆柔性会造成摆弹运动时间延长,柔性摆臂仿真时考虑了弹性变形,在机构设计时应当考虑摆臂柔性带来的影响。
3.3 弹体滑移对摆弹运动的影响
扬弹末端弹体位置会导致摆弹的初始质心偏差,在摆弹过程中弹体也会产生滑移,研究弹体滑移对机构运动特性的影响对提高摆弹机构可靠性与防止掉弹有着重要的意义。对弹体分别施加离心方向0.1m/s2和0.2m/s2的加速度,仿真得到的结果如图9所示。
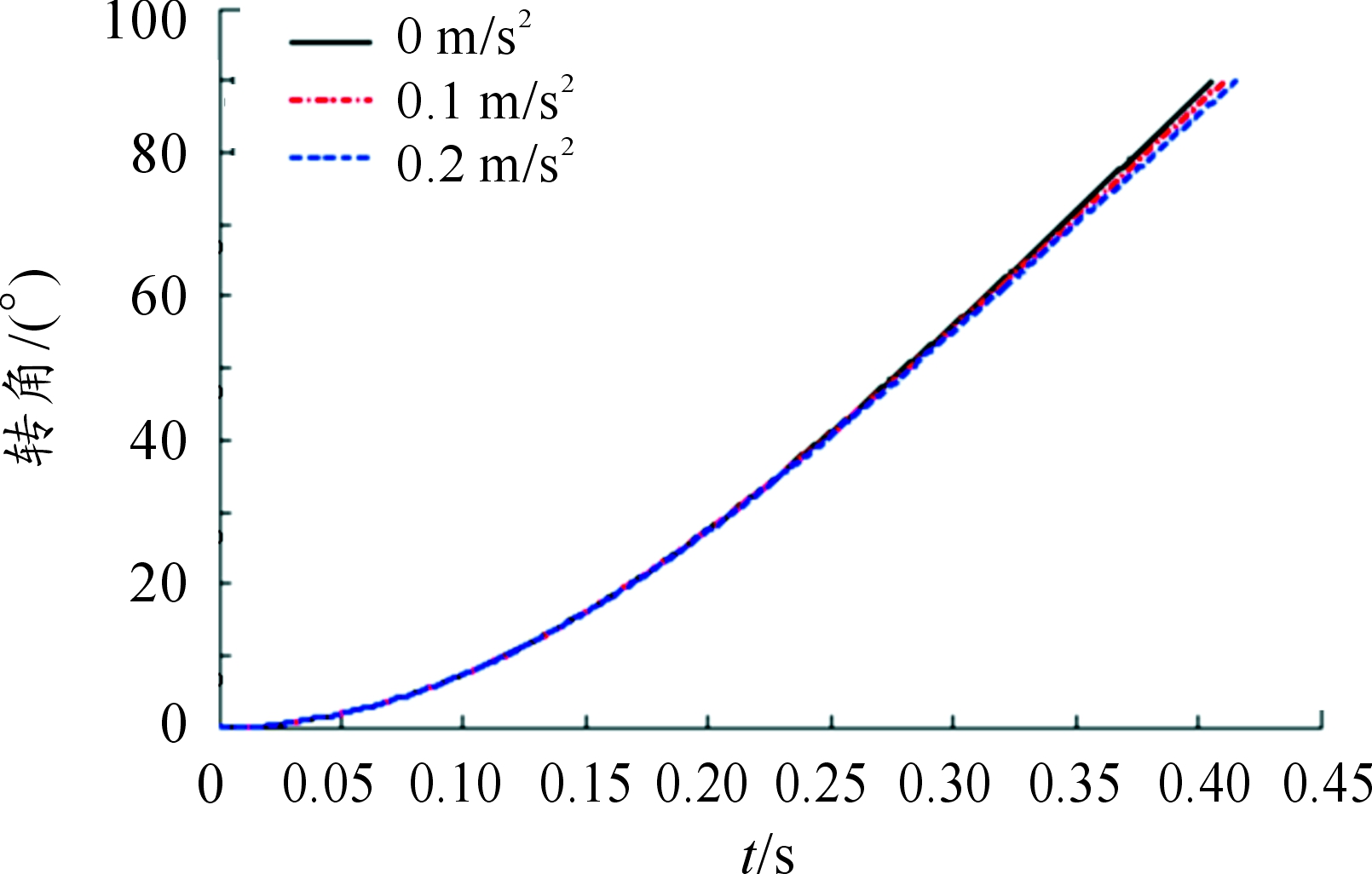
图9 不同滑移加速度时转角与时间的关系曲线
由图9可知在弹体无滑移、滑移加速度为0.1 m/s2和0.2 m/s2时摆弹截止时间t分别为0.406 2 s、0.410 7 s和0.415 8 s,弹体滑移会造成力臂变长,导致摆弹运动时间延长,在机构设计时应当合理设计抱箍给弹体的预紧力,避免产生滑移。
3.4 弹体质量偏差对摆弹运动的影响
弹体存在装药、加工等误差造成的质量偏差,为研究质量偏差对机构运动特性的影响,分别对质量偏差±0.2 kg的弹体进行仿真研究,结果如图10所示。
由图10可知在弹体质量偏差-0.2 kg、无质量偏差和质量偏差0.2 kg时摆弹截止时间t分别为0.379 5 s、0.406 2 s和0.434 4 s,弹体质量偏差对摆弹运动影响较大,随质量偏差越大转角与时间关系曲线偏离理想曲线越远,造成误差的原因是弹体质量偏差导致负载转矩变化。

图10 不同质量偏差时转角与时间的关系曲线
4 结论
1) 间隙导致摆弹存在运动误差,但间隙大小与误差的大小并不成正相关。
2) 刚柔耦合仿真时摆臂柔性对机构运动产生误差,在机构设计中应考虑弹性变形带来的影响,合理选择材料。
3) 弹体滑移导致机构运动截止时间延长,为避免滑移产生,合理设计抱箍预紧力是降低误差的有效办法。
4) 弹体质量偏差会影响到供弹的及时性,保证弹药质量满足规定能有效避免这一误差。
5) 针对不同结构的摆弹机,转动副间隙大小、摆臂柔性、预紧力大小的选择与配合仍有待进一步验证。
[1] 张相炎,郑建国,杨军荣.火炮设计理论[M].北京:北京理工大学,2014.
[2] 程刚,张相炎,董志强.供弹动作可靠性仿真研究[J].海军工程大学学报,2011,23(2):72-75.
[3] 程刚,张相炎,董志强,等.偏离运动仿真在供弹机构故障分析和优化设计中的应用[J].火炮发射与控制学报,2010(01):64-66.
[4] 程刚.高射频自动机及供输弹机构动态特性研究[D].南京:南京理工大学,2011.
[5] 杨丽.自动火炮供弹机可靠性及关键性能评估策略研究[D].沈阳:东北大学,2015.
[6] 胡胜海,古青波,彭浩宸,等.中腹摆弹机构刚—柔耦合建模及摆弹误差分析[J].南京理工大学学报,2013,37(03):398-403.
[7] 胡胜海,古青波,彭浩宸,等.中腹摆弹臂的递归学习输入成形振动抑制方法[J].北京理工大学学报,2013,33(11):1107-1112,1118.
[8] 古青波,彭浩宸,叶小红,等.考虑摆弹臂柔性的中腹摆弹机构动力特性分析[J].应用科技,2013,40(1):30-34.
[9] 可学为,侯健,陈汀峰.考虑摆臂柔性的舰炮摆弹机构动作可靠性及灵敏度分析[J].海军工程大学学报,2014(4):101-104.
[10] 侯健,可学为,魏平,等.大口径舰炮摆弹机构的动态设计[J].南京理工大学学报(自然科学版),2010,34(4):528- 532.
[11] 可学为,侯健,陈汀峰,等.大口径舰炮摆弹机构的动作可靠性分析[J].计算机仿真,2013,30(12):5-8.
[12] 侯健,樊龙龙,可学为.基于ADAMS和MATLAB的大口径舰炮发射系统动力学仿真[J].海军工程大学学报,2009,21(06):62-65.
[13] 唐文献,张丽娟,郭晓冬,等.中腹摆弹机摆臂疲劳特性研究[J].江苏科技大学学报(自然科学版),2015,29(5):474-479.
[14] 李渊明.大口径舰炮供弹系统摆弹机构动力学特性研究[D].哈尔滨:哈尔滨工程大学,2017.
[15] 温诗铸,黄平.摩擦学原理[M].3版.北京:清华大学出版社,2008.
[16] 丁键,赵宇,吴洪涛,等.含多运动副间隙机构动态特性研究[J].组合机床与自动化加工技术,2014(05):9-13.