使用机载吊放声纳进行反潜相比于其他反潜方式具有如下的优势:① 搜潜速度及机动性较高运用更为灵活;② 搜潜效率较高,成功率大;③ 受到潜艇攻击的可能性较低。④吊放声纳工作受直升机平台影响较小。所以使用直升机吊放声纳空中反潜是海军对潜作战的重要手段之一,也是未来发展的主要方向。
以往对于反潜直升机采用吊放声呐进行搜索的效率计算往往采用二维模式。认为水平面上只要潜艇到吊放点的距离小于声呐最大工作半径即为发现潜艇。这种简单的模式与实际情况具有较大的差距[1]。
海水中的声速剖面是连续变化的,这就导致了吊放声呐置于海水中工作在不同深度上拥有不同的传播损失,也就是在不同深度上的有效作用距离不同。本研究正是结合吊放声纳在深度上的作用距离变化与简化的潜艇深度分布模型来对三维情况下反潜直升机搜潜效率计算进行仿真研究。
1 潜艇位置分布
1.1 潜艇水平位置分布
假设初始位置满足服从X和Y两个方向上相互独立的正态分布![]() 则其初始位置概率密度为[2]
则其初始位置概率密度为[2]
(1)
将此式转变为极坐标形式(R,Θ)得到
(2)
R,Θ上的概率密度分别为

(3)
可见初始距离满足瑞利分布,航向满足0到2π上均匀分布[3-4]。伴随潜艇机动时间t,潜艇位置改变为(X1,Y1),同样满足正态分布![]() 则潜艇在此时位置变为(X0+X1,Y0+Y1)。满足概率密度函数。
则潜艇在此时位置变为(X0+X1,Y0+Y1)。满足概率密度函数。
(4)
将![]() 置零,进行极坐标转化并代入r=vt。可求得航速的概率密度分布
置零,进行极坐标转化并代入r=vt。可求得航速的概率密度分布
(5)
记σ1=σvt,则此式变为
![]()
(6)
假设潜艇速度满足均值为vec。则t时刻潜艇位置概率密度函数为
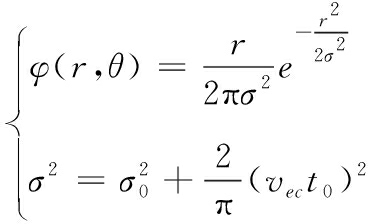
(7)
假设潜艇航速为7节,σ0=2,则t=1 h时潜艇水平分布的概率密度如图1所示。
因为速度与时间的独立性,在以原点为圆心,平均航速与时间乘积为半径圆上概率分布密度最大。以往对于二维平面上的直升机吊放声纳搜潜效率计算仅考虑潜艇水平分布概率模型,在计算时吊放声纳作用距离采取与吊放声纳同一深度下的最大作用距离。这样会导致计算得出的概率与实际情况有一定偏差,影响对于搜潜策略的判断。因此引入潜艇的垂直分布,使所计算的概率与真实情况更为接近。

图1 潜艇水平分布概率密度
1.2 潜艇垂直分布
应召搜索的背景是在跟踪潜艇过程中潜艇目标丢失,分两种情况。一是由声学探潜设备导致的丢失,可能是由于潜艇航行驶出探测范围导致的,这种情况下认为潜艇的垂直分布是深度上的均匀分布。第二种是由磁探仪,红外探测仪,雷达甚至目视观察等针对近海面目标的探测设备导致的丢失,多由潜艇下潜等因素导致,因此需要考虑潜艇垂直方向的分布。本研究主要针对第二种丢失,构建潜艇垂直分布概率密度模型。潜艇的垂直方向运动是一个复杂的控制问题[5],但是如果海区较为平静没有暗流的情况下其大部分时间可以近似看作匀速下潜,至于下潜开始及结束阶段的调整潜艇姿态运动,因为其相较于匀速运动的时间较短,对潜艇搜索的影响较低,故在计算吊声对潜艇的搜潜效率时对潜艇垂直方向上的分布进行一定简化。简化为初始深度满足期望为z0的瑞利分布,下潜速度分布应与平面上的速度同分布即满足期望为vd的瑞利分布,潜艇的下潜具有一定目标深度,不过如果将目标深度代入概率密度的表达并不容易计算,故将其转化为时间的分布。根据潜艇垂直运动的特征以及概率统计相关特性,假定下潜时间满足[tmin,tmax]上的均匀分布其期望为td。三个参量的随机分布概率密度为

(8)
下潜过程因为对时间有一定约束,所以相对平面上的运动概率密度分布要更为复杂。首先,显而易见下潜过程中总的位置Z=Z0+TV,首先设TV=Z1为下潜开始后深度的变化量。所以由统计学原理可构建关于Z1的概率函数
故路程位置变为Z=Z0+Z1。从而得到垂直方向上深度的概率密度
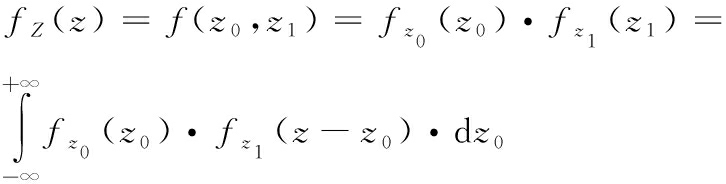
(9)
将各概率密度代入得到
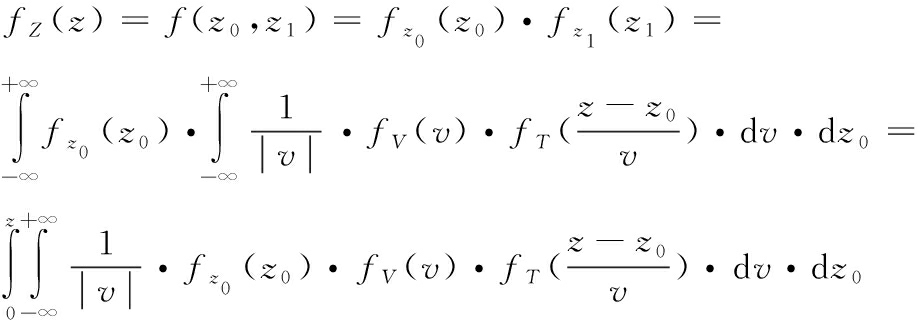
(10)
又根据各个参量概率密度函数性质最终得到
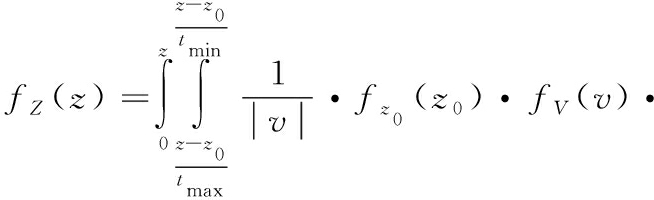
(11)
此方程无法求得具体的积分解析解,但是对于工程应用上求概率密度来讲是可以通过递推自适应算法得到相应一系列数值解的。假设初始深度期望为5 m,下潜速度的期望为2 m/s,下潜的时间分布为[55 s,65 s],在深度上按照步长1 m进行计算得到深度上位置分布概率密度如图2所示,积分结果期望为125 m,与概率性质相符。同时,需要注意的是,此概率密度函数是假设潜艇下潜完成后的概率密度函数。因为在这种浅海假设下潜艇下浅的时间相较于搜潜作业的时间来讲时间很短,考虑运动中的情况对于搜潜效率的计算较为困难且意义不大,因此对下潜过程的运动情况即概率密度随时间的变化进行忽略,只考虑下潜完成后潜艇所在位置的概率密度[6-8]。
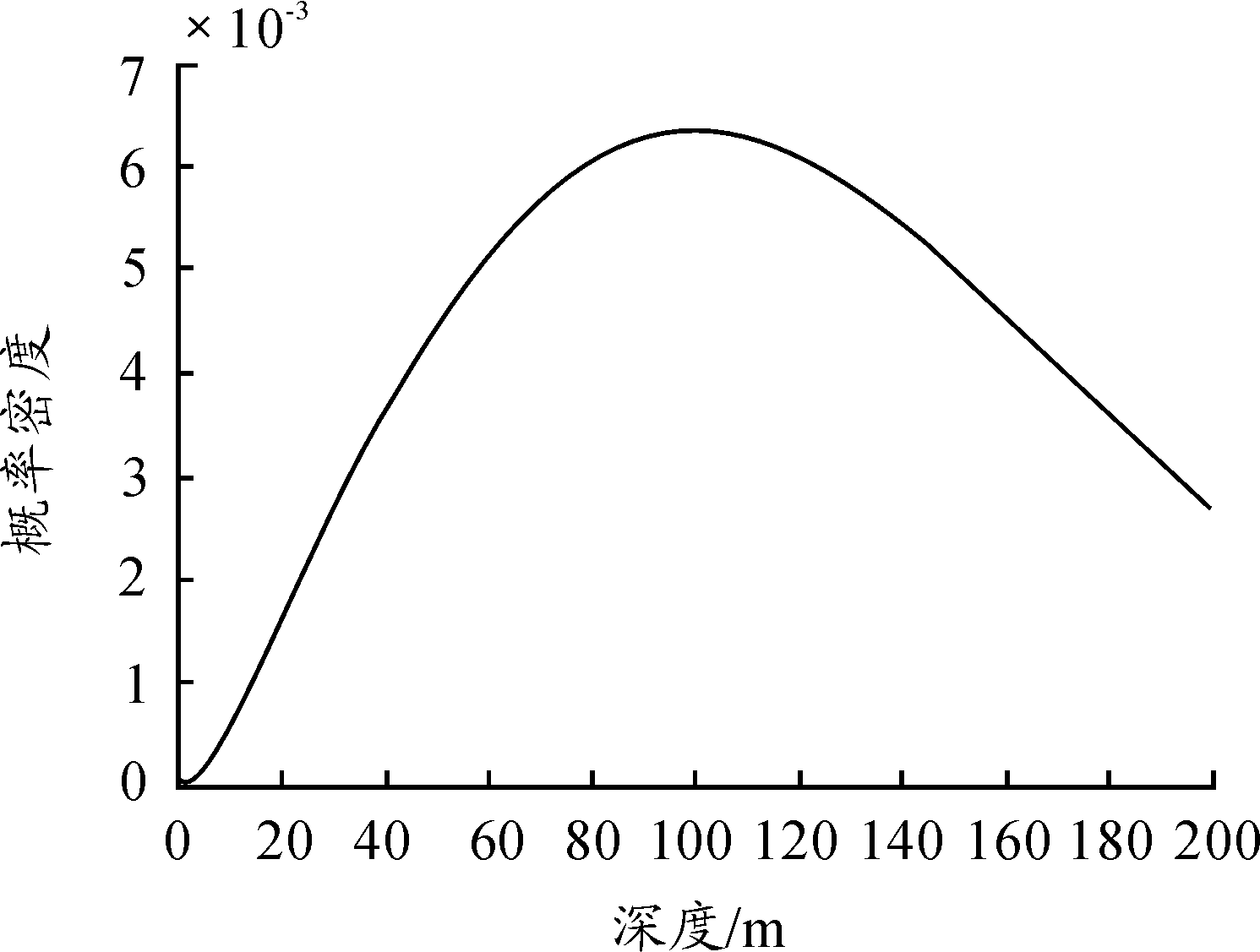
图2 潜艇垂直位置分布概率密度曲线
在简化的潜艇运动模型中,将潜艇的水平运动与垂直运动看作是相互独立的两个运动,所以最终可以得出潜艇三维概率度分布
f (r,θ,z)=φ(r,θ)·fZ(z)
(12)
在搜潜效率计算时将其作为被积函数对吊放声呐区域进行积分即为某一次吊放声纳进行搜潜作业的搜潜效率。
(13)
2 传播损失与吊放声纳作用距离
在传统的二维平面上的搜潜效能研究中,吊放声纳的作用范围被视作半径固定的圆,只要潜艇平面上的位置位于圆内即为发现潜艇。但实际上将声纳置于水中工作时,其在不同深度上的作用距离并不相同[9-10]。当将搜潜效能评估扩展到三维情况时,就必须考虑声纳在不同深度上作用距离的不同。
根据吊放声纳普遍工作频率在1~15 kHz之间的实际情况,研究吊放声纳的作用距离时采用射线声学近似的方式会取得比较好的效果。以如图3的典型浅海负梯度声速剖面为例,这种声速剖面广泛存在于我国夏季浅海地区[11]。

图3 浅海负梯度声速剖面线
声速可由以下公式进行简略描述
cz=csurf+a·z
其中a的绝对值可以反映声速变化的剧烈程度,越大则声速变化越剧烈。将声纳看作点声源置于100 m深度时理想的不考虑其他因素的传播损失如图4。
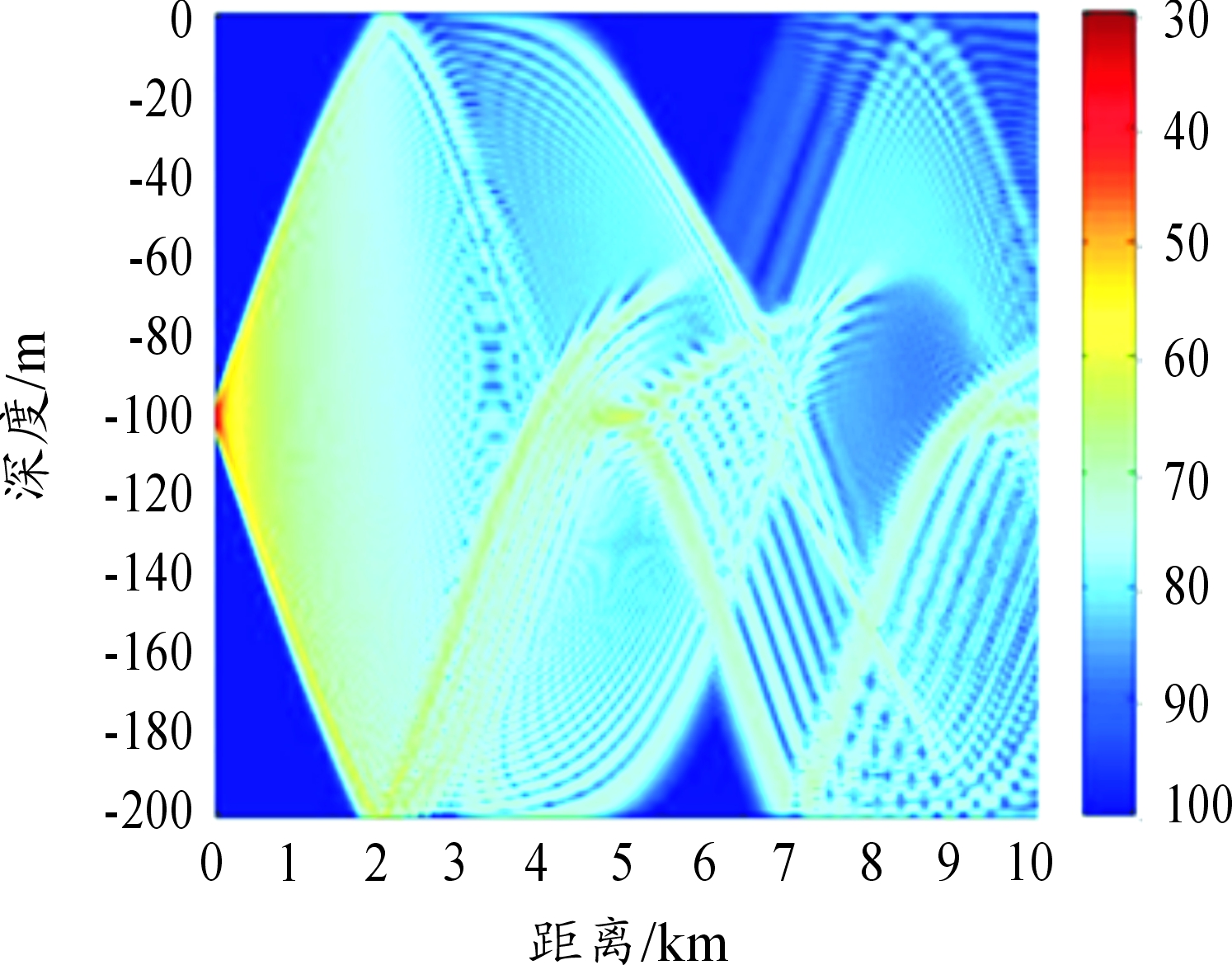
图4 100 m声源深度下的传播损失图
根据声纳方程,可以通过传播损失求得置于某一确定深度声纳在各个深度上的作用距离[12]。由传播损失图可见声纳总是在其相同深度上具有最大的作用距离,且不同深度上作用距离不同。
假定作用距离随深度变化的函数为HZ(z),这个函数没有确定的解析表达形式,能得到的只有各个深度上不同的传播损失数值解拟合出来的一个近似函数,在实际应用中如果将这个函数代入模型中进行搜潜效能计算会极大地提高计算量,显然在应用中并不合理。所以想要取得实际意义必须对这个函数进行一定处理。采用根据潜艇垂直分布的概率密度函数通过离散化权重积分的方式求得一个全深度的声纳作用距离的方法。有两种计算方式,第一种直接对作用距离进行处理
(14)
这样得到的吊放声纳有效作用区域是一个柱状区域。第二种是对最大距离到声源点的距离作为被积函数进行处理。
(15)
这样得到的吊放声纳作用区域是一个球状区域。仿真运算中将对这两种方式进行对比。
3 搜潜效率仿真计算
在进行搜潜效能仿真计算时,假设目标潜艇的运动参数如前文所提即初始位置满足服从X和Y两个方向上相互独立的正态分布N(0,4),其速度满足均值为vec=7 kn航速的瑞利分布,航向在[0,2π]均匀分布。反潜机抵达并开始反潜的延迟时间为0.5 h,直升机反潜作业平均飞行速度vhel=200 km/h。
假设声纳工作在主动模式下,主动模式下声纳优质因数为
![]()
(16)
通常在仿真计算中,传播损失小于此优质因数即为可以检测到目标信号。所处海洋环境为二级海况,根据如下经验公式计算环境噪声
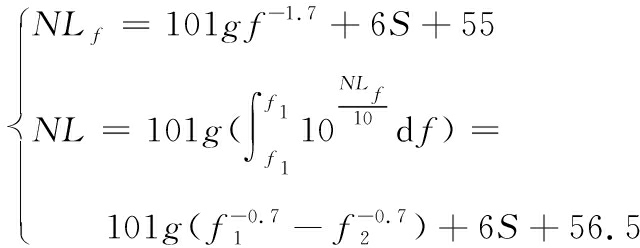
(17)
其中S为海况等级,代入二级海况求得噪声级约60 dB。声纳工作时声源级SL为200 dB,工作频率5 kHz,接收频率为10 Hz~10 kHz,目标强度15 dB,接收指向性为20 dB,阈值为10 dB。同时在考虑传播损失时引入海水吸收系数。将所有条件代入求得所设声纳的优质因数FOM=82.5 dB。
假设所处海区声速剖面如上文中提到的,假定的声呐工作频率为5 kHz,此频率在大部分海水情况下声吸收现象较为明显。因此在计算中引入海水的声吸收系数。吸收系数的计算按照经验公式
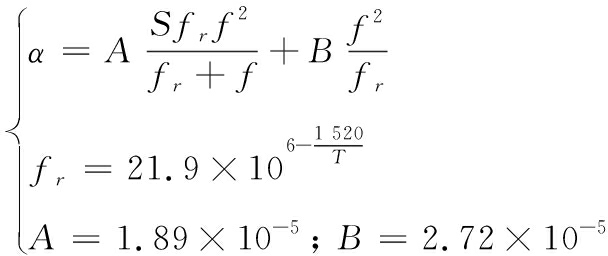
(18)
式中:S为海水盐度; fr为弛豫频率; T为绝对温度下的水温。代入盐度S=35‰,温度T=293.16 K,得到吸收系数α=5.023×10-4 dB·m-1,将这个值代入传播损失模型中进行计算得到新的传播损失如图5如表所示。
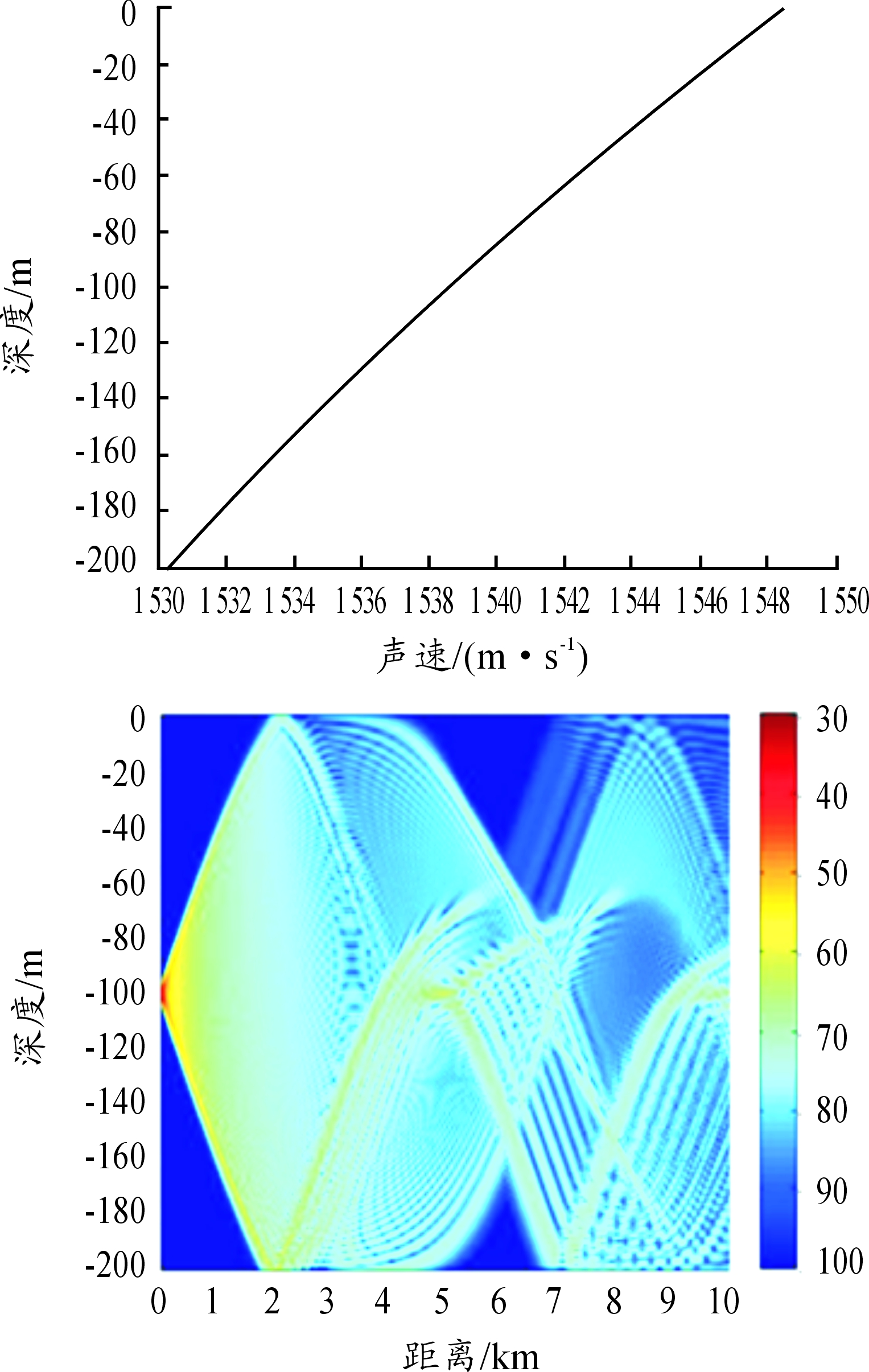
图5 引入声吸收系数后的传播损失图
将声纳优质因数引入得到将所设声源置于100 m深度时各个深度上的采用一次线性拟合的示意图和得到的作用距离如图6所示,常规二维情况下搜潜效率计算中吊声作用半径通常取与声源相同深度的最大作用距离,即8 768 m,这与巨人模型经验公式下的作用距离基本一致。
再根据离散权重积分得到第一种方法下全深度声呐作用距离rcy=6.2 km,第二种方法下得到的球半径为rsp=6.05 km,对应声纳有效作用区域示意图如图7,下一步的搜潜效能将以此值代入进行计算。
仿真以搜潜作业中最常见的扩展方形搜潜方法为例,其搜潜方式如图8所示。
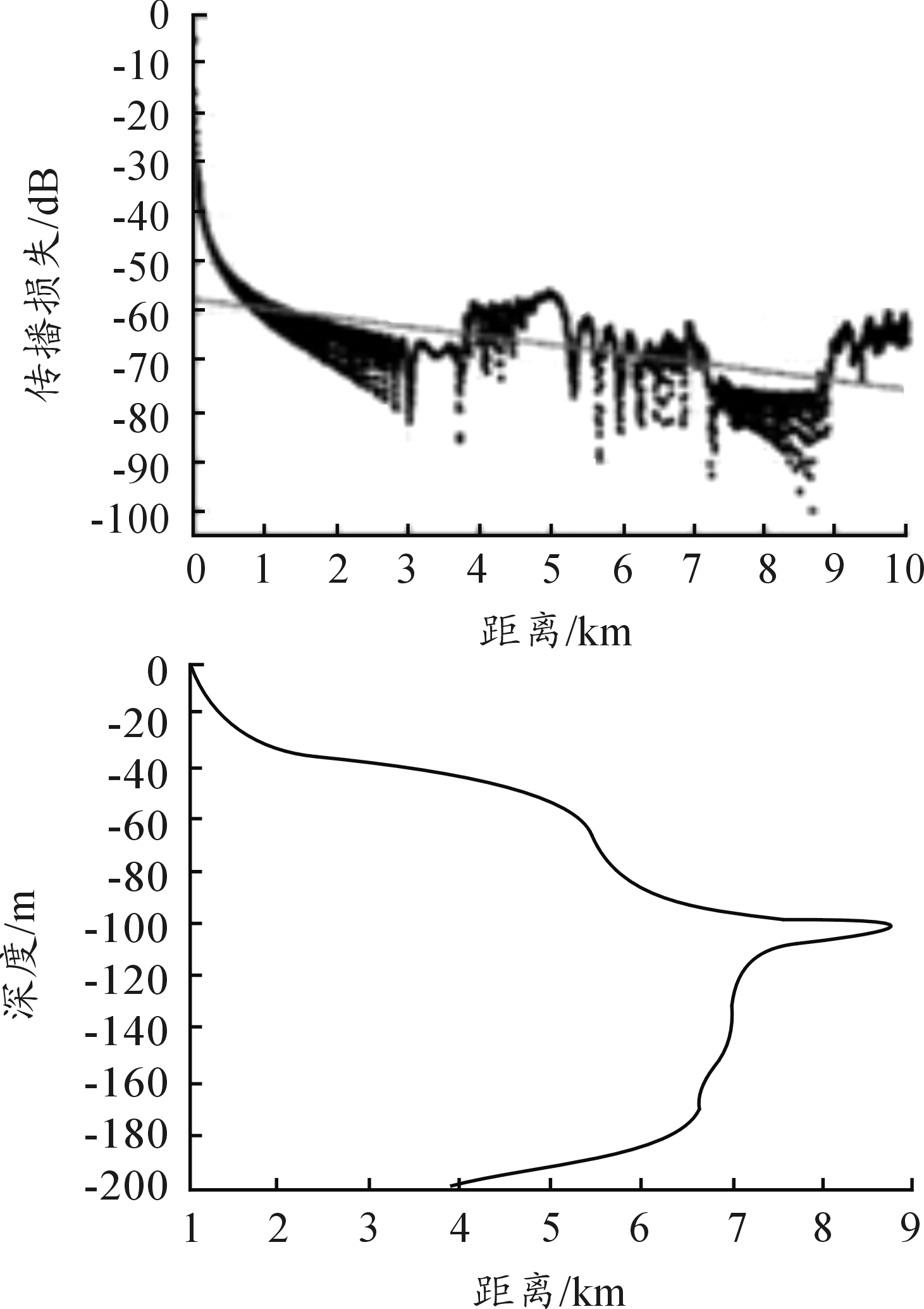
图6 100 m深度上传播损失拟合示意图(上)全深度声纳作用距离(下)
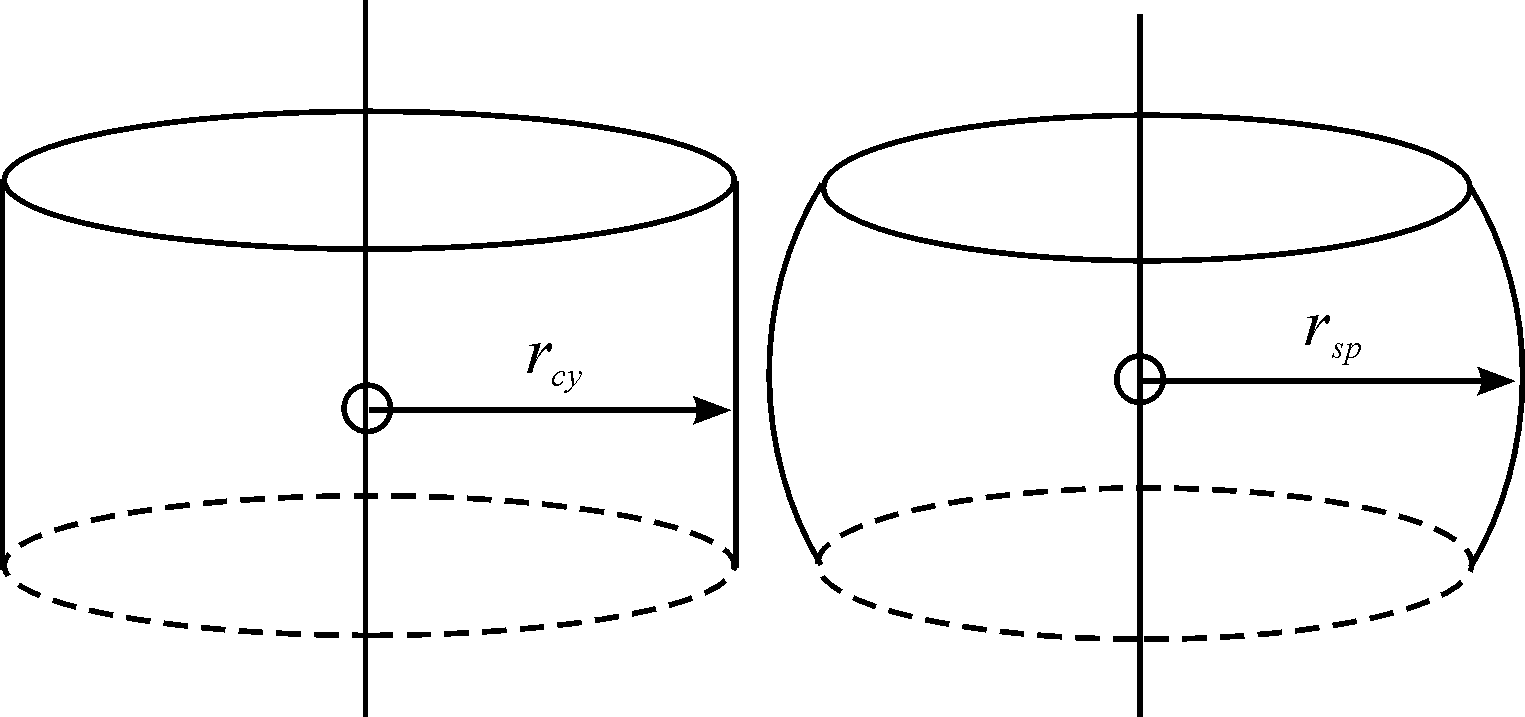
图7 柱状拟合与球状拟合声纳作用区域示意图
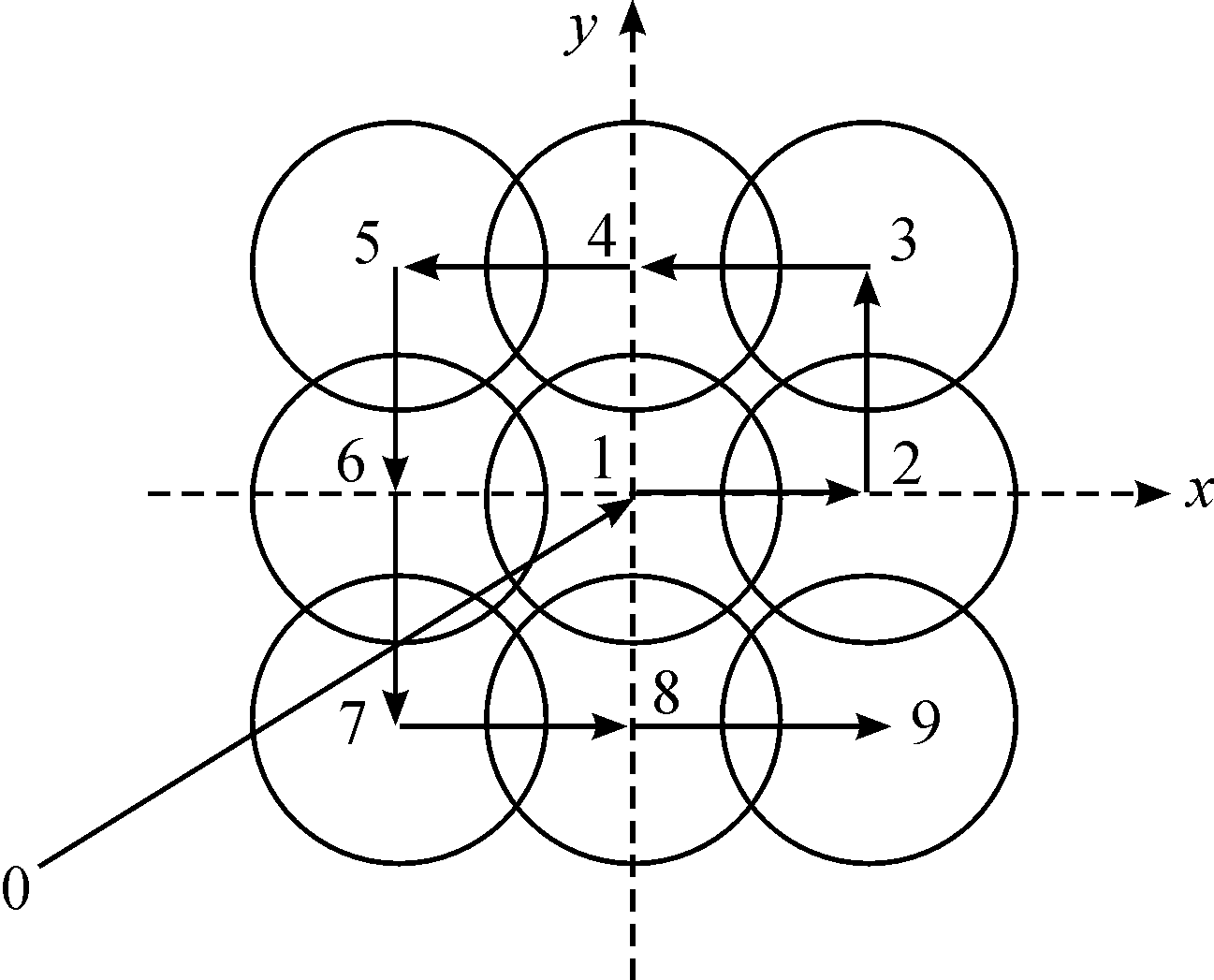
图8 扩展方形搜潜示意图
计算时点0为反潜直升机应召待命点,点1为潜艇疑似初始位置,即潜艇初始概率分布的期望位置。反潜直升机接到命令后按红色路径由0点到9点逐点搜索,相邻点间间隔距离系数D=1.6,即相邻两个吊放点距离为求得吊声作用半径的1.6倍,所以吊放点在不同吊声作用半径下是不相同的。每个吊放点进行吊放声呐搜索作业5 min。将点1作为整个坐标系的原点,点2方向为X轴正方向,点4方向为Y轴正方向。分别对圆柱形,圆球形近似作用区域积分计算仿真搜潜效率,并且与取N=10 000点的蒙特卡罗法按照传播损失模型计算出的吊声作用距离下进行的搜潜效率仿真进行比较。得到各个点情况如表1所示。
表1 各个吊放点搜潜效率情况
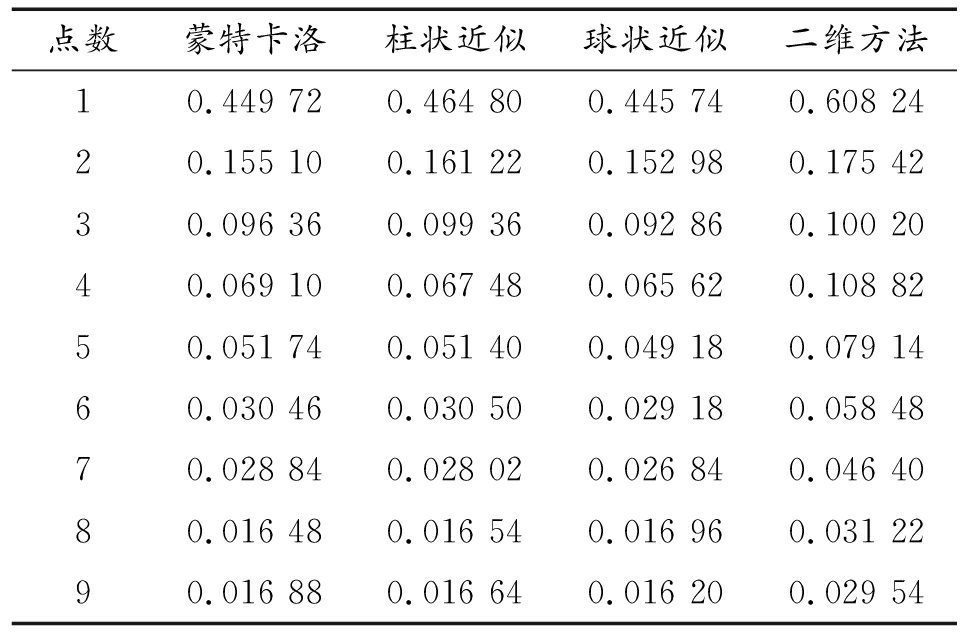
点数蒙特卡洛柱状近似球状近似二维方法10.449 720.464 800.445 740.608 2420.155 100.161 220.152 980.175 4230.096 360.099 360.092 860.100 2040.069 100.067 480.065 620.108 8250.051 740.051 400.049 180.079 1460.030 460.030 500.029 180.058 4870.028 840.028 020.026 840.046 4080.016 480.016 540.016 960.031 2290.016 880.016 640.016 200.029 54
整个搜潜过程的搜潜概率随时间变化曲线如图9所示。
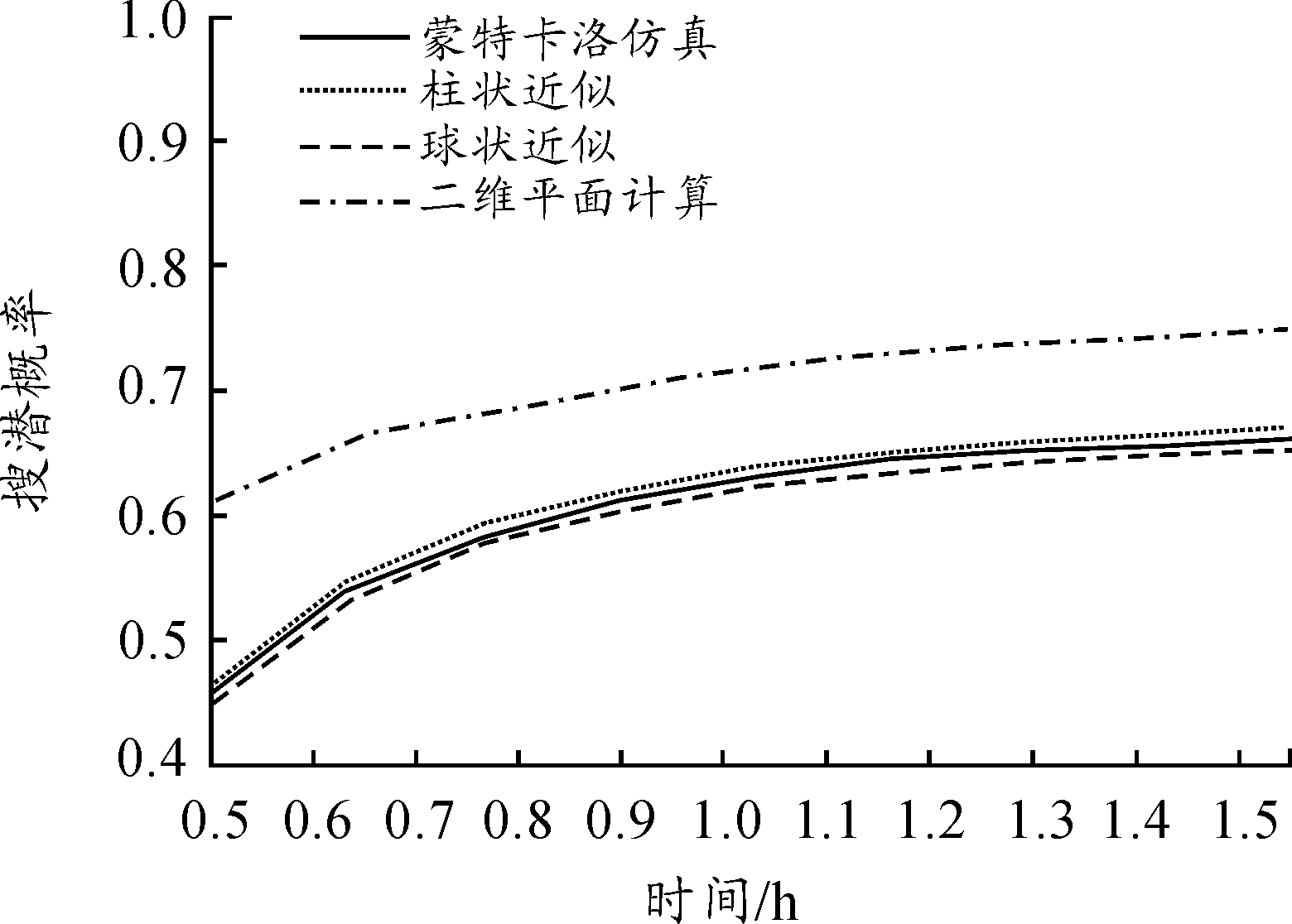
图9 四种方法的搜潜概率随时间变化曲线
柱状近似与球状近似均与蒙特卡洛法结果较为接近,将蒙特卡洛仿真作为标准结果,两种近似与蒙特卡洛方法进行比较的平均误差为:柱状近似0.021,球状近似0.015。而二维方法求得的搜潜概率要高0.15左右。
将柱状近似的吊声作用距离代入到二维方法推导的吊放点中进行计算,搜潜概率随时间变化曲线如图10所示。

图10 搜潜概率随时间变化曲线
更为直观地看出按照传统二维方法进行计算得到的搜潜效率是具有较大误差的。对整个仿真计算进行计时,计算结果如表2所示。
表2 各个模式仿真计算结果

仿真模式蒙特卡洛柱状近似球状近似时间/s50.196 310.233 914.479 3
可见将垂直概率密度代入近似吊声作用距离的计算在保持结果近似的情况下计算时间会大幅降低。
改变声速变化a的值对构建的三维模型与传统的二维模型进行对比仿真,得到两者计算出的搜潜概率差值曲线如图11所示。
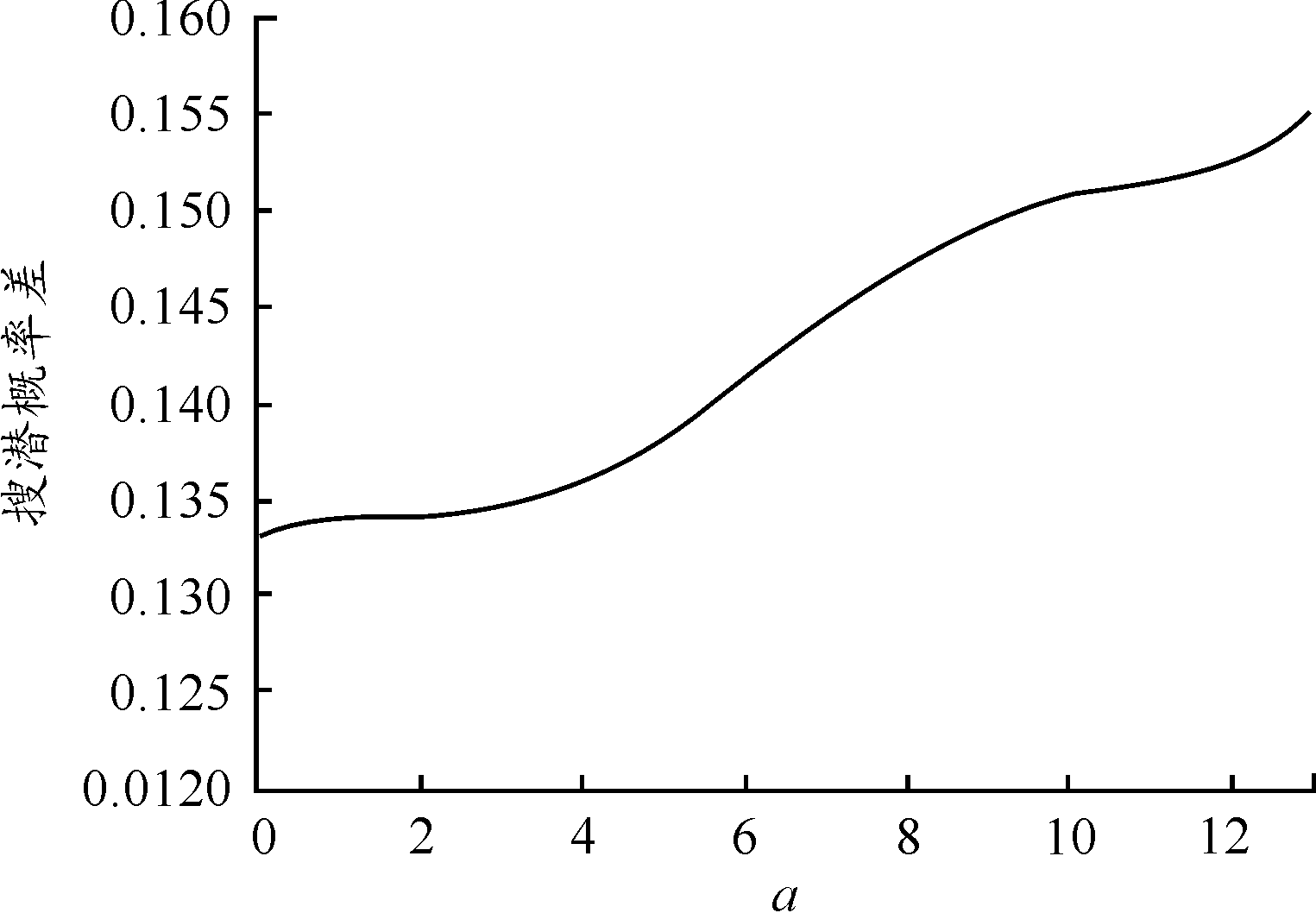
图11 改变声速剖面参数后的搜潜概率差值曲线
声速在垂直方向上变化的越剧烈,传统方法所计算的搜索概率误差越大。
连续改变吊放声呐深度对三维模型进行多次仿真得到的搜潜概率如图12所示。

图12 改变吊放声呐工作深度后的搜潜概率曲线
可以看出吊放声呐在125 m作用工作时会得到最大的搜潜概率,这与潜艇垂直分布的期望值是一致的。因此可以判断将主动吊放声呐使用时置于潜艇期望深度会取得比较好的搜索效果。
4 结论
本研究简化了潜艇垂直方向的运动,构建了一种计算潜艇垂直分布的概率模型。结合这种模型与声纳垂直方向上最大作用距离的不同提出了两种对于吊声搜潜中搜潜范围的选取方案。最终与蒙特卡洛法仿真的真实值进行对比,提出的方案在保证搜潜效率计算误差较小的情况下客观提高了运算速度。
[1] 吴芳,吴铭,杨日杰.反潜机吊放声纳扩展螺旋线性搜潜建模[J].北京航空航天大学学报,2011,9(37):1137-1142.
[2] 陈建勇,冷江,于传健.使用吊放声纳的直升机应召搜潜发现概率[J].海军航空工程学院学报,2004,19(5):559-561.
[3] 吴芳,杨日杰.多机吊放声纳应召搜潜建模与仿真[J].航空学报,2009,30(10):1948-1953.
[4] 屈也频,廖瑛.潜艇位置散布规律与搜潜效能评估模型研究[J].系统仿真学报,2008,20(12):3280-3283.
[5] 赵国良,季鲁慧.潜艇空间运动模型的简化和仿真[J].船舶工程,1991(4):23-31.
[6] 常赛.潜艇近水面航行控制方法研究[D].哈尔滨:哈尔滨工程大学,2011.
[7] ZUBRITZKY M C,ZACHARY W W,RYDER J M.Constructing and Applying Cognitive Models to Mission Management Problems in Air Anti-Submarine Warfare[J].Proceedings of the Human Factors and Ergonomics Society Annual Meeting,1989,33(2):129-133.
[8] DAWSON H C.Anti-submarine warfare:still an essential warfare art[R].ADA26356,1993.
[9] 孙明太,周利辉,赵志允.负梯度浅海混响条件下吊放声纳主动探测深度研究[J].海军航空工程学院学报,2013(3):221-225.
[10] 曲晓慧,单志超,陈建勇,等.深海声速剖面对吊放声纳探测距离的影响研究[J].计算机仿真,2012,29(5):471-476.
[11] 赵志允,孙明太,任东彦.吊放声纳主动工作方式探测域建模与仿真[J].指挥控制与仿真,2013,35(6):49-53.
[12] KETTER T N.Anti-submarine warfare in the 21ts century[R].ADA27660,2003.