作战飞机在进行电磁威胁环境态势感知过程中,需依赖其机载自卫电子对抗系统来降低或消除被敌方机载探测系统、地面监视系统和导弹制导系统发现的威胁,这是提高作战飞机战场生存能力的重要手段。随着各种精确制导武器的不断发展和应用,“发现即摧毁”已是常态,机载自卫电子对抗系统能否正常发挥效能,对作战飞行安全和战斗任务执行至关重要[1]。在装备研制和生产,以及实际使用和训练过程中,对机载自卫电子对抗系统中的雷达告警设备,通过相关检测进行有效性测试与评估是重要科目。目前,基于雷达信号模拟器,通过设置发射信号参数,包括载频、脉冲宽度和脉冲重复间隔等,产生特定雷达目标测试信号是用于相关检测的常用方法[2]。
由于真实战场环境复杂,存在着不同特征和用途的多部雷达同时照射的情况[3],因此,雷达模拟器应该具备多部雷达组合测试信号生成的能力,即将多路脉冲信号融合为一路有序输出[4]。考虑到多个不同雷达脉冲信号的到达时间(Time of Arrival,TOA)存在差异,如果前后两个脉冲到达时间差小于前一个脉冲的脉宽,此时会产生时域脉冲交叠现象[5]。当出现交叠时,常用的处理方法有:脉冲合并、按照优先级进行舍去、通过硬件进行优选等。文献[4]采用设置优先级的方法,按照威胁等级进行脉冲序列选择和合并,但存在致使威胁等级较小的脉冲序列信息改变或丢失的问题。文献[6]采用基于比较电路的纯硬件方法,通过比较多路脉冲信号的到达时间、优先级和脉宽等信息来进行脉冲排列,但对复杂比较电路的硬件设计需求,制约了该方法的推广使用。综上所述,在不断增加雷达信号模拟器输出信号种类和数量的同时,设计能够尽量减小时域脉冲交叠的工程实现方法仍是一个重要的研究课题。本文针对上述需求,从脉冲交叠概率入手,推导出可用于工程实现的交叠概率公式,提出了一种分组脉冲排列的方法,可以有效降低脉冲交叠的数目。
1 脉冲交叠分析
当脉冲流处于高密度雷达信号环境中时,可以看作是随机过程,如果随机过程在某一时间区间内的状态不受这个时间区间以外状态的影响,则称为是无后效的随机过程[7]。那么对于某一时刻t来说,这个随机过程可以近似为一个随机事件来考虑,因此可以从概率统计的角度来分析问题。
若两个脉冲前沿的到达时间差小于前一个脉冲的脉冲宽度时,此时会出现脉冲交叠的现象,后一脉冲的脉内信息就会丢掉。因此,任一脉冲的交叠概率,即是在该脉冲的脉冲宽度内存在其他脉冲的概率[8]。对于某一部雷达来说,由于具有固定的脉冲间隔,所以脉冲信号不存在交叠的现象,计算时应该去除该部雷达产生的脉冲序列[9-10]。另一方面,雷达信号环境复杂,存在高密度流的脉冲信号,所以这些脉冲序列可以看作是相互独立的。同时,在任一时刻雷达信号脉冲存在的概率是相同的。因此,去除某一部雷达所产生的脉冲序列,其他脉冲序列在任一时刻出现的概率即是该部雷达脉冲可能交叠的概率。
单个脉冲序列的占空比公式为:
(1)
单个脉冲序列不存在的概率为1-ri,其他脉冲序列不存在的概率为[11]:
(2)
其中,n为脉冲序列的个数,则脉冲序列出现交叠的概率为:
(3)
对于单个脉冲序列而言,占空比r往往较小,在实践中常把1-r近似为1,所以当脉冲序列数目较多时,上式可简化为:
(4)
由幂级数![]() 可知,当x<<1 时,可简化为:e-x≈1-x,则式(4)可表示为:
可知,当x<<1 时,可简化为:e-x≈1-x,则式(4)可表示为:
(5)
令![]() 其中r表示所有脉冲序列的总占空比,则:
其中r表示所有脉冲序列的总占空比,则:
p2=1-e-r
(6)
由式(6)可知,脉冲交叠的概率与脉冲序列总占空比有关。所以可通过调节脉冲序列的到达时间,使得各组脉冲序列初始时间产生时间差以降低总占空比,达到减小脉冲交叠概率的目的。一方面,可以避免因优先级排列而造成某列脉冲丢失的情况,另一方面不需要设置专门的比较电路,只需要采用专门的软件来实现,降低了外围电路的复杂度。
2 分组脉冲交叠分析
2.1 分组脉冲排列
由于雷达模拟器产生的脉冲数量庞大,当处理器对产生的脉冲序列进行排序时,若脉冲密度越大,即脉冲序列的时域总占空比也越大,调节到达时间差所得到的效果往往不明显,那么雷达模拟器将会有较高的脉冲交叠概率,造成大量的脉冲重叠,使得待检测的机载自卫电子对抗系统侦查告警设备产生漏警,且内部的处理单元计算资源有限,若脉冲密度越大,则处理器的时间越大,占用的资源也相对较多。
所以为了能够从整体上提高实用效能,本研究提出分组脉冲排列的方法。对于前述提出的雷达模拟器,可将产生的脉冲序列根据载频进行平均分组,如对于2~18 GHz这一频段可分为4个组,分别为2~6 GHz、6~10 GHz、10~14 GHz和14~18 GHz,这样每组脉冲序列的数量与脉冲密度比分组前要减少,然后调节各组的到达时间进一步降低占空比,从理论上达到降低脉冲交叠概率的效果。
2.2 分组脉冲交叠概率分析
对于分组后的脉冲序列,都满足:
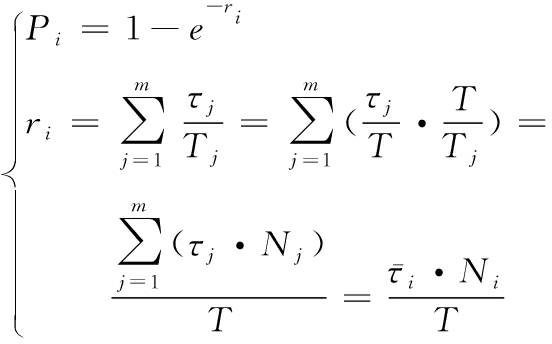
(7)
其中: τj为各组脉冲序列脉宽;![]() 为各组脉冲序列平均脉宽; Ni为各组序列的脉冲总数; T为脉冲排列时间。那脉冲交叠概率为:
为各组脉冲序列平均脉宽; Ni为各组序列的脉冲总数; T为脉冲排列时间。那脉冲交叠概率为:

(8)
式中,m为脉冲序列的分组数。
另一方面,脉冲序列的总占空比![]() 为全部脉冲的平均脉宽,N为脉冲总数[12]。由于模拟器产生的脉冲序列密度较大,可以假设每组的平均脉宽
为全部脉冲的平均脉宽,N为脉冲总数[12]。由于模拟器产生的脉冲序列密度较大,可以假设每组的平均脉宽![]() 近似等于全部脉冲的平均脉宽。由此可以得到每组脉冲序列占空比ri与全部脉冲占空比r之间的关系:
近似等于全部脉冲的平均脉宽。由此可以得到每组脉冲序列占空比ri与全部脉冲占空比r之间的关系:
(9)
把式(7)与式(9)代入式(8)化简得到:

(10)
式(10)为没有考虑各组相互影响的脉冲交叠概率,那是由于在对某组进行脉冲排列后,其他各组与之进行排列时也会产生交叠的现象,所以如果不考虑这种情况,模拟器势必也会产生脉冲交叠。
在进行排列的时间T内,对第k组进行排列后,其他各组与之产生脉冲交叠的数目为:
(11)
式中:m为分组的个数;k为排列后的第k组;Nj为各组与第k组产生交叠的数目。那么对于整个雷达模拟器而言,由各组相互排列所引起的脉冲交叠数目为:
(12)
由于雷达模拟器产生的脉冲数目巨大,脉冲序列可以认为是相互独立的,并且分组后每组包含的频段长度相同,所以各组脉冲存在的概率也是相同的,那么对于某一组来说,脉冲序列存在的概率即为该组内脉冲总占空比rk,由式(9)可知,该组脉冲出现的概率为:
(13)
那该组与其他组产生交叠的数量为:
(14)
将式(14)代入式(12)即为模拟器由于各组相互排列所引起的脉冲丢失数目:
(15)
综上所述,雷达模拟器进行脉冲分组排列时产生交叠的数目为:
(16)
脉冲交叠概率即为:
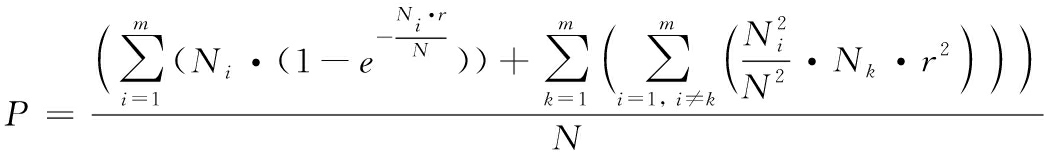
(17)
3 仿真分析
因为导弹控制、地面监视雷达系统和机载雷达的频段大多处于2~18 GHz,所以本文选取这一频段进行研究。为了验证以上分析,现假设雷达模拟器分别产生350万个脉冲和450万个脉冲,其频段的分布如图1和图2所示。

图1 350万脉冲频段分布曲线

图2 450万脉冲频段分布曲线
按照脉冲分组的方法,将上述产生的脉冲序列均分为4组,分别为2~6 GHz、6~10 GHz、10~14 GHz和14~18 GHz。通过式(6)与式(17),设置不同的占空比得到分组前后脉冲序列交叠情况,如表1、表2所示。
表1 350万脉冲交叠概率

脉冲总占空比原脉冲序列交叠概率/%分组脉冲交叠概率/%0.021.980.620.043.921.250.065.821.890.087.692.540.109.523.210.1211.313.880.1413.064.570.1614.795.270.1816.475.980.2018.136.71
表2 450万脉冲交叠概率

脉冲总占空比原脉冲序列交叠概率/%分组脉冲交叠概率/%0.021.980.560.043.921.140.065.821.720.087.692.320.109.522.930.1211.313.550.1413.064.190.1614.794.840.1816.475.500.2018.136.17
分析上述图表可知,随着序列总占空比的增加,分组前后的交叠概率都相应增大,这说明可以通过调节占空比来减少脉冲交叠概率。进一步可知,模拟器产生的脉冲序列在分组前后的交叠情况也差异显著,经过分组排列的脉冲交叠概率要小于原序列的交叠概率,并且原序列脉冲交叠概率增加的幅度也大于分组后的。对于需要产生复杂且数目巨大的雷达模拟器而言,脉冲信号的密度越大,代表着总占空比也越大,所以经过分组排列后的脉冲序列可以有效地降低交叠概率。
上述仿真只采用了四等分组的情况,为了更好说明分组脉冲排列后交叠概率的情况,将原序列划分为不同分组,各分组与原序列交叠概率和占空比的关系如图3所示。
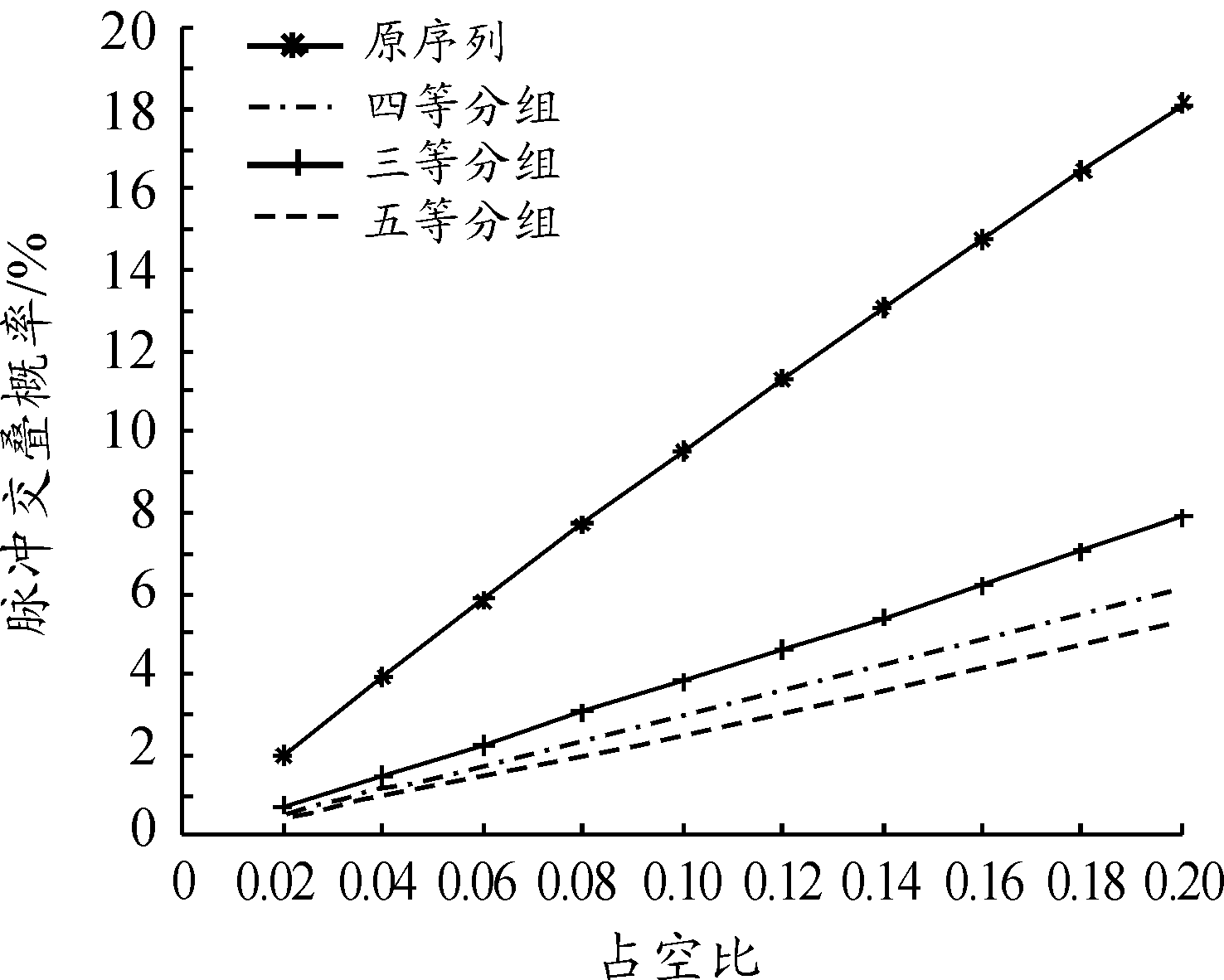
图3 不同分组脉冲交叠概率与占空比的关系曲线
分析图3可知,不同分组后的脉冲交叠概率与上文结果相同,都远远小于原序列的脉冲交叠概率,并且随着占空比的增大,交叠概率增加幅度也比原序列较小。进一步分析可知,在相同占空比的情况下,随着分组数目的增多,脉冲交叠概率也相应减小。
通过上述分析,可以得出结论:脉冲交叠概率与脉冲总占空比呈负相关,可以通过调节总占空比的大小来改变脉冲交叠的数目;经过分组后的脉冲交叠情况与原序列相比有显著的变化,可以有效地降低脉冲交叠概率。所以在雷达模拟器设计时,以脉冲交叠概率作为参考,通过分组脉冲排列调节占空比来降低脉冲交叠,与传统方法相比,因为不再划分优先级,所以可以有效避免低优先级脉冲序列的丢失,另一方面也不需要多余的外围硬件电路,满足了设计的需要。
4 结论
在已有文献的基础上,分析得到脉冲序列交叠概率的一般表达式,为进一步降低雷达模拟器生成信号脉冲交叠概率而对原序列进行分组排列,推导出适用于计算的脉冲交叠公式。通过对原序列与分组排列后脉冲交叠情况的仿真实验,证明了分组脉冲排列可以有效降低交叠概率。需要说明的是,雷达模拟器产生脉冲之间需要一定的恢复时间,推导公式时为了简便没有考虑,并且本文提到的分组脉冲方法是平均划分频段,不均分的情况以及如何分组使脉冲交叠产生最优解还需进一步研究。
[1] 王龙涛,姜宁,戎华.舰载一体化雷达电子对抗系统无源侦察引导效能研究[J].兵器装备工程学报,2018,39(3):15-19.
[2] 刘利民,程呈,韩壮志,等.实时机载雷达告警仿真系统设计与实现[J].系统工程与电子技术,2016,38(4):812-820.
[3] 孙魏,伍度志.基于防御雷达监控的多无人机协同侦察优化模型[J].兵工自动化,2018,37(04):5-9.
[4] 江绪庆.多辐射源雷达信号环境仿真技术[D].成都:电子科技大学,2006.
[5] 辛明,余志斌,谢爱平.密集电磁环境下脉冲信息的丢失概率[J].电子信息对抗技术,2012,27(3):25-27.
[6] 陈正宁,王宁.基于FPGA的雷达信号模型解算与脉冲排序[J].电子设计工程,2018,26(10):160-164.
[7] 祝正威.脉冲丢失概率的计算方法[J].电子信息对抗技术,1990,15(6):21-26.
[8] 秦江.毫米波告警系统截获概率与测向性能分析[D].成都:电子科技大学,2014.
[9] NAWCWPNS T P.Electronic Warfare and Radar System Engineering[J].Washington DC:Naval Air Warfare Center,1997.
[10] ZAHIRNIAK D R,SHAPIN D L,FIELDS T W.A Hardware-efficient,Multirate,Digital Channelized Receiver Architecture[J].IEEE Transactions on Aerospace and Electronic Systems,1998,34(1):28-32.
[11] 童智靖,陈臻.复杂密集电磁环境下低重频雷达信号分选技术[J].舰船电子对抗,2018,41(3):88-91.
[12] 王星,周东青,张曦,等.时分制RWR/ESM处理方法对脉冲丢失的影响[J].电讯技术,2013,53(9):1136-1141.