跳频通信是指在同时同步条件下,收发两端按照预定伪随机变化图案以窄带载波进行的信息通信。由于跳频通信自身具有很强的抗截获、抗干扰能力,使得其在通信领域得到了广泛的使用[1-2]。在非合作通信中,由于收发两端不具有匹配性,接收方往往对接收到信号的调制方式和信号结构等相关信息未知。因此,如何在缺少先验信息条件下对跳频信号进行有效监测,进而在跳频检测和网台分选的基础上对跳频信号进行参数估计,这对于无线电监管、雷达传输、军事通信等领域有着十分重要的意义[3]。目前常用的参数估计方法主要有:时频分析方法、信号分解方法和压缩感知方法等。其中,信号分解方法是通过构建符合跳频信号结构的冗余原子库,从中搜索出最优参数组合原子来进行参数的盲估计[4-6]。该方法抗噪性较好,但搜索算法迭代停止条件选择的得当与否会对估计精度影响较大,且所需的冗余原子库过大导致该方法因计算量过大而难以满足无线电监测的实时性要求。张伟[7]提出了一种基于正交匹配追踪和稀疏线性回归相结合的方法一定程度上改善了计算量过大的问题。东润泽[8]定义无限原子集合,建立了原子范数最小化模型利用其对偶问题方法,改善了构造的基字典与信号不匹配的问题。压缩感知方法以远远少于奈奎斯特采样频率的速率进行对信号的采样并重构出原始信号[9-10]。该方法的重构算法等相关技术及硬件实现目前尚不成熟,需要进一步完善。付卫红[11]提出一种不需要信号进行重构,只需压缩测量值就能完成参数盲估计的方法。在时频分析方法中,维格纳-维尔分布(Wigner-Ville Distribution,WVD)及其改进方法具有理论上最高的时频分辨率,但也存在严重的交叉干扰和阈值效应,其改进方法都以牺牲时频分辨率为代价,且大幅增加了计算量[12-15]。Morlet小波算法由于其自身多分辨率特性导致低频部分分辨率较低[16]。短时傅里叶变换(Short-Time Fourier Transform,STFT)受测不准原理限制,不能很好地兼顾时间和频率,但实时性较强[17]。付卫红[18]通过将STFT与平滑伪WVD分布(SPWVD)结合,提高了参数估计精度。
在无线电监测过程中,由于无线电环境的复杂性,对精度、抗噪性和实时性都有一定的要求,这就使得使用单一参数估计方法难以满足无线电监测过程中多维度的需求。在此提出一种二次估计与阈值修正相结合的方法来兼顾无线电监测的多维需求。使用STFT来对信号进行时频分析并得到信号谱图,对得到的谱图通过加入阈值修正环节来提高跳频信号参数估计的准确度。估计跳变时间后对信号进行分段并使用信号DFT变换系数构造频率修正项的方法来估计载频频率,从而使得此方法在保证一定实时性的同时,还有较高的参数估计精度和一定的抗噪声能力。
1 跳频信号系统模型
跳频信号载波频率在很宽频带范围内按伪随机码进行跳变,可建模为[19]:
(1)
式(1)中: 0<t<T; A为信号幅度; Th为跳频周期; T0为起跳时刻; fk为跳变频率; N为跳变频率数;![]() ω(t)表示高斯白噪声。
ω(t)表示高斯白噪声。
在1946年,Dennis Gabor引入了短时傅里叶变换,对于信号x(t)的STFT定义为[15]:
(2)
为方便计算机处理,一般把信号进行离散化处理,即:
![]()
(3)
谱图法是一种二次型时频分析方法,它的值是STFT模的平方,即:
SPEC(t, f)=![]() =
=
(4)
2 特征参数估计方法
由测不准原理可知,STFT的时频分析结果在时域和频域的分辨率难以兼得。使用较长的滑动距离会导致时域分辨率难以保证,使用较短的滑动距离会造成抗噪性能下降且不利于后续跳频频率的估计,因此在跳频信号每一跳过程中,若取较短的滑动距离可以获得更高的时间分辨率,也势必会增加计算量,从而增加运算时间。在此使用对接收信号进行二次搜索的方法来减少计算量,节省运算时间。先不直接找较精确的跳变时刻,而是根据STFT分析结果找跳变时刻的存在时间区间。使用较长的滑动距离,对接收到的信号进行粗估计,得到跳变时刻所在时间区间并进行标记,然后再对跳变时刻所在时间区间使用较短的滑动距离进行二次搜索。为提高跳变时刻估计的准确性,在二次搜索前要对跳频信号的时频图进行修正,利用修正后的时频图对存在跳变时刻的时间区间进行二次搜索可得到更为精确的跳变时刻。利用估计出的跳变时刻,通过求差可得到跳频信号的跳变周期。利用插值DFT变换系数的频率修正项的频率估计方法得到每跳信号频率。
设使用窗口长度为C,滑动窗每次滑动步长为L0的距离,进行STFT的时频分析可以得到时频分析结果,其中m=0,1,2,…,M-1(M为STFT的频率采样点数),l=0,1,2,…,L-1(L为x(t)所加的窗数)。
由谱图计算公式: B(m,l)=|X(m,l)|2可以得到信号谱图,如图1所示。提取图1中频率脊线,可得到频率脊线,如图2所示。求一阶差分方程可得跳变时刻存在时间区间,第m个跳变时刻存在区间记为im(m=1,2,…,M)(M为跳变时刻总数)。
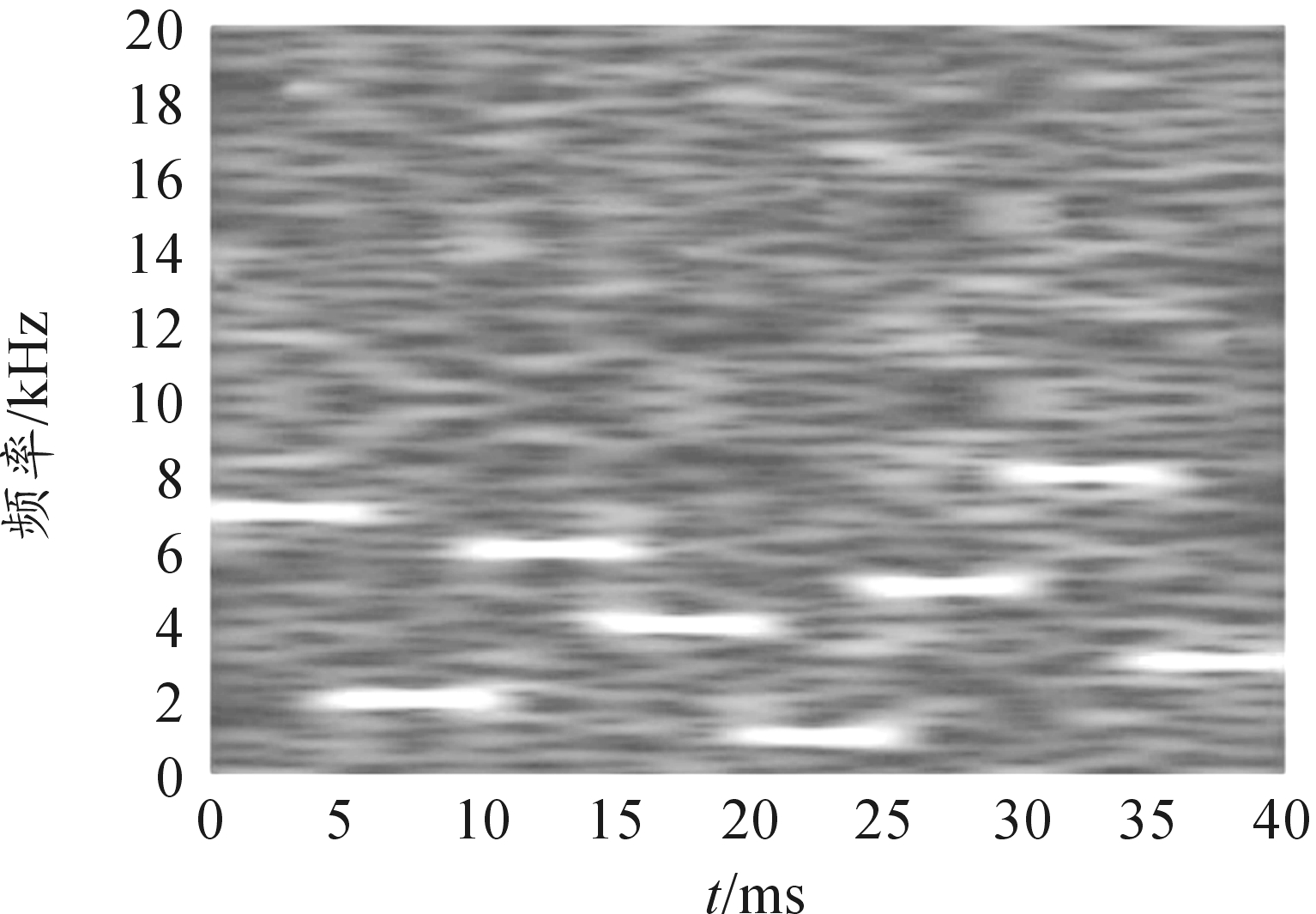
图1 信号谱图
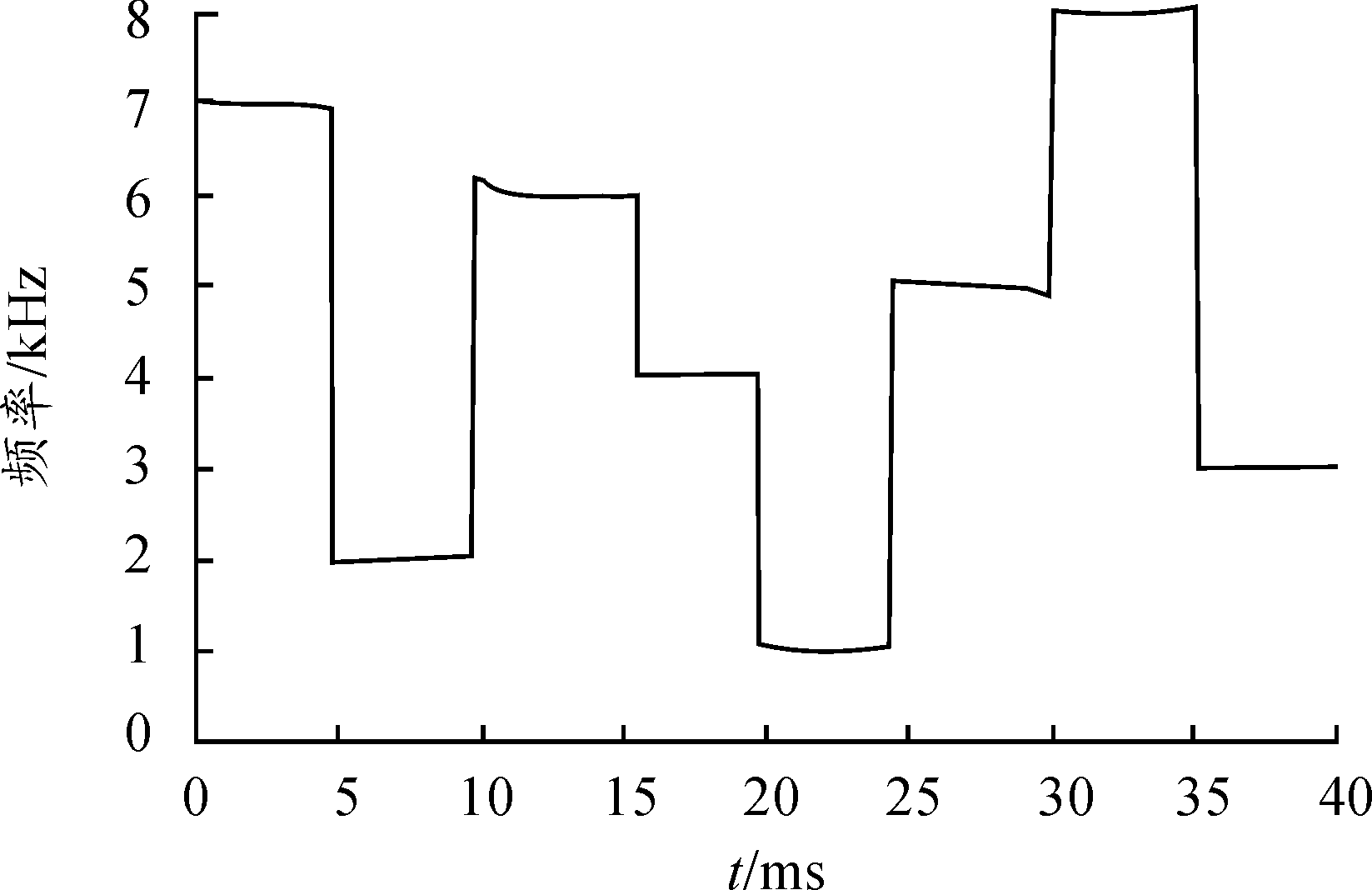
图2 频率脊线
2.1 时频图修正
由于不同检测门限的方法产生的检测结果差别较大,会直接影响各项参数的精确度,因此选择合适的检测门限十分重要。传统的基于能量检测方法,是将各个数据段的短时能量与给定的阈值进行比较来分辨信号的存在。但在背景噪声起伏较大情况下固定阈值方法会失效,因此这里选择自适应门限的方法来对时频谱图进行修正。使用能量分割的方法计算信号短时能量,含有载频段短时能量远大于不含载频段能量,如图3所示。通过将短时能量等距分割可得到初始阈值,利用初始阈值划分噪声段,再进行二次配置得到较强噪声的新阈值,来标记信号中较强的噪声段并进行去除,最后修正不连续的频率值,即可得到更为清晰的时频图。
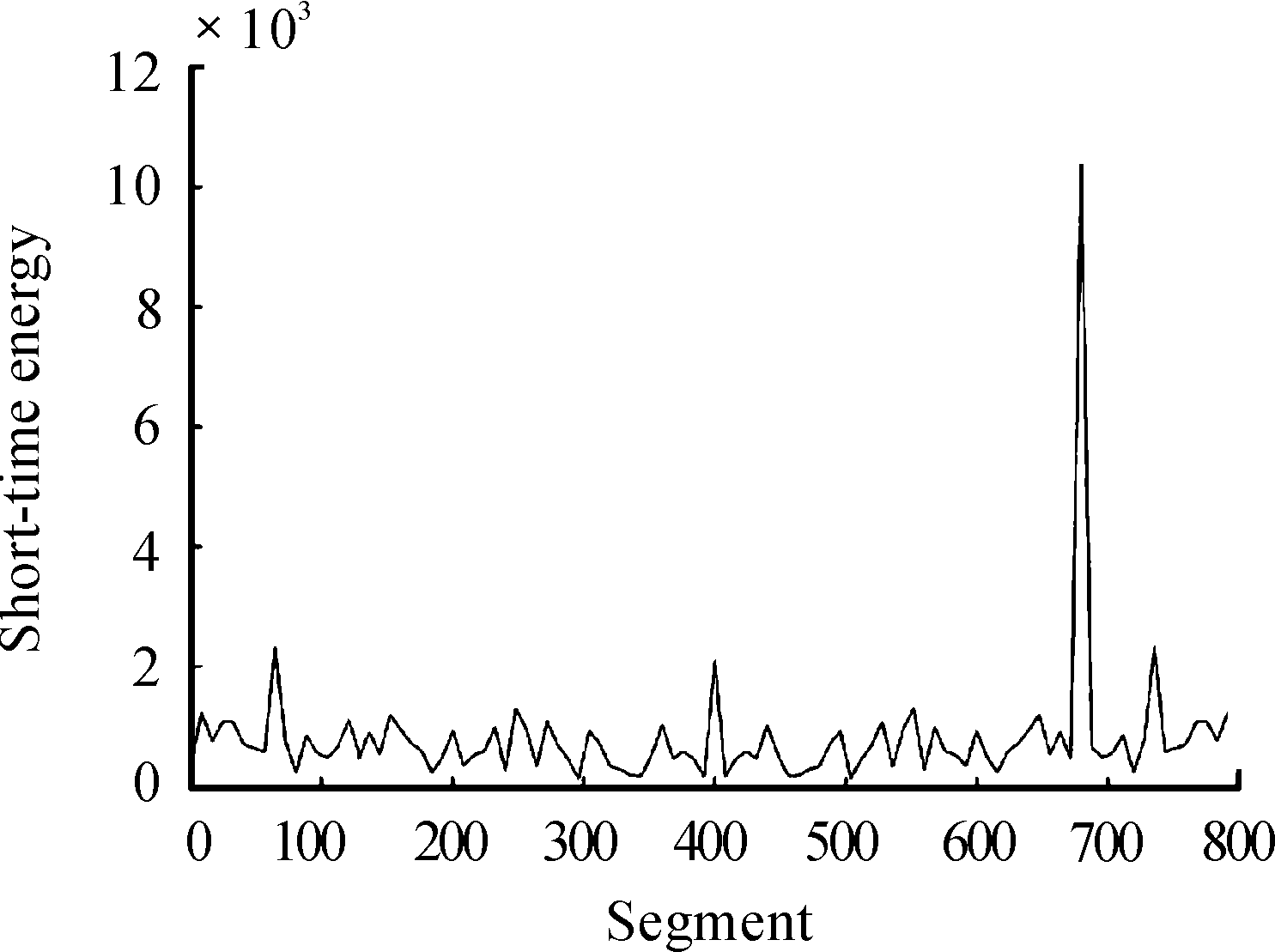
图3 短时能量图
具体时频图修正步骤为:
步骤1 将B(m,l)数据分为k段,每段长L,可以依次计算第k段的短时能量为:
(5)
式(5)中,b为B(m,l)中元素。
对短时能量E进行等间距分割,即:
(6)
得初始阈值为:
(7)
步骤2 将初始阈值γ0与E(k)中的元素进行比较,若E(k)<γ0,则标记为噪声段。将噪声段标记为up(p=1,2,…, P0),将其他非噪声段标记为vq(q=1,2,…,Q0)。
步骤3 为去除含有较强噪声的数据,计算迭代阈值。
将得到的非噪声段取平均能量,有:
(8)
得新阈值为:
(9)
步骤4 再次将E(k)中的元素与新阈值γ1进行比较,若E(k) <γ1,则标记为噪声段,记为up(p=P0+1,P0+2,…,P1)。根据标记将噪声段数据去除,这就导致原数据的不连续。去除数据段两端数据使用插值法填补,即得到修正后的时频图,如图4所示。
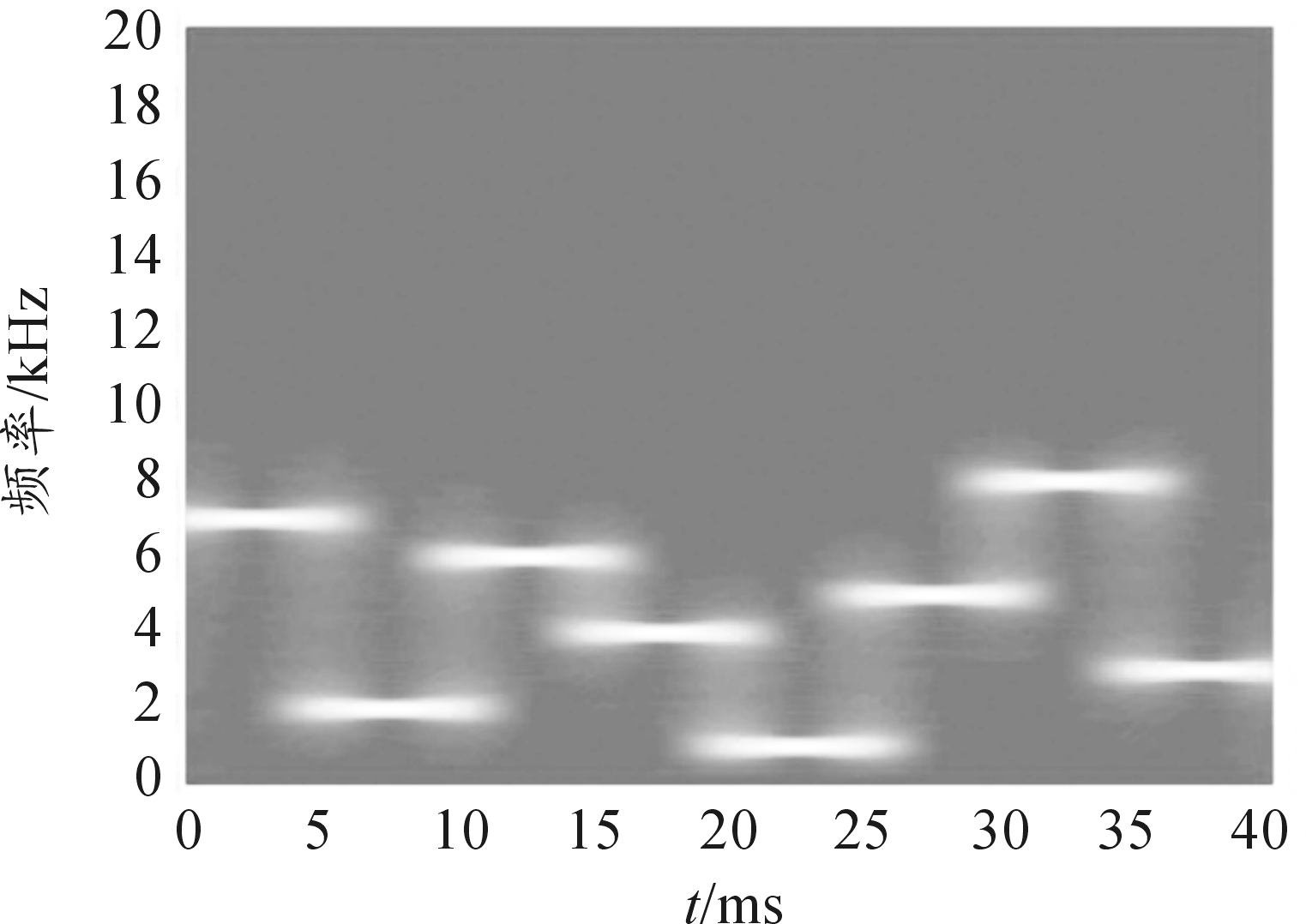
图4 修正后的时频图
2.2 特征参数估计
提取修正后的时频图中频率脊线,如图5所示,对标记的im跳变时刻存在区间内进行二次搜索。对区间内求一阶差分方程,所得极值点时刻即为跳变时刻的估计值Td(d=1,2,…,D)。再通过求两个跳变时刻估计值的差值即可得到跳频信号的跳变周期估计值。
为避免某一估计值对精确度影响过大,这里使用切尾平均数的方法,对所得到的跳变周期估计值去极值求平均值,得到跳周期的估计值计算结果Th(h=1,2,…,H)。
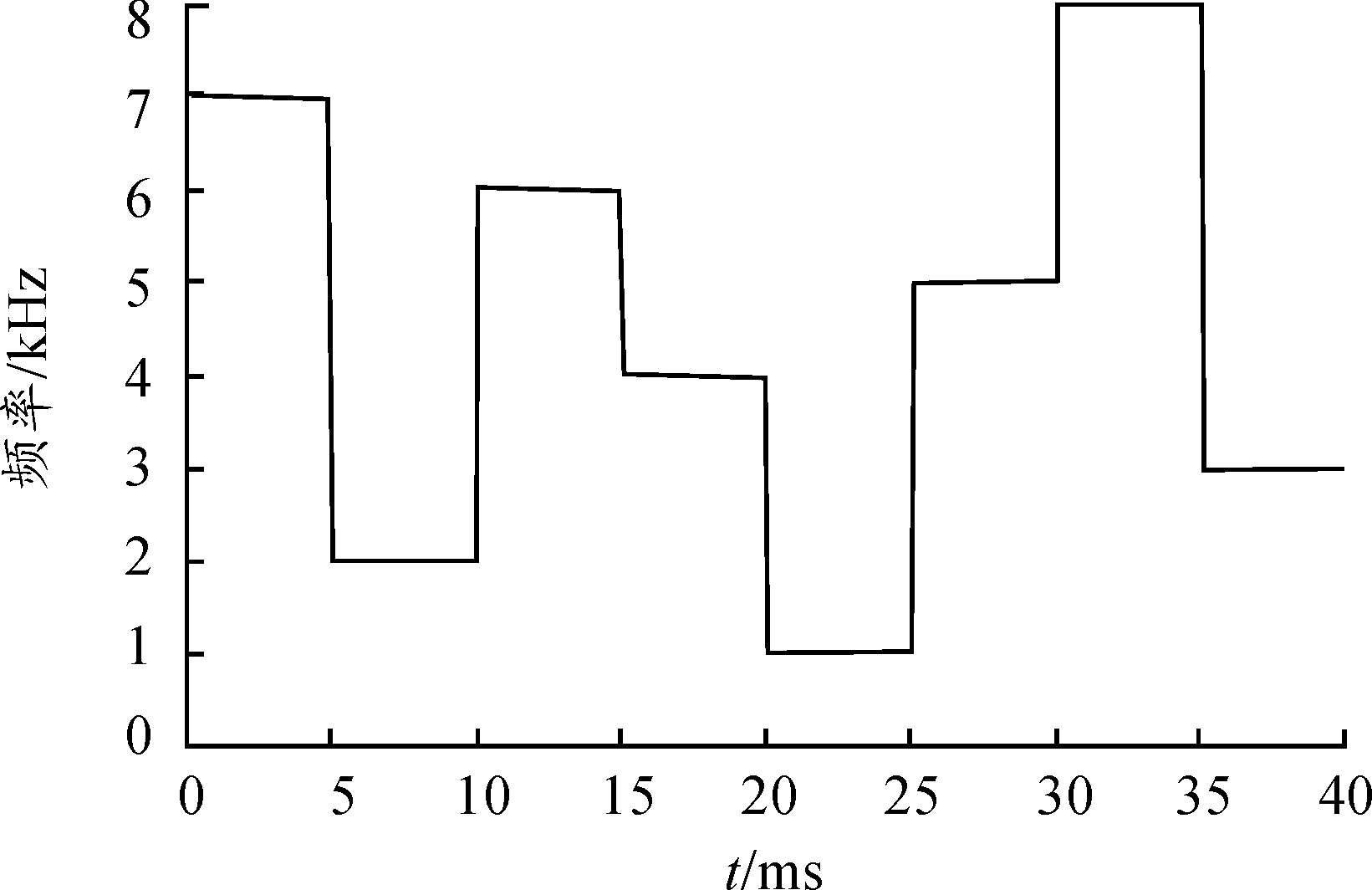
图5 修正后的频率脊线
用得到跳变时刻对信号进行划分,可以得到每一跳信号。实际跳频信号产生过程中,频率跳变并不是即时跳变的,而是在两个稳定的载波频率之间存在转换时间间隙,系统在这个时间间隙内完成一个频点切换到另一个频点的转换。显然,包含转换时间间隙的数据段估计出跳频的频率是有偏差的,跳速越快影响越大。粗估计区间包含了这个转换时间间隙。在此选取每两个标记了粗估计区间之间的数据段,利用峰值前后DFT变换系数的频率修正项的频率估计方法得到每跳信号频率。离散化信号点的DFT系数为:
(10)
则可得信号幅度谱为:
S(k)=|X0(k)|
(11)
幅度峰值点(km,S(km))的前后点,即(km-1,S(km-1))和(km+1, S(km+1))。
当S(km+1)>S(km-1),真实频率在(km,km+1)之间,则:
![]()
(12)
当S(km+1)<S(km-1),真实频率在(km-1,km)之间,则:
![]()
(13)
当S(km+1)=S(km-1),真实频率在km处,则:
Δk0=0
(14)
最终可得该段信号频率为:
(15)
3 仿真实验与结果分析
为不失一般性,验证本文中方法参数盲估计的可行性,通过MatlabR2017b仿真平台进行仿真分析实验证其性能(使用本文方法与常用的SPWVD方法以及文献[9]和文献[12]进行比较)。这里设定的仿真条件和参数为:采样频率fs为20 kHz,观测时间为8个周期共40 ms,采样点数N为800,频率集f为[7,2,6,4,1,5,8,3]kHz,信号跳周期Th为5 ms。
为了进一步分析方法的抗噪性,本文中对同一跳频信号样本在[-3,5]信噪比下情况进行200次蒙特卡洛仿真实验,规定测量精确度:
(16)
式(16)中:n代表第n个测量值;![]() 代表第p次实验真实值;p代表第p次实验。用et表示跳变时刻估计误差,用eT表示跳变周期估计误差,用ef表示跳变频率估计误差。
代表第p次实验真实值;p代表第p次实验。用et表示跳变时刻估计误差,用eT表示跳变周期估计误差,用ef表示跳变频率估计误差。
图6、图7分别为在不同信噪比的情况下,使用本文方法与文献[9]和文献[12]以及SPWVD计算得到的跳变时刻估计误差曲线、跳变周期估计误差曲线。图8为在不同信噪比的情况下,使用本文方法与文献[9]和SPWVD计算得到的跳变频率估计误差曲线。
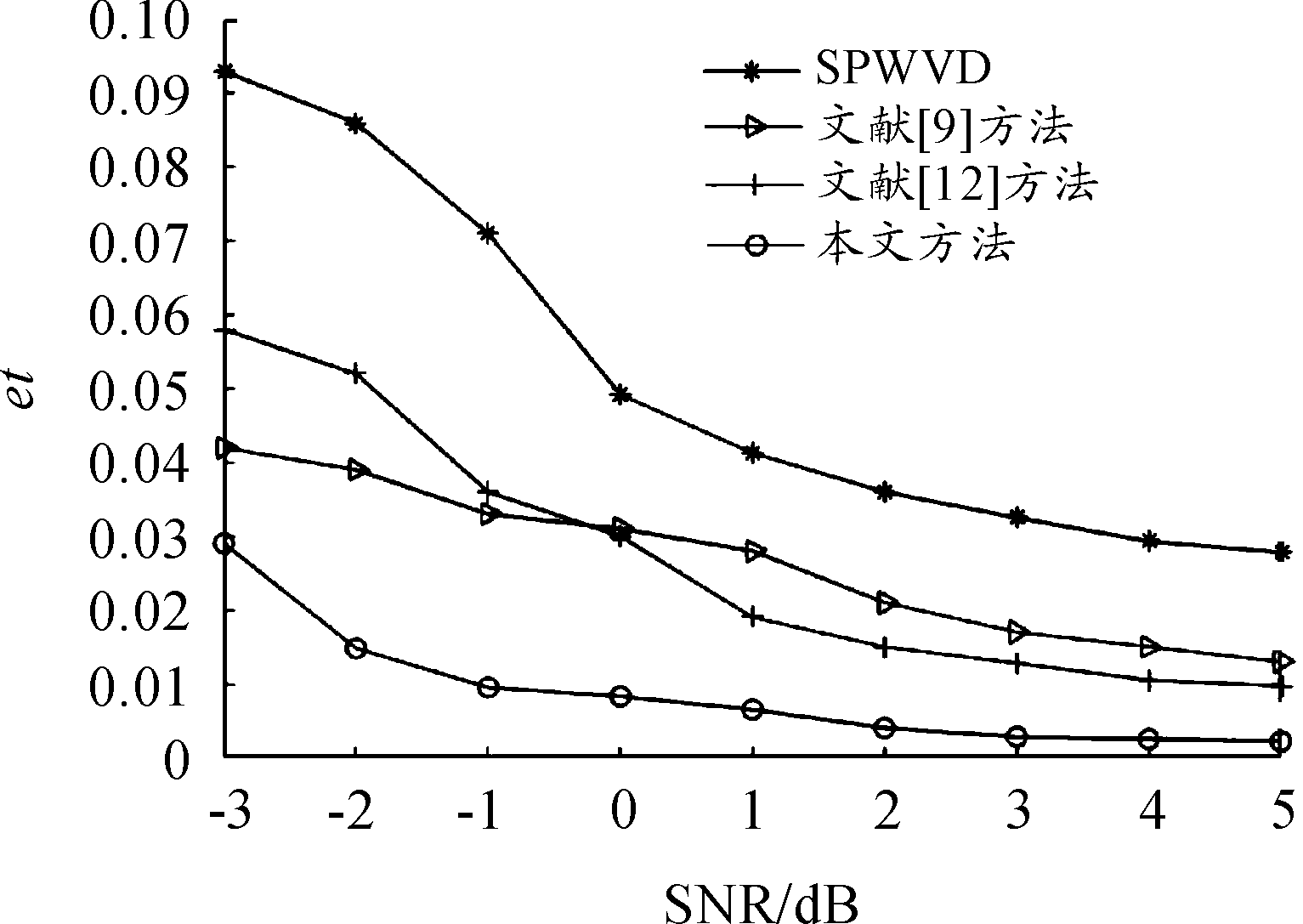
图6 跳变时刻估计误差曲线
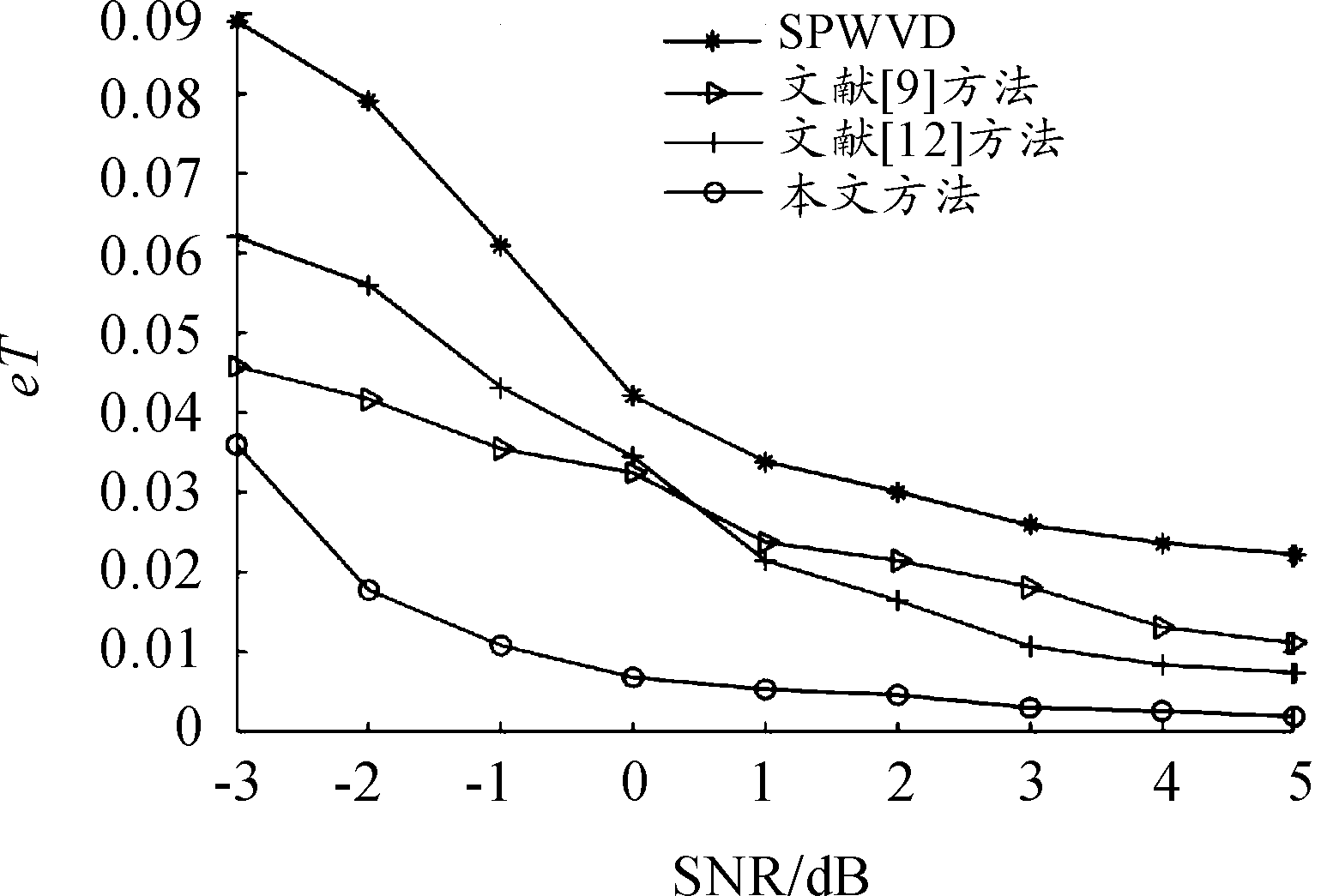
图7 跳变周期估计误差曲线

图8 跳变频率估计误差曲线
由图6、图7可见,在跳变时刻估计和跳变周期估计方面,文献[12]的改进型SPWVD方法、文献[9]的压缩感知方法和本文方法在精度方面都优于传统的SPWVD方法,改善了传统SPWVD方法在SNR=0处附近开始迅速衰减的问题,有着更高的估计精度。文献[9]和本文方法在抗噪性方面更为稳定。由图8可见,在跳变频率估计方面,本文使用信号DFT变换系数构造频率修正项方法的估计精度更高,取得了更好的效果。
4 结论
通过利用本文提出的基于时频分析的跳频信号参数估计方法进行跳频参数估计的仿真实验,证实了本文方法在处理跳频信号时有着更好的抗噪性和更高的估计精度。与SPWVD等方法相比,可以得到更高质量的跳频信号的特征参数盲估计结果。
[1] 孟令杰,张顺健,翟翔.战术电台跳频通信反侦察抗干扰效能分析[J].火力与指挥控制,2018,43(06):76-80.
[2] ROTHMAN T.Random paths to frequency hopping[J].American Scientist,2019,107(1):46-53.
[3] SA SOUSA J,VILELA J P.Uncoordinated Frequency Hopping for Wireless Secrecy Against Non-Degraded Eavesdroppers[J].IEEE Transactions on Information Forensics and Security,2018,13(1):143-155.
[4] 范海宁,郭英,艾宇.基于原子分解的跳频信号盲检测和参数盲估计算法[J].信号处理,2010,26(05):695-702.
[5] ANGELOSANTE D,GIANNAKIS G B,SIDIROPOULOS N D.Estimating Multiple Frequency-Hopping Signal Parameters via Sparse Linear Regression[J].IEEE Transactions on Signal Processing,2010,58(10):5044-5056.
[6] 郭建涛,王宏远.低信噪比下的跳频信号参数估计[J].计算机工程与应用,2010,46(27):142-144.
[7] 张伟,王宇,乔玉龙,张朝柱.基于OMP-SLR的多跳频信号参数估计方法[J].无线电工程,2018,48(10):871-875.
[8] 东润泽,郭英,张坤峰,杨银松.基于原子范数的多跳频信号时频参数估计[J].系统工程与电子技术,2018,40(11):2581-2585.
[9] 任旭,朱卫纲.基于压缩感知的跳频信号参数估计[J].计算机工程与设计,2016,37(4):867-871.
[10] LIU F,MICHAEL W.Compressive sampling for detection of frequency-hopping spread spectrum signals[J].IEEE Transactions on Signal Processing,2016,64(21):5513-5524.
[11] 付卫红,张云飞,韦娟,等.基于压缩感知的跳频信号参数盲估计算法[J].通信学报,2017,38(12):48-56.
[12] 蔡云,刘成皓,张鑫.非协作跳频通信信号参数估计与仿真[J].计算机仿真,2018,35(11):202-206+219.
[13] 冯涛,袁超伟.跳频信号的时频分析新方法[J].北京邮电大学学报,2010,33(3):10-14.
[14] YANG W,MENG L,WANG L,et al.Parameter Estimation of Frequency Hopping Signals Based on Time Frequency Analysis[J].Lecture Notes in Electrical Engineering,2013,187:131-140.
[15] 赵方超,蒋建中,郭军利,等.形态学滤波与组合时频分布跳频信号参数估计[J].太赫兹科学与电子信息学报,2013,11(6):942-947.
[16] ZHENG Y,CHEN X,ZHU R.Frequency hopping signal detection based on wavelet decomposition and Hilbert-Huang transform[J].Modern Physics Letters B,2017.
[17] YU S,YOU X,OU W,et al.STFT-like Time Frequency Representations of Nonstationary Signal with Arbitrary Sampling Schemes[J].Neurocomputing,2016,204(5):211-221.
[18] 付卫红,王璐,贾坤,等.基于STFT与SPWVD的跳频参数盲估计算法[J].华中科技大学学报(自然科学版),2014,42(09):59-63.
[19] 金艳,周磊,姬红兵.基于稀疏时频分布的跳频信号参数估计[J].电子与信息学报,2018,40(3):663-669.