磁悬浮可以用于实现各种机械结构的高速、无摩擦运转，比如运用到高速磁浮列车、高速磁悬浮电机、磁悬浮轴承等[1]。单点悬浮系统是一个非常典型的非线性系统，并且是磁浮列车悬浮控制的基础，尽管在较长时期里有过诸多智能控制算法在单点悬浮系统的控制中的技术尝试，但是在工程实践中，由于难以实现磁浮列车受到轨道不平顺、乘客上下车和在车厢走动的影响而引起的磁浮间隙随机性的即时跟踪，最终此类算法均表现得不尽人意。目前磁浮列车基本上还是依靠PID控制算法实施行驶控制。
1999年韩京清教授提出了具有抗干扰且不依赖被控对象模型的“自抗扰控制”[2](ADRC,Auto Disturbance Rejection Control)，经过近20年的发展，ADRC算法已经在坦克炮控系统、导弹姿态控制、机器人控制等系统中广泛运用。
本文针对单点悬浮系统的动力学特性，将ADRC算法应用于磁浮控制，并与PID进行比较，从中探索出适用于磁浮列车行驶控制的技术特点。
1 系统模型与问题描述
1.1 单点悬浮系统模型
本文以常导磁吸式(EMS)磁浮列车为例，参见图1(a)所示。
为了保证这种悬浮的可靠性和列车运行的平稳性，使直线电机具有较高的功率，必须精确地控制电磁铁中的电流，使磁场保持稳定的强度和悬浮力，使车体与导轨之间保持大约10 cm的间隙。EMS通常采用气隙传感器来实施系统的间隙反馈控制。
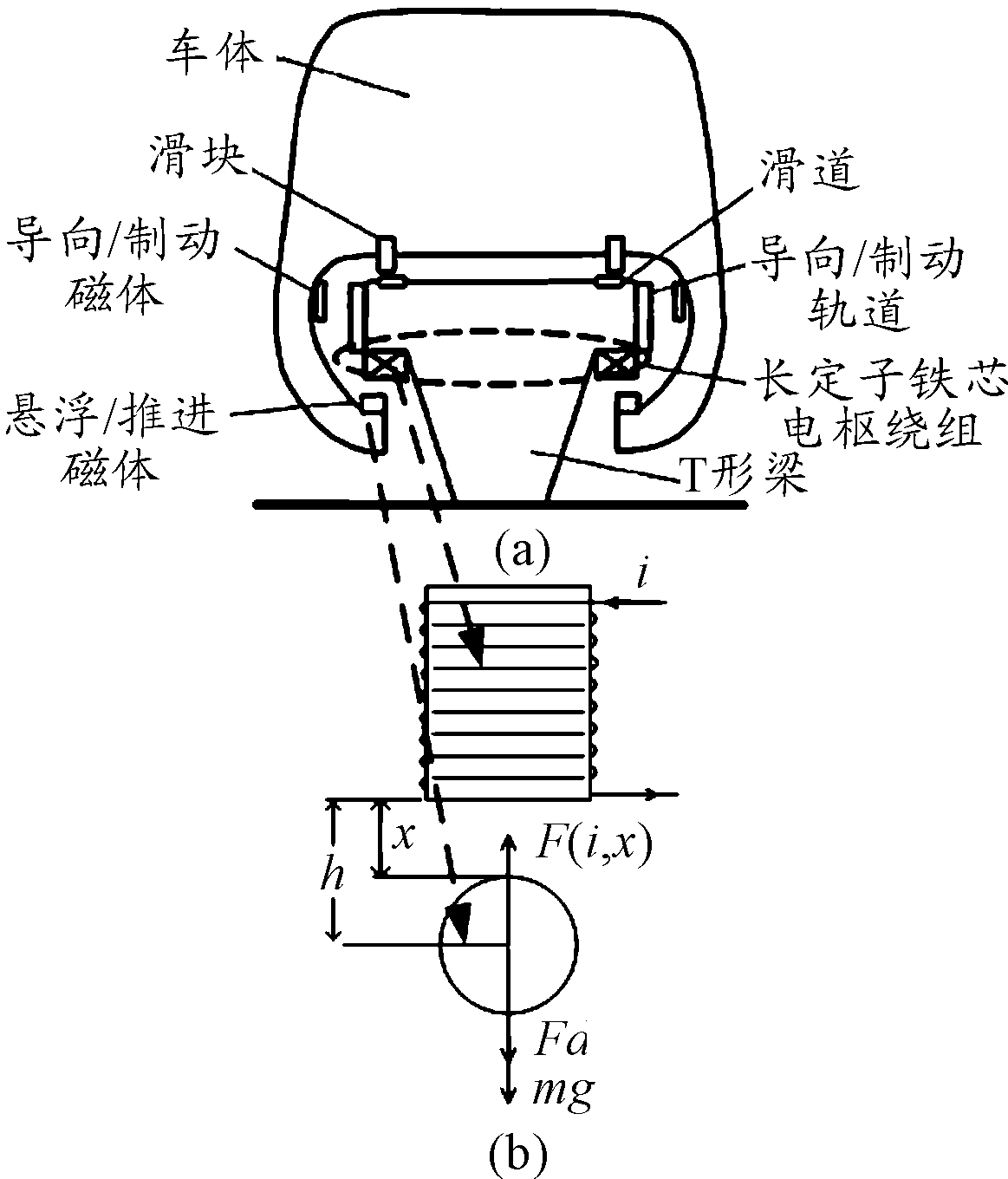
图1 EMS系统原理及其基础动力学模型
为了引入“自抗扰控制”算法，有必要对实际的悬浮系统进行一种抽象与简化，因此可以获得如图1(b)所示的单点悬浮基础动力学模型，该动力学模型即表达了单点悬浮物理系统。图中的虚线(箭头与圆框)系抽象(虚拟)过程的“思维表达线”。
图1(b)中的上方为固定电磁铁，代表设置于轨道的长定子铁心电磁铁，下方的铁磁性球，代表列车模拟体。当电磁铁上的线圈绕组通入电流i时产生的电磁场对下方的铁磁性球便形成吸力F(i,h)。当产生的吸力与铁磁性球的重力相等时，铁磁性球就悬浮在空中，两者之间的间隙x即是列车的悬浮高度。此时，铁磁性球处于不稳定的平衡状态，当铁磁性球受到外力fd干扰时，极易失去平衡。为了使系统维持稳定，势必需要加上反馈环节。为此，必须设计一种控制算法，以确保悬浮达到稳定控制的技术要求。
当列车达到设定的悬浮高度时，电磁吸力和列车重力相等，此时列车就被悬浮起来。可见，单点悬浮系统的控制等价于磁浮列车整车悬浮的控制基础。其动力学方程为
(1)
式中: m为铁磁性球的质量；h为铁磁性球的质心到电磁铁磁极面的距离,h=x+d,d为铁磁性球的半径，x亦即铁磁性球的悬浮高度；g为地球重力加速度； fd为铁磁性球所受的外界干扰力； F即F(i,h)，为铁磁性球所受到的吸力。其中
(2)
式中：i为电磁线圈中的电流；K为定义常数，
为空气磁导率；A为磁通流过铁磁性球截面的导磁面积；N为电磁线圈匝数。由式(1)、式(2)可得
(3)
忽略悬浮铁磁性球位置的变化对电感的影响，可以得到方程
(4)
式中：U为电磁铁两端电压；R为电磁铁等效电阻；L为电磁铁绕组等效电感。
当铁磁性球处于平衡状态时，重力和电磁吸力相等，由牛顿第二定律可得铁磁性球此时所受的合力为零。即
mg+F(i0,h0)=0
(5)
F(i0,h0)为铁磁性球悬浮高度为x0、平衡电流为i0时电磁铁对铁磁性球的电磁吸力。
联立式(3)、式(4)、式(5)后，得
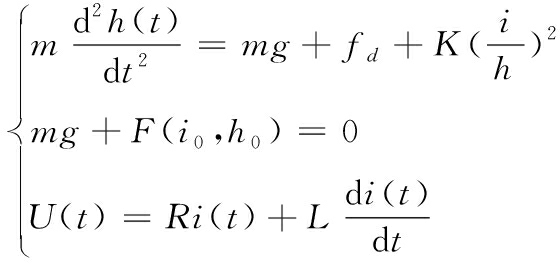
(6)
即为单点悬浮系统运动动力学方程。
1.2 单点悬浮系统模型线性化
对于单点悬浮系统，电磁铁的电流作为控制输入量，并不考虑感抗对于系统的影响时，可在平衡点x0附近对动力学方程进行线性化处理。
对式(2)进行泰勒级数展开并省略高阶项[3]
令
可得单点悬浮系统的线性化模型为
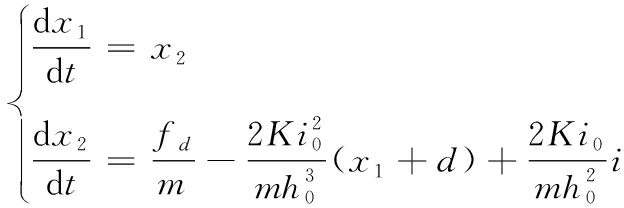
(7)
将式(7)中的
项当作一个新的未知的干扰状态变量，并令
2 自抗扰控制器的设计
ADRC主要由跟踪-微分器(TD)、扩张状态观测器(ESO)、非线性状态误差反馈控制律(NLSEF)组成，用TD安排过渡过程并提取给定输入的微分信号；用ESO估计对象状态和不确定扰动作用[4]；用过渡过程与状态估计间的误差的非线性组合和扰动估计量的补偿来生成控制信号[5]。ADRC实现的核心在于ESO中的扰动补偿项，该项对系统的模型参数变化和未知外扰作用共同给予估计和补偿[6]。
本文设计的单点悬浮系统的ADRC结构如图2所示。
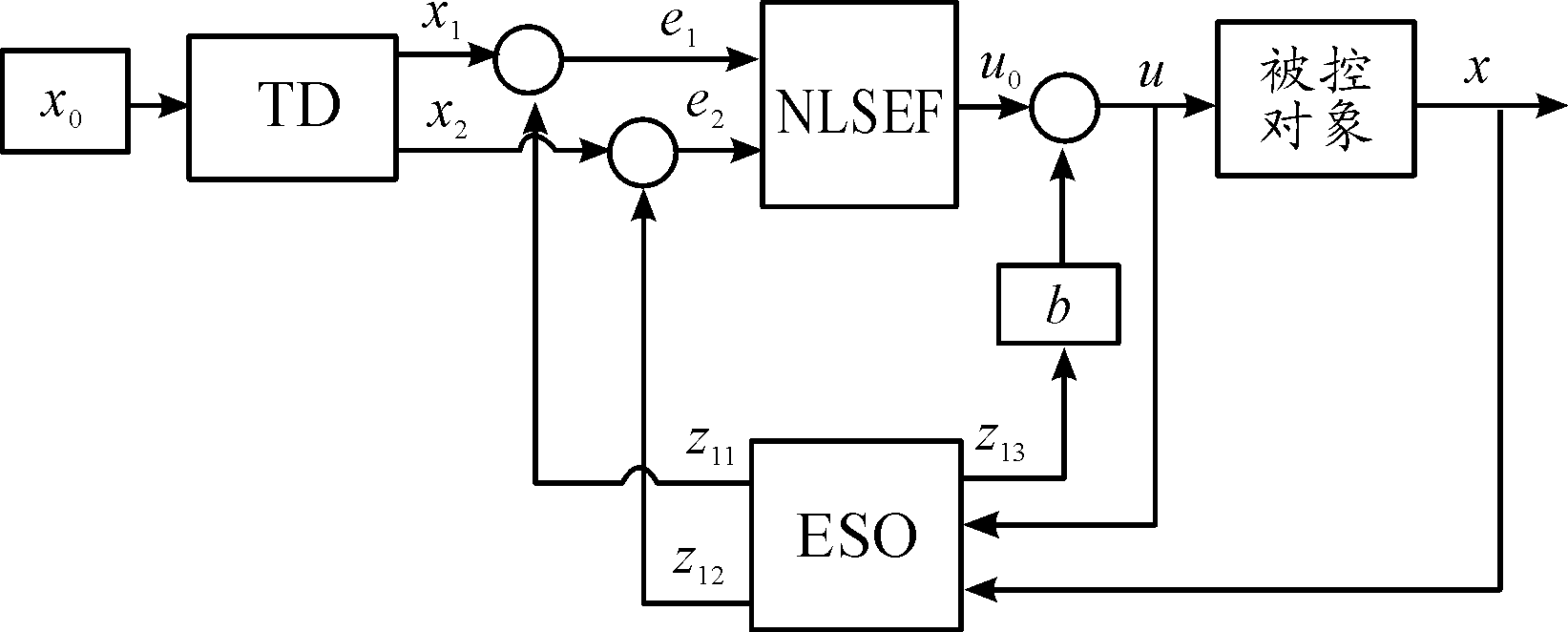
图2 单点悬浮系统自抗扰控制结构框图
图2中x0是单点悬浮系统中铁磁性球的设定悬浮高度，x1是二阶Levant微分器对输入x0的跟踪信号，x2是Levant微分器对输入信号x0微分信号的跟踪，x为铁磁性球的实时悬浮高度，z11为扩张状态观测器对铁磁性球实时悬浮高度x的跟踪输出，z12为扩张状态观测器对铁磁性球实时悬浮高度微分信号
的观测输出，z13为扩张状态观测器对式(7)扩张出来的干扰状态变量x3的跟踪输出，b是补偿因子，e1、e2分别为x1与z11和x2与z11的差值，u10为经过非线性PD控制律计算后的输出，u1为经过补偿后的控制量。
单点悬浮系统需要考虑变化的设定悬浮间隙，并以此判断控制器对于变化的设定悬浮间隙的适应性。为了能快速的跟踪设定悬浮间隙的变化，并且避免因为设定值的突变所造成控制量的剧变而产生超调[6]，将ADRC控制器中的TD环节，设计为二阶Levant微分器[7]，其二阶滑膜微分器的表达式为
(8)
式中，
其中C>0,C是输入信号v(t)的Lipschitz常数上界。采用Levant微分器可实现s跟踪输入信号v(t),u1跟踪输入信号的微分
三阶扩张状态观测器为
(9)
式中， βi>0(i=1,2,3)，饱和函数fal(e,α,δ)的作用就是为了抑制信号的抖振，其表达式为
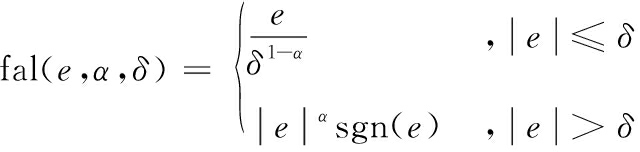
(10)
在扩张状态观测器式(9)中，z11是状态x1的观测量，z12是状态x2的观测量，z13是扩张状态的观测量，可以实现对被控对象式(7)中未知部分的干扰及模型不确定性部分的观测，即对
的观测。扩张状态观测器是ADRC的核心部分，用于解决ADRC技术中扰动观测这一核心问题，将影响被控对象输出的扰动作用扩张成新的状态变量，用特殊的反馈机制来建立能够观测被扩张的状态观测器，这个扩张状态观测器并不依赖生成扰动的模型，也不需要直接测量就能对扰动进行观测，得到估计值，尤其是在实际工程中通过扩张状态观测器可将系统的参数摄动和周围环境的干扰进行观测，这对于解决实际工程中的干扰问题具有较好的应用价值。
本研究采用的非线性控制律为一种PD形式的非线性控制律，其表达式为：
u=β10fal(e1,α10,δ0)+
β20fal(e2,α20,δ0)
(11)
式中：0<α10<1<α20；e1是设定的悬浮位置信号与悬浮小球实际的悬浮位置之差；e2是设定悬浮位置信号微分与悬浮小球速度输出之差；fal(e,α,δ)函数同式(10)表达式相同。
通过扩张状态观测器的变量z13跟踪被控对象中扩张出的未知干扰状态变量x3[8]通过消减x3(即z13)可将原被控对象简化为
(12)
这就变成了一个双重积分器串联单位增益的控制问题，由式(7)、式(12)可得控制量
(13)
式中，
是补偿扰动的分量，
是用非线性反馈去控制积分器串联型分量[9]。
3 参数整定
根据式(7)可得图2中的补偿因子
参数的调节过程中首先调节Levant微分的参数α和λ，使其能够快速稳定的跟踪输入信号；接着给被控对象一个固定的控制量使被控对象有输出即可，同时调节扩张状态观测器的参数β1、 β2、 β3、α1、α2、δ使扩张状态观测器能够快速精确的跟踪状态变量x1、x2、x3，通常将α1取0.5，α2取0.25即可，其余的4个参数按照β1<β2<β3的原则调节，δ尽可能的取一个较小的正值；最后将扩张状态观测器和非线性控制律接入到闭环控制系统中，此时调节非线性PD控制律中的参数β10、 β20、α10、α20、δ0即可。β10、 β20按照β10>β20进行调节，通常β10是β20的10倍左右；，通常α10<α20取α10=0.75,α20=1.5，δ0是扩张状态观测器中参数δ的10倍左右。按照以上参数的整定步骤使被控对象能够稳定的输出设定的悬浮间隙信号。
4 仿真分析
单点悬浮系统的仿真参数如表1所示。
对单点悬浮系统分别采用PID和ADRC控制方式，主要在以下几个方面展开仿真研究：
1) 在系统突然加大负载情况下的冗余能力；
2) 控制器对设定间隙变化的适应性；
3) 控制器对设定参数变化的鲁棒性。
表1 单点悬浮系统仿真参数
参数参数值悬浮小球质量m/g94设定悬浮高度x0/m0.005铁磁性球半径d/m 0.022 5铁磁性球导磁截面积A/m21.239×10-3电磁铁线圈匝数N/匝1 600平衡电流i0/A0.836 3K/(Nm2·A-2)-9.960×10-4
1) 阶跃响应
在图3中，实线为ADRC间隙H阶跃响应曲线，虚线为PID控制的间隙H阶跃响应曲线。由图3可以看出ADRC的动态性能优于PID，ADRC的调节时间为0.085 s，PID控制的调节时间为0.35 s；ADRC超调量小于PID控制的超调量；由此可以看出在单点悬浮系统的间隙阶跃响应中ADRC的性能优于经典的PID控制。
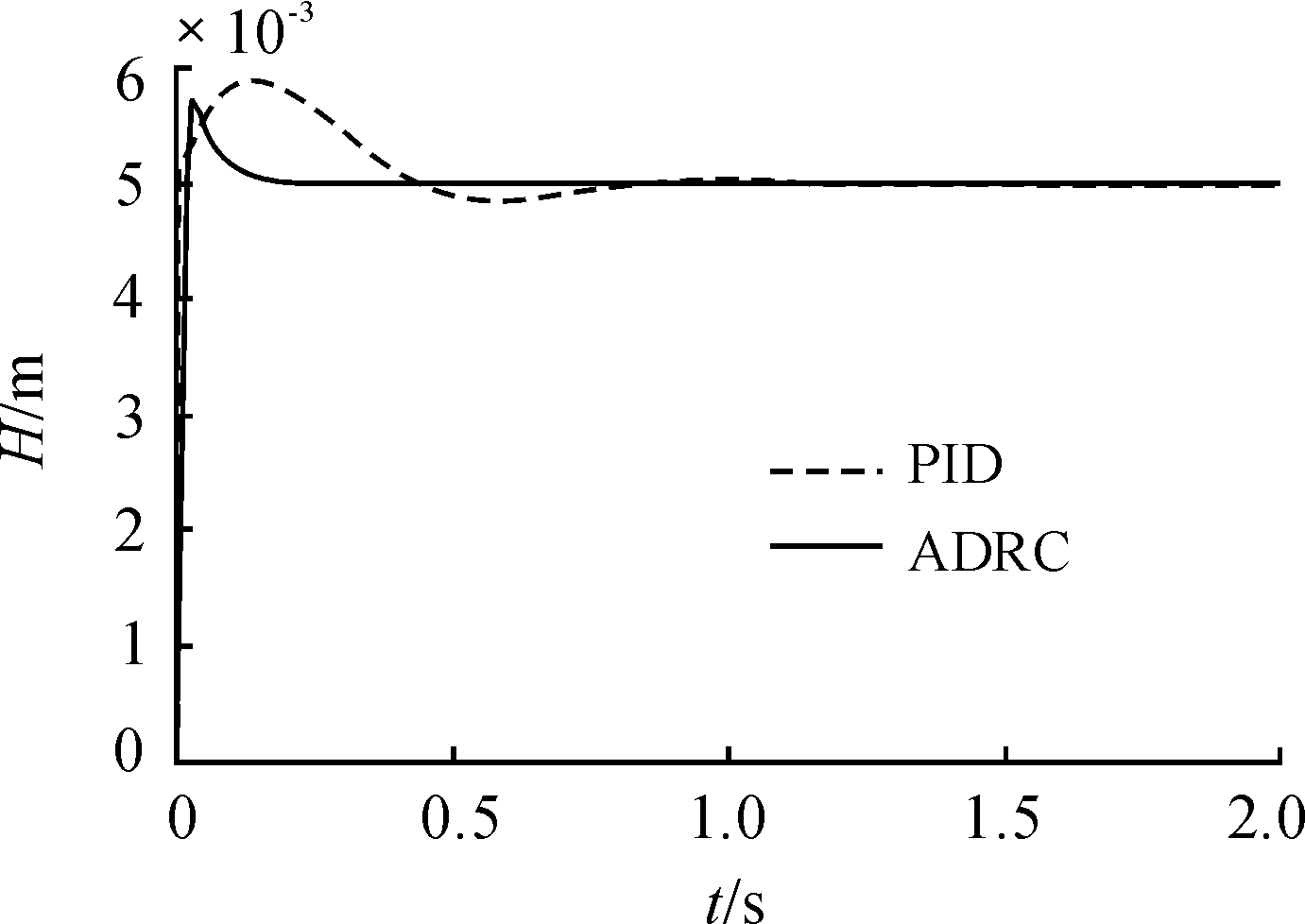
图3 ADRC和PID间隙阶跃响应曲线
如图4所示，从上到下的顺序，实线是阶跃响应中ADRC扩张状态观测器对输出信号x、微分信号y、干扰信号z的观测输出曲线；虚线是单点悬浮系统中实际的悬浮高度输出、微分信号输出和实际干扰信号的输出曲线，可知ADRC的扩张状态观测器可以很好的观测到系统的输出信号、微分信号和干扰信号。
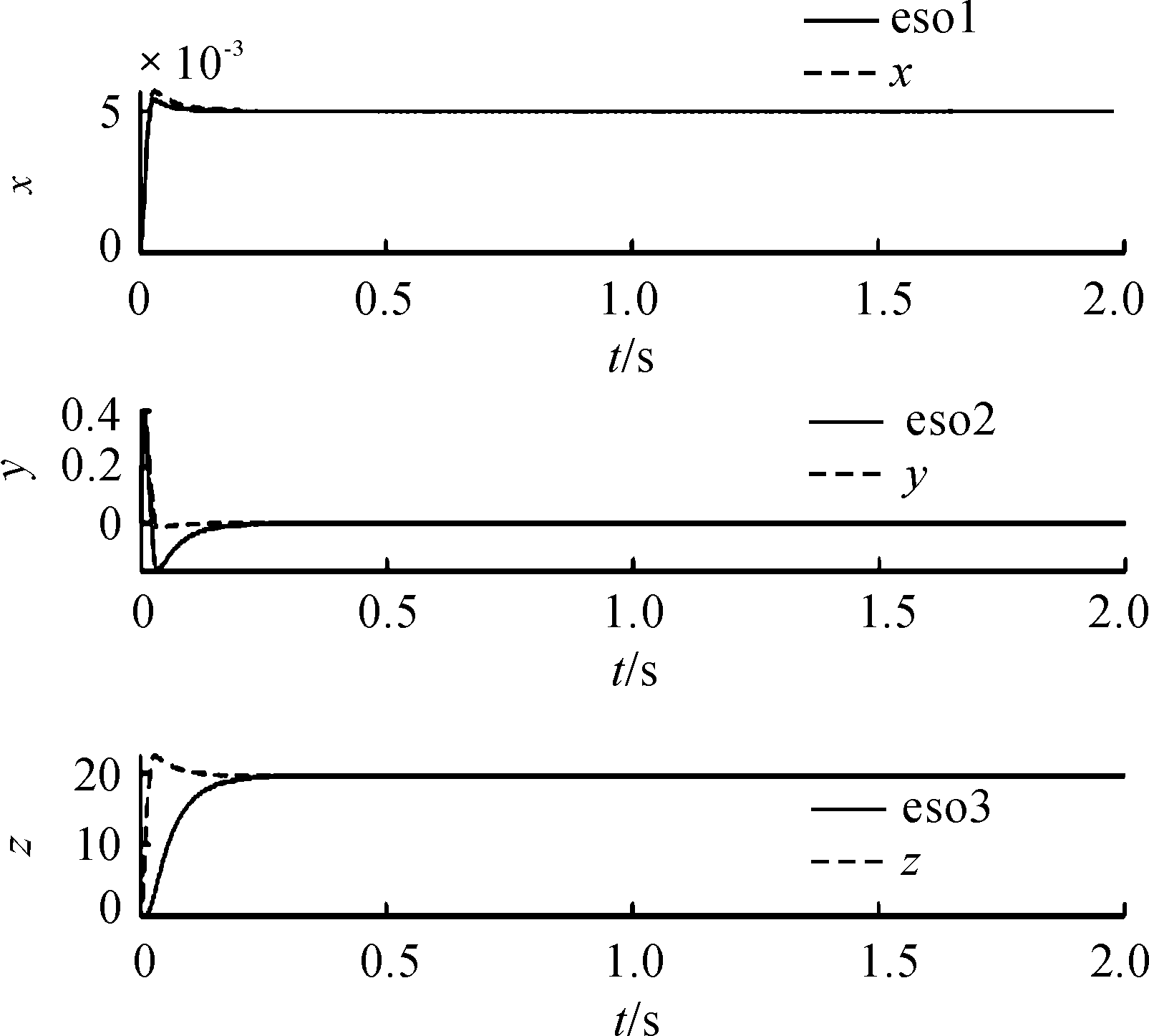
图4 阶跃响应ADRC的扩张状态观测器输出曲线
2) 冗余实验
图5中实线和虚线分别表示采用ADRC和PID控制方法时，在5 s时刻突然加4.7 N阶跃负载的间隙H响应曲线。ADRC和PID两种控制方法在此种情形下最大间隙变化量分别为1.954 mm和2.245 mm：完全恢复到平衡位置ADRC需要0.3 s的时间，PID控制需要1.3 s的时间。此处所加的负载是单点悬浮小球自身质量的5.1倍，由此可知ADRC比PID更能适应大范围负载的变化，ADRC闭环控制系统具有很强冗余能力和抗干扰能力，这也为高速磁悬浮列车搭接结构的冗余控制提供了一条技术思路。
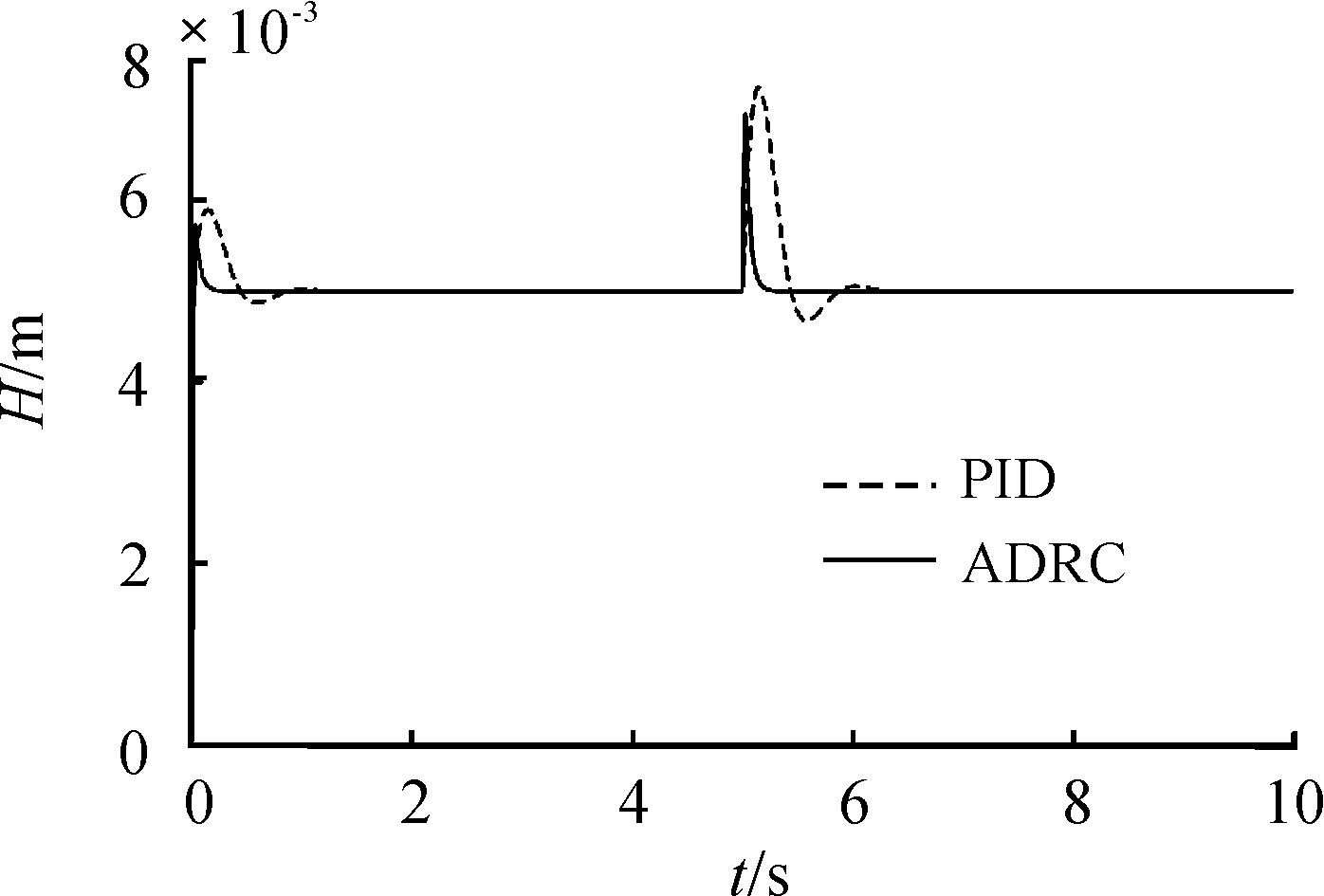
图5 ADRC和PID冗余实验曲线
如图6所示，实线是冗余实验中ADRC的扩张状态观测器对输出信号x、微分信号y、干扰信号z的观测输出曲线；黑色虚线是单点悬浮系统中实际的悬浮高度输出、微分信号输出和实际干扰信号的输出曲线，在5 s时刻突加4.7 N的负载，由式(7)中可知，此时ADRC的扩张状态观测器将4.7 N的负载当作外界的干扰处理，由于 fd前的系数
的影响，此时外界干扰被放大倍后为50 
N,此时总干扰力就为69.598 N,由图6可知，ADRC的扩张状态观测器依然可以很好地观测出系统的外界干扰。
正是由于ADRC控制器中扩张状态观测器的这样一种特殊的性质使得ADRC具有很强的抗干扰能力和天然的解耦性能，给控制不确定对象系统克服其复杂的扰动性提供了解决方案[10]。
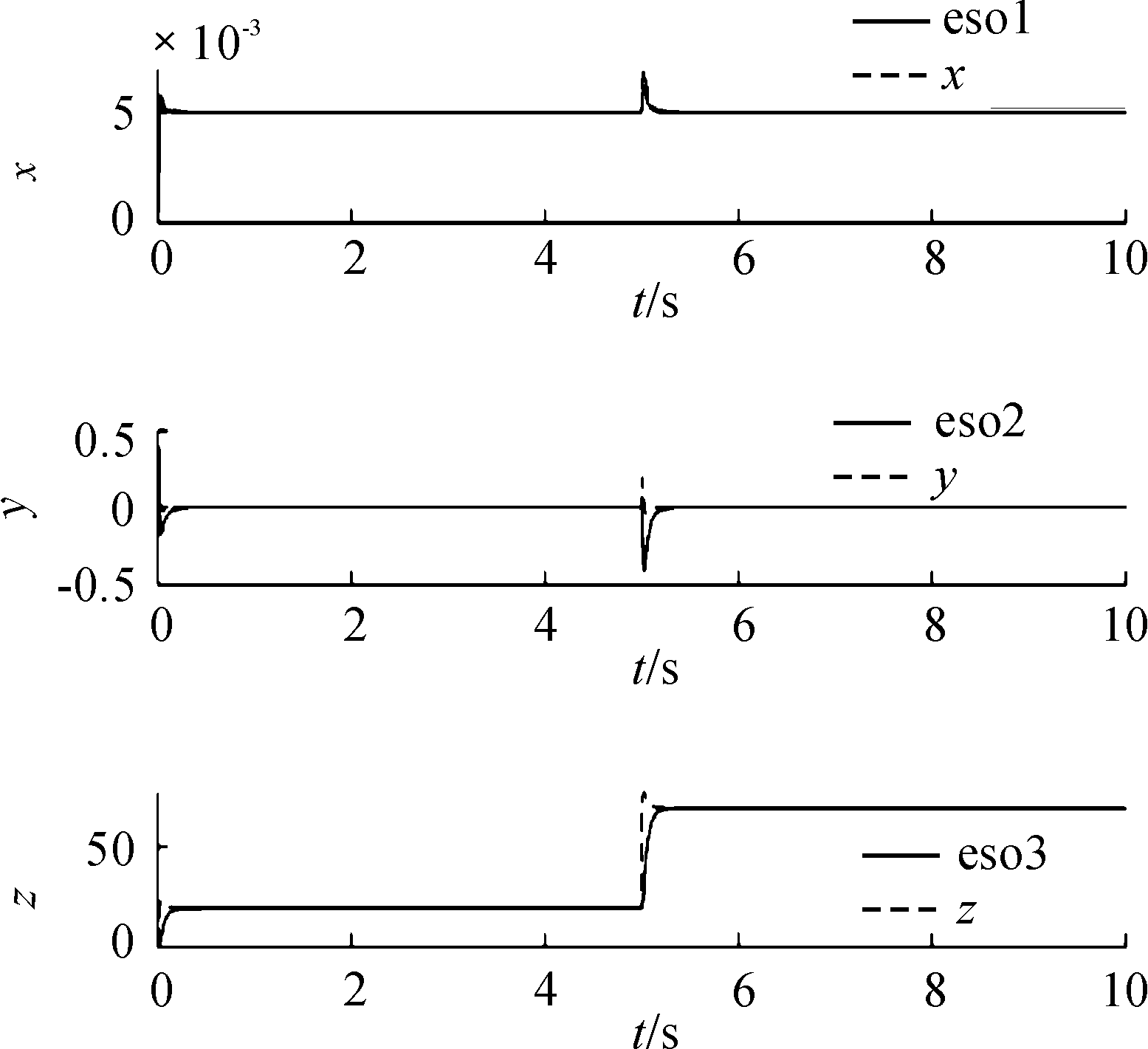
图6 冗余实验ADRC的扩张状态观测器输出曲线
3) 跟随性试验
图7中短虚线为设定的间隙H变化曲线，变化范围在3～9 mm，实线和长虚线分别为ADRC和PID控制输出间隙曲线，可知，ADRC比PID控制能更好地跟踪变化的设定间隙。
图7 ADRC和PID跟随性试验输出曲线
图8中在设定间隙不断变化的情况下，ADRC的扩张状态观测器在观测输出信号x、微分信号y和干扰信号z方面依然展现出很好的观测性能。
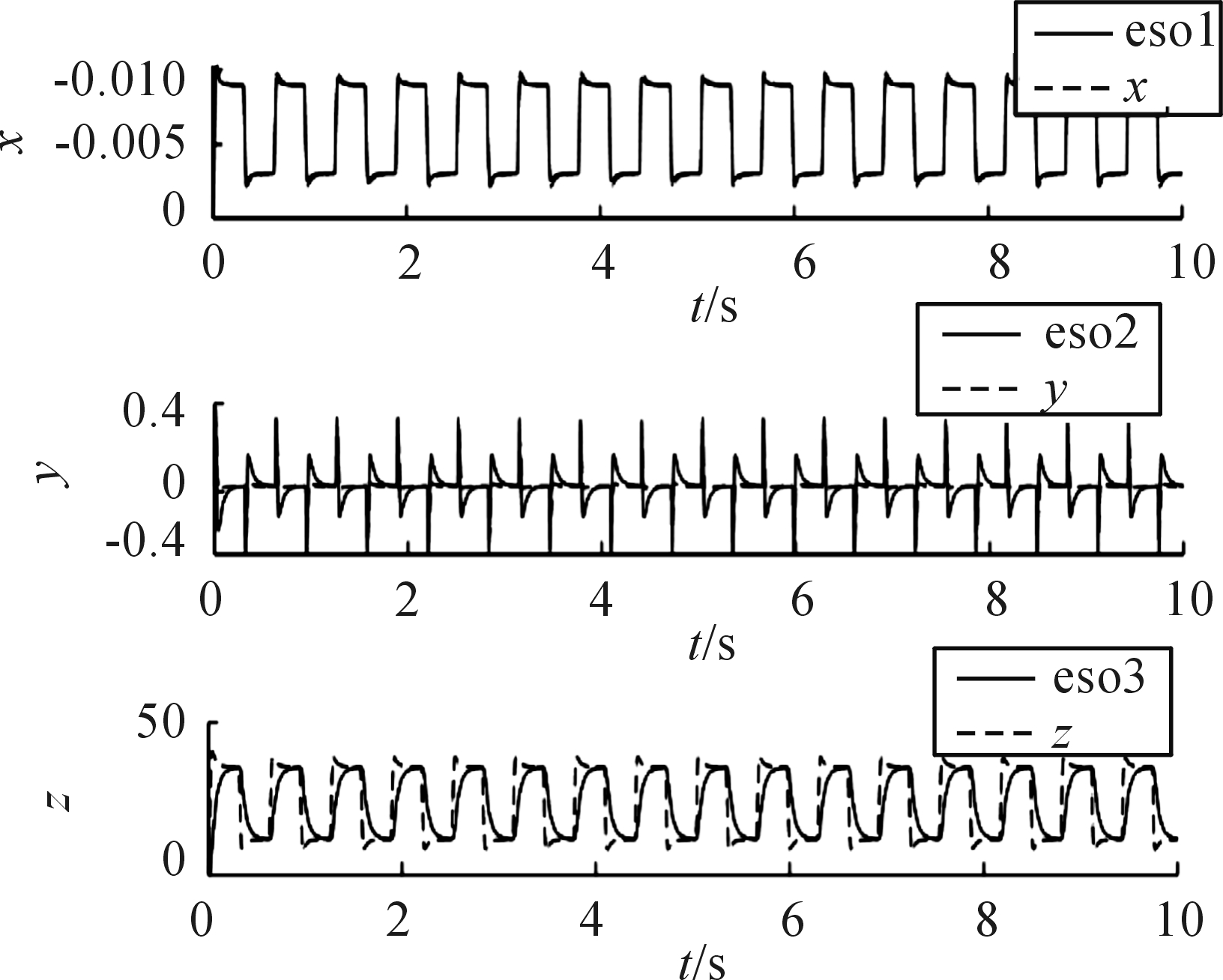
图8 跟随性试验中ADRC扩张状态观测器输出曲线
5 结论
ADRC充分发挥了非线性函数的强功能和高效率，通过Levant微分器在基本无超调的前提下实现信号的快速跟踪，从而解决超调与快速性的矛盾；非线性PD控制律中fal函数中的参数一般取值范围为0<α<1,0<δ≤1，结合公式(10)fal函数的表达式易得该函数实际上蕴含了“小误差大增益，大误差小增益”的控制知识和具有快速收敛的特性，因此这种控制律易于实现，并且具有良好的鲁棒性和适应性。
单点悬浮系统仿真结果表明ADRC在快速性、适应性和克服大扰动能力方面都明显优于经典的PID。
单点悬浮系统的ADRC仿真实验可以为工程实现提供理论指导，对于具体的工程化运用，参数必须结合实际系统的具体特性来调整，才能取得满意的控制效果。
[1] 王玲玲，王宏，梁勇.磁悬浮球控制系统的仿真研究[J].兵器装备工程学报,2017(4)；122-126.
[2] 韩京清.自抗扰控制技术——估计补偿不确定因素的控制技术[M].北京：国防工业出版社，2008:243-280.
[3] 向晓燕,梁平原,张书真,等.优化算法在磁悬浮控制器设计中的应用[J].计算机仿真,2012,29(10):263-267.
[4] 程启明,郑勇,杜许峰,等.自抗扰控制器串级三冲量汽包水位控制系统[J].热能动力工程,2008(1):69-72,108.
[5] 韩启银,杨锦.自抗扰控制器在火电厂主蒸汽温度控制中的仿真研究[J].广东电力,2007(9):20-24。
[6] 何凌云,佘龙华,赵春霞.磁浮列车悬浮系统的双环自抗扰控制[J].兵工自动化,2006(11):59-61.
[7] OBEID H,FRIDMAN L,SALAH,et al.Adaptation of Levant’s differentiator based on barrier function[J].International Journal of Control,2018,91(9).
[8] 唐堂.四旋翼无人机姿态的自抗扰控制算法研究[D].南宁：广西师范大学,2018.
[9] 曹辉,李双跃.基于自抗扰控制的非圆截面数控车削[J].机械设计与研究,2011,27(1):77-79.
[10] HUANG Yi,XUE Wenchao.Active.disturbance rejection control:Methodology and theoretical analysis[J].ISA Transactions,2014,53:963-976.