信息化技术的发展全面推进了军事科技的进步,使得侦察技术与伪装技术的对抗也向着越来越广阔的领域延伸。在图像侦察领域,通过心理物理学实验对侦察照片判读过程进行定量分析是研究图像评价指标的重要方式[1]。
眼动追踪技术最早作为心理学研究手段被提出,Babcock等[2-3]率先将其运用于研究图像特征与注意力关联问题,Alert[4]使用眼动追踪技术对地图地标的明显程度进行了研究,近年间,Traynor等[5-7]将研究重心转向注意力产生机制。国内研究主要集中于技术应用,在媒体、教育、纺织等行业均有基于注意力机制的研究成果出现[8-10]。为基于心理物理学的判读过程定量研究带来了新的实验思路。
目前,国内外对于目标侦察判读的研究主要依靠人员主观评价,缺少可靠的科学评价体系。针对上述问题,运用计算机图像处理技术与仿真技术进行模拟测试在一定程度上缓解了现地实验的较高需求,但也存在数据化的客观评价难以与主观评价相联系的问题。参照部分眼动追踪系统在视觉评价上的应用成果,本研究将眼动仪运用于目标搜寻过程分析,以建立注视指标与目标图片参数之间的联系。
1 基于眼动仪的目标搜寻过程
侦察活动根据其任务目的不同,可分为监视与目标捕获两种类型,而在目标与背景存在某种程度的相似,伪装措施的保护,目标本身尺寸、形状难以发现等情况下,需要观察者进行目视搜寻。通常情况下,搜寻任务是利用某类光电成像系统,完成对侦察地域全景拍摄后进行视场搜寻,观察者在搜寻过程中迅速扫描侦察图像以获取目标信息。
观察者的搜寻过程是随着注视点连续跳动而进行的定点信息搜索、询问以及判断目标存在与否而进行的。这一过程中,视线跳动的移动方式被称为急动,在眼动研究领域也被称为眼跳[11]。急动的速度和长短取决于不同观察对象,因此视觉模型的构建必须考虑典型人眼运动的特性。
眼动仪基于眼动轨迹对视线落点进行追踪,可以精准记录眼球运动、瞳孔缩放与位置等信息,适用于人眼视觉系统分析、心理学、媒体产品设计等诸多领域。
搜寻过程的复杂性多源自于无法通过数据来精准反映,过往研究中多利用搜寻概率模型预告搜寻目标的大体概率。这一模型虽然已在部分科研领域得到验证,但仍存在使用限制较多、视场信息结合较低等不足。因此,本文通过眼动数据分析,研究观察者搜寻过程的具体规律,定量分析侦察照片特征。
2 眼动仪指标选择
常用的眼动仪观测指标包括首次发现时间、注视点、注视时间、注视率等。
首次发现时间指观察者从开始观察时刻起到视线首次接触感兴趣目标经过的时间,通常表明搜索过程中发现目标的难易,能够反映目标在背景中的鲜明程度。
注视点指的是视线在某一位置停留,代表了观察者进行了对观察点的认知过程,在有任务驱动的实验中可以反映观察者对任务目标的肯定。但这一指标过高则倾向于表现出被试难以迅速确定目标,对观察区域信息难以及时辨析。
注视时间反映了观察者处理注视点信息的时间,较长的注视时间通常被认为是难以辨析观察点信息,观察不完善伪装目标或假目标时有一定可能出现此类状况。
注视率为注视时间与注视点数量的比值,反映了观察者对观察区域信息读取的难易度。若注视点较多而注视时间短,则分散在每个注视点的注视时间极短,观察点处于频繁移动并不断分辨信息的状态,即观察者难以确定观察目标或分辨图像信息。反之,则表示图像信息易于辨认,目标明显。
3 实验方案设计
本实验采用Tobii T120型眼动仪,采样频率60 Hz,显示屏为标准17英寸,屏幕分辨率1 920×1 080。试验场景如图1,实验对象面对电脑屏幕,双眼距离屏幕50~60 cm,可平视显示器上三分之一区域。参与实验者共37名,均为在校大学生,年龄在20~24岁,无视觉方面生理缺陷,具有一定的军事常识。

图1 眼动仪实验场景
为减少主观因素影响,实验前确保被试具有基础的先验知识,观察过程以军事目标搜索为任务驱动。
实验图片取自某山区20个地点的无人机航空拍摄照片,为确保目标在无伪装条件下清晰可见,拍摄高度定为距目标水平面40 m,每轮拍摄用时约20 min。采用控制变量法,选取“亮度”与“目标显著度”2个侦察敏感元素为研究对象。通过在一日之内的不同时刻对同一地点进行拍摄来获得具有不同亮度信息的照片,本文采用从早6时至中午11时每隔1 h进行一次拍摄的方式,获得6组不同亮度水平照片,具体数值为使用拍摄地区所测亮度均值;在每5个地点对目标实施不同程度的伪装,最后将拍摄地区分为“无伪装”“实施不完善伪装”“实施完善伪装”“无目标”4类,对应目标显著度由高到低,并对应量化分数为“3”、“2”、“1”、“0”。
为确保被试实验数据的准确性,本文采用间断实验法,设置单张图片观察时间10 s,每两次观察间插入10 s黑幕作为视觉缓冲,尽量确保观察当前图像的第一反应不受前一张图片影响。每位被试将观察20张图片,每张图片的亮度为随机抽选。为最大程度上消除图片顺序对实验结果带来的影响,用均匀设计法对实验进行优化。为减少无意义眼跳及扫描路径对结果分析产生的影响,采用AOI分析法分别确定各个图片的感兴趣区域进行指标统计。
4 实验结果与分析
4.1 指标可靠性分析
不同图片的相同要素,如形状相近的道路、林地等势必会对观察者造成影响,由于眼动仪观察实验要求被试双眼位置保持稳定,预实验中选择插入黑幕的方式,尽量消除当前观察印象对后续观察造成的影响。选择测试过程中同一时刻拍摄的一组图像,对获取的眼动仪指标进行检验。
表1为主成分分析检测结果,以凝视时间,首次发现时间,注视点数目作为参照,可以看出,在显著性P小于0.01的情况下,不同图片3项指标的F值分别为12.537、8.519、14.884,说明各个图片的3种指标均有明显差异,即图片对被试的视觉刺激有显著不同。
表1 不同地点图片间效应检测结果

因变量自由度F值显著性凝视时间4912.537<0.01首次发现时间498.519<0.01注视点数目4914.884<0.001
再对相关数据进行方差齐次检验,各个变量与主要测量指标间方差齐次概率介于0.21~0.57>0.05,说明方差齐次,可进行方差显著性检验,所得指标数据差异具有统计学意义。
4.2 亮度分析
表2给出了一定亮度水平下眼动仪评价指标相关参数,图2为各个指标随亮度变化的趋势。
表2 亮度相关参数均值统计
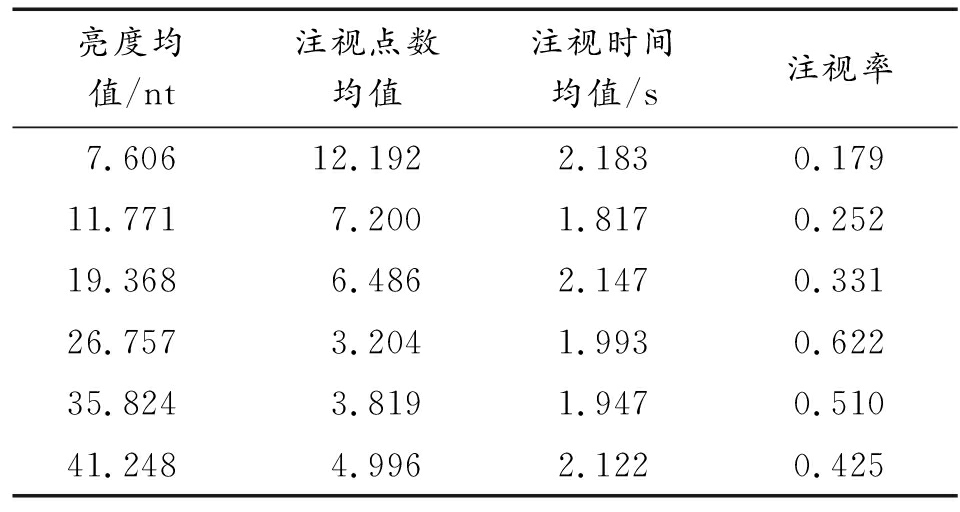
亮度均值/nt注视点数均值注视时间均值/s注视率7.60612.1922.1830.17911.7717.2001.8170.25219.3686.4862.1470.33126.7573.2041.9930.62235.8243.8191.9470.51041.2484.9962.1220.425
综合注视点数、注视时间、注视率三项指标可见,亮度过低时,注视点较多而注视时间短,注视率指较低,表明观察者难以对暗环境下拍摄的照片进行高效地辨识,观察效率较低;而随着亮度提升,注视点数明显下降,注视率逐渐上升,观察效率明显提高。实验表明,注视时间对亮度变化不敏感,而注视点数量受亮度变化影响较大,反映在观察低亮度照片,无法准确获得图像信息时,观察者会产生较多的不确定点。

图2 亮度相关参数变化曲线
4.3 目标显著度分析
4.3.1 注视时间及注释点数量
表3给出了同一亮度水平下不同图片的目标显著度观察参数。图3为各个指标随目标显著度变化的趋势。
表3 目标显著度相关参数均值统计
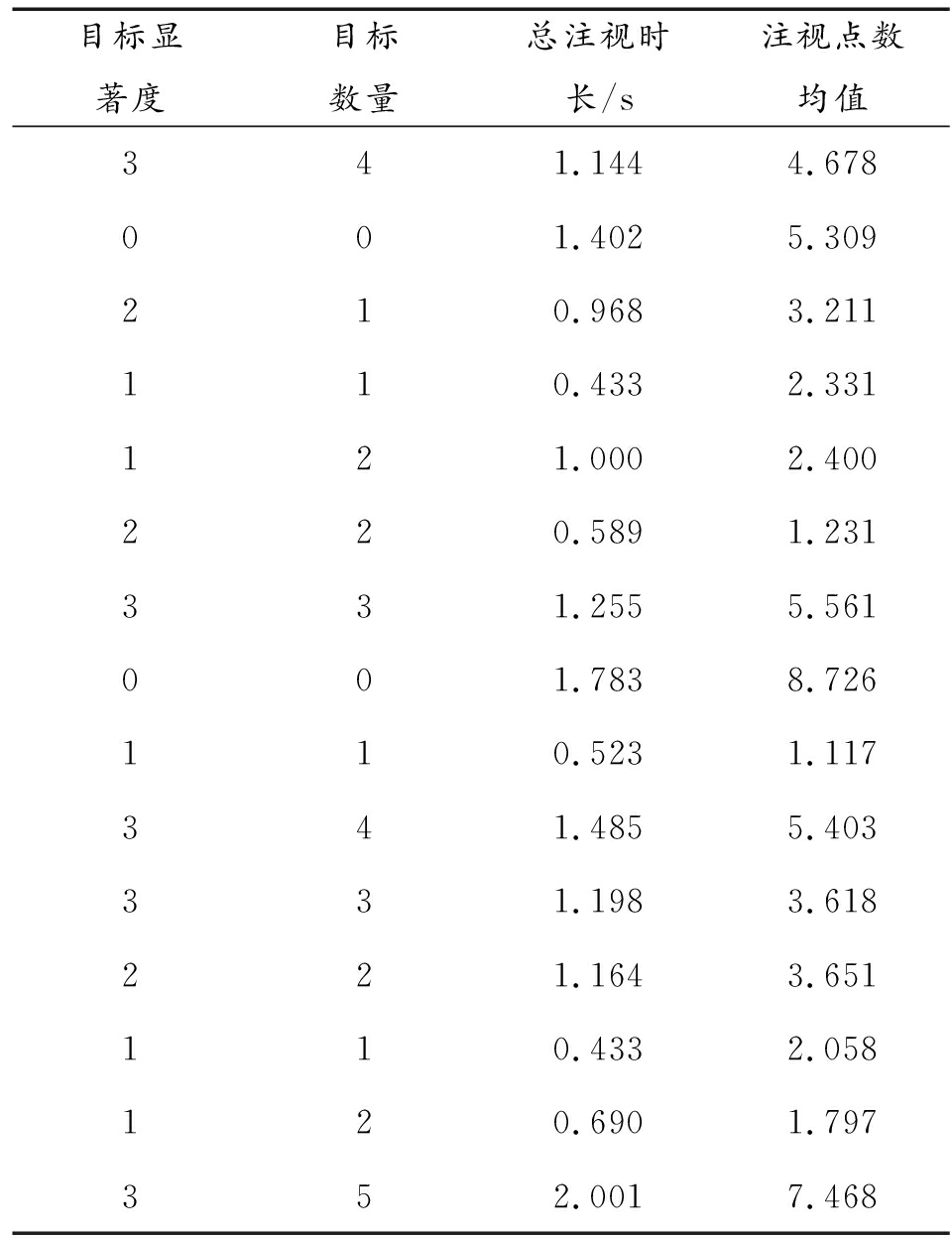
目标显著度目标数量总注视时长/s注视点数均值341.1444.678001.4025.309210.9683.211110.4332.331121.0002.400220.5891.231331.2555.561001.7838.726110.5231.117341.4855.403331.1983.618221.1643.651110.4332.058120.6901.797352.0017.468
续表(表3)

目标显著度目标数量总注视时长/s注视点数均值003.27711.864152.80910.481211.3104.081221.3135.000001.4725.250

图3 目标显著度相关参数变化趋势
从图3可以明显看出,总注视时长与目标显著度、目标数量之间的关系大致相同,显著度和目标数量为0的照片注视时间与注视点数量均偏高,反映出任务驱动下观察者无法迅速寻获目标,始终处于搜索状态;而有目标及伪装设施的图片,其注视点数及注视时间均随着目标显著度和目标数量同时上升,在一定程度上成正相关。
4.3.2 首次发现时间
表4给出了各个图片的平均首次发现时间均值与目标显著度之间的关系。图4反映了二者的关系。
从图4可以看出,仅依靠初步处理的数据,首次发现时间与目标显著度的关系大致呈负相关,说明在对观察区域的目标显著度进行合理设置的情况下,观察者首次发现时间会随着目标显著度的提高而减小,也即目标越明显,越容易被发现。参照Kabaila等对线性归回参数的解读方案,对目标进行线性回归分析以定量评价数据间关联性[12-13]。相关参数见表5所示。
表4 首次发现时间均值统计

目标显著度首次发现时间/s目标显著度首次发现时间/s02.681 0021.482 7501.950 7521.651 5002.899 0021.682 7503.262 0021.334 2512.920 0021.778 7512.188 7531.952 2512.332 7530.650 5012.406 5030.664 7512.583 3331.093 5010.932 7531.477 75

图4 首次发现时间均值与目标显著度的关系变化趋势
表5 线性回归分析参数

拟合优度R2P-相关性SigDurbin-Watson0.576-0.7590.0001.920

图5 标准化残差直方图
对数据拟合效果分析,拟合优度R2为0.576表明拟合效果一般;Pearson相关系数绝对值高于0.7且方差分析显著性小于0.001,表明此模型具有显著统计学意义。
残差检验可以有效分析回归过程中数据的有效性及是否存在干扰及其特征[14]。检验中德宾瓦特逊检验接近2,表明残差基本不具有自相关性。从图5中可以看出,残差基本符合正态分布。综上所述,可以认为在本次实验中,首次观察时间与目标显著度之间存在线性相关。
5 结论
1) 主观过程的眼动追踪参数与解析图像得到的客观数值具有相关性。针对本文所研究的两种参数的变化,被试观察结果也产生了对应的规律性变化。
2) 亮度变化可影响观察者在图像上的注视点数,表明人眼对不同亮度观察条件下拍摄的照片解读能力不同,而并非局限于传统认识上的主要受观察环境亮暗程度影响。
3) 目标显著度及目标数量的变化与注视点数量、注视时间、首次发现时间之间存在可信度较高的线性相关关系,证实了存在将视觉搜索的生理过程量化后寻求与客观参数线性关联的可行性。
4) 首次发现时间在研究生理过程对图像信息量变化而产生的反应方面相较于其他参数更具有与研究价值。对目标显著度的量化方式还有进一步优化的空间。
[1] 刘凯龙,孙向军.基于心理物理学的图象评价技术研究[J].系统仿真学报,2005(2):417-420.
[2] BABCOCK J S,LIPPS M,PELZ J B.How people look at pictures before,during,and after scene capture:Buswell revisited[J].Proceedings of SPIE-The International Society for Optical Engineering,2002,4662:34-47.
[3] EVERETT S P,BYRNE M D,GREENE K K.Measuring the Usability of Paper Ballots:Efficiency,Effectiveness,and Satisfaction[J].Proceedings of the Human Factors and Ergonomics Society Annual Meeting,2006,50(24):2547-2551.
[4] ALBERT W,LIU A.The effects of map orientation and landmarks on visual attention while using an in-vehicle navigation system[C]//Gale AG.Vision in Vehicles.London:Oxford Press,2003:3-28.
[5] TRAYNOR J M,GOUGH A,DUKU E,et al.Eye Tracking Effort Expenditure and Autonomic Arousal to Social and Circumscribed Interest Stimuli in Autism Spectrum Disorder[J].J Autism Dev Disord,2019,49:1988-2002.
[6] PATRICIA A.Alexander,The art (and science) of seduction:Why,when,and for whom seductive details matter[J].Applied Cognitive Psychology,2019,33(1):142-148.
[7] 吴丹,刘春香.交互式信息检索研究中的眼动追踪分析[J].中国图书馆学报,2019,45(02):109-128.
[8] 程时伟,魏千景,张章伟.移动设备交互环境下的注视点感知计算方法[J].计算机辅助设计与图形学学报,2019,31(01):3-11.
[9] 张苏道,薛文良,魏孟媛.眼动仪在服装面料色彩视觉评价中的应用[J].纺织学报,2019,40(03):139-145.
[10] 肖健文,黄燕燕.基于眼动仪的学习者的敏感元素研究[J].中小学电教,2018,466(10):29-34.
[11] 胡凤培,韩建立,葛列众.眼部跟踪和可用性测试研究综述[J].人类工效学,2005,11(2):52-55.
[12] HILL R J,FLACK H D.The Use of the Durbin-Watson d Statistic in Rietveld Analysis[J].Journal of Applied Crystallography,1987,20(5):356-361.
[13] KABAILA P,ALHELLI S,FARCHIONE D,et al.The effect of a Durbin-Watson pretest on confidence intervals in regression[J].2018.
[14] JUV NCIO S.NOBRE,SINGER J M.Leverage analysis for linear mixed models[J].Journal of Applied Statistics,2011,38(5):10.
NCIO S.NOBRE,SINGER J M.Leverage analysis for linear mixed models[J].Journal of Applied Statistics,2011,38(5):10.