随着航空发动机日益向着高推重比、高负荷、高效率的方向发展，其叶片变得更轻薄，结构变得更紧凑。这就使得上下游叶片之间的间距不断减小，叶片间的干涉越来越显著。上下游干涉作用引起的叶片气动弹性、周期性疲劳振动和颤振等问题变得十分突出，对这一问题的研究引起了越来越多的关注[1-3]。Huang等[4]的研究结果甚至显示上游静子的尾流会改变下游转子叶片的气动弹性稳定性，进行叶片颤振预测时应考虑相邻叶排间距的影响。杨慧等[5]使用自行开发的程序详细分析了上游静叶的尾流对转子叶片颤振稳定性的影响。
随着计算机的快速发展，计算流体力学(CFD)以其计算精确和结果可靠的优势已成为研究叶片气动弹性振动问题的主要方法，但是该方法存在着对计算资源消耗过大和耗时久(尤其是面对大型工程问题如航空发动机的内流场计算等)等的问题[6-17]。所以针对CFD技术的这些缺点，20世纪90年代提出了建立非定常气动力降阶模型(ROM)，用于解决CFD计算耗时久和消耗计算资源过大的问题[10-17]。气动力降阶模型以其消耗计算资源少，对气动力描述准确等特点，得到迅速发展和应用。Silva[14]提出了基于 Volterra 级数的非线性气动力降阶模型。Hall等[15]建立了基于谐波平衡法的降阶模型来计算涡轮机械中非定常流动，其结果表明降阶模型的计算效率比直接用CFD求解快1到2个数量级。Thomas[16]建立的POD降阶模型对跨音速条件下的三维机翼进行了颤振分析。Ashcroft等[17]的研究结果表明谐波平衡法可用于在亚音速和跨音速流动条件下准确预测二维压缩机级联的颤振特性。
气动力降阶模型的应用虽然极大的提高了计算效率，节省了计算资源，但在不同的边界条件下其计算精度不同。为了探究影响基于谐波平衡法的气动力降阶模型计算精度的因素，本文在文献[11]的基础上，通过建立不同尾流均值压力和尾流谐波振幅下的气动力降阶模型，预测叶片气动力响应，并与CFD计算结果进行对比，讨论这些因素对气动力降阶模型计算精度的影响。
1 基于谐波平衡法的尾流激励叶片气动力降阶模型
谐波平衡法的主要思想是通过对系统的状态变量进行傅立叶级数展开，将非定常系统问题转换为振幅定常问题求解，以此来直接模拟系统周期性非线性振荡现象。以图1所示的尾流激励的叶片气动力系统为例，根据文献[11]，首先按照傅里叶级数将上游尾流的压力波分解为定常均值部分和N阶谐波部分：
(1)
将展开后的定常均值部分和谐波振荡部分，分别加载在下游流场CFD模型的进口处，利用CFD进行计算，求解出定常状态下叶片气动力均值响应(A0、B0、D0)和各阶压力谐波对应下的叶片气动力谐波振荡的幅值
最后将求得的均值和幅值代入式(2)就可以得到上游尾流激励下的叶片气动力。
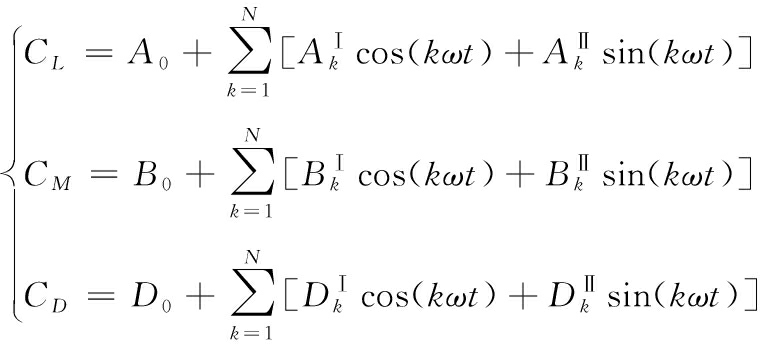
(2)
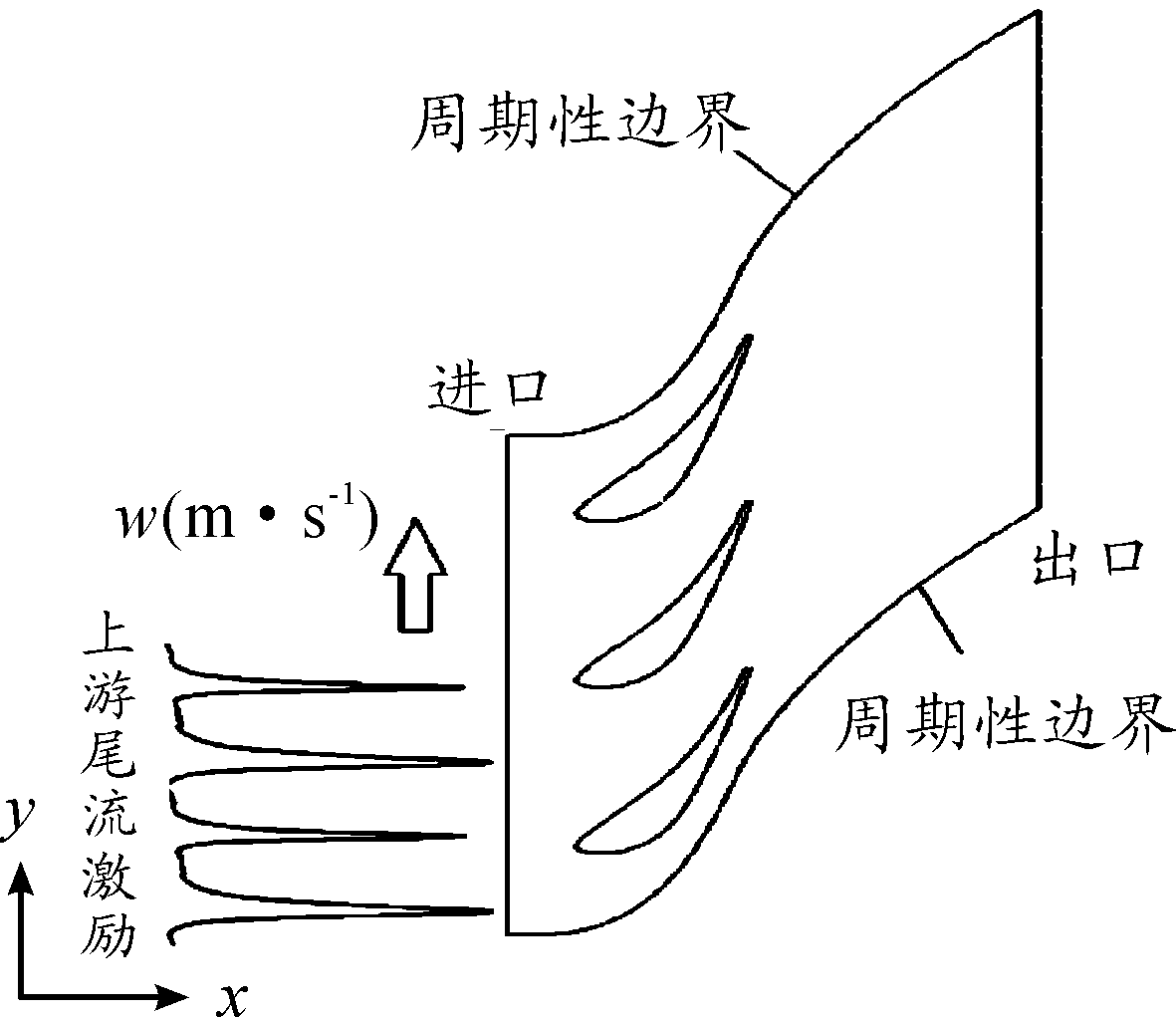
图1 尾流激励的叶片气动力系统
2 压力波均值对气动力降阶模型精度的影响
采用图2所示二维叶片流场的CFD模型验证尾流激励的叶片气动力降阶模型方法。流场采用Fluent求解，理想气体， Spallart-Allmaras模型，计算初始温度300 K，流场出口压力不变，为 101 325 Pa。以流场进口最下方点为压力波基准点，尾流以10 m/s的速度从基准点开始沿着进口向上方移动。
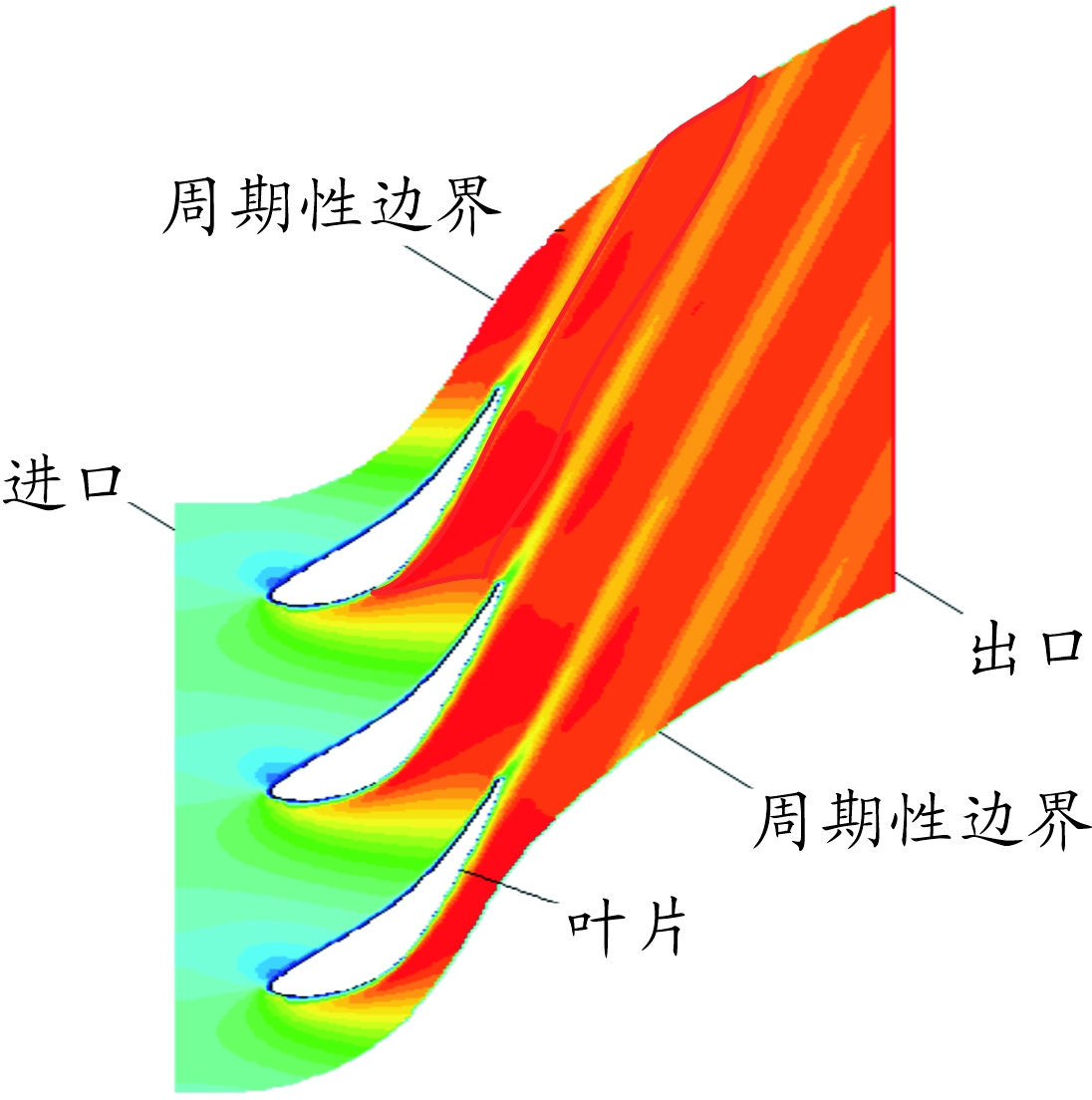
图2 叶片流场的CFD模型
首先研究压力波均值对气动力降阶模型精度的影响。选择多组均值不同波形相同的尾流压力波对基于谐波平衡法的气动力降阶模型进行研究。根据式(1)将这几组尾流压力波进行傅里叶级数展开，取前7阶波形，采用文献[11]中的尾流谐波系数及频率(见表1)，求得各尾流的压力均值p0分别为106 325 Pa，111 325 Pa，124 325 Pa，143 325 Pa，150 325 Pa，160 325 Pa。
表1 尾流分解后的谐波幅值和频率
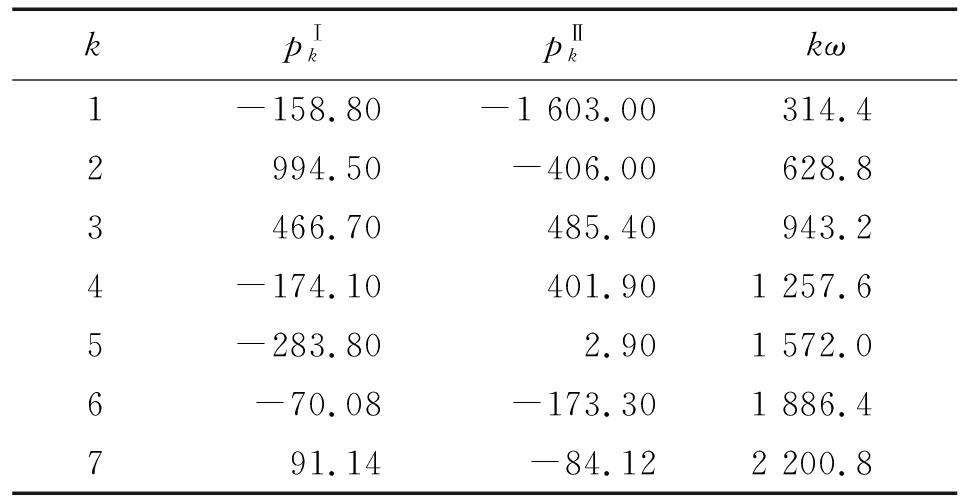
kpⅠkpⅡkkω1-158.80-1 603.00314.42994.50-406.00628.83466.70485.40943.24-174.10401.901 257.65-283.802.901 572.06-70.08-173.301 886.4791.14-84.122 200.8
将进口平均压力(p0)和表1中各谐波分别加载到流场进口处，并根据式(2)建立上述各尾流下的降阶模型预测叶片气动力，并与CFD模型下的计算结果进行对比，结果如图3至图8所示，从图中可以看出随着压力波均值的增大气动力降阶模型的精度增加。
为了更清晰的观察进口平均压力对气动力降阶模型精度的影响，表2给出不同进口平均压力的气动力降阶模型计算的气动力响应结果与CFD结果之间的误差。
图3 p0为106 325 Pa的尾流激励降阶模型的气动力结果
图4 p0为111 325 Pa的尾流激励降阶模型的气动力结果
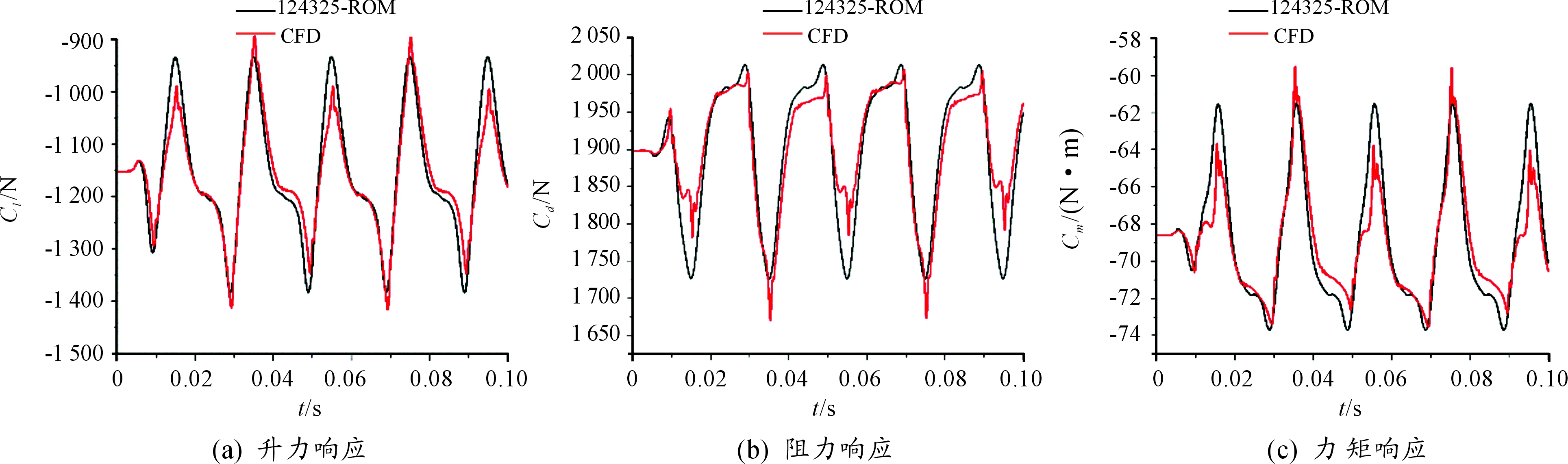
图5 p0为124 325 Pa的尾流激励降阶模型的气动力结果
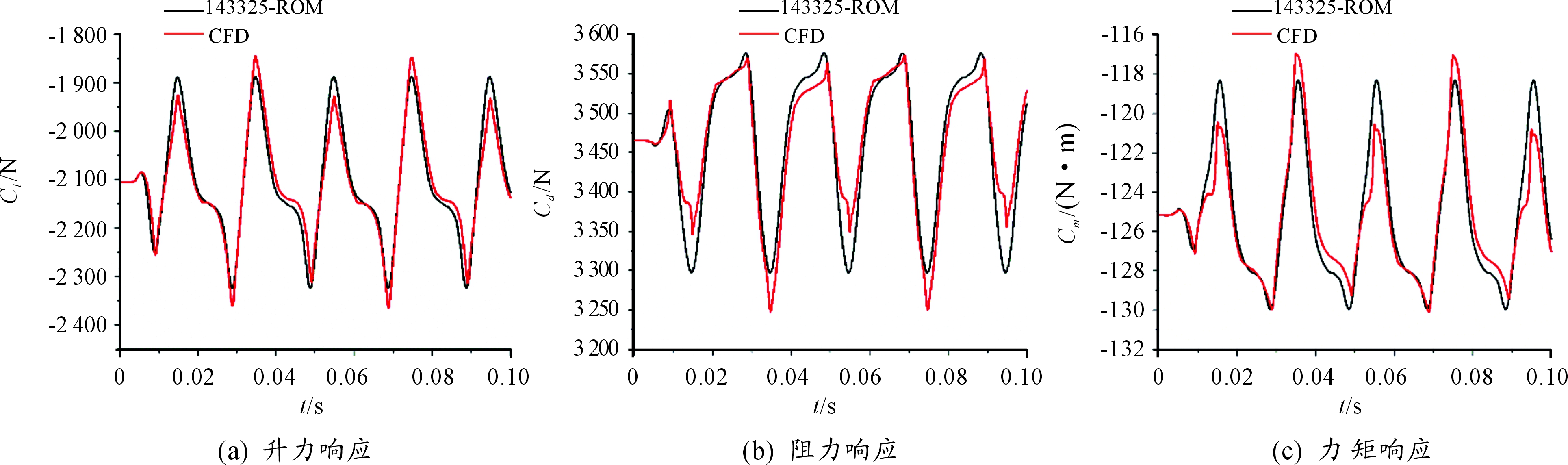
图6 p0为143 325 Pa的尾流激励降阶模型的气动力结果
图7 p0为150 325 Pa的尾流激励降阶模型的气动力结果
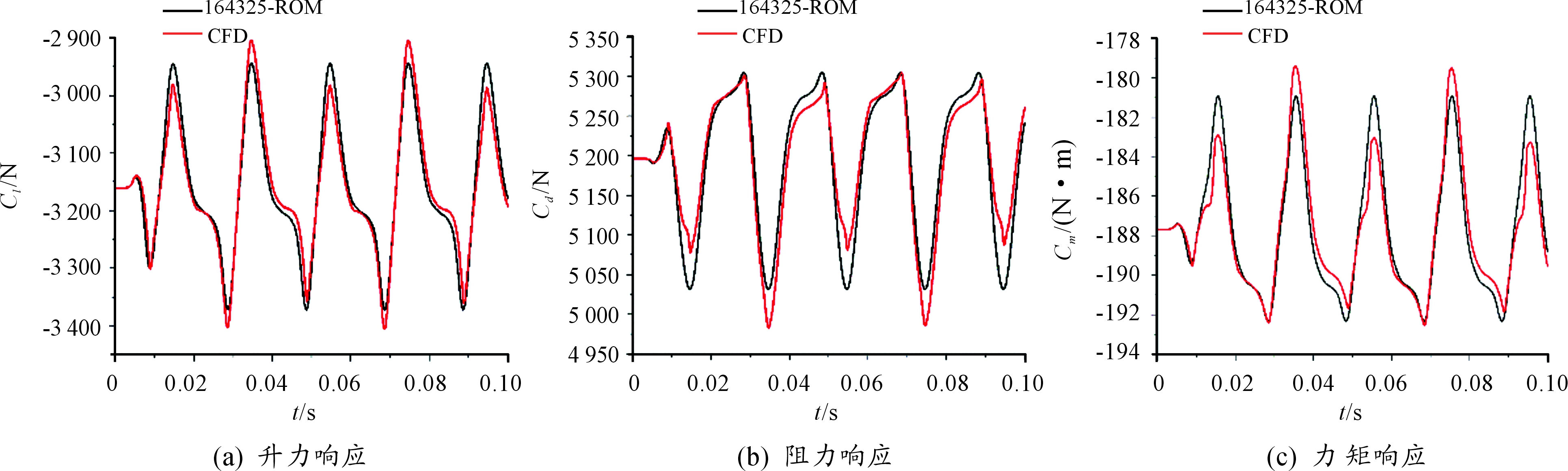
图8 p0为164 325 Pa的尾流激励降阶模型的气动力结果
表2 不同进口平均压力下气动力响应误差分析
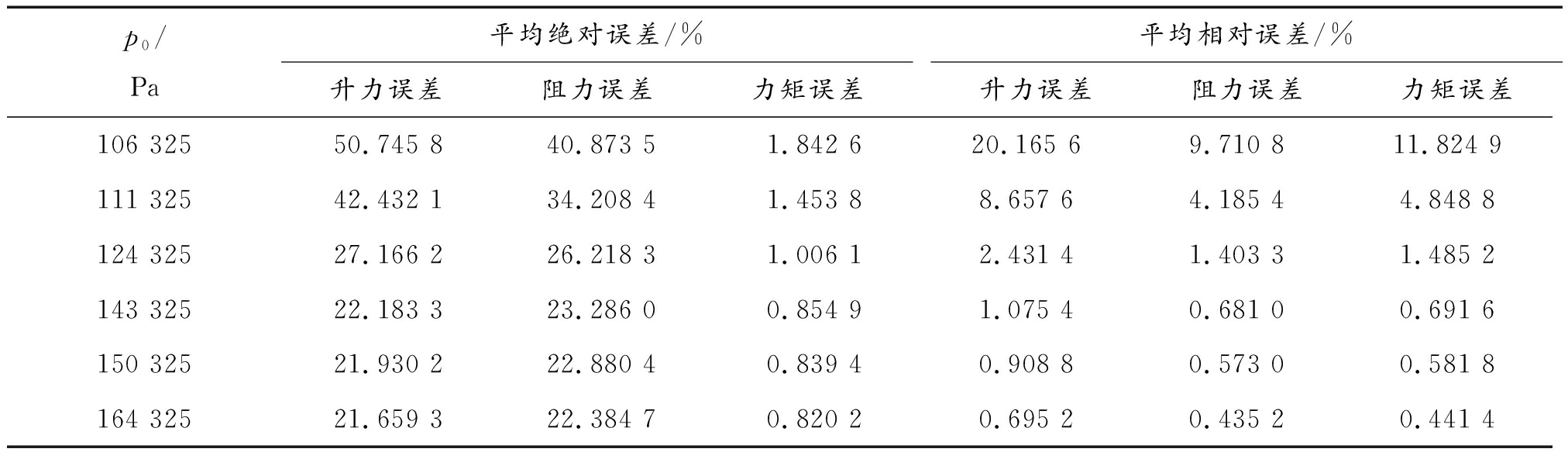
p0/Pa平均绝对误差/%升力误差阻力误差力矩误差平均相对误差/%升力误差阻力误差力矩误差106 32550.745 8 40.873 5 1.842 6 20.165 69.710 811.824 9111 32542.432 1 34.208 4 1.453 8 8.657 64.185 44.848 8124 32527.166 2 26.218 3 1.006 1 2.431 41.403 31.485 2143 32522.183 3 23.286 0 0.854 9 1.075 40.681 00.691 6150 32521.930 2 22.880 4 0.839 4 0.908 80.573 00.581 8164 32521.659 3 22.384 7 0.820 2 0.695 20.435 20.441 4
从表2中进一步可以看出：随着进口尾流平均压力的增大，气动力降阶模型的计算精度逐步提高。这说明尾流压力波均值越大，气动力降阶模型的计算结果越精确。
3 尾流振幅对叶片气动力降阶模型精度的影响
第2节讨论了进口平均压力对气动力降阶模型计算精度的影响，本节将讨论进口压力不变的情况下，尾流谐波振幅对气动力降阶模型计算精度的影响。按照前述尾流压力波形，构造尾流压力波：
(3)
其中，β为尾流谐波的振幅放大系数。
本文为探究尾流谐波幅值对气动力降阶模型计算精度的影响，保持进口尾流平均压力不变(p0=106 325 Pa)，改变尾流谐波的振幅大小，来研究振幅对计算精度的影响。即，尾流各谐波幅值
和频率(kω)取表1值，依次设置尾流谐波振幅放大系数为β=1、β=2/3、β=1/3、β=1/6、 β=1/10。分别用CFD模型和气动力降阶模型计算不同幅值的尾流激励下的叶片气动力，比较研究振幅对气动力降阶模型精度的影响。CFD模型和气动力降阶模型计算结果如图9～图13所示，从结果可以看出随着振幅的减小气动力降阶模型的精度增加。
为进一步更清晰的观察振幅对气动力降阶模型精度的影响，表3给出不同振幅的气动力降阶模型结果与CFD结果之间的误差。
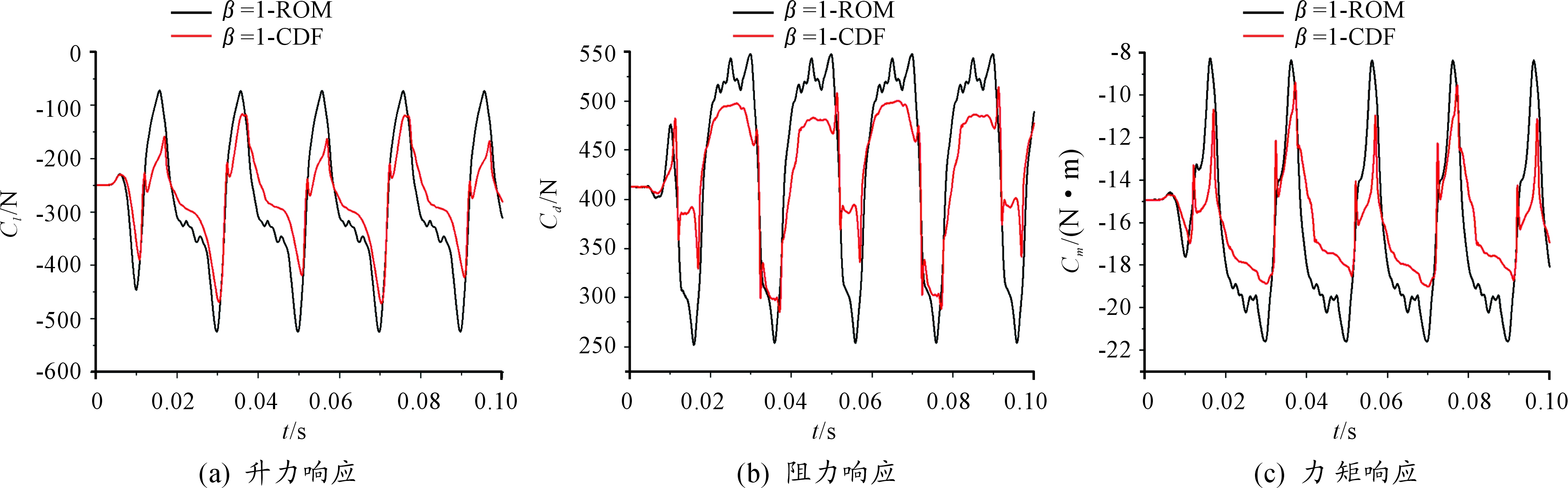
图9 β=1的气动力计算结果
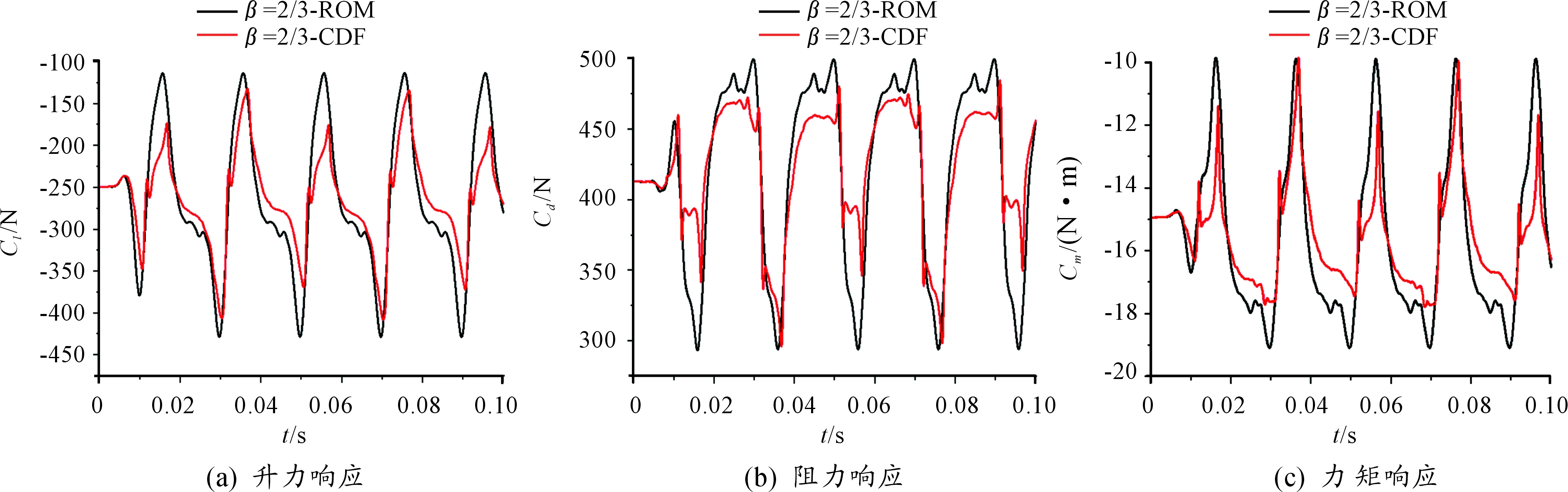
图10 β=2/3的气动力计算结果
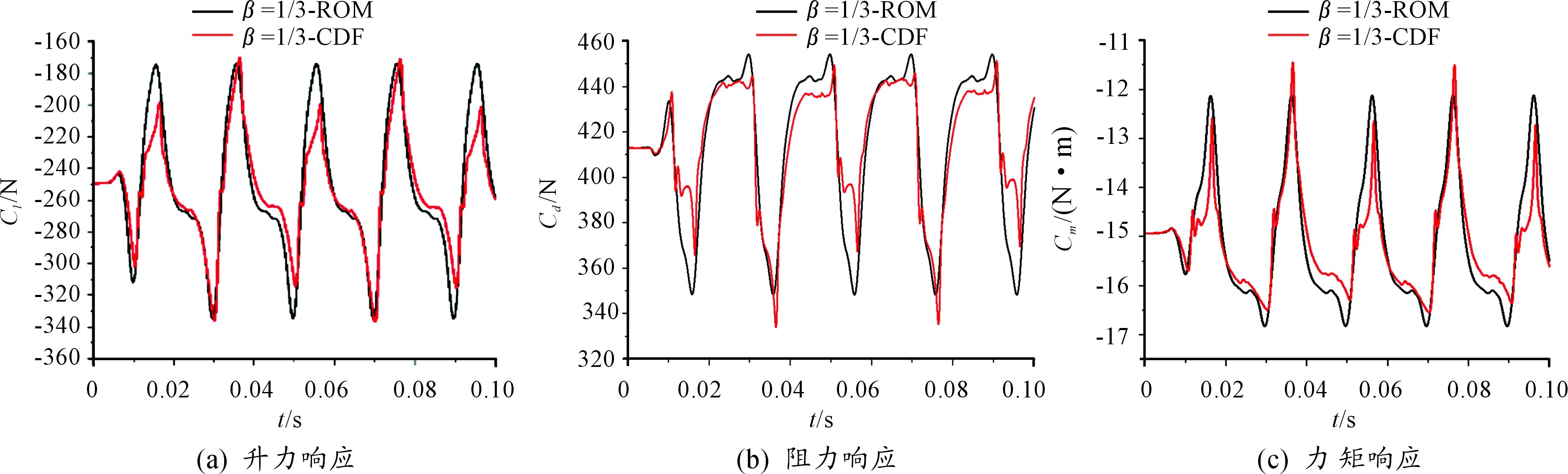
图11 β=1/3的气动力计算结果
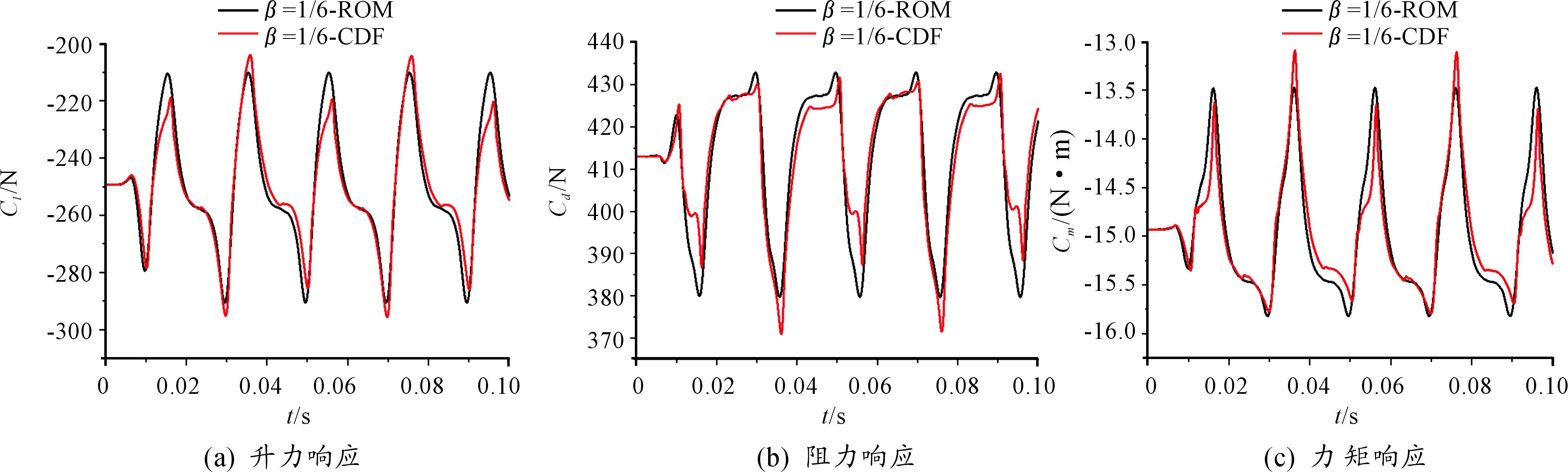
图12 β=1/6的气动力计算结果
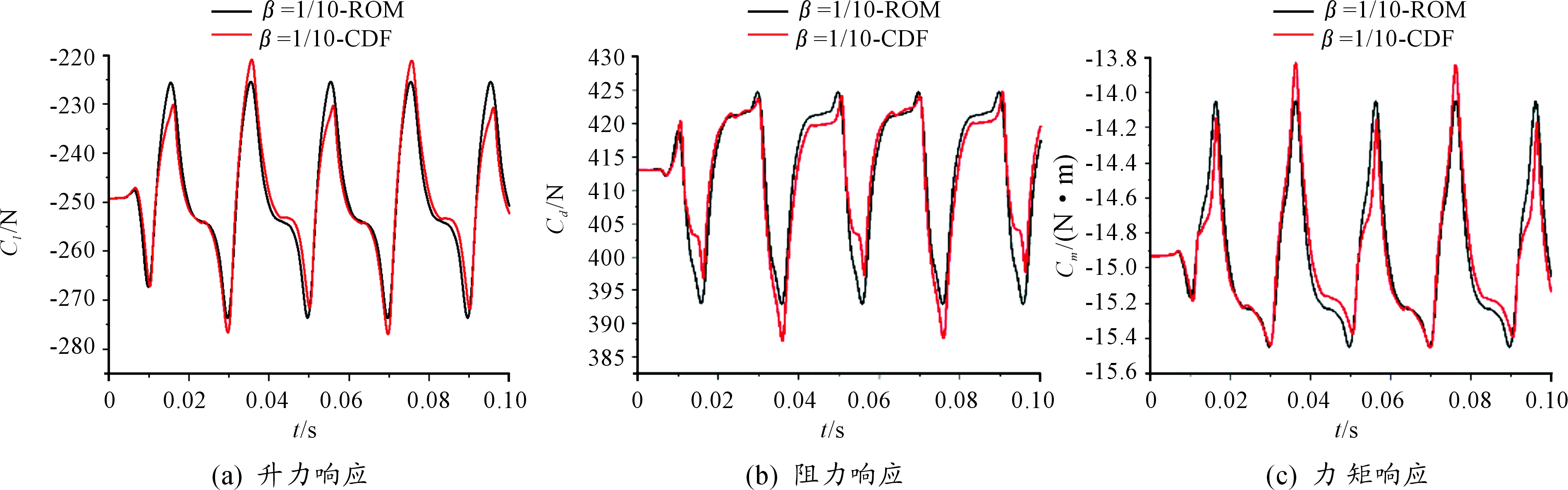
图13 β=1/10的气动力计算结果
表3 不同尾流振幅的气动力响应误差
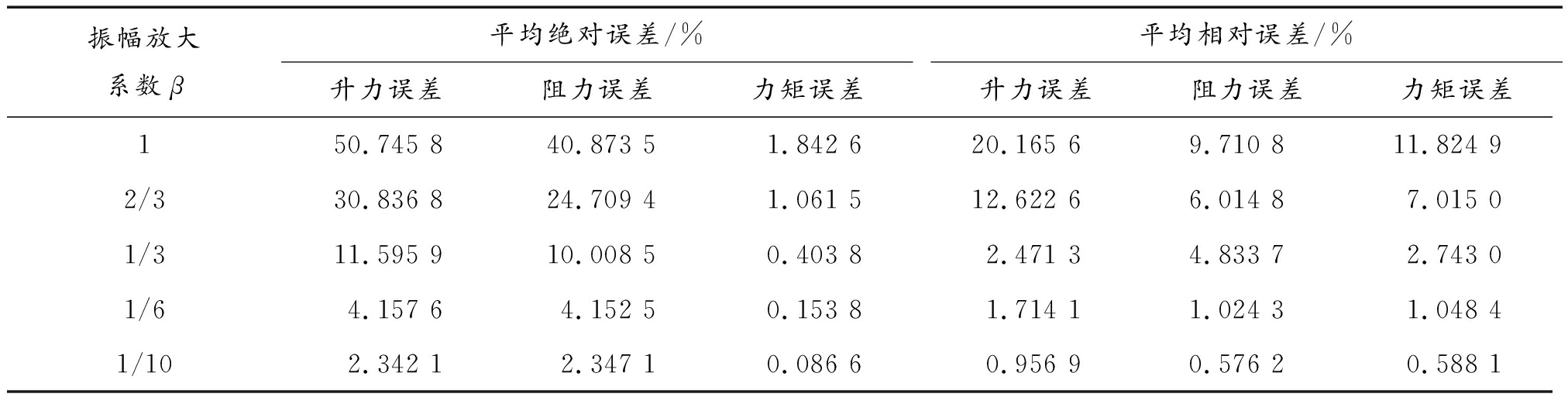
振幅放大系数β平均绝对误差/%升力误差阻力误差力矩误差平均相对误差/%升力误差阻力误差力矩误差150.745 8 40.873 5 1.842 6 20.165 69.710 811.824 9 2/330.836 8 24.709 4 1.061 5 12.622 66.014 87.015 0 1/311.595 9 10.008 5 0.403 8 2.471 34.833 72.743 0 1/64.157 6 4.152 5 0.153 8 1.714 11.024 31.048 4 1/102.342 1 2.347 1 0.086 6 0.956 90.576 20.588 1
从表3中进一步可以看出：随着幅值系数的降低，叶片气动力降阶模型的计算精度逐步提高。这说明尾流谐波扰动部分的振幅越低，气动力降阶模型的计算精度就越高。
4 结论
1) 基于谐波平衡法的气动力降阶模型能快速准确的描述尾流激励下的叶片气动力；
2) 随着进口尾流压力的增大，尾流激励下的叶片气动力降阶模型的计算精度越高；
3) 随着尾流谐波振幅的降低，尾流激励下的叶片气动力降阶模型计算精度逐渐提高。
[1] 张陈安,叶正寅,刘锋,等.进口导流叶片对转子叶片颤振特性的影响[J].推进技术,2010,31(3):335-339.
[2] 陈佐一.流体激振[M].北京:清华大学出版社,1988.
[3] 郭恩民,周盛,陆亚钧.叶片排干涉对叶片颤振和强迫响应影响的研究[J].航空学报,1999,20(4):56-60.
[4] HUANG X Q,HE L,BELL D L.Influence of upstream stator on rotor flutter stability in a low pressure steam turbine stage[J].Proceedings of the Institution of Mechanical Engineers Part A Journal of Power & Energy,2006,220(220):25-35.
[5] 杨慧,李振鹏.转静干涉对转子叶片颤振特性的影响[J].北京航空航天大学学报,2016,42(2):258-264.
[6] KIVANC E,ROBERT E K,KENNETH C H.The Effect of Aerodynamic Asymmetries on Turbomachinery Flutter[J].Journal of Fluids and Structures,2013,36(5):1-17.
[7] THOMAS J,HALL K,DOWELL E.A Harmonic Balance Approach for Modeling Nonlinear Aeroelastic Behavior of Wings in Transonic Viscous Flow[C]//Aiaa/asme/asce/ahs/asc Structures,Structural Dynamics and Materials Conference.2015.
[8] 王梅,江和甫,吕文林.在尾流激振情况下叶片振动应力预估计技术[J].航空动力学报,2007,22(4):608-613.
[9] DOWELL E H.Some recent advances in nonlinear aeroelasticity:Fluid-structure interaction in the 21st century[C]//Proceedings of 51st AIAA/ASME/ASCE/AHS/ASC Structures,Structural Dynamics and Materials Conference.Springer International Publishing,2010:1-23.
[10] 张伟伟,叶正寅.基于CFD的气动力建模及其在气动弹性中的应用[J].力学进展,2008,38(1):77-86.
[11] 罗骁，张新燕，张珺，等.基于谐波平衡法的尾流激励的叶片振动降阶模型方法[J].应用数学和力学,2018,39(8):892-899.
[12] DIMITRIADIS G.Continuation of Higher-Order Harmonic Balance Solutions for Nonlinear Aeroelastic Systems[J].Journal of Aircraft,2008,45(2):523-537.
[13] 陈刚,李跃明.非定常流场降阶模型及其应用研究进展与展望[J].力学进展,2011,41(6):686-701.
[14] WALTER A S.Reduced Order Models Based on Linear and Nonlinear Aerodynamic Impulse Responses[J].AIAA Journal,1999,233(11):1-11.
[15] HALL K C,THOMAS J P,CLARK W S.Computation of Unsteady Nonlinear Flows in Cascades Using a Harmonic Balance Technique[J].Aiaa Journal,2002,40(5):879-886.
[16] THOMAS J P,DOWELL E H,HALL K C.Three-Dimensional Transonic Aeroelasticity Using Proper Orthogonal Decomposition-Based Reduced-Order Models[J].Journal of Aircraft,2012,40(40):544-551.
[17] ASHCROFT G,FREY C,KERSKEN H P.On the Development of a Harmonic Balance Method for Aeroelastic Analysis[C]//The 11th World Congress on Computational Mechanics (WCCM XI).Barcelona,Spain,2014.