缓冲装置在自动武器中有着广泛应用，常用的弹簧缓冲装置具备结构简易，维护性好，成本低的优点，但是缺点是弹簧刚度无法改变，这使得缓冲过程冲击大、不稳定，严重影响了缓冲过程的可靠性。
本课题设计了一种新型的串联弹簧刚度可变式双向缓冲装置，相对于普通弹簧缓冲装置，在相同缓冲距离情况下，可以储存更多能量，能大大降低动力装置在缓冲过程受到的冲击，获得类似于液压减震器的平滑且可靠的缓冲效果。
航炮是口径≥20 mm，装备于飞机上的自动发射武器。航炮特点是射速高且可调，弹丸初速高，威力大。为了适应作战需要，需要解决变射速航炮的后坐力问题。减小后坐力将会改善飞机的安全性能。周乐[1]应用多目标遗传优化算法和动力学数值计算技术对反后坐装置进行结构和总体优化。李世康[2]的缓冲弹簧设计参数的并行优化设计为转管武器缓冲器优化设计提供了参考依据。闫菲[3]建立了一个可改变刚度的弹簧结构振动分析的数学模型，并推导出可改变刚度的弹簧解析解表达式。魏占芳[4]设计了变刚度螺旋弹簧的型式、结构及特性参数，试验表明该弹簧能满足越野车辆在弹性力学特性曲线及疲劳寿命方面的使用要求。Jafari A[5]开发了可变刚度执行器，对不同类型弹簧的变刚度设计方法进行了分析。
纵观已有文献，关于刚度可变弹簧的研究涉及到优化弹簧结构，研究新材料[6]，运用主动控制[7]等，关于刚度可变弹簧减后坐的研究尚未见报导。为大幅度降低火炮的后坐力，本文设计出一种新型刚度可变弹簧缓冲器，并以某航炮为研究对象，对本装置与单簧定刚度缓冲装置缓冲效果进行比较；分析了不同弹簧刚度和不同阻尼条件下炮身所受的后坐力大小，并进行数值计算，验证本装置在缓冲效果上的优势。
1 刚度可变弹簧缓冲器工作原理
新型刚度可变弹簧缓冲器原理如图1所示，其中，前置弹簧8预压缩量为δ1，后置弹簧10预压缩量为δ2。工作原理：套筒1与火炮身管固连，拉杆12与炮架固连。航炮击发时，在火药燃气作用下，套筒1相对于外预压套筒7和拉杆12向右运动。后置弹簧10设置了较为合理的预压力，且大于前置弹簧8的预压力，在缓冲后坐过程中，导引杆3带动前滑板5向右运动，使前置弹簧8不断压缩，此时装置表现为单刚度弹簧缓冲器。当前置弹簧8所受压力大于后置弹簧10预压力时，后滑板9开始向右运动，后置弹簧10受压缩，此时两级弹簧构成串联关系，缓冲装置刚度发生改变，从前置弹簧刚度变为串联弹簧的刚度。
1.套筒；2.销；3.导引杆；4.拉杆挡板；5.前滑板；6.内预压套筒；7.外预压套筒；8.前置弹簧；9.后滑板；10.后置弹簧；11.挡板；12.拉杆
图1 新型刚度可变缓冲器原理示意图
2 基于刚度可变弹簧缓冲的某航炮后坐过程动力学模型
航炮系统在射击时，受到的主要作用力力为击发时膛内高温高压火药气体对膛底的压力。作用于膛底的膛内压力会使炮身后坐，它会直接影响整个航炮发射装置的后坐力、后坐位移的大小和整个航炮系统的动力学特性。如图2所示的某型航炮为本文的研究对象。模型中首先需要确定的作用力主要有膛底压力、膛口制退器制退力、缓冲簧作用力等[8]。
1.炮口制退器；2.身管；3.新型缓冲器；4.自动机部分
图2 基于刚度可变弹簧缓冲的航炮局部示意图
2.1 火药气体内弹道与后效期模型
首先计算内弹道和后效期内膛内和膛口处的气体参数。膛内火药气体对膛底的压力通过Matlab编写的程序计算求得，在后文ADAMS仿真部分中，将得到的压力数据曲线导入ADAMS中，在身管相应位置处添加，载荷的大小为曲线的值乘以膛底面积，同时设置一个传感器来控制仿真时力的触发时间点。
2.2 航炮后坐过程动力学模型
为了研究缓冲器内弹簧刚度对后坐力的影响，便于分析计算，对模型作出如下假设：
1) 运动过程中前后滑板质量忽略不计；
2) 前后滑板与预压套筒之间碰撞忽略不计；
3) 不考虑系统内摩擦力；
4) 以下计算中的位移指套筒的绝对位移，并用弹簧力表示后坐力建立模型。
以前置弹簧预压缩量为δ1时为起始位置建立坐标系，坐标系正方向为向右运动方向。变刚度瞬间位移和速度连续。对于本文建立的单自由度振动系统，系统的微分方程如下：
其中:m为炮身总质量；k1是前置弹簧的刚度；k2是后置弹簧的刚度；k是串联弹簧的总刚度；δ1是前置弹簧的预压缩量；δ2是后置弹簧的预压缩量；b为前置弹簧工作行程；b′为套筒前冲前置弹簧极限压缩行程。
为正值表示缓冲后坐，为负值表示复进。本文只研究缓冲装置从开始后坐至减速为0时的后坐过程，不包括复进过程。
3 数值计算实例及分析
3.1 数值求解模型
单刚度缓冲装置缓冲后坐过程能量转换表达式为：
其中
质量m为炮架质量，经试验测得数值为63 kg，速度v为炮架后坐初速度，经试验测得数值为2 m/s，k是弹簧刚度，δ为弹簧预压缩量，Δx为单刚度缓冲器缓冲后坐位移，根据缓冲器结构得到Δx值为0.02 m。
上式化简后得到
其中F0=kδ，表示缓冲簧初始预压力。因此后坐力可表示为F=kΔx+F0。
前置弹簧刚度为k1，预压缩量为δ1，前置弹簧工作行程为b。后置弹簧刚度为k2，预压缩量为δ2，后置弹簧工作行程为Δx-b，Δx为单刚度缓冲器缓冲工作行程，数值为0.02 m。
当后坐力达到后置弹簧预压力时，后滑板开始运动并压缩后置弹簧，此时有F1+k1b=F2，其中F1=k1δ1为前置弹簧预压力，任取F1和k1即可得δ1。F2=k2δ2为后置弹簧预压力，故
两弹簧串联共同作用时，前置弹簧与后置弹簧之间的弹力相等，有
得到：
炮架后坐时转化为两弹簧的弹性势能，可分解为三部分，为仅前置弹簧工作消耗能量E1，两弹簧串联时前置弹簧消耗能量E2，以及后置弹簧消耗能量E3。
前置弹簧消耗的能量：
和
后置弹簧消耗的能量：
系统消耗的总能量E=E1+E2+E3化简后得到：
而系统消耗的总能量E为航炮后坐时的动能
将上式中
代入系统消耗总能量E的方程可以得到关于δ2的一元二次方程：
其中
由此可根据设定值k1、k2、δ1、Δx求出δ2值，δ2带回公式
求出前置弹簧的工作行程b。至此缓冲器结构参数全部已知，可利用Matlab里的ode45函数即4阶Runge-Kutta数值算法，根据初始工作载荷即可对缓冲装置实时缓冲位移和缓冲速度进行数值计算，根据系统的微分方程得出实时后坐力值
3.2 三种缓冲方式下航炮后坐过程对比分析
为了研究刚度可变弹簧缓冲器比单刚度弹簧缓冲器在缓冲效果上的优势，本文对3种缓冲器用Matlab进行数值计算，通过对微分方程的解析，运用胡克定律和4阶Runge-Kutta数值算法，得出3种装置的缓冲力F、缓冲距离X分别与时间t的关系曲线如图3、图4，缓冲力F和缓冲距离X的关系曲线如图5。
图3 3种缓冲装置的后坐力与时间t的关系曲线
根据第二节内容计算出该型航炮炮架后坐冲量为126 kg·m/s，炮架质量为63 kg，初始后坐速度为2 m/s，缓冲距离设定为20 mm，3种缓冲器的初始预压力为3 500 N。单刚度缓冲器缓冲簧刚度k为280 N/mm，后坐力F为9 100 N。刚度可变缓冲器k1取值1 500 N/mm，k2取值10 N/mm，在阻尼c=0时后坐力F为6 534.24 N，c=100时后坐力F为6 510.18 N。
图4 3种缓冲装置的缓冲位移曲线
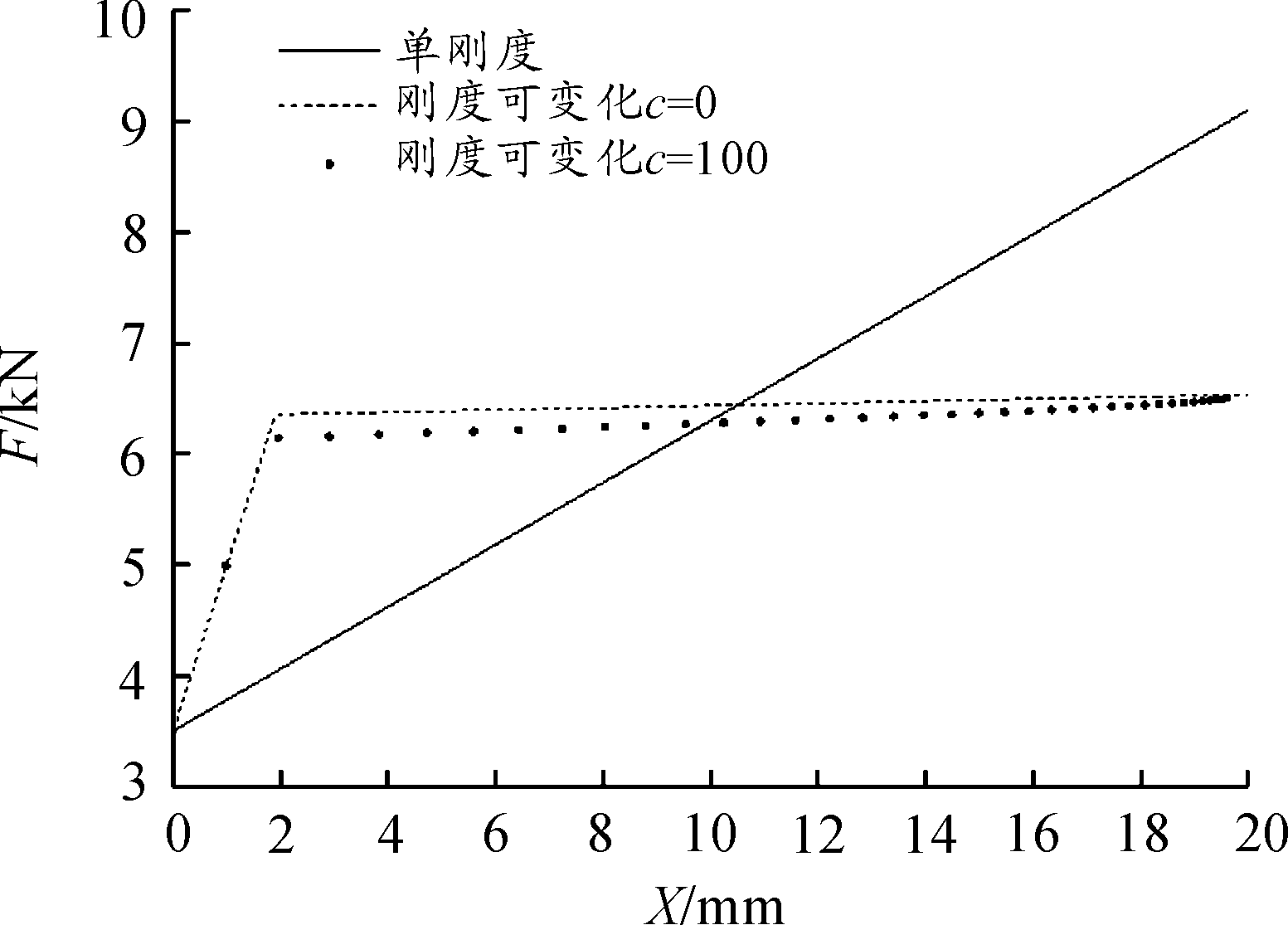
图5 3种缓冲装置的F-X的关系曲线
表1 3种缓冲装置数据
t/msF/NX/mm单刚度17.649 100.0020.00刚度可变c=019.176 534.2420.00刚度可变c=10019.436510.1819.61
由图3、图4、图5和表1可见：
1) 在相同的缓冲距离下，刚度可变结构(c=0)后坐力为6 534.24 N，单刚度结构后坐力为9 100 N，刚度可变结构后坐力降低了28.20%；
2) 刚度可变结构缓冲行程所需的时间大于单刚度结构，增加了1.53 ms，增加7.98%；
3) 刚度可变结构c=0与c=100结构相比较，后者缓冲后坐时间相比多0.26 ms，增加了1.34%，后坐力降低了24.06 N，减小了0.37%，但是阻尼c=100时，此时的缓冲后坐行程变为19.61 mm，减小了0.39 mm，减小1.95%。
因此得出结论，单刚度缓冲后坐工作时间最短，但后坐力最大，刚度可变结构在c=100时，系统具有最小的后坐行程和最小的后坐力，但系统具有最长的工作时间。
3.3 刚度可变弹簧缓冲各因素对后坐力影响分析
如图6所示为不考虑阻尼c时，取不同k1值，最大后坐力Fm与k1的关系曲线。初始值k1取800 N/mm，k2取10 N/mm。k1增量为100 N/mm。从图6可以得出结论，随着k1的增加，最大后坐力Fm减小，且变化量也逐渐减小。
图6 无阻尼时Fm-k1关系曲线
如图7所示为不考虑阻尼c时，取不同k2值，最大后坐力Fm与k2的关系曲线。k1取800 N/mm，k2取10 N/mm。k2增量为10 N/mm。从图7可以得出结论，随着k2的增加，最大后坐力Fm近似线性地增加。
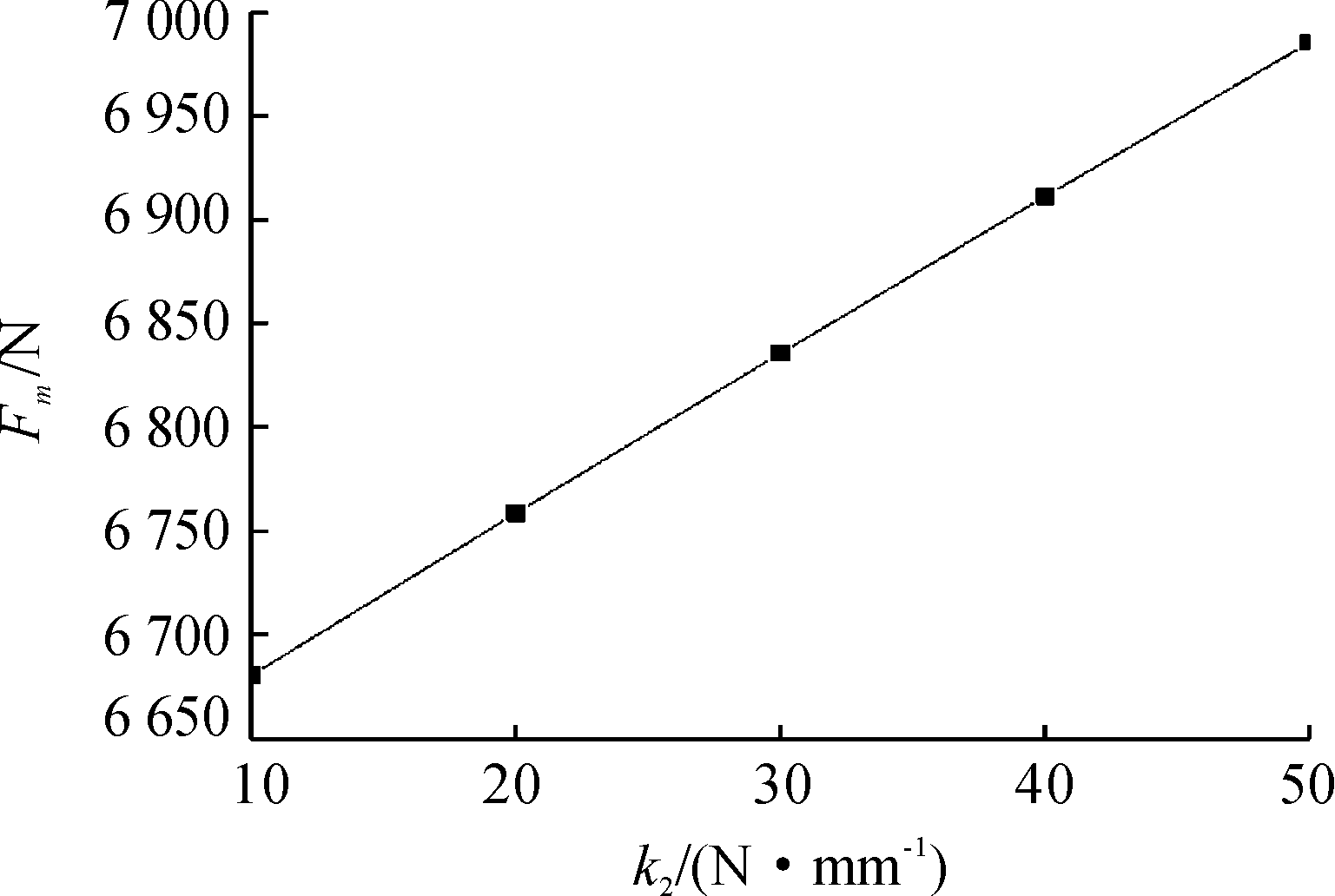
图7 无阻尼时Fm-k2关系曲线
如图8所示为不同阻尼系数下最大后坐力Fm与前置弹簧刚度k1的关系图线。根据图8可以得出结论：阻尼系数c保持不变，k1增加，最大后坐力Fm减小；如果k1保持不变，增加阻尼系数c，那么最大后坐力Fm减小。
图8 不同阻尼时Fm-k1关系曲线
图9显示了不同阻尼系数的最大后坐力Fm与k2之间的关系。根据图9可以得出结论：阻尼系数c保持不变，k2增加，最大后坐力Fm近似线性增加；若k2保持不变，增大阻尼系数c，那么最大后坐力Fm变大。
图9 不同阻尼时Fm-k2关系曲线
3.4 最大后坐力Fm与后置弹簧预压力F2关系
如图10所示为无阻尼系数时最大后坐力Fm与F2的关系曲线。k1选取800 N/mm，k2取值从10 N/mm到90 N/mm，通过图10和表2可以得出结论： 当k2增加时，后置弹簧预压力F2降低，最大后坐力Fm变大。
图10 后置弹簧预压力F2与最大后坐力Fm的关系曲线
表2 Fm与F2数值对应关系
k2102030405060708090100F26 520.026 440.146 360.756 281.836 203.396 125.406 047.865 970.775 894.125 817.89Fm6 680.266 758.666 835.636 911.266 985.527 058.487 130.187 200.677 269.977 338.10
4 动力学仿真
为了验证数值计算的结果，本文使用ADAMS对刚度可变结构进行动力学仿真，得到的曲线如图11所示，并对数值计算与仿真结果的误差进行分析。
航炮后坐载荷由前文数值计算得到的压力数据曲线导入到ADAMS中，在相应位置处添加。刚度可变缓冲装置的结构参数选取与前文相同，前置弹簧刚度k1=1 500 N/mm，后置弹簧刚度k2=10 N/mm，c分别取0和100。
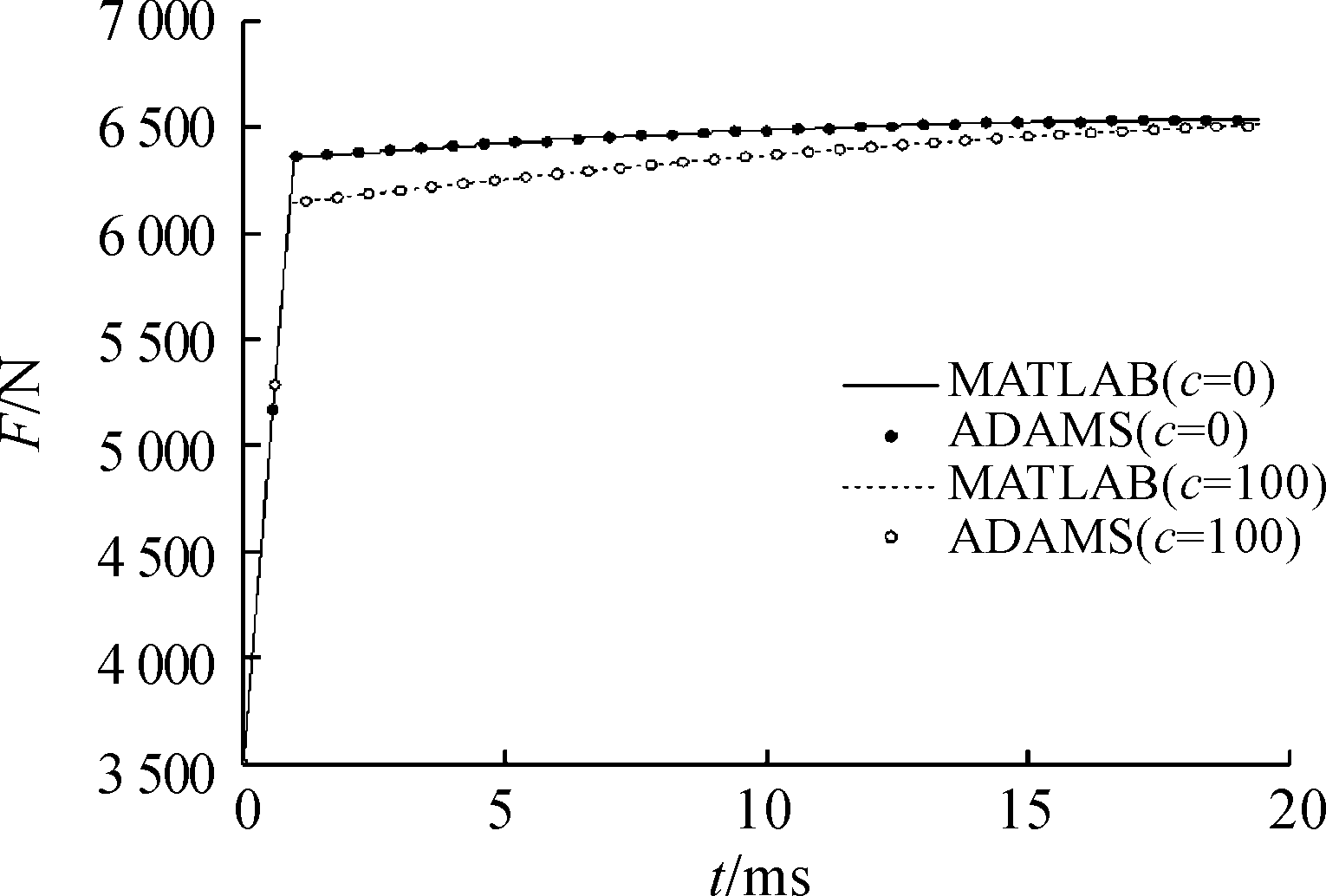
图11 数值计算与动力学仿真曲线
由图11可见：
1) c取0时，Matlab数值计算结果后坐力为6 534.24 N，ADAMS动力学仿真结果中后坐力为6 530 N，误差为0.065%，误差较小。c取100时Matlab数值计算结果后坐力为6 510.08 N，ADAMS动力学仿真结果中后坐力为6 500 N，误差为0.155%，误差较小数值计算结果得到验证。
2) 数值计算中忽略了系统零部件之间的碰撞，而仿真中存在零件间碰撞的能量损失，使得仿真结果略小于数值计算结果。
5 结论
1) 数值计算结果表明，在相同的预压力作用下，刚度可变弹簧缓冲装置的最大后坐力减少了28.20%，明显提高了缓冲效果。数值计算结果与仿真结果误差较小。
2) 增加前置弹簧刚度k1、减小后置弹簧刚度k2和增加后置弹簧的预压力F2可以显著降低缓冲装置的最大后坐力。
3) 根据不同阻尼下的力与时间曲线，阻尼c为100时比无阻尼的缓冲效果提高0.37%，增加阻尼提升缓冲效果不明显，但是能降低缓冲距离。
4) 上述研究结果可以为链式炮减后坐的后续研究提供理论依据和应用参考。
[1]周乐.大口径火炮反后坐装置多目标优化设计研究[D].南京：南京理工大学,2015.
[2]李世康,李强,谭庆,等.基于isight的某转管武器弹簧缓冲器优化设计[J].兵工自动化,2018,37(05):49-51,59.
[3]闫菲，车驰东.变刚度隔振系统动力特性及仿真[J].噪声与振动控制，2014，34(3)：15-19.
[4]魏占芳.重型越野车变刚度螺旋弹簧设计[J].汽车实用技术,2013(08):42-45.
[5]JAFARI A， TSAGARAKIS N G， SARDELLITTI I， et al.How design can affect the energy required to regulate the stiffness in variable stiffness actuators.[C]//IEEE International Conference on Robotics & Automation.IEEE，2012.
[6]高伟,应善强,杨冬,等.越野车变刚度悬架螺旋弹簧的材料研究及应用[J].汽车技术,2011(02):54-59.
[7]GUOPING Y， LIANG W.Research of hydraulic impactor with self-adaptive intelligent buffer[C]//International Asia Conference on Informatics in Control.IEEE Press，2010.
[8]肖俊波，杨国来，李洪强，等.膛口制退器与缓冲器匹配对后坐力的影响研究[J].弹道学报，2017,29(4):86-92.