迷彩伪装是最常用的伪装技术措施,它通过将迷彩涂料作用于目标表面,用以减少目标与背景的颜色、亮度差异[1]。目前制式伪装涂料均为多种颜色的颜料混合而成,而现实情况下背景随地域、季节千变万化,而实践中难以通过经验配色快速、准确的复制背景颜色,急需建立一套配色系统,满足现代战场环境下适应不同背景的高融合智能化迷彩伪装要求[2]。
计算机测色配色技术已被广泛应用于印染、涂料、油墨、汽车配色等与着色有关的各个行业[3-4]。计算机配色技术发展是近几十年科学发展的结果,1931年库贝尔卡-芒克(Kubelka-Munk)定律的发表为计算机配色技术提供了理论基础[5]。近年来,人们将数值分析方法和神经网络技术与计算机配色技术结合起来,在提高配色准确率上取得了一定的研究成果[6-9]。将计算机配色技术运用到迷彩伪装配色实践,能够较好地解决经验配色遇到的问题。本文先是构建伪装基础颜色数据库,建立色度坐标与基础颜色浓度数学模型,然后通过多元回归方法求解并验证模型系数[10],采用Matlab遗传算法[11-13]对色样与已知背景色差函数求最小值,在色偏差允许范围内求出拟合背景的最佳颜料比例。实验中随机选取颜色不同深浅的绿叶,将测量计算的色度值代入色差方程,根据求解出的颜色配比制备色板,验证模型和计算的可靠性。
1 理论基础
迷彩伪装中色样与背景颜色匹配,不仅要求颜色相近,还要求与背景的光谱反射特性相同,即在特定的照明条件下,两种颜色不仅对于特定的标准观察者具有相同的颜色感觉,而且具有相同的光谱分布曲线[14]。只有当色样的三刺激值与背景颜色三刺激值分别相等,两种颜色才完全匹配。当色样与背景的三刺激值不相等时,两者之间的颜色差别称为色差,迷彩伪装中采用的是CIELAB均匀色空间,且要求涂料色样与背景的允许色差小于3L*a*b*标准单位[15]。
理论上,自然界中任一颜色均可由红、黄、蓝按一定比值混合而成。不同于色光加色混合,颜料减色混合没有固定的混色模型,不用的基础颜料混合产生不同的混合结果。只有在固定基础颜料的基础上,通过测试大量不同配比颜料混合后的的色度值,分析并建立色度值与配比之间的模型,求解相关模型,才能获得不同颜色对应的基础颜料配比。
回归分析是建立在大量实验基础上的客观事物变量间的统计关系的研究方法,不仅可以揭示自变量对因变量的影响大小,还可以用回归方程进行预测和控制[16-17]。本文将CIE1976均匀色空间的L*,a*,b*视为随机变量,颜料的质量比(x,y)(x表示黄色基础颜料质量占黄和蓝质量的百分数,y表示红色基础颜料质量占黄和蓝质量的百分数)视为自变量,自变量在定义域内取某些固定值时,因变量的观测值是随机的。如样本数据为![]() 则多元回归模型可表示为
则多元回归模型可表示为
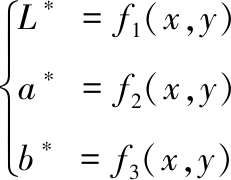
假设回归模型为多项式模型,以![]() 二元二次多项式回归模型可表示为
二元二次多项式回归模型可表示为
L*=q0+q1x+q2y+q3x2+q4y2+q5xy
(1)
通过控制变量法分析L*与x、y之间的关系,对回归项进行筛选,通过SPSS软件中回归分析工具包对实验数据进行回归分析,得出回归方程,观测复相关系数R值、拟合系数R方值以及回归系数t检验的显著性sig值判断回归效果好坏。一般当R值、R方值尽可能接近于1,sig值小于0.05时,判断模型回归效果良好[18-19]。
2 计算机配色模型建立与求解
基于同谱同色伪装性能的要求,本实验所使用颜料为钴蓝、镉红、镉黄三种基础颜料,将选取的颜料以相同质量分数与树脂、溶剂混合,研磨60 min获得基础颜色色浆,再按多种比例配制不同颜色色板。使用分光光度仪测量色板的光谱反射率,利用Excel中的VLOOKUP函数[20],计算颜色三刺激值和均匀色空间的色度坐标。分析色空间坐标与颜色质量浓度之间的关系,建立并求解数学模型。
2.1 色空间坐标L*,a*,b*与颜料质量浓度(x,y)回归曲线分析
将基础颜料按不同黄蓝比(x)配制色样,再固定黄蓝比例添加不同比值(y)的红色颜料色样,测试其光谱反射率,计算颜色三刺激值和均匀色空间的色度坐标,构建色坐标(L*,a*,b*)与基础颜料配比的基础色配方库。根据已知数据,利用Excel绘制样品L*,a*,b*值与基础颜料质量比(x,y)的散点图,并利用回归分析方法分别进行多次函数拟合,选取最适合的回归分析方程。
1) 当y=0,L*,a*,b*与x的关系曲线如图1所示。由图1可知,当色样中不含红色颜料时,L*,b*与x近似成线性关系,a*与x近似成二次非线性关系。
2) 当x=50,L*,a*,b*与y的关系曲线如图2所示。由图2可知,当色样中黄蓝比例为1∶1不变时,L*,a*,b*与y近似成线性关系,且拟合程度较好。
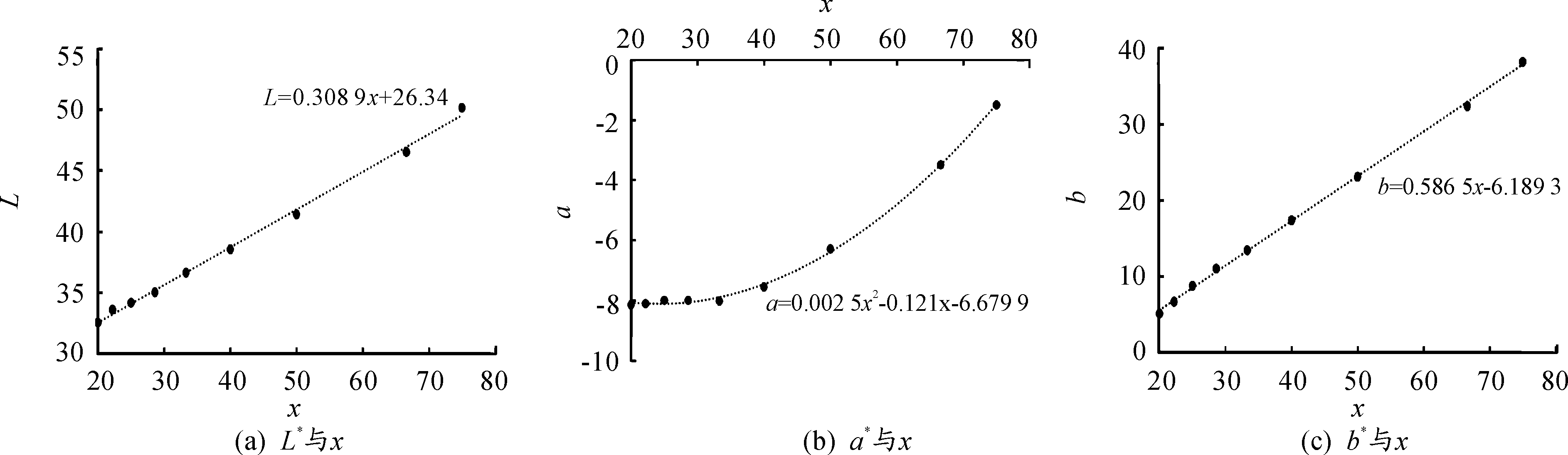
图1 L*,a*,b*与x的回归曲线(y=0)
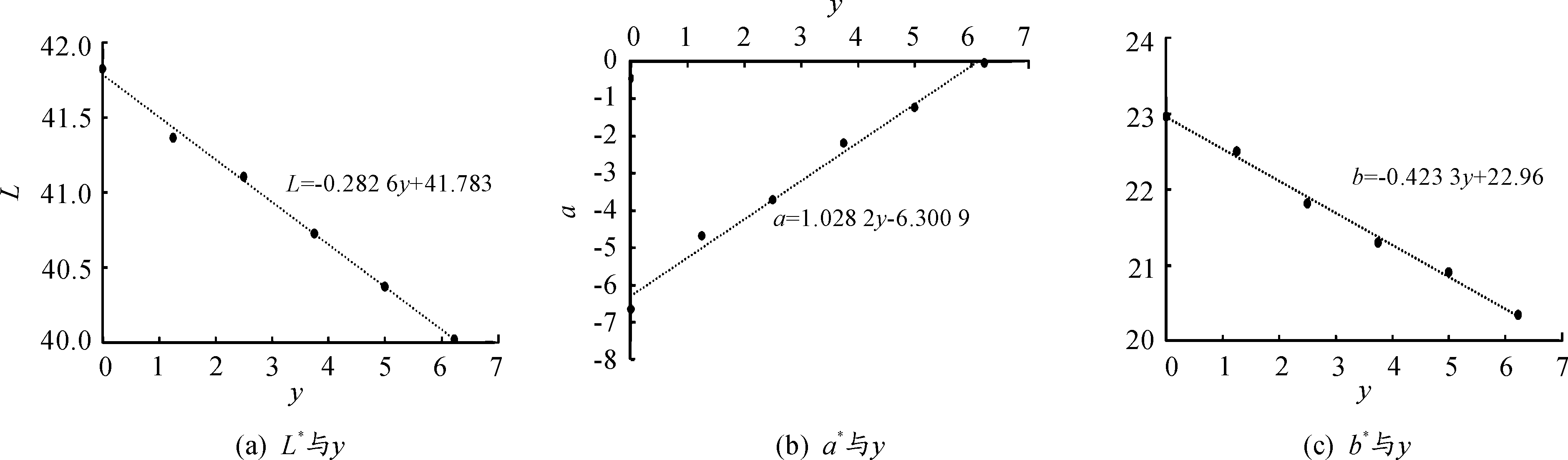
图2 L*,a*,b*与y的回归曲线(x=50)
2.2 色空间坐标L*,a*,b*与颜料质量浓度(x,y)数学模型建立与求解
采用控制变量法分析色空间坐标L*,a*,b*与颜料质量浓度(x,y)之间的关系可知,L*,a*,b*分别与(x,y)的一次和二次有关联,选取其中有关联的回归项建立回归方程,并通过SPSS软件求解回归项系数。
(1) L*与(x,y)的模型建立与求解。由数据分析可知,当y不变时,L*与x成近似线性关系,当x不变时,L*与y成近似线性关系,故假设L*与(x,y)的二元回归模型为
L*=q0+q1x+q2y
(2)
L*=q0+q1x+q2y+q3xy
(3)
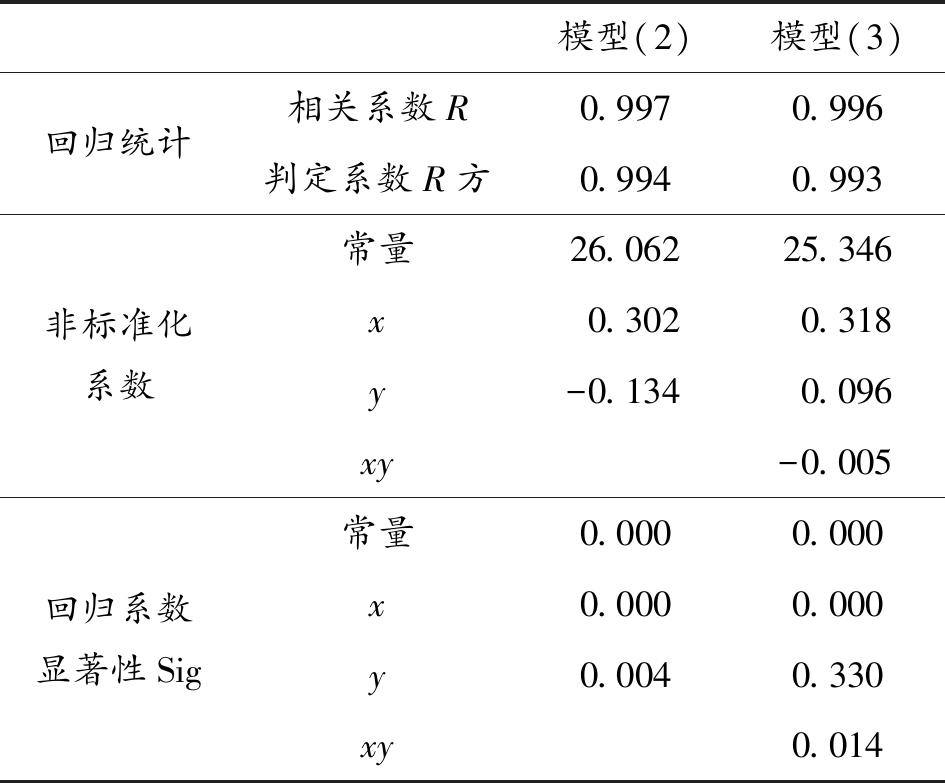
通过SPSS软件中数值分析的回归工具包,分别用模型(2)、模型(3)对实验数据进行回归分析,结果如表1所示。
从表1可以看出:模型(2)、模型(3)决定系数R方和调整后的R方均较大,说明两个模型都较为显著,但从回归系数t检验的显著性,模型(1)常量x、y的sig值均小于0.05,优于模型(3),所以选择模型(2)作为L*与(x,y)的二元回归模型,其回归表达式为
L*=22.062+0.302x-0.134y
(4)
(2) a*与(x,y)的模型建立与求解。由数据分析可知,当y不变时,a*与x成近似二元非线性关系,当x不变时,a*与y成近似线性关系,故假设a*与(x,y)的二元回归模型如下:
a*=q0+q1x+q2y+q3x2+q4xy+q5x2y
(5)
同理,用模型(5)对实验数据进行回归分析,结果如表2所示。
由表2可知:决定系数R方和调整后的R方均较大,表明模型总体上是显著的,但从回归系数t检验的显著性来看,x、xy、x2y的sig值均大于0.05,说明模型中可能存在多重共线性。因此,将其中不显著项x2y去掉得到模型(6):
a*=q0+q1x+q2y+q3x2+q4xy (6)
表1 L*与(x,y)模型回归分析及显著性检验结果
模型(2)模型(3)回归统计相关系数R0.9970.996判定系数R方0.9940.993非标准化系数常量26.06225.346x0.3020.318y-0.1340.096xy-0.005回归系数显著性Sig常量0.0000.000x0.0000.000y0.0040.330xy0.014
表2 a*与(x,y)模型回归分析及显著性检验结果
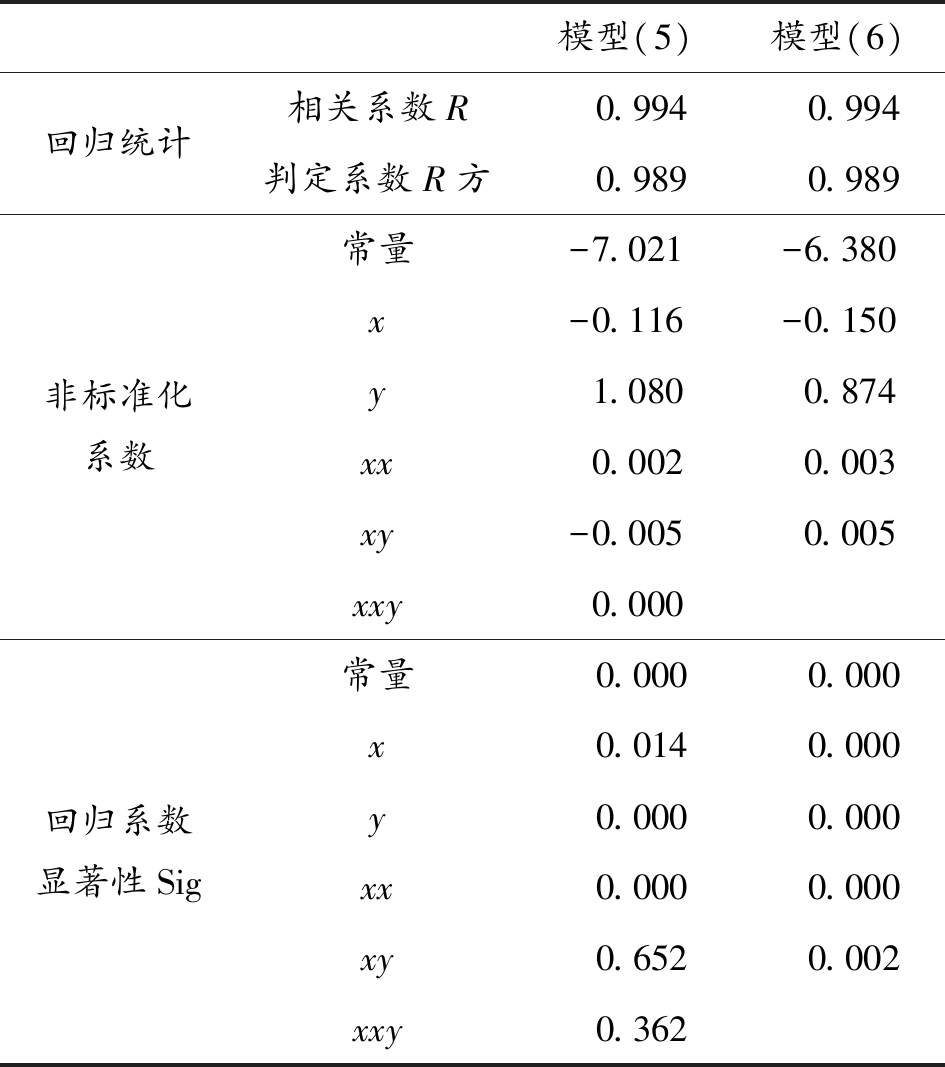
模型(5)模型(6)回归统计相关系数R0.9940.994判定系数R方0.9890.989非标准化系数常量-7.021-6.380x-0.116-0.150y1.0800.874xx0.0020.003xy-0.0050.005xxy0.000回归系数显著性Sig常量0.0000.000x0.0140.000y0.0000.000xx0.0000.000xy0.6520.002xxy0.362
用SPSS对其进行回归分析,从表2数据可以看出,决定系数R方和调整后的R方均较大,表明模型显著,且回归系数t检验的显著性每一项均小于0.05,说明该模型(6)优于模型(5),故选模型(6)作为a*与(x,y)的二元回归模型,其回归表达式为
a*=-6.38-0.15x+0.003x2+
0.874y+0.005xy
(7)
(3) b*与(x,y)的模型建立与求解。由实验分析可知,当y不变时,b*与x成近似线性关系,当x不变时,b*与y成近似线性关系,故假设b*与(x,y)的二元回归模型如下:
b*=q0+q1x+q2y
(8)
b*=q0+q1x+q2y+q3xy
(9)
通过SPSS中分析回归工具包,分别用模型(8)、模型(9)对实验数据进行回归分析,结果如表3所示。
从表3可以看出:模型(8)、模型(9)的决定系数R方和调整后的R方均较大,且回归系数t检验的显著性每一项均小于0.05,说明两个模型都能很好的解释b*与x,y的关系,比较可以看出模型(9)更优,故选模型(9)作为b*与x,y的二元回归模型,其回归表达式为
b*=-6.770+0.591x+0.447y-0.015xy
(10)
根据上述数值分析和回归计算,可以得出L*,a*,b*分别与x,y的相关性方程:
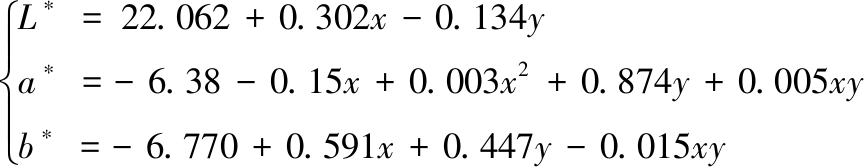 (11)
(11)
表3 b*与(x,y)模型回归分析及显著性检验结果
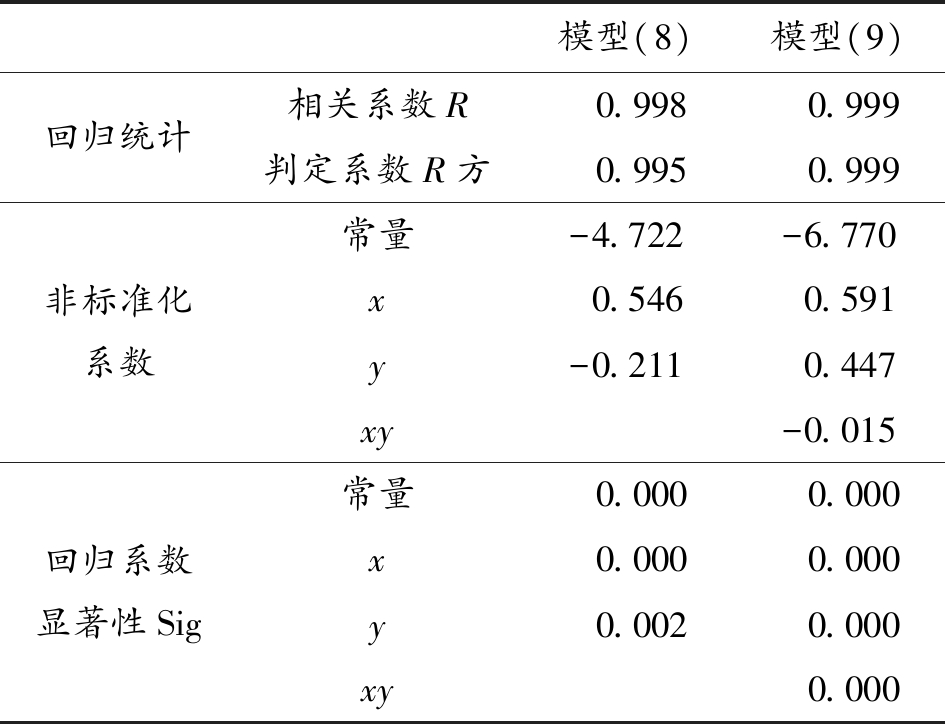
模型(8)模型(9)回归统计相关系数R0.9980.999判定系数R方0.9950.999非标准化系数常量-4.722-6.770x0.5460.591y-0.2110.447xy-0.015回归系数显著性Sig常量0.0000.000x0.0000.000y0.0020.000xy0.000
3 遗传算法极值寻优求解基础颜料质量比
在CIE1976Lab均匀色空间中两种色样的色差可用式(12)计算:
ΔE=[(ΔL*)2+(Δa*)2+(Δb*)2]1/2
(12)
为使调配的色样符合迷彩伪装配色要求,其需与所模拟的背景颜色色差小于3L*a*b*单位,即求解基础颜料配比(x,y)按式(11)得出的色空间坐标与所模拟的背景颜色色空间坐标之间的距离小于3。
3.1 目标函数的建立
假设所模拟背景颜色的色度坐标为Li,ai,bi,则其与颜料的质量比为(x,y)配得颜色的色差为
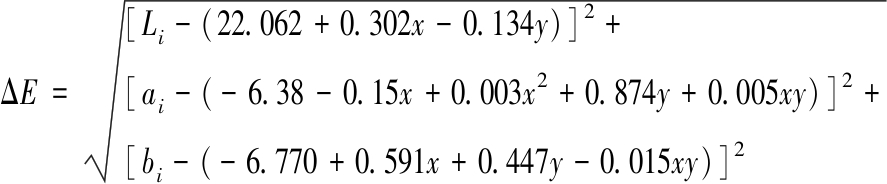
(13)
为使配色得出的色样与所模拟背景的色差小于3,只需目标函数ΔE取最小极值且该值小于3。假使当(x,y)取值为(xi,yi)时ΔE取得最小值,则按颜料质量比(xi,yi)配色得出的色样与背景颜色色差最小。
3.2 遗传算法求极值
针对二元函数ΔE求最小值,本文利用Matlab软件采用遗传算法进行迭代计算,通过将二元函数ΔE设定为适应度函数,并调整算法参数(迭代次数103、种群规模20、交叉概率0.4、变异概率0.4)进行优化迭代计算最优值。
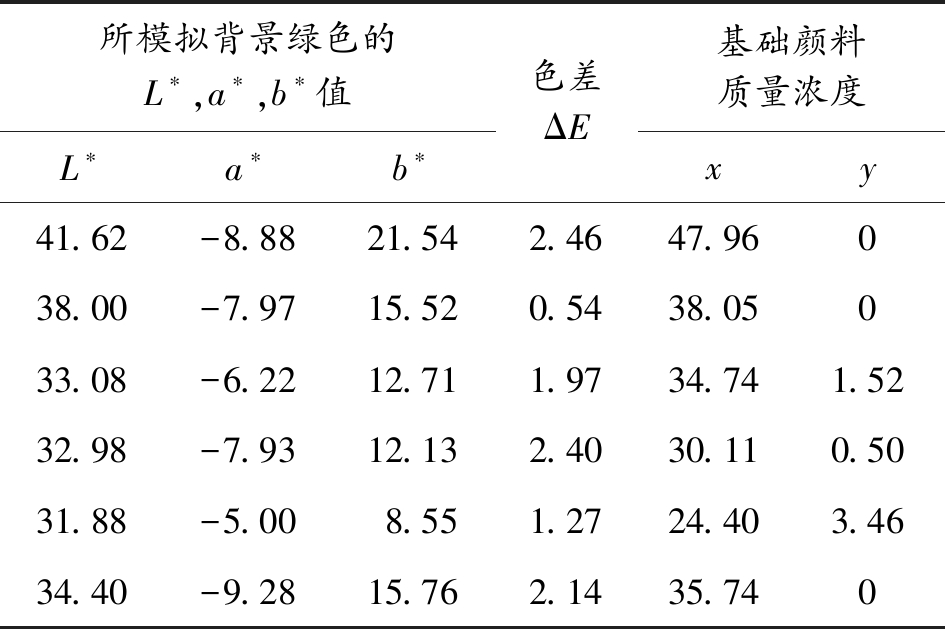
任取自然界中六处背景绿色,测试其光谱反射曲线,计算其色坐标,将其代入上述方程中,计算所需基础颜料的质量分数,表4为通过遗传算法计算的获得最小色差时的基础颜料质量浓度。
由表4可以看出:根据回归模型求解出的基础颜料质量比配出的L*,a*,b*值,与所模拟的背景色色差满足色差小于3L*a*b*的要求。因此所建立的回归模型能够较好的满足迷彩伪装计算机配色要求。
表4 与已知背景颜色最小色差的基础颜色质量浓度
所模拟背景绿色的L∗,a∗,b∗值L∗a∗b∗色差ΔE基础颜料质量浓度xy41.62-8.8821.542.4647.96038.00-7.9715.520.5438.05033.08-6.2212.711.9734.741.5232.98-7.9312.132.4030.110.5031.88-5.008.551.2724.403.4634.40-9.2815.762.1435.740
3.3 优化结果分析
通过MARLAB软件进行数值计算后已经求解出在满足minΔE的条件下,x,y相应的数值,下面我们需要进行反向验证:根据求得的颜色质量浓度x,y制作色板,测出它们的光谱反射率,计算出相应色板的L*,a*,b*值,再与表4中测量到的不同颜色的树叶的L*,a*,b*值作对比,具体色差如表5所示。
表5 实际色板与背景颜色理论色差和实际色差

ΔE12.262.392.162.661.632.76ΔE22.460.541.972.401.272.14
其中,ΔE1表示理论计算色差,即在数值计算中满足的最小色差值,ΔE2是根据模型计算获得的色样配比的色板与树叶的真实色差,从上述结果来看,它们的大小均小于 3L*a*b* 的色差单位,完全满足迷彩伪装配色的要求,说明所建立的回归模型能够较好的处理迷彩伪装中的计算机配色问题。
4 结论
利用SPSS回归分析工具包,对实验数据配色小样值与基础颜料质量比进行回归分析,得出配色小样L*,a*,b*值与基础颜料质量比的数学模型,通过Matlab遗传算法求解出与所模拟背景颜色色差最小的基础颜料配比。通过从背景中实际取样进行配色对比,证明所建立的回归模型能够较好的处理迷彩伪装中的计算机配色问题,提供的颜色配比与真实背景的颜色偏差小于3L*a*b*单位,完全满足迷彩伪装配色的准确性和高效性要求,对实现适应不同背景的高融合迷彩伪装具有重要的军事应用价值。
[1]胡江华.伪装技术[M].北京:国防工业出版社,2010.
[2]LIU G,CHEN Q,CHEN G.Research on Theory and Application of Computer Ink Color Matching[C]//Proceedings of the Advanced Graphic Communications and Media Technologies,Singapore:Springer Singapore,2017.
[3]ALLEN E.Basic Equations Used in Computer Color Matching[J].Journal of the Optical Society of America,1966,56(9):1256-1257.
[4]ALMAN D H.Inter-society Color Council Annual Meeting and International Colour Association Interim Meeting on Computer Color Matching[J].Color Research & Application,1993,18(1):64-66.
[5]BARRRON V,TORRENT J.Use of the Kubelka-Munk Theory to Study the Influence of Iron Oxides on Soil Colour[J].European Journal of Soil Science,2010,37(4):499-510.
[6]BOLDRIN E,SCHETTINI R.Cross-media Color Matching Using Neural Networks[J].Lecture Notes in Computer Science,2006,32(3):335-342.
[7]许瑞馨,何明辉.浅析电脑配色系统中的配色方法[J].印刷质量与标准化,2008(9):51-53.
[8]李含春,张秉森,聂晴晴,等.织物染色计算机配色的数值分析方法[J].计算机工程,2009,35(5):255-256.
[9]李晖,李晓惠,吴伟,等.计算机配色技术[J].沈阳化工大学学报,1991(3):219-226.
[10]丁海霞.回归分析在织物染色计算机配色中的应用研究[D].青岛:青岛大学,2011.
[11]WANG T S,YU T T,LEE S T,et al.MATLAB Code to Estimate Landslide Volume from Single Remote Sensed Image Using Genetic Algorithm and Imagery Similarity Measurement[J].Computers & Geosciences,2014,70(9):238-247.
[12]查普曼.MATLAB编程[M].北京:科学出版社,2011.
[13]王小川.MATLAB神经网络43个案例分析[M].北京:北京航空航天大学出版社,2011.
[14]朱正芳.现代颜色技术原理及应用[M].北京:北京理工大学出版社,2007.
[15]BERBS R.颜色技术原理[M].北京:化学工业出版社,2002.
[16]谢宇.回归分析[M].北京:社会科学文献出版社,2010.
[17]张启锐.实用回归分析[M].北京:地质出版社,1988.
[18]NIMON K,GAVRILOVA M.Commonality Analysis:Demonstration of an SPSS Solution for Regression Analysis[J].Commonality Analysis,2010(10):54-59.
[19]张文彤.SPSS统计分析基础教程[M].南京:高等教育出版社,2011.
[20]陈国良.Excel 2010函数公式[M].北京:电子工业出版社,2010.