信息的精准获取已成为当前决定战争走势的重要因素。传统的以单个传感器进行目标探测的方法极容易导致信息决策有误，因此，使用多个传感器进行组网配合非常必要[1]。但是，在组网数据处理过程中，由于雷达系统误差的存在，不进行系统误差的估计补偿，很难获得高精度的多雷达融合航迹，极有可能产生错误的跟踪航迹。因此，组网雷达数据处理中必须进行误差配准。
根据系统偏差估计的时机，多雷达误差配准可以分为批处理[2-3]、实时处理[4-6]以及联合估计[5]。其中，批处理方式是一种离线处理方法，其无法对滤波状态进行实时更新，实时处理方式是能够时间推移持续对系统偏差进行动态估计，而联合估计能将雷达探测目标状态向量与系统偏差组合成一个新的扩维向量实现实时联合估计。扩维误差配准方法(Augmented State Extended Kalman Filter，ASEKF)[5]即是一种较好的目标状态与系统偏差联合实时配准算法，其将扩展卡尔曼滤波与双阶卡尔曼滤波结合，实现了非线性系统的实时估计。后续扩维算法又与UKF[6]、CKF等[7]结合，都取得了一定效果，但是状态向量维数增加导致运算量增加的问题一直没有得到解决。Freidland[8]提出了双阶卡尔曼滤波的思想，将扩维滤波分成无偏滤波器与偏差滤波器分别进行估计，提升了运算速度，减少计算量。理论上，在双阶扩展卡尔曼滤波系统的噪声统计特性准确已知的条件下，能够获得良好的滤波结果。然而，实际应用中无法对量测噪声参数进行准确获取或在设置时存在一定的误差，致使滤波精度不高，甚至出现滤波发散现象。
本文在当前研究基础上，为降低非线性系统下扩维算法计算量大的问题，首先提出一种双阶扩展卡尔曼滤波方法(Two-Stage Extended Kalman Filter，TSEKF)。然后为克服量测噪声未知或不准确而产生的滤波精度降低，将Sage-Husa自适应滤波[9]引入到无偏滤波器中，在进行无偏滤波的同时根据通过量测输出在线实时修正量测噪声。将其应用到多雷达误差配准上，提出一种双阶自适应扩展卡尔曼滤波(Two-Stage Sage-HusaExtended Kalman Filter，TSSH-EKF)误差配准算法。
1 系统模型与问题描述
设存在两坐标雷达探测模型，其量值为(r,θ)，真实值为
令其随机误差为(δr,δθ)，系统偏差为(λr,λθ)，则量测存在如下关系：
(1)
两部雷达同时对一批目标进行探测，其观测向量定义为Z=[r1,θ1,r2,θ2]。为了实现对目标与系统偏差的实时估计，定义扩维向量
其中
为目标运动向量，b=[λr1,λθ1,λr2,λθ2]′为两部雷达的系统偏差向量。则其量测方程和状态方程为
X(k+1)=F(k)X(k)+G(k)L(k)
(2)
对于固定系统偏差，
(3)
其中
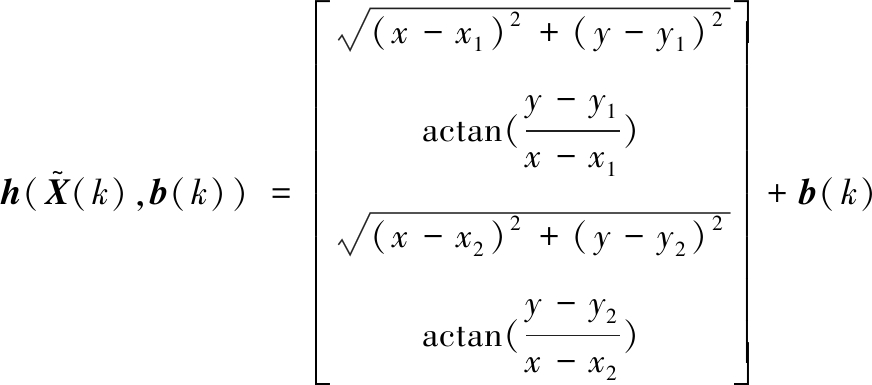
(4)
(x1,y1)，(x2,y2)分别为雷达A、B的坐标。
利用扩展卡尔曼滤波实现目标状态和系统偏差的非线性联合估计：
(5)
P(k+1|k)=F(k)P(k|k)F′(k)+Q(k)
(6)
(7)
式中hX(k)是雅可比矩阵，即
hX(k) = 
(8)
(9)
(10)
(11)
L(k)、W(k)为白色高斯的随机变量，其方差阵分别为Q(k)、R(k)。利用扩维滤波能够对目标运动状态与系统偏差进行实时估计，但运算量增加导致计算量增大。而双阶滤波在对扩维滤波解耦后，能够在达到扩维滤波效果下大大减小系统的计算负担，但其滤波的精确估计是基于噪声统计特性准确已知的条件下，而在实际应用中，量测噪声未知或存在一定的误差，严重时会出现滤波发散现象，因此，本文利用Sage-Husa自适应滤波对双阶扩展卡尔曼滤波进行改进，提高精度的同时，减少滤波计算的收敛时间。
2 改进的双阶自适应滤波算法
2.1 TSEKF算法
本文所提TSEKF算法滤波结构如图1所示。
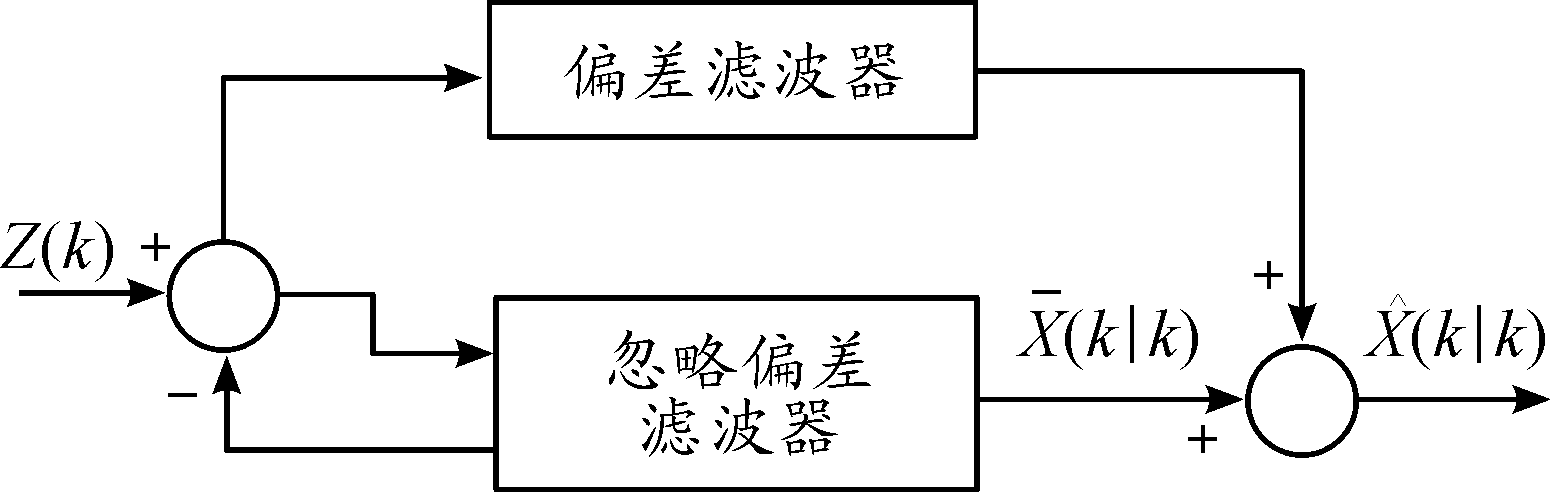
图1 双阶扩展卡尔曼滤波结构示意图
1) 忽略偏差滤波器。忽略偏差滤波器结构与标准扩展卡尔曼滤波器相似，即进行状态方程与对应滤波误差协方差的递推更新。此时，假设不存在系统偏差，对目标状态
进行EKF滤波，
为其预测值。则一步预测方程为
(12)
(13)
量测预测协方差与滤波增益分别为
(14)
(15)
滤波更新为
(16)
(17)
其中
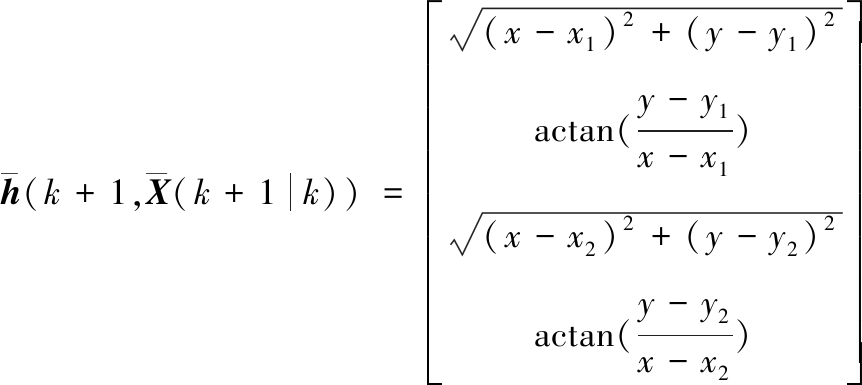
其中h的雅克比矩阵为
2) 偏差滤波器。设b(k)为系统偏差估计值，则由文献[8-10]可设计系统偏差滤波器。
其一步预测方程为
b(k+1|k)=b(k|k)
(18)
Pb(k+1|k)=Pb(k|k)+Qb(k)
(19)
量测预测协方差与滤波增益分别为
(20)
(21)
系统偏差滤波更新为
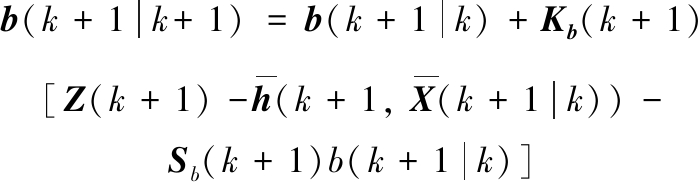
(22)
(23)
其中
U(k+1)=A(k)V(k)
U(k+1)+C(k+1))
式中I与C(k)均为4×4的单位矩阵。
3) 融合滤波。对忽略系统偏差滤波和系统偏差滤波进行融合，即可得到融合后目标状态估计
更新为
V(k)b(k+1|k+1)
(24)
U(k+1)b(k+1|k)
(25)
其协方差矩阵
更新为
V(k+1)Pb(k+1|k+1)V′(k+1)
(26)
U(k+1)Pb(k+1|k)U′(k+1)
(27)
2.2 改进的TSSH-EKF自适应滤波
因为量测噪声方差阵R(k)未知，所以需要对R(k)进行自适应估计。不难理解，滤波系统的量测误差会对其输出产生影响，因此，量测输出中必定隐含关于滤波系统的状态信息，当系统参数不准确时可利用量测输出对不准确参数进行重新评估建模。
已知在扩展卡尔曼滤波中，观测向量的预测误差(亦称为新息)为
(28)
由于状态估计一步预测误差
和量测噪声W(k)之间互不相关，且其均值都为零，可知新息
的均值也为零，对式(28)两边同时求方差并移项，即可得到量测噪声方差阵R(k)的表达式为
(29)
对R(k)进行等加权递推估计，其递推公式可表示为
(30)
为减小陈旧量测噪声对当前估计的影响，引入减消记忆指数加权因子[11]，构造限定记忆加权递推公式为
(31)
其中，0<b<1称为减消因子，初值β0设为1。且当k充分大时，近似有βk≈1-b，陈旧噪声对当前估计的影响随b取值的变小而变小，通常取b=0.9～0.999。由式(31)可知，当滤波系统的量测噪声相较与理论值偏小，则
会较小；若量测噪声值设置相较与理论值偏大，则
较大。因此，无论是哪种情形都有机率使得
导致
非正定，使滤波出现异常。为避免该问题发生，本文引入序贯思想对对角线上的各元素大小进行限制。
假设量测噪声方差阵为对角线矩阵，利用序贯滤波对第i个标量进行量侧更新，则
简记
利用式(32)设定下限
使
保持正定，设定上限
快速降低Zi(k)的可信度，同时若ρi(k)超过所设定上限，则判定为量测异常，放弃本次量测更新。
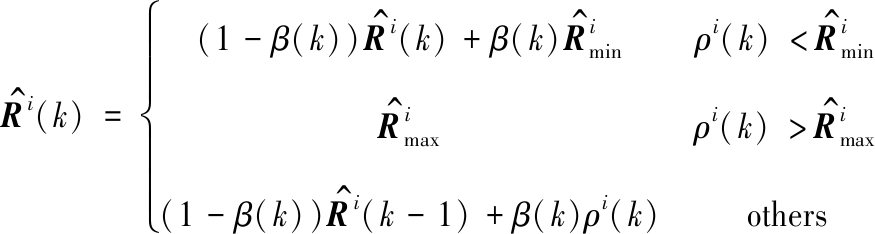
(32)
通过将噪声方差阵限制在
之间，使R(k)具有良好的自适应能力及稳定性。如图2即为本文所提改进的双阶自适应滤波结构图。
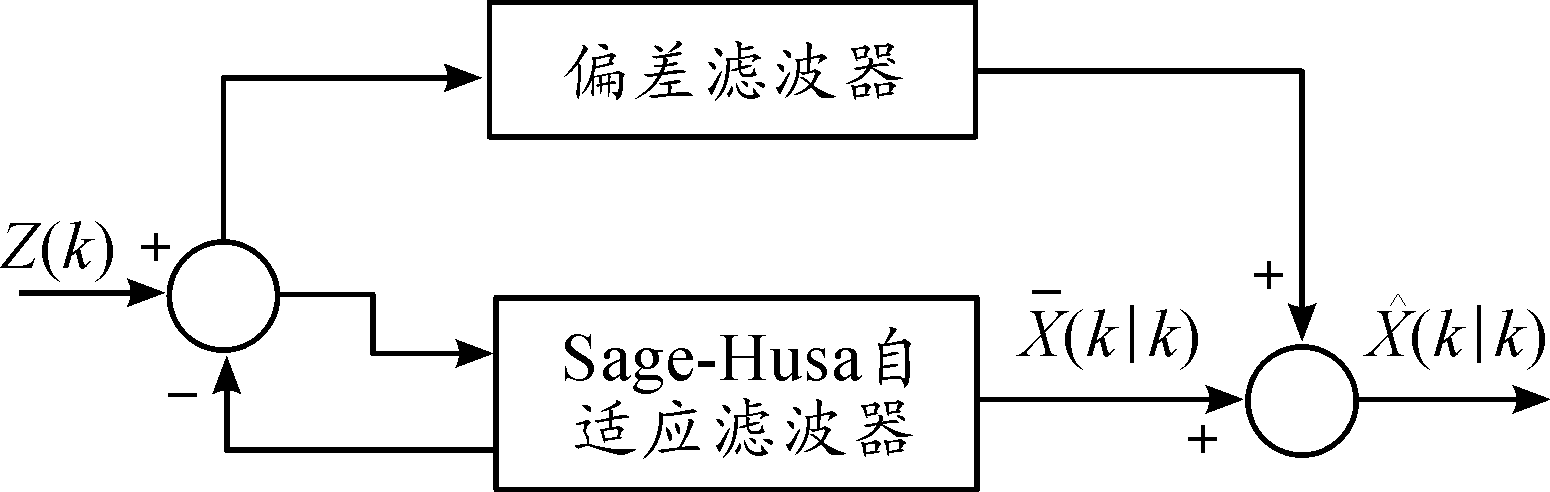
图2 双阶自适应滤波结构示意图
3 仿真实验
利用仿真实验说明本文所提量测未知时组网雷达误差配准的有效性。假设两部雷达坐标分别为原点和(u,v)，其中u=185 200 m，v=0，两部雷达A和B的量测精度均为σrA=σrB=100 m，σθA=σθB=1°。雷达A距离量测系统误差λrA=2 000 m，角度量测系统误差λθA=0.008 7°；雷达B距离量测系统误差λrB=1 500 m，角度量测系统误差λθB=0.004 7°。目标初始状态为(6 000,50,50 000,-10)，迭代步数为3 000。
由于传统ASEKF方法将目标状态向量扩维，导致计算量随维度增加而增加，而本文所提方法对扩维向量进行解耦，在不影响误差配准前提下，能显著降低计算量，因此，仿真实验首先对此两个方法进行收敛时间对比，验证算法在降低计算量的有效性。图3、图4即是本文所提TSSH-EKF方法与对文献[7]ASEKF算法复现后利用A，B两部雷达进行系统误差配准后的结果，可以看出：本文所提改进算法较ASEKF算法收敛速度更快，计算效率得到了提高。
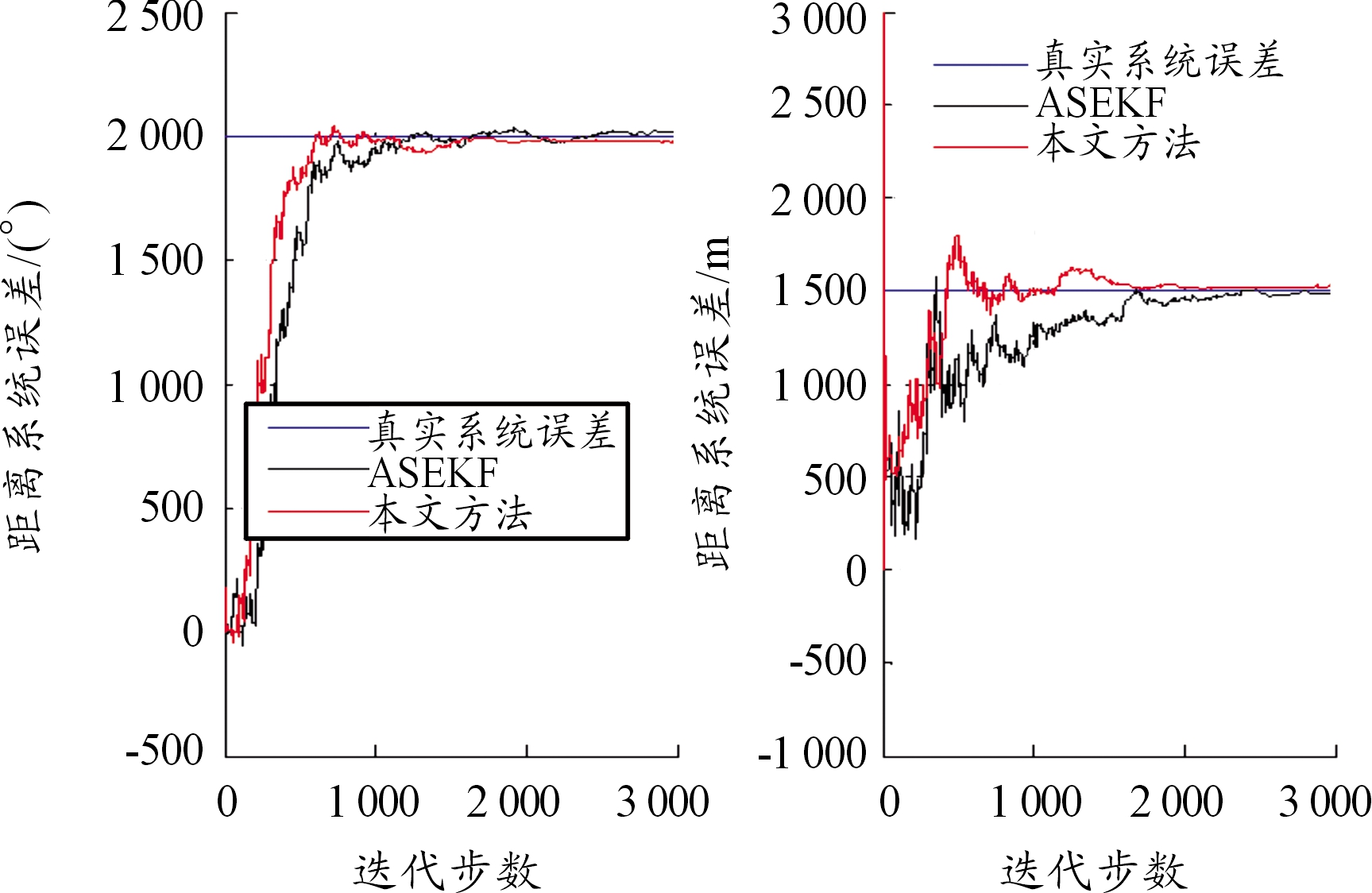
图3 本文所提方法与ASEKF方法距离误差配准结果
图4 本文所提方法与ASEKF方法角度误差配准结果
由于在量测噪声未知或与理论值存在较大差距时，虽然TSEKF算法会降低计算量，但收敛精度会受到量测噪声的较大影响。因此引入序贯的Sage-Husa滤波对其进行改进。图5、图6即是在量测噪声未知时分别利用本文所提TSSH-EKF方法与TSEKF算法对A，B两部雷达进行系统误差配准后的结果。可以看出，双阶扩展卡尔曼滤波方法因为量测误差不定，当量侧误差过大时，无法对系统偏差进行有效的配准。而所提改进方法因将量测误差限定在有效范围内，能够快速收敛于真实系统误差值，滤波精度明显较高，滤波效果比较理想。
传统扩维误差配准算法因状态维数增加导致计算量增大，而本文将双阶卡尔曼滤波应用到联合误差配准中，对扩维向量进行解耦，并引入序贯的Sage-Husa滤波，显著降低了计算时间，增加了收敛精度。表1为本文算法与ASEKF算法、传统TSEKF算法的收敛步数，可以看出，单一的TSEKF算法因受量测误差影响收敛较差，本文所提改进算法在进行系统误差配准时能够快速收敛且收敛速度明显快于ASEKF算法，计算效率得到了提高。
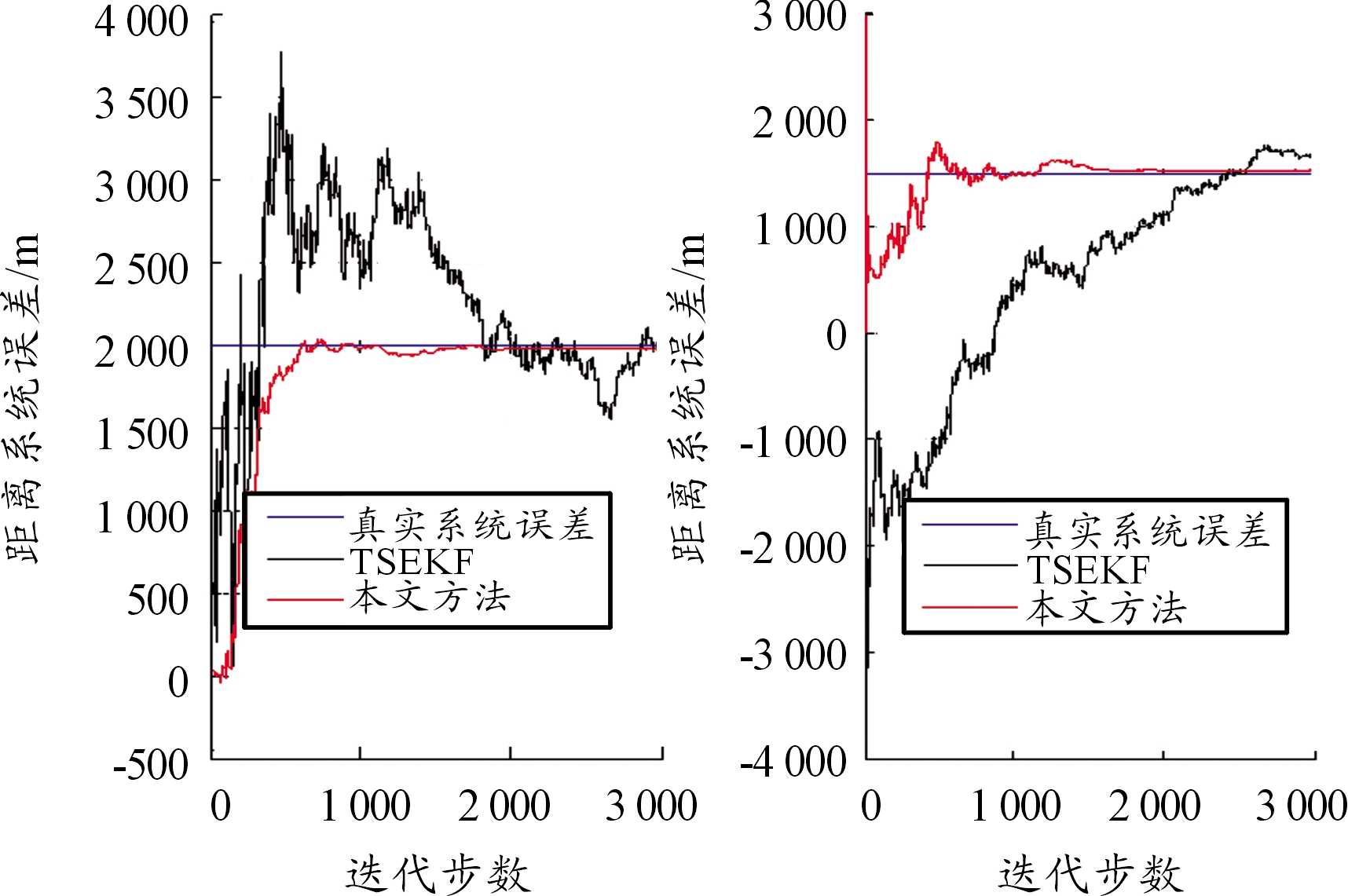
图5 本文所提方法与TSEKF方法距离误差配准结果
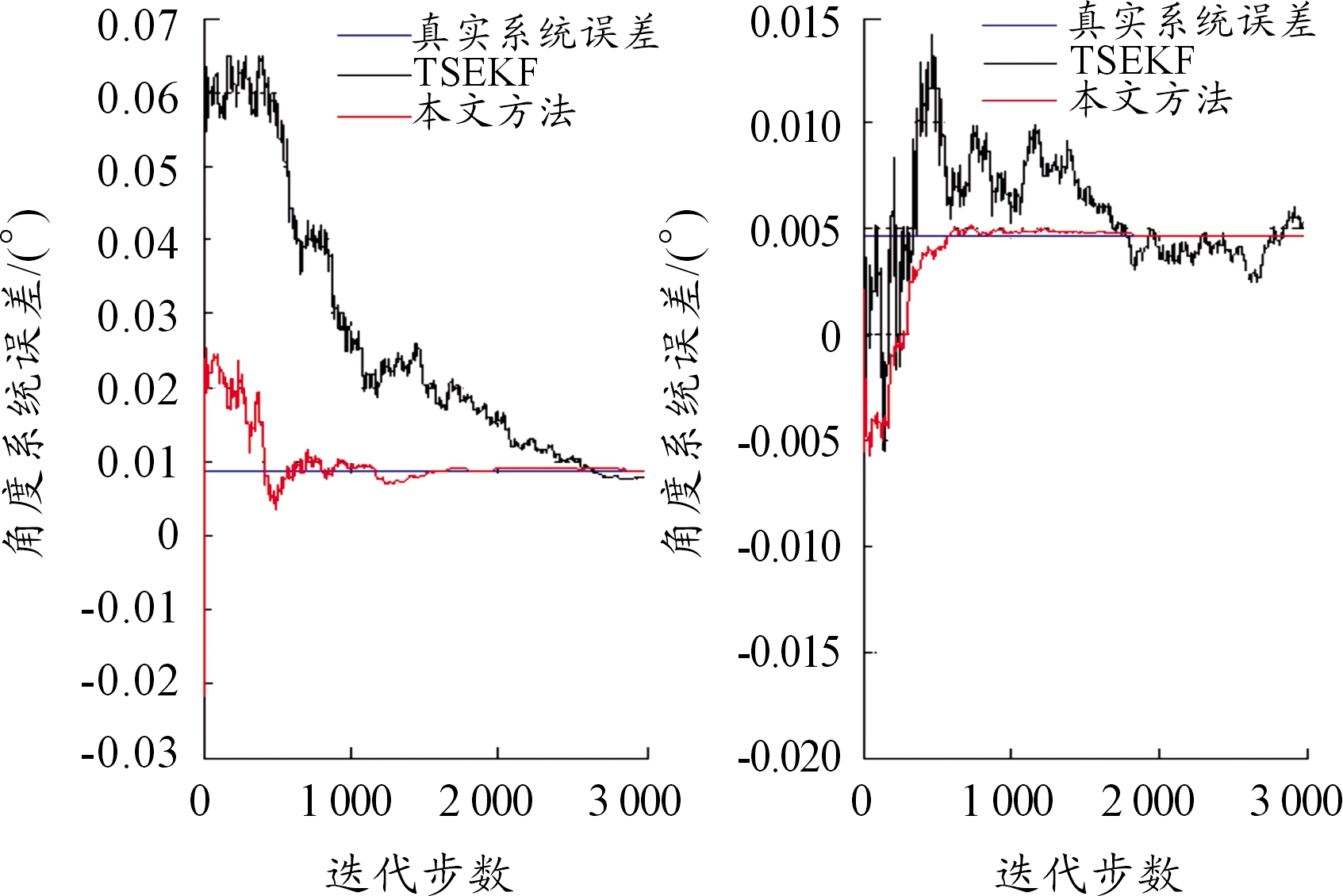
图6 本文所提方法与TSEKF方法角度误差配准结果
表1 滤波收敛时间
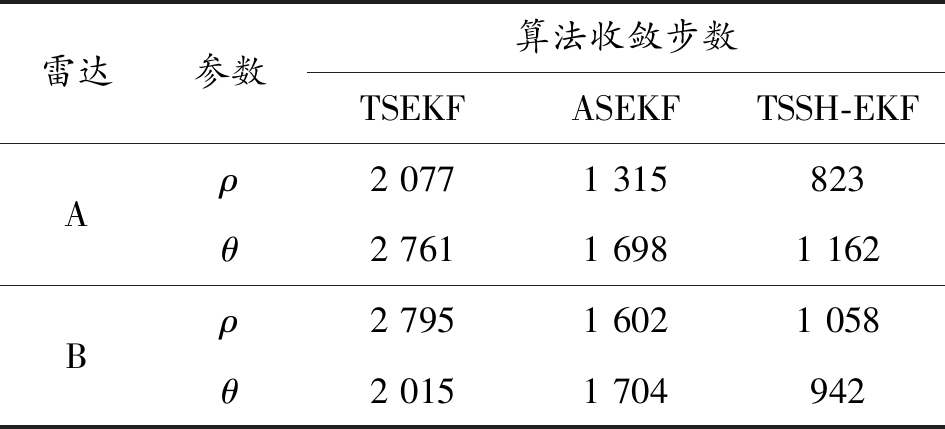
雷达参数算法收敛步数TSEKFASEKFTSSH-EKFAρ2 0771 315823θ2 7611 6981 162Bρ2 7951 6021 058θ2 0151 704942
4 结论
考虑到扩维误差配准算法中状态维度的增加会导致计算量增大的问题，提出一种状态解耦的双阶扩展卡尔曼滤波误差配准方法，并引入序贯Sage-Husa自适应思想解决了TSEKF中无偏滤波器存在滤波精度较低的问题。通过仿真对所提算法的性能进行了分析，验证了所提算法性能上的有效性。
[1]何友,修建娟,关欣.雷达数据处理及应用[M].北京：电子工业出版社,2013.
[2]周学平,李佳杰,邹瑾涛,等.基于极大似然的联合数据关联与空间配准[J].现代雷达,2019,41(3):48-52.
[3]刘锦昌,黄树彩,庞策,等.末段反导防御系统探测误差对拦截效果的影响[J].火力与指挥控制,2018,43(01):74-79.
[4]章涛,李海,吴仁彪.基于概率假设密度滤波的多目标雷达空间误差配准算法[J].控制与决策,2018,33(8):88-94.
[5]宋强,何友,董云龙.一种目标状态与系统偏差的联合估计算法[J].弹箭与制导学报,2007,27(4):312-315.
[6]程然,何科峰.基于CKF的联合扩维误差配准算法[J].航空科学技术,2018，29(5)：66-73.
[7]赵季红,谢志勇,曲桦,等.基于最大互相关熵UKF的传感网目标状态和系统偏差联合估计算法[J].计算机应用研究,2019,36(02):256-259.
[8]FRIEDLAND B.Treatment of Bias in Recursive Filtering[J].IEEE Transactions on Automatic Control,1969,14(4):359-367.
[9]李果,刘旭焱,马建晓.Sage-Husa自适应滤波简化算法[J].计算机工程与设计,2019(5):1360-1364.
[10]ALOUANIA T,XIA P,RICE TR,et al.On the Optimality of Two-Stage State Estimation in the Presence of Random Bias[J].IEEE Transactions on Automatic Control,1993,38(8):1279-1282.
[11]徐景硕,秦永元,彭蓉.自适应卡尔曼滤波器渐消因子选取方法研究[J].系统工程与电子技术,2004(11):1552-1554.