关于航材的预测，国内外学者采用了多种方法进行试验拟合，其中包括线性回归、神经网络、支持向量机等方法[1-5]。线性回归模型对缺少明确变化趋势、离散型数据拟合较差，但其算法固定，通过规定的算法得出唯一结果，且其延伸性能较好；支持向量机是一种优秀的机器学习预测算法，能较好解决局部最优、过度学习等问题，对小样本信息预测效果较好，但其对于较大步幅预测，由于缺少样本支撑，经常拟合效果较差。
对某型引俄直升机航材消耗建立模型时，需要考虑两个特点：一是机型较新、服役时间短，难以获取足够数据，不能划分训练集；二是机型备件国产化水平低，大部分要依靠进口，补给难度较大且易受多种因素影响，对该机型航材消耗，不仅要预测T+1时刻，还要预测T之后较长步幅的区间。基于上述问题，本文使用非参数回归算法建立模型。非参数回归是一种不对模型参数做任何假设的回归算法[6]，仅规定一些一般性条件，近年来该算法在多学科运用较为广泛[7-13]。
1 非参数回归分析
回归分析是应用最广的统计分析方法，其一般模型数学表达式为：
Y=m(X)+U
(1)
式(1)中：X预测变量；Y是X的响应变量；U是随机误差，且满足E(U|X)=0，E(U2|X)=σ2(X)；m(·)是光滑函数[14]。若m(·)模型已知，参数未知即为参数回归。对于模型的估计，需要一定的先验知识做出强假设，否则会有较大偏差。当m(·)模型未知，该回归函数即为非参数回归，在分析时不做任何参数假定。
对该型直升机，预测时可以根据相似机型基础上修正，计算出足够量的先验知识，利用贝叶斯大数定律预测[15-17]。但是类比推测的过程中不可避免会产生误差，并且使用参数回归形式一旦固定，经常拟合效果差。在这种情况下，当数据样本容量足够，使用非参数回归具有一定的可行性，且应用范围更广，性能更稳健[18]。使用非参数回归建模，不需要对数据样本做先验估计，仅依靠数据自身规律进行拟合，通过每个数据计算权重，使得回归曲线具有整体性，对长步幅区间的预测效果较好[6]，能较好解决该机型样本数据少、预测长区间等问题。
非参数回归有多种算法，最经典的是局部核回归，对m(·)估计的数学表达式为：
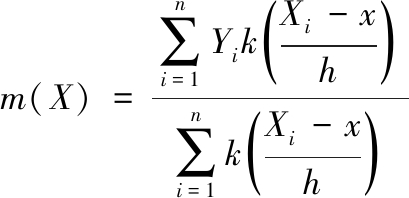
(2)
式(2)中：k(·)是核函数；h是带宽；Xi、Yi分别为预测变量与响应变量。如式(2)所示，平滑函数仅与X、Y相关，通过选取适当的核函数与带宽，建立预测模型。
2 基于非参数回归的航材消耗预测
2.1 航材消耗序列
选取某型引俄直升机一种关键航材，统计8年的航材消耗数据。在8年时间内，该型飞机由于各种原因服役数量存在波动，在本文中，转换为单机月平均消耗件数，方便预测模型的建立。其消耗序列如图1所示，可以初步看出，消耗序列较为离散，有缓慢上升趋势。利用非参数回归模型，对数据样本不做先验假设，依据数据样本自身特点进行回归运算。
2.2 局部多项式回归算法
局部核回归存在边界带估计偏差较大的缺点，对其回归算法进行改进，建立局部多项式回归[7]。其主要方法是在x的一个邻域内，用多阶多项式去估计光滑函数m(·)，然后进行核函数加权，求出m(·)及各阶系数。p阶局部多项式估计是求下式最小值的解，即：
(3)
式(3)中：Yi为响应变量即为每个月单机消耗量；Xi为预测变量即为月份。设
使式(3)达到最小值β=(β0,β1,…,βp)T的值，则β0即回归函数m(x)的估计，βs是
的估计，ms(x)是m(x)的s 阶导数，可以看出，当p=0时，即为局部核估计[19]。令
(4)
Y=(Y1,Y2,…,Yn)′
(5)
β=(β0,β1,…,βp)′
(6)
(7)
将式(3)转化为：
M=(Y-Xxβ)TWx(Y-Xxβ)
(8)
即转化为求式(4)的最小二乘问题。
取p=1，有：
(9)
经计算可得
(10)
式(10)中：
是核函数；Xi、Yi分别代表预测变量与响应变量；h代表带宽。由式(6)～式(9)可以看出，在选定核函数后，关于x的光滑函数需要确定带宽h。
图1 航材消耗序列图
2.3 模型选择
核函数有多种选择，通常有Triangle、Epanechnikov、Quartic、Triweight、Gaussian等核函数，有学者指出当带宽h合适时，核函数的选择对于回归结果影响较小[20-22]。针对上述数据较为离散、变化趋势不明显的问题，使用高次方函数精确性会有一定提高[23]，使用Triweight函数作为备选函数，其数学表达式为：
(11)
在试验中发现，使用Triweight核函数，在序列两端偏差较大，高次幂对权重影响较大，对该核函数改造为：
K(x)=(1-3x2+0.5x4)(1-0.2x2)
(12)
由此能有效降低高次幂在两端的影响，一定程度消除偏差。
对于带宽h的选择优化问题，有了较多的研究，较多学者使用交叉验证选取[20-24]。交叉验证是通过构建均方误差最小的估计量来确定最优带宽，通过剩余数据量来预测响应变量，但对于预测外延有一定误差，本文使用经典拇指法则[6]，其数学表达式为：
h=1.06σn-0.2
(13)
式(13)中：σ为样本方差；n为样本个数。
3 仿真实验
为有效对比非参数回归模型准确性，使用多种方法对消耗数据进行建模。使用前72个数据建立模型，预测73-84数据，与真实数据做对比。
3.1 数据检验
数据检验是回归建模的基础工作，对数据的平稳性做出检验，若不满足要求，在回归拟合前需要进行偏差处理。使用Eviews进行单位根检验，检验结果如图2所示。
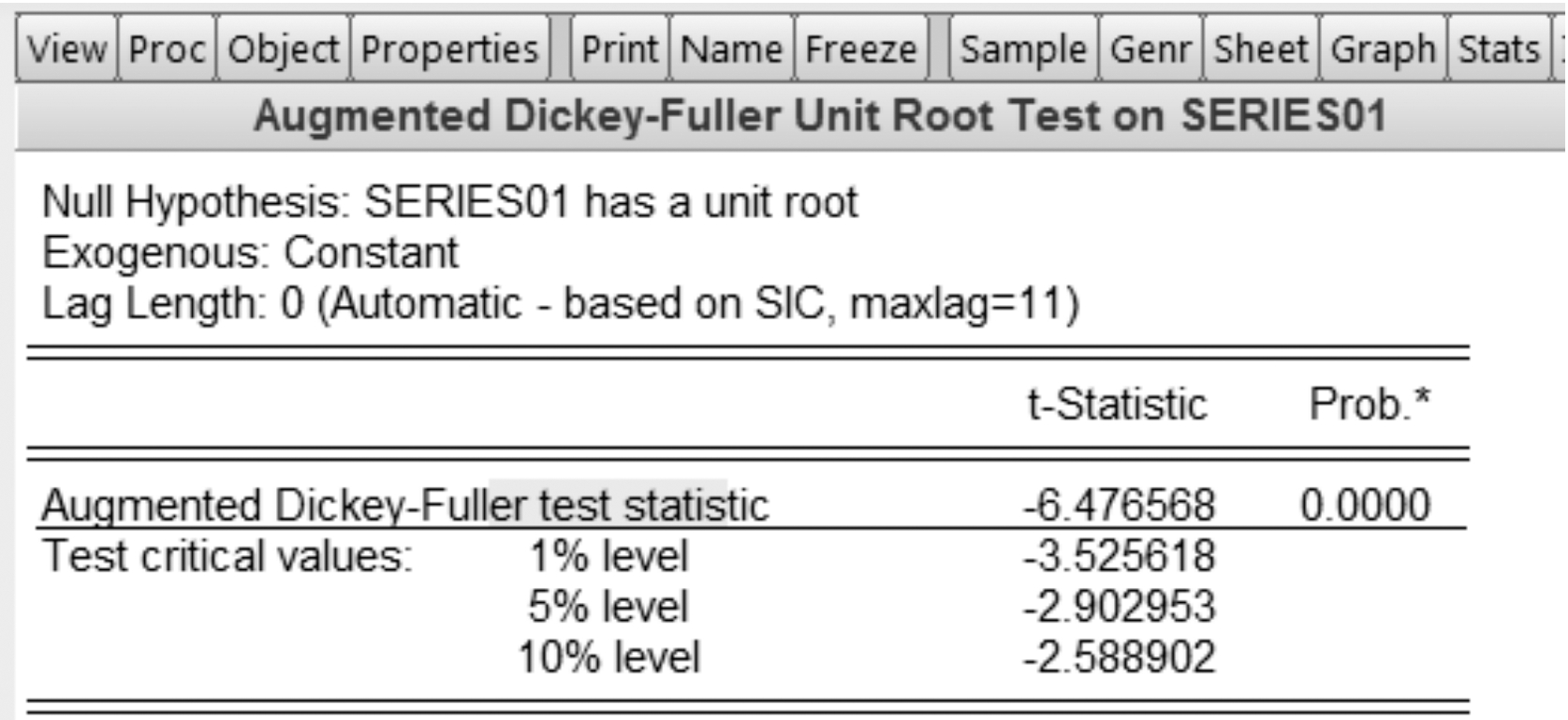
图2 平稳性检验结果
通过ADF(Augmented Dickey-Fuller)检验T值满足要求显著性检验，P值为0，认为消耗序列平稳，无需进行差分运算[15]。
3.2 试验对比
分别使用最小二乘法 (Least Square Method)2阶、3阶、4阶，自回归滑动平均模型(Autoregressive Moving Average Model)、非参数回归(Non-parametric Regression)等方法建模，仿真曲线如图3所示。
由图3可以看出，自回归滑动平均模型对于长步距预测效果较差，最小二乘法拟合曲线由于序列自身波动性较大而缺少明显趋势，拟合过于平滑，但3阶算法预测结果与实际消耗趋势相同。非参数回归由于两端高次幂影响偏差较大，通过改进后模型有了较好优化，曲线拟合与实际消耗情况相近。
图3 回归仿真曲线
支持向量机(Support Vector Machine)对小样本预测较为理想，多名学者在此基础上进行了改进，取得了一定的成果[25]。为充分对比，本文使用SVM对上述仿真进行建模。在上文建模仿真中，73至84数据设为未知，因此在设计SVM试验时，设置[1,60]数据为训练集、[61，72]数据为标准集，对[61-84]数据预测拟合，其推导原理及试验过程在此不做描述，仿真结果如图4所示。
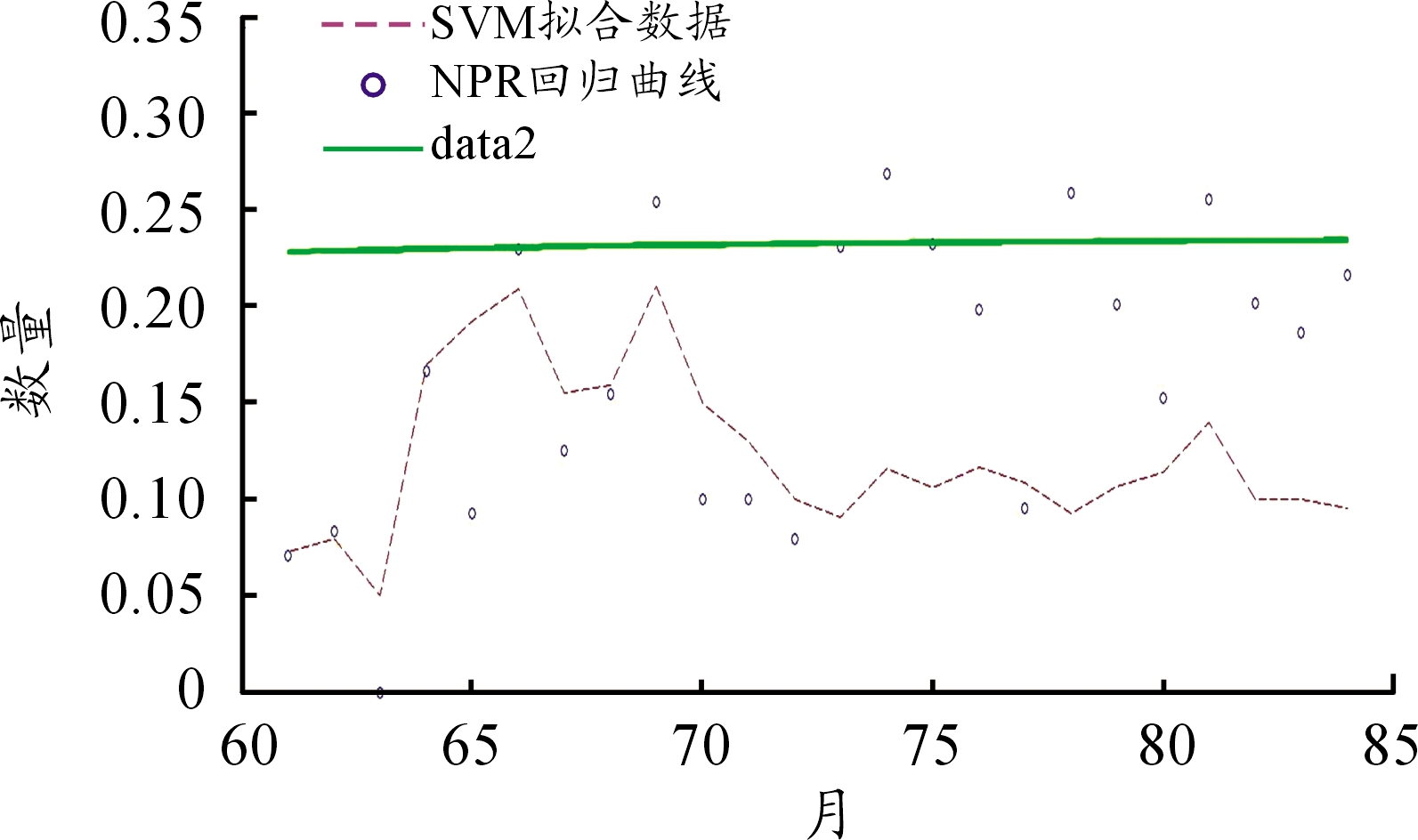
图4 SVM仿真曲线
由图4可以看出，由于前期数据支撑，对于近邻阶段预测效果较好，61～72仿真数据拟合较为理想，对比回归曲线更加接近数据样本。但74之后数据拟合效果较差，对于消耗数据上升趋势未做有效预测分析。
为有效评价模型拟合效果，使用以下两个指标分析对比不同模型的预测准确性。
1) 均值百分比误差MAPE。其数学表达式为[10]：
(14)
2) 均方根差RMSE。其数学表达式为[10]：
(15)
式(15)中：yi为实际值；
为预测值。
对其后12项数据预测结果如表1所示。由表1可以看出，最小二乘3阶模型与非参数局部多项式回归预测效果接近，而改进后非参数局部多项式回归预测效果明显较好。
表1 预测效果对比
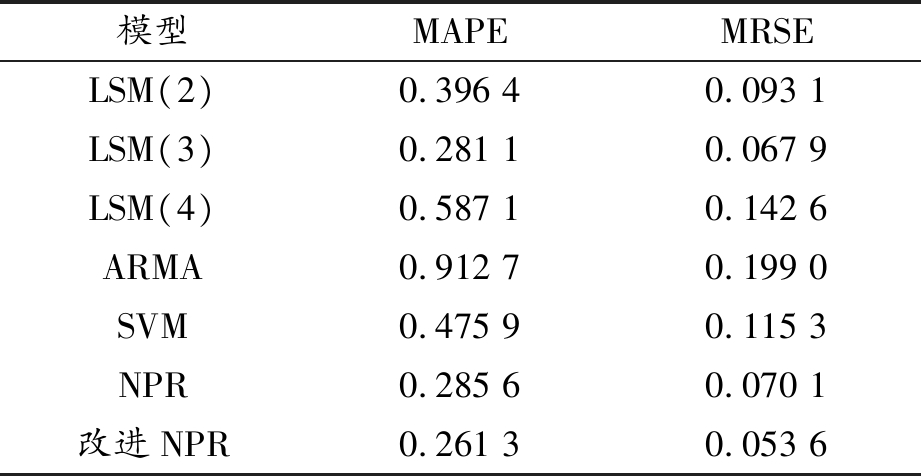
模型MAPEMRSELSM(2)0.396 40.093 1LSM(3)0.281 10.067 9LSM(4)0.587 10.142 6ARMA0.912 70.199 0SVM0.475 90.115 3NPR0.285 60.070 1改进NPR0.261 30.053 6
4 结论
基于非参数回归算法建立航材消耗预测模型，在建模时不对变量作强假设推定，通过样本数据自身进行拟合，使得模型具有自适应性。利用局部多项式回归算法建立模型，并根据数据特点修正模型，仿真实验表明，对于多种回归算法，基于非参数回归的航材消耗预测模型拟合效果更好、预测误差更小，具有较高的准确性。
[1]刘旭,周丽华,朱臣.基于PCA-SVM的航材需求预测方法研究[J].舰船电子工程,2017,37(07):105-109.
[2]汪娅,王超峰.基于约束调度的消耗性航材备件需求预测分析[J].科学技术与工程,2019,19(02):243-247.
[3]李文强,段振云,赵文辉.基于偏最小二乘模型的无人机航材需求预测方法[J].系统工程理论与实践,2018,38(05):1354-1360.
[4]陈博,徐常凯,任佳成.基于灰色神经网络的携行航材消耗预测[J].指挥信息系统与技术,2018,9(05):86-90.
[5]韩玉,张作刚,张海军.基于粗糙集和神经网络的舰载直升机航材消耗预测研究[J].舰船电子工程,2017,37(09):96-99.
[6]龙伟芳,叶绪国.未知误差分布下线性回归模型的非参数自适应估计[J].西北师范大学学报(自然科学版),2019,55(01):26-34.
[7]华祖林,韩爱秋.基于非参数回归改进的太湖总磷压力-响应模型[J].水资源保护,2019,35(01):20-4，46.
[8]李春雨.α-混合误差下非参数回归函数加权核估计的相合性[J].广西民族大学学报(自然科学版),2019,25(01):59-61.
[9]李庆,杨青龙.模型指导的单指标非参数期权定价[J].数理统计与管理,2018,37(06):1086-1094.
[10]戴秀菊,舒志彪.基于非参数核回归模型的隐含波动率预测[J].福州大学学报(自然科学版),2018,46(02):156-162.
[11]夏丽丽,田茂再.零—膨胀泊松回归模型的非参数统计分析及其应用[J].数理统计与管理,2019,38(02):235-246.
[12]许梁,孙涛,徐箭,等.基于函数型非参数回归模型的中长期日负荷曲线预测[J].电力自动化设备,2015,35(07):89-94，100.
[13]姚海祥,李仲飞.基于非参数估计框架的期望效用最大化最优投资组合[J].中国管理科学,2014,22(01):1-9.
[14]ASSAF A G,TSIONAS M.Non-parametric regression for hypothesis testing in hospitality and tourism research[J].International Journal of Hospitality Management,2019,76(2):125-139.
[15]CHAGNY G,ROCHE A.Adaptive estimation in the functional nonparametric regression model[J].Journal of Multivariate Analysis,2016,146(4):23-31.
[16]GIORDANO F,PARRELLA M L.Bias-corrected inference for multivariate nonparametric regression:Model selection and oracle property[J].Journal of Multivariate Analysis,2016,143(1):165-181.
[17]HL
VKA Z,HU
KOV M,MEINTANIS S G.Tests for independence in non-parametric heteroscedastic regression models[J].Journal of Multivariate Analysis,2011,102(4):215-232.
[18]HU Y,YANG Y,WANG C,et al.Imputation in nonparametric quantile regression with complex data[J].Statistics and Probability Letters,2017,127(4):111-135.
[19]KRIEF J M.Direct instrumental nonparametric estimation of inverse regression functions[J].Journal of Econometrics,2017,39(1):54-69.
[20]MANGILI F.A prior near-ignorance Gaussian process model for nonparametric regression[J].International Journal of Approximate Reasoning,2016,78(1):89-103.
[21]MOREIRA C,U
A-LVAREZ J D,MEIRA-MACHADO L.Nonparametric regression with doubly truncated data[J].Computational Statistics and Data Analysis,2016,93(3):129-141.
[22]PARK C G,KIM I,LEE Y S.Error variance estimation via least squares for small sample nonparametric regression[J].Journal of Statistical Planning and Inference,2012,142(8):239-251.
[23]TUFFAHA H W,STRONG M,GORDON L G,et al.Efficient Value of Information Calculation Using a Nonparametric Regression Approach:An Applied Perspective[J].Value in Health,2016,19(4):187-206.
[24]WANG W,YU P.Asymptotically optimal differenced estimators of error variance in nonparametric regression[J].Computational Statistics and Data Analysis,2017,105(1):63-87.
[25]张作刚,宋大勇,宫明慧,等.基于EEMD-SVM的不稳定需求航材消耗预测研究[J].环境技术,2018,36(05):70-73.