随着武器设计精度的不断提高，对于武器测试系统要求也越来越高。弹丸姿态作为评定武器性能的重要参数，是在武器研发测试中必须获取的参数，对武器的性能分析有重要的作用[1]。
文中提出一种基于三目视觉对高速运动弹丸进行姿态测量的方法，利用3台高分辨率CCD相机，在不同位置获取目标弹丸在飞行过程中同一时刻的3幅图像，使用图像处理技术中的边缘直线检测提取到弹丸直线，并于每副图片中提取得到两条直线，利用双目视觉三维重构出弹丸空间中轴线，根据弹丸中轴线计算在相机拍摄时刻运动弹丸的俯仰角和偏航角。相较于在弹丸姿态测量过程中广泛应用的双目视觉原理，三目视觉测量系统有明显的优势。一方面，利用3台数字相机之间的关联性，求解三维姿态的方法使得所测弹丸姿态更为准确。相较于单一双目视觉系统，该模型集中了3个双目视觉测量系统，使得有效测量视场范围更大，可以检测活动范围更为广泛的弹丸。另一方面，由于三目视觉测量系统的每一部分都可以单独完成测量工作，在实际工程应用中的系统容错率和稳定性更高，在复杂应用场景下可以更好地发挥作用。
1 三目测量原理
1.1 双目姿态测量原理
因为弹丸是一个回转体，所以采用中轴线法测量弹丸的姿态角，弹丸在两个相机中所成图像中轴线与各自光心所成的两个平面相交于一条直线，这条直线就是所求弹丸的中轴线[3]。弹丸中轴线与相机光心可以确定为的空间视平面，根据几何关系，可以知道弹丸中轴线在相机上的像就是视平面与成像平面的交线。因为本研究只需要被测弹丸的姿态角度，所以只要将两个平面的法向量叉乘，就可以得到所求中轴线的方向向量，由方向向量即可得到弹丸的俯仰角和偏航角。
1.2 三目姿态测量模型
三目立体视觉模型是由3台摄像机组成，如图1所示，这3台摄像机的光轴分别成一定角度，可以看作是3个双目视觉模型。利用3台摄像机在成像平面上投影。若没有任何误差存在，摄像机1和摄像机2组成的双目系统的测量值l12，摄像机1和摄像机3组成的双目系统的测量值l13，摄像机2和摄像机3组成的双目系统的测量值l23；都应该与被测线l的实际坐标重合[4]，即3个面m1,m2,m3只应交于空间的同一条直线。但实际场景下，由于双目视觉测量系统的误差，l12,l13,l23被测线l的实际坐标并不重合。实际上这3个面会交于空间3条不同的直线，它们分别是各自光心与中轴线组合而成的3个平面的两两相交的线，它们的姿态角度可以经双目视觉的定位算法求出。
由上述推导可看出由于双目视觉测量系统的误差，双目视觉测量系统求解出的被测点坐标偏差比较大，本文提出的三目视觉融合求解被测物三维坐标的方法可以通过l12,l13,l23的优化，求解出更为准确的被测物姿态。
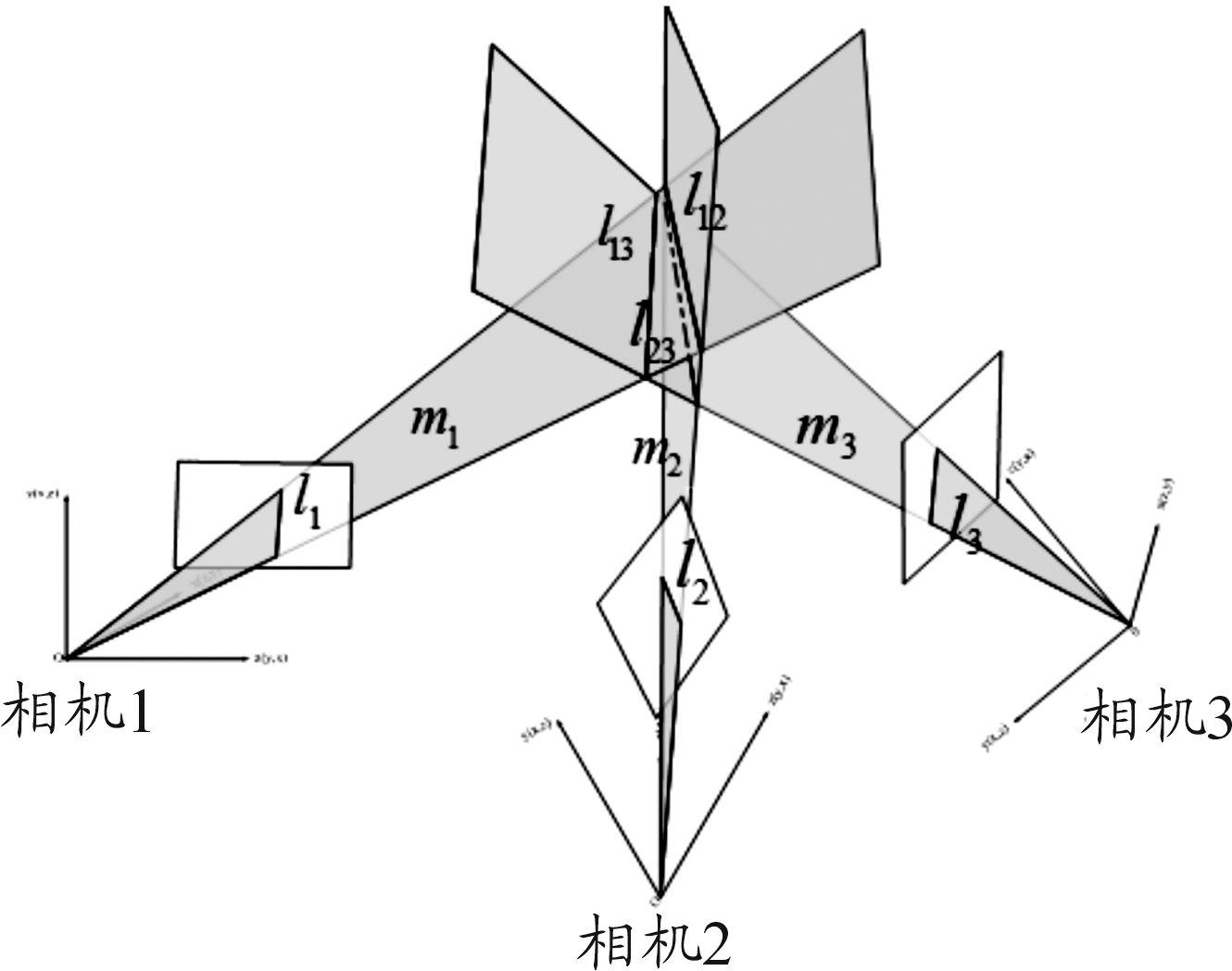
图1 三目姿态测量模型
求中轴线的姿态角度，设直线l测量的单位方向向量v=(X Y Z);
l12的单位方向向量为v1=(X1 Y1 Z1)；
l13的单位方向向量为v2=(X2 Y2 Z2)；
l23的单位方向向量为v3=(X3 Y3 Z3)；
则其最优估计值应满足目标函数：
F=min(||v-v1||+||v-v2||+||v-v3||)
(1)
要满足式(1)只需同时满足下列条件：
(2)
由各变量与算术平均数的离差平方和最小，可知最优的(X Y Z)的值为[5]：
该式即为l的单位方向向量v=(X Y Z)的最优估计，此法也称为求被测物的重心法[5]。
1.3 中轴线法的模型误差[6]
为了方便研究像平面上中轴线误差对结果的影响，假设一台相机有误差，另一台相机无误差；定义一个全局坐标系O-xyz，假设有误差的相机光心位于全局坐标系原点O，无误差相机光心与目标中轴线所确定的平面，与全局坐标系的O-xy平行。
中轴线提取误差对计算结果的影响，假设带有误差的像平面上的方程为：
xcosw+ysinw-p=0
(3)
角度和距离误差分别为wθ和pr，则带有误差的中轴线方程为:
xcos(w+wθ)+ysin(w+wθ)-(p+pr)=0
(4)
假设w和p均为0则中轴线的方程为：
xcoswθ+ysinwθ-pr=0
(5)
相机的高低角和方位角分别为E和A，经计算可以得到角度误差为
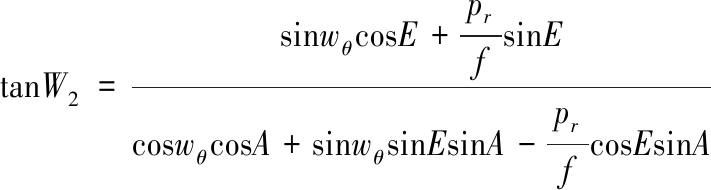
(6)
其中，W2为中轴线的角度误差。
将方向误差和距离误差分开讨论，讨论其中一个误差将另一个置零。对于角度误差，令pr= 0，则公式写成：
(7)
因为sinwθ<<1所以
由分析可知若使图像平面提取角度误差在双目交会时不被严重放大，交会角度应尽量接近90°夹角控制在60°～120°之间时，轴线提取误差与姿态角度测量误差保持在一个数量级，实际测量效果较好。
令wθ= 0，式(7)可写成：
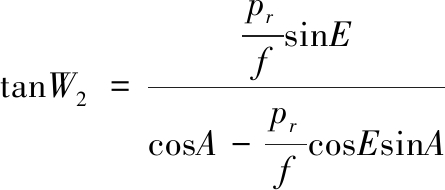
(8)
由于
所以
由于pr误差带来的中轴线角度误差较小，可以忽略不计。两个相机之间的基线长度、测量距离等因素都与两相交平面的夹角有关，这个角度保持在60°～120°之间误差最小。
所以在相机摆放平面与弹丸运动轨迹垂直，12相机和23相机之间间隔60°，这样，就有了两个60°夹角和一个120°夹角的双目姿态测量系统。
在60°和120°时，摆放夹角所产生的误差是一样的，由重心法可得到更加精确的姿态角度。
2 系统实现
2.1 图像捕捉
这种测量方式主要应用于炮口附近的弹丸姿态测量，弹丸发射后有一个炮口触发信号产生，作为系统的启动信号，弹丸进入每个站点的范围，经过红外触发靶有效区域后产生的触发信号作为系统时序控制器的启动信号，时序控制器经过上位机设置的延时分别向激光器和相机发出触发信号，使激光器在相机打开的时间内闪光，从而捕捉到弹丸在激光器闪光时刻的图像。
在图像清晰度方面，相机曝光时间是影响运动拖影的关键因素，为了保证弹丸在图像中的拖影不超过1/2个像素，应保证弹丸在CCD上成像的曝光时间内的位移不超过1/2个像素单位。对于弹丸高速运动而产生的图像拖影，可以采用超短脉冲激光光源的脉宽来控制相机曝光时间。相机快门打开，处于等待状态，通过激光光源的脉冲持续时间控制相机的曝光时间，这样高速飞行的弹丸的图像拖影就取决于脉冲激光的持续时间。此次试验选用的是像素边长为5.5 μm的B6620CCD相机，采用50 mm的定焦镜头，假设弹丸与相机相距2 m，则每一像素边长在弹丸平面内的距5.5 μm×(2 m,/50 mm)=0.22 mm。一般采用波长为532 nm,脉冲宽度为8 ns激光光源，假设弹丸速度为1 000 m/s，拖影长度为8 ns×1 000 m/s=0.008 mm，远小于0.22 mm，可以满足拍摄要求。
2.2 实验流程
实验流程如图2所示。
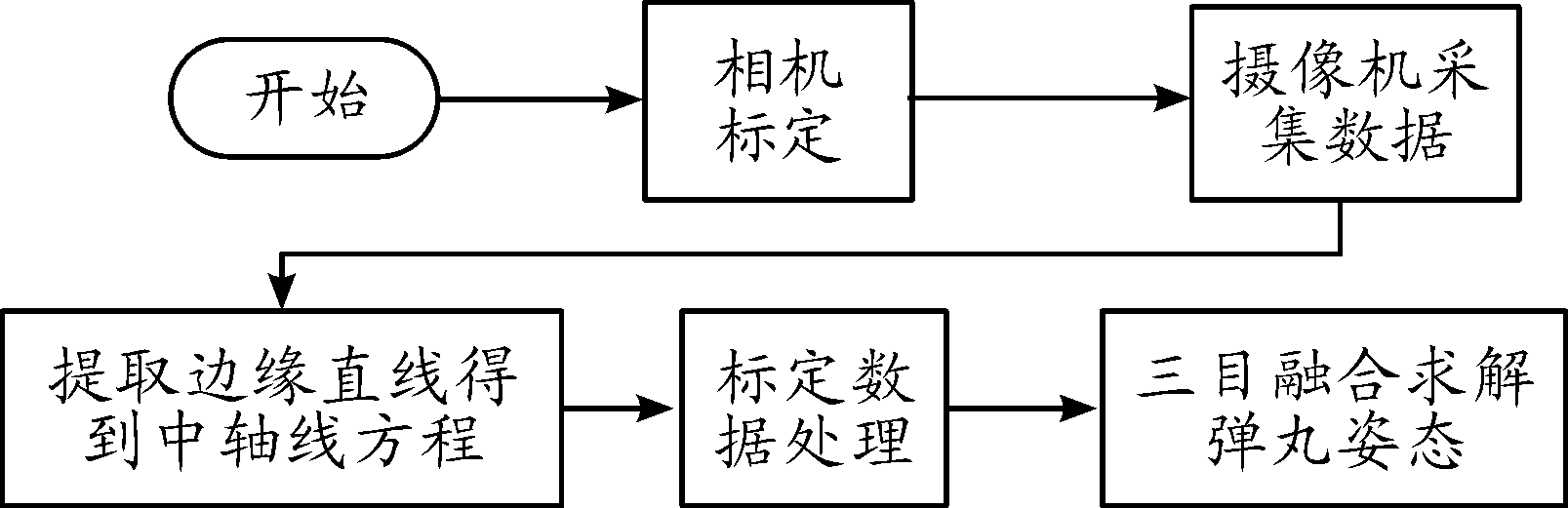
图2 实验流程框图
2.3 相机标定
摄像机标定是指在被测物的三维坐标和相应的二维坐标间建立映射关系[7]，它依据摄像机的成像原理，根据已知特征点的世界坐标和像素坐标的关系可以计算出摄像机的内外参数。上述摄像机标定的结果得到三台摄像机之间的相对位置关系，只有明确了三台摄像机间的相互位置关系，才能通过本研究提出的三目视觉融合方法求解出被测物的三维坐标。
标定选用张正友标定方法[8]，作为普遍应用的张友正标定法，主要是对非线性相机进行标定的一种方法。相机标定的主要思想是先对相机内参数的五个线性参数进行标定，这时并不考虑相机畸变的影响，获得线性参数的初始值后，利用线性参数的初始值对加入畸变系数的非线性模型进行标定。第一次非线性和线性的标定精度都很低，接下来要做的是再次利用非线性标定的结果再一次进行线性标定。按照这种方法反复利用前一次的结果进行迭代运算，直到线性标定和非线性标定的结果全部收敛为止。该方法灵活方便，仅需要通过很少的方向角度去拍摄二维平面图案，步骤包括求解初值，然后再基于最大似然估计进行非线性优化[9]。这种方法与传统标定方法相比的优点是，传统标定方法对标定物的精度要求很高，而这种方法采用的标定模板很容易获取。和自标定方法相比，该方法有较高的精度和更好的鲁棒性。本次的标定板是300 mm×300 mm光学标定板，方格尺寸为20 mm×20 mm，测量总不确定度为±2 μm，能满足相机标定的精度要求。
基本原理：
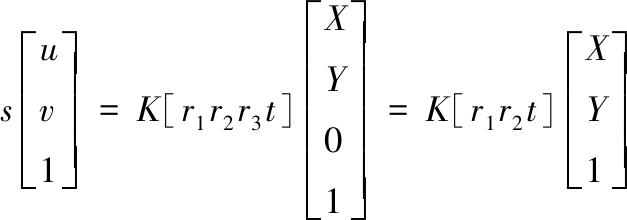
(9)
假定模板平面在世界坐标系Z=0的平面上，K为摄像机的内参数矩阵，M=[X Y 1]T为模板平面上点的齐次坐标，m=[u v 1]T为模板平面上的点投影到像平面上对应的其次坐标。[r1 r2 r3]和t 分别为摄像机坐标系相对于世界坐标系的旋转矩阵和平移量。
设H=[h1 h2 h3]= λ[r1 r2 r3]其中
根据旋转矩阵的性质，即
和|| r1||=|| r2||=1，每副图像可以获得以下两个对内参数的基本约束：
(10)
由于摄像机有 5 个未知参数a、b、r、u0、v0,所以当所拍得的图像数目不小于3 时，就可以求出唯一的一组解。
2.4 数据处理
由张正有标定法可以得到3个相机之间的旋转平移关系，设相机1坐标系到相机2坐标系的旋转矩阵为R12，相机2坐标系到世界坐标系的旋转矩阵为R2。
由Canny边缘检测得到弹丸的边缘线如图3所示，再由Hough变换直线法得到弹丸两条对称的边缘直线如图4所示[10]，两条直线的角平分线即为弹丸的中线。
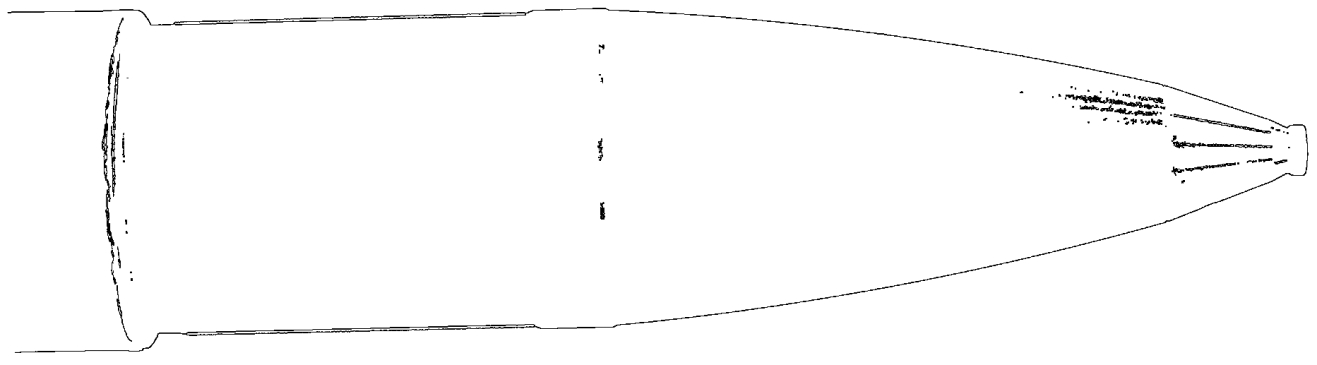
图3 弹丸的边缘线
图4 弹丸的两条边缘直线
设这条直线在图像坐标系中的方程为
ax+by+c=0
(11)
图像坐标系所在的平面在相机坐标系z=f焦距)平面内，O点在z轴上,且x轴y轴与相机坐标系的x轴y轴平行，摄像机的成像过程可以利用针孔模型给出[11]，所以过相机坐标系原点以及z=f(焦距)处直线在相机坐标系的平面方程为
(12)
这个平面的法向量为
设相机1拍到的图片延伸出平面在相机1坐标系下的法向量为F1，设相机2拍到的图片延伸出平面在相机2坐标系下的法向量为F2。因为设相机1坐标系到相机2坐标系的旋转矩阵为R12，则F1在相机2坐标系下为
两平面的交线的法向量即为F1叉乘F12。最后得到的向量再与相机2坐标系到世界坐标系的旋转矩阵R2相乘可得到在世界坐标系下的方向向量，同理可得到相机1与相机3，相机2与相机3双面相交所得直线的方向向量，就可以得出三目姿态测量的方向向量，再由方向向量可得俯仰角和偏航角。
这样计算只用考虑各相机坐标系之间的旋转关系，而不用考虑平移转换，可以消除平移变换所产生的误差。
3 实验
对测试系统进行静态试验，将相机架在三脚架上，以60°的夹角摆放如图5、图6所示，拍摄照片提取边缘直线，计算角度。
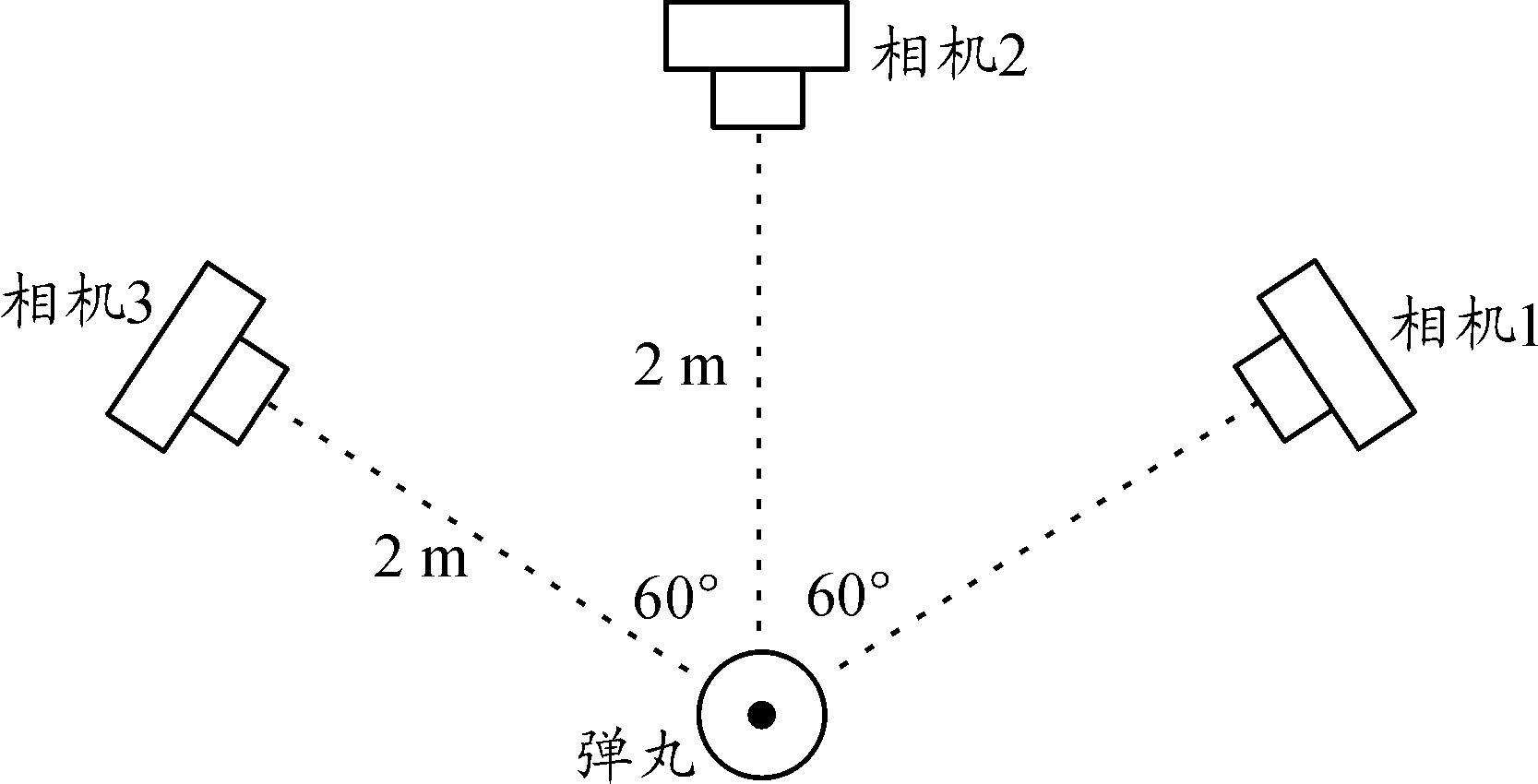
图5 相机摆放示意图(俯视)
图6 现场布置图
表1 计算得到的弹丸姿态角度及误差
实际值/(°)双目检测/(°)双目误差/(°)三目检测/(°)三目误差/(°)1俯仰-4.437 30-4.417 300.020 05-4.420 100.0172 4101偏航8.440 488.670 410.229 938.673 460.232 9782俯仰-2.726 70-2.709 400.017 23-2.656 800.069 8422偏航1.929 602.233 490.303 892.178 630.249 0253俯仰2.255 412.279 030.023 622.291 750.036 3403偏航6.259 886.533 150.273 276.518 340.258 4604俯仰1.891 281.950 910.059 622.029 520.138 2374偏航-5.413 30-5.011 600.401 67-5.087 700.325 6245俯仰-0.270 20-0.213 300.056 95-0.134 300.135 9115偏航0.252 820.628 480.375 660.551 410.298 591
通过三目视觉的弹丸姿态测量系统计算得到弹丸的俯仰角和偏航角将计算结果与实际结果对比后可知系统可以得出有效的姿态角度，且对角度的测量误差不大于0.35°，相比于双目姿态测量系统视场范围变大，也更加稳定。
4 结论
利用3个相机构建三目立体视觉系统，采用投影面交线法重建弹丸中轴线的方向向量从而得出弹丸的姿态角，并搭建系统进行实验验证。在室内进行实验，多次试验表明三目姿态测量系统可以有效测出弹丸的姿态角，且静态误差小于0.35°，相对于双目检测系统具有更高的稳定性和可靠性,与传统的阴影照相法[12]相比，不用搭建复杂的光路系统，对野外等复杂环境更加适应。
[1]杨榜林岳全发.军事装备试验学[M].北京:国防工业出版社,2002:1-7.
[2]赵昕扬,刘仰川,高万荣,等.一种基于多目立体视觉的手术器械跟踪定位策略[J].江苏大学学报(自然科学版),2018,39(1):57-63.
[3]崔彦平,林玉池,黄银国.回转体目标空间三维姿态测量方法研究[J].传感技术学报,2007,20(1):146-149.
[4]钱萍,王惠南.基于三目视觉测量的航天器交会对接相对位姿确定算法[J].宇航学报,2010,31(6):1575-1581.
[5]辛乐.三目视觉坐标测量系统的设计与实现[D].哈尔滨：哈尔滨工程大学2018.
[6]于起峰,孙祥一,陈国军.用光测图像确定空间目标俯仰角和偏航角的中轴线法[J].国防科技大学学报,2000,22(2):15-19.
[7]李孟.三目立体相机的标定研究[J].计算机技术与发展,2015(2):69-73.
[8]ZHANG Z.Flexible Camera Calibration by Viewing a Plane from Unknown Orientations[C]//The Proceedings of the Seventh IEEE International Conference on Computer Vision.IEEE,1999:666-673 vol.1.
[9]李海,张宪民,陈忠.基于直线检测的棋盘格角点自动提取[J].光学精密工程,2015,23(12)：3480-3489.
[10]陈志强,高磊,吴黎慧,等.一种优化的Canny算子边缘检测法[J].电子测试,2011(6):43-46.
[11]马颂德，张正友.计算机视觉-计算理论与算法基础[M].北京:科学出版社，1998:52-59.
[12]顾金良,陈平,夏言,等.数字式靶道阴影照相系统[J].弹道学报,2009,21(4):38-41.