火炮在现代化战场上具有重要的作用。链式弹仓作为火炮供输弹系统的重要组成部分，其定位精度的优劣直接影响到火炮的射速[1-3]。链式弹仓作为一种特种机械设备，为保证其动力传输的可靠性以及工作效率，常常采用链传动方式作为弹仓的传动系统。由于链传动多边形效应所引起的速度变化造成了弹仓系统存在冲击与振动，使得弹仓系统模型中存在时变性扰动与不确定性[4]。此外，非线性摩擦也是造成弹仓系统模型存在不确定性的主要因素之一。滑模控制(Sliding Mode Control，SMC)作为一种非线性控制方法，因具有良好的鲁棒性和抗干扰能力，所以常被用在存在不确定性因素的系统中，但其造成控制量的抖振现象严重制约了滑模控制的发展与应用[5-6]。目前，国内外针对削弱滑模系统抖振的方法主要有以下几种。自适应控制 (Adaptive Control)：自适应控制能够有效估计系统不确定性因素的界限[7]。文献[8]中以自适应控制理论和滑模控制理论为基础，为一类不确定性系统设计了自适应滑模控制律(Adaptive Sliding Mode Control)，在保证鲁棒性的前提下改善了滑模切换项的不连续性，削弱了抖振。趋近律(Reaching Law)：中国学者高为炳[9]提出的趋近律概念，首次对滑模趋近运动的轨迹做了明确的规划，改善了滑模趋近运动的动态品质。文献[10]中提出的一种基于指数趋近律构造的模糊滑模控制系统不仅解决了因负载变化所导致的非线性系统控制精度不足问题，而且设计的模糊系统实现了对趋近律参数的在线调节，改善了整体控制系统的性能。扰动观测器(Disturbance observer，DOB)：利用扰动观测器估计外界干扰以及不确定性，并加以补偿不仅能够有效降低滑模切换项增益，削弱滑模控制的抖振，而且还能提高系统的抗干扰能力[11]。文献[12]中将滑模控制与扰动观测器引入永磁同步电机的调速环节，通过积分补偿了系统的稳态误差，降低了抖振现象。
针对存在时变性扰动的链式弹仓系统的位置控制问题[14-15]，本研究在对滑模控制、自适应律以及扰动观测器理论等算法研究的基础上，以及上述文献的综合启发作用下，提出了一种基于干扰观测器的弹仓趋近自适应滑模控制。干扰观测器有效估计了系统中存在的扰动和不确定性，并通过控制输出量进行了补偿；通过引入指数趋近律改善了滑模动态品质，设计的滑模切换自适应律有效削弱了控制量的抖振，使得链式弹仓系统获得了较高的位置控制精度。
1 系统的动力学模型
链式弹仓系统主要组成部分包括：弹仓本体、链式传动机构、减速器以及永磁同步伺服电机等。伺服电机对回转弹仓系统进行位置控制，忽略电机内部电流环特性，采用id=0的矢量控制法，驱动器根据上位机算法输出控制电流iq，电机电磁转矩方程为
Te=1.5pnφfiq=Ktiq
(1)
其中：pn为电机磁极对数；φf为转子磁链；Kt为电机转矩常数。
链式弹仓伺服系统的动力学方程为：
(2)
式中： J为链式弹仓系统等效至电机转子的等效转动惯量(包括转子的转动惯量)；B为弹仓系统等效至电机转子的等效阻尼系数(包括转子的阻尼)；dt为链式弹仓系统存在的扰动力矩，包括负载力矩、非线性摩擦、参数扰动以及其他未建模动态。
进一步的，可以写成更为一般形式的数学模型
(3)
其中：x1=θ为电机转子角位移；
为电机转子角速度；其中，
为控制力矩。
2 控制系统设计
2.1 扰动观测系统的设计
针对本研究的二阶伺服系统采用如下扰动观测器[13]：
(4)
其中：
为扰动观测估计项；参数
为对系统角速度的估计项；λ1>0，λ2>0，λ1，λ2均为扰动观测器系数。通常情况下在实际的系统中，存在的扰动都是有界的，且假设其为慢时变函数，即
比较小，通过合理设置参数λ1和λ2能够保证扰动观测系统的稳定。
设计扰动观测系统Lyapunov函数如下
(5)
其中
为扰动估计误差且估计误差有界即
为角速度估计误差。
求导得：
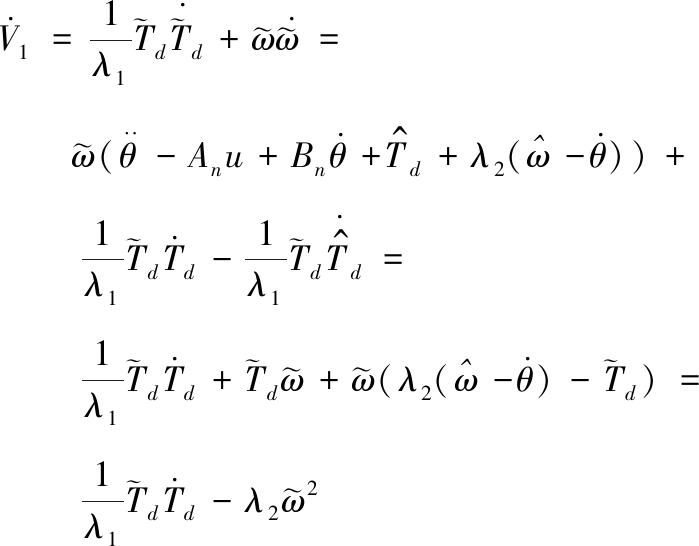
(6)
在前文假设条件下比较小，所以当λ1取较大的值时，有
从而证明了此扰动观测系统是稳定的。构造的扰动观测系统能够有效观测弹仓系统中存在的扰动特性，为下一步构造基于扰动观测器的趋近滑模控制系统奠定基础。
2.2 基于扰动观测的趋近滑模控制系统的设计
设系统角位移误差e=θd-θ；θd为期望角位移轨迹，取滑模面函数为
其中c为滑模面参数。为改善滑模动态特性，设计滑模指数趋近律如下：
(7)
即有
其中，sgn(s)为符号函数；k>0为指数趋近律参数。
将2.1小节中得到的扰动观测项代入式(7)得到基于扰动观测的趋近滑模控制律为：
(8)
设计趋近滑模控制系统Lyapunov函数如下
(9)
求导得：
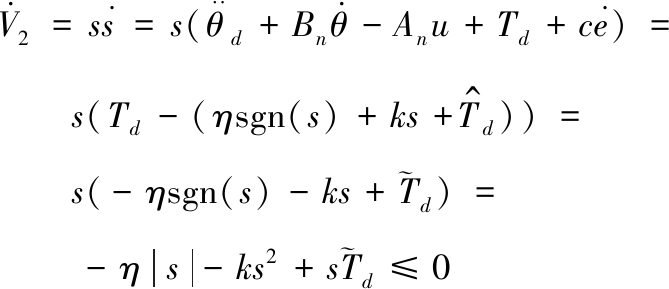
(10)
所以采用式(8)的控制律时，证明控制系统是稳定的。为改善控制系统的动态性能，引入自适应算法，为控制系统设置合理的自适应律，能够有效削弱滑模控制系统中存在的抖振问题。
2.3 基于扰动观测滑模自适应控制系统的设计
在滑模控制系统中，参数η往往难以估计。如果参数η取值过大则会导致系统产生抖振；如果参数η取值过小则会引起系统的不稳定。所以文中为此参数设计了自适应律如下：
(11)
式中，自适应参数μ>0。
以自适应估计值
代替固定值，得到最终控制律如下：
(12)
设计整个闭环控制系统的Lyapunov函数如下
(13)
式中，
为自适应估计误差。求导得：
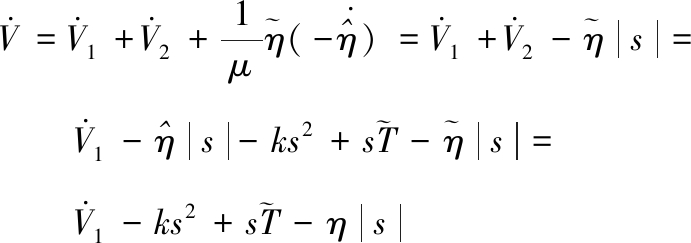
(14)
所以
整个闭环控制系统是稳定的。
3 参数设计及仿真分析
为了检验本研究所设计的算法对于各种工作情况下弹仓的位置控制的有效性。设置弹仓在空载、半载以及满载3种带载状态条件下，进行算法的仿真。由于在实际弹仓控制系统中，采用的是点到点的位置轨迹曲线，所以在仿真时设计了如图1所示的速度梯形轨迹曲线。图1中，最大角位移为600 rad，最大角速度为300 rad/s，最大角加速度为600 rad/s2，整个轨迹运动时间为5s，加速、减速时间各为0.5 s，匀速时间为1.5 s。
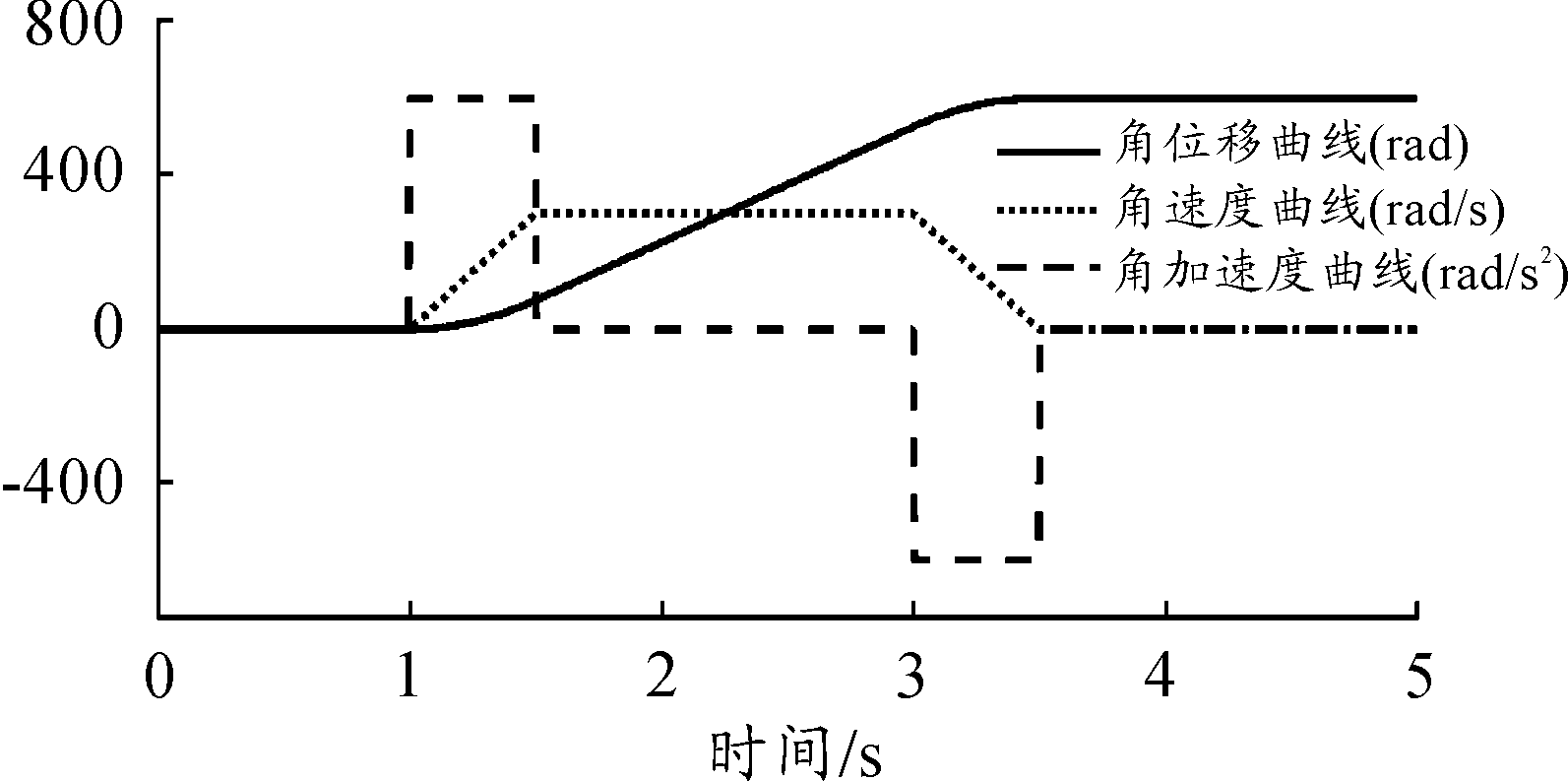
图1 速度梯形轨迹曲线
本研究基于干扰观测器的弹仓趋近自适应滑模控制参数设计如下：
λ1=5000，λ2=500，c=40，k=40，μ=0.5
3种载荷下弹仓动力学模型中的固有参数值如表1所示。
表1 弹仓模型固有参数
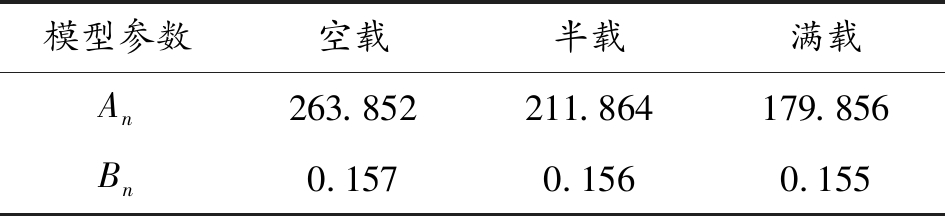
模型参数空载半载满载An263.852211.864179.856Bn0.1570.1560.155
伺服电机转矩常数Kt=0.072，本研究设计的算法能够估计弹仓系统中存在的扰动，从而控制电机输出力矩克服扰动，进而获得较高精度的位置控制。为模拟弹仓系统中存在的时变性扰动特性，本研究为3种载荷状况下的弹仓设置了3种幅值不同的随机函数扰动曲线如图2所示。满载扰动的幅值为2 N·m，半载扰动幅值为1.5 N·m，空载扰动为1 N·m。
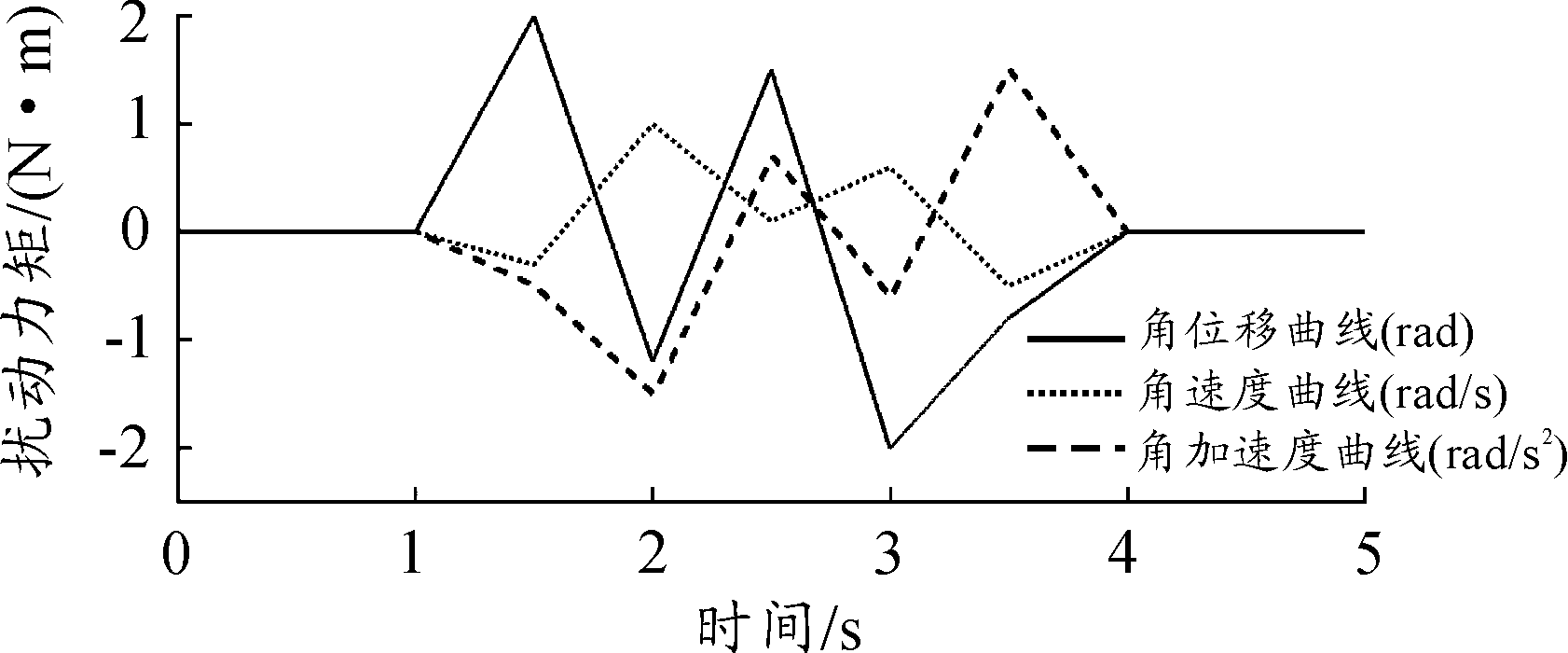
图2 随机函数扰动曲线
利用Matlab软件中的Simulink仿真工具，搭建基于扰动观测器的弹仓趋近自适应滑模控制系统，设置固定仿真步长为0.004 s，仿真时间为5 s。根据本研究所设计的控制算法，用Matlab语言进行程序的编写。控制系统结构如图3所示。
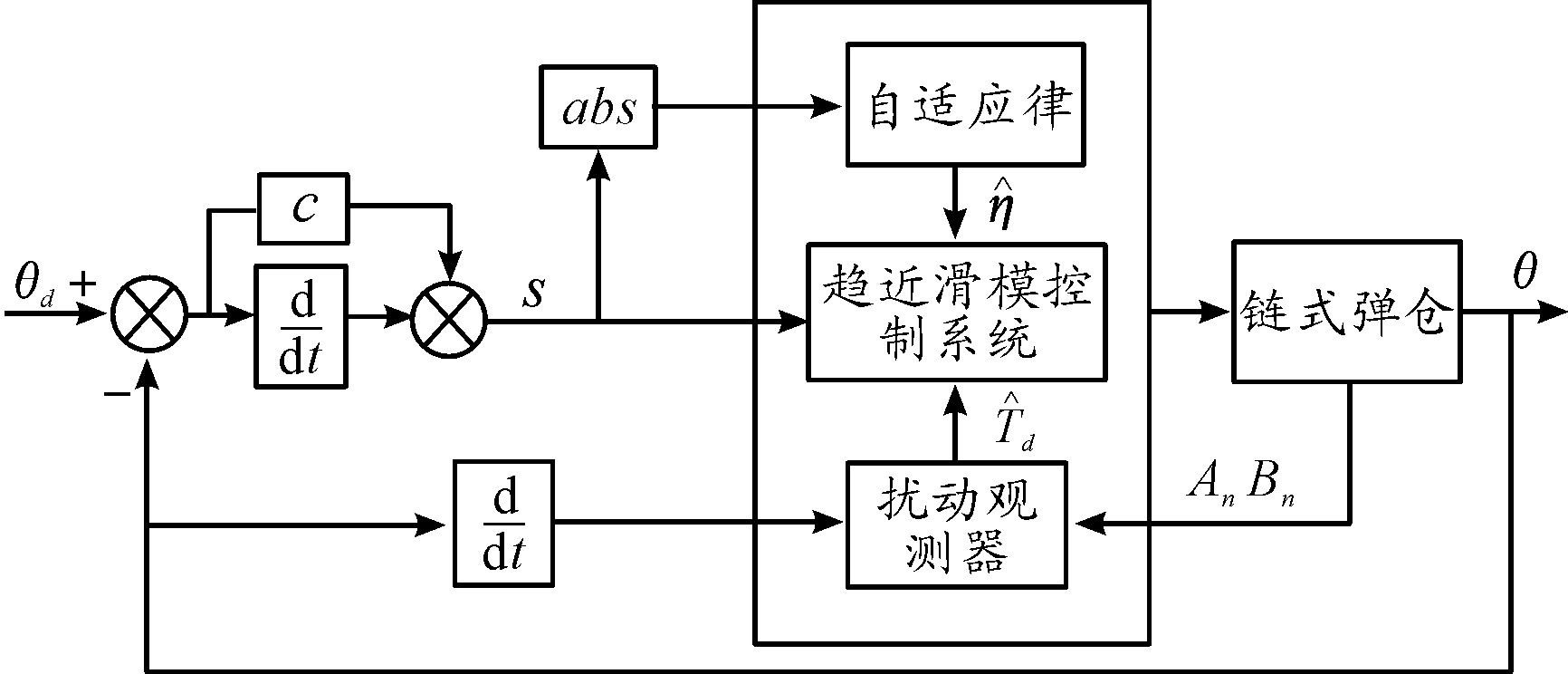
图3 弹仓控制系统结构框图
在Simulink中的scope模块输出弹仓控制系统的仿真结果，并绘制曲线。具体仿真曲线如图4～图9所示。
图4 空载控制输出力矩曲线
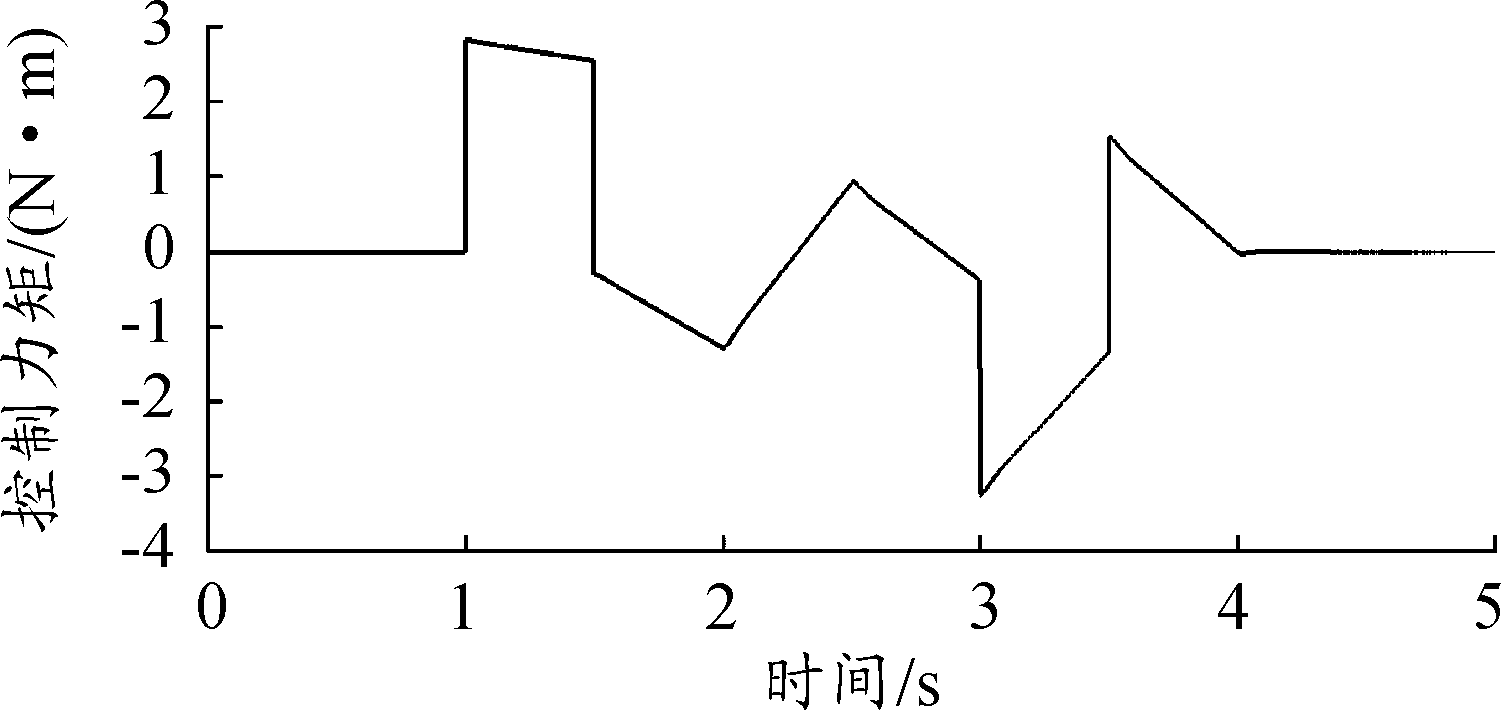
图5 半载控制输出力矩曲线
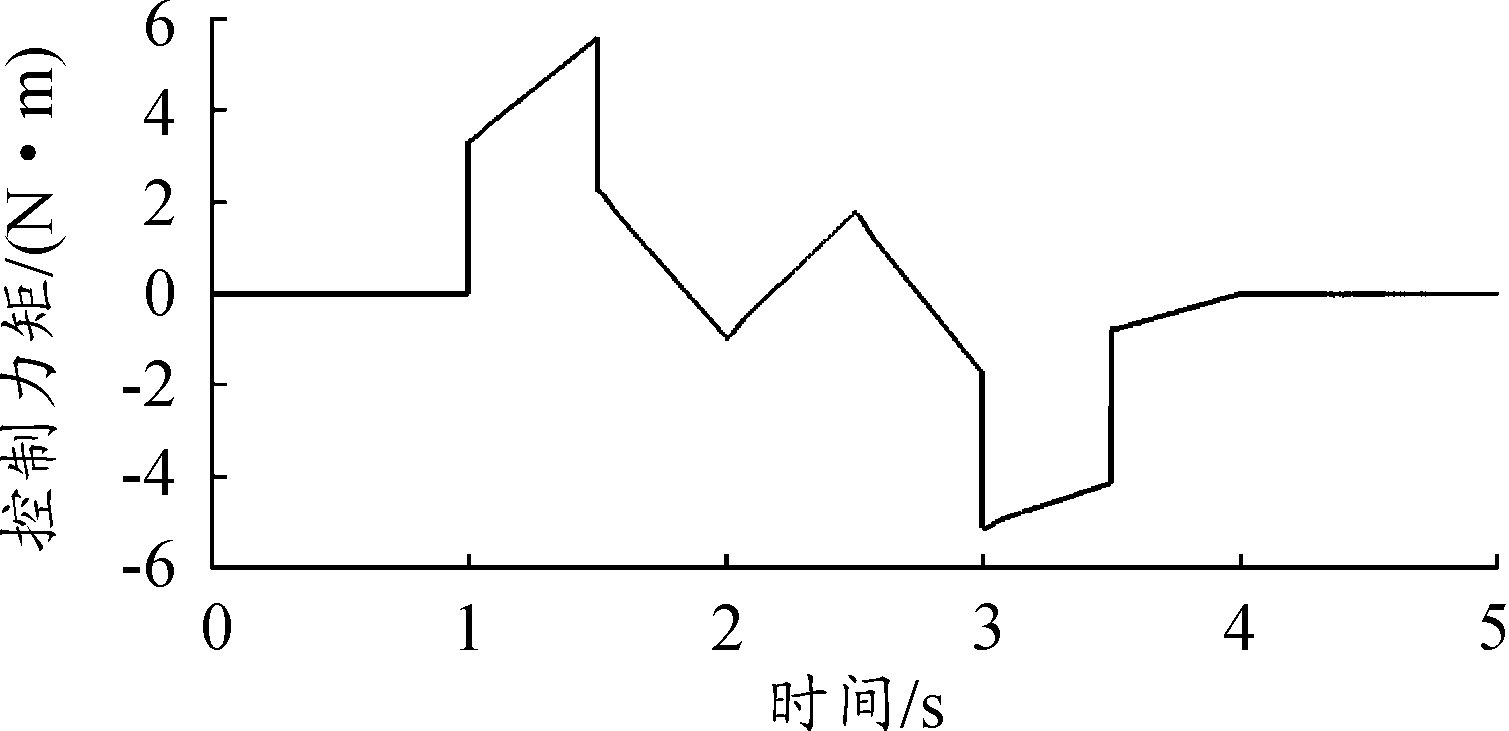
图6 满载控制输出力矩曲线
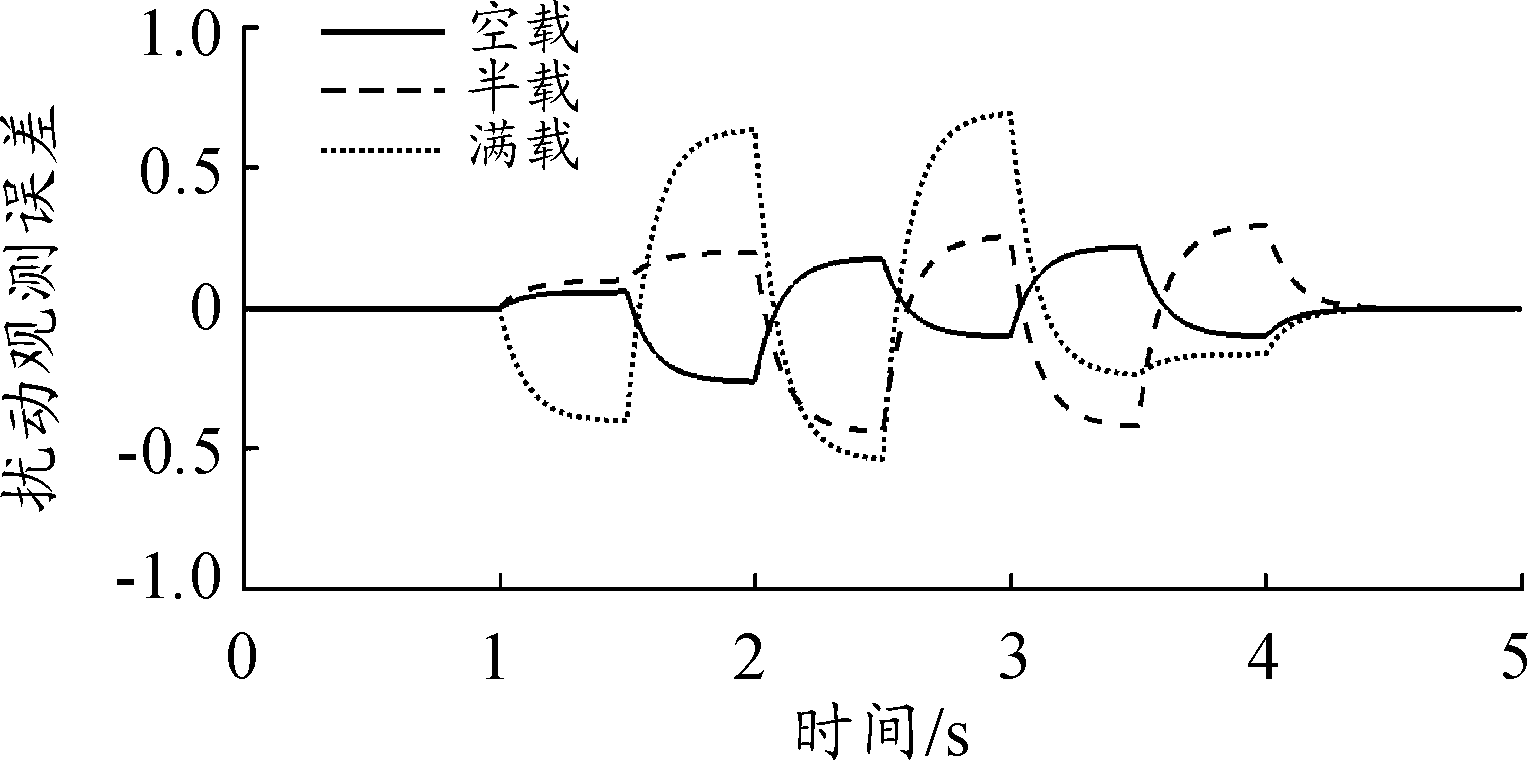
图7 扰动观测误差曲线
图4～图6为3种负载情况下，控制系统输出的力矩曲线；图7为3种负载情况下，扰动观测器估计的扰动误差曲线。由图4～图6曲线的变化趋势以及图7扰动估计的误差可以看出，本文提出的基于干扰观测器的弹仓趋近自适应滑模控制算法有效估计了弹仓系统中存在的扰动并控制输出相应的力矩对其进行了补偿。
图8为3种负载情况下，滑模控制系统的自适应参数估计曲线。从曲线变化趋势可以看出，本研究设计的自适应律根据滑模系统状态的变化，实现了对滑模切换系数的实时在线调整，有效削弱了控制量的抖振，改善了控制系统性能。
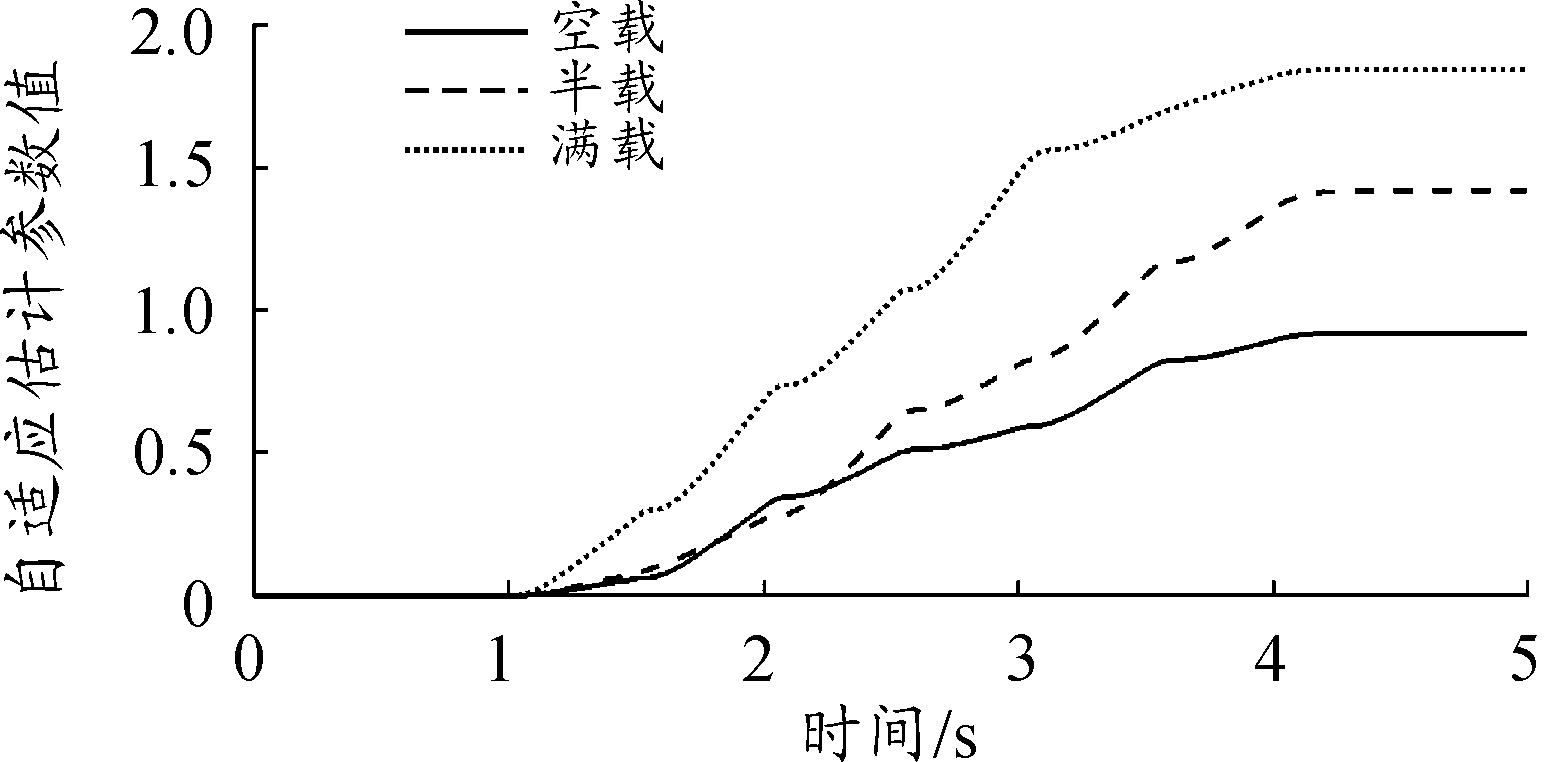
图8 自适应参数曲线
图9为3种负载情况下，系统角位移跟踪误差曲线。分析图9可以得到，随着载荷的增加，弹仓系统的角位移跟踪误差有所增加，但整体仍保持在±0.04 rad以内。以上的仿真结果表明：本研究提出的基于干扰观测器的弹仓趋近自适应滑模控制算法具有较高精度的位置控制效果。
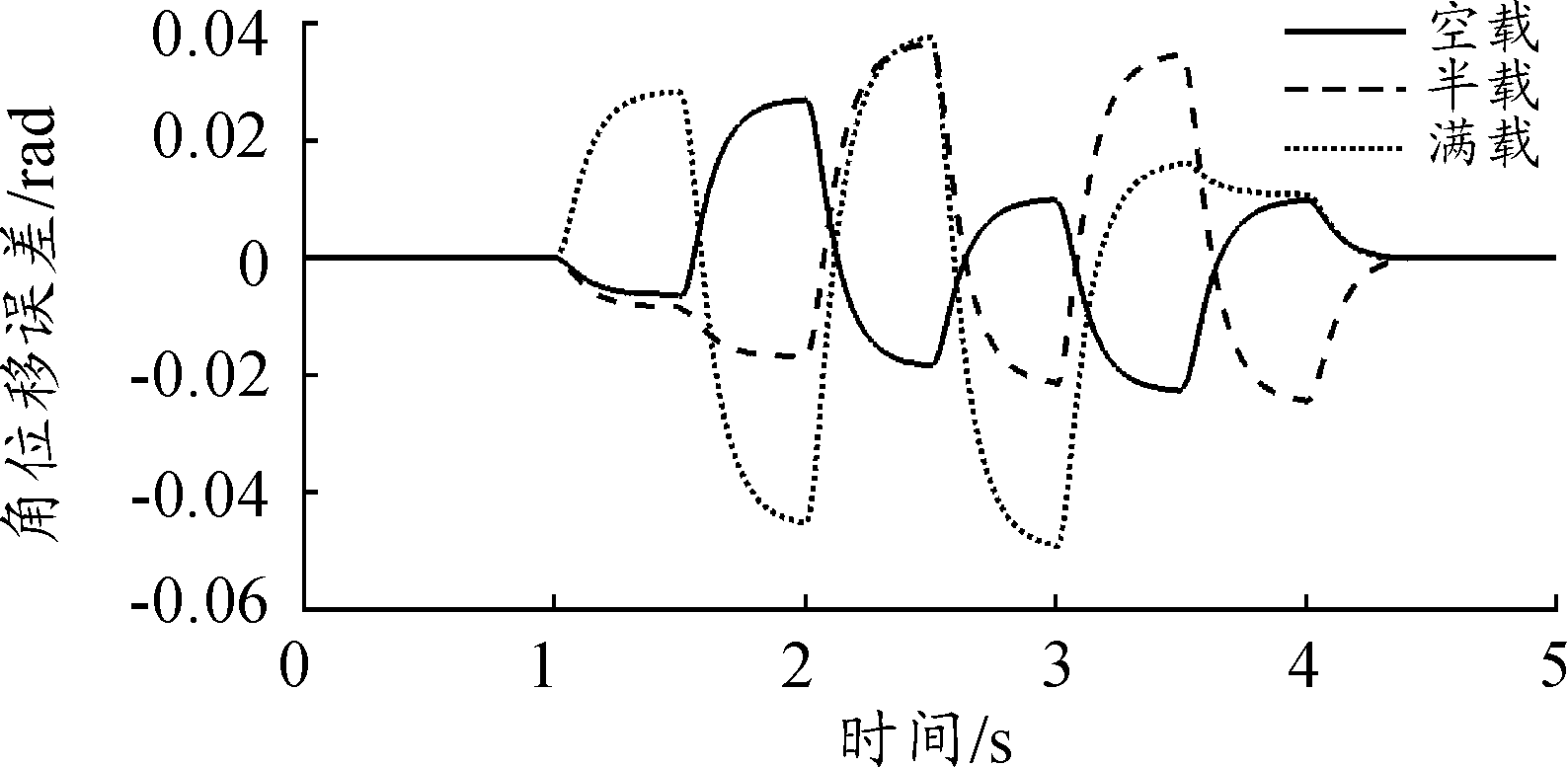
图9 跟踪误差曲线
4 结论
基于干扰观测器的弹仓趋近自适应滑模控制算法，可通过为弹仓系统设置合理的扰动观测器，实现对系统中存在的时变性扰动的有效估计并对此扰动进行控制补偿，扰动观测器的估计误差由滑模控制系统消除。为了削弱控制量的抖振，改善弹仓系统的整体控制效果，为滑模系统设置了自适应律，在3种载荷状态下的仿真结果表明：所提出控制算法不仅具有良好的控制精度，而且较强的鲁棒性。
[1]梁辉,马春茂,潘江峰,等.大口径火炮弹药自动装填系统研发现状和趋势[J].火炮发射与控制学报,2010(3):103-107.
[2]张相炎,郑建国,袁人枢.火炮设计理论[M].北京：北京理工大学出版社,2014.
[3]刘琮敏,孙大鹏,范志国,等.中大口径火炮弹药自动装填技术[J].火炮发射与控制学报,2013(3):93-96.
[4]唐逸雄,陈龙淼,高波.链式回转弹仓的RBF神经网络滑模控制[J].兵器装备工程学报,2018,39(11):141-145.
[5]LIU J K,SUN F C.Research and development on theory and algorithms of sliding mode control[J].Control Theory & Applications,2007,24(3):407-418.
[6]刘金琨.滑模变结构控制MATLAB仿真[M].2版.北京：清华大学出版社,2005.
[7]董绍阳,陈龙淼,张彤.火炮自动装填机械手的自适应动态面滑模控制[J].兵器装备工程学报,2018,39(1):97-101.
[8]HUANG Y J,KUO T C,CHANG S H.Adaptive sliding-mode control for nonlinear systems with uncertain parameters[J].IEEE Transactions on Systems Man & Cybernetics Part B Cybernetics A Publication of the IEEE Systems Man & Cybernetics Society,2008,38(2):534-539.
[9]高为炳.非线性系统的变结构控制[J].自动化学报,1989,15(5):408-415.
[10]岳才成,钱林方,徐亚栋,等.基于指数趋近律链传动弹仓自适应模糊滑模控制[J].上海交通大学学报,2018,52(6):750-756.
[11]CHEN W H.Disturbance Observer Based Control for Nonlinear Systems[J].IEEE/ASME Transactions on Mechatronics,2005,9(4):706-710.
[12]刘颖,周波,方斯琛.基于新型扰动观测器的永磁同步电机滑模控制[J].中国电机工程学报,2010,30(9):80-85.
[13]KAWAMURA A,ITO H,SAKAMOTO K.Chattering reduction of disturbance observer based sliding modecontrol[J].IEEE Trans.on Ind.appl,1992,30(2):456-461.
[14]闫鹏程,郝驰宇,孙华刚,等.基于RecurDyn的开式链传动输弹机动力学联合仿真研究[J].火炮发射与控制学报,2015,036(002):31-35.
[15]董振乐,马大为,姚建勇,等.强冲击载荷下火箭炮位置伺服系统跟踪控制[J].火炮发射与控制学报,2015(03):61-65.