发动机振动是机舱噪声的主要来源[1]。为了降低舱内振动噪声带来的不良影响,必须对发动机振动及其传递进行有效控制[2]。发动机安装系统作为连接飞机吊挂与发动机的重要机械构件系统,其在满足传递发动机推力及各种附加载荷的同时,还应该具备隔振功能[3-4]。目前,对于涡扇发动机安装系统的研究,大多基于有限元模型进行安装系统的强度分析[5-7],少数人对涡扇发动机振动传递进行了研究。宋波涛等[8]建立了飞机翼下吊挂的等效模型,分析了不同实测载荷工况下吊挂结构的减振特性,但仅考虑了载荷通过吊挂向机翼的传递,并未考虑发动机安装节的影响。李诗哲[9]针对某型大涵道比涡扇发动机的两种不同形式安装节结构建立了不同形式安装节结构建立了有限元模型,通过理论计算了两种结构的振动特性分析,在安装节建模过程中,将球铰用Joint连接单元简化模拟,并在后安装节及各连杆上附加弹簧单元来实现后安装节与吊挂的柔性连接;陈熠[10]针对A320飞机建立了“吊挂-机翼-机身”有限元模型,分析了发动机振动通过机翼向机身结构的传递特性,建模时,把安装节简化为弹簧单元。由此可见,在目前为数不多的涉及涡扇发动机振动向机身传递的研究中,安装节部分均简化为线性弹簧单元进行建模,未考虑安装节的自身结构特性。发动机安装节作为分布式动力学机构,其自身结构参数对发动机振动传递的影响应展开研究。
本文首先以涡扇发动机安装系统前安装节为例,采用多体动力学理论推导了其动力学微分方程,明确了多体理论在涡扇发动机安装系统动力学特性分析中的实现过程;进一步基于Π相似定理[11]建立了某型涡扇发动机安装系统的缩比研究模型,采用多体动力学软件对模型进行了仿真分析,研究了铰接连杆式安装系统不同的结构参数对其振动传递的影响。
1 理论推导
某型涡扇发动机安装系统采用的空间铰接连杆式安装系统,由前、后安装节及推力杆组成。其中,前后安装节主要传递发动机产生的侧向载荷、垂向载荷及扭矩载荷,推力杆主要传递发动机产生的推力,并通过后安装节主体传递至吊挂上。发动机通过前、后安装节悬吊于置于机翼下方的吊挂上。其安装系统如图1所示。
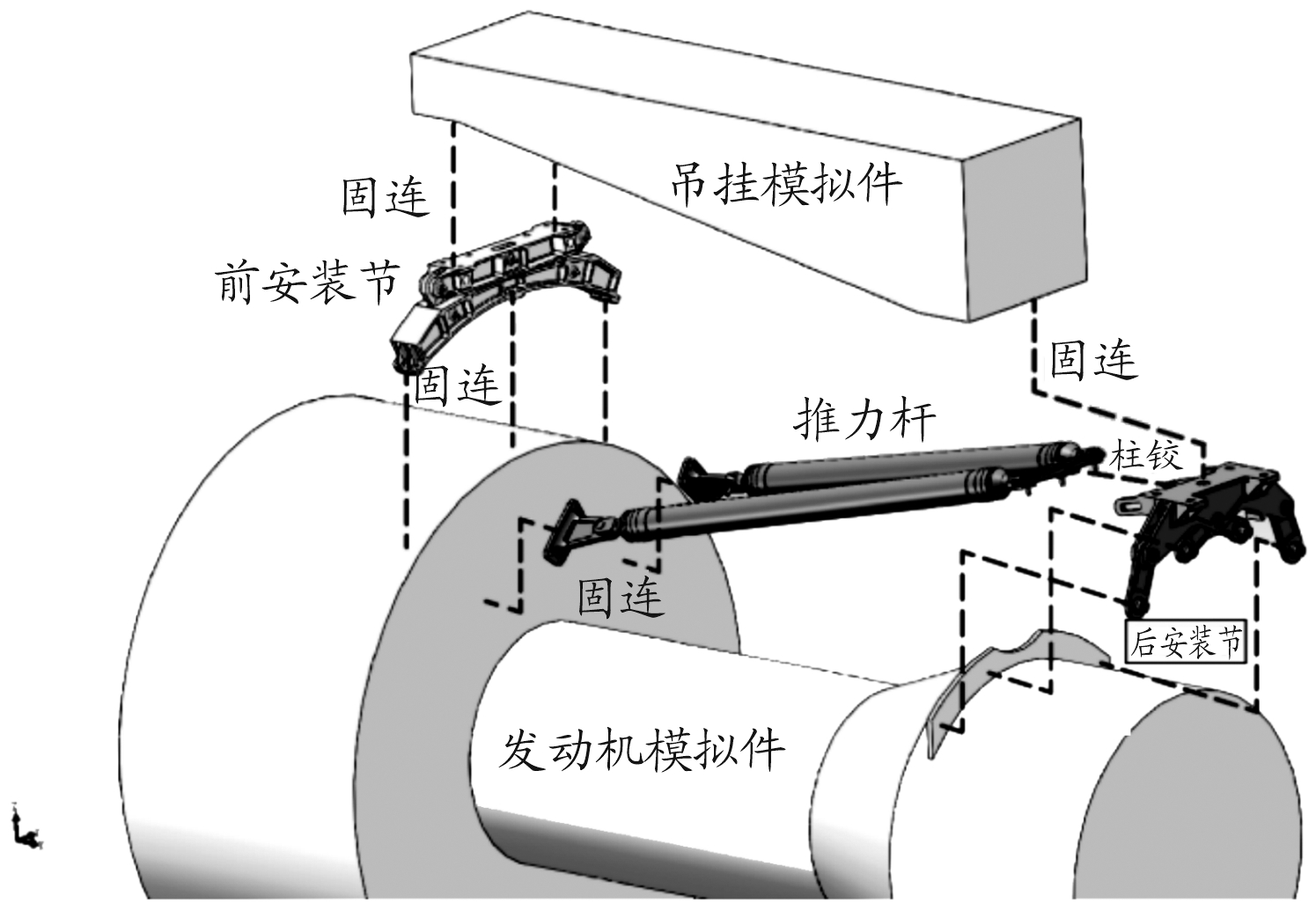
图1 发动机安装系统示意图
图1所示的前、后安装节均采用了多连杆的结构形式,去除冗余杆件,简化结构如图2所示。
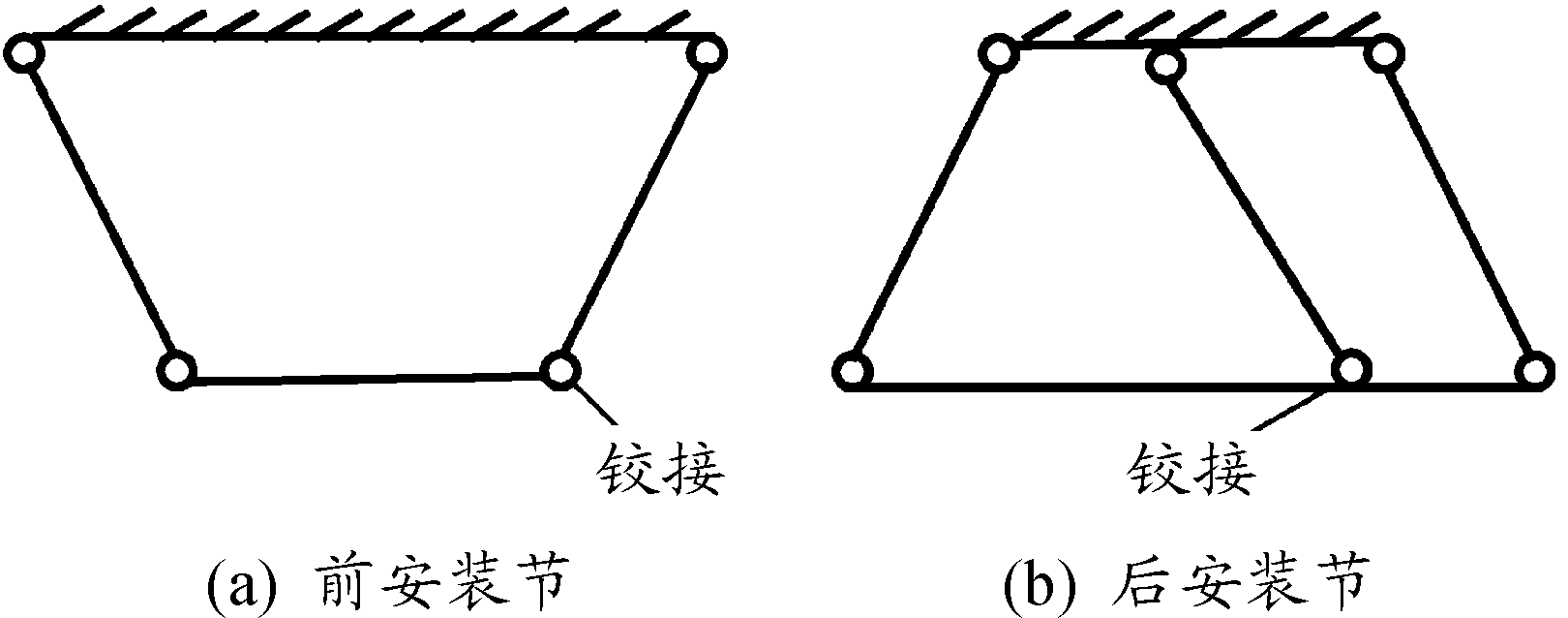
图2 铰接连杆式安装系统前、后安装节简化结构
多连杆结构具有大位移,小变形的特点,适用于采用多体动力学方法进行分析。多体动力学方法常用于描述复杂的运动系统,其从系统总体出发,采用广义坐标来确定系统的位置,并利用系统的动能与功来描述系统的运动量和相互作用,用拉格朗日方程等导出系统的运动微分方程[12]。
拉格朗日方程描述如下:
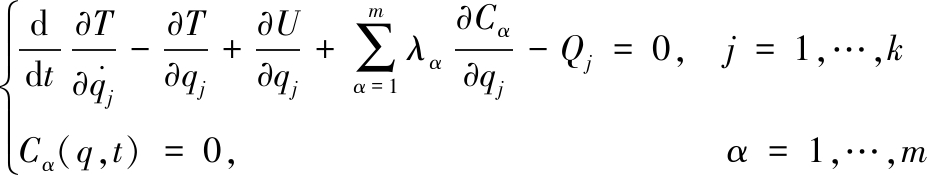
(1)
方程中前两项表示系统的惯性力,第三项表示系统有势力,第四项表示系统的约束力,最后一项Qj表示系统除有势力之外的其他力。具体的符号表示:T为系统动能,U为系统势能,Cα为系统约束方程,qj为系统广义变量。
本文以前安装节为例,阐述多体动力学方法在涡扇发动机铰接连杆式安装系统动力学分析中的具体实现过程。采用多体动力学理论对前安装节进行数学建模,考虑到在安装节的真实结构中,各连接球铰均含有一定间隙,不能简单采用连接副描述,为了准确描述安装节中连接球铰的特性,各含间隙球铰采用赫兹接触模型[13]进行描述。
选取的前安装节的简化结构如图3,l、m、φ分别为连杆长度、质量、角度。选取连杆角度φ为广义变量,分别求得四连杆机构的动能T、势能U、约束方程C1、C2:
T=![]()
(2)
U=(m1+2m2)g(l1/2)cosφ1+m2g(l2/2)cosφ2+
m3g(l3/2)cosφ3
(3)
C1∶l3cosφ3-l1cosφ1-l2cosφ2=0
(4)
C2∶l3sinφ3+l1sinφ1+l2sinφ2-d=0
(5)
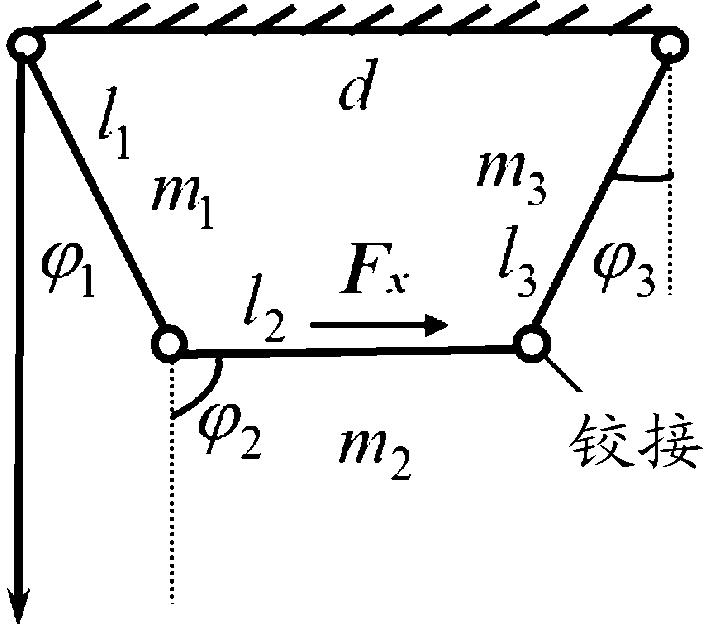
图3 前安装节简化结构
根据赫兹接触及库伦摩擦定义[14],各间隙铰之间的碰撞摩擦力表述如下:
(6)
式(6)中:n为碰撞法向单位矢量;t是切向单位矢量;k为碰撞接触刚度;e为嵌入深度指数;c为接触阻尼系数;δ为嵌入深度; μ为摩擦因数;vt为切向相对速度。
将式(2)~式(6)代入式(1)可得前安装节的动力学微分方程为:
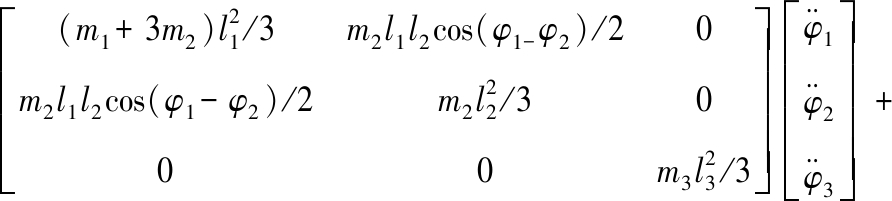
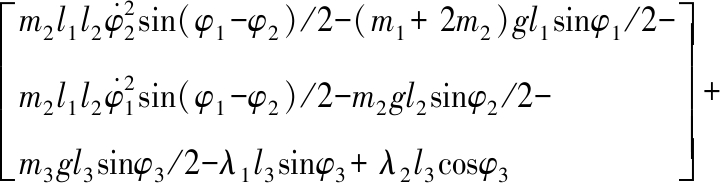

(7)
(8)
T = Fc/ F0
(9)
本文通过力传递率研究安装系统的振动传递特性。联立式(4)、式(5)、式(7)、式(8),可得固支边界的约束反力Fc,因输入力载荷F0已知,因此根据式(9)即可得到前安装节的力传递率T上述分析即是多体动力学方法在涡扇发动机安装系统动力学分析中的基本过程。
2 涡扇发动机安装系统仿真结果与分析
2.1 涡扇发动机安装系统缩比模型建立
为了研究铰接连杆式安装系统的动力学特性,本文针对图1所示的某型涡扇发动机安装系统,将其前、后安装节中冗余设计部分进行了简化, 并基于Π相似定理[10]对安装系统缩比模型进行了设计。
为了保证原模型与缩比模型具有相似的动力学特性,令时间缩比λt=t原/t缩=1,此时原模型与缩比模型的固有频率相同,同时令原模型与缩比模型尺寸缩比λl=l原/l缩=3,质量缩比λm=m原/m缩=15,则对应的转动惯量缩比λI=I原/I缩=λmλl2=135,连接球铰接触刚度缩比λk=k原/k缩=λm=15。
基于上述原则,某发动机质量 m1= 3 500 kg,转动惯量Ix1=1.2×109kg·mm2,Iy1=5.7×109kg·mm2,Iz1=5.7×109kg·mm2,连接球铰刚度k1=1.6×106N/mm;通过缩比计算,得到缩比模型中发动机假件质量m2=230 kg,转动惯量Ix2=8.8×106kg·mm2,Iy2=42×106kg·mm2,Iz2=42×106kg·mm2,连接球铰接触刚度k2=1×105N/mm。
最终设计的缩比模型如图4所示。
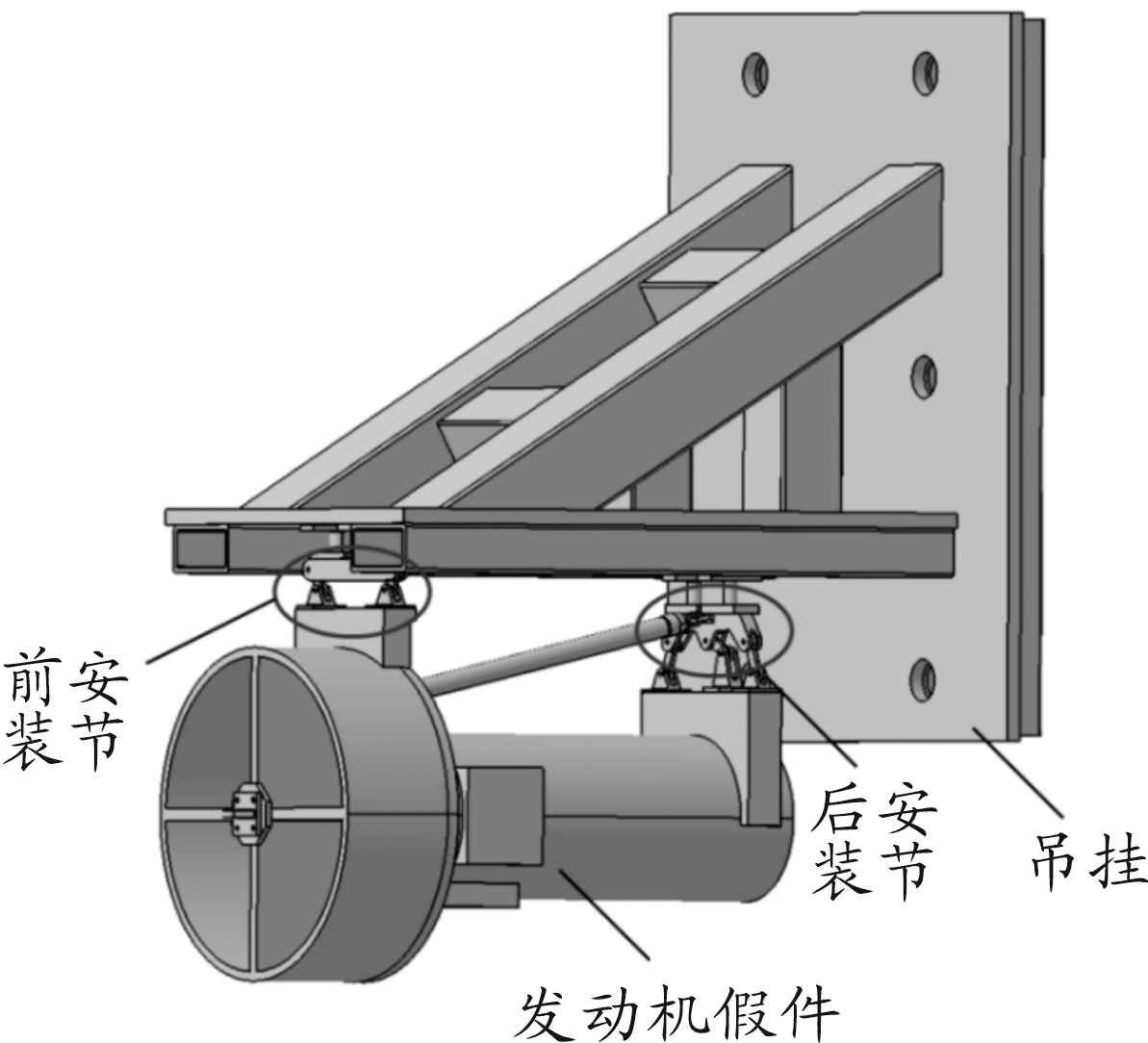
图4 安装系统缩比模型示意图
2.2 结构参数对安装系统振动传递率的影响分析
下面将针对图4所示的铰接连杆式安装系统缩比模型,研究不同的结构参数对安装系统振动传递的影响。
采用多体动力学软件Adams进行仿真建模。考虑到安装系统中各部件自身固有频率(经计算均大于1 000 Hz)远高于安装系统整体频率,因此在低频振动分析时,各部件自身的动态特性不会对安装系统的动力学特性有很大影响,而涡扇发动机的振动主要表现为N1转速对应频率处的振动[10],某涡扇发动机巡航工况下N1转速对应频率约57 Hz,远低于其各部件自身频率,因此本文在建立仿真模型时,忽略了安装系统中部件柔性的影响,将发动机安装系统中各部件均视为刚体,仅考虑安装系统作为一个多自由度系统的振动特性;发动机假件仅用来模拟发动机的质量及转动惯量,按刚性体建模,间隙球铰采用赫兹接触建模,赫兹接触模型中各参数赋值:k=1×105、c=100、μ=0.01、间隙值d=0.005 mm;本文的主要目的是考核发动机安装系统的动力学特性,因此暂不考虑吊挂及机翼的影响,安装系统前后安装节均采用固支边界条件。
发动机安装系统作为一个多自由度系统,当前、后安装节作刚性体处理时,结构参数的变化主要体现在连杆的长度及角度的变化。为了研究连杆长度、连杆角度等参数对发动机安装系统振动传递率的影响,采用控制变量法,在控制其他参数一定的条件下,选取其中的一个参数的4~5个不同参数水平,设置不同条件的算例矩阵,通过计算结果对比分析,研究这些参数对安装系统振动传递的影响规律。
分别选取前安装节中连杆长度l、角度φ作为变量,其取值如表1所示。
发动机的振动主要由于发动机转子叶片的不平衡引起,仅在发动机转动平面内存在较严重的振动,即发动机主要存在侧向及垂向两个方向的振动,因此,本文将主要研究在受到侧向及垂向激励时,安装系统的动力学特性。分别对图4所述仿真模型施加垂向与侧向正弦扫频激励,频率范围为0~140 Hz,通过测量安装节与吊挂连接前后点载荷总值Fc,及输入载荷F0,即可由式(9)得到力传递率T。
连杆长度对系统振动传递率影响的仿真分析结果如图5、图6所示。
表1 算例参数
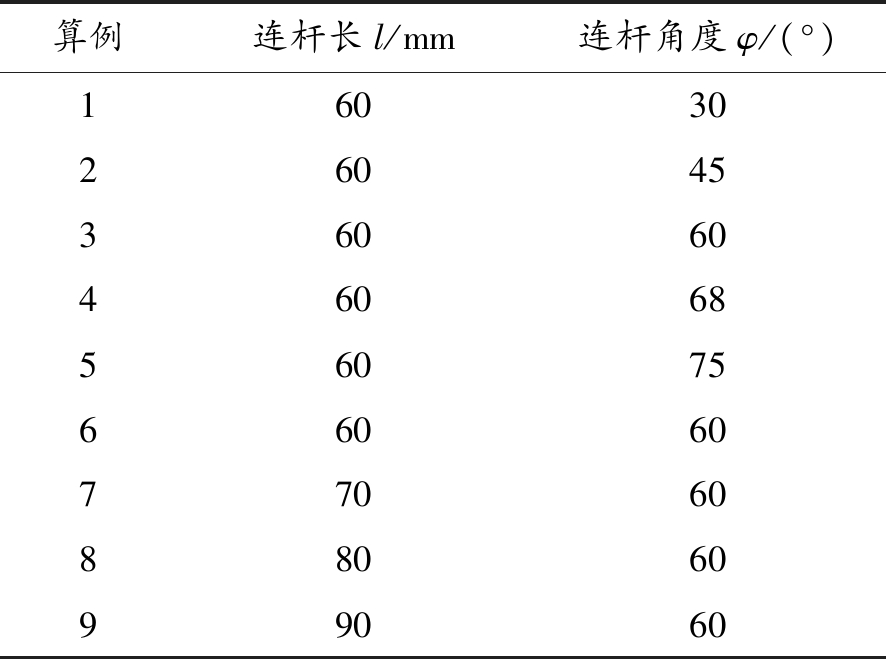
算例连杆长l/mm连杆角度φ/(°)160302604536060460685607566060770608806099060
2.2.1 连杆长度对系统振动传递率的影响
由图5可知:连杆长度对安装系统垂向及侧向传递率的影响均较小。
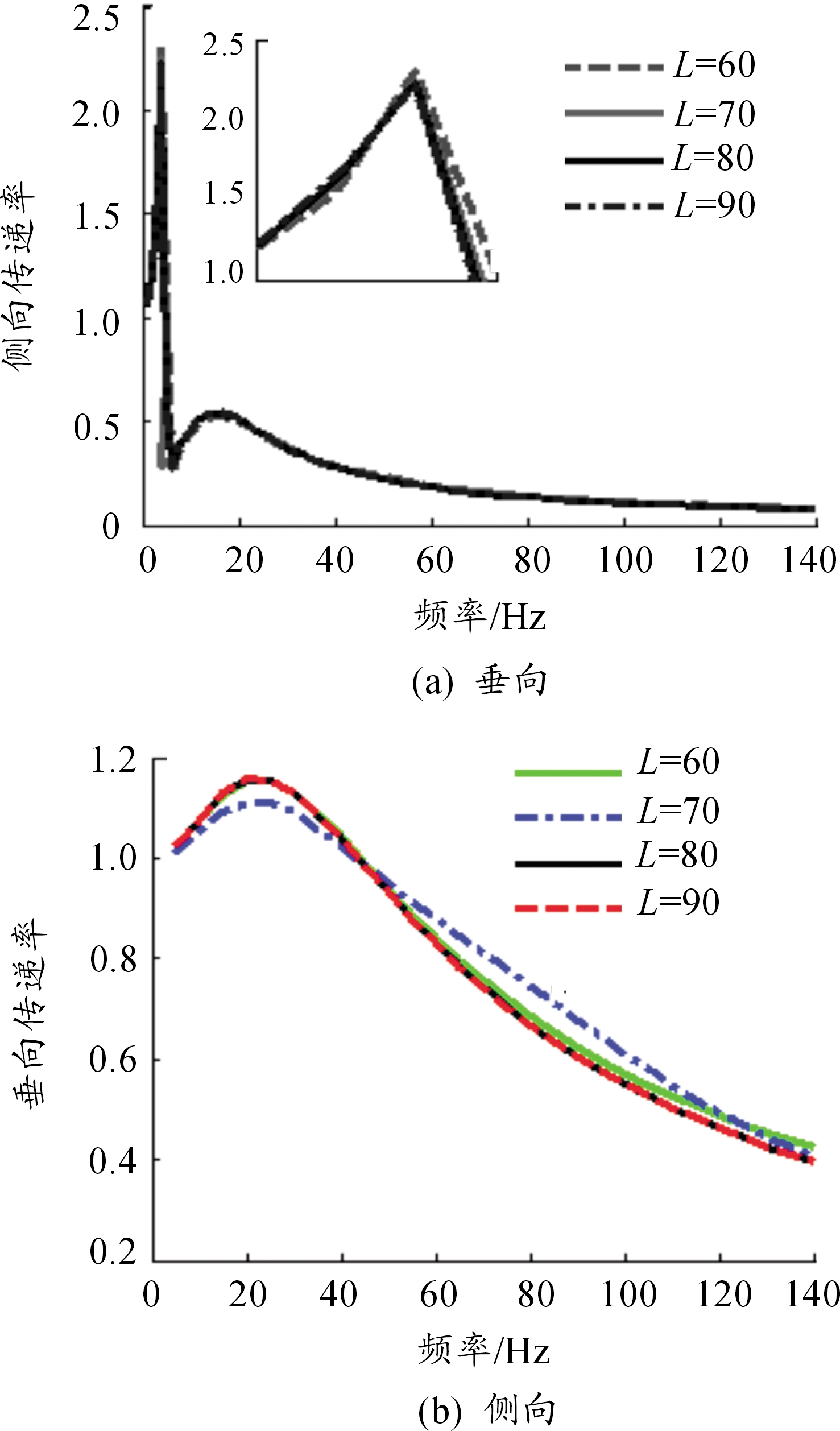
图5 连杆长度对系统振动传递率的影响
2.2.2 连杆角度对系统振动传递率的影响
由图6可知:
1) 随着连杆角度的增大(小于60°时),系统垂向固有频率增大,固有频率处幅值相应降低,而高频处(大于57 Hz)振动传递率幅值逐渐增大,隔振效率下降;当连杆角度大于60°时,角度对系统垂向传递率的影响不再明显。
2) 当连杆角度介于30°~68°时,随着连杆角度的增加,系统侧向固有频率逐渐增大,并出现“双共振峰”现象,而当角度进一步增加到75°时,系统侧向固有频率进一步增大,“双共振峰”现象消失;整个角度变化范围内,除角度为68°对应的“双共振峰”现象,其余情况对系统侧向固有频率处振动传递率幅值影响较小;系统在高频处(大于57 Hz)振动传递率幅值接近20%。

图6 连杆角度对系统振动传递率的影响曲线
3 结论
1) 通过理论推导得到了涡扇发动机前安装节的动力学微分方程,明确了多体动力学理论在涡扇发动机安装系统动力学分析中的应用,建立了某涡扇发动机安装系统缩比模型,
2) 通过对该模型的仿真分析,知连杆角度对安装系统的振动传递率的影响,而连杆长度对系统振动传递率影响较小。
3) 安装节设计时,应兼顾发动机及吊挂预留空间及连接位置的基础上,通过选配合理的连杆角度,使铰接连杆式安装系统在发动机工作频段范围内处于隔振状态。
[1]CROW D E.A comprehensive approach to engine noise reduction technology[C]//ISABE-International Symposium on Air Breathing Engines.2001:3-7.
[2]杨其,苏国华,刘庆宝,等.纵向振动对捷联惯导误差影响半解析表达式研究[J].兵器装备工程学报,2017,38(08):14-16.
[3]刘亚奇,胡锦旋,刘星北,等.翼下发动机吊架及其与机翼连接结构研究[J].民用飞机设计与研究,2009(1):74-76.
[4]陈永辉,陈春兰,苏尔敦,等.涡桨发动机安装系统动力学设计方法研究[J].科学技术与工程,2017,35(6):23- 27.
[5]郑继波.民航飞机发动机吊挂结构优化设计[D].武汉:武汉理工大学,2013.
[6]孙滨,林鸿志,谭伟,等.发动机吊挂与机翼连接接头强度分析与试验[J].航空工程进展,2012,3(3):300-304.
[7]李卫平,谭伟,薛彩军,等.民用飞机发动机吊挂部段静力试验与静强度分析[J].南京航空航天大学学报,2012,43(6):732-737.
[8]宋波涛,贺尔铭,张钊.翼吊发动机吊架结构等效建模及减振特性分析[J].科学技术与工程,2012,12(4):832-835.
[9]李诗哲.典型大涵道比发动机发动机安装形式对振动特性的影响及其弹性安装减振研究[D].上海:上海交通大学,2015.
[10]张培忠,郑建福,苏伟丽,等.机载预警雷达转台的疲劳寿命相似物理模型设计[J].兵器装备工程学报,2017,38(05):10-13.
[11]陈熠.翼吊发动机振动传递特性研究[D].西安:西北工业大学,2012.
[12]方同,薛璞著.振动理论及应用[M].西安:西北工业大学出版社,2004.
[13] JOHNSON K L.Contact mechanics[M].Cambridge New York:Cambridge University Press,1985.
[14]谈庆明.量纲分析[M].合肥:中国科学技术大学出版社,2005.