现今世界总体形式是“和平与发展”,但局部战争和冲突不断。虽然美军从阿富汗撤离,并且国际公约已经明令禁止地雷的大量使用,但作为不对称作战中经常遭遇的路边炸弹、简易爆炸装置(IED)、地雷等武器仍长期存在,未来数年国际安全援助部队仍将重点关注使用这些武器的恐怖分子,防雷车仍然是今后战场及维和部队不可或缺的装备。战场上,地雷是威胁装甲车辆和乘员生命最主要的手段。地雷的防护指数仍然作为研发、生产、制造防雷车最主要的考量标准。
近年来,已有大量学者对空爆载荷下靶板的动态响应进行研究,地雷爆炸与空中爆炸的关系,为该领域的研究热点。
板壳结构具有构造简单、自重较小且能承受较大荷载的特点,广泛用于坦克和各种车辆结构上。实际使用中这些结构常常受到地雷爆炸冲的毁伤考验,因此板壳结构在地雷爆炸作用下响应的研究引起人们的普遍重视。
Hashen Gharababaei等[1]研究了受到较小当量爆炸载荷作用的夹紧圆形靶板,靶板材料分别为软钢,铜和铝圆板的响应。给出了关于中心偏转变化的实验结果,运用近似能量分析对圆板中点偏转厚度比建模。同时,A.Neuberger等[2-4]讨论了夹持圆形板在近距离和大药量球形爆炸载荷作用下的动态响应,研究表明,大当量近距离的地雷和空爆载荷作用下的高强钢靶板的响应可以采用缩比模型进行评估。H.M.Wen[5]提出了一个近似理论来预测受均匀分布冲击载荷作用的夹持圆形加工硬化板的变形和撕裂。结果表明,当考虑材料应变速率敏感性时,最大永久性横向位移量和引起板的拉伸断裂失效的临界输入脉冲,理论预测与实验观察结果完全一致。Zakrisson等[6]进行了半尺寸实验,并测量了地雷爆炸作用下的结构变形和脉冲转移。研究了埋藏深度和沙子含水量的影响。研究表明,平板上的总脉冲随着埋藏深度的增加而增加,尽管50mm和150mm掩埋深度实验的总脉冲有重叠。相反,随着掩埋深度从0变化到50 mm,板变形增加,但是大于50 mm的DOB,板变形减小。吴义田等[7-8]采用量纲理论对结构在冲击波载荷作用下的几何相似模型律进行分析,得到了结构满足几何相似模型律的条件,研究表明,一定药量TNT的球形装药的爆炸过程进行数值仿真,得到靶板的挠度峰值与厚度、靶板的速度峰值与靶板厚度的倒数均呈线性关系。张中英等[9]则研究了爆炸冲击波对常见V形车底防护结构的影响,指出V形板的夹角在一定角度范围内与爆炸冲击的加速度峰值呈指数的关系,建议V形板的理想夹角取140°。王芳等[10]对方形板壳结构在爆炸冲击载荷下的结构响应进行了理论分析与试验研究,其边界条件是方形板块四边进行全约束。国内牟金磊、朱锡等[11]为了预测加筋板结构在爆炸冲击载荷作用下的变形程度,将加筋板的变形分为整体变形和局部变形,借助数值计算拟合了两者能量分配关系,进而提出了爆炸冲击作用下加筋板结构变形的理论计算方法,并与实验结果进行比较,结果吻合较好。
浅埋地雷爆炸的载荷作用过程较为复杂,且有较多的影响因素。因此,对于浅埋地雷爆炸载荷的全局预测较为困难。本文通过建立固支方板在浅埋地雷爆炸作用下的数值仿真模型,研究固支方板在浅埋地雷爆炸作用下的响应,为装甲车辆防雷设计提供技术参考,具有极为重要的工程意义。
1 有限元模型的建立及验证
1.1 有限元模型及参数设置
英国巴克斯顿谢菲尔德大学爆炸与冲击实验室共进行了24次爆炸载荷作用的固支方板响应测试[12]。试验采用1 m×1 m夹持、方形Armour 440t靶,净跨距为655 mm×655 mm。将板夹在专门建造的框架内,其设计具有半径边缘,以尽量减少支架周围集中剪切载荷的影响,并且板由大型EN24T钢衬套约束,其尺寸和间距被固定。TNT装药当量从400~1 000 g不等,装药径高比3∶1,埋于砂土表面以下50 mm,钢板距离砂土表面150 mm。
依据试验设置,建立有限元仿真模型,如图1所示。靶架采用实体单元,钢板为壳单元,钢板及靶架四周固支。选取试验的4个工况进行仿真对比,工况设置如表1所示。
表1 试验工况
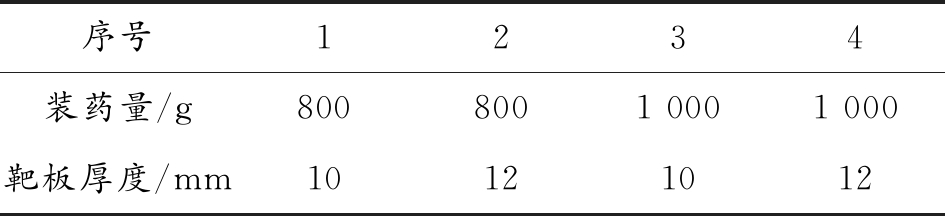
序号1234装药量/g8008001 0001 000靶板厚度/mm10121012
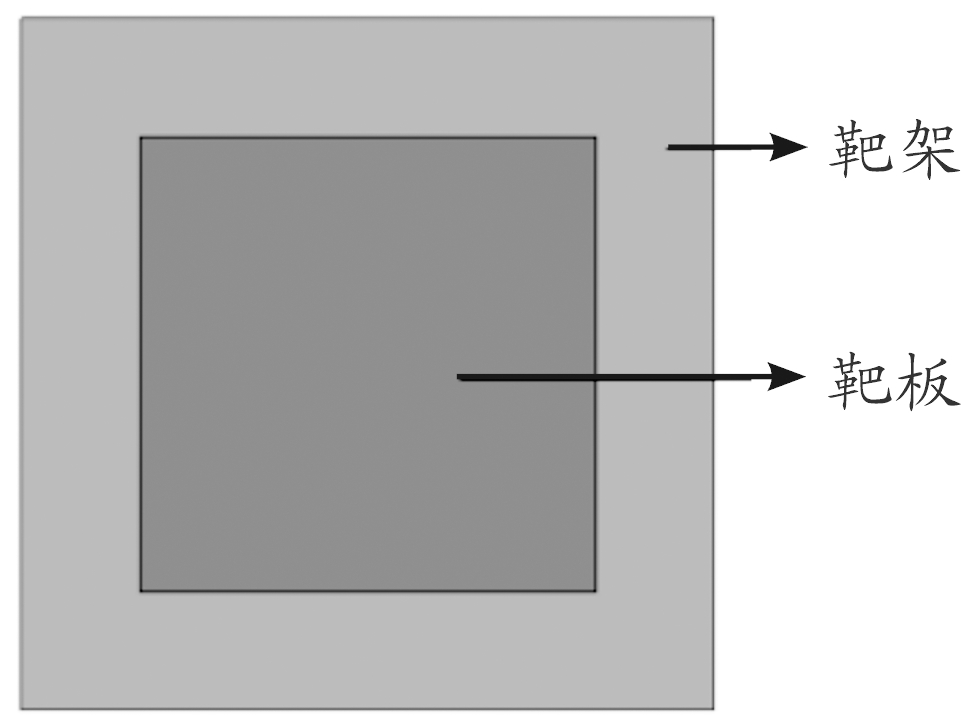
图1 钢板及靶架有限元模型示意图
土壤、炸药、空气材料模型选取与文献中相同,具体参数按照试验相同状态设置,此处不做过多赘述[12,14]。靶架采用刚体材料模型,靶板采用双线性弹塑性体材料模型,其参数如表2。
表2 靶板材料参数

密度/(kg·m-3)杨氏模量E/MPa泊松比/Pr屈服强度σy/MPa失效应变7 8502 1000.31 1000.12
1.2 地雷作用过程分析
浅埋地雷爆炸载荷的作用过程更为复杂,大体可以分为爆炸冲击波的作用、弓形空气冲击波的作用、高速土帽和爆炸产物的冲击3个部分,其中爆炸冲击波的作用和弓形空气冲击波的作用很小,可以忽略。高速土帽和爆炸产物的冲击过程可以分为2个阶段:第一阶段为高速土帽的冲击和推动高速土帽的爆轰产物高压产生的超压效应组成,该部分作用强度大,作用时间短,提供大约50%的冲量,第二阶段为膨胀爆轰产物扩展压力和土壤喷射物的动量传递,该部分作用强度较小,但作用时间长,约为第一阶段的10倍,提供大约50%的冲量。
以工况4为例,浅埋装药爆炸与靶板的耦合过程,如图2所示。0 ms时刻,TNT装药开始起爆,装药起爆后爆轰产物向一方面向四周和向下压实砂土,另一方面向上推动砂土层;0.2 ms时刻,高速砂土层已经作用到靶板,引起靶板的变形;0.8 ms时刻,爆轰产物继续对靶板作用,靶板的变形程度加大;到2.5 ms时刻,爆轰产物已经基本作用到整个靶板,爆轰产物的扩散过程将持续到5 ms时刻。
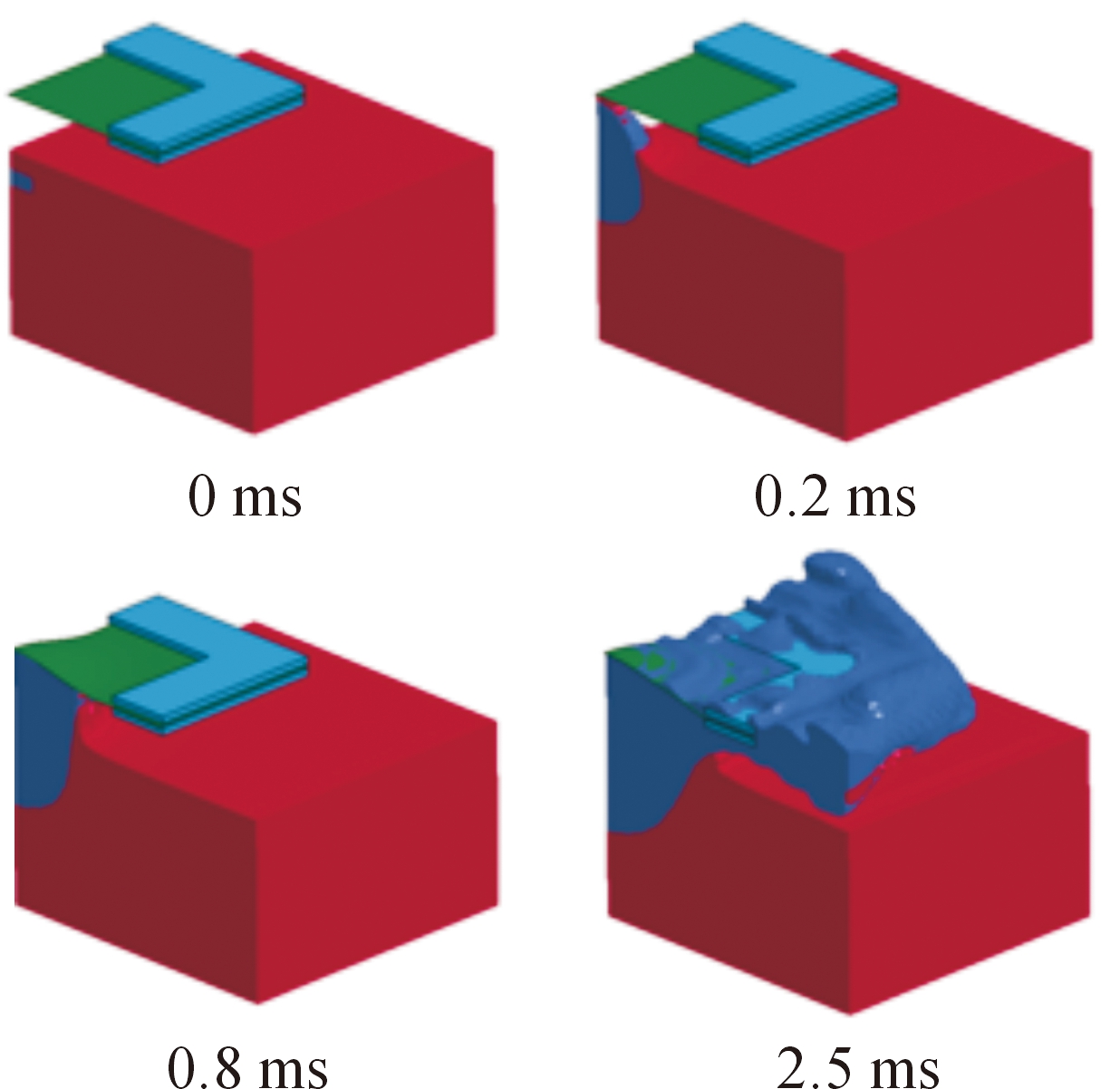
图2 装药爆炸与靶板耦合过程
由图3所示的5 ms内靶板中心点位移与压力的时间曲线也可以看出,靶板中心点位置的反射压力在0.5 ms左右达到峰值32 MPa,靶板中心点位移在1.2 ms左右达到最大值,之后持续振动。这说明靶板中心点位移达到最大值是在浅埋地雷爆炸载荷两个阶段作用之后,而不是在冲击最大的第一加载阶段。由反射压力时间曲线可以看出,5 ms的加载时间已经足够。
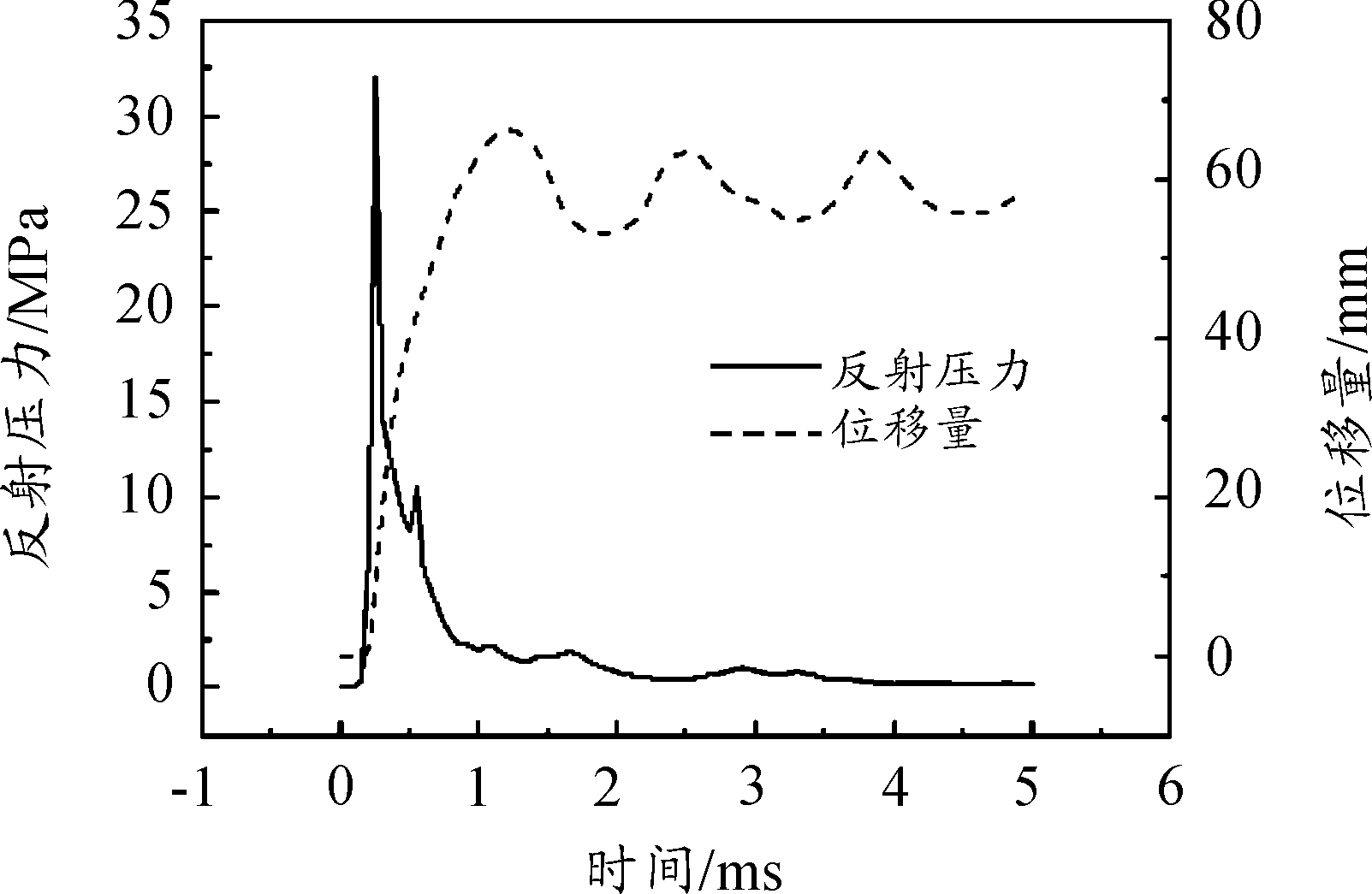
图3 靶板中心点位移及反射压力时间曲线
1.3 仿真模型验证
图4给出了Case4在30 ms时刻的横向位移图以及钢板变形形状与试验结果[11]。通过数值模拟得到的变形形状曲线与试验得到的曲线吻合较好。
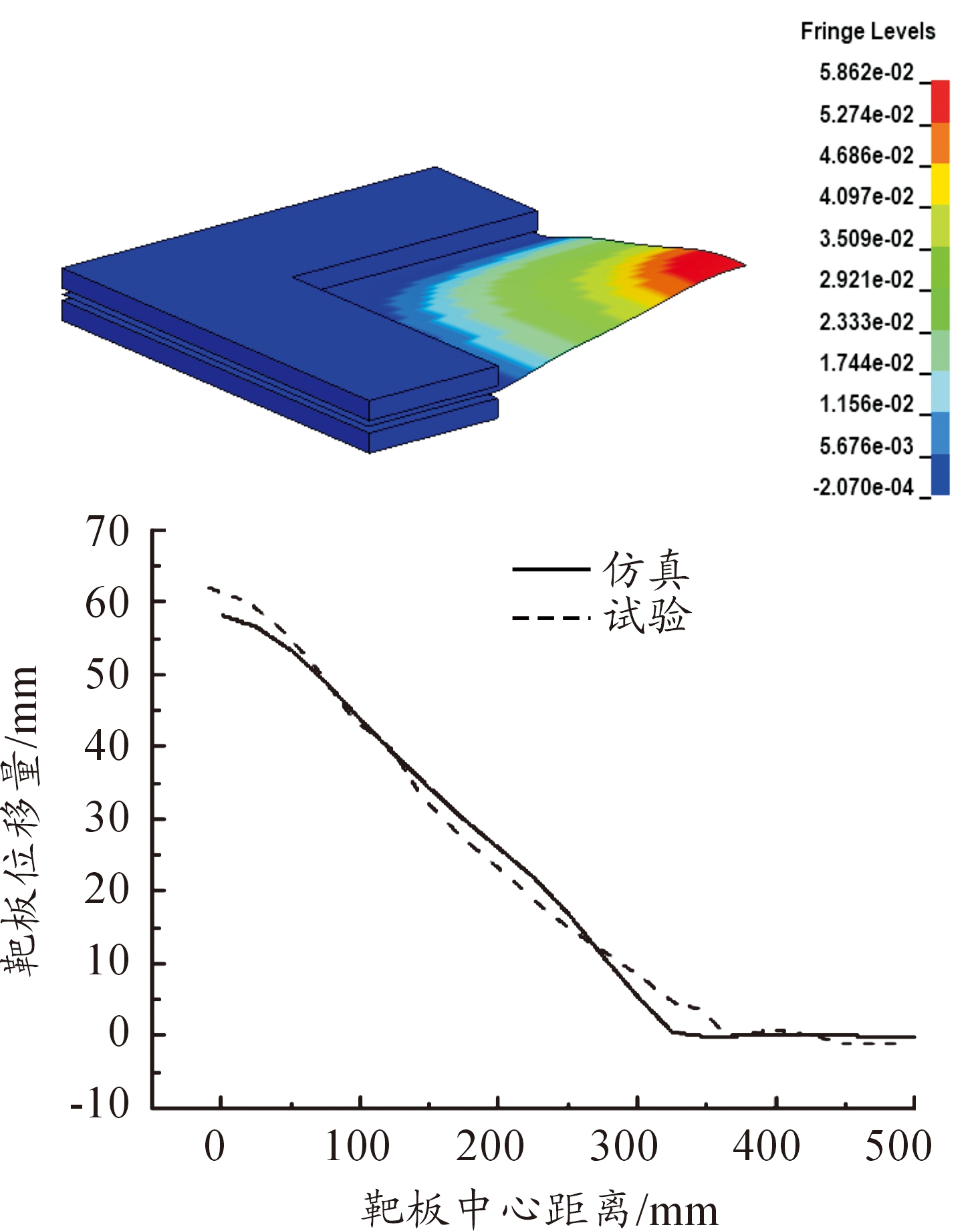
图4 靶板挠度数值模拟曲线与试验曲线
仿真结果与试验结果如表3,所作出的曲线如图5,由4个工况钢板中心点最终变形量的仿真结果与试验得到的结果吻合较好,误差均在10%以内,符合工程的要求,该仿真工况的设置及参数的选取有效。
表3 仿真结果与试验结果
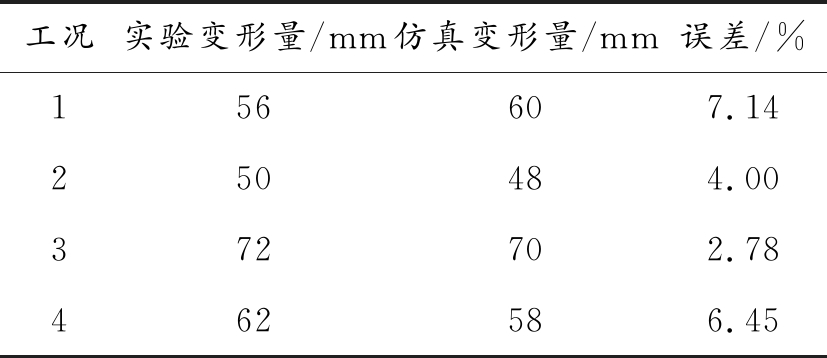
工况实验变形量/mm仿真变形量/mm误差/%156607.14250484.00372702.78462586.45
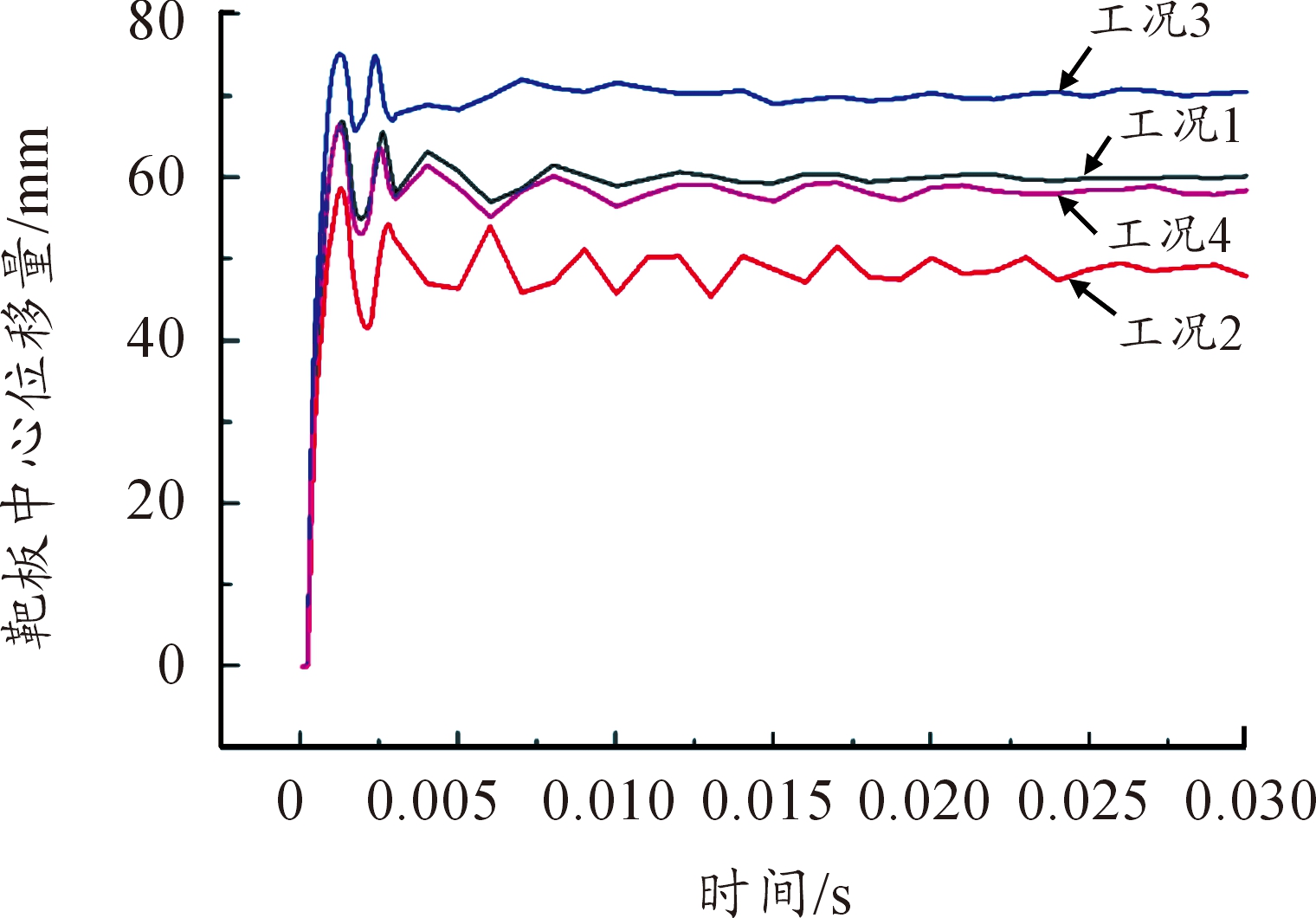
图5 钢板中心点位移时间曲线
2 靶板变形的影响因素分析
为考察固支方板在浅埋地雷爆炸载荷作用下的塑性大变形,选取12 mm厚的Armour 440 t方形钢板,在上一节验证试验工况设置的基础上,增加仿真工况:靶板受到当量为0.8、0.9、1.0、1.1、1.2、1.5 kg TNT,地雷埋深为20、50、80、100、120 mm,离地间隙为130、140、150、160、180、200、300 mm。增设21个计算工况对该问题进一步研究。
2.1 炸药当量的影响
图6所示为钢板变形形状随炸药当量的变化,由于装药的掩埋深度和钢板的离地间隙不变,各工况下钢板的变形形状相似,都为比较均匀的全局球形变形。这说明在0.8~1.5 kg的炸高区间内,靶板的塑性变形模式为受到均布载荷的形式。
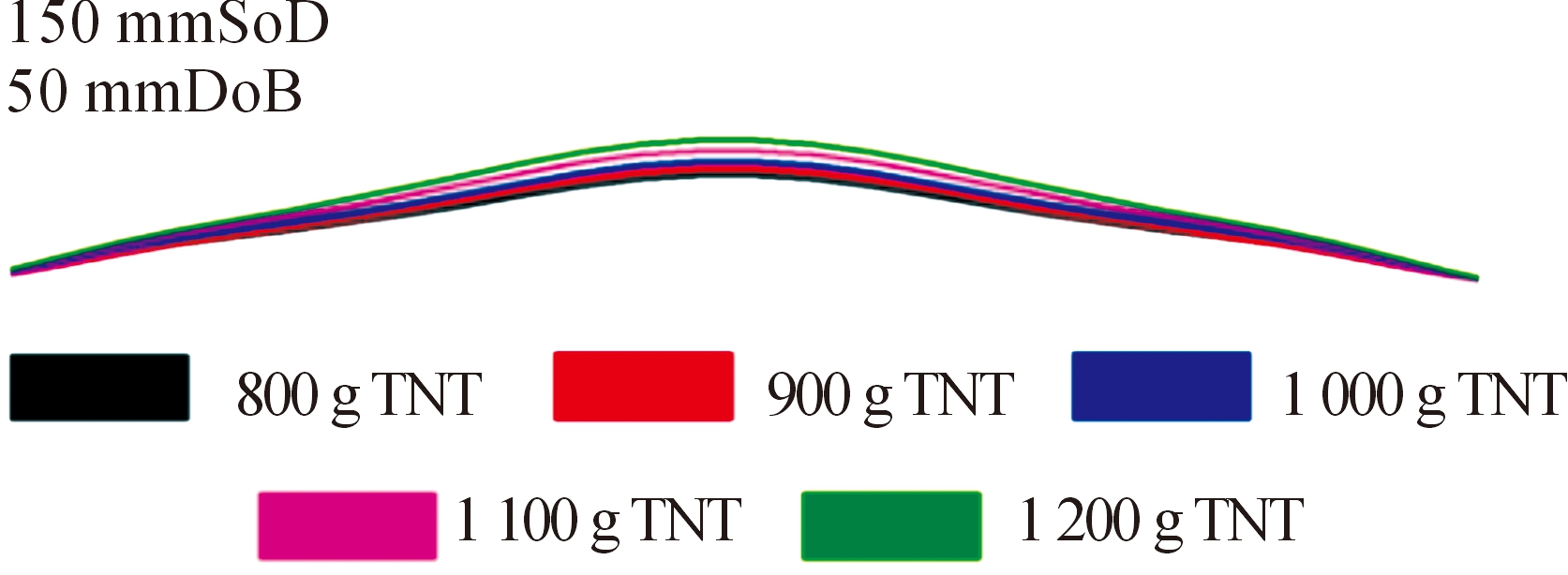
图6 钢板变形形状随炸药当量的变化示意图
图7所示为钢板离地间隙和装药掩埋深度相同,而装药质量不同时钢板的最终变形挠度曲线。钢板的中心变形量随着装药当量的增加而增加。
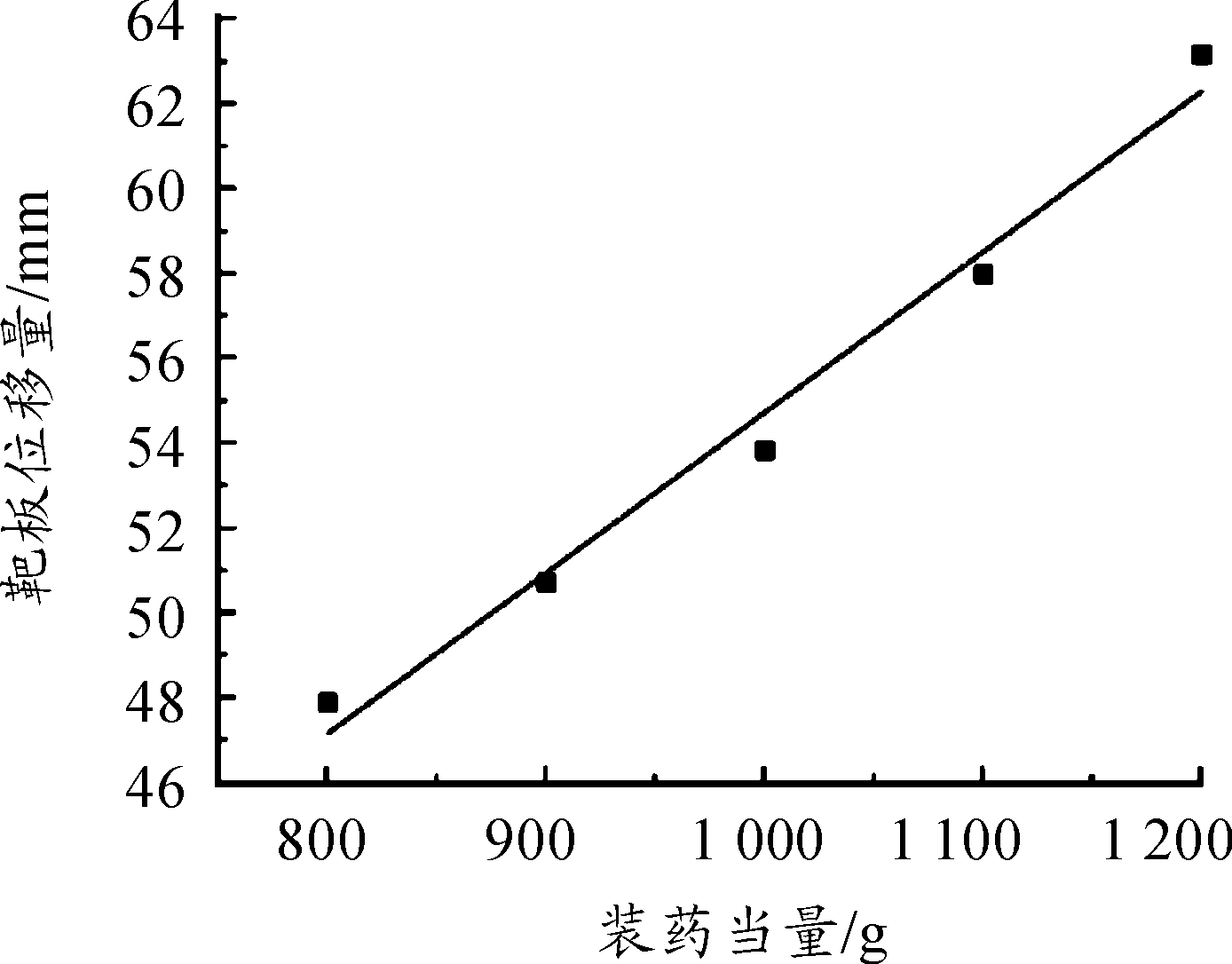
图7 随装药当量变化的钢板中心点变形挠度曲线
2.2 离地间隙的影响
图8所示为装药质量和装药掩埋深度相同,钢板中点挠度随钢板离地间隙(SOD)的变化曲线。图9所示为钢板变形形状随离地间隙的变化。可以看出,随着离地间隙的增加,钢板中点挠度值不断减小。随着离地间隙的增加,钢板越来越呈现出均匀的球形变形。而在离地间隙达到130 mm时,钢板的变形呈现出比较明显的中心外凸内圆顶的形状。
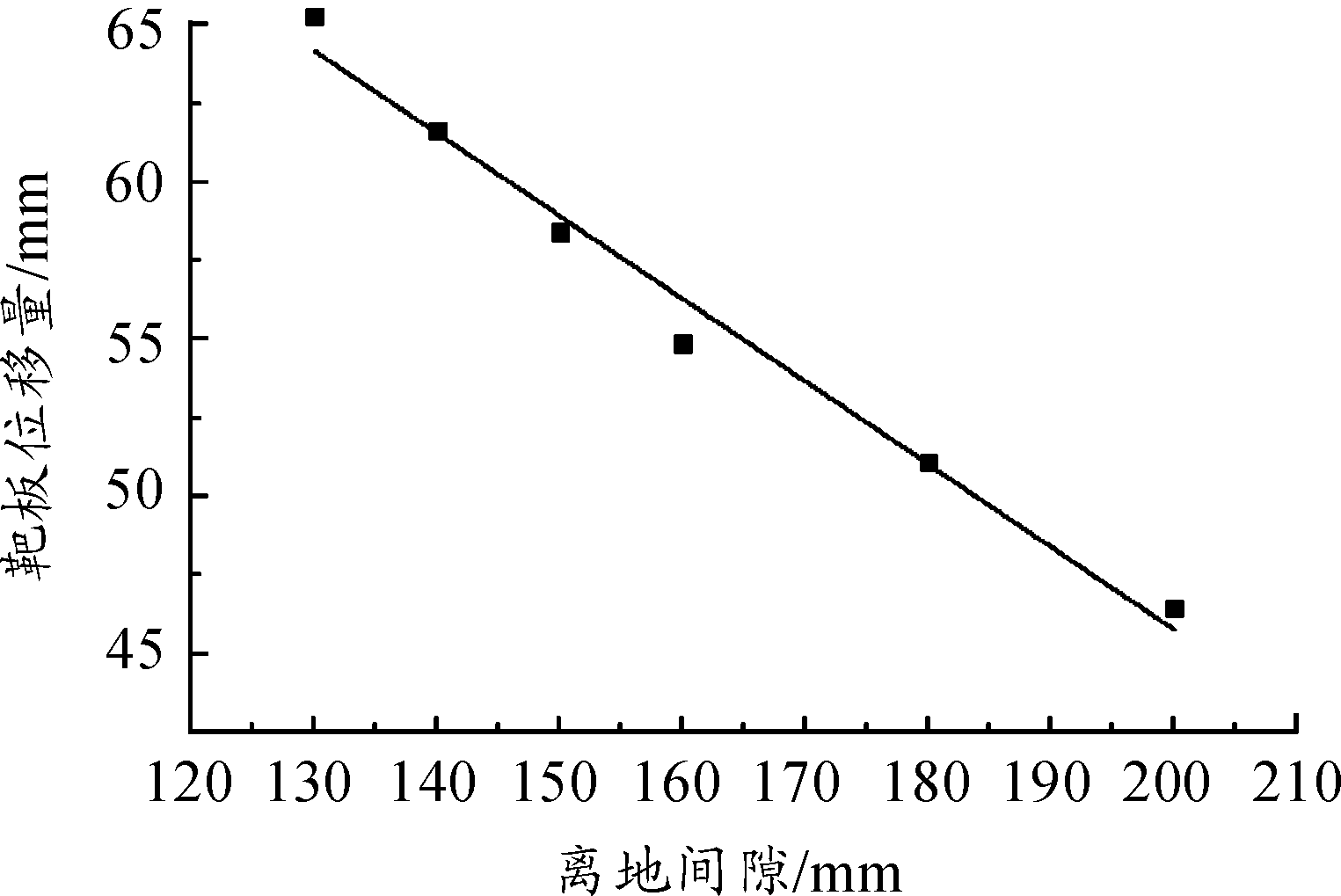
图8 钢板中心点变形挠度随离地间隙的变化曲线
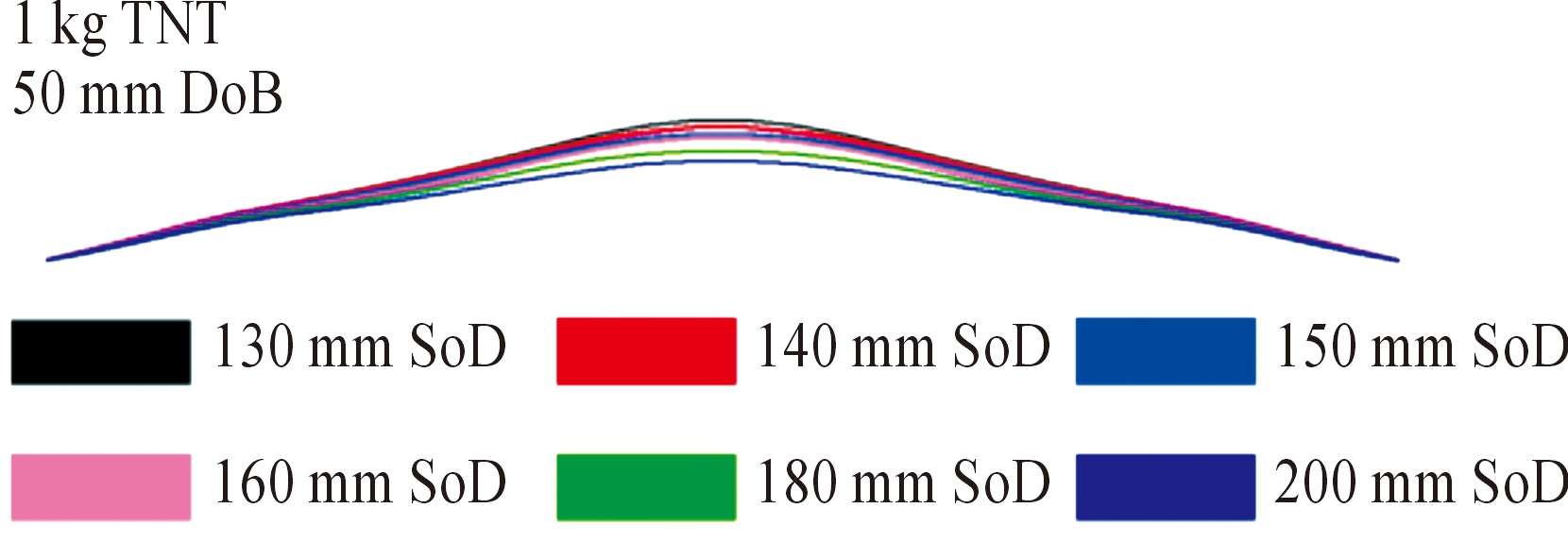
图9 钢板变形形状随离地间隙的变化示意图
2.3 地雷埋深的影响
图10所示为装药当量与钢板离地间隙相同,而装药的掩埋深度(DOB)不同时各工况钢板的最终变形形状。在工况范围内,钢板的中点偏转量随着埋深的增加而减小。
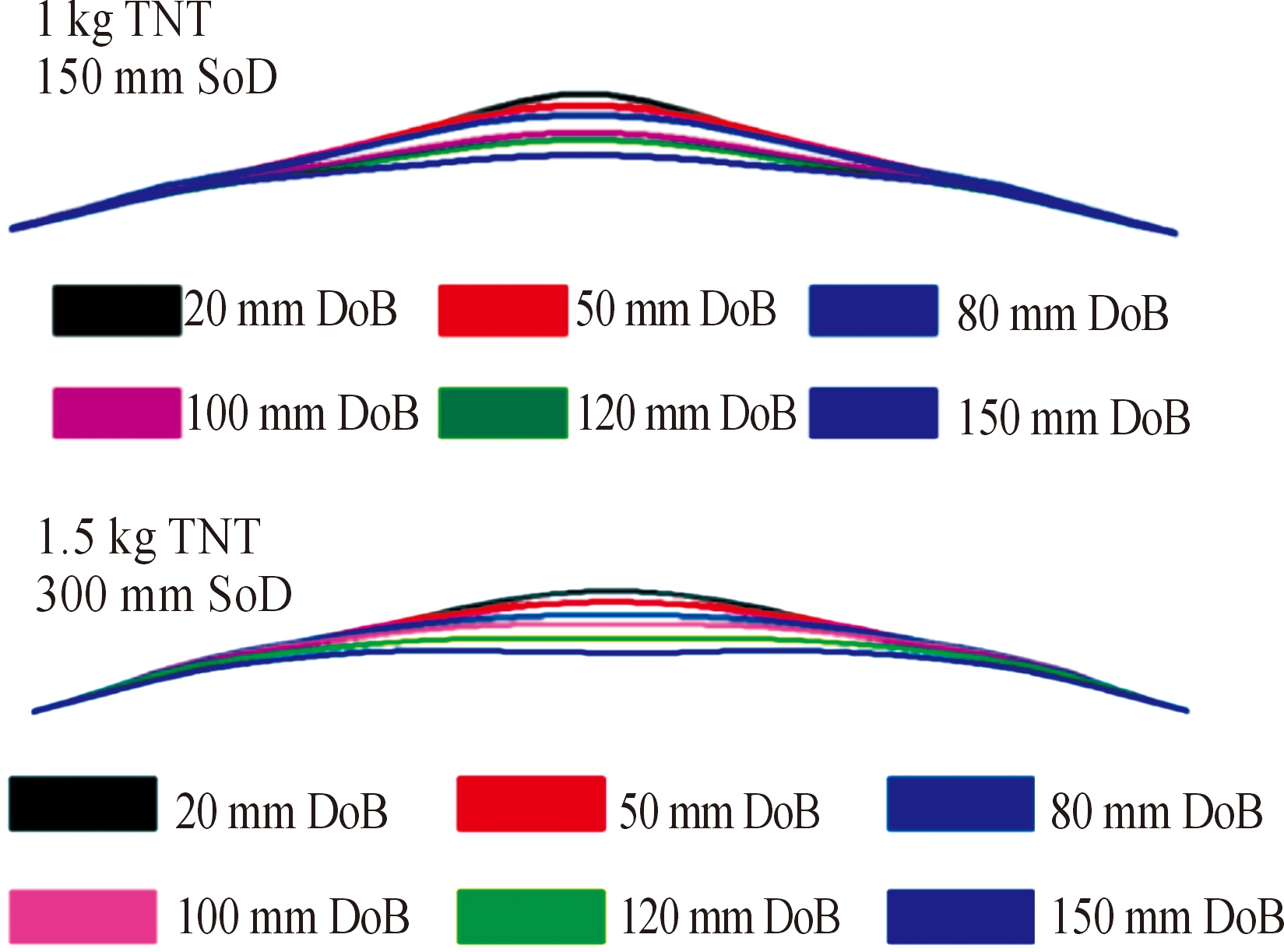
图10 钢板变形形状随地雷埋深的变化示意图
图11所示为中点挠度随地雷埋深的变化曲线。当掩埋深度较小(20 mm)时,钢板的变形剖面呈现出全局的球形变形圆顶上有中心内圆顶的形状,这接近于Jacob等[4]所述的空气中的局部爆炸载荷所形成的变形形状。随着掩埋深度的增加,钢板的变形剖面越来越呈现出均匀的球形变形,接近于Chung Kim Yuen和Nurick [13]描述的空气中的均匀爆炸载荷所形成的变形形状。分析可知[14],随着埋深的增大,钢板中心点位置的比冲量是减小的,而靠近钢板边缘的位置,比冲量的值是略有增大的,也就是说,随着埋深的增大,比冲量在钢板的分布越来越均匀,距离钢板中心各位置处的比冲量的差值减小,而钢板的变形形态与掩埋深度对于地雷爆炸比冲量分布的影响规律基本一致。
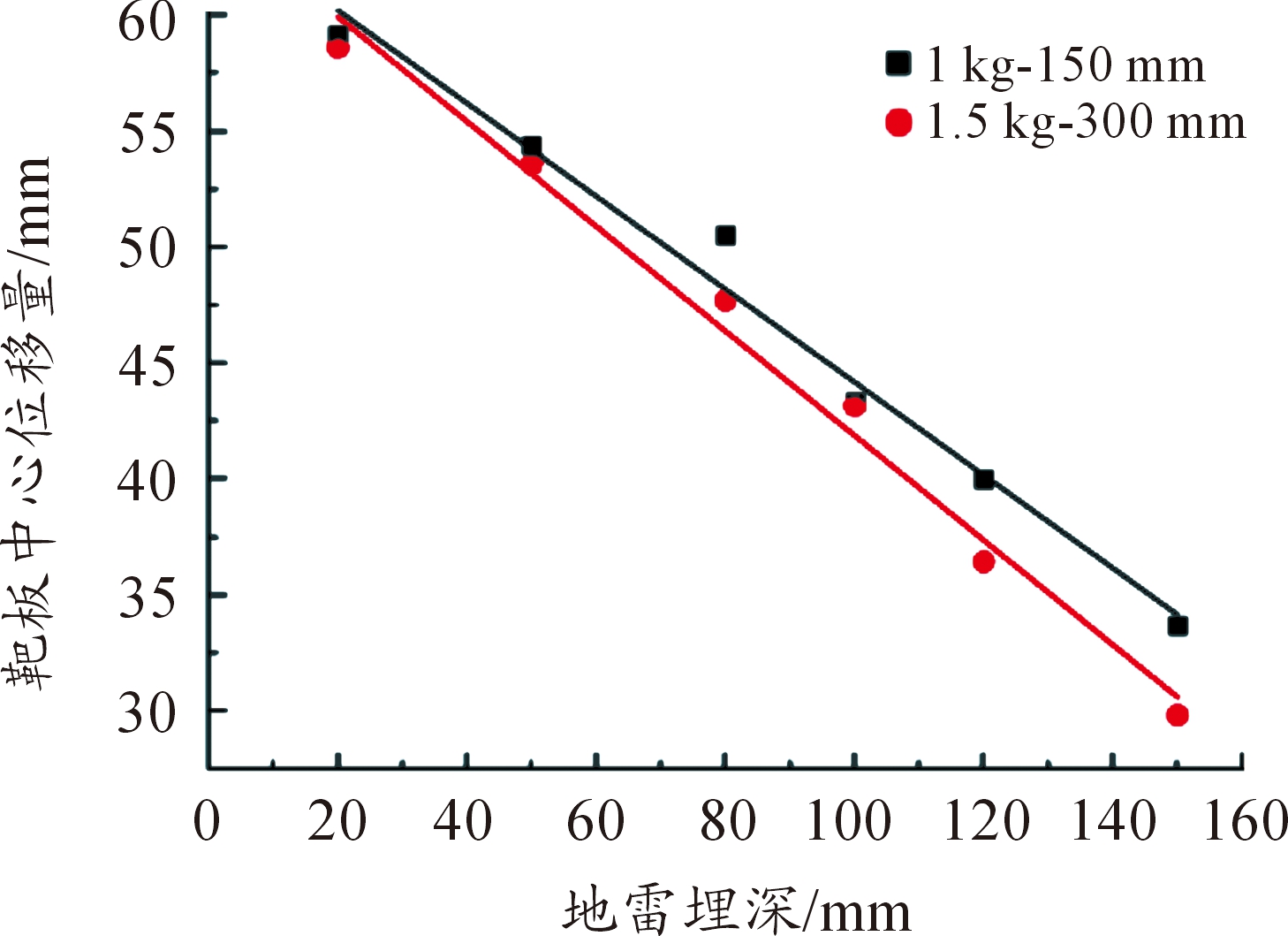
图11 钢板中心点变形挠度随掩埋深度的变化曲线
2.4 中心比冲量的影响
图12所示为钢板中心点变形量随比冲量的变化关系曲线。在各工况下,钢板中心点变形量与地雷爆炸作用到钢板的中心点比冲量基本呈线性关系。因此,浅埋地雷爆炸作用虽然有土壤的作用,但依然可以用中心比冲量的大小得到靶板中心点的挠度。
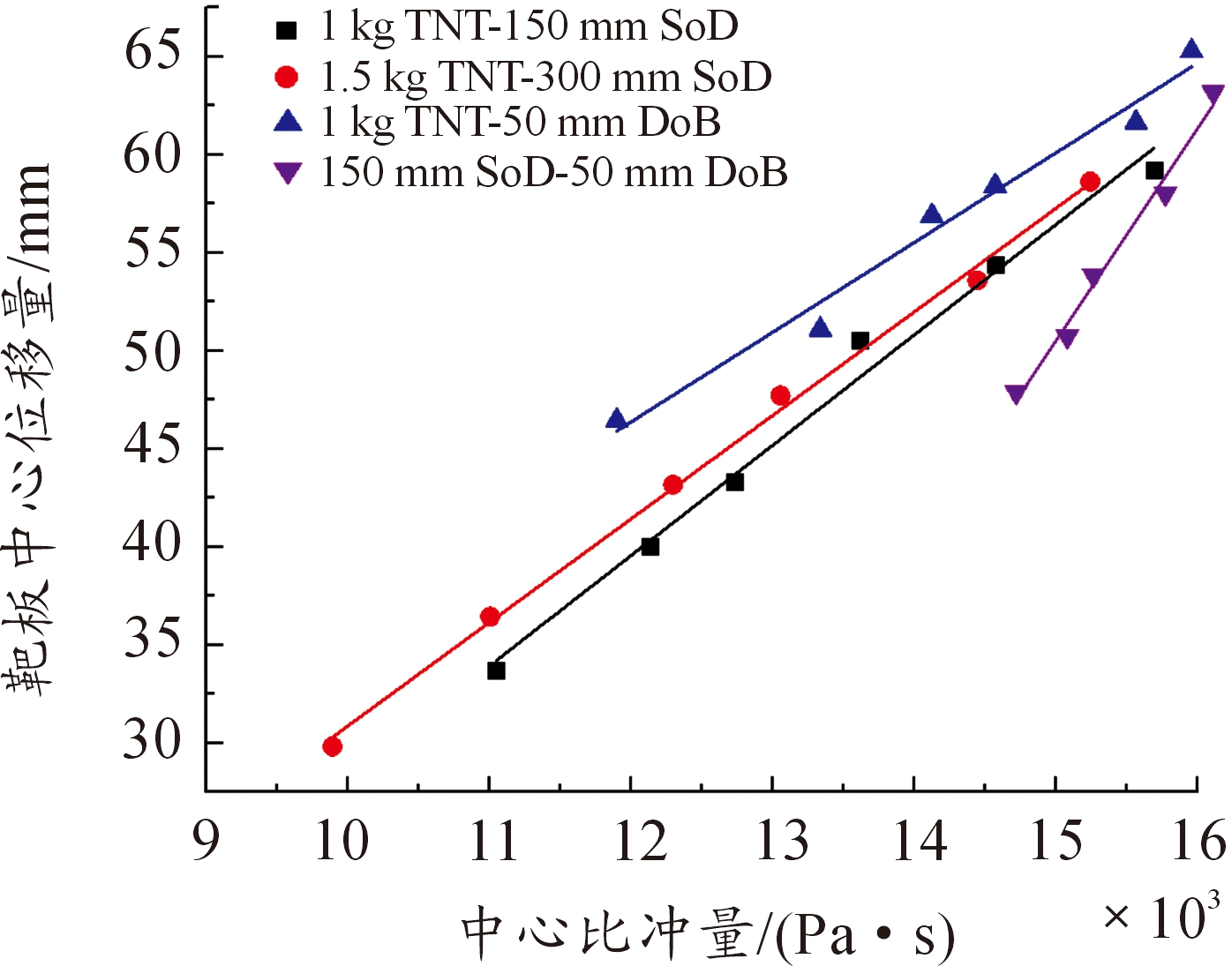
图12 钢板中心变形挠度与比冲量关系曲线
3 量纲分析
地雷载荷作用下高强钢板的动态响应问题,涉及的独立变量如表4。输入变量有:几何尺寸参数、材料属性、炸药参数、土壤参数。响应参数主要研究靶板中心最终位移量和传入靶板中心的比冲量。
表4 影响参数的输入变量

参数分类输入变量土壤参数剪切模量G1,含水率ε炸药参数炸药当量M,炸药半径r,炸药高度h,Ee靶板参数杨氏模量E,屈服强度δy,长度a,宽度b,厚度t空间参数地雷埋深H2,靶板离地间隙H3响应参数靶板中心位移量δ,靶板中心比冲量i
量纲分析可得无量纲π项为:![]() 上述无量纲π项反映了影响靶板的中心位移量参数之间的无量纲关系。因此,靶板的无量纲函数关系为
上述无量纲π项反映了影响靶板的中心位移量参数之间的无量纲关系。因此,靶板的无量纲函数关系为
π3= f(π1,π2,π4,π5)
(1)
代入得
(2)
整理得
(3)
式(3)可应用于不同土壤参数、不同靶板材料和尺寸、不同炸药当量以及不同空间几何位置对靶板中心位移。本文计算工况,靶板尺寸和靶板材料参数、土壤参数均为固定值。
![]()
(4)
式(4)代入式(3)得
(5)
代入仿真结果,拟合得
δ=9.95·(H3)-0.389·(H2)-0.173·(iM3/2)0.45
(6)
如表5,可以看出无量纲计算模型与仿真值的最大误差不超过15%。其中,工况8和工况12的模型计算值对应1.3节中试验4和试验2测量值的误差分别6.15%和4.41%,说明所建立的模型可取,可以较好的预测浅埋地雷作用下方板的变形挠度。
表5 靶板挠度无量纲模型计算值与仿真值
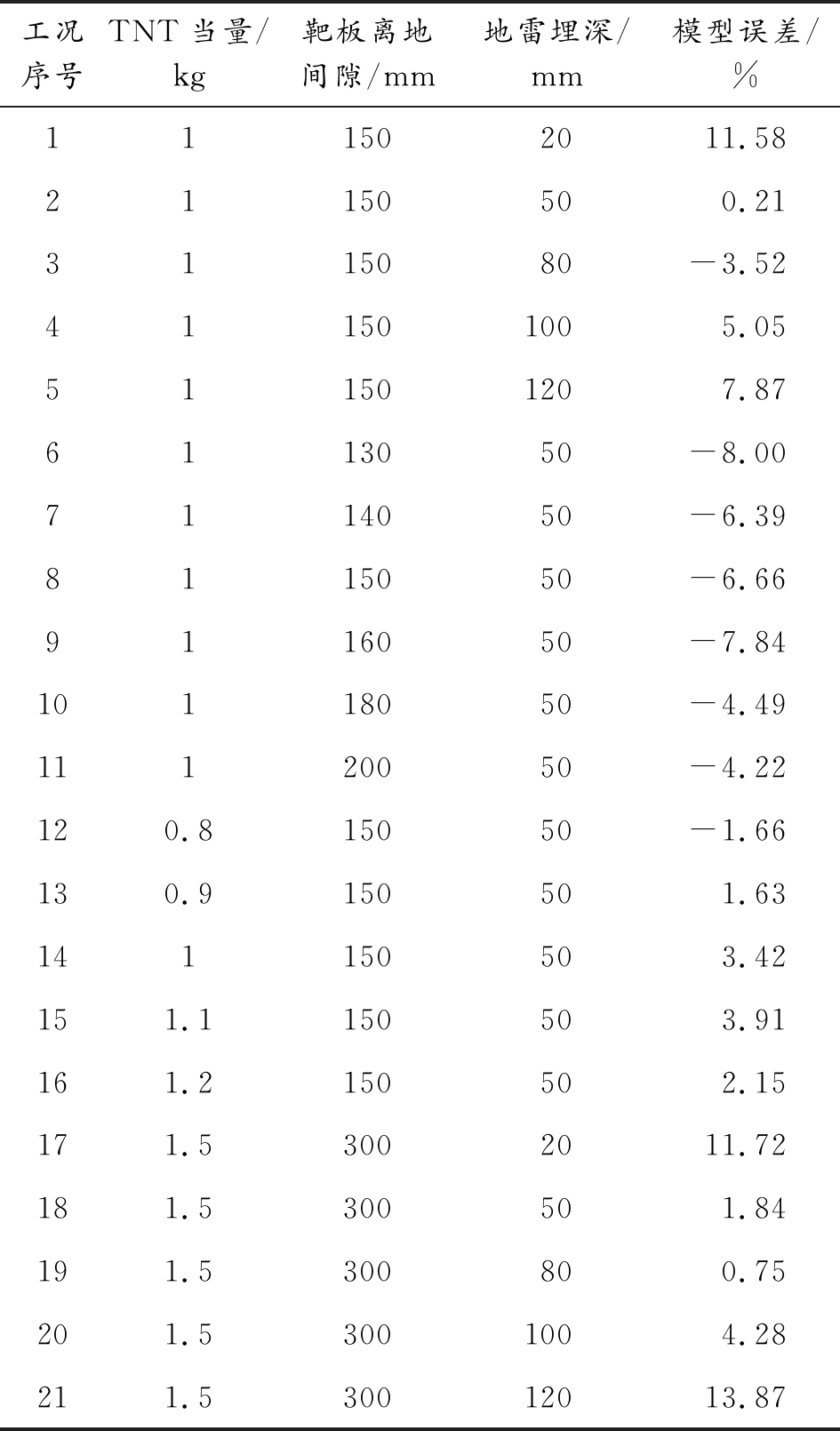
工况序号TNT当量/kg靶板离地间隙/mm地雷埋深/mm模型误差/%111502011.5821150500.213115080-3.52411501005.05511501207.876113050-8.007114050-6.398115050-6.669116050-7.8410118050-4.4911120050-4.22120.815050-1.66130.9150501.63141150503.42151.1150503.91161.2150502.15171.53002011.72181.5300501.84191.5300800.75201.53001004.28211.530012013.87
4 结论
1) 对浅埋地雷爆炸作用下固支方板的响应,掩埋深度增大或者靶板离地间隙增大,钢板的变形形态接近均布载荷作用下的变形形状,即均匀的圆顶形。
2) 浅埋地雷爆炸下靶板的变形受砂土喷射的作用,靶板的中心点变形量与传入钢板的中心点比冲量呈线性关系。
3) 建立适用于不同材料属性、靶板尺寸、土壤属性、不同炸药当量以及不同炸药空间位置的无量纲公式,导出关于中心挠度的无量纲关系式。并计算得到经验模型,与试验和仿真模型的误差均小于15%,可以有效预测浅埋地雷作用下方板的变形挠度。
[1] GHARABABAEI H,DARVIZEH A.Analytical and experimental studies for deformation of circular plates subjected to blast loading[J].Journal of Mechanical Science and Technology 2010 24(9):1855-1864.
[2] NEUBERGER A,PELES S.Scaling the response of circular plates subjected to large and close-range spherical explosions.Part I:Air-blast loading[J].International Journal of Impact Engnieering 2007,34:859-873.
[3] NEUBERGER A,PELES S.Scaling the response of circular plates subjected to large and close-range spherical explosions.Part II:Buried charges[J].International Journal of Impact Engnieering 2007,34:874-882.
[4] NEUBERGER A,PELES S.Springback of circular clamped armor steel plates subjected to spherical air-blast loading [J].International Journal of Impact Engnieering 2009,36:53-60.
[5] WEN H M.Deformation and tearing of clamped circular work-hardening plates under impulsive loading[J].International Journal of Pressure Vessels and Piping,1998,75:67-63.
[6] ZAKRISSON B, WIKMAN B, JOHANSSON B,Johansson B.Half scale experiments with rig for measuring structural deformation and impulse transfer from land mines[C].Lancaster,PA:24th Int.Symp.Ballistics,2008:497-504.
[7] 吴义田,张庆明,顾忠明.冲击波载荷作用下结构响应的模型律分析[J].北京理工大学学报,2006,26(8):664-667.
[8] 吴义田,张庆明.近距离爆炸下不同厚度靶板的动态响应分析[J].北京理工大学学报,2007,27(7):568-571.
[9] 张中英,何洋扬,王乐阳,等.车底结构对爆炸冲击波响应特性影响研究[C].2009全国仿真技术学术会议论文集.中国计算机用户协会仿真应用分会,九江:2009.
[10] 王芳,冯顺山,俞为民.爆炸冲击波作用下靶板的塑性大变形响应研究[J].中国安全科学学报,2003,13(3):58.
[11] 牟金磊,朱锡,张振华,等.爆炸冲击作用下加筋板结构变形研究[J].海军工程大学学报,2007,19(6):12-16.
[12] FULLER B J,WARREN J A.Assessing the performance of protective systems subject to buried charge blasts[J].ResearchGate,2017.
[13] JACOB N,CHUNG S,KIM Y.Scaling aspects of quadrangular plates subjected to localized blast loads—experiments and predictions[J].International Journal of Impact Engineering 2004,30:1179-1208.
[14] 李晓坤,郭香华,张庆明.浅埋地雷爆炸载荷分布的数值仿真分析[J].兵器装备工程学报,2019,38(5).