当前用于测试冲击振动信号的传感器多为压电式传感器，此类传感器大多以电荷为输出形式。上升时间短暂、峰值较高的特点使得对电荷信号调理电路的动态特性有较高的要求。于是传感器的输出也具有与冲击信号相似的特点[1-4]。对具有以上特点的电荷信号进行采集分析，就需要设计能够切合信号特性的电荷放大电路。在理论上实现对电荷的转换以及放大之后，经过实验发现电荷放大电路的动态特性难以符合要求，前人对此的解决方法是：运用更高一级的标准仪器，对电路多次输入冲击信号，并对电路的输出进行处理得出其动态特性。本文采用将系统辨识相关的知识应用于模拟电路的方法，运用最小二乘辨识算法对电路的输入输出数据进行处理，估计出数学模型并与实际响应曲线进行比较，之后运用反滤波器技术改进动态特性。经过试验验证之后发现，此方法有效可行。
1 电荷放大电路设计
电荷输出型传感器具有内阻极高但是信号极其微弱的特点，要对电荷信号进行采集首先必须搭建可靠的前置放大电路。此类传感器的输出特点决定调理电路的特性，要求电荷放大电路拥有较高的输入阻抗，同时具有极低的偏置电流，要求偏置电流低于信号幅值。因为传感器的输出所形成的电流只有pA级[5]。运算放大器的选型方面：低输入偏置电流，低输入失调电压，较宽的工作频带，较高的增益和极高的输入阻抗[6]。考虑选择静电型集成运放OPA128。输入电阻选择必须高于反馈电阻，这样可以达到减小低频漂移的效果。电荷放大部分是由积分负反馈电路组成。反馈电容选择聚苯乙烯电容。电容量的大小要考虑到电压增益、寄生电容干扰等问题。图1中，为防止输入过高而增加电阻R1；电容C4～C11是滤除电源的波动。此电路可分为三部分。第一部分为电荷—电压转换电路。电荷信号经输入端输入经过这一部分电路，电荷信号被转化为电压信号，并且输出电压Uo=Q/C3，其中Q为输入电荷的大小；第二部分将第一部分输出的电压转换为两个大小相等，相位相差180° 的电压；为了使电路有比较稳定的静态工作点，此电荷放大电路的第三部分设计了一个差分放大器，一个稳定的静态工作点可以有效抑制共模信号。此电路的输入电压叠加后即可得输出电压。其中R11与R6并联后的阻值等于R7和R10并联后的阻值，R10/R7=R9/R8。输出电压U=R11(Ui2-Ui1)/R7,其中Ui2和Ui1为同相输入端和反相输入端的电压。
图1 电荷放大电路图
2 电荷放大电路模型参数辨识以及动态性能补偿
2.1 最小二乘辨识法
所谓系统辨识是在假定的一些模型中寻找与系统实际最为相近的模型，此过程中需要已知系统输入输出数据，依据这些条件确定模型参数。基本原理如图2所示。经过系统辨识的一系列算法将得到模型参数θ，假设k时，以前一时刻的模型参数估计值
做为参照，可以计算出该时刻的模型输出，也就是系统输出的预测值。即：
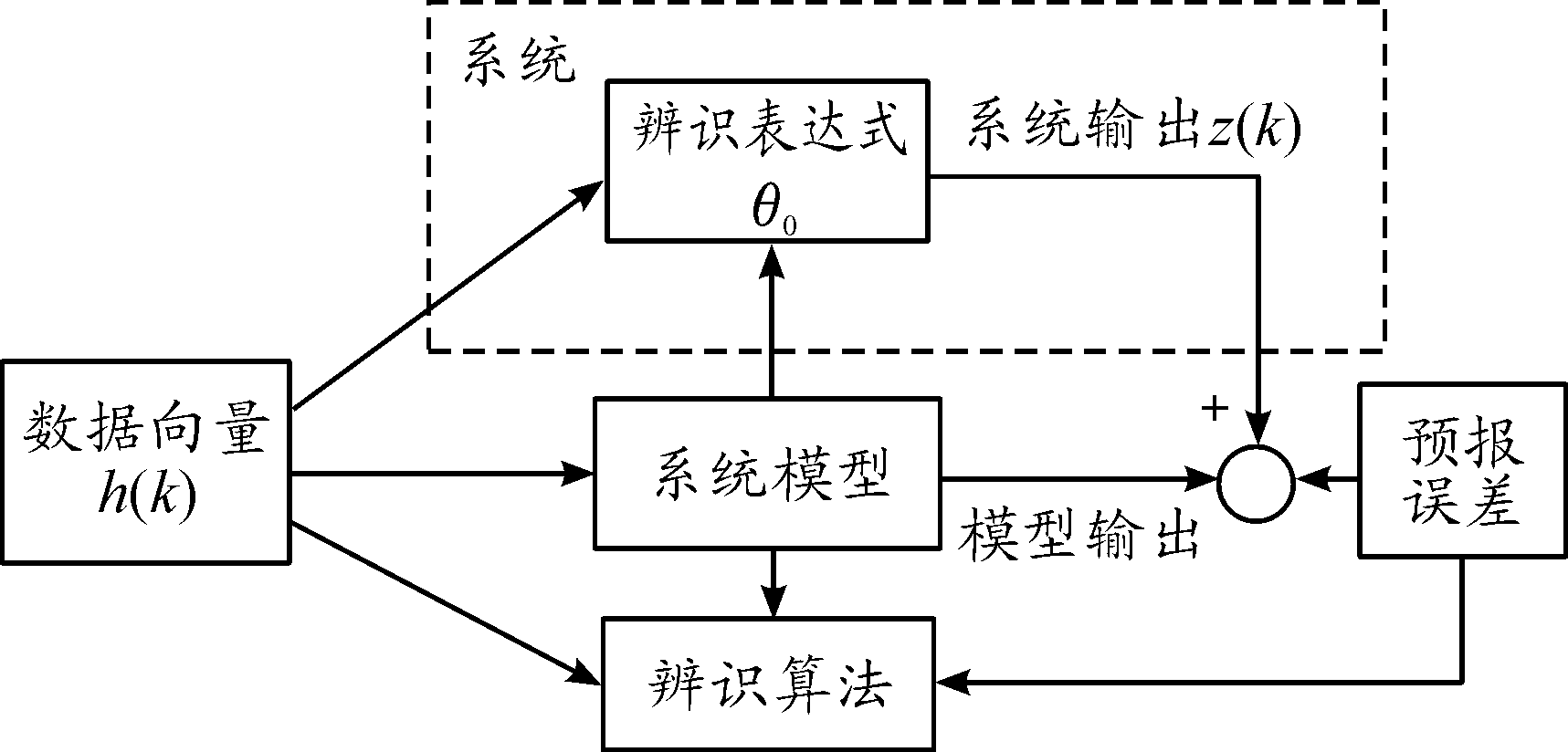
图2 系统辨识原理框图
(1)
式(1)中，h(k)是可观测的数据向量。
预测误差
是将系统输出z(k)和模型输出
进行比较之后得到的。辨识算法利用之前得到的输出预测误差
在确定的准则下，计算出k时刻的模型参数估计值，然后用这个估计值去更新系统模型函数。在反复反馈和迭代中，预测误差将达到极小值。此时的模型输出在该准则意义下最接近系统输出z(k)，这个模型便是辨识到的最终结果。将系统的输入和输出构造成最小二乘格式为：
z(k)=hT(k)θ+n(k)
(2)
式(2)中：z(k)为系统的输出；h(k)是输入输出数据组成的向量；n(k)是均值为零的随机噪声。
利用数据序列{z(k)}和{h(k)}，极小化如下准则函数为：
(3)
即可求得模型参数θ的最小二乘估计值
此时的模型输出便可以很好地代表真实系统的输出[8-10]。
2.2 反滤波技术
一般情况下搭建的模拟电路都具有动态特性方面的缺陷，比如电路的工作频带无法覆盖传感器的信号有效带宽。后续的采集电路采集到的信号将与实际信号存在较大的动态误差，于是需要拓展此电路的工作频带，以提高它的动态性能[11]。假设该系统为线性时不变系统，测试系统的输出响应为激励x(t)x(t)与系统的脉冲响应h(t)h(t)的卷积：
(4)
时域的卷积对应频域的乘积，由此可以对输出响应作快速傅里叶变换，有：
(5)
通过式(5)计算输入信号的傅里叶变换，再通过反傅里叶变换得到输入信号，这样的过程被称为反卷积。在此过程中有如下两个难点：判据准则的选取以及怎样依靠这样的准则来优化设定的参数。通过对多个模型在对噪声的抑制、精度、适用范围和复杂度等多个方面的考虑，我们选择采用以下模型：
(6)
式(6)中：H′(k)为H(k)的共轭；ar为可优化的参数。
3 具体实现方法
由于仪器原因电荷信号发生器无法输出此阶跃信号数据，只能将方波信号的上升沿作为阶跃信号。经过电荷放大电路后的信号由采集存储电路将其存储在Flash(闪存)内。采集端选用10 MHz采样频率。将采集到的信号经Matlab处理，取其中重要部分的20 000个点，绘制可得电荷放大电路的响应曲线如图3所示。
图3 电荷放大电路的归一化响应曲线
按照最小二乘格式将输入和输出的关系表达为：
z(k)=hT(k)θ+e(k)
(7)
式(7)中：
(8)
式(8)中：u(k)是电路第k个输入数据，u(k-1)为电路的第(k-1)个输入数据；z(k)为电路的第k个输出数据，z(k-1)为电路的第(k-1)个输出数据；e(k)为零均值随机噪声；k=1,2,…,L，L是数据的长度，在此L=20 000；na和nb是系统模型的阶次，根据电路理论可知电路阶次为二阶。在此将阶次参数na和nb都设为2。输入输出关系可以联立线性方程组，得：
zL=HL(k)θ+eL(k)
(9)
式(9)中:
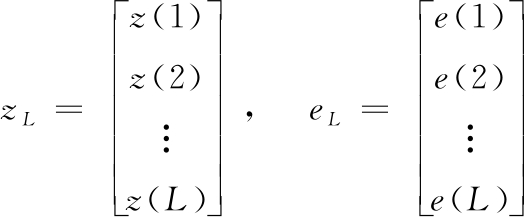
(10)
(11)
根据准则函数可得:
(zL-HLθ)T(zL-HLθ)
(12)
求出J(θ)的极小值，此时所得的参数θ的值即为模型参数的估计值，算法如下：
设
使得
于是有:
(13)
运用向量微分公式[12]有：
(14)
(15)
可以解得：
(16)
导入输入输出数据解出参数矩阵。由此可知电路传递函数为：
(17)
根据辨识出的电路传递函数进行动态特性补偿，利用反滤波技术对电路的工作频带进行拓宽。反滤波的方法给出了测试信号的估计值以及确定的误差范围。
4 实验验证
首先对电荷放大电路进行理论仿真实验，利用Multisim 14软件，但该软件中不存在电荷源这样的工具，于是根据电荷生成的原理与特性，采用双极电压源和电容串联的方式来生成电荷，取代电荷源[7]。根据实际需求可以双击电压源设置输出信号的正负脉冲电压值、占空比、频率、上升时间和下降时间等参数。此次项目所用冲击传感器频率最高达50 kHz，输出的电荷量在4 000 pC左右，其自身的等效电容约是200 pF。最终设置电压源的脉冲上升时间为5 ns，脉冲宽度为50 ns，脉冲下降时间为5 ns，脉冲幅度为1 V的矩形脉冲作为等效仿真信号源，计算可知等效电荷源的输出脉冲电荷为4 000 pC。在电荷放大电路的输出端放置示波器，点击运行后双击示波器，通过分析波形发现电路在理论状态中可以将信号正常放大且没有失真。
对运用最小二乘辨识算法所辨识出的电路模型以相同的输入信号，观测并记录其响应，处理数据可以绘制出辨识模型的响应曲线图。图4为系统实验输出响应曲线与辨识模型的响应曲线图。
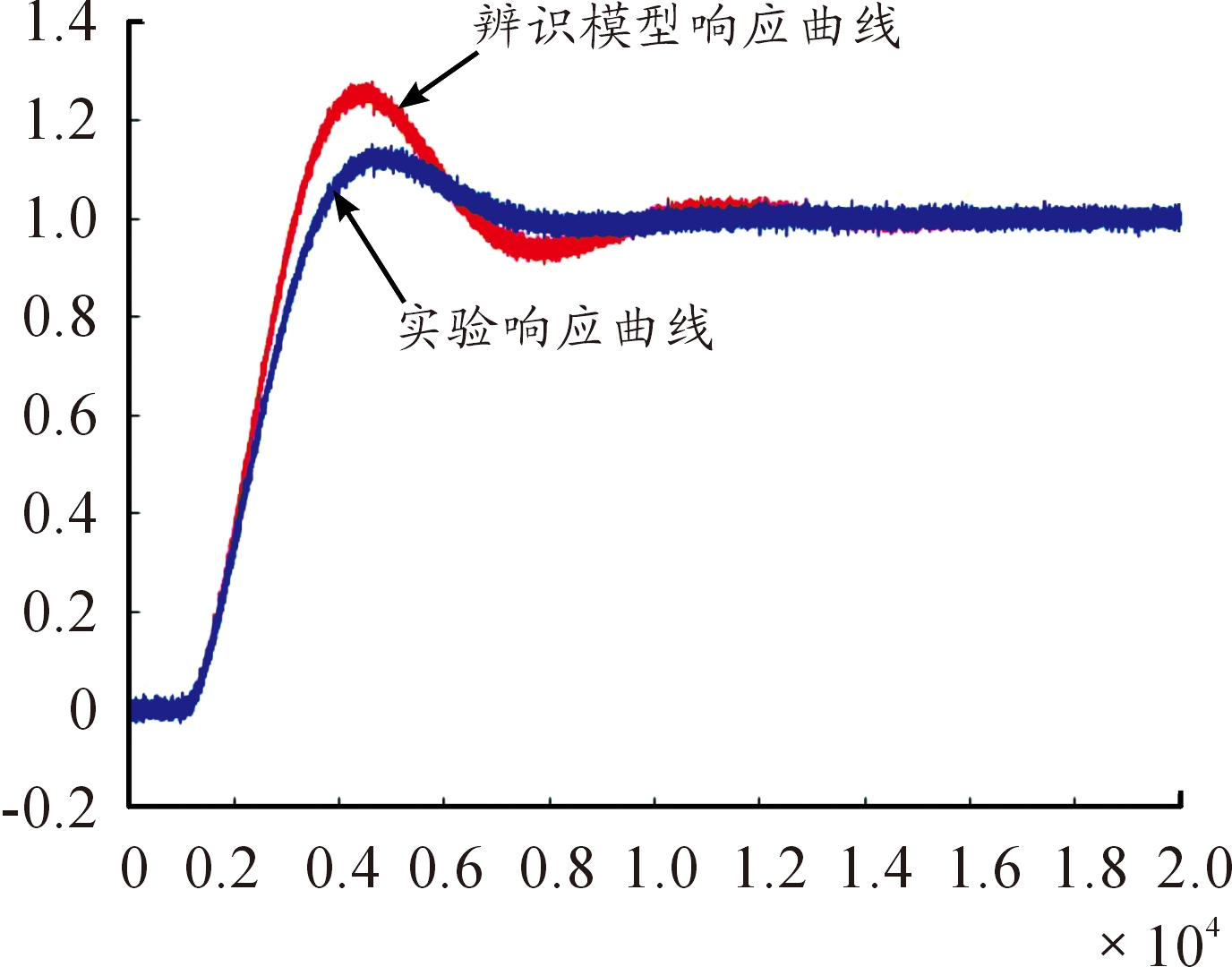
图4 系统实验输出响应曲线与辨识模型的归一化响应曲线
依据上文利用系统辨识算法所计算出的传递函数，可以得到幅频特性曲线如图5所示。
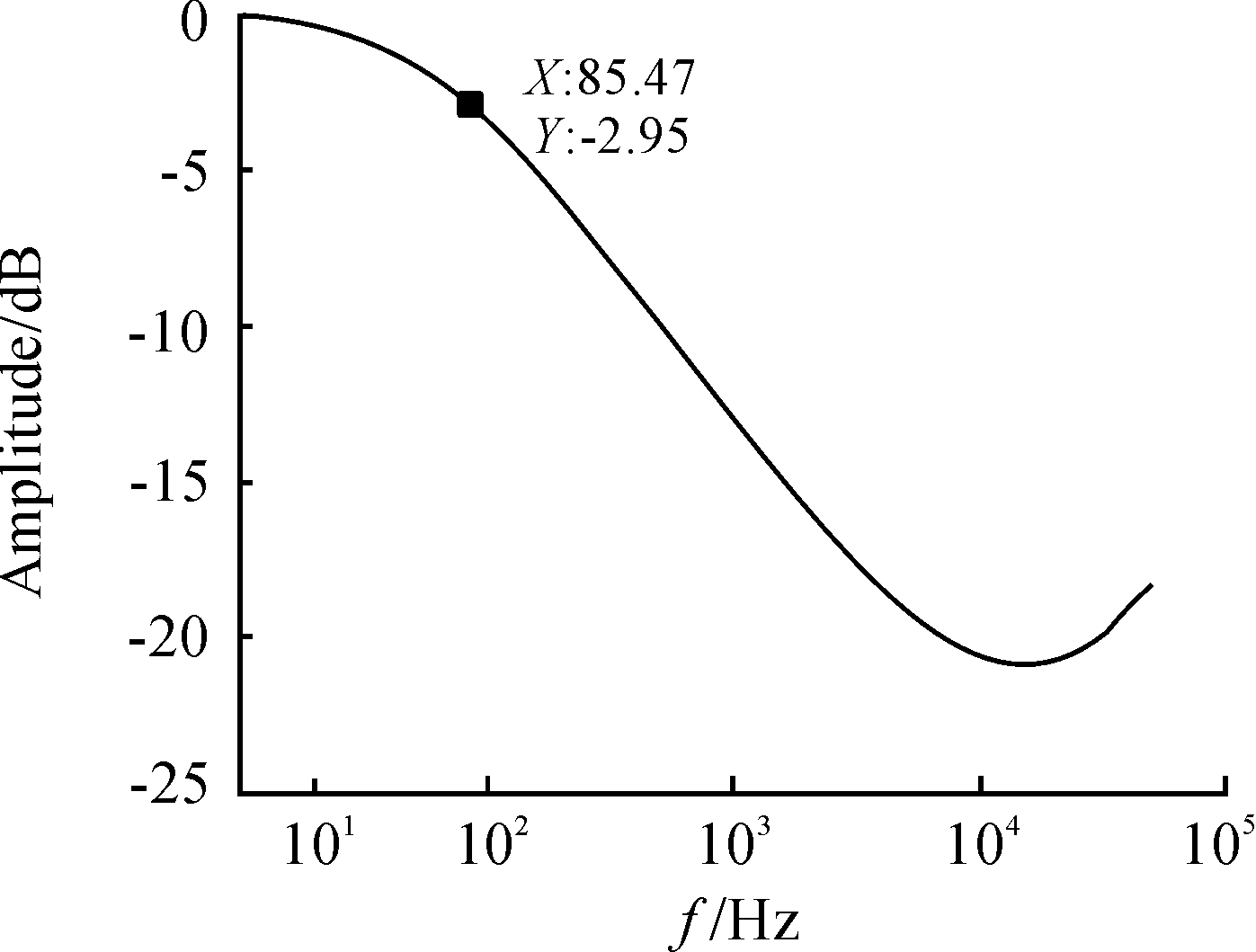
图5 幅频特性曲线
当信号衰减3 dB时的带宽为工作频带，图5中取点可知工作频带为 0～90 kHz。但是根据实际要求工作频带要达到150 kHz左右，此时就需要运用反滤波技术加宽电路的工作频带。反滤波器的实现方法是根据之前介绍的模型，并结合电路的传递函数和采样数据的点数进行计算，构造并分析离散输入信号的估计值。图6为补偿前后系统幅频特性曲线。图7为补偿前后系统的相频特性曲线。
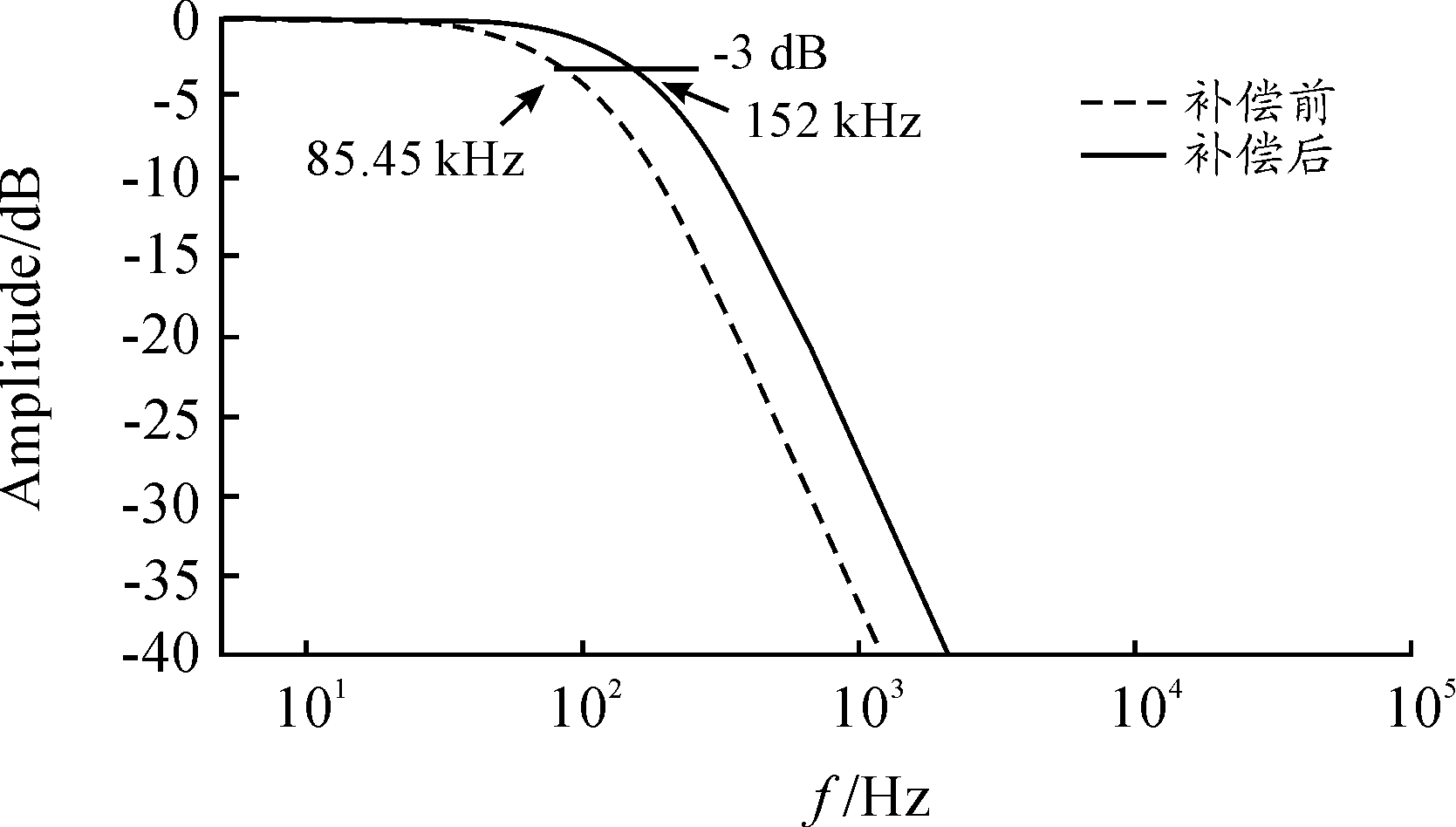
图6 补偿前后系统幅频特性曲线
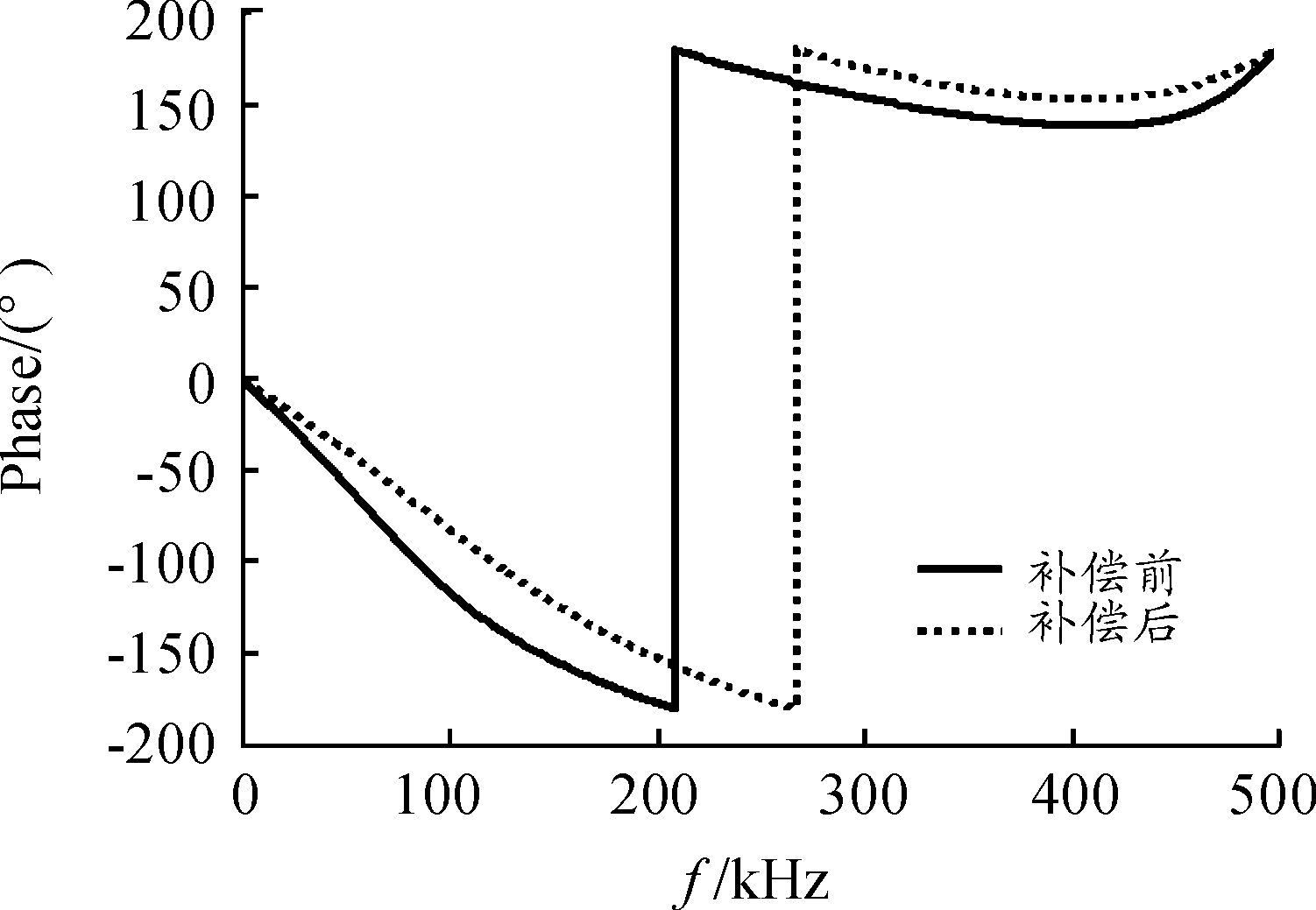
图7 补偿前后系统的相频特性曲线
分析由反滤波器校正后的幅频特性与补偿前对比图可以得知，电路的工作频带由补偿前的0～85 kHz，拓宽到0～152 kHz，并且在工作频带内幅频特性曲线的平直度明显提高，补偿后系统获得了更好的群延迟特性以及更宽的通频带,显著提高了电路的动态特性。电路的工作频带的提高和工作频带内的平滑度的提高，预示着此系统在工作频带内，增益随着信号频率的改变不会发生太大的波动，系统的误差会同时大幅减小。
5 结论
致力于更加精准地采集冲击波形而设计的电荷放大电路，为适应冲击信号上升时间短暂，峰值较高的特点，将系统辨识方法应用于模拟电路，能比较精确地辨识电路的传递函数，接近实际地观察电路的动态性能。在此基础上对电路进行软件补偿可以有效提高电路的动态特性，从而减小在测试冲击信号时存在的误差。
[1] 刘浩.冲击波测试系统与动态特性补偿研究[D].太原：中北大学,2017.
[2] 杜红棉,祖静.无线冲击波超压测试系统研究[J].火力与指挥控制,2012,37(01):198-200.
[3] 尤文斌,祖静,范锦彪,等.冲击波存储测试技术[J].仪器仪表学报,2006,27(z2):1228-1229.
[4] 杨帆,梁永烨,杜红棉,等.毁伤威力场冲击波无线分布式测试方法研究[J].传感技术学报,2015,28(01):71-76.
[5] 徐爱华,王健,许昊,等.电荷放大器校准的研究[J].计量与测试技术,2018,45(06):42-43+46.
[6] 张微,高国旺,李汉兴,等.新型压电式传感器前置放大电路的设计[J].电子测试,2010(06):10-14.
[7] 邓维礼,秦岚,刘俊,等.基于Multisim的准静态电荷放大器仿真分析[J].国外电子测量技术,2009,28(04):24-26,35.
[8] 倪二男,张大力.一种基于最小二乘的离散模型参数自适应辨识方法[J].哈尔滨工业大学学报,1994(2):60-66.
[9] 樊高辉,魏明,刘卫超.基于系统辨识的电路脉冲响应建模[J].电讯技术,2011,51(10):117-121.
[10] 耿彦章,吕海峰,安君,等.基于LabVIEW的SISO系统传递函数估计虚拟仪器设计[J].中国测试,2017,43(06):103-107.
[11] 邹虹,杨德猛,陈志军,等.冲击波压杆测试系统动态特性补偿技术研究[C]//第十届全国冲击动力学术会议论文集.中国力学学会爆炸力学专业委员会冲击力学专业组等，太原：2011.
[12] 袁东,马晓军,曾庆含,等.二阶系统线性自抗扰控制器频带特性与参数配置研究[J].控制理论与应用,2013,30(12):1630-1640.