捷联惯导系统初始对准是通过捷联在载体上的惯性元件输出,解算载体初始时刻姿态问题的技术[1]。一般初始对准可以分为粗对准和精对准两个过程[2],粗对准是利用双矢量定姿原理,确定初始时刻的姿态角[3];精对准是利用卡尔曼滤波等技术实现对初始姿态失准角的估计[4-5]。
无论粗对准还是精对准都要利用惯性元件输出,所以惯性元件输出将很大程度上影响初始对准精度[6]。但是目前高精度惯性元件成本较高,功耗较大,所以利用低精度、低成本、低功耗的惯性元件实现高精度初始对准是目前研究热点[7-8]。旋转调制技术是较常用的一种惯性元件误差补偿方法[9],通过误差补偿提高输出精度,进而提高初始对准精度[10-12]。旋转调制技术操作简单、成本低,具有一定应用价值。
本研究通过将旋转调制和传统解析粗对准结合,提出一种旋转调制解析粗对准方法,该方法能够有效解决惯性元件常值误差对粗对准精度影响。通过建立旋转调制下捷联惯导系统的误差状态方程,提高了精对准速度。
1 连续旋转调制原理
旋转调制是一种有效补偿惯性测量器件常值误差的技术,该技术通过驱动惯性测量装置相对某一固定坐标系(一般为载体坐标系)周期性旋转,使得与旋转轴正交方向的缓变误差调制成整周期积分为零的周期变化形式,通过积分实现对缓变误差的自补偿,提高惯性测量装置测量精度。
连续旋转调制的基本原理为:
若惯性元件3个方向上分别有漂移误差εx、εy、εz,在旋转台的带动下绕Z轴以恒定角速度ω旋转,则在任意时刻t该漂移误差在载体坐标系下的分量为:

(1)
式中

(2)
为惯性器件坐标系到载体坐标系的转换矩阵。然后对式(1)在时间(0,t)上进行积分,可得:

(3)
垂直于旋转轴的惯性传感器的常值误差通过惯性元件旋转被调制成正弦或余弦函数形式的周期信号,使得它们在整个旋转周期中的积分为零,这是旋转调制的基本原理。如果惯性传感器误差是缓慢变化的随机误差而不是常数时,此时对调制信号的积分不完全为零,但对于完整的旋转周期接近于零。旋转调制大大减少常值误差,从而提高了计算精度。由于沿旋转轴的惯性元件误差不能被调制,其积分与时间成比例,或者仍然遵循非旋转调制系统的误差传播规律。值得注意的是,惯性元件本身的误差并没有消失,但通过使用旋转调制,可以减小该误差对姿态角解算过程中的影响,从而提高初始对准精度。
2 旋转调制初始对准原理
2.1 旋转调制粗对准算法
传统解析粗对准算法,主要是通过地球自转角速度ωie和重力加速度g在载体坐标系和导航坐标系下的分量,利用双矢量定姿的原理实现对对准矩阵的求取。但该方法无法解决惯性元件自身误差所造成初始对准精度低的问题。旋转调制技术能有效对惯性元件进行误差补偿,从而提高惯性元件输出精度,基于旋转调制的解析粗对准原理如图1所示。
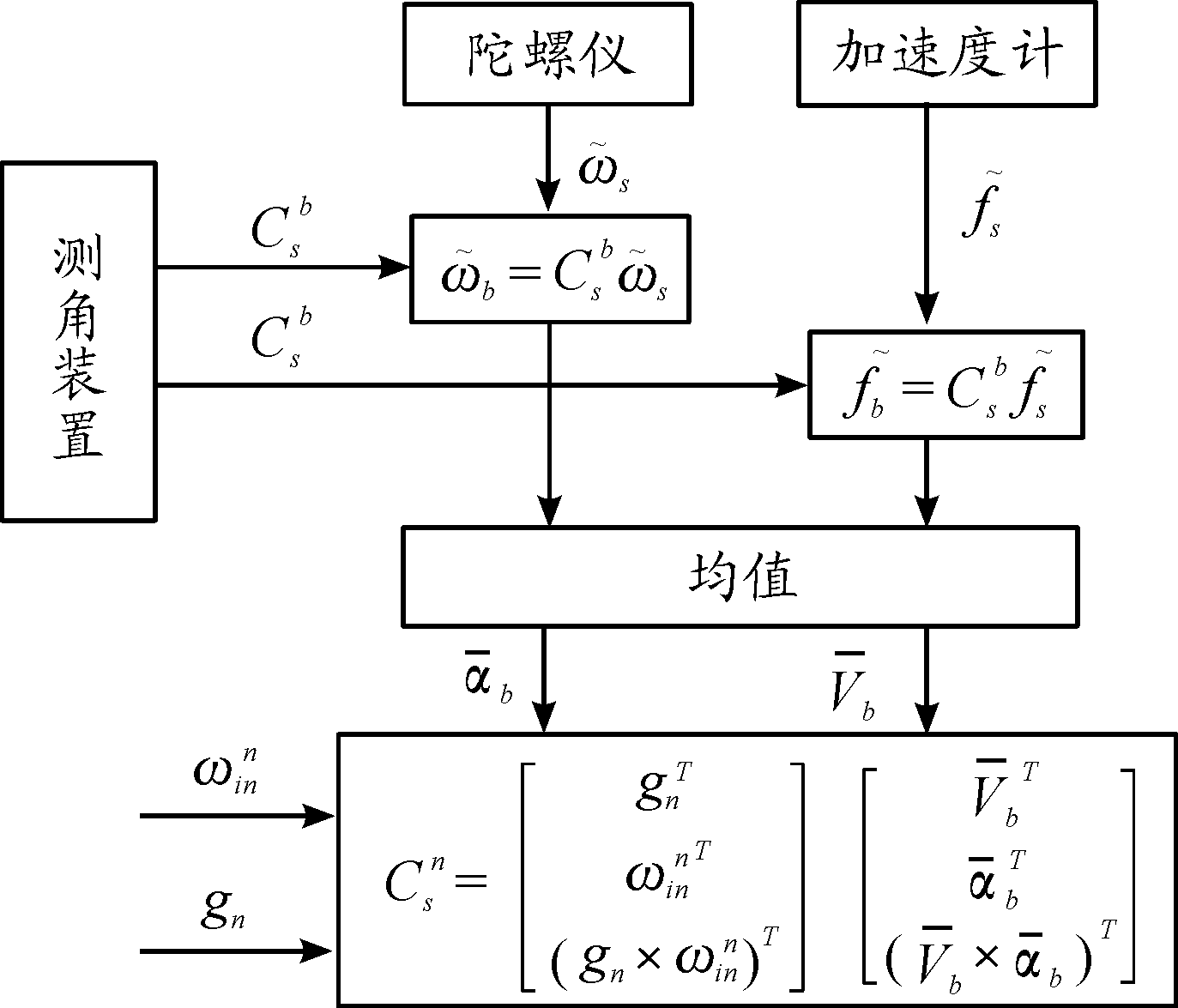
图1 旋转调制粗对准原理框图
未采用旋转调制载体坐标系下加速度计的实际输出模型为:
(4)
其中: fc为常值误差; fr为随机误差。
未采用旋转调制载体坐标系下陀螺仪的实际输出模型为:
(5)
其中:Kr为标度因数误差;Kg为安装误差ωc为常值误差;ωr为随机误差。
为降低常值误差对对准精度的影响,采用单轴连续旋转调制技术对常值误差进行补偿。其主要是利用旋转机构带动惯性元件绕Z轴进行周期性旋转,得到惯性元件坐标系下输出为:
(6)
(7)
将陀螺仪输出和加速度计输出转换到载体坐标系下可得:
(8)
(9)
对两边同时积分得:
(10)
(11)
设
(12)
(13)
根据双矢量定姿的方法可以得到对准矩阵为
![]() ♂
♂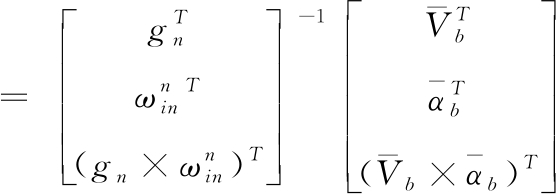
(14)
最后根据对准矩阵和姿态角之间的关系进行解算就能够得到粗对准结果。该方法利用均值代替积分过程,方便后续精对准过程中参数的更新。且在求均值的过程中将多个矢量信息包含于一个矢量内,可以提高粗对准精度。
2.2 旋转调制精对准算法
精对准主要是在粗对准得到初始状态的基础上,建立正确的误差状态方程,利用卡尔曼滤波技术对初始失准角进行估计的过程。因为旋转调制技术的引入,精对准的状态方程也要做适当调整,其原理如下:
误差状态方程:
(15)
(16)
(17)
(18)
(19)
其中▽为加速度计的随机常值误差,ε为陀螺仪的随机常值误差。所以有如下关系
(20)
(21)
可以得到捷联惯导系统静基座对准的误差状态方程:
(22)
其中状态变量X=[δVEδVNφEφNφU▽x▽yεxεyεz]T; 其中δVE,δVN为东向和北向速度误差;φE,φN为水平失准角,φU为方位失准角。
(23)
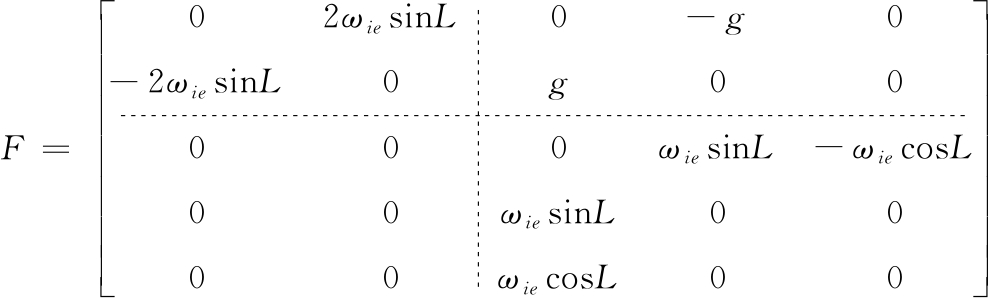
(24)

(25)
其中Cij为![]() 中所对应的元素。W(t)为N(0,Q)的高斯白噪声。选取两个水平速度误差作为观测量,则观测方程为:
中所对应的元素。W(t)为N(0,Q)的高斯白噪声。选取两个水平速度误差作为观测量,则观测方程为:
Z=HX+V
(26)
其中:H=[I2×2 02×8];V是系统观测噪声,为N(0,R)的高斯白噪声过程。
但是当旋转机构带动整体进行旋转时,此时惯性元件坐标系不与载体坐标系重合。所以式(20)、(21)转换为:
(27)
(28)
故状态方程中T变为
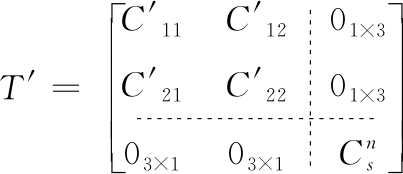
(29)
其中![]() 为
为![]() 中所对应的元素。观测方程仍采用式(26)。
中所对应的元素。观测方程仍采用式(26)。
新的初始对准误差模型建立之后,再利用卡尔曼滤波技术对水平失准角和方失准角进行估计。
离散型卡尔曼滤波过程如下:
状态一步预测
(30)
状态估计
(31)
滤波增益
(32)
一步预测均方误差
(33)
估计均方误差
Pk=(I-KkHk)Pk/k-1
(34)
3 仿真及结果分析
3.1 仿真条件
为对上述方法进行验证,利用Matlab进行仿真,仿真条件设置如下:静基座下姿态角为,俯仰角θ=5°、航向角φ=7°、横滚角γ=3°。位置信息为东经116.35°、北纬39.97°。陀螺仪的常值误差为0.02(°)/h、随机误差为0.01(°)/h;加速度计的常值误差为1×10-4 g、随机误差为5×10-5 g。仿真时间为300 s,其中粗对准120 s,精对准180 s。旋转调制角速度为10(°)/s。陀螺仪的标度因数误差为10-5,安装误差为10-5 rad,卡尔曼滤波初始条件如下:
P(0)=diag[(0.1 m/s)2,(0.1 m/s)2,(1°)2,(1°)2,
(1°)2,(100 μg)2,(100 μg)2,(0.02(°)/h)2,
(0.02(°)/h)2,(0.02(°)/h)2]
Q=diag[(50 μg)2,(50 μg)2,(0.01(°)/h)2,
(0.01(°)/h)2,(0.01(°)/h)2,0,0,0,0,0]
R=diag[(0.1 m/s)2,(0.1 m/s)2]
3.2 仿真结果分析
如图2、图3所示为加速度计和陀螺仪的旋转调制仿真结果,从其中可以看出当陀螺仪和加速度计存在常值和随机误差的情况下,仿真结果和理想结果之间存在较大偏差。利用旋转调制技术进行误差补偿后,惯性元件开始的输出波动比较大,但是随着积分对波动的消除,X轴和Y轴最终与理想结果趋于一致,由于Z轴的误差未被调制,所以Z轴结果仍存在偏差。对仿真数据进行分析可以得出表1、表2的结果。
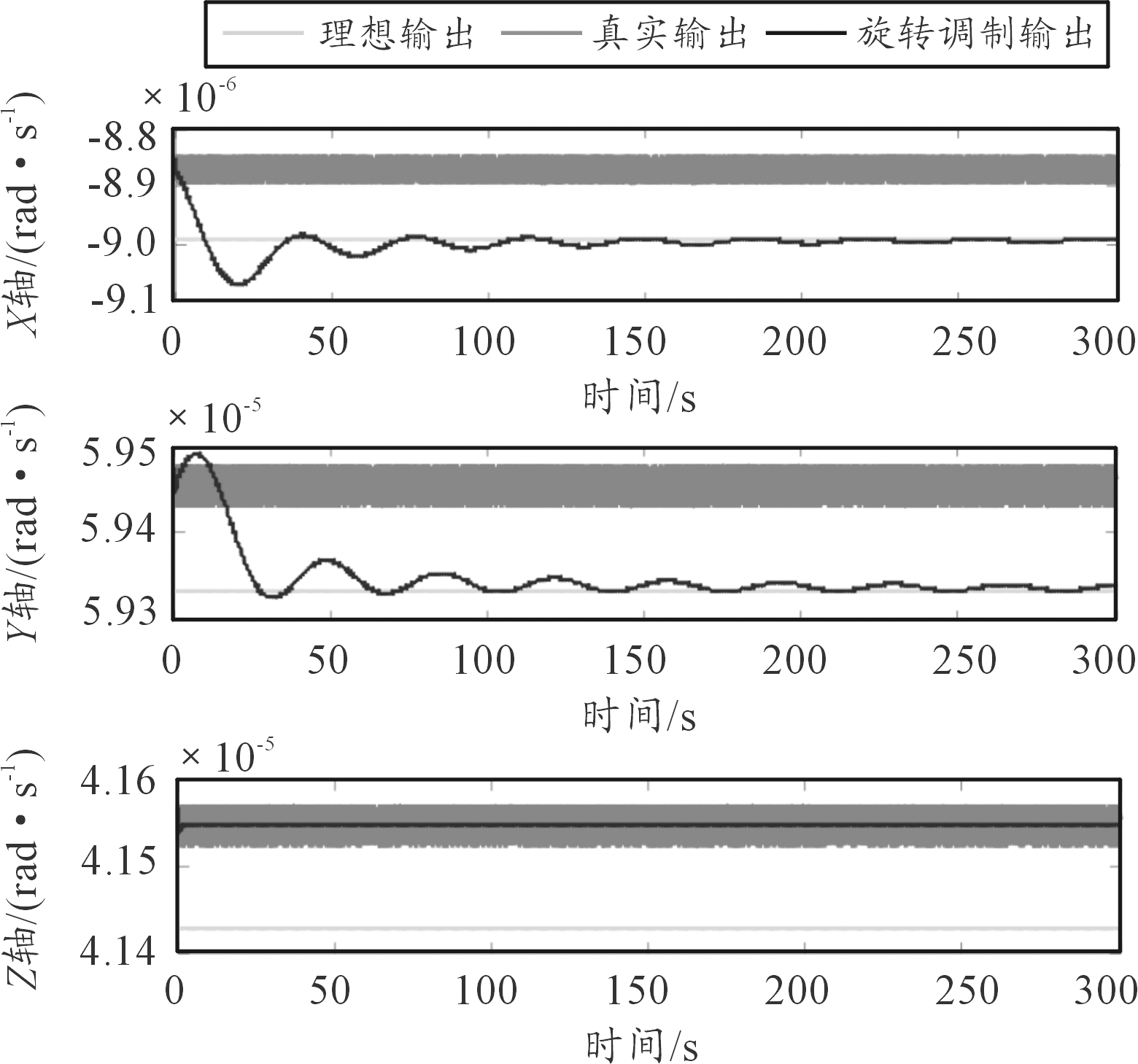
图2 陀螺仪仿真输出结果
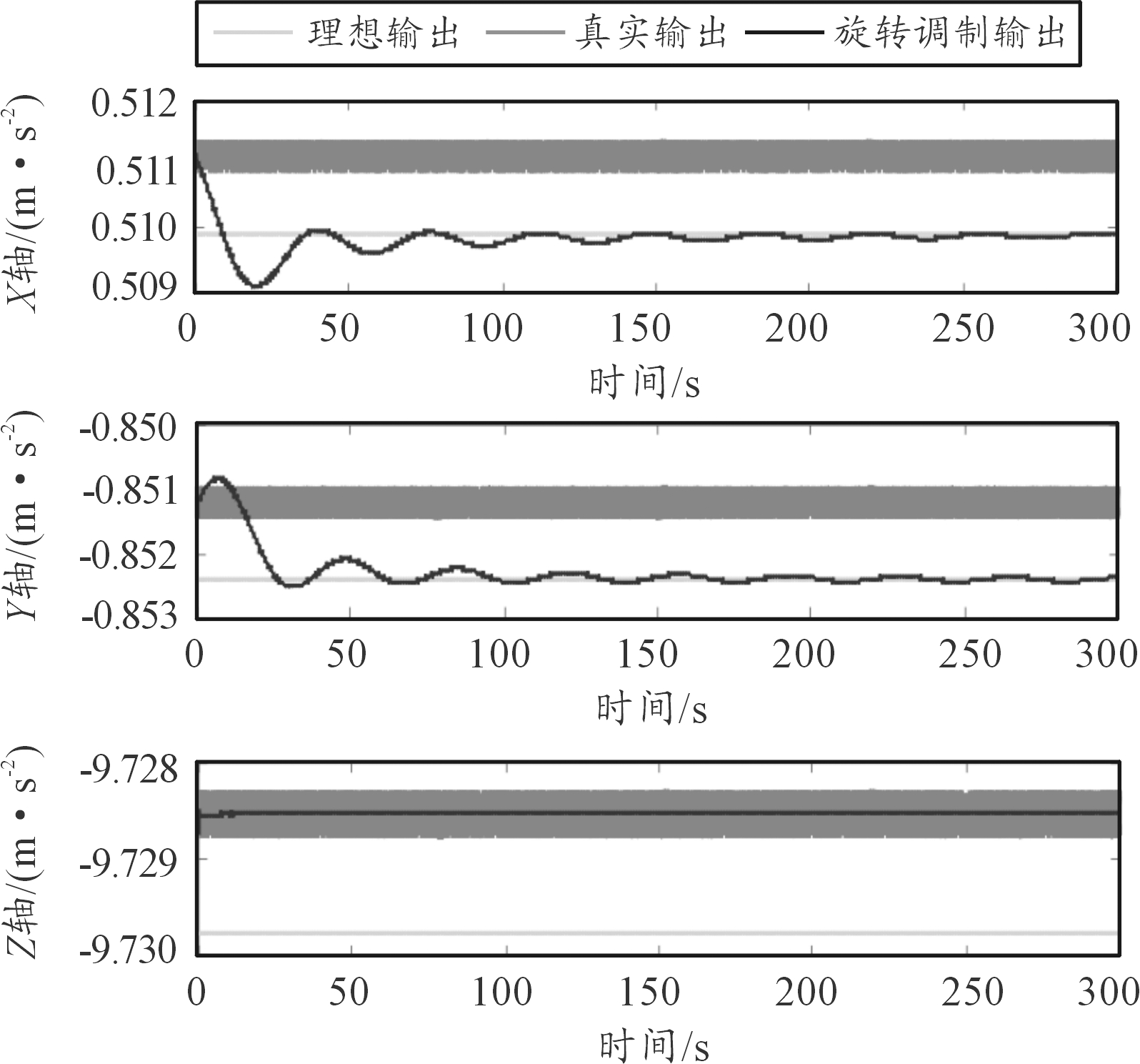
图3 加速度计仿真输出结果
表1 陀螺仪输出结果

仿真条件X轴/(m·s-2)Y轴/(m·s-2)Z轴/(m·s-2)理想值-8.990 2×10-65.933 4×10-54.142 7×10-5实际值-8.869 0×10-65.945 5×10-54.154 8×10-5旋转调制值-8.990 9×10-65.933 5×10-54.154 8×10-5
表2 加速度计输出结果
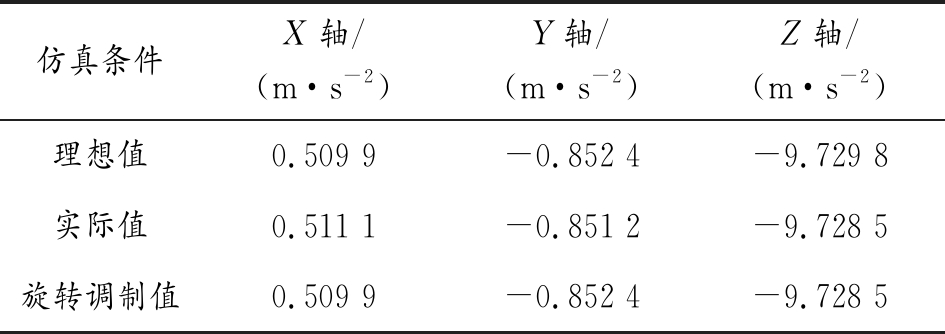
仿真条件X轴/(m·s-2)Y轴/(m·s-2)Z轴/(m·s-2)理想值0.509 9-0.852 4-9.729 8实际值0.511 1-0.851 2-9.728 5 旋转调制值0.509 9-0.852 4-9.728 5
静基座条件下旋转调制解析粗对准仿真结果如图4所示。当惯性元件未经旋转调制时,即采用传统解析粗对准时,由于惯性元件存在常值误差和随机误差,解算出姿态角与理想结果之间大致存在一个常值偏移。当利用旋转调制解析粗对准时,由于旋转调制技术能够对常误差进行补偿,所以仿真结果最终会与理想结果一致。分析数据可得到表3的结果,传统解析粗对准方法得到的结果,俯仰角相对误差为14‰,横滚角误差为25‰,航向角误差为217‰;旋转调制解析粗对准结果,俯仰角相对误差为1‰,横滚角误差为0.33‰,航向角误差为0.56‰。
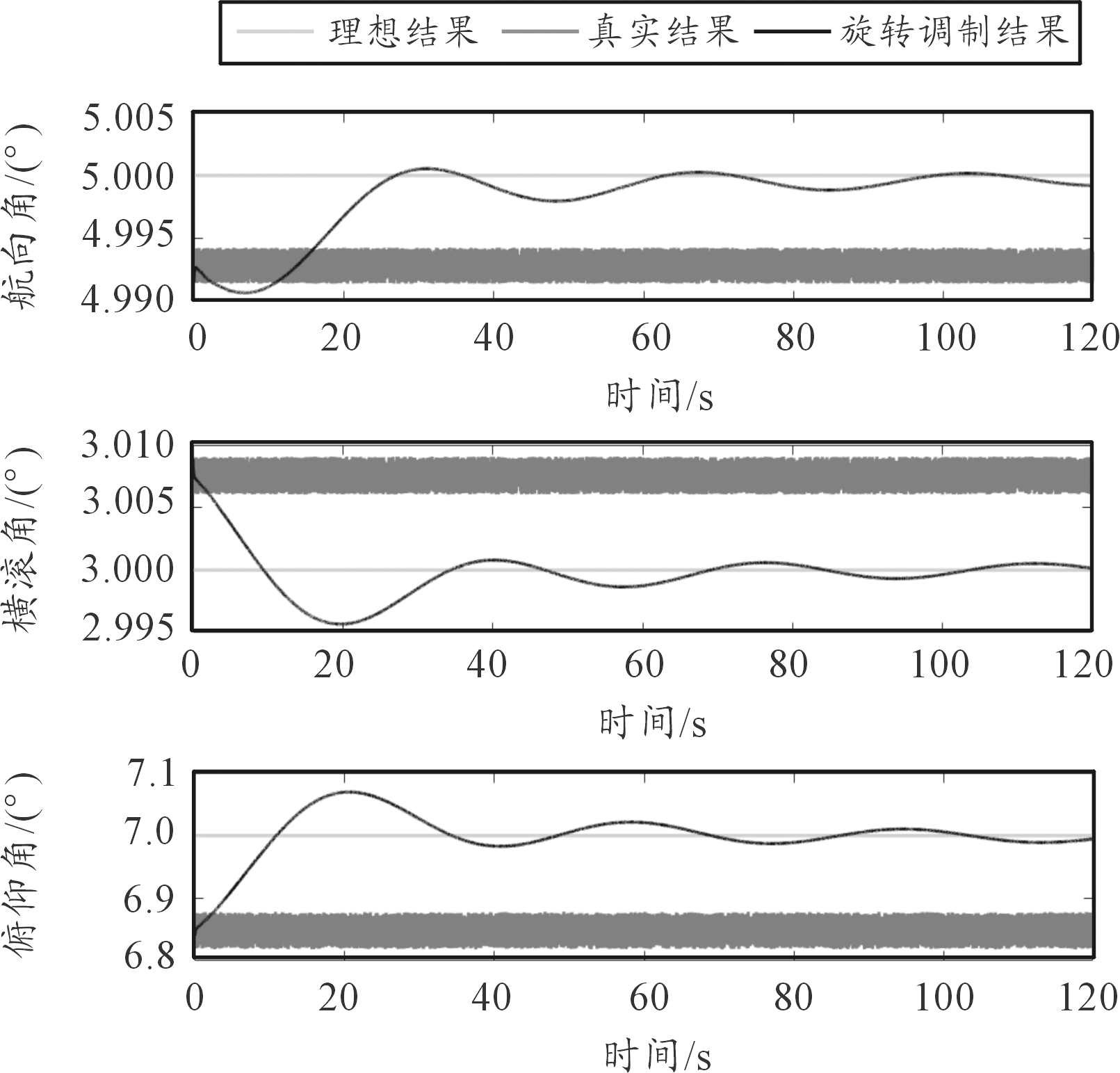
图4 旋转调制解析粗对准仿真结果
表3 不同方法求解姿态角仿真结果

粗对准方法俯仰角/(°)横滚角/(°)航向角/(°)传统解析粗对准4.992 83.007 66.848 2旋转调制解析粗对准4.999 53.000 16.996 1
为对比旋转调制解析粗对准和传统解析粗对准结果对整个初始对准精度的影响,采用卡尔曼滤波精对准技术对失准角进行估计。初始对准方案如表4所示,仿真结果如图5所示,从图5中可以看出,利用旋转调制解析粗对准方法,其精对准过程比传统解析粗对准方法速度快,且精度高。但是旋转调制精对准误差状态方程要进行修正,其修正后的仿真结果如图6所示,从图6中可以明显看出,由于修正后的误差状态方正更加准确,故精对准过程用时更短。
表4 两种初始对准方案

方案1传统解析粗对准(120 s)+卡尔曼滤波精对准(180 s)方案2旋转调制解析粗对准(120 s)+卡尔曼滤波精对准(180 s)
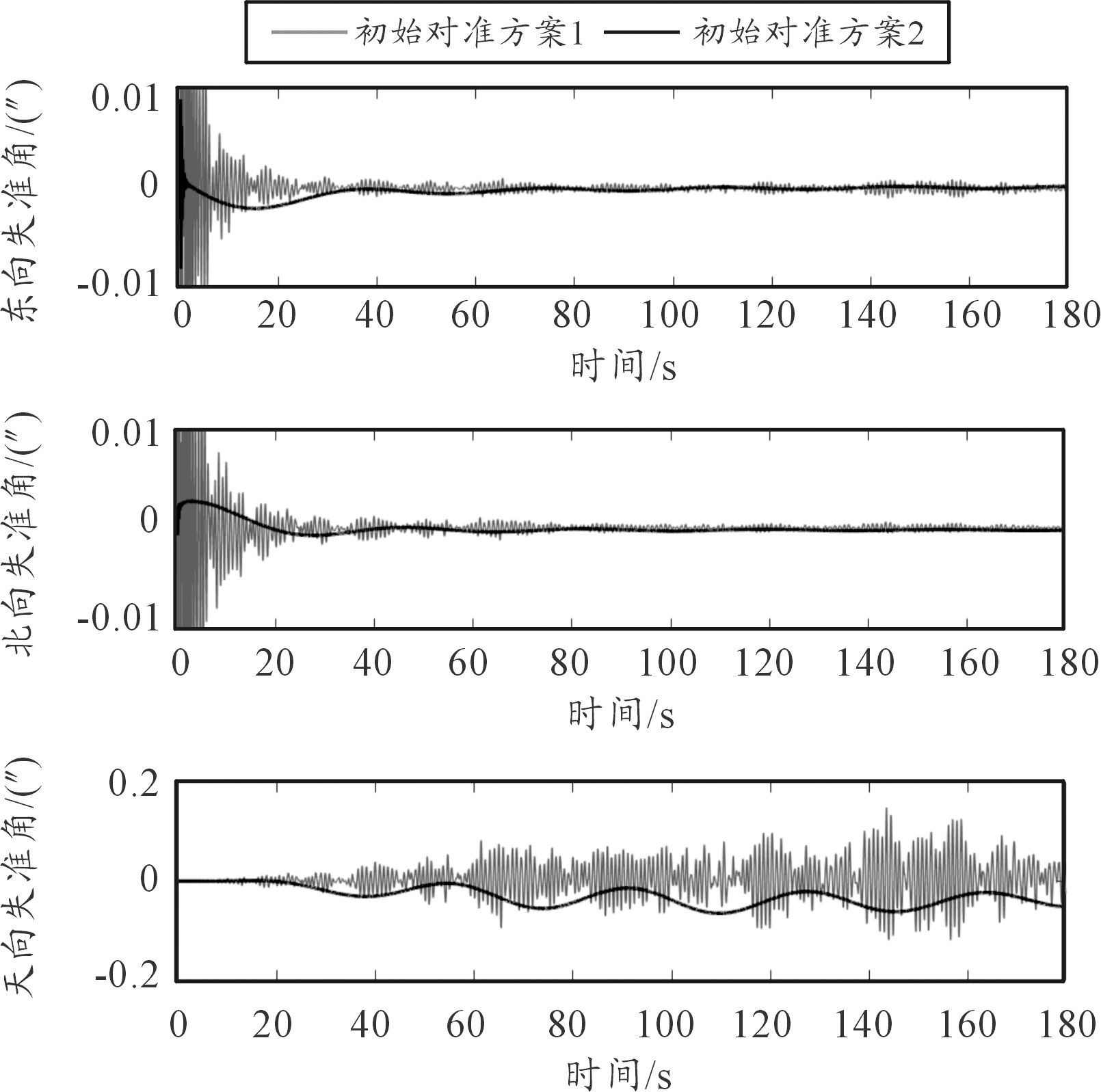
图5 两种初始对准方案仿真结果
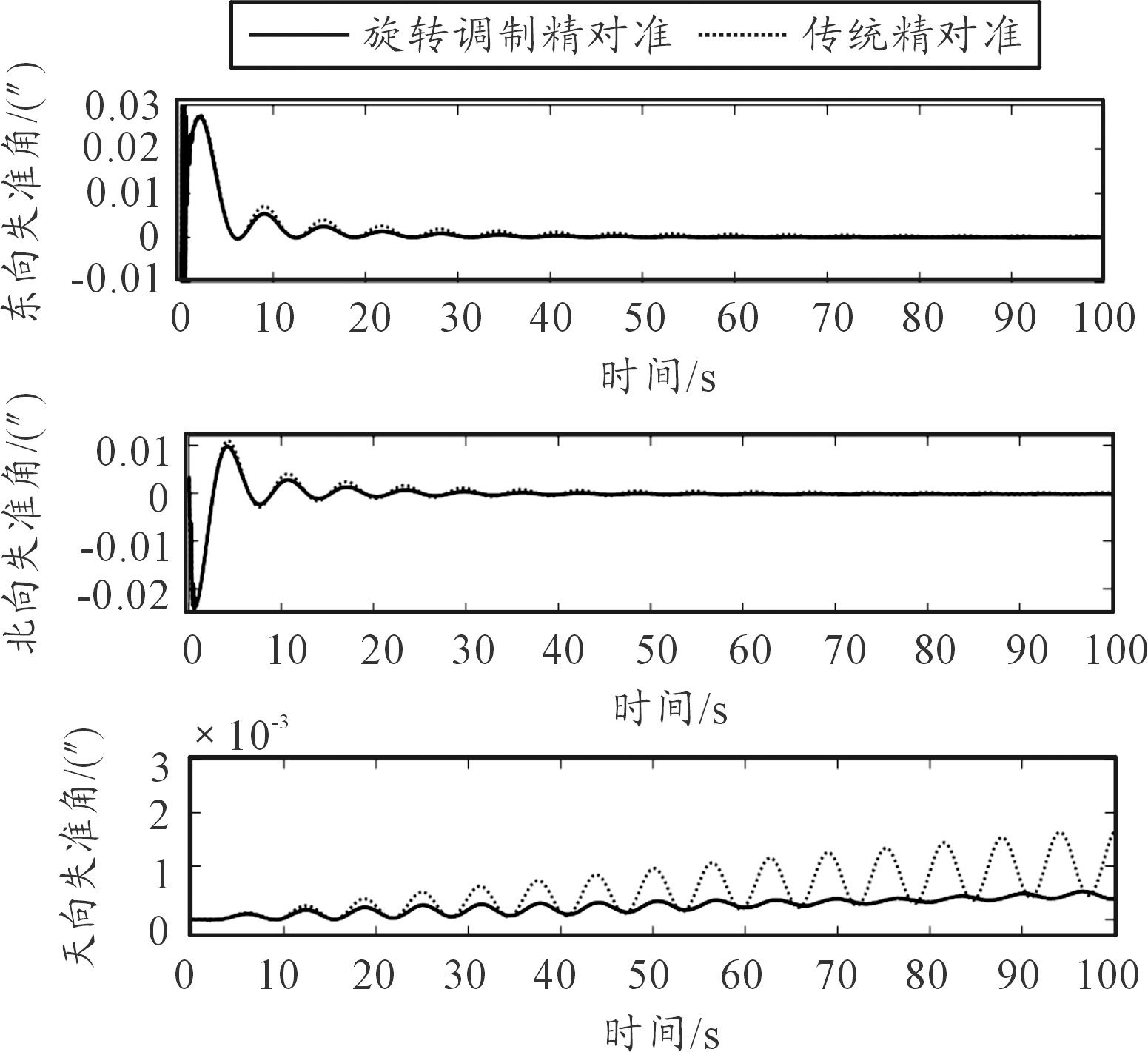
图6 两种误差状态方程对准仿真结果
4 结论
本研究提出了基于旋转调制静基座条件下捷联惯导系统初始对准方法,将旋转调制技术融入初始对准过程中,提出了旋转调制解析粗对准方法,修正了旋转调制下精对准的误差状态方程。通过仿真验证了该方法能够有效提高粗对准的精度,提高精对准速度。
[1] 秦永元.惯性导航[M].北京:科学出版社,2009.
[2] REDDY N S,MURRAY J.Transfer Orbit stage Gyrocompass Alignment Algorithm Twist and SwayEnvironment for Mars Observer Mission on Commercial Titan[J].Aerospace and Electronic Systems Magazine,1991,6(2):3-7.
[3] SCHIMELEVICH L,NAOR R.New approach to coarse alignment[J].Position Location and Navigation Symposium,Atlanta,GA,1996:324-327.
[4] TITTERTON DH,WESTON JL.Strapdown Inertial NavigationTechnology[M] 2nd ed.Stevenage:Institution of Electrical Engineers,2004:10.
[5] 李鲁明,赵鲁阳,唐晓红,等.基于模糊卡尔曼滤波的姿态估计算法[J].仪表技术与传感器,2019(04):100-105,110.
[6] 刘生攀,王文举,饶兴桥.单轴旋转捷联惯性导航系统误差分析与转位方案研究[J].兵工学报,2018,39(09):1749-1755.
[7] DEPPE O,DOMER G,KONIG S,et al.MEMS and FOG Technologies forTactical and Navigation Grade Inertial Sensors—Recent Improvements and Comparison[J].Sensors,2017(17):567.
[8] YAMMANE D,KONISHI T,SAFU T,et al.Long-term Vibration Characteristics of MEMS Inertial Sensors by Multi-layer Metal Technology[J].In Proceedings of the 2017 19th International Conference on Solid-State Sensors,Actuators andMicrosystems(TRANSDUCERS),Kaohsiung,Taiwan,2017,18(22):2187-2190.
[9] 姬晓琴,陈文辉,杨 业.旋转惯导的发展及应用[J].航天控制,2019,37(1):27-33.
[10] XINGH F,CHEN Z Y,YANG H T,et al.Self-alignment MEMSIMUMethod Based on the Rotation Modulation Technique on a Swing Base[J].Sensors,2018,18(4):1178-1200.
[11] ZHANG J Y,LI J,ZHANG X,et al.Analysis and Compensation of Modulation Angular Rate Error Based on Missile-borne Rotation Semi-strapdown Inertial Navigation System[J].Sensors,2018,18(5):1430-1447.
[12] JIA Y,LIS L,QIN Y Y,et al.Error Analysis and Compensation of MEMSRotation Modulation Inertial Navigation System[J].IEEE Sensors Journal,2018,18(5):2023-2030.