adaptive
通过建立诸如轨迹长度最短、运动时间最少的优化目标,找到复杂环境中起点和终点之间的最优路径,实现移动机器人的路径规划,是机器人自主导航的关键问题之一[1-3]。目前,以人工势场法、视图法、单元分解法为代表的传统方法,在解决路径规划中存在执行效率低和易陷入局部最优的问题。因此,近年来以遗传算法、粒子群算法、蚁群算法、人工蜂群算法为代表的启发式智能优化算法得到了越来越多学者的关注。
文献[4]将人工神经网络、模糊神经网络引入机器人的路径规划中,借助神经网络的并行计算和出色的学习能力,提高了路径规划的效率和精度。文献[5]采用蚁群算法对机器人进行路径规划,取得了较好的效果。文献[6]对粒子群算法进行了改进,并将改进后的算法用于机器人的路径规划。此外,飞蛾优化算法、人工蜂群算法等在机器人路径规划中同样具有较高的应用价值。
人工蜂群(Artificial Bee Colony,ABC)算法作为一种新的群智能优化算法具有收敛速度快、精度高的优点[7-8],但同时,也存在早熟收敛等不足。文献[9]提出了自适应进化策略的人工蜂群优化算法,使得算法的收敛速度更快、精度更高。文献[10]结合粒子群算法提出了粒子蜂群算法,测试结果表明算法具有更快的收敛速度和更高的寻优精度。因此,本文在对蜜源位置更新策略进行改进的基础上,基于Bootstrap采样策略,在蜂群位置更新公式中增加随机搜索因子和自适应位置更新系数的基础上,提出了改进人工蜂群算法,并对所提算法进行了验证。最后,将所提算法用于机器人的路径规划,取得了较好的效果。
1 Bst-ABC算法模型
1.1 ABC算法
ABC算法通过模拟蜜蜂采蜜过程,以实现寻优的目的。ABC算法将蜂群分为三类:引领蜂、观察蜂和侦查蜂。其中,引领蜂数量和观察蜂数量相等,主要任务是开采蜜源,设置侦查蜂的目的是为了增加蜜源种类[7-8]。对目标优化问题,蜜源的位置被看作是所求问题的解,花蜜数量被视为所求问题的函数值,问题求解的过程即为寻找最优蜜源的过程。具体为:设优化问题的解为D维,随机产生2N个解为蜜源位置,即种群数量(引领蜂个数=观察蜂个数=N),选取N个作为蜜源位置。蜜蜂搜索蜜源的过程主要由三部分组成:1) 引领蜂对当前蜜源进行邻域搜索,发现新蜜源,记录蜜源的信息;2) 观察蜂根据引领蜂提供的蜜源信息,选择一个食物源,进行邻域搜索;3) 一个蜜源被放弃,引领蜂变成侦查蜂,随机寻找新的蜜源。
在搜索过程中按照式(1)随机产生蜜源,即:
xij=r1(ub-lb)+lb
(1)
式(1)中:r1为[0,1]之间的随机数;ub,lb分别为变量x的上、下限。
引领蜂和观察蜂按式(2)对蜜源进行邻域搜索,即:
vij=xij+r(xij-xkj)
(2)
式(2)中:vij为新蜜源位置;r∈[-1,1]是一个随机数;k∈1,2,…,N且k≠i,为随机产生的整数; j为第i个蜜源中第j维的位置, j∈1,2,…,D。
观察蜂按照式(3)选择蜜源,即:

(3)
式(3)中, fi为花蜜适应度。按式(4)进行计算,即:
![]()
(4)
式(4)中, f(i)为第i个解的目标函数值。在一定循环次数之后若蜜源质量没有提高,则该蜜源被放弃,同时,相应的引领蜂转变为侦查蜂,按式(5)随机产生新蜜源,即:
xij=r2(0,1)(uj-lj)+lj
(5)
式(5)中:r2为[0,1]之间的随机数;uj,、lj分别为当前循环内得到的解的第j维最大值和最小值。
1.2 蜜源位置公式的改进
梯度下降算法为了实现优化的目的,使得变量沿负梯度方向更新。其自变量迭代量Δxt的形式为:
![]()
(6)
为避免算法早熟,提高算法优化性能,将式(6)和式(2)相结合,取出式(6)中分母表示前后两次迭代的函数值差,提出如式(7)改进的蜜源位置更新公式。同时,考虑到引领蜂和观察蜂进行邻域搜索的早期,蜜源位置随机性较大,此时,为了快速获得最优解,蜜源位置更新时应该具有较大的迭代步长。在搜索后期,蜜源的位置逐渐接近最优位置,此时,解的搜索范围逐渐缩小,引领蜂和观察蜂进行邻域搜索的过程中应该具有更小的搜索迭代步长。鉴于以上思路,对式(2)进行了改进,如式(7)所示。式(7)中主要增加了基于sigmoid函数的自适应调整系数w和随机搜索因子c∈[0,1],以实现随机搜索的目的。
vij=wcxij+r(fbest-fi)(xij-xkj)
(7)
![]()
式(7)中:t为迭代次数; fbest为当前最优蜜源的适应度值; fi为第i个蜜源的适应度值。其中,(fbest-fi)代表当前最优适应度值与当前适应度值的差值,r和梯度下降算法中的(xi+1-xi)具有相同的作用,此处取为[-1,1]的一个随机数。式(7)的改进与梯度下降算法的思想一致。
1.3 改进人工蜂群算法(Bst-ABC)
Bootstrap是对已有样本进行有放回的随机抽样,使得数据集中出现概率大的样本被抽取到的次数较多。该方法对包含有n个样本的数据集进行n次抽样,从而形成新的样本数据集。在ABC算法中,引领蜂和观察蜂在搜索的过程中依据随机选择的方法进行邻域搜索,这就使得当前较优蜜源不能很好的被利用,降低了算法搜索效率,无法充分开发当前最优解。同时,算法在计算适应度时也未能优先考虑当前最优解,使得最优解的利用效率降低。鉴于上述思想我们引入Bootstrap采样策略,使得算法在每次迭代时能够充分利用当前最优解,从而加快算法收敛速度,提高算法精度。Bst-ABC具体算法步骤如下:
步骤1 初始化参数,根据式(1)随机产生初始种群M,种群规模为2N,找到初始蜜源;
步骤2 根据Bootstrap对蜜源进行采样,选择要进行邻域搜索的蜜源位置。引领蜂根据式(7)对蜜源进行邻域搜索,形成新的种群M1;
步骤3 根据Bootstrap对种群M1进行采样形成新的种群M2;
步骤4 计算种群M2中个体适应度(函数值);
步骤5 观察蜂根据式(3)选择蜜源;
步骤6 观察蜂根据式(7)对蜜源进行邻域搜索,形成新的种群M3;
步骤7 根据Bootstrap对种群M3进行采样形成新的种群M4;
步骤8 观察蜂计算种群M4中个体适应度(函数值),用式(3)选择较好的蜜源;
步骤9 判断有无蜜源需要抛弃,如果有侦查蜂根据式(5)发现新的蜜源;
步骤10 记录迄今为止最好的蜜源,判断是否满足终止条件,如果是,输出最优解,否转至步骤7。
Bst-ABC算法流程如图1所示。
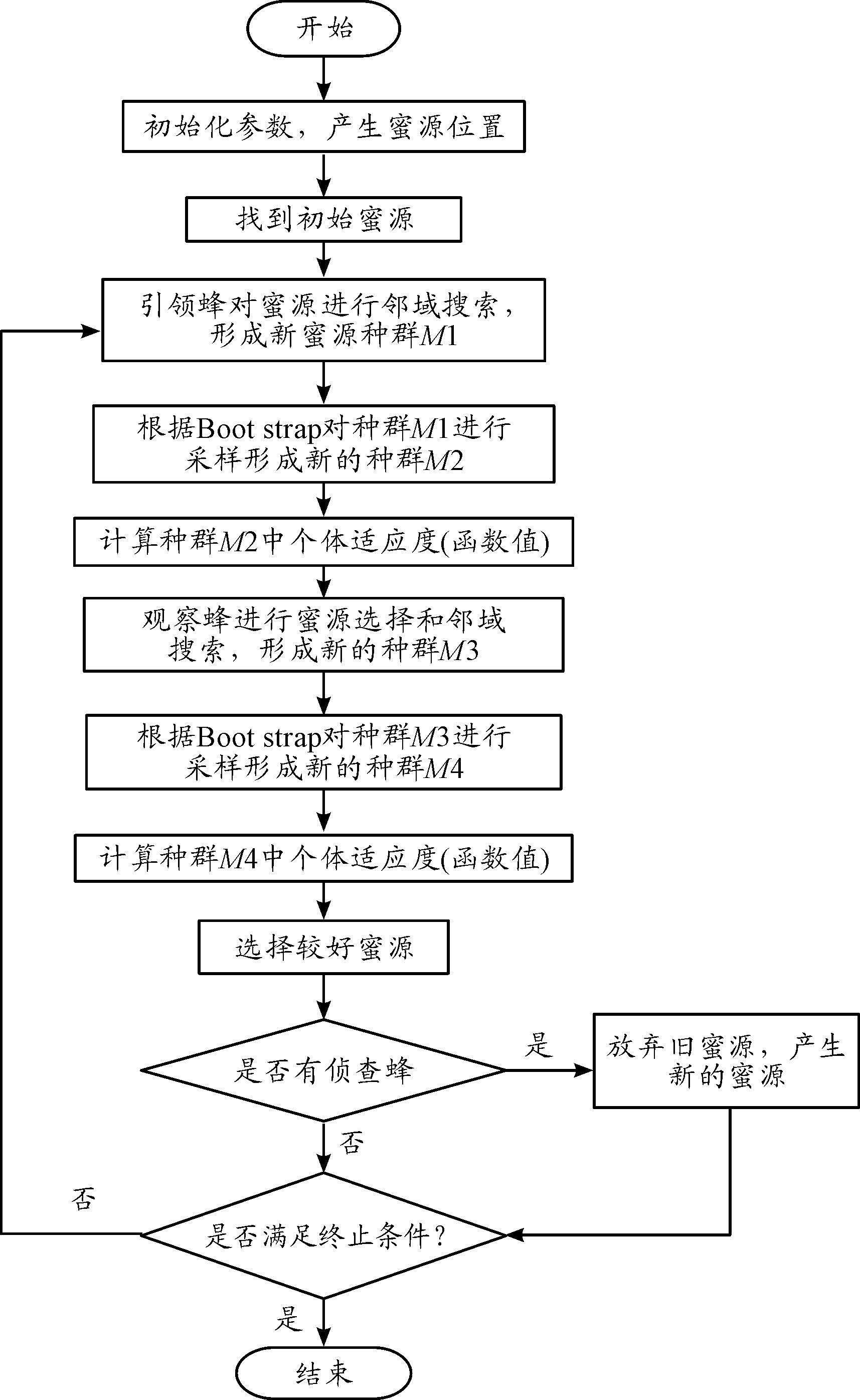
图1 Bst-ABC算法流程框图
为了验证Bst-ABC算法的有效性,对所提算法在以下标准测试函数[11] (选用研究者普遍使用的几个测试函数)上进行了测试,并和传统ABC算法及目前改进效果较好的LRABC[11]、FSABC[12]、ABCP[13]算法进行了比较。结果显示,无论是在迭代次数还是精度方面Bst-ABC算法都要优于其他几种算法。由此可见,本文算法具有良好的搜索能力。因此,所提Bst-ABC算法可以用来优化SVM的惩罚因子和核函数参数。算法具体测试参数为引领蜂、观察蜂、蜜源的数量为50;蜜源循环次数limit为50;迭代次数cycles为 1 000。为了测试算法的有效性,算法随机运行50,取测试结果的平均值、最优值、最差值、方差来衡量所提算法的性能。测试函数信息见表1,测试结果见表2,为了更加直观的对比几种算法的优劣性,图2(横坐标为进化次数,纵坐标为适应度的对数值)给出了几个测试函数具有最优测试结果时的进化过程曲线。
表1 测试函数信息

序号函数 f(x)范围目标值10.5 + sin2(x21+x22)-0.51+0.001(x21+x22)2[-5.12,5.12]0214 000∑Di=1x2i+∏Di=1cos(xii) + 1 [-600,600]03∑Di=1[x2i-10cos(2πxi)+10] [-5.12,5.12]04100(x2-x21)2+(1-x1)2[-30,30]0
表2 Bst-ABC算法测试结果
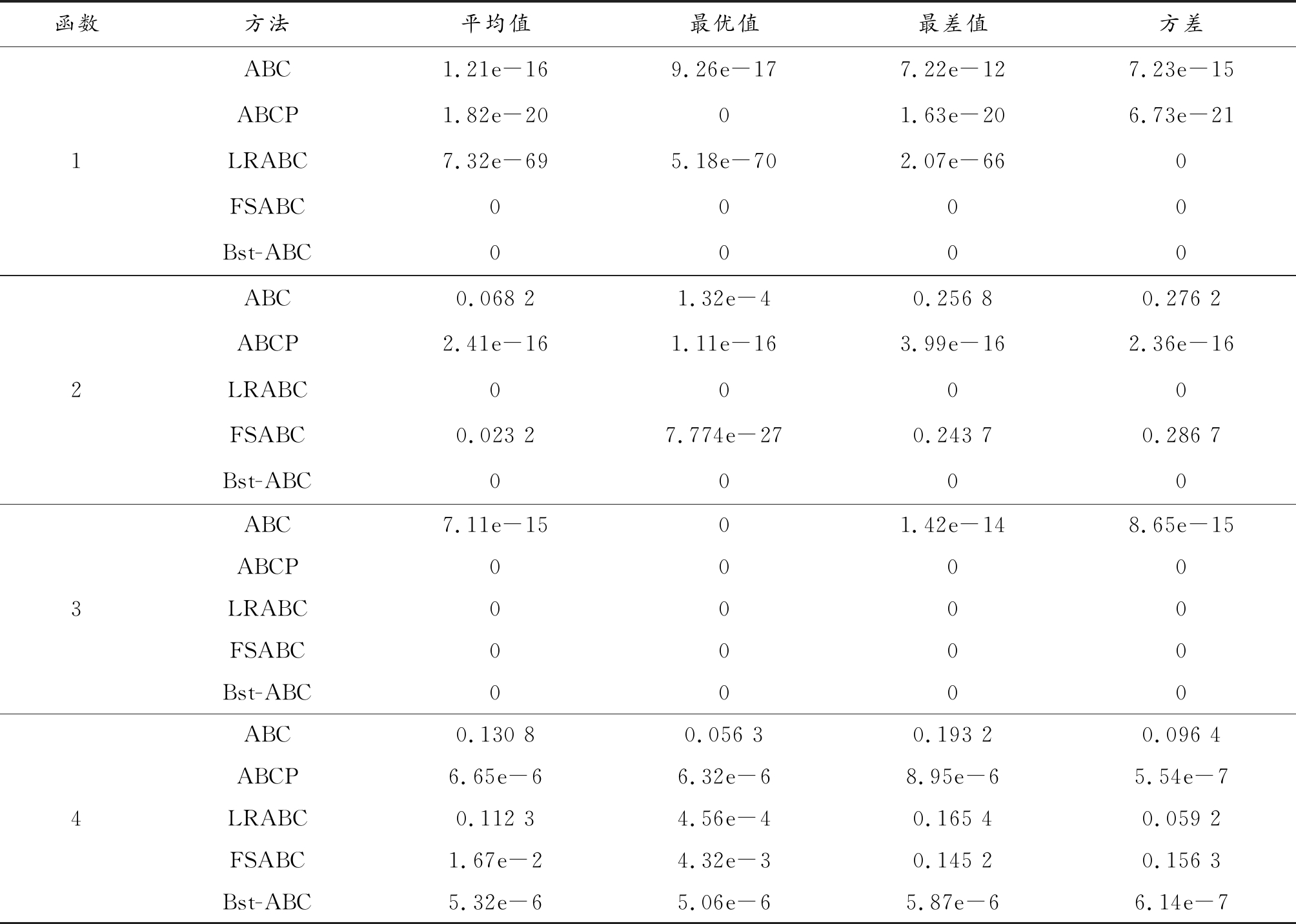
函数方法平均值最优值最差值方差1ABC1.21e-169.26e-177.22e-127.23e-15ABCP1.82e-2001.63e-206.73e-21LRABC7.32e-695.18e-702.07e-660FSABC0000Bst-ABC00002ABC0.068 21.32e-40.256 80.276 2ABCP2.41e-161.11e-163.99e-162.36e-16LRABC0000FSABC0.023 27.774e-270.243 70.286 7Bst-ABC00003ABC7.11e-1501.42e-148.65e-15ABCP0000LRABC0000FSABC0000Bst-ABC00004ABC0.130 80.056 30.193 20.096 4ABCP6.65e-66.32e-68.95e-65.54e-7LRABC0.112 34.56e-40.165 40.059 2FSABC1.67e-24.32e-30.145 20.156 3Bst-ABC5.32e-65.06e-65.87e-66.14e-7

图2 5种算法的进化过程比较
由表2中的结果数据可以看出,所提Bst-ABC算法在解的精度和鲁棒性方面要明显优于其他四种算法。图2直观的反映了Bst-ABC在迭代初期收敛速度就高于其他几种ABC算法,而且相比其他ABC算法Bst-ABC能收敛速度更快,且能收敛到更高精度解。
2 路径规划
将本文所提蜂群算法用于机器人的路径规划,检验算法的实际应用效果。
2.1 参数选择
采用如图3所示的环境模型,其中起点和终点坐标分别为(0,0)和(100,100)。图3中以绿色圆代表障碍物,其位置表达式为:
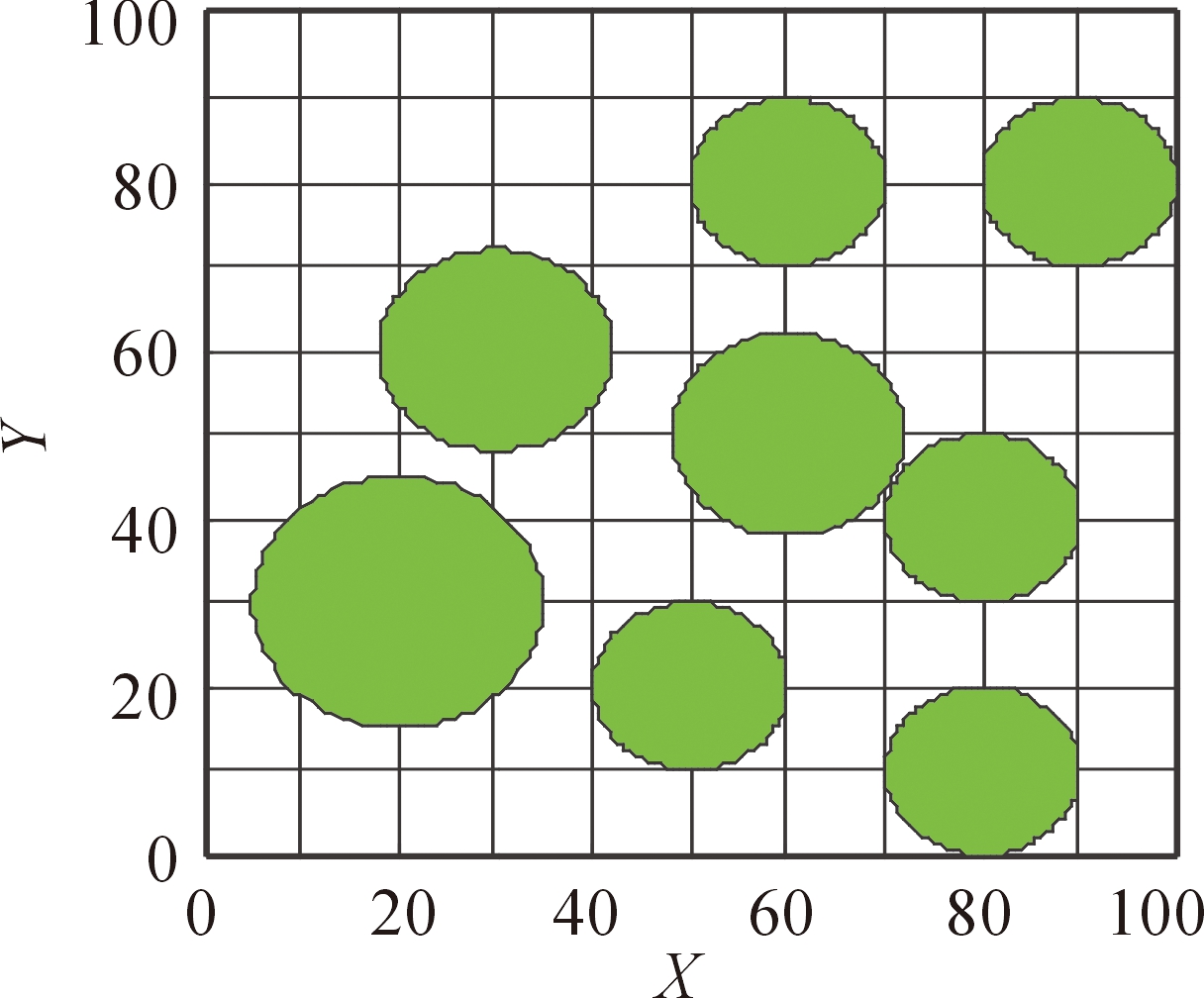
图3 基本环境模型示意图
r2=(x-a)2+(y-b)2
(8)
式(8)中:(a,b)为障碍物的圆心;r为半径。
以图3中起点(0,0)、目标点(100,100),构建一条不经过障碍物的平滑路径,使得该条路径长度最短。建立如下目标函数[6]:
(9)
式(9)中:l(k)为避障约束函数;R(k)为第k个障碍物的半径;K为障碍物个数;ε为权重系数,设为100。
2.2 路径规划仿真
将本文所提Bst-ABC算法和对比结果较优的FSABC算法用于路径规划仿真实验。设置两种算法具有相同的参数,分别为:引领蜂、观察蜂、蜜源的数量分别为50;蜜源循环次数limit为50;迭代次数cycles为1 000。实验环境为 Matlab 2015a,分别将两种算法进行30次实验,获得每次算法路径规划结果,如图4所示。图4中横坐标为算法的实验次数,纵坐标为每次规划的路径长度。结果显示,相较FSABC算法的规划结果,本文所提算法30次实验的最终规划曲线波动较小,说明该算法稳定性高。而FSABC算法的结果曲线相对波动较大,算法稳定性较差。图5为本文所提算法在目标环境中的规划结果。图5中信息显示,算法的路径规划结果更加平稳、距离更短,30次规划结果都能很好的避开障碍物,具有较高的成功率。而图6所示的FSABC算法规划结果效果更差,规划成功的概率更低。两种规划结果也能直观反映出,本文改进算法具有更高的路径规划精度和鲁棒性。

图4 两种算法规划结果曲线
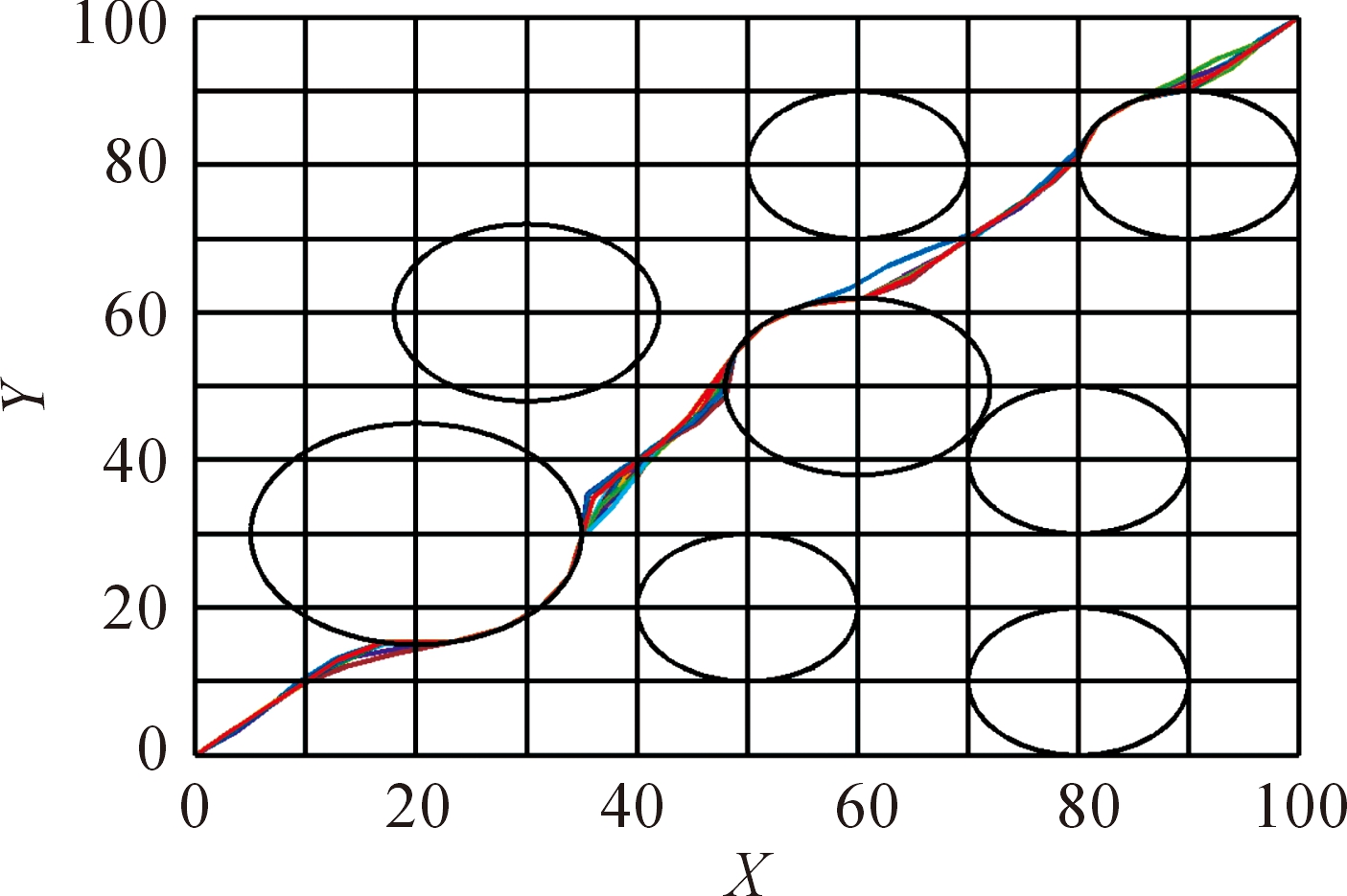
图5 Bst-ABC算法规划结果

图6 FSABC算法规划结果
3 结论
在增加随机搜索因子和基于sigmoid函数的自适应位置更新系数的基础上,将Bootstrap采样理论引入ABC算法,提出了基于Bootstrap采样策略的改进ABC算法(Bst-ABC),以解决ABC算法早熟及优化精度不高的问题。在部分研究者普遍采用的优化函数上的测试结果表明了所提算法相较其他的改进较优的算法具有更高的优化精度。最后将所提算法用于机器人的路径规划,表明算法具有应用价值。
[1] DEWANG H S,MOHANTY P K,KUNDU S.A Robust Path Planning For Mobile Robot Using Smart Particle Swarm Optimization[J].Procedia Computer Science,2018:290-297.
[2] 陆皖麟,雷景森,邵炎.基于改进A*算法的移动机器人路径规划[J].兵器装备工程学报,2019,40(04):197-201.
[3] 曲道奎,杜振军,徐殿国,徐方.移动机器人路径规划方法研究[J].机器人,2008(02):97-101,106.
[4] MOHANTY P K,PARHI D.Navigation of autonomous mobile robot using adaptive network based fuzzy inference system[J] Springer- Journal of Mechanical Science and Technology,2014,28(2):2861-2868.
[5] 刘建华,杨建国,刘华平等.基于势场蚁群算法的移动机器人全局路径规划方法[J].农业机械学报,2015,46(09):18-27.
[6] 康玉祥,姜春英,秦运海,等.基于改进PSO算法的机器人路径规划及实验[J].机器人,2020,42(1):71-78.
[7] KARABOGA D,BASTURK B.A powerful and efficient algorithm for numerical function optimization:artificial bee colony (ABC) algorithm[J].Journal of Global Optimization,2007,39(3):459-471.
[8] KARABOGA D,AKAY B.A comparative study of Artificial Bee Colony algorithm[J].Applied Mathematics & Computation,2009,214(1):108-132.
[9] 张强,李盼池,王梅.基于自适应进化策略的人工蜂群优化算法[J].电子科技大学学报,2019,48(04):560-566.
[10] 王继超,李擎,崔家瑞,等.一种改进的人工蜂群算法——粒子蜂群算法[J].工程科学学报,2018,40(07):871-881.
[11] 刘三阳,张平,朱明敏.基于局部搜索的人工蜂群算法[J].控制与决策,2014,29(01):123-128.
[12] 毕晓君,王艳娇.改进人工蜂群算法[J].哈尔滨工程大学学报,2012,33(01):117-123.
[13] LIU X B,CAI Z X.Artificial Bee Colony Programming Made Faster[C]//Proc.of the International Conference on Natural Computation.IEEE,2009:154-158.