传统水下发射系统一般分为干发射和湿发射,干发射是指采用密封式发射方式,湿发射是指采用淹没式发射方式。其中干发射的水下发射系统具有较好的内弹道性能,较高的炮口初速,更易形成弹丸航行的超空炮,同时还能降低水对内膛的腐蚀,因此应用较为广泛[1-2]。对于干发射水下发射系统的动密封装置,如能降低密封口处的水压,将在一定程度上提升水下动密封的性能,同时有利于弹丸发射后中间弹道的加速过程与飞行稳定[3]。部分学者提出利用空化原理在密封口周围产生空化区,从而降低密封口处的压力,甚至在密封口处形成空气泡,以达到提高密封性能与弹丸飞行稳定的效果。
空化是因为液体的局部压力低于相同状态温度下的饱和蒸气压而导致的空泡初生、发展乃至溃灭的过程,空化技术的应用已在水下航行器等方面有了较多的研究。Savchenko[4]、牟晴[5]等通过对超空泡航行体的理论研究,运用多体动力学方法建立了带超空泡的航行体动力学模型,并提出了稳定超空泡技术与工程化应用方面的设想。张志宏[6] 、吕忠波[7] 、齐江辉[8]、葛新峰[9]、刘晓雄[10]等在研究超声速细长体运动、水下枪弹运动、空化器、水下高速转盘、自激振荡腔中的空化问题时,建立了超空泡流动的非线性积分-微分方程,采用数值模拟的方式,对建立的流场空化模型进行仿真模拟,为理论计算空化效应提供了求解的思路。空化技术在降压密封方面应用较少。
本文在此基础研究一种用于水下发射系统的基于空化原理的水下降压腔,该水下降压腔通过诱导翼片绕发射密封口高速旋转,在诱导翼片背水面产生空化、形成空泡,利用四周空泡与中心水域的压力差使水向四周流动,从而降低发射密封口部分的水压。本研究通过对该水下降压腔原理分析,建立该装置的仿真模型,分析其特性与影响因素,并进行相应的验证实验。
1 水下降压腔分析模型建立
1.1 工作原理
基于空化原理的水下降压腔原理如图1。图1中诱导翼片在转筒的带动下高速旋转,通过控制转筒转速与翼片形状,可在翼根背水面处形成空化区,利用转轴部分与空化区的压力差使转轴区域水填补空化区,空化区又形成新的空化,如此反复累加在旋转轴形成低压区,当压力足够低时,甚至形成空泡,达到密封减压的效果,减压效果与转筒的转速、诱导翼片的形状与数量有关。
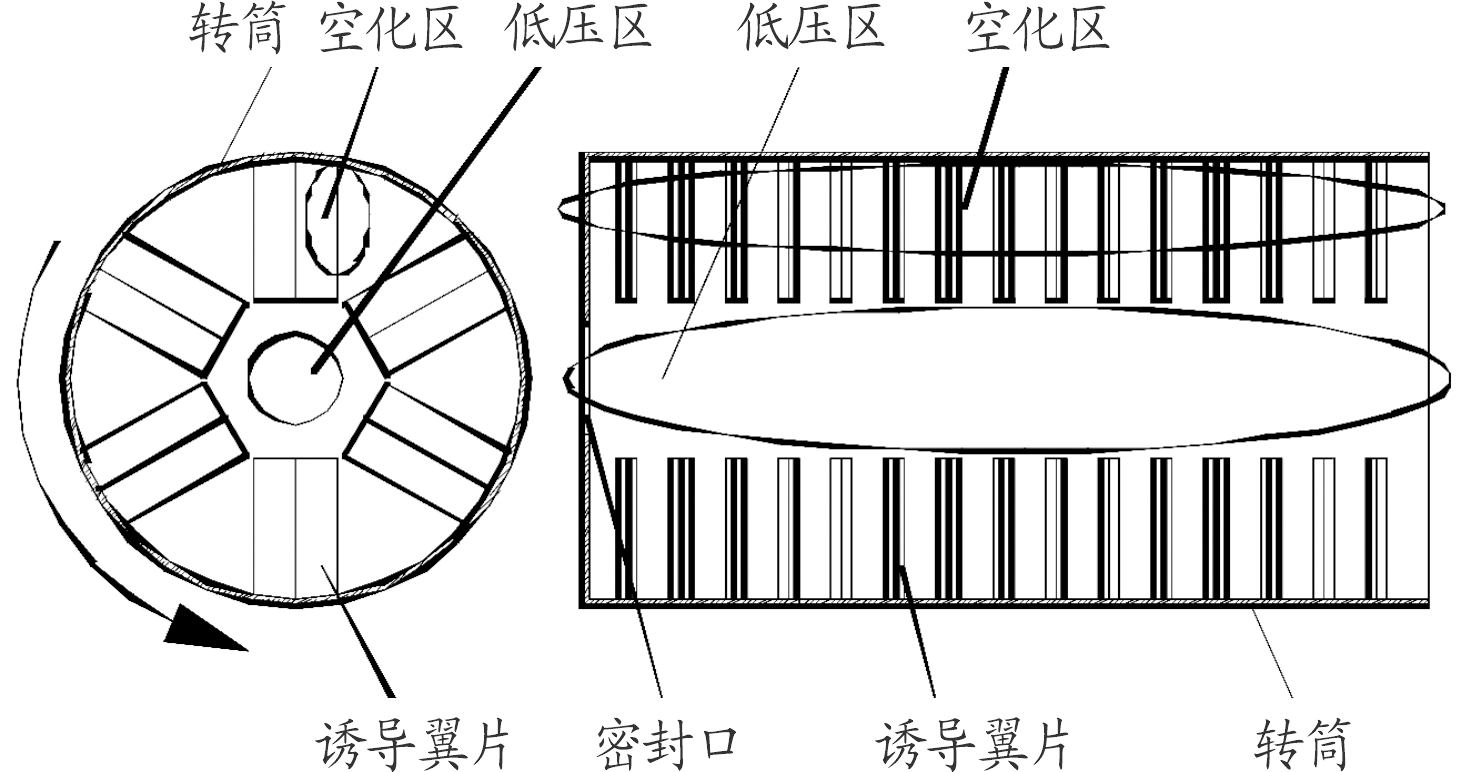
图1 基于空化原理的水下降压腔原理图
1.2 模型建立
由于诱导翼片在转筒上周期分布,因此使用周期对称边界的方案简化模型,如图2所示。水下降压腔减压效果与诱导翼片的结构有关,主要有诱导翼片夹角α,诱导翼片边长l,两诱导翼片间距D、d以及周向分布数量n,如图3所示。

图2 简化模型 图3 模型尺寸符号
2 空化求解方法
2.1 控制方程
本研究采用标准k-ε双方程湍流模型和增强型近壁面函数法,压力速度耦合采用coupled算法,其他项变量采用具有绝对稳定特性的一阶迎风格式,采用Mixture多相流混合模型中Singhal空化模型来处理气液两相流。利用连续方程、动量方程、湍动能-湍流耗散率方程和蒸气相质量运输方程来求解流场中的速度、压力和质量组分。
1) 连续方程
(1)
式中: ρ为流场混合相密度;t为时间;u为流场速度矢量;div为散度符号。
2) 动量方程
div{(μl+μt)[grad(u)+grad(uT)]-grad(p)}
(2)
式中:p为流场压力;grad为梯度符号;μl为层流黏性系数;μt为湍流黏性系数。
(3)
式中:k为湍动能;ε为湍流耗散率; Cμ为经验常数,一般取0.09[11]。
3) 湍动能-湍流耗散率方程
Gk+Gb-ρε-Ym
(4)
(5)
式中:σk、σε分别为k、ε的prandtl数;C1ε、C2ε、C3ε为经验常数;Gk、Gb、Ym为湍动能系数,分别与平均速度梯度、浮力及可压湍流中的脉动扩张有关。
4) 蒸气质量分数运输方程
(6)
式中:Re、Rc分别表示气泡增加的质量和气泡减少的质量
(7)
(8)
式中: ζ为液体表面张力系数; ρl、 ρv分别为液体、水蒸气的密度;pv为水蒸气压力; fv、 fg分别为水蒸气和不可凝结气体质量分数;Ce、Cc为经验常数[11]。
2.2 边界条件与网格模型
由上述工作原理可知,诱导翼片随转筒在流场域绕旋转轴以一定速度旋转,诱导翼片、转筒壁面均为固壁限制水及气泡的流动;为降低周围水域对转筒的影响,在远离转筒位置设置压力出口边界;翼片绕圆周对称,把流域按翼片等分,在等分边界处设置旋转周期边界;当有多层翼片时,假设每层翼片作用效果相同,其分界面设置为镜像对称边界。边界条件设置如图4所示。
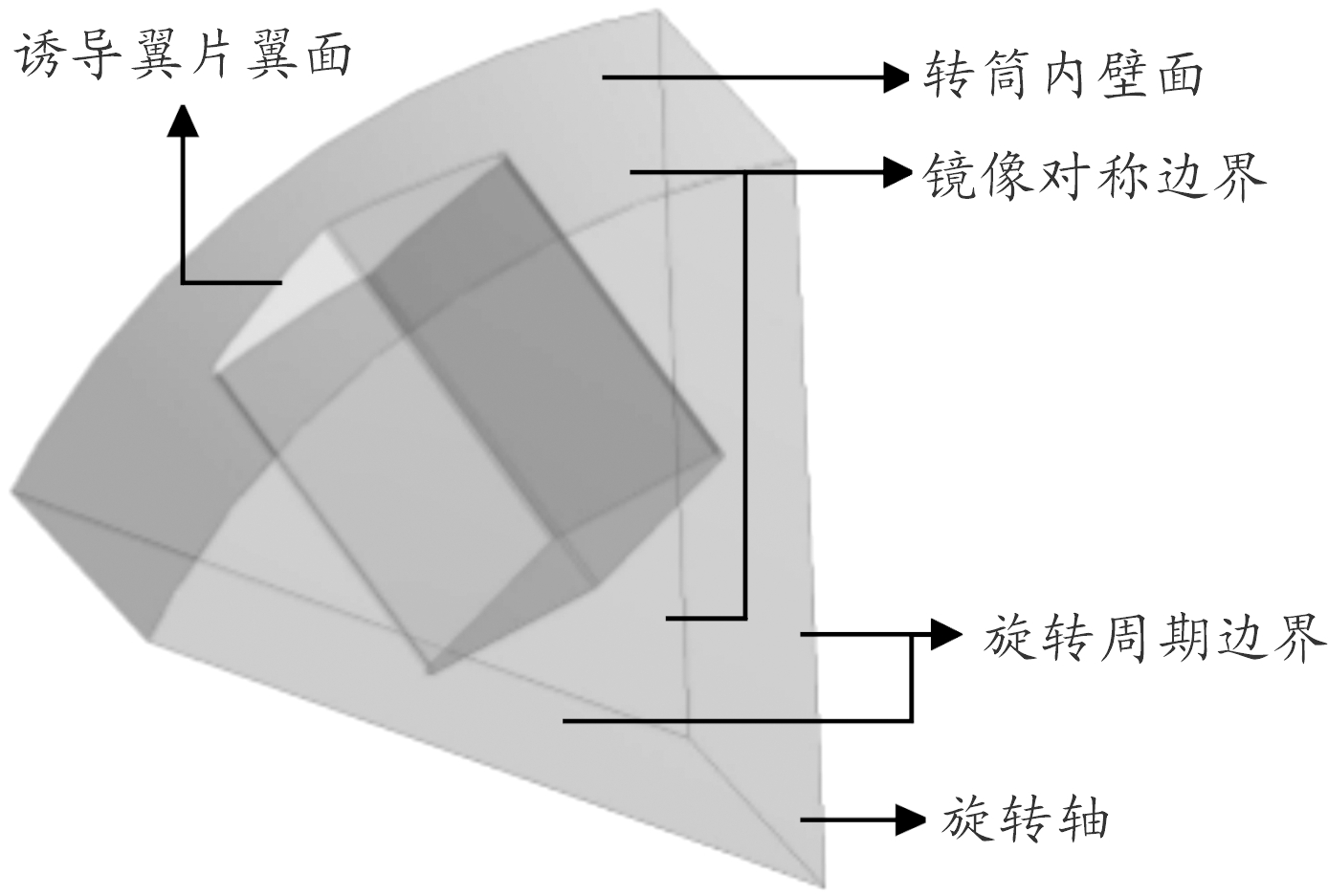
图4 工质模型及边界条件示意图
根据几何模型,建立流场区域工质模型,并划分多面体网格。图5为计算网格模型,在叶片近壁面布置了10层网格进行加密,使y+值分布在1~5。图6为网格无关性验证曲线,考虑计算精度和计算成本,选取计算网格总数为35万。

图5 网格模型曲线
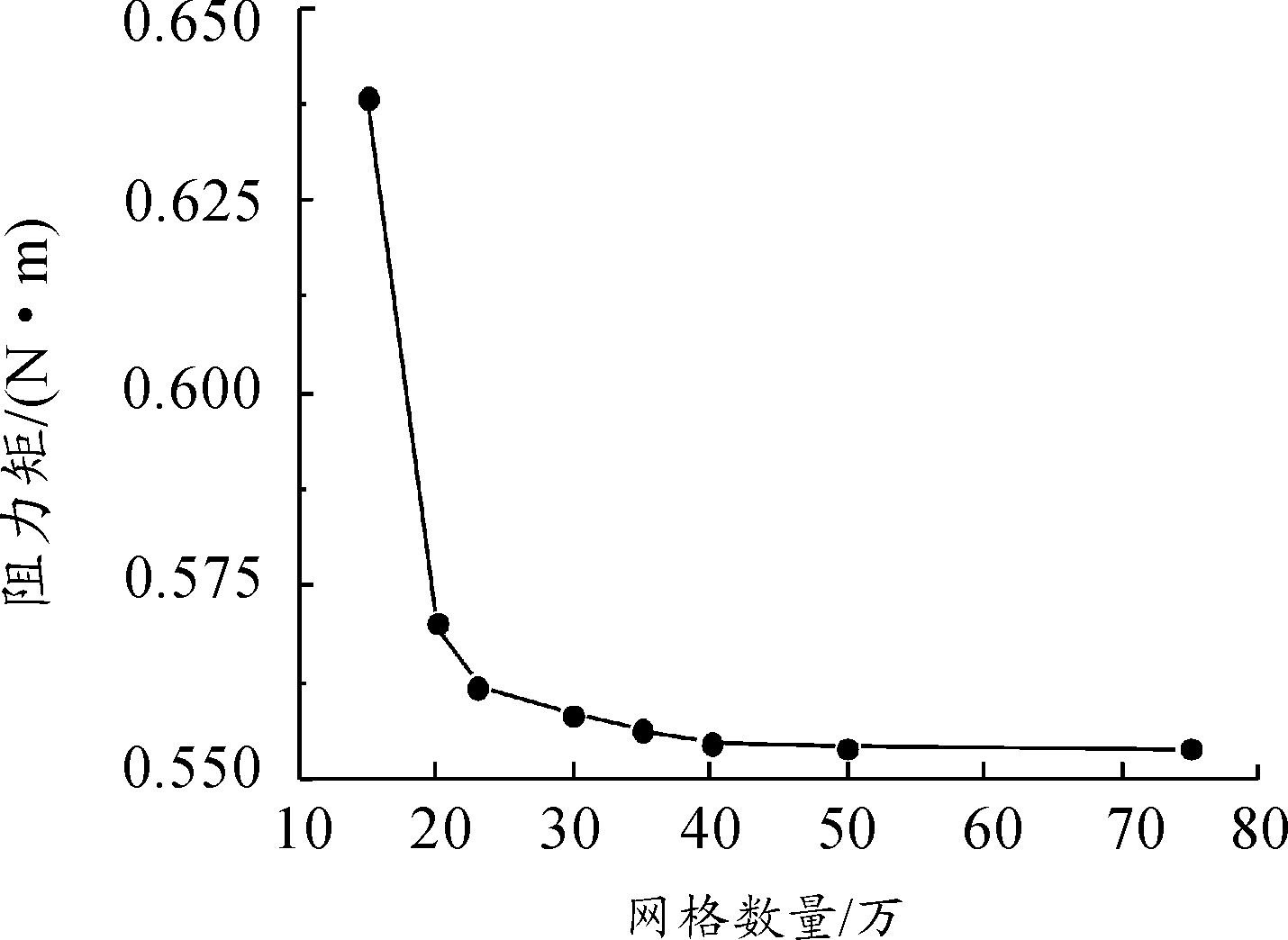
图6 网格无关性验证
根据上述分析,在浅水条件下分别考虑转筒转速、诱导翼片高度和夹角、诱导翼片数量对中心区域压降的影响。
3 仿真结果及分析
3.1 转筒转速的影响
在诱导翼片高度为90 mm,夹角为35°,6个诱导翼片的情况下,研究转筒转速对中心区域压降的影响。保持诱导翼片高度、夹角和数量不变,改变转筒转速分别为1 750、2 000、2 250、2 500和2 750 r/min,模拟计算结果如图7、图9、图9所示。
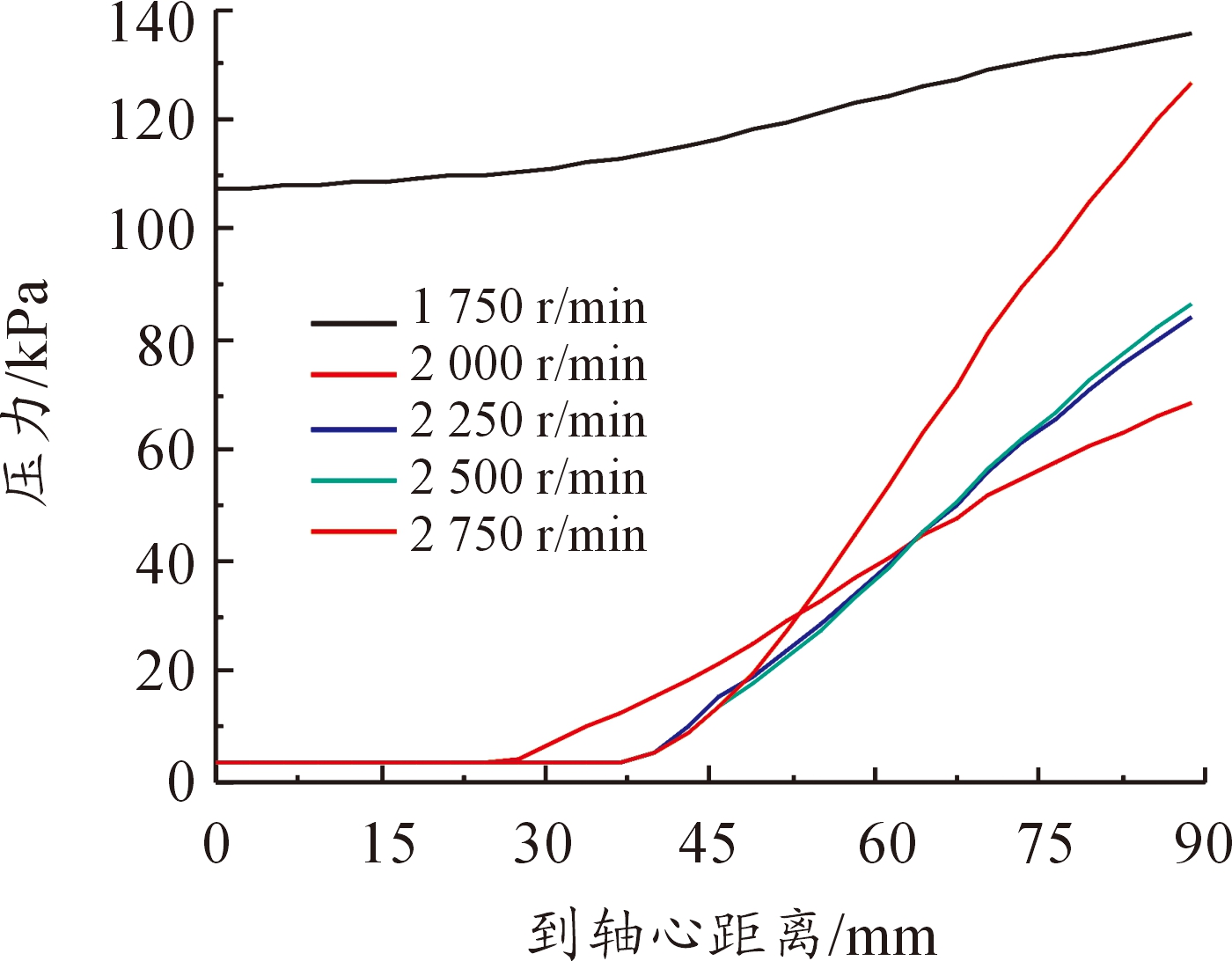
图7 压力随轴心距离的变化曲线
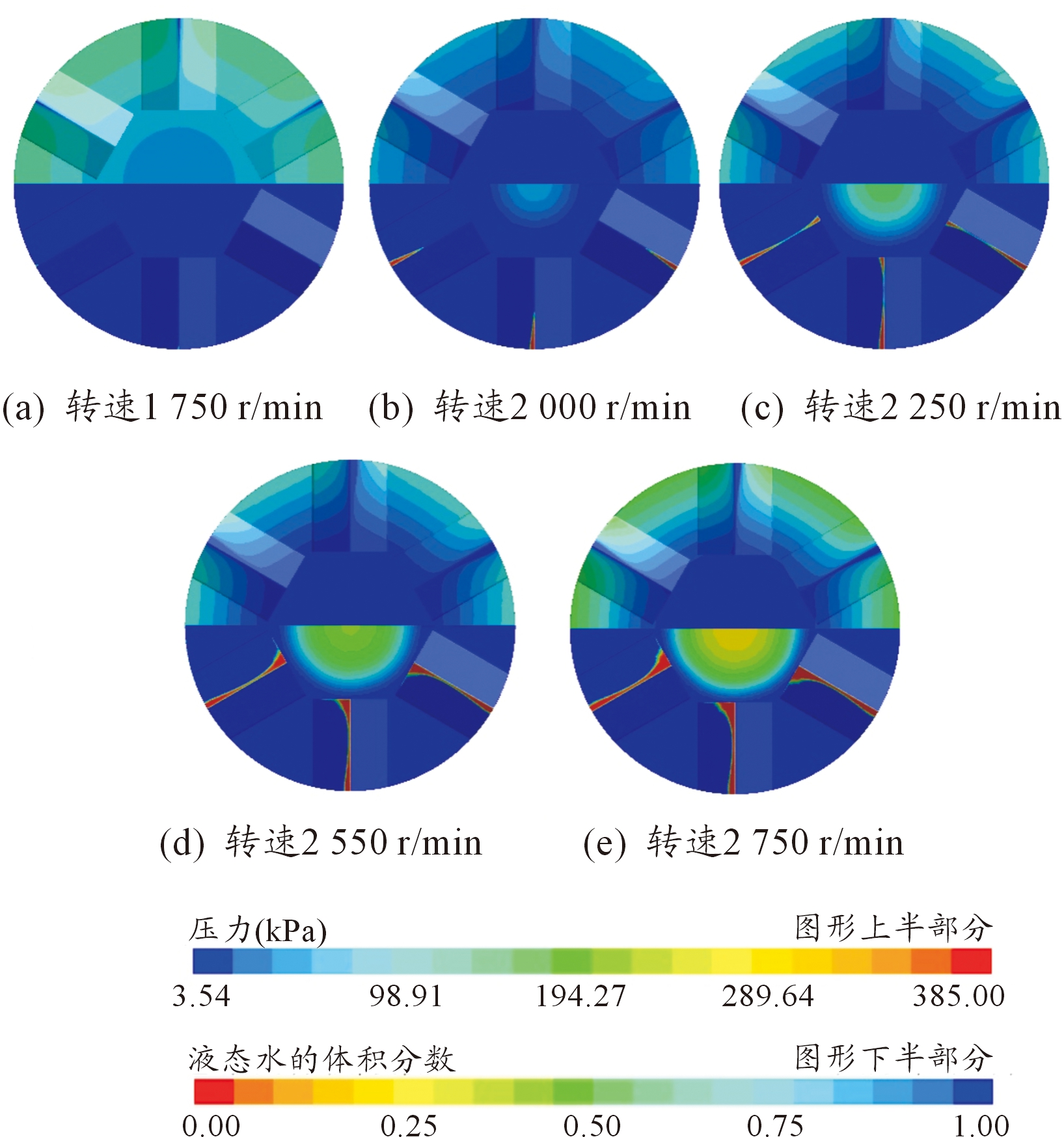
图8 压力(上部)与空化(下部)云图
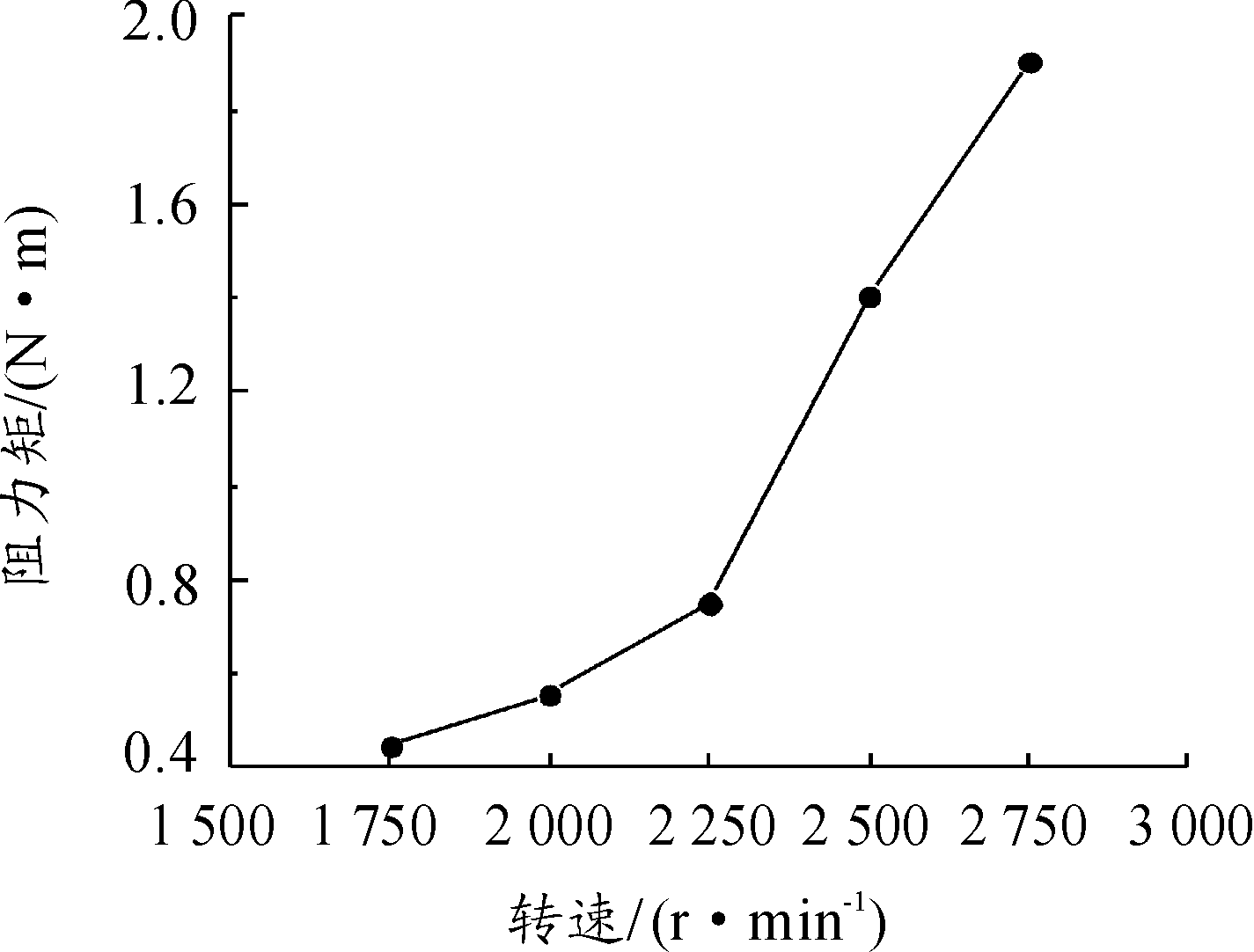
图9 阻力矩随转速的变化曲线
图8中每一部分上半为压力云图,下半为液态水体积分数云图,在压力云图中,越蓝的部分表示压力越低,即降压效果越明显;在液态水体积分数云图中,越红的部分液态水体积分数越低,即产生的空化效果越明显,下文与之类似。图8中可以看出,由于诱导翼片根部线速度最快,空泡最开始在翼根背水面处形成,翼片上越靠近轴心空化区越小;由于中心压力高,空化区域压力低,水会向四周流动,空泡会向中心汇聚,中心轴处出现降压效果;最大压力形成在翼片翼根的迎水面,是形成阻力的主要原因。
图8(a)到图8(e)说明,当转速为1 750 r/min时,翼片根部刚好形成好泡,随着转速增大,翼片在水中线速度越大,所形成的空化作用更强,使中心轴处汇聚的空泡更多、降压区域更大。图7表示了转筒区域内轴心距离与压力的关系,其中当转速为1 750 r/min时,中心区域并未堆积空泡,因此中心压力较高;当转速从2 000 r/min变化到2 750 r/min时,中心低压区面积逐渐扩大,也说明转速的增大能使中心汇聚的空泡增多,但增幅在逐渐减小,同时翼片翼根处压力随着转速增大而增大,与图9相互印证了,转速越高,即翼片翼根处线速度越大,所受到的阻力也越大,且从图9的斜率上看,阻力增大的速度也越快。
3.2 诱导翼片高度的影响
在诱导转筒转速为2 000转/min,夹角为35°,6个诱导翼片的情况下,研究翼片高度对中心区域压降的影响。保持转筒转速、诱导翼片夹角、数量不变,改变诱导翼片高度分别为70、80、90、100和110 mm,模拟计算结果如图10、图11、图12所示。

图10 压力(上部)与空化(下部)云图
从图10中可以看出诱导翼片高度的增大,整个腔室的体积随之增大,同时在相同转速下越高的诱导翼片翼根处线速也就越大,这对于空化区的形成是有利的;但在相同的线速度条件下,较低翼片形成的空化区域更大,如图10(e)中的90 mm处的空化区域小于图10(c)中90 mm处的空化区域,这说明在一定的转速和翼片形状下,翼片上维持的最大空化区域几乎不变。
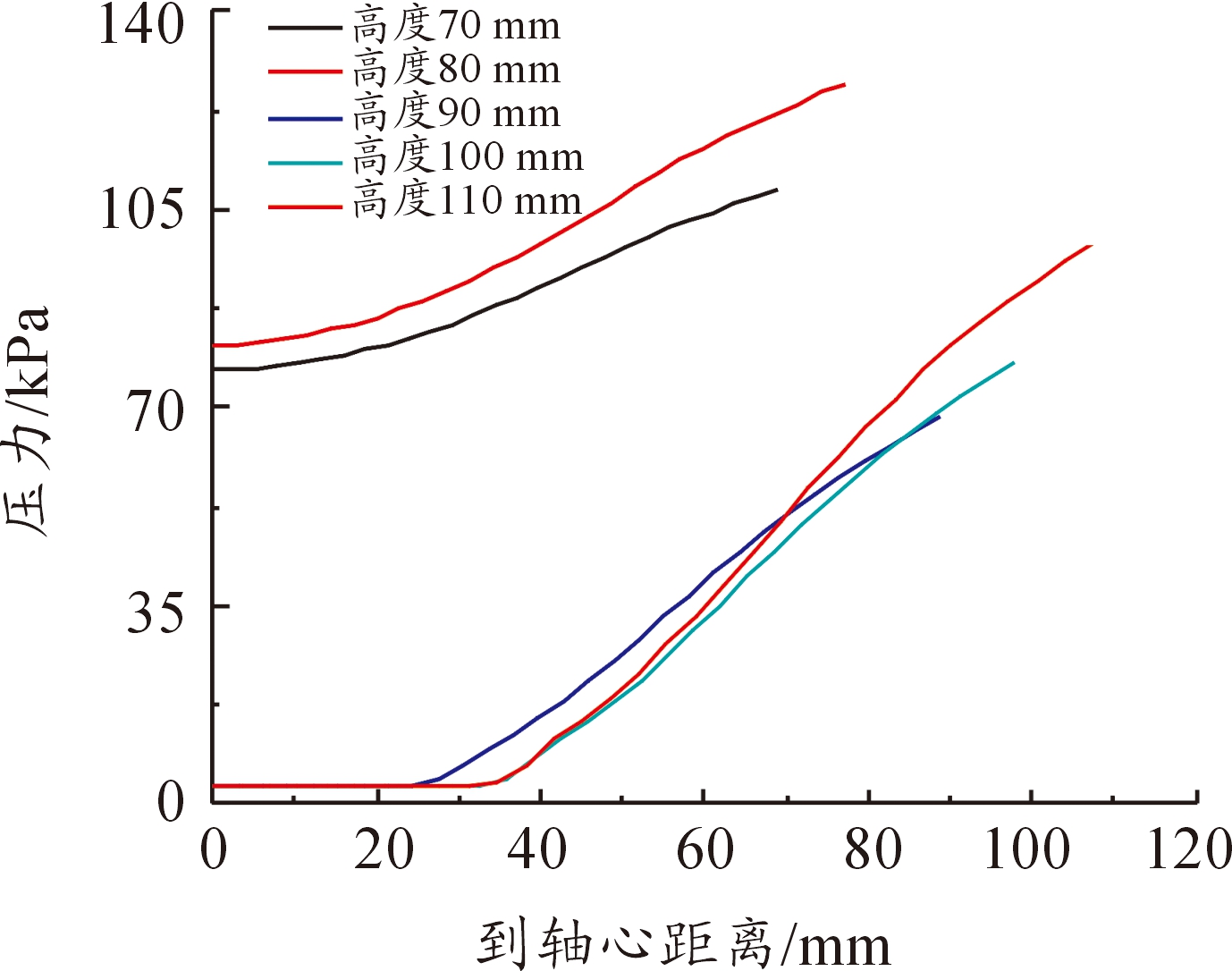
图11 压力随轴心距离的变化
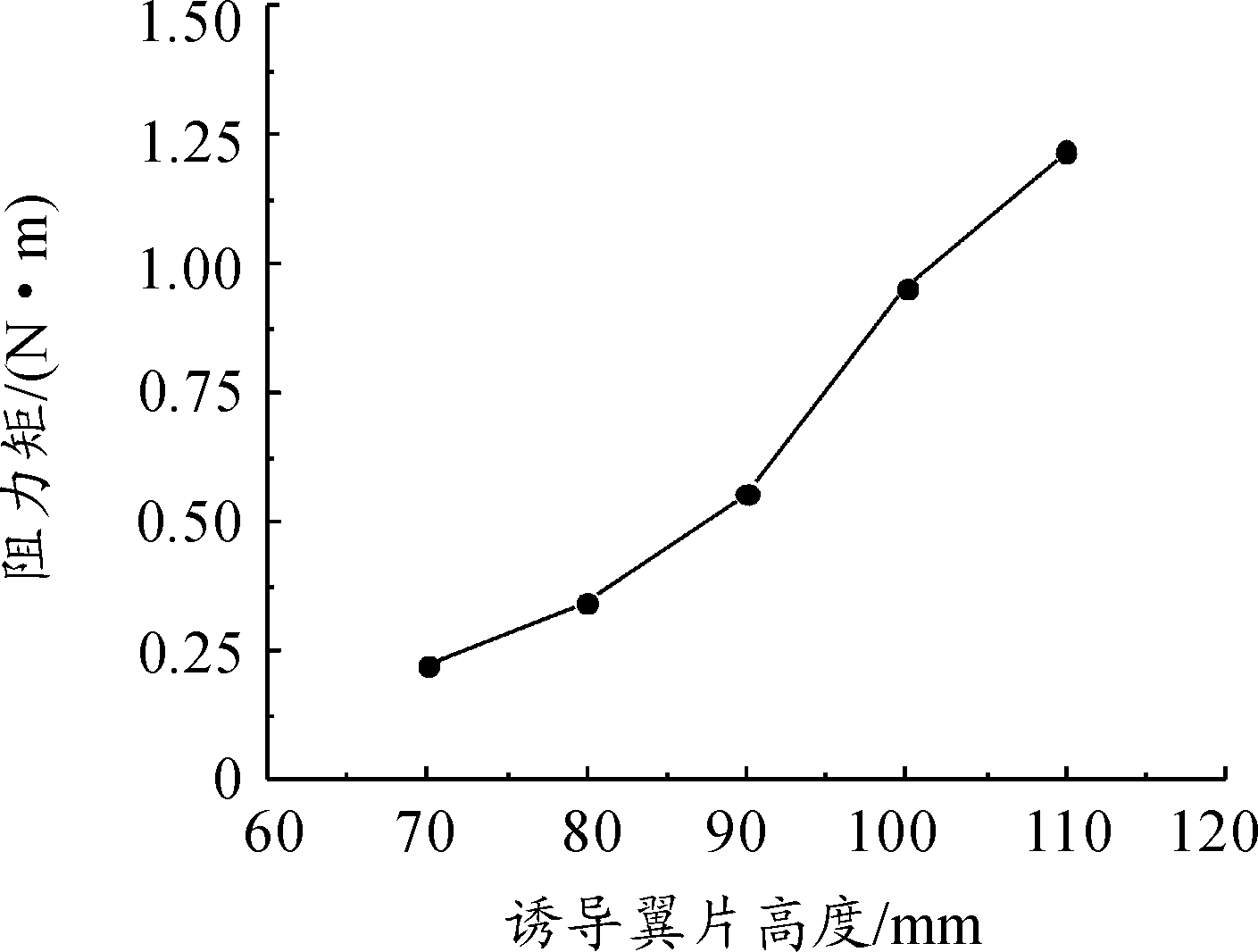
图12 阻力矩随转速的变化
图10(a)到图10(e)说明,高度为70 mm、80 mm时均在翼根处产生少量空泡,随着高度增大,即线速翼根处线速度增大,所形成的空化作用更强,使中心轴处汇聚的空泡更多、降压区域更大。图11可以看出在高度为70 mm、80 mm中心未堆积空泡时,翼片高度增大反而会使压力增大,这是因为更大的翼片使水受到更大的压缩作用;翼片高度继续增大中心低压区面积逐渐扩大,但增幅逐渐减小,同时翼片翼根处压力随着转速增大而增大,与图12相互印证了,转速越高,即翼片翼根处线速度越大,所受到阻力也越大。
3.3 诱导翼片夹角的影响
在诱导转筒转速为2 000转/min,诱导翼片高度为90 mm,6个诱导翼片的情况下,研究诱导翼片夹角对中心区域压降的影响。保持转筒转速、诱导翼片高度、数量不变,改变诱导翼片夹角分别为20°、25°、30°、35°和40°,模拟计算结果如图13、图14、图15所示。
图13中体现了诱导翼片角度变化的影响,可以看出诱导翼片越尖锐,即角度越小,翼片根部迎水面所受到的压力越小,相应的背水面处压力越高,由空化原理可以知道压力越小越易形成的空化区域,因此角度越大越利于空化的产生;同时角度的增大也是水流形成的增加,即角度越大翼片根部水流的线速度也就越大,更利于空泡的形成。
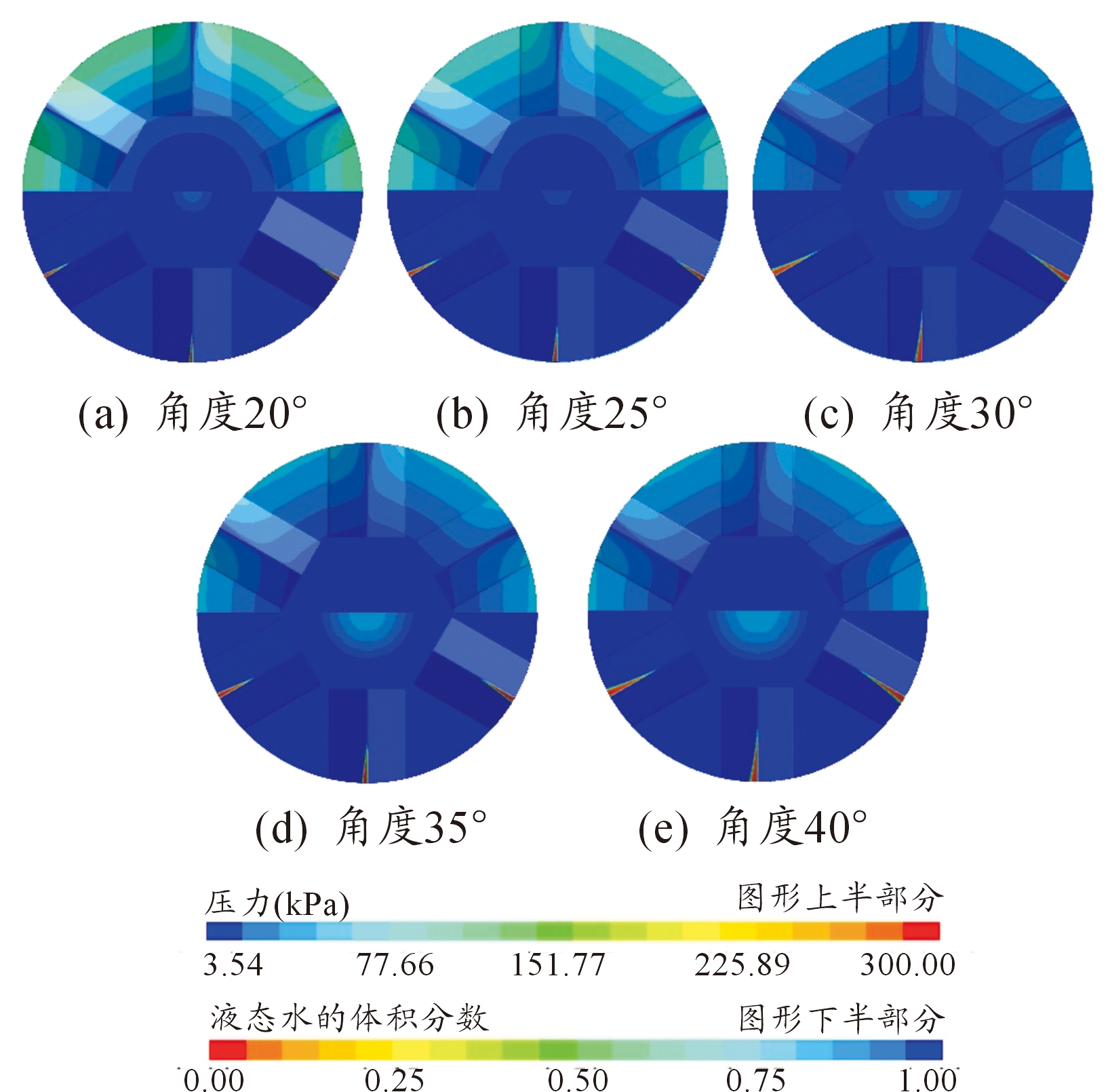
图13 压力(上部)与空化(下部)云图

图14 压力随轴心距离的变化
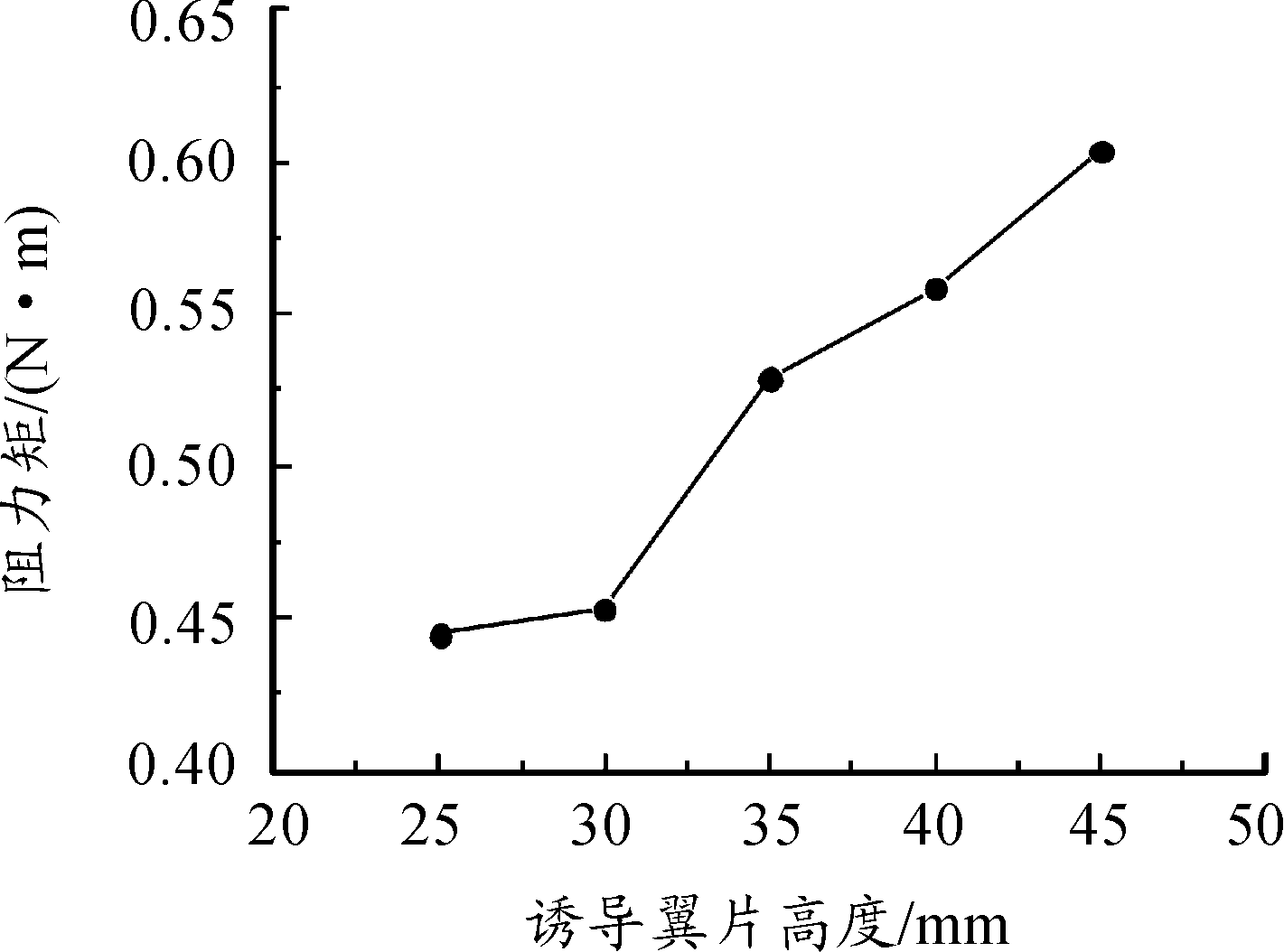
图15 阻力矩随转速的变化
图13(a)到图13(e)说明随着翼片夹角增大,所形成的空化作用更强,使中心轴处汇聚的空泡更多、降压区域更大。图14也可看出中心汇聚的空泡随压力增大也逐渐增多,结合图15还说明了随着翼片夹角增大,转筒和翼片所受到的阻力也相应增大。
3.4 诱导翼片数量的影响
在诱导转筒转速为2 000转/min,诱导翼片高度为90 mm,夹角为35°的情况下,研究诱导翼片数量对中心区域压降的影响。保持转筒转速、诱导翼片高度、夹角不变,改变诱导翼片数量分别为3、4、5和6个,模拟计算结果如图16、图17、图18所示。

图16 压力随轴心距离的变化
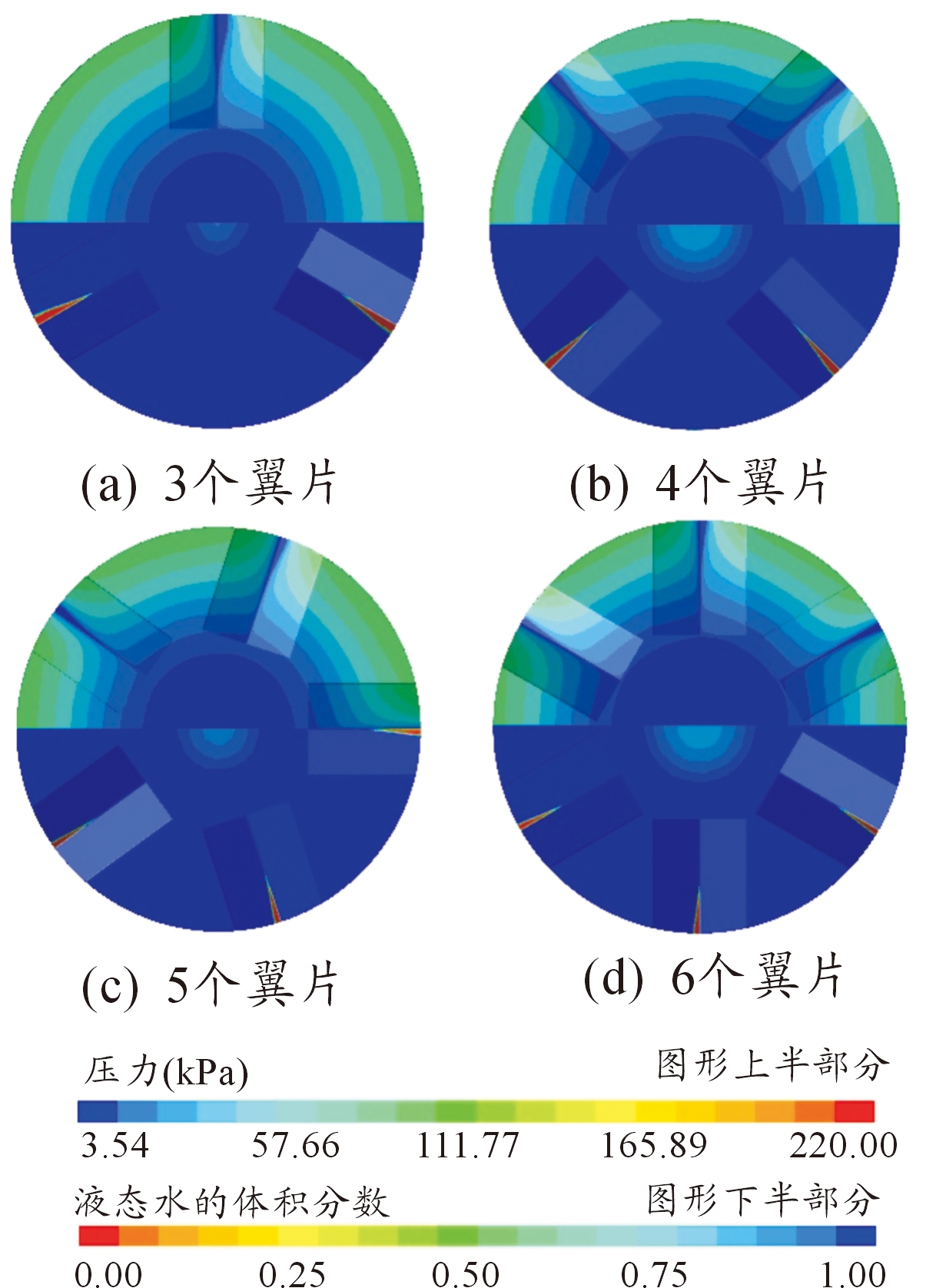
图17 压力(上部)与空化(下部)云图
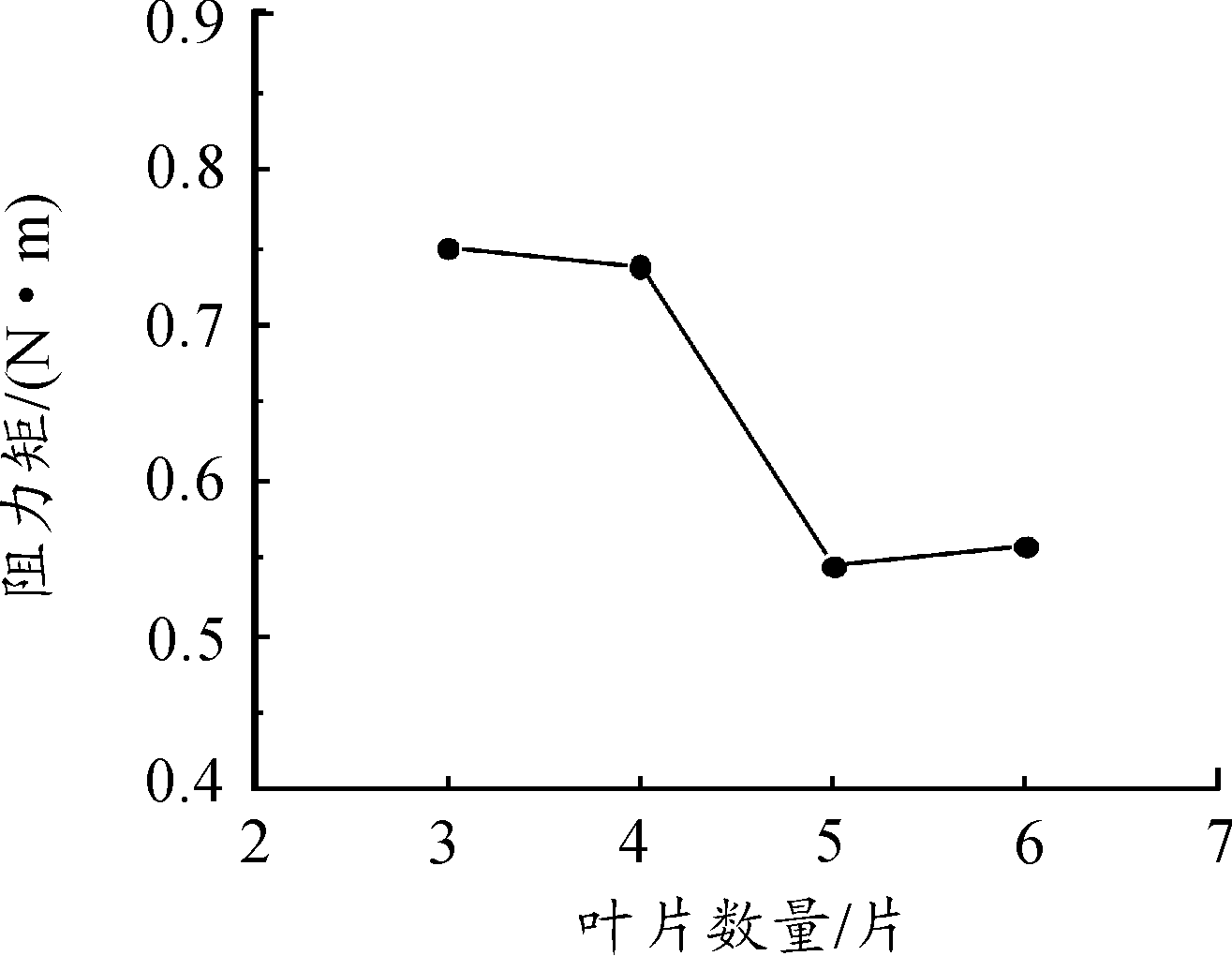
图18 阻力矩随转速的变化
诱导翼片的数量较少时,每片翼片所需要挤压的水域空间越大,翼片翼根迎水面所受到的压力越大,相应的背水面处压力越低,更加容易形成空化,这也就说明图17中翼片数少时,翼片上空化区反而更大;而中心的空泡是由翼片根部产生汇聚过去的,即是说当翼片数量增多时,中心区域能够汇聚更多方向的空泡,从而使中心空泡区域变大。
图17(a)到图17(e)结合图16说明,中心轴降压效果与翼片数量有关,翼片4片、6片的降压效果优于翼片3片、5片的降压效果,因为4片翼片时单个翼片具有更大的空化区,而6片翼片具有更多产生空泡的区域,使汇聚在中心的空泡区域增大。从图18中可以看出随着翼片数量增加,转筒和翼片所受到的阻力由下降趋势。
4 结论
1) 基于空化原理的水下降压腔能够实现降压效果,形成一定的空化区,为实现水下干发射提供便利;
2) 水下降压腔降压性能随着转筒转速增大、诱导翼片高度与夹角增大而提高,同时降压性能还与诱导翼片数量有关;
3) 水下降压腔运动阻力会随着水下降压腔性能提高而增大。
[1] 赵嘉俊,余永刚.侧喷孔分布对多股燃气射流在充液室中扩展特性的影响[J].工程力学,2017,34(07):241-248.
[2] 周良梁,余永刚,刘东尧,等.水下火炮气幕式发射过程中燃气射流与液体工质相互作用特性研究[J].兵工学报,2016,37(08):1373-1378.
[3] 谢浩怡,杨国伟,王全伟,等.2维弹道修正技术研究综述[J].兵工自动化,2018,37(09):66-69.
[4] SAVCHENKO Y.Supercavitation-Problems and Perspectives[J].Proceedings of 4th International Symposium on Cavitation,Califonia,USA 2001.
[5] 牟晴,赵潇雨,周维.超空泡技术在小口径炮弹上的应用[J].四川兵工学报,2010,31(04):31-33.
[6] 张志宏,孟庆昌,金永刚,等.超声速细长锥型射弹超空泡流动数值计算方法[J].华中科技大学学报(自然科学版),2014,42(01):39-43,109.
[7] 吕忠波,张霖,张元军,等.水下枪弹自然超空泡数值模拟[J].四川兵工学报,2015(5):11-13.
[8] 齐江辉,郑亚雄.空化器形状对超空泡流场影响的数值模拟[J].兵器装备工程学报,2018,39(09):85-88.
[9] 葛新峰,徐旭,来亦姝,等.旋转圆盘内不同转速的空化特性研究[J].人民黄河,2019,41(08):112-116.
[10] 刘晓雄,聂松林,纪辉,等.自激振荡腔空化特性的数值仿真及试验研究[J].液压与气动,2019(07):7-13.
[11] 王福军.计算流体动力学分析——CFD软件原理与应用[M].北京:清华大学出版社,2004:120-124.